
Рекурсивтік ішкі программалар
Программалау тілінде кезкелген ішкі прогрaммалардың өзін-өзі шақыра алу мүмкіндігі бар. Мысалы, fun ішкі программасы берілген және оның өзінің құрылымында қайтадан өзін шақыратын fun операторы болса, онда мұндай өзін-өзі шақыра алатын ішкі программмаларды рекурсивті деп, ал бүкіл процесті рекурсия деп атайды.
Рекурсия кей жағдайда анықталмаған болады. Мысалы, fun ішкі программасы sum-ішкі прграммасын, ал ол өз кезегінде қайтадан fun ішкі программасын шақыра алатын болса, онда мұндай жағдайда рекурсивтік тізбек құрылады.
Мысалы, факториалды есептеуді рекурсия тәсілмен жазып көрелік:
n!=1*2*3*…*(n-1)*n, немесе бұл формуланы келесі кезекте мына түрде жазуға да болады: n!=(n-1)!*n одан кейін n!=(n-2)!*(n-1)*n т.с.с
Мысалы: 4!=1*2*3*4 деп жазуға, немесе
4!=3!*4, түрінде жазуға болады келесі кезекте:
3!=2!*3,
2!=1!*2,
1!=1.
Рекурсивті процестерді құру үшін міндетті түрде рекурисияның аяқталу шарты (тірелу шарты) болуы тиіс. Шартта рекурисивті есептеудің нәтижесінде табылатын, процесті тоқтатуды қамтамасыз ететін белгілі бір мән анықталады. Берілген мысал үшін бұл мән 1!=1 болады. Олай болса кез келген рекурсивті процесс үшін міндетті түрде екі элемент болуы керек: ол біріншіден аяқталу шарты, екіншіден кезекті қадамды алдыңғы қадамның көмегімен орындау әдісі (яғни негізгі формуласы). Енді осы тақырып бойынша бірнеше мысалдар қарастырып көрелік.
1 мысал:
Енді жоғарыдағы мысалды (факториалды есептеуді) рекурсивті функцияның көмегімен есептеудің программасын C++ және Python программалау тілдерінде жазып көрелік:
C++
#include <iostream>
using namespace std;
int factorial (int x)
{ if (x==1 ) return 1;
return x* factorial (x-1);
}
int main()
{
int n;
cin>>n;
cout << factorial(n);
return 0;
}
Python
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n - 1)
n = int(input("Натурал n санын енгізіңіз: "))
print(factorial(n))
Енді осы программаның орындалу барысына талдау жасап көрелік. Мыалы: N=4 болсын.
1 қадам f:=4*f(3) n=4
2 қадам f:=4*3*f(2) n=3
3 қадам f:=4*3*2*f(1) n=2
4 қадам f:=4*3*2*1 n=1
2 мысал:
Натурал n саны берілген, n-ден 1-ге дейінгі барлық сандарды шығаратын рекурсивті функциясы бар бағдарламаны жазыңыз. Негізгі бағдарламада бастапқы деректердің кірісі (n саны) және функция шақыруы болуы керек.
C++
#include <iostream>
using namespace std;
int Numbers(int n) {
if (n < 1) {
return 0;
}
// Санды шығару
cout << n << " ";
// Рекурсивті шақыру
Numbers(n - 1);
}
int main() {
int n;
cout << "Натурал n санын енгізіңіз: ";
cin >> n; // Пернетақтадан n санын енгізу
printNumbers(n); // Функцияны шақыру
return 0;
}
Python
def print_numbers(n):
# Негізгі жағдай
if n < 1:
return
# Рекурсивті шақыру
print(n, end=' ')
print_numbers(n - 1)
# Пайдалану: пернетақтадан n санын енгізу
n = int(input("Натурал n санын енгізіңіз: "))
print_numbers(n)
Бұл бағдарламада:
-
print_numbers функциясы анықталады, ол ( n ) санын қабылдайды.
-
Негізгі жағдайда, егер ( n ) 1-ден кем болса, функция тоқтайды.
-
Әйтпесе, функция ( n ) санын бір жолға шығарады және өзін ( n - 1 ) аргументімен қайта шақырады.
-
Пайдаланушыдан ( n ) санын енгізу үшін input функциясы қолданылады.
3 мысал:
Екі санның ең үлкен ортақ бөлгішін анықтау.
C++
#include <iostream>
using namespace std;
int eoyb(int x,int y)
{ if (x!=0)
return eoyb(y % x,x);
else return y;
}
int main()
{ int n,m;
cin>>n>>m;
cout <<eoyb(n,m);
return 0;
}
Python
def eoyb(a, b):
if b == 0:
return a
else:
return eoyb(b, a % b)
a = int(input("Бірінші санды енгізіңіз: "))
b = int(input("Екінші санды енгізіңіз: "))
result = eoyb(a, b)
print(f"{a} және {b} сандарының ең үлкен ортақ бөлгіші: {result}")
4 мысал:
Екі санның ең кіші ортақ еселігін анықтау.
Екі санның ең кіші ортақ еселігін (ЕКОЕ) анықтау үшін, алдымен ЕҮОБ (Ең үлкен ортақ бөлгіш) табу керек. Себебі, ЕКОЕ формуласы мынадай:
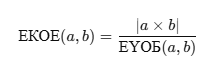
Ендеше, рекурсивті шешімді жазайық.
C++
#include <iostream>
#include <cmath>
using namespace std;
// ЕҮОБ табу (рекурсивті әдіс)
int eyob(int a, int b) {
if (b == 0)
return a;
return eyob (b, a % b);
}
// ЕКОЕ табу (рекурсивті әдіс)
int ekoe(int a, int b) {
return abs(a * b) / eyob (a, b);
}
int main() {
int a, b;
cout << "Бірінші санды енгізіңіз: "; cin >> a;
cout << "Екінші санды енгізіңіз: "; cin >> b;
cout << a << " және " << b << " сандарының ең кіші ортақ еселігі: " << ekoe(a, b) << endl;
return 0;
}
eyob() функциясы:
Егер b == 0 болса, a — ЕҮОБ.
Әйтпесе, eyob (b, a % b) формуласын қолданады.
ekoe() функциясы:
|a * b| / gcd(a, b) формуласы арқылы ЕКОЕ анықталады.
Python
def eyob(a, b):
# "ЕҮОБ табу (рекурсивті әдіс) "
if b == 0:
return a
else:
return eyob(b, a % b)
def ekoe(a, b):
# ЕКОЕ табу
return abs(a * b) // eyob(a, b)
a = int(input("Бірінші санды енгізіңіз: "))
b = int(input("Екінші санды енгізіңіз: "))
result = ekoe(a, b)
print(f"{a} және {b} сандарының ең кіші ортақ еселігі: {result}")
Алдымен, eyob (a, b) функциясы арқылы ЕҮОБ табамыз.
Содан кейін, ekoe (a, b) функциясы арқылы ЕКОЕ анықталады.
5 мысал:
Осы тақырыпқа тағыда бір мысал ды қарастырып көрелік:
Санамақ ойыны.
Балалар шеңбер боймен сағат тілі бағытымен 1, 2, ... , N -ге дейінгі реттік нөмірмен орналасқан. Одан кейін сағат тілімен бағытымен бірірінші баладан бастап бастап M-ге дейін санайды да (балалар шеңбер бойымен тұрғандықтан, санағанда N -нен кейінгі бірінші нөмір болады), осы M-ші бала шеңберден шығады, одан кейін келесі баладан бастап, қайтадан M бала санайды, осылай шенбер бойында бір бала қалғанға дейін қайталанады.
Берілген N мен M сандары бойынша, табу керек:
а) шенберде қалған баланың реттік нөмірін;
б) k нөмірлі бала шеңберде қалу үшін қай нөмірден санауды бастау керек?
Шешуі: а)
Есепті рекурсия тәсілін пайдаланып шешіп көрелік. Ол үшін келесі қадамды алдыңғы қадамның көмегімен орындау формуласын және тірелу шартын анықтап алуымыз керек.
Есептің берілуі бойынша шеңберде қалған соңғы баланың нөмірін анықтау керек.
Іздеп отырған нөмірді U(m, n) арқылы белгілейік. Мұндағы m санақ саны ал n шеңбердегі балалар саны. Осы U(m,n) саны мына рекурренттік қатынасты қанағаттандырады:
U(m,n)=(m+U(m,n-1)-1) % n+1
мұндағы % бөліндінің қалдығын анықтайды.
Шынымен де, шеңберден бірінші шығатын баланың нөмірі:
m1=(m-1) % n+1 формуласымен анықталады
Шеңберде қалған балалардың нөмірлерін (m1+1)-ден бастап, яғни шеңберден шығып кеткеннен кейінгі баладан бастап қайтадан 1,2,...,n-1 сандарымен нөмірлейміз. Жаңадан нөмірлеу бойынша «санамақ жеңімпазының» нөмірі анықтама бойынша U(m, n-1)болады да, ал бастапқы формула бойынша:
(m1+U(m,n-1)-1) % n+1)
Сондықтан
U(m,n)=((m-1) % n+1+U(m,n-1)-1) % n+1
Осы есептеулерден ішкі қалдықты есептеуді алып тастауға болатынын байқауға болады, және де рекурсияның тірелу шарты U(m,1)=1 екені айқын.
Бұл классикалық Иосиф Флавий (Josephus) мәселесі деп аталады. Мәселе бойынша N бала шеңбер бойында орналасқан, әр M-ші бала шеңберден шығады, ал соңында бір бала ғана қалады. Сол баланың реттік нөмірін табуымыз керек.
Олай болса есептің шешімін C++ және Python тілдеріндегі бағдарламасын жазып көрелік:
C++
а)
#include <iostream>
using namespace std;
int sanamak(int n, int m) {
if (n == 1)
return 1;
else
return (sanamak(n - 1, m) + m - 1) % n + 1;
}
int main() {
int n, m,result ;
cout << "Балалар саны (N): " ; cin >> n;
cout << "Санайтын сан (M): "; cin >> m;
result = sanamak(n, m);
cout << "Шеңберде қалған баланың реттік нөмірі: " << result << endl;
return 0;
}
Python
def sanamak (n, m):
if n == 1:
return 1
else:
return (sanamak (n - 1, m) + m - 1) % n + 1
n = int(input("Балалар саны (N): "))
m = int(input("Санақ саны (M): "))
result = josephus_recursive(n, m)
print(f"Рекурсивті шешім бойынша қалған бала: {result}")
Егер:
Балалар саны (N): 7
Санақ саны (M): 3
Шығады: Шеңберде қалған соңғы баланың нөмірі: 4
Енді қадам-қадаммен, нақты мысалдармен талдау жасап көрелік:
Мысал:
-
N = 7 (7 бала бар)
-
M = 3 (әр 3-ші бала шығарылады)
Балалар шеңбер бойымен мынадай ретпен орналасқан: 1 2 3 4 5 6 7
1-қадам:
-
Бірінші баладан бастап санаймыз: 1, 2, 3
-
3-ші бала шеңберден шығады.
-
Қалған балалар: 1 2 4 5 6 7
2-қадам:
-
4-тен бастап қайтадан санаймыз: 4, 5, 6
-
6-шы бала шығады.
-
Қалған балалар:1 2 4 5 7
3-қадам:
-
7-ден бастап санаймыз: 7, 1, 2
-
2-ші бала шығады.
-
Қалған балалар: 1 4 5 7
4-қадам:
-
4-тен бастап санаймыз: 4, 5, 7
-
7-ші бала шығады.
-
Қалған балалар:1 4 5
5-қадам:
-
1-ден бастап санаймыз: 1, 4, 5
-
5-ші бала шығады.
-
Қалған балалар:1 4
6-қадам:
-
1-ден бастап санаймыз: 1, 4, 1
-
1-ші бала шығады.
-
Қалған жалғыз бала:4
Сонымен, соңғы қалған бала — 4-ші бала.
Алғазы Серік Сәбитұлы.
Алматы қаласы.
КеАҚ "Республикалық физика-математика мектебі" информатика пәні мұғалімі.
Педагог-шебер.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Рекурсивтік ішкі программалар
Рекурсивтік ішкі программалар
Рекурсивтік ішкі программалар
Программалау тілінде кезкелген ішкі прогрaммалардың өзін-өзі шақыра алу мүмкіндігі бар. Мысалы, fun ішкі программасы берілген және оның өзінің құрылымында қайтадан өзін шақыратын fun операторы болса, онда мұндай өзін-өзі шақыра алатын ішкі программмаларды рекурсивті деп, ал бүкіл процесті рекурсия деп атайды.
Рекурсия кей жағдайда анықталмаған болады. Мысалы, fun ішкі программасы sum-ішкі прграммасын, ал ол өз кезегінде қайтадан fun ішкі программасын шақыра алатын болса, онда мұндай жағдайда рекурсивтік тізбек құрылады.
Мысалы, факториалды есептеуді рекурсия тәсілмен жазып көрелік:
n!=1*2*3*…*(n-1)*n, немесе бұл формуланы келесі кезекте мына түрде жазуға да болады: n!=(n-1)!*n одан кейін n!=(n-2)!*(n-1)*n т.с.с
Мысалы: 4!=1*2*3*4 деп жазуға, немесе
4!=3!*4, түрінде жазуға болады келесі кезекте:
3!=2!*3,
2!=1!*2,
1!=1.
Рекурсивті процестерді құру үшін міндетті түрде рекурисияның аяқталу шарты (тірелу шарты) болуы тиіс. Шартта рекурисивті есептеудің нәтижесінде табылатын, процесті тоқтатуды қамтамасыз ететін белгілі бір мән анықталады. Берілген мысал үшін бұл мән 1!=1 болады. Олай болса кез келген рекурсивті процесс үшін міндетті түрде екі элемент болуы керек: ол біріншіден аяқталу шарты, екіншіден кезекті қадамды алдыңғы қадамның көмегімен орындау әдісі (яғни негізгі формуласы). Енді осы тақырып бойынша бірнеше мысалдар қарастырып көрелік.
1 мысал:
Енді жоғарыдағы мысалды (факториалды есептеуді) рекурсивті функцияның көмегімен есептеудің программасын C++ және Python программалау тілдерінде жазып көрелік:
C++
#include <iostream>
using namespace std;
int factorial (int x)
{ if (x==1 ) return 1;
return x* factorial (x-1);
}
int main()
{
int n;
cin>>n;
cout << factorial(n);
return 0;
}
Python
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial(n - 1)
n = int(input("Натурал n санын енгізіңіз: "))
print(factorial(n))
Енді осы программаның орындалу барысына талдау жасап көрелік. Мыалы: N=4 болсын.
1 қадам f:=4*f(3) n=4
2 қадам f:=4*3*f(2) n=3
3 қадам f:=4*3*2*f(1) n=2
4 қадам f:=4*3*2*1 n=1
2 мысал:
Натурал n саны берілген, n-ден 1-ге дейінгі барлық сандарды шығаратын рекурсивті функциясы бар бағдарламаны жазыңыз. Негізгі бағдарламада бастапқы деректердің кірісі (n саны) және функция шақыруы болуы керек.
C++
#include <iostream>
using namespace std;
int Numbers(int n) {
if (n < 1) {
return 0;
}
// Санды шығару
cout << n << " ";
// Рекурсивті шақыру
Numbers(n - 1);
}
int main() {
int n;
cout << "Натурал n санын енгізіңіз: ";
cin >> n; // Пернетақтадан n санын енгізу
printNumbers(n); // Функцияны шақыру
return 0;
}
Python
def print_numbers(n):
# Негізгі жағдай
if n < 1:
return
# Рекурсивті шақыру
print(n, end=' ')
print_numbers(n - 1)
# Пайдалану: пернетақтадан n санын енгізу
n = int(input("Натурал n санын енгізіңіз: "))
print_numbers(n)
Бұл бағдарламада:
-
print_numbers функциясы анықталады, ол ( n ) санын қабылдайды.
-
Негізгі жағдайда, егер ( n ) 1-ден кем болса, функция тоқтайды.
-
Әйтпесе, функция ( n ) санын бір жолға шығарады және өзін ( n - 1 ) аргументімен қайта шақырады.
-
Пайдаланушыдан ( n ) санын енгізу үшін input функциясы қолданылады.
3 мысал:
Екі санның ең үлкен ортақ бөлгішін анықтау.
C++
#include <iostream>
using namespace std;
int eoyb(int x,int y)
{ if (x!=0)
return eoyb(y % x,x);
else return y;
}
int main()
{ int n,m;
cin>>n>>m;
cout <<eoyb(n,m);
return 0;
}
Python
def eoyb(a, b):
if b == 0:
return a
else:
return eoyb(b, a % b)
a = int(input("Бірінші санды енгізіңіз: "))
b = int(input("Екінші санды енгізіңіз: "))
result = eoyb(a, b)
print(f"{a} және {b} сандарының ең үлкен ортақ бөлгіші: {result}")
4 мысал:
Екі санның ең кіші ортақ еселігін анықтау.
Екі санның ең кіші ортақ еселігін (ЕКОЕ) анықтау үшін, алдымен ЕҮОБ (Ең үлкен ортақ бөлгіш) табу керек. Себебі, ЕКОЕ формуласы мынадай:
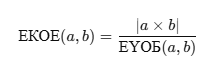
Ендеше, рекурсивті шешімді жазайық.
C++
#include <iostream>
#include <cmath>
using namespace std;
// ЕҮОБ табу (рекурсивті әдіс)
int eyob(int a, int b) {
if (b == 0)
return a;
return eyob (b, a % b);
}
// ЕКОЕ табу (рекурсивті әдіс)
int ekoe(int a, int b) {
return abs(a * b) / eyob (a, b);
}
int main() {
int a, b;
cout << "Бірінші санды енгізіңіз: "; cin >> a;
cout << "Екінші санды енгізіңіз: "; cin >> b;
cout << a << " және " << b << " сандарының ең кіші ортақ еселігі: " << ekoe(a, b) << endl;
return 0;
}
eyob() функциясы:
Егер b == 0 болса, a — ЕҮОБ.
Әйтпесе, eyob (b, a % b) формуласын қолданады.
ekoe() функциясы:
|a * b| / gcd(a, b) формуласы арқылы ЕКОЕ анықталады.
Python
def eyob(a, b):
# "ЕҮОБ табу (рекурсивті әдіс) "
if b == 0:
return a
else:
return eyob(b, a % b)
def ekoe(a, b):
# ЕКОЕ табу
return abs(a * b) // eyob(a, b)
a = int(input("Бірінші санды енгізіңіз: "))
b = int(input("Екінші санды енгізіңіз: "))
result = ekoe(a, b)
print(f"{a} және {b} сандарының ең кіші ортақ еселігі: {result}")
Алдымен, eyob (a, b) функциясы арқылы ЕҮОБ табамыз.
Содан кейін, ekoe (a, b) функциясы арқылы ЕКОЕ анықталады.
5 мысал:
Осы тақырыпқа тағыда бір мысал ды қарастырып көрелік:
Санамақ ойыны.
Балалар шеңбер боймен сағат тілі бағытымен 1, 2, ... , N -ге дейінгі реттік нөмірмен орналасқан. Одан кейін сағат тілімен бағытымен бірірінші баладан бастап бастап M-ге дейін санайды да (балалар шеңбер бойымен тұрғандықтан, санағанда N -нен кейінгі бірінші нөмір болады), осы M-ші бала шеңберден шығады, одан кейін келесі баладан бастап, қайтадан M бала санайды, осылай шенбер бойында бір бала қалғанға дейін қайталанады.
Берілген N мен M сандары бойынша, табу керек:
а) шенберде қалған баланың реттік нөмірін;
б) k нөмірлі бала шеңберде қалу үшін қай нөмірден санауды бастау керек?
Шешуі: а)
Есепті рекурсия тәсілін пайдаланып шешіп көрелік. Ол үшін келесі қадамды алдыңғы қадамның көмегімен орындау формуласын және тірелу шартын анықтап алуымыз керек.
Есептің берілуі бойынша шеңберде қалған соңғы баланың нөмірін анықтау керек.
Іздеп отырған нөмірді U(m, n) арқылы белгілейік. Мұндағы m санақ саны ал n шеңбердегі балалар саны. Осы U(m,n) саны мына рекурренттік қатынасты қанағаттандырады:
U(m,n)=(m+U(m,n-1)-1) % n+1
мұндағы % бөліндінің қалдығын анықтайды.
Шынымен де, шеңберден бірінші шығатын баланың нөмірі:
m1=(m-1) % n+1 формуласымен анықталады
Шеңберде қалған балалардың нөмірлерін (m1+1)-ден бастап, яғни шеңберден шығып кеткеннен кейінгі баладан бастап қайтадан 1,2,...,n-1 сандарымен нөмірлейміз. Жаңадан нөмірлеу бойынша «санамақ жеңімпазының» нөмірі анықтама бойынша U(m, n-1)болады да, ал бастапқы формула бойынша:
(m1+U(m,n-1)-1) % n+1)
Сондықтан
U(m,n)=((m-1) % n+1+U(m,n-1)-1) % n+1
Осы есептеулерден ішкі қалдықты есептеуді алып тастауға болатынын байқауға болады, және де рекурсияның тірелу шарты U(m,1)=1 екені айқын.
Бұл классикалық Иосиф Флавий (Josephus) мәселесі деп аталады. Мәселе бойынша N бала шеңбер бойында орналасқан, әр M-ші бала шеңберден шығады, ал соңында бір бала ғана қалады. Сол баланың реттік нөмірін табуымыз керек.
Олай болса есептің шешімін C++ және Python тілдеріндегі бағдарламасын жазып көрелік:
C++
а)
#include <iostream>
using namespace std;
int sanamak(int n, int m) {
if (n == 1)
return 1;
else
return (sanamak(n - 1, m) + m - 1) % n + 1;
}
int main() {
int n, m,result ;
cout << "Балалар саны (N): " ; cin >> n;
cout << "Санайтын сан (M): "; cin >> m;
result = sanamak(n, m);
cout << "Шеңберде қалған баланың реттік нөмірі: " << result << endl;
return 0;
}
Python
def sanamak (n, m):
if n == 1:
return 1
else:
return (sanamak (n - 1, m) + m - 1) % n + 1
n = int(input("Балалар саны (N): "))
m = int(input("Санақ саны (M): "))
result = josephus_recursive(n, m)
print(f"Рекурсивті шешім бойынша қалған бала: {result}")
Егер:
Балалар саны (N): 7
Санақ саны (M): 3
Шығады: Шеңберде қалған соңғы баланың нөмірі: 4
Енді қадам-қадаммен, нақты мысалдармен талдау жасап көрелік:
Мысал:
-
N = 7 (7 бала бар)
-
M = 3 (әр 3-ші бала шығарылады)
Балалар шеңбер бойымен мынадай ретпен орналасқан: 1 2 3 4 5 6 7
1-қадам:
-
Бірінші баладан бастап санаймыз: 1, 2, 3
-
3-ші бала шеңберден шығады.
-
Қалған балалар: 1 2 4 5 6 7
2-қадам:
-
4-тен бастап қайтадан санаймыз: 4, 5, 6
-
6-шы бала шығады.
-
Қалған балалар:1 2 4 5 7
3-қадам:
-
7-ден бастап санаймыз: 7, 1, 2
-
2-ші бала шығады.
-
Қалған балалар: 1 4 5 7
4-қадам:
-
4-тен бастап санаймыз: 4, 5, 7
-
7-ші бала шығады.
-
Қалған балалар:1 4 5
5-қадам:
-
1-ден бастап санаймыз: 1, 4, 5
-
5-ші бала шығады.
-
Қалған балалар:1 4
6-қадам:
-
1-ден бастап санаймыз: 1, 4, 1
-
1-ші бала шығады.
-
Қалған жалғыз бала:4
Сонымен, соңғы қалған бала — 4-ші бала.
Алғазы Серік Сәбитұлы.
Алматы қаласы.
КеАҚ "Республикалық физика-математика мектебі" информатика пәні мұғалімі.
Педагог-шебер.

шағым қалдыра аласыз















