Иргизская средняя общеобразовательная школа №2
ОТКРЫТЫЙ УРОК
Тема: «Решение систем нелинейных уравнений с двумя переменными»
Учитель: Мыркымбай Назгуль Болатовна
Иргиз 2020г
Тема урока: «Решение систем нелинейных уравнений с двумя переменными»
Класс: 9 класс
Учитель: Мыркымбай Н.Б
Предмет: алгебра
Тип: Урок обобщения и систематизации знаний.
Базовая компетентность: умение учиться.
Составляющая компетентность:коммуникативная, познавательная, формирование личного самосовершенствования
Цель урока: систематизировать знания и умения у учащихся, решать системы различными способами
Задачи:
- образовательные аспекты:
-
повторить способы решения систем
- развивающий аспект:
-
способствовать развитию логического мышления, математической интуиции;
-
развивать умения самостоятельной учебно-познавательной деятельности;
- воспитательный аспект:
-
воспитывать трудолюбие, умение работать в коллективе, умение слушать одноклассников
Средства обучения: текст теста, карточки для работ по группам, интерактивная доска
План урока:
1. Мотивация
2. Актуализация знаний (устная работа)
3. Практическая работа
4. Осмысление и применение (тестовое задание)
5. Коррекция знаний
6. Инструктаж по выполнению домашнего задания
7. Рефлексия
Содержание урока
-
Мотивация:( 3 мин)
Здравствуйте! Сегодня у нас необычный урок у нас гости, и мы должны показать свои знания и умения по теме «Системы нелинейных уравнений с двумя переменными». Данный урок является последним перед контрольной работой.
Девизом нашего урока будут слова: Дорогу осилит идущий, а математику –мыслящий»
-
Актуализация знаний (устная работа)
(в это время 2 ученика решают системы методом подстановки и методом сложения)
![]()
Ответ: (2;2) (-3;7) Ответ: (5;1) ( -1;-5)
Вопросы :
-
Что является решением системы уравнений с двумя переменными? (пара чисел, которые при постановке в эту систему превращают каждое ее уравнение в верное равенство)
Что значит решить систему уравнений с двумя переменными? ( найти все
ее решения или установить , что их нет)
-
Какие существуют способы решения систем уравнений с двумя переменными?
-
Рассмотрим
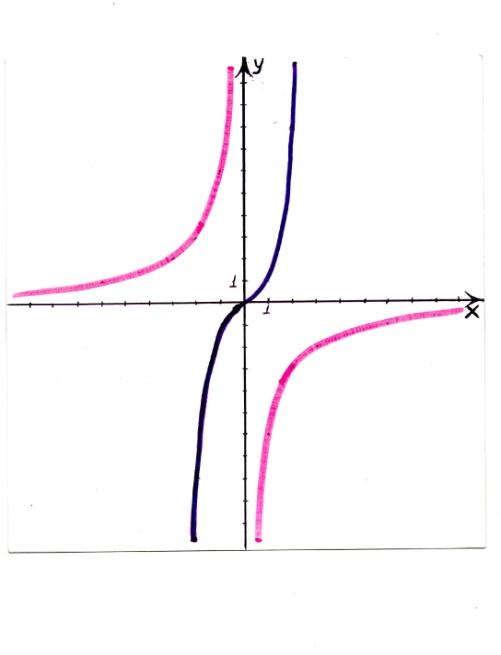
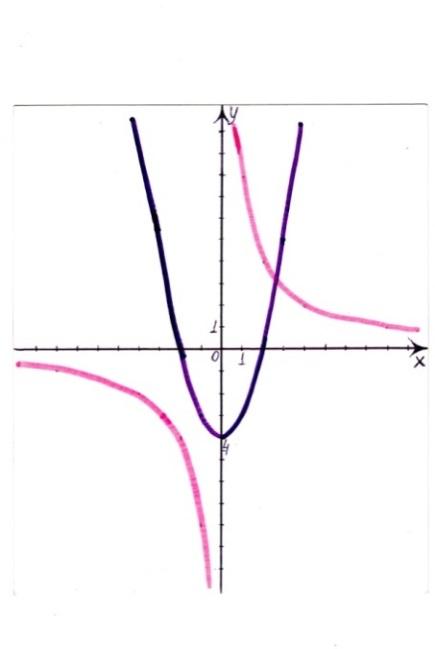
Сколько решений имеет система, если графики изображены на рисунках. (слайд)
|
1. |
2.
|
3
|
|
4
|
5
|
6
|
5.
На рисунке дано графическое решение системы уравнений. Назовите
решение каждой системы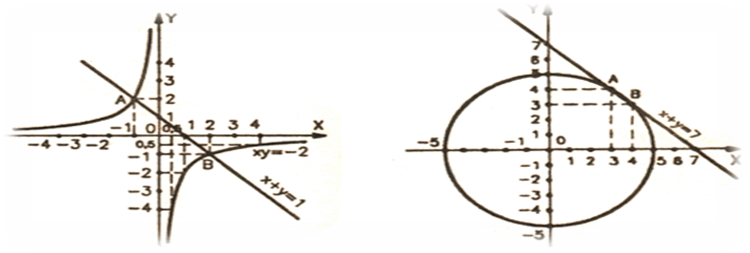
Ответ: (3;4) (4;3)
-
Используя метод подбора на знании теоремы обратной теоремы Виета,
![]() найдите решения системы
найдите решения системы
Ответ(-10;2) (2;-10)
(Проверка учащихся решения систем у доски )
-
Какой способ вы считаете самым не рациональным в решении систем? И почему?
-
Проверка умений применять на практике полученные знания.
-
Работа в группах ( дифференцированно)
1 группа ( слабая)
-
Решите систему наиболее рациональным способом:
![]() Ответ: (2;3)
(-4;15)
Ответ: (2;3)
(-4;15)
2. Выберите систему уравнений, соответствующую
условию задачи и решите ее.
Сумма двух чисел равна 12, а их произведение равно 32. Найти эти
числа
а) ![]()
![]() б)
б) ![]()
![]() Ответ: 4 и 8
Ответ: 4 и 8
3. Какая из нижеуказанных пар чисел является решением системы уравнений:
![]()
1. (-3;2); 2. (1;4); 3. (8;-3); 4. (3;2 ) Ответ (8;-3)
2 группа (средняя)
1. Решить систему наиболее рациональным способом:
![]()
Ответ: (-7; 11) (3;1)
2. Решить
задачу:
Площадь прямоугольного земельного участка равна
20м2. Участок обнесен изгородью длиной 18 м. Найдите
длину и ширину участка.
Ответ: 4м и 5м
-
Какая из указанных пар чисел, является решением системы уравнений:
![]()
1. (-6;8); 2. (0;-2); 3. (-8;6); 4. (7;-9)
Ответ: ( -8; 6)
-
Осмысление и применение (тестовое задание)
1. Какие из перечисленных уравнений являются нелинейными уравнениями?
А)
х – 2у = 1, Б) хуz + 3у = -18,
В) ![]() +2у = 5, Г) –х – у =
-11.
+2у = 5, Г) –х – у =
-11.
2. Даны уравнения, график какого, уравнения является парабола?
А)
у =![]() , б) 5х + 4у = 20, в) ху = 12. , г) у
=
, б) 5х + 4у = 20, в) ху = 12. , г) у
= ![]() ,
,
3.
Какая пара чисел является решением системы
уравнений ![]()
А) (6; 3), б) (2; -1), в) (-3; -6), Г) (3; 0).
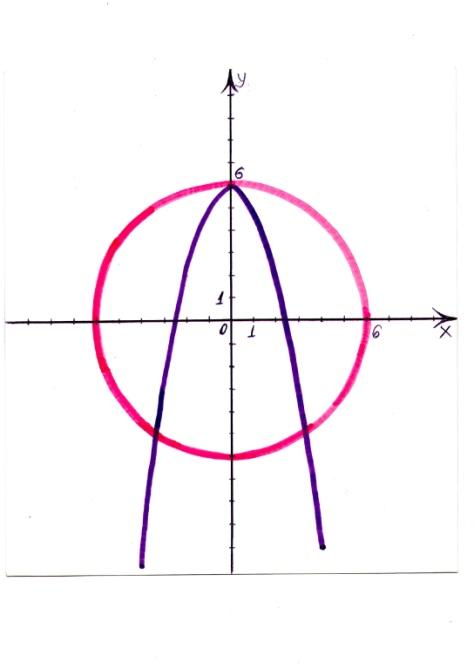
4. С помощью графика, изображенного на рисунке, определите, сколько решений имеет система уравнений?
А) Одно решение; б) Два решения; в) Три решения; г) Четыре решения;
д) Нет решений;
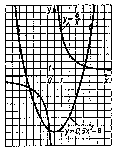
5. Если система состоит из двух уравнений второй степени с двумя переменными, то каким способом легче удается найти ее решение?
А) способом подстановки; б) способом сложения; в) графическим способом;
|
№1 |
№2 |
№3 |
№4 |
№5 |
|
б,в |
г |
б |
в |
б |
- Проверьте, отметив на листах итог вашей работы.
-
Коррекция знаний
Дополнительное задание:
1) Подберите решение системы
уравнений:![]()
А)
2) Найдите х + у :
![]()
Решение : ( х – у) (х + у) = 16 х – у =2 2(х +у) 16 х + у =16:2 х + у=8
-
Задание на дом Инструктаж по выполнению домашнего задания
4А.25(б), 4А26(б)
Рефлексия
( презентация)
1 группа
-
Решите систему наиболее рациональным способом:
![]()
2. Выберите систему уравнений, соответствующую
условию задачи и решите ее.
Сумма двух чисел равна 12, а их произведение равно 32. Найти эти
числа
а) ![]()
![]() б)
б) ![]()
![]()
-
Какая из нижеуказанных пар чисел является решением системы уравнений:
![]()
1. (-3;2); 2. (1;4); 3. (8;-3); 4. (3;2)
2 группа
1. Решить систему наиболее рациональным способом:
![]()
2. Решить
задачу:
Площадь прямоугольного земельного участка равна
20м2. Участок обнесен изгородью длиной 18 м. Найдите
длину и ширину участка
3. Какая из указанных пар чисел, является решением системы уравнений:
![]()
1. (-6;8); 2. (0;-2); 3. (-8;6); 4. (7;-9)
Фамилия Имя ученика___________________________________
тест
1. Какие из перечисленных уравнений являются нелинейными уравнениями?
А)
х – 2у = 1, б) хуz + 3у = -18,
в) ![]() +2у = 5, г) –х – у =
-11.
+2у = 5, г) –х – у =
-11.
2. Даны уравнения, график какого, уравнения является парабола?
А)
у =![]() , б) 5х + 4у = 20, в) ху = 12. , г) у
=
, б) 5х + 4у = 20, в) ху = 12. , г) у
= ![]() ,
,
3. Какая пара чисел является решением системы уравнений
![]()
А) (6; 3), б) (2; -1), в) (-3; -6), Г) (3; 0).
4. С помощью графика, изображенного на рисунке, определите, сколько решений имеет система уравнений?
А) Одно решение; б) Два решения; в) Три решения; г) Четыре решения;
д) Нет решений;

5. Если система состоит из двух уравнений второй степени с двумя переменными, то каким способом легче удается найти ее решение?
А) способом подстановки; б) способом сложения; в) графическим способом;
|
№1 |
№2 |
№3 |
№4 |
№5 |
|
|
|
|
|
|
|
|
|
|
|
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Решение систем нелинейных уравнений с двумя переменными
Решение систем нелинейных уравнений с двумя переменными
Иргизская средняя общеобразовательная школа №2
ОТКРЫТЫЙ УРОК
Тема: «Решение систем нелинейных уравнений с двумя переменными»
Учитель: Мыркымбай Назгуль Болатовна
Иргиз 2020г
Тема урока: «Решение систем нелинейных уравнений с двумя переменными»
Класс: 9 класс
Учитель: Мыркымбай Н.Б
Предмет: алгебра
Тип: Урок обобщения и систематизации знаний.
Базовая компетентность: умение учиться.
Составляющая компетентность:коммуникативная, познавательная, формирование личного самосовершенствования
Цель урока: систематизировать знания и умения у учащихся, решать системы различными способами
Задачи:
- образовательные аспекты:
-
повторить способы решения систем
- развивающий аспект:
-
способствовать развитию логического мышления, математической интуиции;
-
развивать умения самостоятельной учебно-познавательной деятельности;
- воспитательный аспект:
-
воспитывать трудолюбие, умение работать в коллективе, умение слушать одноклассников
Средства обучения: текст теста, карточки для работ по группам, интерактивная доска
План урока:
1. Мотивация
2. Актуализация знаний (устная работа)
3. Практическая работа
4. Осмысление и применение (тестовое задание)
5. Коррекция знаний
6. Инструктаж по выполнению домашнего задания
7. Рефлексия
Содержание урока
-
Мотивация:( 3 мин)
Здравствуйте! Сегодня у нас необычный урок у нас гости, и мы должны показать свои знания и умения по теме «Системы нелинейных уравнений с двумя переменными». Данный урок является последним перед контрольной работой.
Девизом нашего урока будут слова: Дорогу осилит идущий, а математику –мыслящий»
-
Актуализация знаний (устная работа)
(в это время 2 ученика решают системы методом подстановки и методом сложения)
![]()
Ответ: (2;2) (-3;7) Ответ: (5;1) ( -1;-5)
Вопросы :
-
Что является решением системы уравнений с двумя переменными? (пара чисел, которые при постановке в эту систему превращают каждое ее уравнение в верное равенство)
Что значит решить систему уравнений с двумя переменными? ( найти все
ее решения или установить , что их нет)
-
Какие существуют способы решения систем уравнений с двумя переменными?
-
Рассмотрим
Сколько решений имеет система, если графики изображены на рисунках. (слайд)
|
1. |
2.
|
3
|
|
4
|
5
|
6
|
5.
На рисунке дано графическое решение системы уравнений. Назовите
решение каждой системы
Ответ: (3;4) (4;3)
-
Используя метод подбора на знании теоремы обратной теоремы Виета,
![]() найдите решения системы
найдите решения системы
Ответ(-10;2) (2;-10)
(Проверка учащихся решения систем у доски )
-
Какой способ вы считаете самым не рациональным в решении систем? И почему?
-
Проверка умений применять на практике полученные знания.
-
Работа в группах ( дифференцированно)
1 группа ( слабая)
-
Решите систему наиболее рациональным способом:
![]() Ответ: (2;3)
(-4;15)
Ответ: (2;3)
(-4;15)
2. Выберите систему уравнений, соответствующую
условию задачи и решите ее.
Сумма двух чисел равна 12, а их произведение равно 32. Найти эти
числа
а) ![]()
![]() б)
б) ![]()
![]() Ответ: 4 и 8
Ответ: 4 и 8
3. Какая из нижеуказанных пар чисел является решением системы уравнений:
![]()
1. (-3;2); 2. (1;4); 3. (8;-3); 4. (3;2 ) Ответ (8;-3)
2 группа (средняя)
1. Решить систему наиболее рациональным способом:
![]()
Ответ: (-7; 11) (3;1)
2. Решить
задачу:
Площадь прямоугольного земельного участка равна
20м2. Участок обнесен изгородью длиной 18 м. Найдите
длину и ширину участка.
Ответ: 4м и 5м
-
Какая из указанных пар чисел, является решением системы уравнений:
![]()
1. (-6;8); 2. (0;-2); 3. (-8;6); 4. (7;-9)
Ответ: ( -8; 6)
-
Осмысление и применение (тестовое задание)
1. Какие из перечисленных уравнений являются нелинейными уравнениями?
А)
х – 2у = 1, Б) хуz + 3у = -18,
В) ![]() +2у = 5, Г) –х – у =
-11.
+2у = 5, Г) –х – у =
-11.
2. Даны уравнения, график какого, уравнения является парабола?
А)
у =![]() , б) 5х + 4у = 20, в) ху = 12. , г) у
=
, б) 5х + 4у = 20, в) ху = 12. , г) у
= ![]() ,
,
3.
Какая пара чисел является решением системы
уравнений ![]()
А) (6; 3), б) (2; -1), в) (-3; -6), Г) (3; 0).
4. С помощью графика, изображенного на рисунке, определите, сколько решений имеет система уравнений?
А) Одно решение; б) Два решения; в) Три решения; г) Четыре решения;
д) Нет решений;

5. Если система состоит из двух уравнений второй степени с двумя переменными, то каким способом легче удается найти ее решение?
А) способом подстановки; б) способом сложения; в) графическим способом;
|
№1 |
№2 |
№3 |
№4 |
№5 |
|
б,в |
г |
б |
в |
б |
- Проверьте, отметив на листах итог вашей работы.
-
Коррекция знаний
Дополнительное задание:
1) Подберите решение системы
уравнений:![]()
А)
2) Найдите х + у :
![]()
Решение : ( х – у) (х + у) = 16 х – у =2 2(х +у) 16 х + у =16:2 х + у=8
-
Задание на дом Инструктаж по выполнению домашнего задания
4А.25(б), 4А26(б)
Рефлексия
( презентация)
1 группа
-
Решите систему наиболее рациональным способом:
![]()
2. Выберите систему уравнений, соответствующую
условию задачи и решите ее.
Сумма двух чисел равна 12, а их произведение равно 32. Найти эти
числа
а) ![]()
![]() б)
б) ![]()
![]()
-
Какая из нижеуказанных пар чисел является решением системы уравнений:
![]()
1. (-3;2); 2. (1;4); 3. (8;-3); 4. (3;2)
2 группа
1. Решить систему наиболее рациональным способом:
![]()
2. Решить
задачу:
Площадь прямоугольного земельного участка равна
20м2. Участок обнесен изгородью длиной 18 м. Найдите
длину и ширину участка
3. Какая из указанных пар чисел, является решением системы уравнений:
![]()
1. (-6;8); 2. (0;-2); 3. (-8;6); 4. (7;-9)
Фамилия Имя ученика___________________________________
тест
1. Какие из перечисленных уравнений являются нелинейными уравнениями?
А)
х – 2у = 1, б) хуz + 3у = -18,
в) ![]() +2у = 5, г) –х – у =
-11.
+2у = 5, г) –х – у =
-11.
2. Даны уравнения, график какого, уравнения является парабола?
А)
у =![]() , б) 5х + 4у = 20, в) ху = 12. , г) у
=
, б) 5х + 4у = 20, в) ху = 12. , г) у
= ![]() ,
,
3. Какая пара чисел является решением системы уравнений
![]()
А) (6; 3), б) (2; -1), в) (-3; -6), Г) (3; 0).
4. С помощью графика, изображенного на рисунке, определите, сколько решений имеет система уравнений?
А) Одно решение; б) Два решения; в) Три решения; г) Четыре решения;
д) Нет решений;

5. Если система состоит из двух уравнений второй степени с двумя переменными, то каким способом легче удается найти ее решение?
А) способом подстановки; б) способом сложения; в) графическим способом;
|
№1 |
№2 |
№3 |
№4 |
№5 |
|
|
|
|
|
|
|
|
|
|
|
|

шағым қалдыра аласыз