Материалдарды шектеусіз жүктеңіз ҚМЖ, ашық сабақтар, презентациялар, көрнекіліктер, дидактикалық материалдар, авторлық бағдарламалар және тағы басқа 400 000-астам материалды шексіз жүктеп алғыңыз келе ме?

Толығырақ

Тақырып бойынша 11 материал табылды

Республикалық онлайн олимпиадаларға белсенді қатысқаны үшін

Материал туралы қысқаша түсінік

Құрметті Кеулімжайқызы Әйгерім! Сіздің республикалық онлайн олимпиадаларда көрсеткен біліміңіз бен еңбегіңізді көрсеткеніңіз үшін алғыс білдіреміз!

Материалдың қысқаша нұсқасы

Сабақ жоспары

10.3В - бөлім

Негізгі тригонометриялық функциялар

Химия-биология бағытындағы НЗМ Атырау қаласы

Күні: 26.01.2017 ж

Шайхиева Н.Ш.

Сынып: 10 в

Қатысқандар саны: 10

Қатыспағандар саны:

Сабақ тақырыбы: №15-16

Тригонометриялық функциялардың графигі және қасиеттері

Оқу мақсаттары (оқу бағдарламасына сілтеме)

АТ 10.3

бірлік шеңбердің көмегімен тригонометриялық функцияның жұптылығын (тақтылығын),периодтылығын ,таңба тұрақтылық аралығын және монотондылығын түсіндіреді;

МН 10.14

Функциялардың анықтамаларына сүйене отырып, тригонометриялық функциялардың графиктерін сызады, мысалы у = 3cos(x-45⁰), сонымен қатар бағдарламалық қамтамасыз етуді пайдаланады;

Сабақ мақсаттары

Тригонометриялық функциялардың анықтамаларын біледі;

Функциялардың анықтамаларына сүйене отырып, тригонометриялық функциялардың графиктерін сызады, сонымен қатар бағдарламалық қамтамасыз етуді пайдаланады

Жетістік критерийлер

Білу және түсіну

Бұрылу бұрыштарының синусы, косинусы, тангенсі, котангенсі анықтамаларын біледі

Білімін қолдану

Функция периодтылығын сипаттайды

Тригонометриялық функциялардың жұп-тақтығын сипаттайды

Тригонометриялық функциялардың таңба тұрақтылықтылығын сипаттайды

Тригонометриялық функциялардың монотонды аралықтарын сипаттайды

Тілдік мақсаттар

Оқушылар:

Тригонометриялық функциялардың графиктерін түрлендіруді қарастырады және көрсете алады

Пәнге қатысты лексика мен терминология

тригонометриялық функциялар: синус, косинус, тангенс, секанс, косеканс, котангенс функция графигін салу, асимптоталар,максимум нүктесі, тұрақты мән, периоды, амплитуда тригонометриялық функциялардың графиктерін түрлендіру созу, сығу, координата осі бойымен параллель көшіру, симметриялы кескіндеу, Диалогқа/жазылымға қажетті тіркестер y = n sin x графигі вертикальды сығылады немесе созылады: · n>1 болғанда, n- көбейткішке байланысты ордината осі бойымен график созылады · 0<n<1 ордината осі бойымен график сығылады · n<0 график x осіне қарағанда симметриялы бейнелейді y= sin n x график көлденең (горизонталь) өзгереді : · n>1 график n- көбейткішке байланысты абсцисса осі бойымен сығылады · 0<n<1 график абсцисса осі бойымен созылады · n<0 болғанда y осіне қарағанда симметриялы бейнелейді y= sin (x+c) графигі x осінің бойымен параллель көшіріледі: · егер c>0,онда график солға қарай жылжиды; y= sin (x-c) графигі оңға қарай жылжиды

Құндылықтарды дарыту

сыни тұрғыдан ойлау арқылы білімге деген сүйіспеншілікті қалыптастыру.

Пәнаралық байланыстар

Алгебра 9 сынып

АКТ қолдану дағдылары

Презентация

Бастапқы білім

Тригонометриялық функциялардың анықтамасын біледі.

Сабақ барысы

Сабақтың жоспарланған кезеңдері

Сабақтағы жоспарланған іс-әрекет

Ресурстар

Басы

3 – мин

І. Ұйымдастыру.

Амандасу. Көңіл күйлерін смайликтер арқылы білу.

Үй тапсырмасын, оқушылар бір-бірінің дәптерлерін қарап тексереді.

5 - мин

Ой – түрткі: С – 1: Синус және косинус функциялары үшін ең кіші оң периоды қандай сан? С – 2: Тангенс (котангенс) функциялары үшін ең кіші оң периоды қандай сан ? С – 3: Синустың анықталу облысы қандай? С -4: Косинустың анықталу облысы қандай? С – 5: Тангенстың анықталу облысы қандай? С – 6: Котангенстың анықталу облысы қандай? С – 7: Синустың мәндерінің облысы қандай? С -8: Косинустың мәндерінің облысы қандай? С -9: Тангенстың мәндерінің облысы қандай? С – 10: Котангенстың мәндерінің облысы қандай? С – 11: Тригонометриялық функциялардың жұптығы туралы не айтуға болады?

20 – мин

15 - мин

Жаңа сабақ

Тригонометриялық функциялардың графигі және қасиеттері

у= sin x функциясының қасиеттері және графигі

1)Функцияның анықталу облысы барлық нақты сандар жиыны.,яғни х .

2)мәндер жиыны [-1;1]кесіндісі.,яғни y [-1;1].

3)Функция тақ,өйткені sin(-x) = sinx.

4) sin(x +2 ) = sinx.функция периодты, ең кіші периоды 2 .

5) [-π/2+2πk; π/2+2πk] кесінділерінде бір сарынды өспелі

[π/2+2πk; 3π/2+2πk] кесінділерінде бір сарынды кемімелі

У=sinx функциясының графигін синусоида қысығы деп атайды.

y=cosx функциясының графигі

1) Анықталу облысы: R
2) Мәндер жиыны: [-1; 1];
3) Функция жұп;
4) Функцияның ең кіші оң периоды 2π;
5) Функция [2πn; π+ 2πn] аралығында кемімелі және [-π+ 2πn; 2πn] аралығында өспелі.

y=cosx функциясының графигі косинусоида қисығы деп атайды.

y=tgx функциясының графигі

y=ctgx функциясының графигі

Тригонометриялық функциялардың графиктеріне қарапайым түрлендірулер қолдануға мысалдар

У=sinx

У= 2sinx

Y=sinx+1

Синус функциясының графигіне қарап, оның қасиеттерін анықтаңыз. 3; 4 - жаттығу

http://bilimland.kz/kk/#lesson=5988

15 - мин

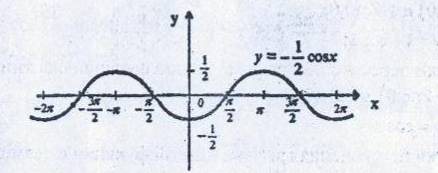
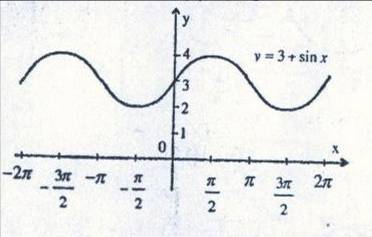
Жалпы сыныптық жұмыс.

№1. А) y= - cosx D(y)=R cosx €[-1:1]., E(y)=

X	-2π	-	-π	-π/2	0	π/2	π		2π
y=- cosx	-1/2	0	1/2	0	1/2	0	1/2	0	-1/2

Ә) y=3+sinx D(y)=R ,E(y)=[-4;-2] sinx €[-1:1]

2π

-π

-π/2

π/2

2π

y=3+sinx

20 - мин

Топтық жұмыс

І топ

1) Бір координаталық жазықтыққа салу y = sin x;

y = 3 sin x; y = sin x – 2

2) Функцияның анықталу, мәндер облысын , жұп – тақтылығын,

периодын тауып у = cos 2x + 3 функцияның графигін салыңдар

және монотонды аралықтарын табыңдар.

ІІ топ

1. Бір координаталық жазықтыққа салу y = сos x;

y = cos 2x; y = cos 2x – 1

Жүктеу

Бөлісу

ЖИ арқылы жасау

Файл форматы:

docx

Химия Оқушылар жұмысы 10 сынып

11.10.2020

755

Жүктеу

ЖИ арқылы жасау

Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз,
шағым қалдыра аласыз

Қазақстандағы ең үлкен материалдар базасынан іздеу

Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз

Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз!

Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі.

Оқу-ағарту министірлігінің ресми жауабы

Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!

Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз!

Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!

Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз!

Министірлікпен келісілген курс саны 12