Сабақ тақырыбы:αrcsinα, αrccosα, αrctgα, анықтамалары 1 курс

Ұзақ мерзімді жоспар бөлімі: 10.2АТригонометрия

Нұр-Сұлтан қаласы «Құрылыс-техникалық колледжі»

Күні: 27.01.2022

Мұғалімнің аты-жөні: Кульсейтова Салтанат Амантаевна

Курс:1

Қатысқандар саны:

Қатыспағандар:

Сабақ тақырыбы:

αrcsinα, αrccosα, αrctgα, анықтамалары

Осы сабақта қол жеткізілетін оқу мақсаттары

10.2.4.1 αrcsinα, αrccosα, αrctgα, анықтамаларын білу және қолдану

Сабақ мақсаттары:

Білім алушылар:

• αrcsinα, αrccosα, αrctgα анықтамаларымен танысады, анықтаманы есептеулерде қолдана алады;

• құрамында αrcsinα, αrccosα, αrctgα бар өрнектердің мәнін табады;

Тілдік мақсаттар

Оқытудың тілдік мақсаты

Білім алушылар:

• өзара кері функциялардың анықтамасы негізінде кері тригонометриялық функциялардың анықтамаларымен танысады, олардың қасиеттерінқолдана алады;

Бөлім бойынша лексика және терминология

• арксинус, арккосинус, арктангенс, арккотангенс;

Диалогқа/ жазылымға қажетті тіркестер

• m санының арккосинусы (арксинусы) деп, xбұрышының мәні … ;

• m санының арктангенсы (арккотангенсы) деп, xбұрышының мәні … ;

• құрамында кері тригонометриялық функциясы бар өрнектің мәнін табу үшін … .

Құндылықтарды

дарыту

Білім алушылардың өзара әрекеттестігі арқылы бір-біріне деген құрмет, бір-бірінің пікірін тыңдау, бағалау, өз пікірін білдіру дағдыларын қалыптастыру.

Пәнаралық

байланыстар

Тригонометрия биология, медицина, химия, сандартеориясын, архитектура, машинақұрастыру, компьютерлік графика, салалардақолданылады.

Бастапқы білім

Негізгі тригонометриялық функцияларды анықтау білімі. Бірлік шеңберде тригонометриялық функцияның қасиеттерін анықтай білу, негізгі тригонометриялық тепе-теңіктерді және келтіру формулаларын өрнектердің мәндерін табуда, өрнектерді ықшамдауда, теңдіктерді дәлелдеуде қолдану.

Сабақ барысы

Сабақтың жоспарланған кезеңдері

Сабақтағы жоспарланған іс-әрекет

Ресурстар

Сабақтың басы

І. Ұйымдастыру мәселелері

ІІ. 1. Үй жұмысына берілген кестенің толтырылуын өзара тексеру.

2. Өткен тақырып бойынша қайталауды топтарда ұйымдастыру.

Білім алушылар топтарда бір-біріне анықтамаларды айтып беріп, мысал келтіреді және сұрақтарға жауап береді.

Сабақтың ортасы

1. arcsinx функциясы . у= sin анықталған және үздіксіз.
1. сан осінің аралығында қарастырылған у= sin функциясы арксинус деп аталатын кері функцияға ие, және ол
х=arcsinу деп жазылады, мұндағы у–тәуелсіз айнымалы, ал х– тәуелді айнымалы.Әдеттегідей тәуелсіз айнымалыны – х,ал тәуелді айнымалы –у деп белгілесек, онда у=arcsin х деп жазамыз.

Осыдан және sin(arcsinх) = х.

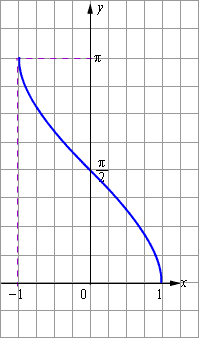
2.arccosx функциясы . у= cosx анықталған және үздіксіз.
сан осінің аралығында қарастырылған у= sin функциясы арккосинус деп аталатын кері функцияға ие, және ол
х=arcсоsу деп жазылады мұндағы у –тәуелсіз айнымалы,ал х– тәуелді айнымалы.Әдеттегідей тәуелсіз айнымалыны – х,ал тәуелді айнымалы–у деп белгілесек,онда у=arccosх деп жазамыз.

Осыдан және cos(arccosх)=х.

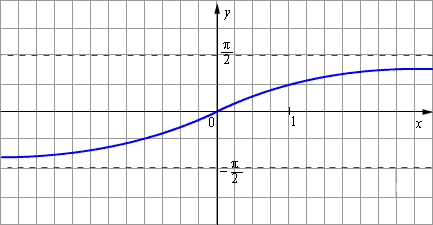
3. arctgx функциясы . у= arctgх функциясы өзінің анықталу облысында (яғни, + тең емес, барлық х үшін) үздіксіз.
сан осінің аралығында қарастырылған

у= tgx функциясы арктангенс деп аталатын кері функцияға ие, және ол х=arctgу деп жазылады, мұндағы у –тәуелсіз айнымалы, ал х– тәуелді айнымалы. Әдеттегідей тәуелсіз айнымалыны – х,ал тәуелді айнымалы –у деп белгілесек,онда у=arctgх деп жазамыз.Осыдан және tg (arctgх)=х.

4. arcctgx функциясы . у= сtgх функциясы өзінің анықталу облысында(яғни, тең емес, барлық х үшін) үздіксіз.
сан осінің аралығында қарастырылған, у= сtg функциясы арккотангенс деп аталатын кері функцияға ие, және ол
х=arcсtgу деп жазылады, мұндағы у –тәуелсіз айнымалы, ал х– тәуелді айнымалы. Әдеттегідей тәуелсіз айнымалыны – х, ал тәуелді айнымалы–у деп белгілесек, онда у=arcctgх деп жазамыз

Осыдан және сtg(arcctgх) = х.

.

.

Кері тригонометриялық функциялардың мәндерін есептеу: