
Алматы қаласы білім басқармасы
Алматы мемлекеттік бизнес колледжі
КЕЛІСІЛДІ БЕКІТІЛДІ
Директордың ОӘБ бойынша Директордың ОЖ бойынша
орынбасары__________ Сагимбекова А.Б. орынбасары ________Сатанова Г.У.
«____» ______________2015 ж. «____» ______________2015 ж.
«ЛОГАРИФДІК ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫҢ ЖҮЙЕЛЕРІ»
Математика пәні бойынша
сабақтың әдістемелік өңдемесі
«Математика- жаратылыстану»
циклдік отырысында
қаралды және талқыланды.
Хаттама № _______________
«___»_____________201 ж
Цикл төрайымы ______ Әбдісана Ұ.Ә.
Дайындаған: Әбдісана Ұ.Ә.
Алматы 2018 ж.
МАЗМҰНЫ
-
Атаулы санат
-
Сабақ жоспары:
-
Сабаққа дейін:
-
Сабақ мақсаттары.
-
Сабақ түрі және әдісі.
-
Алғышарттары-білім, ептілік және дағдылар.
-
Пәнаралық байланыс.
-
Сабақ қорытындысының талдамасы және бағасы.
-
Қажетті материалдар– студенттерге арналған әдебиет, ОТҚ,сабақты дидактикалық қамтамасыз ету.
-
Сабақтың негізгі кезеңдері және олардың уақыт бойынша ұзақтығы.
-
Оқыту үшін топтастыру.
-
Болжалды нәтижені суреттеу.
-
-
Сабақ кезінде – сабақ барысы:
-
Ұйымдастыру кезеңі.
-
Оқу материалын баяндау.
-
Оқытылатын материалды тексеру.
-
Сабақ нәтижесін бағалау.
-
-
Сабақтан кейін.
-
-
Пайдаланылған әдебиеттер.
-
Қосымшалар.
Атаулы санат
Мамандық: 0516 000- «Есеп және аудит»
Біліктілігі: Бухгалтер –экономист
Топ: 1 Уч «В»
Оқу пәні : Математика
Бөлім: III тарау. Көрсеткіштік, логарифмдік дәрежелік функциялар
Сабақтың тақырыбы: Логарифмдік теңдеулер және олардың жүйелері
2. Сабақ жоспары
2.1 Сабаққа дейін
2.1.1. Сабақ мақсаттары және міндеттері
Әдістемелік мақсат: оқушылардың сабаққа деген ынтасын, қызығушылығын жаңа технологиямен көтеру.
Үйретушілік мақсат: Логарифмдік теңдеулер менолардың жүйелерін шешу тәсілдерімен таныстыру , логарифмдік теңдеуді және теңдеулер жүйелерін шешіп жаттығу.
Дамытушылық мақсат: Логарифмдік функцияның қасиетерін қолдана отырып логарифмдік теңдеуді шешу,есептер шығарып жаттығу, білім, білік дағдыларын қалыптастыру
Тәрбиелік мақсат: Азаматтық жауапкершілікке тәрбиелеу, жинақылыққа, логикалық ойлау қабілетін дамыту.
Сабақ кезеңдеріне қойылатын міндеттер:
-
логарифмнің негізгі қасиеттерін, оларға амалдар қолдана білу
-
логарифмдік функцияның қасиеттерін білу
-
логарифмдік теңдеулерді түрлендіре отырып шешу
2.1.2. Сабақ түрі: аралас (түсіндірмелі, көрнектілікті)
Сабақ әдісі: үш өлшемді деңгейлеп оқыту технологиясын қолдану, сұрақ-жауап, жекелей, топтық жұмыс,практикалық есептер шығару.
2.1.3. Алғышарттар:
Тапсырмаларды орындау барысында үйренушілерге қажетті білім:
Пән – Алгебра және анализ бастамалары 10-11сынып
Тақырыбы Логарифмдік функциялар ,қасиеттері ,графигі
Тапсырмаларды орындау барысында үйренушілерге қажетті ептілік:
-
теңдікті н/е есептеу құралдарын пайдалана отырып логарифмдік өрнектің мәнін есептеуді
-
математиканың негізгі бағыттарын анықтауды
Тапсырмаларды орындау барысында үйренушілерге қажетті дағдылар:
-
математиканың басқа пәндермен байланысын
-
әр түрлі теңдеулерді түрлендіре отырып шеше білу
2.1.4 Пәнаралық байланыс
Пән –«Алгебра және анализ бастамалары 10-11сынып»
Тақырыбы– Тарихи мағлұматтар
Пән – Информатика.
Тақырыбы– «MS Microsoft бағдарламалары»
-
2.1.5 Сабақ қорытындысының талдамасы және бағасы.
Есептер шығару, қатемен жұмыс жасау, оқушылар білімін бағалау, Жұмыс дәптерлерінің қортындысын шығару
2.1.6. Қажетті материалдар
Үйренушілерге арналған әдебиет:
-
А.Е.Әбілқасымова11с ,98б,229-233
-
А.Н. Колмогоров. «Алгебра және анализ бастамалары 10-11сынып» Алматы-2003
-
Электрондыоқулықтар. Оқытудың техникалық құралдары:
-
Мультимедиалық проектор
-
Электронды оқулықтар
-
Жұмыс дәптерлері
-
Компьютер.
Сабақты оқу-әдістемелік құралдарымен қамтамасыз ету:
-
Тірек конспектілер
-
Презентация
-
Жұмыс дәптерін толтыру
-
Есептер картасы
-
Тапсырмалар.
2.1.7. Сабақтың негізгі кезеңдері және олардың ұзақтығы
|
Сабақ кезеңі |
Уақыты |
Тапсырма түрі |
Әдіс |
|
Ұйымдастыру кезеңі |
10 мин |
Амандасу. Психологиялық икемдеу. |
Оқытушының алғы сөзі |
|
Түгендеу |
Журнал |
||
|
Өтілген тақырыпты қайталау |
Қосымша 1 |
||
|
Тақырып бойынша оқу материалын баяндау: Тақырып бойынша бекітілген материалдарды беру Жұмыс дәптерлерін толтыру |
40 минут |
|
Қосымша 2 Қосымша 3 Жұмыс дәптерлерін толтыру |
|
Сабақты бағалау Тақырыпты бекіту және игергендігін тексеру. Оқушылар білімін бағалау |
25 минут 5 мин |
Есептер шығару |
Қосымша 4 |
|
Оқушылардың ауызша жауап беруі. |
Қосымша 5 |
||
|
Рефлексия |
Қосымша 6 |
2.1.8. Оқыту үшін топтастыру
-
Жеке жұмыс түрі;
-
Жалпы топтық жұмыс түрі;
2.22.Сабақ барысында
Сабақ барысы
2.2.1 Ұйымдастыру кезеңі
-
Амандасу
-
Психологиялық икемдеу
-
Сабақта жоқ білім алушыларды журнал бойынша түгендеу;
2.2.2. Оқу материалын баяндау
-
Логарифмдік теңдеуге анықтама беру
-
Логарифмдік теңдеулерді шешу тәсілдерімен таныстыру , мысалдар талдау
-
Логарифмдік теңдеудің екі жақ бөлігінде бірдей негізге келтіру әдісі
-
Логарифмдік теңдеуге жаңа айнымалы енгізу арқылы шешу әдісі
-
Логарифмдік теңдеулер жүйесін шешу әдістерін қарастыру
-
Есептер шығару,тақтамен, жеке оқушылармен жұмыс
2.2.3.Оқытылатын материалды тексеру
-
Логарифмдік функцияның қасиетін тұжырымдаңдар.
-
Логарифмдік теңдеудің шешу тәсілдерін талдаңдар?
2.2.4. Сабақ нәтижесін бағалау
2.3. Сабақтан кейін
2.3.1. Үй тапырмасы
-
Пайдаланылған әдебиеттер
Негізгі әдебиет:
-
А.Е.Әбілқасымова. Алг. ж/е анализ баст. §15, 102б,№229-233 Қосымша әдебиет:
-
Н. Колмогоров. «Алгебра және анализ бастамалары 10-11сынып» §11, 252бет№468-469
Әдістемелік әдебиет:
-
Жұмыс дәптерлері
-
Электронды оқулық
-
Оқу әдістемелік кешені.
-
Қосымшалар
ҚОСЫМША 1
-
Нақты көрсеткішті дәрежелердің қасиеттерін тұжырымдаңдар?
-
Көрсеткіштік функция қасиеттерін тұжырымдап ,оларды дәлелдеңдер?
-
Теріс санның логарифмі бола ма?
-
Логарифмдік функция деп қандай функцияна атайты?
-
Логарифмдік және оның қасиеттерін тұжырымдаңдар?
-
Логарифмдік функцияның графиктері негізі a > 1 болғанда, ал 0 < a < 1 болғанда қалай орналасады?
-
Жаңа негізге көшу қасиеті қай уақытта қолданылады?
-
Потенцалдау кезінде логарифмнің негізі ескеліле ме?
ҚОСЫМША 5
-
Логарифмдік функцияға анықтама беріңдер?
-
Логарифмдік функцияның қасиетін тұжырымдаңдар.
-
Логарифмдік теңдеудің шешу тәсілдерін талдаңдар?
ҚОСЫМША 6
Оқушылардың жаңа сабақта алған білімдерін пысықтау, сабаққа белсенді қатысқан оқушыларды мадақтау.
-
Жеке оқушылар білімін бағалау.
-
Жалпы оқушылардың сабаққа қатысуының сапасын бағалау
-
Сабақ не туралы?
-
Нені пайдаландың ? Нені үйрендің ?
-
Бүгінгі сабақ өмірде қажет пе ?
-
Көңіл күйің қандай ?
ҚОСЫМША 3
Оқушылырға жұмыс дәптерлерімен жұмыс жасату ол үшін алдын ала теориялық материал беріледі сол бойынша оқушы «Жұмыс дәптерлерін» толтыру керек.Кезеңдермен орындайды.
Сабақтың жұмыс дәптері
|
Бұ л «Көпір» тапсырмаларын оқушылар үйде орындап, бүгінгі сабаққа дайындалып келеді |
I кезең Бос орынға қажет сөздерді және формулаларды жаз.
___________ ______________________________ деп атайды.
3. Логарифмнің қасиеттері. _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ ______________________________________________________________________________________________________________________________
4. Логарифмдік функцияның қасиеттері. _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ ______________________________________________________________________________________________________________________________ 5.Ондық логарифм. __________________________________________________________________ 6. Натурал логарифм _______________________________________________________________ |
|
IV. Жаңа сабақ: Сабақтың мақсатымен таныстыру. |
|
|
«Білу» тапсырмалары Кім? Не? Қалай? Қашан? Қандай? |
II кезең
Т 1 . _____________________________________________
2 ___________________________________________
3 ___________________________________
4. ___________________________________________
5. ______________________________________________
6. ___________________________________________
|
|
«Түсіну» тапсырмалары Неліктен? Неге? Не үшін? Не себепті? |
Бос орынға қажетi формулаларды жаз.
|
|
«Талдау» тапсырмалары |
____________________________________________________________
|
|
«Жинақтау» тапсырмасы |
Логарифмдік теңдеулерді шешуге оның анықталу облысын ескеру қажет пе? Жауабын түсіндір. |
|
«Қолдану» тапсырмалары |
1. Л
Демек, мәні теңдеуді қанағаттандырады. Ж 2. А
немесе
Жауабы:6 |
|
«Баға» беру |
|
|
«Кері байланыс» «Білу» теориясы Тәжірибе |
III кезең 1 деңгей (5 балл) «3»
Логарифмнің қандай қаасиеттерін қолданамыз. |
|
« Түсіну» теория Тәжірибе |
2 деңгей (5 +4 балл) «4»
Шыққан теңдеуді негізін 2-ге тең етіп логарифмдейік:
|
|
«Жинақтау» «Талдау» Теория Тәжірибе |
3
x1=4 x1= Жауабы: 4 және 1 2 3 4. 5. 6. |
Қосымша 2
3.7. Логарифмдік теңдеулер және олардың жүйелері
Анықтама: loga f (x) = loga g (x), ( a > 0, a ≠ 1, f (x) >0, g (x) >0) (1) түрінде берілген немесе осы түрге келетін теңдеуді логарифмдік теңдеу деп атайды.
Логарифмдік теңдеуді шешу үшін:
-
Теңдеудің екі жақ бөлігін бірдей негізге келтіру;
-
Жаңа айнымалы енгізу;
-
Потенциалдау қолданылады;
Логарифмдік теңдеулерді шешкенде, логарифмдік функцияның анық-талу облысы оң сандар екенін ескеріп, х айнымалысының мүмкін мән-дер жиынын анықтап алуға болады. Содан кейін теңдеуді шешіп, түбірлердің анықталған жиынға тистілігін тексерсек жеткілікті.

loga f (x) = loga g (x) теңдеуінен f (x) = g (x) теңдігіне ауысуды потенциалдау деп атайды.
1-Мысал.Теңдеуді шешіңдер:
Шешуі: Логарифмнің негізі 7 болатындай етіп жазамыз.


a)  x > 1 теңсіздігін
x > 1 теңсіздігін
қанағаттандыратын теңдеудің түбірі x = 3 болады.
б) 
М.М.Ж ескерсек x = -3 теңдеудің шешімі болмайды.
Жауабы. 0, 3, −7.
2-Мысал: Теңдеуді шешіңдер:

|
|





 , 3x – 4 = 0
, 3x – 4 = 0



x = 0
және х=
3. x = 0 теңдеудің бөгде
түбір, себебі х айнымалысының мүмкін мәндер жиынына тиісті емес.
Жауабы.  , 3.
, 3.
3-мысал. logx4 = 2 теңдеуін шешейік.
Шешуі. (1) бойынша 4 = x2; 22 =
x2;
x = 2. Логарифмнің негізі теріс сан болмайды, яғни x>0. Жауабы:
x = 2.
4-Мысал.  теңдеуінің түбірлерін
табыңдар.
теңдеуінің түбірлерін
табыңдар.
Шешуі: х айнымалысының мүмкін мәндер жиынын анықтайық:

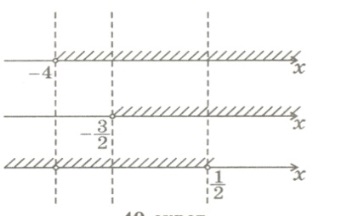 ,Теңсіздіктер жүйесінің әрбір
теңсіздігінің мәндер жиынын Координаталық түзуге түсірейік.
Сондa х айнымалысының мәні -1,5< х < 0,5 теңсіздігін
қанағаттандыру керек.
,Теңсіздіктер жүйесінің әрбір
теңсіздігінің мәндер жиынын Координаталық түзуге түсірейік.
Сондa х айнымалысының мәні -1,5< х < 0,5 теңсіздігін
қанағаттандыру керек.
Логарифмдік теңдеуді (1) теңдеудің түріне келтірейік. Ол үшін теңдеудің сол жақ бөлігін тепе-тең түрлендіреміз:

П![]()
13-сызба
отенциалдау арқылы келесі мәндес теңдеуді аламыз.(2x+8)∙(2x+3)=2-4x, x2+13x+11=0,түбірлері x1= -5,5 және x2= -1. x= -5,5бөгде түбір, себебі х айнымалысының мүмкін мәндер жиынына тиісті емес. Берілген теңдеудің түбірі x= -1
5-мысал. 
 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі. Логарифм таңбасының астындағы сан теріс болмауы
керек.

 . (x-1)(5x+3) =
. (x-1)(5x+3) =  . (x-1)(5x+3) = 36 немесе 5x2-2x-39 = 0. Бұл теңдеуді
шешсек, x1 = 3, x2
= -
. (x-1)(5x+3) = 36 немесе 5x2-2x-39 = 0. Бұл теңдеуді
шешсек, x1 = 3, x2
= - . Жауабы x = 3
. Жауабы x = 3
Анықтама: Құрамында логарифмдік теңдеулері бар теңдеулер жүйесін логарифмдік теңдеулер жүйесі деп атаймыз.
Логарифмдік теңдеулер жүйесін шешу үшін логарифмдік теңдеулерді және алгебралық теңдеулер жүйесін шешу тәсілдері қолданылады.
4-Мысал.  жүйесін шешейік.
жүйесін шешейік.
Шешуі: х
және у айнымалыларының мүмкін болатын мәндер
жиыны оң сандар. Логарифмнің қасиеттерін қолданып, берілген жүйені
түрлендіреміз. Сонда  теңдулер жүйесін аламыз, ал шыққан
теңдеулер жүйесі келесі жүйемен мәндес
теңдулер жүйесін аламыз, ал шыққан
теңдеулер жүйесі келесі жүйемен мәндес  соңғы теңдеулер жүйесін орын
ауыстыру тәсілі арқылы у2 + 8у-9=0 квадрат теңдеуін
аламыз, Виет теоремасын пайдаланып теңдеу түбірлері
у1=1, у2
= -9, онда сәйкесінше х1=9, х2
= -1. х
және у айнымалыларының мүмкін болатын мәндер
жиыны оң сандар болғандықтан теңдеулер жүйесінің жауабы:
(9; 1)
соңғы теңдеулер жүйесін орын
ауыстыру тәсілі арқылы у2 + 8у-9=0 квадрат теңдеуін
аламыз, Виет теоремасын пайдаланып теңдеу түбірлері
у1=1, у2
= -9, онда сәйкесінше х1=9, х2
= -1. х
және у айнымалыларының мүмкін болатын мәндер
жиыны оң сандар болғандықтан теңдеулер жүйесінің жауабы:
(9; 1)
ҚОСЫМША 4
Теңдеуді шеш:
-

-
 =
=
-

-
 =
=
-

-
log2х+log2(x-1)=1
-
log4(3-4x) =-1
-
log3(
 )=0
)=0 -
 (2x-4) =-
3
(2x-4) =-
3 -
 (x-1) =
-2
(x-1) =
-2
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Сабақтың әдістемелік өңдемесі
Сабақтың әдістемелік өңдемесі
Алматы қаласы білім басқармасы
Алматы мемлекеттік бизнес колледжі
КЕЛІСІЛДІ БЕКІТІЛДІ
Директордың ОӘБ бойынша Директордың ОЖ бойынша
орынбасары__________ Сагимбекова А.Б. орынбасары ________Сатанова Г.У.
«____» ______________2015 ж. «____» ______________2015 ж.
«ЛОГАРИФДІК ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫҢ ЖҮЙЕЛЕРІ»
Математика пәні бойынша
сабақтың әдістемелік өңдемесі
«Математика- жаратылыстану»
циклдік отырысында
қаралды және талқыланды.
Хаттама № _______________
«___»_____________201 ж
Цикл төрайымы ______ Әбдісана Ұ.Ә.
Дайындаған: Әбдісана Ұ.Ә.
Алматы 2018 ж.
МАЗМҰНЫ
-
Атаулы санат
-
Сабақ жоспары:
-
Сабаққа дейін:
-
Сабақ мақсаттары.
-
Сабақ түрі және әдісі.
-
Алғышарттары-білім, ептілік және дағдылар.
-
Пәнаралық байланыс.
-
Сабақ қорытындысының талдамасы және бағасы.
-
Қажетті материалдар– студенттерге арналған әдебиет, ОТҚ,сабақты дидактикалық қамтамасыз ету.
-
Сабақтың негізгі кезеңдері және олардың уақыт бойынша ұзақтығы.
-
Оқыту үшін топтастыру.
-
Болжалды нәтижені суреттеу.
-
-
Сабақ кезінде – сабақ барысы:
-
Ұйымдастыру кезеңі.
-
Оқу материалын баяндау.
-
Оқытылатын материалды тексеру.
-
Сабақ нәтижесін бағалау.
-
-
Сабақтан кейін.
-
-
Пайдаланылған әдебиеттер.
-
Қосымшалар.
Атаулы санат
Мамандық: 0516 000- «Есеп және аудит»
Біліктілігі: Бухгалтер –экономист
Топ: 1 Уч «В»
Оқу пәні : Математика
Бөлім: III тарау. Көрсеткіштік, логарифмдік дәрежелік функциялар
Сабақтың тақырыбы: Логарифмдік теңдеулер және олардың жүйелері
2. Сабақ жоспары
2.1 Сабаққа дейін
2.1.1. Сабақ мақсаттары және міндеттері
Әдістемелік мақсат: оқушылардың сабаққа деген ынтасын, қызығушылығын жаңа технологиямен көтеру.
Үйретушілік мақсат: Логарифмдік теңдеулер менолардың жүйелерін шешу тәсілдерімен таныстыру , логарифмдік теңдеуді және теңдеулер жүйелерін шешіп жаттығу.
Дамытушылық мақсат: Логарифмдік функцияның қасиетерін қолдана отырып логарифмдік теңдеуді шешу,есептер шығарып жаттығу, білім, білік дағдыларын қалыптастыру
Тәрбиелік мақсат: Азаматтық жауапкершілікке тәрбиелеу, жинақылыққа, логикалық ойлау қабілетін дамыту.
Сабақ кезеңдеріне қойылатын міндеттер:
-
логарифмнің негізгі қасиеттерін, оларға амалдар қолдана білу
-
логарифмдік функцияның қасиеттерін білу
-
логарифмдік теңдеулерді түрлендіре отырып шешу
2.1.2. Сабақ түрі: аралас (түсіндірмелі, көрнектілікті)
Сабақ әдісі: үш өлшемді деңгейлеп оқыту технологиясын қолдану, сұрақ-жауап, жекелей, топтық жұмыс,практикалық есептер шығару.
2.1.3. Алғышарттар:
Тапсырмаларды орындау барысында үйренушілерге қажетті білім:
Пән – Алгебра және анализ бастамалары 10-11сынып
Тақырыбы Логарифмдік функциялар ,қасиеттері ,графигі
Тапсырмаларды орындау барысында үйренушілерге қажетті ептілік:
-
теңдікті н/е есептеу құралдарын пайдалана отырып логарифмдік өрнектің мәнін есептеуді
-
математиканың негізгі бағыттарын анықтауды
Тапсырмаларды орындау барысында үйренушілерге қажетті дағдылар:
-
математиканың басқа пәндермен байланысын
-
әр түрлі теңдеулерді түрлендіре отырып шеше білу
2.1.4 Пәнаралық байланыс
Пән –«Алгебра және анализ бастамалары 10-11сынып»
Тақырыбы– Тарихи мағлұматтар
Пән – Информатика.
Тақырыбы– «MS Microsoft бағдарламалары»
-
2.1.5 Сабақ қорытындысының талдамасы және бағасы.
Есептер шығару, қатемен жұмыс жасау, оқушылар білімін бағалау, Жұмыс дәптерлерінің қортындысын шығару
2.1.6. Қажетті материалдар
Үйренушілерге арналған әдебиет:
-
А.Е.Әбілқасымова11с ,98б,229-233
-
А.Н. Колмогоров. «Алгебра және анализ бастамалары 10-11сынып» Алматы-2003
-
Электрондыоқулықтар. Оқытудың техникалық құралдары:
-
Мультимедиалық проектор
-
Электронды оқулықтар
-
Жұмыс дәптерлері
-
Компьютер.
Сабақты оқу-әдістемелік құралдарымен қамтамасыз ету:
-
Тірек конспектілер
-
Презентация
-
Жұмыс дәптерін толтыру
-
Есептер картасы
-
Тапсырмалар.
2.1.7. Сабақтың негізгі кезеңдері және олардың ұзақтығы
|
Сабақ кезеңі |
Уақыты |
Тапсырма түрі |
Әдіс |
|
Ұйымдастыру кезеңі |
10 мин |
Амандасу. Психологиялық икемдеу. |
Оқытушының алғы сөзі |
|
Түгендеу |
Журнал |
||
|
Өтілген тақырыпты қайталау |
Қосымша 1 |
||
|
Тақырып бойынша оқу материалын баяндау: Тақырып бойынша бекітілген материалдарды беру Жұмыс дәптерлерін толтыру |
40 минут |
|
Қосымша 2 Қосымша 3 Жұмыс дәптерлерін толтыру |
|
Сабақты бағалау Тақырыпты бекіту және игергендігін тексеру. Оқушылар білімін бағалау |
25 минут 5 мин |
Есептер шығару |
Қосымша 4 |
|
Оқушылардың ауызша жауап беруі. |
Қосымша 5 |
||
|
Рефлексия |
Қосымша 6 |
2.1.8. Оқыту үшін топтастыру
-
Жеке жұмыс түрі;
-
Жалпы топтық жұмыс түрі;
2.22.Сабақ барысында
Сабақ барысы
2.2.1 Ұйымдастыру кезеңі
-
Амандасу
-
Психологиялық икемдеу
-
Сабақта жоқ білім алушыларды журнал бойынша түгендеу;
2.2.2. Оқу материалын баяндау
-
Логарифмдік теңдеуге анықтама беру
-
Логарифмдік теңдеулерді шешу тәсілдерімен таныстыру , мысалдар талдау
-
Логарифмдік теңдеудің екі жақ бөлігінде бірдей негізге келтіру әдісі
-
Логарифмдік теңдеуге жаңа айнымалы енгізу арқылы шешу әдісі
-
Логарифмдік теңдеулер жүйесін шешу әдістерін қарастыру
-
Есептер шығару,тақтамен, жеке оқушылармен жұмыс
2.2.3.Оқытылатын материалды тексеру
-
Логарифмдік функцияның қасиетін тұжырымдаңдар.
-
Логарифмдік теңдеудің шешу тәсілдерін талдаңдар?
2.2.4. Сабақ нәтижесін бағалау
2.3. Сабақтан кейін
2.3.1. Үй тапырмасы
-
Пайдаланылған әдебиеттер
Негізгі әдебиет:
-
А.Е.Әбілқасымова. Алг. ж/е анализ баст. §15, 102б,№229-233 Қосымша әдебиет:
-
Н. Колмогоров. «Алгебра және анализ бастамалары 10-11сынып» §11, 252бет№468-469
Әдістемелік әдебиет:
-
Жұмыс дәптерлері
-
Электронды оқулық
-
Оқу әдістемелік кешені.
-
Қосымшалар
ҚОСЫМША 1
-
Нақты көрсеткішті дәрежелердің қасиеттерін тұжырымдаңдар?
-
Көрсеткіштік функция қасиеттерін тұжырымдап ,оларды дәлелдеңдер?
-
Теріс санның логарифмі бола ма?
-
Логарифмдік функция деп қандай функцияна атайты?
-
Логарифмдік және оның қасиеттерін тұжырымдаңдар?
-
Логарифмдік функцияның графиктері негізі a > 1 болғанда, ал 0 < a < 1 болғанда қалай орналасады?
-
Жаңа негізге көшу қасиеті қай уақытта қолданылады?
-
Потенцалдау кезінде логарифмнің негізі ескеліле ме?
ҚОСЫМША 5
-
Логарифмдік функцияға анықтама беріңдер?
-
Логарифмдік функцияның қасиетін тұжырымдаңдар.
-
Логарифмдік теңдеудің шешу тәсілдерін талдаңдар?
ҚОСЫМША 6
Оқушылардың жаңа сабақта алған білімдерін пысықтау, сабаққа белсенді қатысқан оқушыларды мадақтау.
-
Жеке оқушылар білімін бағалау.
-
Жалпы оқушылардың сабаққа қатысуының сапасын бағалау
-
Сабақ не туралы?
-
Нені пайдаландың ? Нені үйрендің ?
-
Бүгінгі сабақ өмірде қажет пе ?
-
Көңіл күйің қандай ?
ҚОСЫМША 3
Оқушылырға жұмыс дәптерлерімен жұмыс жасату ол үшін алдын ала теориялық материал беріледі сол бойынша оқушы «Жұмыс дәптерлерін» толтыру керек.Кезеңдермен орындайды.
Сабақтың жұмыс дәптері
|
Бұ л «Көпір» тапсырмаларын оқушылар үйде орындап, бүгінгі сабаққа дайындалып келеді |
I кезең Бос орынға қажет сөздерді және формулаларды жаз.
___________ ______________________________ деп атайды.
3. Логарифмнің қасиеттері. _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ ______________________________________________________________________________________________________________________________
4. Логарифмдік функцияның қасиеттері. _______________________________________________________________ _______________________________________________________________ _______________________________________________________________ ______________________________________________________________________________________________________________________________ 5.Ондық логарифм. __________________________________________________________________ 6. Натурал логарифм _______________________________________________________________ |
|
IV. Жаңа сабақ: Сабақтың мақсатымен таныстыру. |
|
|
«Білу» тапсырмалары Кім? Не? Қалай? Қашан? Қандай? |
II кезең
Т 1 . _____________________________________________
2 ___________________________________________
3 ___________________________________
4. ___________________________________________
5. ______________________________________________
6. ___________________________________________
|
|
«Түсіну» тапсырмалары Неліктен? Неге? Не үшін? Не себепті? |
Бос орынға қажетi формулаларды жаз.
|
|
«Талдау» тапсырмалары |
____________________________________________________________
|
|
«Жинақтау» тапсырмасы |
Логарифмдік теңдеулерді шешуге оның анықталу облысын ескеру қажет пе? Жауабын түсіндір. |
|
«Қолдану» тапсырмалары |
1. Л
Демек, мәні теңдеуді қанағаттандырады. Ж 2. А
немесе
Жауабы:6 |
|
«Баға» беру |
|
|
«Кері байланыс» «Білу» теориясы Тәжірибе |
III кезең 1 деңгей (5 балл) «3»
Логарифмнің қандай қаасиеттерін қолданамыз. |
|
« Түсіну» теория Тәжірибе |
2 деңгей (5 +4 балл) «4»
Шыққан теңдеуді негізін 2-ге тең етіп логарифмдейік:
|
|
«Жинақтау» «Талдау» Теория Тәжірибе |
3
x1=4 x1= Жауабы: 4 және 1 2 3 4. 5. 6. |
Қосымша 2
3.7. Логарифмдік теңдеулер және олардың жүйелері
Анықтама: loga f (x) = loga g (x), ( a > 0, a ≠ 1, f (x) >0, g (x) >0) (1) түрінде берілген немесе осы түрге келетін теңдеуді логарифмдік теңдеу деп атайды.
Логарифмдік теңдеуді шешу үшін:
-
Теңдеудің екі жақ бөлігін бірдей негізге келтіру;
-
Жаңа айнымалы енгізу;
-
Потенциалдау қолданылады;
Логарифмдік теңдеулерді шешкенде, логарифмдік функцияның анық-талу облысы оң сандар екенін ескеріп, х айнымалысының мүмкін мән-дер жиынын анықтап алуға болады. Содан кейін теңдеуді шешіп, түбірлердің анықталған жиынға тистілігін тексерсек жеткілікті.

loga f (x) = loga g (x) теңдеуінен f (x) = g (x) теңдігіне ауысуды потенциалдау деп атайды.
1-Мысал.Теңдеуді шешіңдер:
Шешуі: Логарифмнің негізі 7 болатындай етіп жазамыз.


a)  x > 1 теңсіздігін
x > 1 теңсіздігін
қанағаттандыратын теңдеудің түбірі x = 3 болады.
б) 
М.М.Ж ескерсек x = -3 теңдеудің шешімі болмайды.
Жауабы. 0, 3, −7.
2-Мысал: Теңдеуді шешіңдер:

|
|





 , 3x – 4 = 0
, 3x – 4 = 0



x = 0
және х=
3. x = 0 теңдеудің бөгде
түбір, себебі х айнымалысының мүмкін мәндер жиынына тиісті емес.
Жауабы.  , 3.
, 3.
3-мысал. logx4 = 2 теңдеуін шешейік.
Шешуі. (1) бойынша 4 = x2; 22 =
x2;
x = 2. Логарифмнің негізі теріс сан болмайды, яғни x>0. Жауабы:
x = 2.
4-Мысал.  теңдеуінің түбірлерін
табыңдар.
теңдеуінің түбірлерін
табыңдар.
Шешуі: х айнымалысының мүмкін мәндер жиынын анықтайық:

 ,Теңсіздіктер жүйесінің әрбір
теңсіздігінің мәндер жиынын Координаталық түзуге түсірейік.
Сондa х айнымалысының мәні -1,5< х < 0,5 теңсіздігін
қанағаттандыру керек.
,Теңсіздіктер жүйесінің әрбір
теңсіздігінің мәндер жиынын Координаталық түзуге түсірейік.
Сондa х айнымалысының мәні -1,5< х < 0,5 теңсіздігін
қанағаттандыру керек.
Логарифмдік теңдеуді (1) теңдеудің түріне келтірейік. Ол үшін теңдеудің сол жақ бөлігін тепе-тең түрлендіреміз:

П![]()
13-сызба
отенциалдау арқылы келесі мәндес теңдеуді аламыз.(2x+8)∙(2x+3)=2-4x, x2+13x+11=0,түбірлері x1= -5,5 және x2= -1. x= -5,5бөгде түбір, себебі х айнымалысының мүмкін мәндер жиынына тиісті емес. Берілген теңдеудің түбірі x= -1
5-мысал. 
 теңдеуін шешейік.
теңдеуін шешейік.
Шешуі. Логарифм таңбасының астындағы сан теріс болмауы
керек.

 . (x-1)(5x+3) =
. (x-1)(5x+3) =  . (x-1)(5x+3) = 36 немесе 5x2-2x-39 = 0. Бұл теңдеуді
шешсек, x1 = 3, x2
= -
. (x-1)(5x+3) = 36 немесе 5x2-2x-39 = 0. Бұл теңдеуді
шешсек, x1 = 3, x2
= - . Жауабы x = 3
. Жауабы x = 3
Анықтама: Құрамында логарифмдік теңдеулері бар теңдеулер жүйесін логарифмдік теңдеулер жүйесі деп атаймыз.
Логарифмдік теңдеулер жүйесін шешу үшін логарифмдік теңдеулерді және алгебралық теңдеулер жүйесін шешу тәсілдері қолданылады.
4-Мысал.  жүйесін шешейік.
жүйесін шешейік.
Шешуі: х
және у айнымалыларының мүмкін болатын мәндер
жиыны оң сандар. Логарифмнің қасиеттерін қолданып, берілген жүйені
түрлендіреміз. Сонда  теңдулер жүйесін аламыз, ал шыққан
теңдеулер жүйесі келесі жүйемен мәндес
теңдулер жүйесін аламыз, ал шыққан
теңдеулер жүйесі келесі жүйемен мәндес  соңғы теңдеулер жүйесін орын
ауыстыру тәсілі арқылы у2 + 8у-9=0 квадрат теңдеуін
аламыз, Виет теоремасын пайдаланып теңдеу түбірлері
у1=1, у2
= -9, онда сәйкесінше х1=9, х2
= -1. х
және у айнымалыларының мүмкін болатын мәндер
жиыны оң сандар болғандықтан теңдеулер жүйесінің жауабы:
(9; 1)
соңғы теңдеулер жүйесін орын
ауыстыру тәсілі арқылы у2 + 8у-9=0 квадрат теңдеуін
аламыз, Виет теоремасын пайдаланып теңдеу түбірлері
у1=1, у2
= -9, онда сәйкесінше х1=9, х2
= -1. х
және у айнымалыларының мүмкін болатын мәндер
жиыны оң сандар болғандықтан теңдеулер жүйесінің жауабы:
(9; 1)
ҚОСЫМША 4
Теңдеуді шеш:
-

-
 =
=
-

-
 =
=
-

-
log2х+log2(x-1)=1
-
log4(3-4x) =-1
-
log3(
 )=0
)=0 -
 (2x-4) =-
3
(2x-4) =-
3 -
 (x-1) =
-2
(x-1) =
-2

шағым қалдыра аласыз


 апсырманы орында.
апсырманы орында. .
. .
.











 огарифмнің анықтамасы бойынша
огарифмнің анықтамасы бойынша
 ауабы:2
ауабы:2 нықталу облысын табамыз:
нықталу облысын табамыз:



















 деңгей
деңгей





 .
. .
.














