
Қазақстан Республикасының білім және ғылым министрлігі
№81 жалпы білім беретін орта мектеп
Жұмыс авторы:
Тлеубергенова Диана, Дюсенбеков Ануар,
6 -сынып
Жоба тақырыбы: Шапшаң есептеудің әдістері
Секция: математика
Жетекші: Ихсанова А.Т.
Қарағанды, 2014 жыл
Мазмұны:
-
Кіріспе.
-
Негізгі бөлім.
А) Арифметиканың пайда болуы туралы тарихи мәлімет.
В) Шапшаң есептеу әдістері.
-
Қорытынды.
 «Санау мен есепшот –
бастағы тәртіптің негізі.»
«Санау мен есепшот –
бастағы тәртіптің негізі.»
Песталоцци
Кіріспе
Шапшаң есептеудің әртүрлі әдістері қолданылып келеді. Ауызша есептеу дағдылары математикалық білімнің маңызды элементі болып табылады. Соңғы жылдардағы компьютер, калькулятордың өмірге көптеп енуі оқушылардың шапшаң есептеу дағдыларына, ойлау қабілетінің тежелуіне әсер етуде.
Мақсаты: Натурал сандарды шапшаң
есептеу әдістерін меңгеру.
Міндеттері:
-
Есепшоттың пайда болу тарихымен танысу;
-
Шапшаң есептеу арқылы ойлау мәдениетін қалыптастыру;
-
Натурал сандарды қосу, азайту, көбейту және бөлуде әртүрлі әдіс- тәсілдерді пайдалану.
Зерттеу әдістері:
-
Әртүрлі дерекнамалардан ақпарат іздестіру (арнаулы әдебиеттерден, интернет ресурстарынан);
-
Практикалық жұмыс.
Арифметиканың пайда болуы туралы.
Математиканың адам өміріндегі мәні орасан зор. Санай білмей, сандарды қосуды, азайтуды, көбейтуді, бөлуді дұрыс орындай білмей тұрып адам қоғамының дамуы мүмкін деп ойлауға болмайды. Арифметикалық төрт амал, ауызша және жазбаша есептеу ережелері бастауыш сыныптардан бастап оқылады. Бұл ережелерді бір адам ойлап шығарған немесе тапқан емес. Арифметика күнделікті практика талаптарына, адамдардың еңбектеніп әрекет жасауындағы өмірлік мұқтаждықтарынан туған. Арифметика өте баяу және ұзақ уақыт дамыған.
Есептеу аспаптары туралы.
Адам ерте кездің өзінде-ақ есептеу жұмысын жеңілдету мақсатымен әр түрлі құралдар мен аспаптарды пайдаланған. Алғашқы, ең ежелгі «есептеу машинасы» адам қолдарының саусақтары мен аяқтарының башайлары болған. Сол арқылы адам едәуір үлкен сандарды есептеуді үйренген. Саусақтарын түрліше бүге отырып, адам тек бірліктер мен ондықтарды ғана емес, тіпті жүздіктер мен мыңдарды кескіндеп көрсете білген. Адам миллионға дейінгі сандарды осылайша қолдарымен меңзеп кескіндей білген.


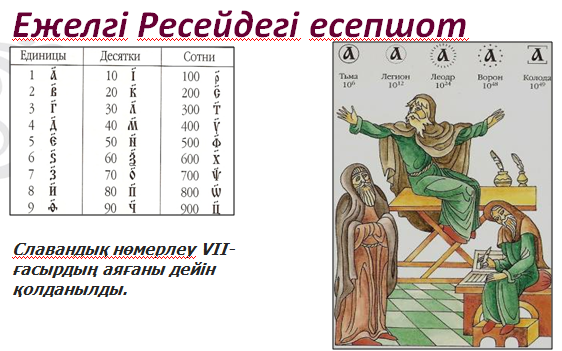



Ежелгі заманда саудагерлер
(финикиялық, вавилондық, т.б. саудагерлері) есеп – қисаптарын
жүргізгенде астық дәндерін, ұсақ тастарды, бақалшақтарды
пайдаланған, сонда оларды кейініректе құм деп аталған арнаулы тақта
бетіне жайып салып есептейтін. Құмды гректер мен римдіктер одан әрі
жетілдіре түсіп, ол өзіміздің қазіргі есепшотымыз тәрізді есептеу
тақтасына, есептеу аспабына айналған. Ең көне есептеу аспаптарының
бірі – қытайдың «суан – пан» деп аталатын есепшоты, ол Қытайда
казір де қ
 олданылады. Басқа бір ескі есептеу аспабы – жапон
«соробаны».
олданылады. Басқа бір ескі есептеу аспабы – жапон
«соробаны».
Саусақпен санау орта ғасырда да практикалық өмірде кең тараған болатын.
«Уақытпен санау хақында» кітап жазған Ирландия ғалымы монах Беда Достопочтенный (673-735) саусақпен санауға бүтін бір тарауды арнаған.
Мәселен, 13-ті 14-ке көбейту былайша орындалатын еді.
1)10*10=100 екені белгілі.
Бұдан кейін:
2) бір қолдың 3 саусағын, екінші қолдың 4 саусағын бүгеді.
3)3+4=7 , бұл - ондықтар, яғни 7*10=70
4)3*4=12, бұл бірліктер.
Сонымен:
5)13*14=10*10+7*10+3*4=182 және де
13*14=(1×1)жүздік+(1×(3+4))ондық+(3×4)=182
Орта ғасырдағы арифметикада саусақтармен санауға байланысты, римдік автор Боэцийден (480-524) бастап, сандар «саусақтарға» (бірліктерге), «буындарға» (ондықтарға) және «құрама сандарға» (басқа қалған сандарға) бөлінетін еді. Бұл сияқты атаулар Л.Ф.Магницкийдің «Арифметикасында» да кездеседі: «саусақтар», «буындар» және «құрамалар». Француздар осы уақытқа дейін бірліктерді «саусақтар» деп атаған.
Көне мысырлық тәсілге «орысша көбейту тәсілі» деп аталатын тәсіл жақын, оны революцияға дейінгі ауыл шаруалары қолданылып келген. Ол біреуі қайталанып екі еселенетін, ал екіншісі бір саны шыққанға дейін екіге бөлінетін екі көбейткіштің көбейтіндісін тізбектеп алмастыруға негізделген.
Мысал: 27×16. Көбейткіштердің біреуі бір бағанның басына жазылып, қайтадан екі еселенеді, екінші көбейткіш екінші бағанның басына жазылып, қайталап екіге бөлінеді.
27 16
54 8
108 4
216 2
432 1
Сонымен, арифметиканың пайда
болуы және дамуы адамдардың еңбектену әрекеттерімен, қоғамның
дамуымен байланысты.
Біз қолданатын осылайша санау тәсілі, яғни он-оннан топтап санау
ондық санау жүйесі немесе ондық нөмерлеу деп
аталады.
Шапшаң есептеу әдістері.
1-мен аяқталатын сандарға көбейту
81×31=
8×3=24 жүздік
8+3=11ондық
1×1=1
___________________
2511
Натурал сандарды шапшаң қосу мен азайту әдістері
Егер қосылғышты бірнеше бірлікке арттырса, қосындыны сонша бірлікке кеміту керек.
Мысалы:564+292=564+(292+8)-8=564+300-8=864-8=856.
Егер бір қосылғышты бірнеше бірлікке арттырса, екінші қосылғышты сонша бірлікке кеміту қосынды мәнін өзгертпейді.
Мысалы: 997+445=(997+3)+(455-3) =1000+452=1452
Егер азайғышты бірнеше бірлікке арттырса, азайтқышты да сонша бірлікке арттырып айырма мәнін өзгермейді.
Мысалы: 2454-1996=(2454+4)-(1996+4) =2458-2000=458
Егер екі санның қосындысынан сол сандардың айырмасын шегерсе, нәтижесінде екі еселенген кіші санның мәні шығады.
(а+в)-(а-в) =2в
Мысалы: (77+15)-(77-15) = 30= 2 * 15
Егер екі санның қосындысына сол сандардың айырмасын қосса, нәтижеде үлкен санның екі еселенген мәні шығады.
(а+в)+(а-в) =2а
(54+16)+(54-16) = 2 х 54=108
Натурал сандарды шапшаң көбейту мен бөлу әдісі
Көбейтудің қосу мен азайтуға байланысты үлестірімділік заңын пайдаланамыз.
Мысалы:
7 * 219 = 7 * (210+9) = 1470+63 = 1533
9 * 186 = 9 * (180+6) =1620+54 = 1674
Ферроль әдісімен көбейту
Айқастырып көбейту.
Көбейтіндінің бірлігін алу үшін көбейткіштердің бірліктерін көбейтеді. Ондығын алу үшін біреуінің ондығын бірлігіне және керісінше көбейтіп, қосындыға ойға алған санды қосады, жүздігін алу үшін ондықтарын көбейтеді, ойға алған санды қосады. Бұл әдіс мына теңдіктен шығады:
(10 а+b)(10с+d) =100 ас+10(аd+bс)+bd
Мысалы: 27*38 =1026
а) 7×8 =56; 6-ны жазамыз, 5-ті ойға аламыз.
б) 2×8+7×3+5 =42, 2 жазылады, 4 ойға алынады.
в) 2×3+4 =10, 10-ды жазамыз
Мысалы: 23*48 көбейтіндісін төмендегідей түрлендіріп көбейтуге болады
2*4*102 + (2*8 + 3*4)*101 + 3*8*100=800+280+24=1104
Графиктік түрде былай жазуға болады:
23 23 23
![]()
48 48 48
![]() 24
304
1104
24
304
1104
Мұндағы « » және « » сызықтары көбейтілетін сандарды байланыстырады.
Үш таңбалы сандарды көбейту осы әдіске ұқсас:
235 235 235 235 235
![]()
![]()
![]()
174 174 174 174 174
20 490 3890 20890 40890
(2*4+3*7)+5*1=(8+21)+5*1=29+5*1=29+5=34 т.с.с.
Пирамида әдісімен көбейту.
Бұл әдісті қысқаша көбейтудің жалпы әдісі деп те атайды.
Мысалы:
216×453
-
Бір-бірінің астында тұрған сандарды көбейтіп, нәтижесін 2 цифрмен жазу;
-
Көршілес цифрларды айқастырып көбейту. Нәтижесін 1 орын солға жылжытып, 1-қадам нәтижесінің астына жазу;
-
Айқастырып көбейту қадамын бір позицияға «ажырату»;
-
Соңында әр қадам нәтижесін қосу керек.
![]() 2 1 6
(2×4=8) 2 1 6
(2×5+1×4=14) 2 1 6
(2×3+6×4=30)
2 1 6
(2×4=8) 2 1 6
(2×5+1×4=14) 2 1 6
(2×3+6×4=30)
| | | (1×5=5) X X (1×3+6×5=33)
4 5 3 (6×3=18) 4 5 3 4 5 3
08 05 18 080 518 080 518
14 33 14 33
3 0 1
97 848
Көп таңбалы сандарды көбейту мына схема түрінде беріледі:
Ферроль әдісімен 10-нан 20-ға дейінгі екі орынды сандарды шапшаң көбейту.
Мысалы:12×14 =168
а) 2×4 = 8
ә)1×2+1×4 =6
б) 1×1 =1
Осы әдіспен үш орынды санды екі орынды санға көбейтуге болады.
Мысалы:125×23 =2857
а) 3×5 =15, 5 жазылады, 1 ойға алынады.
ә) 2×3+2×5+1 = 17, 7 жазылады, 1 ойда
б) 2×2+1×3+1 = 8, 8 жазылады
в)2×1 = 2, 2 жазылады.
Ондықтары бірдей, бірліктерінің цифрларының қосындысы онға тең сандарды шапшаң көбейту әдісі.
Көбейткіштердің біреуінің ондығын өзінен бірге артық санға көбейтіп, алдыңғы көбейткен нәтижеге тіркеп жазады. Бұл әдіс мына теңдікке негізделген.
(10а+в)(10а+с) = 100а(а+1)+bс, егер b+с=10
Мысалы: 23×27=621
23*27=(10*2+3)*(10*2+7)=100*2*(2+1)+3*7=600+21=621
а) 2× (2+1) =6, бірінші 6 саны жазылады
б) 3×7=21, соңынан 21 жазылады.
204×20=420224
а)20× (20+1) =420
б) 4×6=24, 24 санын 420 санының оң жағынан тіркеп жазамыз.
11 санына шапшаң көбейту әдісі
{АС*11}. 11 санына көбейту
келесі формуламен есептеледі:
АС*11=А||(А+С)||С,
мұндағы
(А+С<10)
АС*11=(А*10+(А+С))||C
11-ге көбейтілетін санның
соңғы цифрын жазамыз.Тізбектей оңнан солға қарай цимфрларының
қосындысын табамыз, содан соң көбейтілетін санның бірінші цифрын
жазамыз.
Мысалы:54×11=594
а) 4*1=4, 4-ті жазамыз
ә) 4+5=9, 4-тің сол жағына азылады
б) 5-ті жазамыз
Бұл әдіс төмендегі математикалық теңдікпен түсіндіріледі:
(10а + b)* 11 = 110*а+ 11 * b = 100*а + 10 * (a + b) + b
Тағы бір мысал формула бойынша жазсақ:
124×11=1|| (1+2) || (2+4) ||4=1364
Егер көрші цифрлардың қосындысы 9-дан артық болса, бірлігі жазылып, ондығы ойға алынады, келесі қосындыға бір саны қосылады.
Мысалы: 58×11=638
а) 8-ді жазамыз
ә) 5+8=13, 3-ті жазып, 1- ді ойға аламыз.
б) 5+1=6, 6- ны жазамыз.
Бір таңбалы немесе екі таңбалы санды 37 санына көбейту әдісі
Бұл әдіс 2×37=74, 3×37=111 теңдіктеріне негізделген
Мысалы:
6×37=37×3×2=222
8×37=(6+2) ×37=222+74=296
45×37=(48-3)×37=12×4×37-3×37=16×3×37-3×37=3×37(16-1)=111×15=1665
37-ге ауызша көбейту үшін, бұл санды 3-ке бөліп, 111-ге көбейту керек:
27 × 37 = 27 : 3 × 111 = 9 × 111 = 999
81 × 37 = 81 : 3 × 111 = 27 ×111 = 2997
Берілген санды 75-ке бөлу үшін, бұл санды 300-ге бөліп, 4-ке көбейту керек
2400 : 75 = 2400 : 300 × 4 = 32
600 : 75 = 600 : 300 × 4 = = 8
37-ге бөлу тәсілінде, керісінше, алдымен 111-ге бөліп, 3-ке көбейту керек.
888 : 37= 888 : 111 × 3 = 8 × 3 = 24
555 : 37= 555 : 111 × 3 = 5 × 3 = 15
5, 25, 125 сандарына шапшаң бөлу әдісі
Ол үшін сәйкесінше берілген санды 2-ге, 4-ке, 8-ге көбейтіп 10-ға, 100-ге, 1000-ға бөлу керек.
Мысалы:
220:5=(220×2):10=44
1300:25=(1300×4):100=52
9250:125=(9250*8):1000=74
Кейде амалдар тәртібін ауыстыруға болады, әуелі 10, 100, 1000 сандарына бөліп, сосын 2, 4, 8 сандарына көбейтуді орындауға болады.
Ондықтар разрядында тұрған цифрлардың қосындысы 10-ға тең болғанда, бірліктері бірдей сандарды көбейту
62×42=(6×4+2)×100+2×2=2604 34×74=(3×7+4)×100+4×4=2516
Екі таңбалы сандарды 101 ге көбейту
33×101=3333 56×101=5656
47×101=4747 99×101=9999
Үш таңбалы сандарды 1001-ге көбейту
316 × 1001= 316316 648 × 1001= 648648
527 × 1001 = 527527 473 × 1001=473473
Қорытынды
«Шапшаң есептеудің әдістері» математикада есептеу жұмысын жеңілдетуге, күнделікті өмірде және қазіргі қоғамда шапшаң есептеу дағдысын қалыптастыруға көмектеседі. Бұл жұмысты зерттеу барысында көптеген өзіме қажетті жаңалықтарды аштым. Сонымен, жоғарыда көрсетілген әдістерді, келтірілген мысалдарды меңгеріп алсақ, кез-келген жағдайда есепшотсыз шапшаң есептеуге болады. Болашақта жоғары сыныптарда «Шапшаң есептеудің әдістері» тақырыбы әлі де зерттеліп, толықтырылады.
Қолданылған әдебиеттер тізімі
1. Перельман Я.И. Быстрый счёт. 30 простых приёмов устного счёта.
2. Математика анықтамалығы.
3. «Информатика, физика,математика» журналдары.
4. Г.И.Глейзер «Мектептегі математика тарихы»
5. http://www.superidea.ru Развитие творческого мышления и интеллекта
2
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
"Шапшаң есептеудің әдістері" жоба
"Шапшаң есептеудің әдістері" жоба
Қазақстан Республикасының білім және ғылым министрлігі
№81 жалпы білім беретін орта мектеп
Жұмыс авторы:
Тлеубергенова Диана, Дюсенбеков Ануар,
6 -сынып
Жоба тақырыбы: Шапшаң есептеудің әдістері
Секция: математика
Жетекші: Ихсанова А.Т.
Қарағанды, 2014 жыл
Мазмұны:
-
Кіріспе.
-
Негізгі бөлім.
А) Арифметиканың пайда болуы туралы тарихи мәлімет.
В) Шапшаң есептеу әдістері.
-
Қорытынды.
 «Санау мен есепшот –
бастағы тәртіптің негізі.»
«Санау мен есепшот –
бастағы тәртіптің негізі.»
Песталоцци
Кіріспе
Шапшаң есептеудің әртүрлі әдістері қолданылып келеді. Ауызша есептеу дағдылары математикалық білімнің маңызды элементі болып табылады. Соңғы жылдардағы компьютер, калькулятордың өмірге көптеп енуі оқушылардың шапшаң есептеу дағдыларына, ойлау қабілетінің тежелуіне әсер етуде.
Мақсаты: Натурал сандарды шапшаң
есептеу әдістерін меңгеру.
Міндеттері:
-
Есепшоттың пайда болу тарихымен танысу;
-
Шапшаң есептеу арқылы ойлау мәдениетін қалыптастыру;
-
Натурал сандарды қосу, азайту, көбейту және бөлуде әртүрлі әдіс- тәсілдерді пайдалану.
Зерттеу әдістері:
-
Әртүрлі дерекнамалардан ақпарат іздестіру (арнаулы әдебиеттерден, интернет ресурстарынан);
-
Практикалық жұмыс.
Арифметиканың пайда болуы туралы.
Математиканың адам өміріндегі мәні орасан зор. Санай білмей, сандарды қосуды, азайтуды, көбейтуді, бөлуді дұрыс орындай білмей тұрып адам қоғамының дамуы мүмкін деп ойлауға болмайды. Арифметикалық төрт амал, ауызша және жазбаша есептеу ережелері бастауыш сыныптардан бастап оқылады. Бұл ережелерді бір адам ойлап шығарған немесе тапқан емес. Арифметика күнделікті практика талаптарына, адамдардың еңбектеніп әрекет жасауындағы өмірлік мұқтаждықтарынан туған. Арифметика өте баяу және ұзақ уақыт дамыған.
Есептеу аспаптары туралы.
Адам ерте кездің өзінде-ақ есептеу жұмысын жеңілдету мақсатымен әр түрлі құралдар мен аспаптарды пайдаланған. Алғашқы, ең ежелгі «есептеу машинасы» адам қолдарының саусақтары мен аяқтарының башайлары болған. Сол арқылы адам едәуір үлкен сандарды есептеуді үйренген. Саусақтарын түрліше бүге отырып, адам тек бірліктер мен ондықтарды ғана емес, тіпті жүздіктер мен мыңдарды кескіндеп көрсете білген. Адам миллионға дейінгі сандарды осылайша қолдарымен меңзеп кескіндей білген.







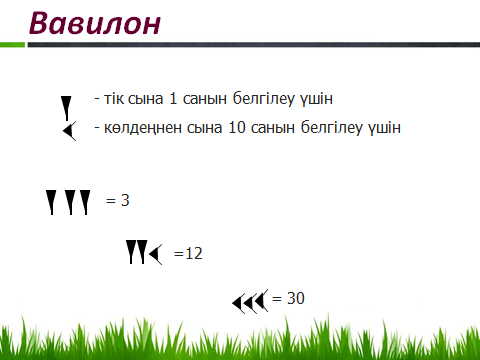
Ежелгі заманда саудагерлер
(финикиялық, вавилондық, т.б. саудагерлері) есеп – қисаптарын
жүргізгенде астық дәндерін, ұсақ тастарды, бақалшақтарды
пайдаланған, сонда оларды кейініректе құм деп аталған арнаулы тақта
бетіне жайып салып есептейтін. Құмды гректер мен римдіктер одан әрі
жетілдіре түсіп, ол өзіміздің қазіргі есепшотымыз тәрізді есептеу
тақтасына, есептеу аспабына айналған. Ең көне есептеу аспаптарының
бірі – қытайдың «суан – пан» деп аталатын есепшоты, ол Қытайда
казір де қ
 олданылады. Басқа бір ескі есептеу аспабы – жапон
«соробаны».
олданылады. Басқа бір ескі есептеу аспабы – жапон
«соробаны».
Саусақпен санау орта ғасырда да практикалық өмірде кең тараған болатын.
«Уақытпен санау хақында» кітап жазған Ирландия ғалымы монах Беда Достопочтенный (673-735) саусақпен санауға бүтін бір тарауды арнаған.
Мәселен, 13-ті 14-ке көбейту былайша орындалатын еді.
1)10*10=100 екені белгілі.
Бұдан кейін:
2) бір қолдың 3 саусағын, екінші қолдың 4 саусағын бүгеді.
3)3+4=7 , бұл - ондықтар, яғни 7*10=70
4)3*4=12, бұл бірліктер.
Сонымен:
5)13*14=10*10+7*10+3*4=182 және де
13*14=(1×1)жүздік+(1×(3+4))ондық+(3×4)=182
Орта ғасырдағы арифметикада саусақтармен санауға байланысты, римдік автор Боэцийден (480-524) бастап, сандар «саусақтарға» (бірліктерге), «буындарға» (ондықтарға) және «құрама сандарға» (басқа қалған сандарға) бөлінетін еді. Бұл сияқты атаулар Л.Ф.Магницкийдің «Арифметикасында» да кездеседі: «саусақтар», «буындар» және «құрамалар». Француздар осы уақытқа дейін бірліктерді «саусақтар» деп атаған.
Көне мысырлық тәсілге «орысша көбейту тәсілі» деп аталатын тәсіл жақын, оны революцияға дейінгі ауыл шаруалары қолданылып келген. Ол біреуі қайталанып екі еселенетін, ал екіншісі бір саны шыққанға дейін екіге бөлінетін екі көбейткіштің көбейтіндісін тізбектеп алмастыруға негізделген.
Мысал: 27×16. Көбейткіштердің біреуі бір бағанның басына жазылып, қайтадан екі еселенеді, екінші көбейткіш екінші бағанның басына жазылып, қайталап екіге бөлінеді.
27 16
54 8
108 4
216 2
432 1
Сонымен, арифметиканың пайда
болуы және дамуы адамдардың еңбектену әрекеттерімен, қоғамның
дамуымен байланысты.
Біз қолданатын осылайша санау тәсілі, яғни он-оннан топтап санау
ондық санау жүйесі немесе ондық нөмерлеу деп
аталады.
Шапшаң есептеу әдістері.
1-мен аяқталатын сандарға көбейту
81×31=
8×3=24 жүздік
8+3=11ондық
1×1=1
___________________
2511
Натурал сандарды шапшаң қосу мен азайту әдістері
Егер қосылғышты бірнеше бірлікке арттырса, қосындыны сонша бірлікке кеміту керек.
Мысалы:564+292=564+(292+8)-8=564+300-8=864-8=856.
Егер бір қосылғышты бірнеше бірлікке арттырса, екінші қосылғышты сонша бірлікке кеміту қосынды мәнін өзгертпейді.
Мысалы: 997+445=(997+3)+(455-3) =1000+452=1452
Егер азайғышты бірнеше бірлікке арттырса, азайтқышты да сонша бірлікке арттырып айырма мәнін өзгермейді.
Мысалы: 2454-1996=(2454+4)-(1996+4) =2458-2000=458
Егер екі санның қосындысынан сол сандардың айырмасын шегерсе, нәтижесінде екі еселенген кіші санның мәні шығады.
(а+в)-(а-в) =2в
Мысалы: (77+15)-(77-15) = 30= 2 * 15
Егер екі санның қосындысына сол сандардың айырмасын қосса, нәтижеде үлкен санның екі еселенген мәні шығады.
(а+в)+(а-в) =2а
(54+16)+(54-16) = 2 х 54=108
Натурал сандарды шапшаң көбейту мен бөлу әдісі
Көбейтудің қосу мен азайтуға байланысты үлестірімділік заңын пайдаланамыз.
Мысалы:
7 * 219 = 7 * (210+9) = 1470+63 = 1533
9 * 186 = 9 * (180+6) =1620+54 = 1674
Ферроль әдісімен көбейту
Айқастырып көбейту.
Көбейтіндінің бірлігін алу үшін көбейткіштердің бірліктерін көбейтеді. Ондығын алу үшін біреуінің ондығын бірлігіне және керісінше көбейтіп, қосындыға ойға алған санды қосады, жүздігін алу үшін ондықтарын көбейтеді, ойға алған санды қосады. Бұл әдіс мына теңдіктен шығады:
(10 а+b)(10с+d) =100 ас+10(аd+bс)+bd
Мысалы: 27*38 =1026
а) 7×8 =56; 6-ны жазамыз, 5-ті ойға аламыз.
б) 2×8+7×3+5 =42, 2 жазылады, 4 ойға алынады.
в) 2×3+4 =10, 10-ды жазамыз
Мысалы: 23*48 көбейтіндісін төмендегідей түрлендіріп көбейтуге болады
2*4*102 + (2*8 + 3*4)*101 + 3*8*100=800+280+24=1104
Графиктік түрде былай жазуға болады:
23 23 23
![]()
48 48 48
![]() 24
304
1104
24
304
1104
Мұндағы « » және « » сызықтары көбейтілетін сандарды байланыстырады.
Үш таңбалы сандарды көбейту осы әдіске ұқсас:
235 235 235 235 235
![]()
![]()
![]()
174 174 174 174 174
20 490 3890 20890 40890
(2*4+3*7)+5*1=(8+21)+5*1=29+5*1=29+5=34 т.с.с.
Пирамида әдісімен көбейту.
Бұл әдісті қысқаша көбейтудің жалпы әдісі деп те атайды.
Мысалы:
216×453
-
Бір-бірінің астында тұрған сандарды көбейтіп, нәтижесін 2 цифрмен жазу;
-
Көршілес цифрларды айқастырып көбейту. Нәтижесін 1 орын солға жылжытып, 1-қадам нәтижесінің астына жазу;
-
Айқастырып көбейту қадамын бір позицияға «ажырату»;
-
Соңында әр қадам нәтижесін қосу керек.
![]() 2 1 6
(2×4=8) 2 1 6
(2×5+1×4=14) 2 1 6
(2×3+6×4=30)
2 1 6
(2×4=8) 2 1 6
(2×5+1×4=14) 2 1 6
(2×3+6×4=30)
| | | (1×5=5) X X (1×3+6×5=33)
4 5 3 (6×3=18) 4 5 3 4 5 3
08 05 18 080 518 080 518
14 33 14 33
3 0 1
97 848
Көп таңбалы сандарды көбейту мына схема түрінде беріледі:
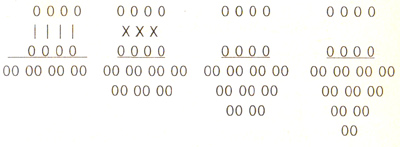
Ферроль әдісімен 10-нан 20-ға дейінгі екі орынды сандарды шапшаң көбейту.
Мысалы:12×14 =168
а) 2×4 = 8
ә)1×2+1×4 =6
б) 1×1 =1
Осы әдіспен үш орынды санды екі орынды санға көбейтуге болады.
Мысалы:125×23 =2857
а) 3×5 =15, 5 жазылады, 1 ойға алынады.
ә) 2×3+2×5+1 = 17, 7 жазылады, 1 ойда
б) 2×2+1×3+1 = 8, 8 жазылады
в)2×1 = 2, 2 жазылады.
Ондықтары бірдей, бірліктерінің цифрларының қосындысы онға тең сандарды шапшаң көбейту әдісі.
Көбейткіштердің біреуінің ондығын өзінен бірге артық санға көбейтіп, алдыңғы көбейткен нәтижеге тіркеп жазады. Бұл әдіс мына теңдікке негізделген.
(10а+в)(10а+с) = 100а(а+1)+bс, егер b+с=10
Мысалы: 23×27=621
23*27=(10*2+3)*(10*2+7)=100*2*(2+1)+3*7=600+21=621
а) 2× (2+1) =6, бірінші 6 саны жазылады
б) 3×7=21, соңынан 21 жазылады.
204×20=420224
а)20× (20+1) =420
б) 4×6=24, 24 санын 420 санының оң жағынан тіркеп жазамыз.
11 санына шапшаң көбейту әдісі
{АС*11}. 11 санына көбейту
келесі формуламен есептеледі:
АС*11=А||(А+С)||С,
мұндағы
(А+С<10)
АС*11=(А*10+(А+С))||C
11-ге көбейтілетін санның
соңғы цифрын жазамыз.Тізбектей оңнан солға қарай цимфрларының
қосындысын табамыз, содан соң көбейтілетін санның бірінші цифрын
жазамыз.
Мысалы:54×11=594
а) 4*1=4, 4-ті жазамыз
ә) 4+5=9, 4-тің сол жағына азылады
б) 5-ті жазамыз
Бұл әдіс төмендегі математикалық теңдікпен түсіндіріледі:
(10а + b)* 11 = 110*а+ 11 * b = 100*а + 10 * (a + b) + b
Тағы бір мысал формула бойынша жазсақ:
124×11=1|| (1+2) || (2+4) ||4=1364
Егер көрші цифрлардың қосындысы 9-дан артық болса, бірлігі жазылып, ондығы ойға алынады, келесі қосындыға бір саны қосылады.
Мысалы: 58×11=638
а) 8-ді жазамыз
ә) 5+8=13, 3-ті жазып, 1- ді ойға аламыз.
б) 5+1=6, 6- ны жазамыз.
Бір таңбалы немесе екі таңбалы санды 37 санына көбейту әдісі
Бұл әдіс 2×37=74, 3×37=111 теңдіктеріне негізделген
Мысалы:
6×37=37×3×2=222
8×37=(6+2) ×37=222+74=296
45×37=(48-3)×37=12×4×37-3×37=16×3×37-3×37=3×37(16-1)=111×15=1665
37-ге ауызша көбейту үшін, бұл санды 3-ке бөліп, 111-ге көбейту керек:
27 × 37 = 27 : 3 × 111 = 9 × 111 = 999
81 × 37 = 81 : 3 × 111 = 27 ×111 = 2997
Берілген санды 75-ке бөлу үшін, бұл санды 300-ге бөліп, 4-ке көбейту керек
2400 : 75 = 2400 : 300 × 4 = 32
600 : 75 = 600 : 300 × 4 = = 8
37-ге бөлу тәсілінде, керісінше, алдымен 111-ге бөліп, 3-ке көбейту керек.
888 : 37= 888 : 111 × 3 = 8 × 3 = 24
555 : 37= 555 : 111 × 3 = 5 × 3 = 15
5, 25, 125 сандарына шапшаң бөлу әдісі
Ол үшін сәйкесінше берілген санды 2-ге, 4-ке, 8-ге көбейтіп 10-ға, 100-ге, 1000-ға бөлу керек.
Мысалы:
220:5=(220×2):10=44
1300:25=(1300×4):100=52
9250:125=(9250*8):1000=74
Кейде амалдар тәртібін ауыстыруға болады, әуелі 10, 100, 1000 сандарына бөліп, сосын 2, 4, 8 сандарына көбейтуді орындауға болады.
Ондықтар разрядында тұрған цифрлардың қосындысы 10-ға тең болғанда, бірліктері бірдей сандарды көбейту
62×42=(6×4+2)×100+2×2=2604 34×74=(3×7+4)×100+4×4=2516
Екі таңбалы сандарды 101 ге көбейту
33×101=3333 56×101=5656
47×101=4747 99×101=9999
Үш таңбалы сандарды 1001-ге көбейту
316 × 1001= 316316 648 × 1001= 648648
527 × 1001 = 527527 473 × 1001=473473
Қорытынды
«Шапшаң есептеудің әдістері» математикада есептеу жұмысын жеңілдетуге, күнделікті өмірде және қазіргі қоғамда шапшаң есептеу дағдысын қалыптастыруға көмектеседі. Бұл жұмысты зерттеу барысында көптеген өзіме қажетті жаңалықтарды аштым. Сонымен, жоғарыда көрсетілген әдістерді, келтірілген мысалдарды меңгеріп алсақ, кез-келген жағдайда есепшотсыз шапшаң есептеуге болады. Болашақта жоғары сыныптарда «Шапшаң есептеудің әдістері» тақырыбы әлі де зерттеліп, толықтырылады.
Қолданылған әдебиеттер тізімі
1. Перельман Я.И. Быстрый счёт. 30 простых приёмов устного счёта.
2. Математика анықтамалығы.
3. «Информатика, физика,математика» журналдары.
4. Г.И.Глейзер «Мектептегі математика тарихы»
5. http://www.superidea.ru Развитие творческого мышления и интеллекта
2

шағым қалдыра аласыз















