
|
2020 год |
В помощь учителю математики Сборник работ для суммативного оценивания по алгебре и началам анализа 10 класс общественно-гуманитарное направление |

|
|
|
ТВГ учителей математики |
В помощь учителю математики Сборник работ для суммативного оценивания по алгебре и началам анализа 10 класс общественно-гуманитарное направление |
Содержание
|
Введение |
|
|
Суммативное оценивание за раздел «Функция, ее свойства и график» |
|
|
Суммативное оценивание за раздел «Тригонометрические функции» |
|
|
Суммативное оценивание за раздел «Тригонометрические уравнения и неравенства» |
|
|
Суммативное оценивание за раздел «Вероятность» |
|
|
Суммативное оценивание за раздел «Производная» |
|
|
Суммативное оценивание за раздел «Применение производной» |
|
|
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики» |
|
|
Суммативное оценивание за 1 четверть |
|
|
Суммативное оценивание за 2 четверть |
|
|
Суммативное оценивание за 3 четверть |
|
|
Суммативное оценивание за 4 четверть |
|
Творческая группа авторов-составителей:
Руководитель группы – Середкин В.П. учитель математики, педагог-мастер, Павлодарская область, Павлодарский район, КГУ Чернорецкая СОШ № 1.
Модератор группы – Айтмуханова Ж.А., учитель математики, педагог-эксперт, Акмолинская область, город Кокшетау, КГУ СОШ № 4.
Состав группы - Демец З.Л. - учитель математики, педагог-исследователь, Карагандинская область, Осакаровский район, КГУ СОШ № 25
Цыганов А.Ю. – учитель математики, высшая категория, Акмолинская область, город Кокшетау, КГУ СОШ № 4
Рецензент -
ВВЕДЕНИЕ
Данный сборник составлен в помощь учителю при планировании, организации и проведении суммативного оценивания за раздел и четверть по предмету алгебра общественно-гуманитарного направления для учащихся 10 классов.
Сборник работ по суммативному оцениванию составлен на основе ГОСО, типовой учебной программы и учебного плана. Данные работы позволяют учителю определить уровень достижения учащимися запланированных целей обучения.
Все работы сборника разработаны учителями-практиками на основе своих наблюдений и опыта работы в рамках обновленного содержания образования
В курсе математики 5 класса в соответствии с учебной программой и долгосрочным планом изучаются следующие разделы – «Натуральные числа и нуль», «Делимость натуральных чисел», «Обыкновенные дроби», «Действия над обыкновенными дробями», «Текстовые задачи», «Десятичные дроби и действия над ними», «Множества», «Проценты», «Углы. Многоугольники», «Диаграммы. Развертки пространственных фигур». Каждая из представленных работ для проведения суммативного оценивания за раздел и суммативного оценивание за четверть, состоит из четырех вариантов. Количество вариантов, используемое при проведение суммативного оценивания каждый учитель определяет самостоятельно.
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК»
Тема Свойства функции. Понятие обратой и сложной функции
Цели обучения
10.3.1.4 уметь описывать по заданному графику функции ее свойства:
1) область определения функции;
2)область значений функции;
3) нули функции;
4)промежутки монотонности функции;
7) наибольшее и наименьшее значение функции;
11) экстремумы функции;
10.3.1.5 знать определения обратной функции и уметь находить функцию, обратную заданной и знать свойство расположения графиков взаимно обратных функций
10.3.1.6
уметь
распознавать сложную функцию  и составлять композицию функции;
и составлять композицию функции;
10.3.1.1 - знать определение и способы задания функции;
Критерий оценивания Обучающийся:
-
Исследует свойства функции по ее графику;
-
Применяет алгоритм нахождения обратной функции;
-
Применяет алгоритм нахождения сложной функции;
-
Вычисляет значение функции
Уровень мыслительных навыков Применение
Время выполнения 25 минут
ЗАДАНИЯ
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
5 |
2 |
2 |
3 |
|
итого |
12 баллов |
|||
1 ВАРИАНТ
-
Дан график функции
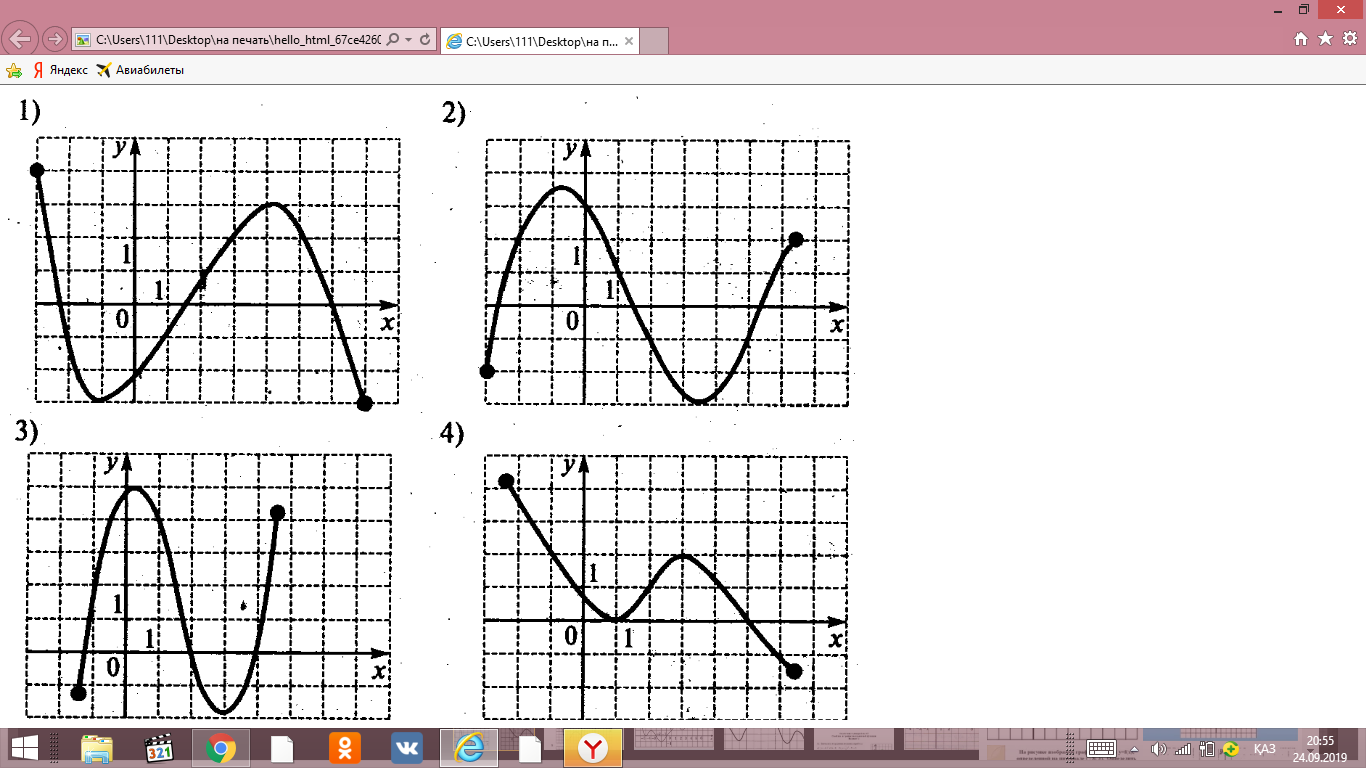
a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
.
Вычислите: 
-
ВАРИАНТ
-
Дан график функции

a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
.
Вычислите: 
-
ВАРИАНТ
-
Дан график функции
a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
.
Вычислите: 
-
ВАРИАНТ
-
Дан график функции

a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
Вычислите:
.
Вычислите: 
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Исследует свойства функции по ее графику; |
1 |
Определяет область определения функции; |
1 |
|
Определяет множество значений функции; |
1 |
||
|
Определяет промежутки монотонности функции; |
1 |
||
|
Определяет промежутки знакопостоянства функции |
1 |
||
|
Определяет наибольшее и наименьшее значения функции; |
1 |
||
|
Применяет алгоритм нахождения обратной функции; |
2 |
Определяет обратную функцию; |
1 |
|
Находит
корень уравнения |
1 |
||
|
Применяет алгоритм нахождения сложной функции; |
3 |
Составляет
сложную функцию |
1 |
|
Составляет
сложную функцию |
1 |
||
|
Вычисляет значение функции |
4 |
Вычисляет значение первой функции |
1 |
|
Вычисляет значение второй функции |
1 |
||
|
Вычисляет значение выражения |
1 |
||
|
И того: |
12 |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания
за раздел «Функция, ее свойства и график»
ФИ обучающегося :_____________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
|||
|
Низкий |
Средний |
Высокий |
||
|
Исследует свойства функции по ее графику |
Затрудняется в определении свойств функции по ее графику |
Допускает ошибки при определении области определения / промежутков знакопостоянства / максимума / минимума / четности функции |
Oпределяет свойства функции по ее графику |
|
|
Применяет алгоритм нахождения обратной функции |
Затрудняется в использовании алгоритма нахождения обратной функции |
Допускает ошибки при нахождения обратной функции |
Применяет алгоритм и находит обратную функцию |
|
|
Применяет алгоритм нахождения значения сложной функции |
|
Затрудняется нахождения значения сложной функции |
Допускает ошибки в преобразованиях для нахождения значения сложной функции |
Находит значение сложной функции |
|
Вычисляет значение функции |
|
Затрудняется в вычислении значений функций |
Допускает ошибки в вычислении значений функций |
Вычисляет значение функции |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ»
Тема: Тригонометрические функции, их свойства и графики. Арксинус, арккосинус, арктангенс, арккотангенс.
Цели обучения 10.1.3.1 - знать определения, свойства тригонометрических функций и уметь строить их графики;
10.1.3.2 - уметь строить графики тригонометрических функций с помощью преобразований;
10.1.3.4 - находить значения выражений, содержащих обратные тригонометрические функции.
Критерий оценивания Обучающийся:
-
Применяет свойства тригонометрических функций
-
Строит графики тригонометрических функций с помощью преобразований
-
Находит значения выражений, содержащих обратные тригонометрические функции.
Уровень мыслительных навыков Применение
Время выполнения 25 минут
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
8 |
3 |
4 |
|
итого |
15 баллов |
||
1 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=соs x |
y=tg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=sin(x+

-
Вычислите значение выражения:

2 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=sin x |
y=ctg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=cos(x+

-
Вычислите значение выражения:

3 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=cos x |
y=ctg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=cos(x+
 [3
балла]
[3
балла] -
Вычислите значение выражения:

4 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=sin x |
y=tg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=sin3x [3 балла]
-
Вычислите значение выражения:

|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Использует свойства тригонометрических функций |
1 |
находит область определения тригонометрической функции cos x \ tg x (sin x\ ctg x); |
2 |
|
находит область значений тригонометрической функции cos x \ tg x (sin x\ ctg x); ; |
2 |
||
|
Определяет четность (нечетность) тригонометрической функции cos x \ tg x (sin x\ ctg x); |
2 |
||
|
определяет периодичность тригонометрической функции cos x \ tg x (sin x\ ctg x); |
2 |
||
|
Строит график тригонометрических функций |
2 |
Строит график функции у= sin x |
1 |
|
Применяет преобразование графика функции у= sin x |
1 |
||
|
Строит
график функции
y=sin(x+ |
1 |
||
|
Находит значения выражений, содержащих обратные тригонометрические функции. |
3 |
Вычисляет первое значение |
1 |
|
Вычисляет второе значение |
1 |
||
|
Вычисляет третье значение |
1 |
||
|
Вычисляет значение выражения |
1 |
||
|
Всего баллов |
15 |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания
за раздел «Тригонометрические функции»
ФИ обучающегося : _____________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Применяет свойства тригонометрических функций |
Затрудняется в использовании свойств тригонометрических функции |
Допускает ошибки при определении четности/ нечетности, использовании монотонности/ нахождении области определения/ периода/ максимального/ минимального значения тригонометрических функций |
Использует свойства тригонометрических функций |
|
Строит график тригонометрических функций |
Затрудняется в построении графиков тригонометрических функций |
Допускает погрешности в построении графиков синуса/ косинуса |
Выполняет построение графиков тригонометрических функций |
|
Находит значения выражений, содержащих обратные тригонометрические функции. |
Затрудняется в вычислении обратных тригонометрических функций |
Допускает ошибки в вычислении обратных тригонометрических функций |
Вычисляет значение обратных тригонометрических функций |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА».
|
Тема |
Простейшие тригонометрические уравнения. Методы решения тригонометрических уравнений. Решение простейших тригонометрических неравенств. |
|
Цели обучения |
10.1.3.5 Уметь решать простейшие тригонометрические уравнения. 10.1.3.8 Уметь решать однородные тригонометрические уравнения. 10.1.3.6 Уметь решать тригонометрические уравнения методом разложения на множители. 10.1.3.9 Уметь решать простейшие тригонометрические неравенства. |
|
Критерии оценивания |
Обучающийся: Находит решение простейших тригонометрических уравнений. Решает однородные тригонометрические уравнения. Использует разложение на множители для решения тригонометрических уравнений. Решает простейшие тригонометрические неравенства. |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
25 мин |
ЗАДАНИЯ.
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
5 |
5 |
3 |
3 |
|
итого |
16 баллов |
|||
ВАРИАНТ 1.
-
Решите уравнение:
-
2sinx =
 ;
; -
ctgx + 3 = 0.
-
Решите уравнение: 2cos2x +
 sin2x – 3sin2x = 0.
sin2x – 3sin2x = 0. -
Решите уравнение: tg2x - 4 tgx = 0.
-
Решите неравенство: 3 cosx < 1,5.
ВАРИАНТ 2.
-
Решите уравнение:
-
– cosx =
 ;
; -
tgx - 12 = 3.
-
Решите уравнение: 3sin2x –sinxcosx -2cos2x = 0.
-
Решите уравнение: 2sin2x + sinx = 0.
-
Решите неравенство: 5ctg x ≤ - 2,5.
ВАРИАНТ 3.
-
Решите уравнение:
-
2sinx =
 ;
; -
21 + ctgx = 0.
-
Решите уравнение: sin2x – 2,5sin2x + 6cos2x = 0.
-
Решите уравнение: 2cos2x -
 cosx = 0.
cosx = 0. -
Решите неравенство: 3tgx ≥
 .
.
ВАРИАНТ 4.
-
Решите уравнение:
-
– 2cosx =
 ;
; -
tgx + 14 = 4.
-
Решите уравнение: - 5cos2x – 4 sinxcosx + sin2x = 0.
-
Решите уравнение: 2ctg2x + 3ctgx = 0.
-
Решите неравенство: 2sinx >
 .
.
Вариант 1.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию sinx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего синус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию ctgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего котангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу синуса двойного аргумента; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители ; |
1 |
|
использует формулы нахождения корней для тангенса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции cosx или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Вариант 2.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию cosx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего косинус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию tgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего тангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу основного тригонометрического тождества; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители; |
1 |
|
использует формулы нахождения корней для синуса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции ctg x или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Вариант 3.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию sinx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего синус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию ctgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего котангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу синуса двойного аргумента; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители; |
1 |
|
использует формулы нахождения корней для косинуса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции tg x или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Вариант 4.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию cosx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего косинус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию tgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего тангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу основного тригонометрического тождества; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители; |
1 |
|
использует формулы нахождения корней для котангенса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции sinx или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Тригонометрические уравнения и неравенства».
ФИ обучающегося : ______________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Находит решение простейших тригонометрических уравнений |
Затрудняется в нахождении решения простейших тригонометрических уравнений |
Допускает ошибки при решении простейших тригонометрических уравнений, содержащих синус / косинус / тангенс / котангенс |
Решает простейшие тригонометрические уравнения |
|
Решает однородные тригонометрические уравнения |
Затрудняется в решении однородных тригонометрических уравнений |
Выбирает метод решения однородного тригонометрического уравнения, допускает ошибки при выполнении преобразований / решении эквивалентного уравнения |
Решает однородные тригонометрические уравнения |
|
Использует разложение на множители для решения тригонометрических уравнений |
Затрудняется в использовании разложения на множители для решения тригонометрических уравнений |
Использует разложение на множители, допускает ошибки при выполнении преобразований / нахождении решения на заданном промежутке |
Использует разложение на множители для решения тригонометрических уравнений |
|
Решает простейшие тригонометрические неравенства |
Затрудняется в нахождении решения простейших тригонометрических неравенств |
Допускает ошибки при решении простейших тригонометрических неравенств, содержащих синус / косинус / тангенс / котангенс |
Решает простейшие тригонометрические неравенства |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ВЕРОЯТНОСТЬ»
|
Тема |
Вероятность события и её свойства. Правила сложения и умножения вероятностей |
|
Цель обучения |
10.2.1.1 - знать понятие случайного события, виды случайных событий и приводить их примеры; 10.2.1.2 - вычислять вероятность случайных событий, применяя свойства вероятностей; 10.2.1.3 - понимать и применять правила сложения и умножения вероятностей * P(A ∙ B) = P(A) ∙ P(B); * P(A + B) = P(A) + P(B); * P(A +B) = P(A)+P(B)–P(A ∙ B); |
|
Критерии оценивания |
Обучающийся: Применяет понятие случайного события, виды случайных событий и приводит их примеры Применяет свойства вероятностей Применяет правила сложения и умножения вероятностей при решении зада |
|
Уровень мыслительных навыков |
Применение |
|
Время для выполнения |
25 минут |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
2 |
5 |
4 |
|
итого |
11 баллов |
||
ВАРИАНТ 1.
-
Установите соответствие:
-
Событие
Вид события
-
«На березе растут яблоки»
1. Равновозможное
-
«При бросании игральной кости выпала цифра 6»
2. Достоверное
-
«За летом наступает осень»
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо..
Б) На тарелке лежат пирожки: 7 с картошкой, 9 с капустой и 4 с вареньем. Сауле наугад выбирает один пирожок. Найдите вероятность того, что он окажется с капустой.
-
Вероятность попадания в цель одним стрелком равна 0,7. Вероятность попадания в цель другим стрелком равна 0,9. Найти вероятность попадания в цель хотя бы одним стрелком.
ВАРИАНТ 2.
-
Установите соответствие:
-
Событие
Вид события
1. После ночи всегда наступает день
1. Равновозможное
2. Новый год отмечают зимой
2. Достоверное
3. В Казахстане всегда лето
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°C равна 0,87. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8°C или выше.
Б) В урне 9 красных, 6 жёлтых и 5 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
3. Рабочий обслуживает три станка. Вероятность того, что в течение смены первый станок потребует настройки, равна 0,3, второй – 0,75, третий – 0,4. Найти вероятность того, что в течение смены все станки потребуют настройки.
ВАРИАНТ 3.
-
Установите соответствие:
-
Событие
Вид события
1. Зимой холодно
1. Равновозможное
2. Летом отмечают Наурыз
2. Достоверное
3. В игральном кубике выпало число 5
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) В магазине стоят два платежных автомата. Оба могут быть неисправны с вероятностью 0,0025. Найдите вероятность того, что хотя бы один автомат исправен.
Б) В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
3. Экзаменационный билет состоит из трех вопросов. Вероятность того, что студент ответит на первый вопрос 0,7; на второй – 0,9; на третий – 0,6. Найти вероятность того, что студент, выбрав билет ответит на все вопросы.
ВАРИАНТ 4.
-
Установите соответствие:
-
Событие
Вид события
1. 5+5=11
1. Равновозможное
2. На сосне растут бананы
2. Достоверное
3. Зимой падает снег
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) В среднем из 300 шариковых ручек 9 не пишут. Найдите вероятность того, что наугад взятая ручка будет писать.
Б) На семинар приехали 5 ученых из Португалии, 3 из Финляндии и 2 из Болгарии. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что седьмым окажется доклад ученого из Финляндии.
3. Шахматисту в турнире предстоит сыграть с двумя соперниками, вероятность выигрыша у которых равна 0,6 и 0,8 соответственно. Определите вероятность выигрыша хотя бы у одного из них.
|
Критерий оценивания. |
№ задания. |
Дескриптор |
Балл. |
|
Обучающийся. |
|||
|
Применяет понятие случайного события, виды случайных событий и приводит их примеры |
1 |
Находит одно соответствия |
1 |
|
находит все соответствия |
1 |
||
|
Применяет свойства вероятностей
|
2а |
Применяет понятие противоположного события |
1 |
|
Вычисляет вероятность противоположного события. |
1 |
||
|
2б |
находит число всевозможных исходов; |
1 |
|
|
определяет число благоприятствующих исходов по условию; |
1 |
||
|
находит вероятность по формуле. |
1 |
||
|
Применяет правила сложения и умножения вероятностей при решении задач |
3 |
Находит вероятность первого события |
1 |
|
Находит вероятность второго события |
1 |
||
|
Применяет правила сложения и умножения вероятностей |
1 |
||
|
Находит вероятность попадания в цель хотя бы одним стрелком |
1 |
||
|
Итого: |
11 баллов |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Вероятность»
ФИ обучающегося : __________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Применяет понятие случайного события, виды случайных событий и приводит их примеры |
Затрудняется в понятие случайного события, виды случайных событий и приводит их примеры |
Допускает ошибки понятия случайного события, виды случайных событий и приводит их примеры |
Использует понятие случайного события, виды случайных событий и приводит их примеры |
|
Применяет свойства вероятностей |
Затрудняется в применении свойств вероятностей |
Допускает ошибки при применении свойств вероятностей |
Применяет свойства вероятностей |
|
Применяет правила сложения и умножения вероятностей при решении задач |
Затрудняется в применении правил сложения и умножения вероятностей при решении задач |
Допускает ошибки в применении правил сложения и умножения вероятностей при решении задач |
Применяет правила сложения и умножения вероятностей при решении задач |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПРОИЗВОДНАЯ»
|
Тема |
Предел функции в точке и на бесконечности. Правила нахождения производных. Физический и геометрический смысл производной. Уравнение касательной к графику функции. Производная сложной функции. Производные тригонометрических функц |
|
Цель обучения |
10.3.1.7 Знать определение предела функции в точке и на бесконечности 10.3.1.10 Находить производные постоянной функции и степенной функции 10.3.1.11 Знать и применять правила дифференцирования 10.3.3.1 Решать прикладные задачи, опираясь на физический смысл производной 10.3.1.12 Составлять уравнение касательной к графику функции в заданной точке 10.3.1.14 Знать определение сложной функции и находить её производную 10.3.1.13 Находить производные тригонометрических функций |
|
Критерии оценивания |
Обучающийся: Вычисляет предел функции Находит производную степенной функции Решает задачи, используя физический смысл производной Находит производную тригонометрической функции Находит производную сложной функции Составляет уравнение касательной |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время для выполнения |
20 минут |
ЗАДАНИЯ
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
4 |
2 |
4 |
7 |
|
итого |
17 баллов |
|||
1 ВАРИАНТ
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = 3 5
5 -4x
-6
-4x
-6
3.
Материальная точка движется прямолинейно по закону s(t) 19t
3t2 t3 , где s(t) – путь в метрах,
t – время в секундах. Найдите мгновенную скорость  (t) и ускорение g(t) в момент времени t =
5 с.
(t) и ускорение g(t) в момент времени t =
5 с.
4. Дана функция ? = - 3???2?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
2 ВАРИАНТ
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = -4 -6
-6 +2x
+ 9
+2x
+ 9
3.
Материальная точка движется прямолинейно по закону s(t) t3
+4t2 -10t , где s(t) – путь в метрах, t – время в
секундах. Найдите мгновенную скорость  (t) и ускорение g(t) в момент времени t =
4 с.
(t) и ускорение g(t) в момент времени t =
4 с.
4. Дана функция ? = - 3?in3?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
3 ВАРИАНТ
Задания
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = - 10
10 -9x
+8
-9x
+8
3.
Материальная точка движется прямолинейно по закону s(t) 12t
5t2 2t3 , где s(t) – путь в метрах,
t – время в секундах. Найдите мгновенную скорость  (t) и ускорение g(t) в момент времени t =
2 с.
(t) и ускорение g(t) в момент времени t =
2 с.
4. Дана функция ? = -4???4?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
4 ВАРИАНТ
Задания
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = 5 1
1 -12x -12
-12x -12
3.
Материальная точка движется прямолинейно по закону s(t) 10t3 -8t2 -8t, где
s(t) – путь в метрах, t – время в секундах. Найдите мгновенную
скорость  (t) и
ускорение g(t)
в момент времени t = 3 с.
(t) и
ускорение g(t)
в момент времени t = 3 с.
4. Дана функция ? = 5?in5?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Вычисляет предел функции |
1a |
выполняет преобразования; |
1 |
|
находит значение предела в точке; |
1 |
||
|
1b |
делит числитель и знаменатель на переменную в старшей степени; |
1 |
|
|
находит предел функции на бесконечности; |
1 |
||
|
Находит производную степенной функции |
2 |
находит производную степени с отрицательным показателем; |
1 |
|
находит производную степени с рациональным показателем; |
1 |
||
|
Решает задачи, используя физический смысл производной |
3 |
находит производную функции; |
1 |
|
вычисляет, мгновенную скорость в момент времени t; |
1 |
||
|
находит производную от скорости |
1 |
||
|
Вычисляет ускорение в момент времени t; |
1 |
||
|
Находит производную тригонометрической функции. Находит производную сложной функции |
4a |
использует формулу производную сложной функции; |
1 |
|
находит производную косинуса (синуса); |
1 |
||
|
находит производную сложной функции; |
1 |
||
|
Составляет уравнение касательной |
4b |
находит значение функции в точке; |
1 |
|
находит значение производной в точке; |
1 |
||
|
использует формулу уравнения касательной; |
1 |
||
|
записывает уравнение касательной. |
1 |
||
|
Итого: |
17 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «ПРОИЗВОДНАЯ»
ФИ обучающегося: _________________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Вычисляет предел функции |
Затрудняется в вычислении предела функции в точке, на бесконечности |
Допускает вычислительные ошибки при нахождении предела функции в точке / на бесконечности |
Вычисляет предел функции в точке, на бесконечности |
|
Находит производную степенной функции |
Затрудняется в нахождении производной степенной функции. |
Допускает ошибки при нахождении производной функции с отрицательным / рациональным показателем |
Находит производную степенной функции. |
|
Решает задачи, используя физический смысл производной |
Затрудняется в применении физического смысла производной при решении задач |
Допускает ошибки в применении физического смысла производной/ вычислительные ошибки при решении задач |
Применяет физический смысл производной при решении задач |
|
Находит производную тригонометрической функции. Находит производную сложной функции |
Затрудняется в нахождении производной тригонометрических функций, сложной функции. |
Допускает ошибки при нахождении производной тригонометрических функций / преобразованиях при нахождении производной сложной функции. |
Находит производную тригонометрических функций и производную сложной функции |
|
Составляет уравнение касательной |
Затрудняется в составлении уравнения касательной |
Допускает ошибки в преобразованиях / вычислениях при составлении уравнения касательной |
Составляет уравнение касательной |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
|
Тема |
Признаки возрастания и убывания функции. Критические точки и точки экстремума. Исследование функции с помощью производной и построение её графика. Наибольшее и наименьшее значения функции на отрезке |
|
Цель обучения |
10.3.1.17 Находить критические точки и точки экстремума функции 10.3.1.15 Знать и применять необходимое и достаточное условие возрастания (убывания) функции на интервале 10.3.1.18 Исследовать свойства функции с помощью производной и строить её график 10.3.1.19 Находить наибольшее и наименьшее значения функции на отрезке 10.3.3.3 Решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции |
|
Критерии оценивания |
Обучающийся: Находит критические точки функции Использует условие возрастания (убывания) функции и находит промежутки монотонности Строит график функции, используя результаты исследования функции Решает задачи на нахождение наибольшего (наименьшего) значения функции |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время для выполнения |
25 минут |
ЗАДАНИЯ
|
Разбаловка заданий работы |
||
|
№ задания |
1 |
2 |
|
Количество баллов |
11 |
6 |
|
итого |
17 баллов |
|
1 ВАРИАНТ
1. Дана
функция f(x) =  х3 – 4х2 + 15х - 7 .
х3 – 4х2 + 15х - 7 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
=  х3 – 4х2 + 15х – 7 при х0 = 1
х3 – 4х2 + 15х – 7 при х0 = 1
d) Для функции f(x) =  х3 – 4х2 + 15х - 7
х3 – 4х2 + 15х - 7
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 80 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
2 ВАРИАНТ
1. Дана
функция f(x) =  х3 –
х3 –  х2 - 5х + 17 .
х2 - 5х + 17 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
=  х3 –
х3 –  х2 - 5х + 17, при х0 = 3
х2 - 5х + 17, при х0 = 3
d) Для функции f(x) =  х3 –
х3 –  х2 - 5х + 17
х2 - 5х + 17
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 96 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
3 ВАРИАНТ
1. Дана
функция f(x) =6
+  х2 –х3 .
х2 –х3 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
= 6 +
 х2 –х3 , при х0 = 0,5
х2 –х3 , при х0 = 0,5
d) Для функции f(x) = 6 +  х2 –х3
х2 –х3
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 102 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
4 ВАРИАНТ
1. Дана
функция f(x) = 4
-  х2 –3х5 .
х2 –3х5 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
= 4 -
 х2 –3х5 , при х0 = - 0,5
х2 –3х5 , при х0 = - 0,5
d) Для функции f(x) = 4 -  х2 –3х5
х2 –3х5
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 88 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся Находит критические точки функции |
1а |
Использует правило дифференцирования степенной функции |
1 |
|
Находит производную функции |
1 |
||
|
решает уравнение; |
1 |
||
|
находит критические точки; |
1 |
||
|
Использует условие возрастания (убывания) функции и находит промежутки монотонности |
1b |
определяет знаки производной; |
1 |
|
записывает промежутки монотонности; |
1 |
||
|
Строит график функции, используя результаты исследования функции |
1c |
Находит значение функции в данной точке |
1 |
|
Находит значение производной функции в данной точке |
1 |
||
|
Составляет уравнение касательной в данной точке |
1 |
||
|
1d |
Находит область определения функции |
1 |
|
|
строит эскиз графика функции |
1 |
||
|
Решает задачу на нахождение наибольшего (наименьшего) значения функции |
2 |
выражает одну переменную через другую, используя периметр фигуры |
1 |
|
составляет функцию для нахождения площади |
1 |
||
|
находит производную функции |
1 |
||
|
находит экстремумы функции |
1 |
||
|
находит максимальное значение, учитывая ограничения |
1 |
||
|
находит необходимые размеры |
1 |
||
|
Итого: |
17 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
ФИ обучающегося :_______________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
|||
|
Низкий |
Средний |
Высокий |
||
|
Находит критические точки функции
|
Затрудняется в нахождении критических точек функции |
Допускает ошибки при нахождении критических точек функции |
Находит критические точки функции |
|
|
Использует условие возрастания (убывания) функции и находит промежутки монотонности |
|
Затрудняется в использовании условия возрастания (убывания) функции и нахождения промежутков монотонности |
Допускает ошибки в использовании условия возрастания (убывания) функции и нахождения промежутков монотонности |
Использует условие возрастания (убывания) функции и находит промежутки монотонности |
|
Строит график функции, используя результаты исследования функции |
|
Затрудняется в построении графика функции, используя результаты исследования функции |
Допускает погрешности в построении графика функции, используя результаты исследования функции |
Выполняет построение в построении графика функции, используя результаты исследования функции |
|
Решает задачу на нахождение наибольшего (наименьшего) значения функции |
|
Затрудняется в решении задач на вычисление наибольшего (наименьшего) значения функции |
Допускает ошибки в решении задач на вычисление наибольшего (наименьшего) значения функции |
Решает задачу на нахождение наибольшего(наименьшего) значения функции |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ»».
|
Тема |
Дискретные и непрерывные случайные величины Числовые характеристики дискретных случайных величин. |
|
Цели обучения |
10.2.1.6 Составлять таблицу закона распределения некоторых дискретных случайных величин. 10.2.1.8 Вычислять математическое ожидание дискретной случайной величины. 10.2.1.9 Вычислять дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины. |
|
Критерии оценивания |
Обучающийся: Использует закон распределения дискретных случайных величин. Использует свойства математического ожидания дискретной случайной величины. Вычисляет дисперсию и стандартное отклонение дискретной случайной величины. |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
25 мин |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
2 |
6 |
6 |
|
итого |
14 баллов |
||
ВАРИАНТ 1
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 9; 8; 10; 12; 11. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
12
10
-5
11
6
р
֍
0,3
֍
֍
0,1
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны числам 1 : 3 : 2 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(-4Х+2).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
5
8
-5
х4
р
0,2
0,3
0,4
0,1
-
-
Найдите х4, зная, что М(Х) = 2.
-
Найдите дисперсию и среднее квадратическое (стандартное ) отклонение дискретной случайной величины.
ВАРИАНТ 2.
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 13; 5; 7; 6; 9. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
15
12
8
-11
9
р
0,2
֍
֍
֍
0,3
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны числам 2 : 1: 2 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(6Х -1).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
4
х2
-5
2
р
0,1
0,3
0,2
0,4
-
-
Найдите х2, зная, что М(Х) = 2,3.
-
Найдите дисперсию и среднее квадратическое (стандартное ) отклонение дискретной случайной величины.
ВАРИАНТ 3.
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 4; 13; 15; 10; 8. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
9
-13
6
10
7
р
֍
0,05
֍
0,15
֍
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны числам 2 :3: 3 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(-3Х + 4).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
10
-6
х3
4
р
0,1
0,3
0,4
0,2
-
-
Найдите х3, зная, что М(Х) = 4.
-
Найдите дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины.
ВАРИАНТ 4.
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 9; 7; 11; 5; 8. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
-8
15
-4
12
6
р
֍
֍
0,25
֍
0,15
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны
числам 1:2: 3 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(10Х - 6).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
х1
10
-5
5
р
0,2
0,1
0,4
0,3
-
-
Найдите х1, зная, что М(Х) = 2,7.
-
Найдите дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Использует закон распределения дискретных случайных величин |
1 |
находит вероятности значений дискретной случайной величины; |
1 |
|
составляет закон распределения дискретной случайной величины; |
1 |
||
|
2А |
составляет выражение для вычисления долей неизвестных вероятностей; |
1 |
|
|
находит неизвестную переменную; |
1 |
||
|
находит доли неизвестных вероятностей; |
1 |
||
|
Использует свойства математического ожидания дискретной случайной величины |
2В |
использует формулу математического ожидания дискретной случайной величины; |
1 |
|
вычисляет математическое ожидание дискретной случайной величины; |
1 |
||
|
2С |
применяет свойства математического ожидания дискретной случайной величины; |
1 |
|
|
3А |
составляет выражение, для нахождения неизвестного значения случайной величины, используя формулу математического ожидания; |
1 |
|
|
находит неизвестное значение дискретной случайной величины; |
1 |
||
|
Вычисляет дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины |
3В |
использует формулу дисперсии дискретной случайной величины; |
1 |
|
вычисляет дисперсию дискретной случайной величины; |
1 |
||
|
использует формулу среднего квадратического (стандартного) отклонения дискретной случайной величины; |
1 |
||
|
вычисляет среднее квадратическое (стандартное) отклонение дискретной случайной величины. |
1 |
||
|
Общий балл |
14 баллов |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Случайные величины и их числовые характеристики».
ФИ обучающегося : ______________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Использует закон распределения дискретных случайных величин |
Затрудняется в составлении и использовании закона распределения дискретных случайных величин |
Допускает вычислительные ошибки при составлении / использовании закона распределения дискретных случайных величин |
Составляет и использует закон распределения дискретных случайных величин |
|
Использует свойства математического ожидания дискретной случайной величины |
Затрудняется в нахождении математического ожидания дискретной случайной величины |
Допускает вычислительные ошибки при нахождении математического ожидания дискретной случайной величины |
Находит математическое ожидание дискретной случайной величины |
|
Вычисляет дисперсию и стандартное отклонение случайной величины |
Затрудняется в вычислении дисперсии и стандартного отклонения дискретной случайной величины |
Допускает вычислительные ошибки при нахождении дисперсии / стандартного отклонения дискретной случайной величины |
Вычисляет дисперсию и стандартное отклонение дискретной случайной величины |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 1 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 7 заданий, включающих вопросы с множественным выбором ответов, с кратким и развернутым ответом.
В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде
численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла.
Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов.
Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол.заданий |
№ задания |
Тип задания |
Время выполн. |
балл |
Балл за раздел |
|
Функция, её свойства и график |
10.3.1.1 Знать определение и способы задания функции |
Знание и понимание |
1 |
1 |
КО |
2 |
1 |
10 |
|
10.3.1.2 Уметь выполнять преобразования графика функции (параллельный перенос, сжатие и растяжение) |
Применение |
1 |
2 |
РО |
7 |
2 |
||
|
10.3.1.5 Знать определение обратной функции и уметь находить функцию, обратную заданной и знать свойство расположения графиков взаимно обратных функций |
Применение |
1 |
3 |
РО |
7 |
4 |
||
|
10.3.1.6 Уметь распознавать сложную функцию f(g(x)) и составлять композицию функций |
Применение |
1 |
4 |
РО |
6 |
3 |
||
|
Тригонометрические функции |
10.1.3.2 Уметь строить графики тригонометрических функций с помощью преобразований |
Применение |
1 |
5 |
РО |
7 |
4 |
10 |
|
10.1.3.3 Знать определения арксинуса, арккосинуса, арктангенса, арккотангенса и уметь находить их значения |
Знание и понимание |
1 |
6 |
КО |
3 |
2 |
||
|
10.1.3.4 Находить значения выражений, содержащих обратные тригонометрические функции |
Применение |
1 |
7 |
РО |
7 |
4 |
||
|
итого |
|
|
|
|
|
|
40 |
20 |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
1 ВАРИАНТ
-
Из указанных функций выберите линейную:
-
2х+у-4=0
-
У=(х-2)2
-

-

-

2. Используя график функции у=х2, постройте график функции у=х2+2
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=5x-125, g(x)=x2. Решите уравнение f(g(x))=0
5. Постройте график функции y=sin x+1. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 1.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
1 |
1 |
|
|
2 |
Строит график функции у=х2 |
1 |
|
|
Строит график функции у=х2+2 |
1 |
|
|
|
3 |
(2х-5)у=4х-3 |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=5х2-125 |
1 |
|
|
5х2-125=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y=sin x |
1 |
|
|
Определяет перемещение графика функции y=sin x |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[0;2] |
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Всего: |
20 |
|
|
2 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
-
1. Из указанных функций выберите квадратичную:
-
2х+у-4=0
-
у=(х-2)2
-

-

-

2. Используя график функции у=х2, постройте график функции у=(х+3)2
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=х2, g(x)=2х-4. Решите уравнение f(g(x))=0
5. Постройте график функции y=cos x-2. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 2.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
2 |
|
|
|
2 |
Строит график функции у=х2 |
1 |
|
|
Строит график функции у=(х+3)2 |
|
|
|
|
3 |
y(x-4)=3x-2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=(2x-4)2 |
1 |
|
|
2x-4=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y=cosx |
1 |
|
|
Определяет перемещение графика функции y= cosx |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[-2;-1] |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
Всего: |
20 |
|
|
3 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
-
1. Из указанных функций выберите обратно-пропорциональную:
-
2х+у-4=0
-
У=(х-2)2
-

-

-

2. Используя график функции у=-х2, постройте график функции у=-х2+2
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=2х+3, g(x)=-6х+9. Решите уравнение f(g(x))=0
5. Постройте график функции y=sin x+1. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 3.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
5 |
|
|
|
2 |
Строит график функции у=-х2 |
1 |
|
|
Строит график функции у=-х2+2 |
|
|
|
|
3 |
y(2x-3)=4x+5 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=-12х+21 |
1 |
|
|
-12х+21=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y=sinx |
1 |
|
|
Определяет перемещение графика функции y=sinx |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[0;2] |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
Всего: |
20 |
|
|
4 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
-
1. Из указанных функций выберите степенную:
-
2х+у-4=0
-
У=(х-2)2
-

-

-

2. Используя график функции у=-х2, постройте график функции у=-х2-3
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=2х-5, g(x)=5х+7. Решите уравнение f(g(x))=0
5. Постройте график функции y=cos x+1. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 4.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
4 |
|
|
|
2 |
Строит график функции у=-х2 |
1 |
|
|
Строит график функции у=-х2-3 |
|
|
|
|
3 |
y(x-4)=3x-2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=10х+9 |
1 |
|
|
10х+9=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y= cos x |
1 |
|
|
Определяет перемещение графика функции y= cos x |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[0;2] |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
Всего: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 7 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла.
Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных
частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Тригонометрические уравнения и неравенства |
10.1.3.5 Уметь решать простейшие тригонометрические уравнения |
Применение |
1 |
5а |
КО |
5 |
2 |
10 |
|
10.1.3.7 Уметь решать тригонометрические уравнения, приводимые к квадратному уравнению |
Применение |
5b |
РО |
10 |
5 |
|||
|
10.1.3.9 Уметь решать простейшие тригонометрические неравенства |
Применение |
1 |
4 |
КО |
5 |
3 |
||
|
Вероятность |
10.2.1.2 Вычислять вероятность случайных событий, применяя свойства вероятностей * P(A ∙ B) = P(A) ∙ P(B); * P(A + B) = P(A) + P(B); * P(A +B) = P(A)+P(B)–P(A ∙ B) |
Применение |
3 |
1 |
КО |
2 |
1 |
10 |
|
2 |
КО |
3 |
2 |
|||||
|
3 |
КО |
5 |
2 |
|||||
|
Применение |
2 |
6 |
КО |
5 |
2 |
|||
|
7 |
РО |
5 |
3 |
|||||
|
ИТОГО: |
|
|
7 |
|
|
40 |
20 |
20 |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1 ВАРИАНТ
1. Вероятность того, что Асхат опоздает на работу равна 0,3. Какова вероятность того, что Асхат не опоздает на работу?
2. В
коробке лежат маленькие кубики разных цветов: белые и синие. Всего
21 кубик. Вероятность того, что случайным образом из коробки
достанут синий кубик равна  . Сколько белых
кубиков в коробке?
. Сколько белых
кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство: 3tg( x +
x +
 )
)
 .
.
5. a) Определите, имеют ли решения следующие тригонометрические уравнения:
1) cos x 3 2) cos x 1.
Поясните ответ и найдите решение, если оно существует.
b) Решите
уравнение 4sin2x+8sinx= 8 sin60o
, на отрезке
2;
sin60o
, на отрезке
2;
6. В двух коробках лежат ручки. В коробке А – 15 ручек: 6 красных, 7 синих и 2 зелёных.
В коробке В – 21 ручка: n синих и остальные красные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно,
что вероятность того, что Рамазан и Асель достанут обе синие ручки,
равна  Сколько синих ручек в коробке
В?
Сколько синих ручек в коробке
В?
7. Имеется девять карточек с числами
1
2
2
2
2
3
3
3
4
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
2 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1.
Вероятность того, что Артур опоздает на работу равна 0,1. Какова
вероятность того, что Артур не опоздает на работу? 2. В коробке
лежат маленькие кубики разных цветов: белые и чёрные. Всего 24
кубика. Вероятность того, что случайным образом из коробки достанут
белый кубик равна  . Сколько
чёрных кубиков в коробке?
. Сколько
чёрных кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство:  tg
(
tg
( x -
x -  ) >
1.
) >
1.
5. a) Определите, имеют ли решения, следующие тригонометрические уравнения:
1) sin x 3 2) cos x -1.
Поясните ответ и найдите решение, если оно существует.
b) Решите уравнение 4 cos2x + 4 cos x = 16 cos 60o , на отрезке ; 2
6. В двух коробках лежат ручки. В коробке А – 9 ручек: 2 красных, 6 синих и 1 зелёная.
В коробке В – 14 ручек: n синих и остальные зелёные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно,
что вероятность того, что Рамазан и Асель достанут обе синие ручки,
равна  Сколько синих ручек в коробке
В?
Сколько синих ручек в коробке
В?
7. Имеется восемь карточек с числами
1
2
2
3
3
3
3
4
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
3 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1.
Вероятность того, что Асхат опоздает на работу равна 0,16. Какова
вероятность того, что Асхат не опоздает на работу? 2. В коробке
лежат маленькие кубики разных цветов: белые и синие. Всего 27
кубик. Вероятность того, что случайным образом из коробки достанут
синий кубик равна  . Сколько белых
кубиков в коробке?
. Сколько белых
кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство:  tg
(
tg
( x -
x -  )
)
 .
.
5. a) Определите, имеют ли решения следующие тригонометрические уравнения:
1)
sin x  2)
sin x - 1.
2)
sin x - 1.
Поясните ответ и найдите решение, если оно существует.
b) Решите уравнение 2sin2x – 10 sinx= -8 sin 90o , на отрезке 2;
6. В двух коробках лежат ручки. В коробке А – 18 ручек: 7 красных, 8 синих и 3 зелёных.
В коробке В – 8 ручек: n зелёных и остальные красные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно,
что вероятность того, что Рамазан и Асель достанут обе зелёные
ручки, равна  Сколько зелёных
ручек в коробке В?
Сколько зелёных
ручек в коробке В?
7. Имеется одиннадцать карточек с числами
1
2
2
2
2
3
3
3
4
3
3
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
4 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1.
Вероятность того, что Артур опоздает на работу равна 0,25. Какова
вероятность того, что Артур не опоздает на работу? 2. В коробке
лежат маленькие кубики разных цветов: белые и чёрные. Всего 18
кубиков. Вероятность того, что случайным образом из коробки
достанут белый кубик равна  . Сколько
чёрных кубиков в коробке?
. Сколько
чёрных кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство:  tg
(
tg
( x -
x -  )>
)> .
.
5. a) Определите, имеют ли решения следующие тригонометрические уравнения:
1)
cos
x  2)
cos
x 0.
2)
cos
x 0.
Поясните ответ и найдите решение, если оно существует.
b) Решите уравнение 6 cos2x + 9 cos x = 12 cos 60o, на отрезке 2; 2
6. В двух коробках лежат ручки. В коробке А – 12 ручек: 5 красных, 4 синих и 3 зелёная.
В коробке В – 9 ручек: n красных и остальные зелёные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно, что вероятность того, что Рамазан и Асель достанут обе красные ручки,
равна  Сколько красных
ручек в коробке В?
Сколько красных
ручек в коробке В?
7. Имеется семь карточек с числами:
1
2
2
2
3
3
4
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 1 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,7 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не имеет решения, т.к. 31;1 |
1 |
|
|
2) имеет
решение и x 2 |
1 |
|
|
|
5b |
sin2 x + 2 sin x – 3 = 0 |
1 |
|
|
t2 2t 3 0 |
1 |
Использует метод замены переменной |
|
|
t1 3, t2 1 |
1 |
|
|
|
x = |
1 |
Принимать решения только в радианной мере |
|
|
x = - |
1 |
||
|
6 |
|
1 |
|
|
12 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 2 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,9 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не имеет решения, т.к. - 31;1 |
1 |
|
|
2) имеет
решение и x |
1 |
|
|
|
5b |
cos2 x + cos x – 2 = 0 |
1 |
|
|
t2 t 2 0 |
1 |
Использует метод замены переменной |
|
|
t1 2, t2 1 |
1 |
|
|
|
x = 0 |
1 |
Принимать решения только в радианной мере |
|
|
x = 2 |
1 |
||
|
6 |
|
1 |
|
|
6 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 3 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,84 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не
имеет решения, т.к. |
1 |
|
|
2) имеет
решение и x |
1 |
|
|
|
5b |
sin2 x - 5 sin x + 4 = 0 |
1 |
|
|
t2 - 5t + 4 0 |
1 |
Использует метод замены переменной |
|
|
t1 4, t2 1 |
1 |
|
|
|
x = |
1 |
Принимать решения только в радианной мере |
|
|
x = - |
1 |
||
|
6 |
|
1 |
|
|
2 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 4 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,75 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не
имеет решения, т.к.- |
1 |
|
|
2) имеет
решение и x |
1 |
|
|
|
5b |
2cos2 x + 3 cos x – 2 = 0 |
1 |
|
|
2t2 3t 2 0 |
1 |
Использует метод замены переменной |
|
|
t1
2, t2
|
1 |
|
|
|
x = |
1 |
Принимать решения только в радианной мере |
|
|
x = |
1 |
||
|
6 |
|
1 |
|
|
2 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов.
Характеристика заданий суммативного оценивания за 3 четверть
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Производная |
10.3.1.7 Знать определение предела функции в точке и на бесконечности |
Знание и понимание |
1 |
1 |
КО |
2 |
3 |
11 |
|
10.3.3.1 Решать прикладные задачи, опираясь на физический смысл производной |
Применение |
1 |
3 |
КО |
5 |
2 |
||
|
10.3.1.14 Знать определение сложной функции и находить её производную |
Применение |
1 |
4а |
РО |
|
2 |
||
|
10.3.1.12 Составлять уравнение касательной к графику функции в заданной точке |
Применение |
4b |
РО |
|
3 |
|||
|
10.3.1.11 Знать и применять правила дифференцирования |
Применение |
1 |
2a |
РО |
12 |
1 |
||
|
Применение производной |
10.3.1.17 Находить критические точки и точки экстремума функции |
Применение |
2b |
РО |
2 |
9 |
||
|
10.3.1.15 Знать и применять необходимое и достаточное условие возрастания (убывания) функции на интервале |
Применение |
2c |
КО |
2 |
||||
|
10.3.3.3 Решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции |
Навыки высокого порядка |
1 |
5 |
РО |
10 |
5 |
||
|
ИТОГО: |
|
|
5 |
|
|
40 |
20 |
20 |
ЗАДАНИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ
1 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = х3 -3х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 7t3 +6t2 +1, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 2 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке (2;1)
.
в точке (2;1)
.
5. Прямоугольный участок площадью 4900 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
2 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = 5х3 -15х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 12t3 +5t2 +11, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 4 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке
(1;2).
в точке
(1;2).
5. Прямоугольный участок площадью 8100 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
3 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = 7х3 -14х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 7t3 - t2 +2, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 3 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке
(1;3).
в точке
(1;3).
5. Прямоугольный участок площадью 14400 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
4 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = 2х3 -3х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 6t3 - 9 t2 +6, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 3 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке
(1;2).
в точке
(1;2).
5. Прямоугольный участок площадью 289 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 1 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: -2 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит
ответ: |
1 |
|
|
|
2а |
y ’ = 3х2 -6х |
1 |
|
|
2b |
3х2 - 6х=0 |
1 |
|
|
x=0, x= 2 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает: (0; 2) |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
108 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(2)= 2 |
1 |
|
|
y ’(2)=1 |
1 |
|
|
|
y=1 |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 70- точка минимума на интервале |
|
|
70м, 70м |
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 2 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: 1 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит
ответ: |
1 |
|
|
|
2а |
y ’ = 15х2 -30х |
1 |
|
|
2b |
15х2 - 30х=0 |
1 |
|
|
x=0, x= 2 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает: (0; 2) |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
616 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(1)= 4 |
1 |
|
|
y
’(1)=1 |
1 |
|
|
|
y=1 |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 81- точка минимума на интервале |
|
|
81м, 81м |
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 3 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: -20 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит ответ: -2 |
1 |
|
|
|
2а |
y ’ = 21х2 -28х |
1 |
|
|
2b |
21х2 - 28х=0 |
1 |
|
|
x=0,
x=1 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает:
(0; 1 |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
183 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(1)=3 |
1 |
|
|
y ’(1)=
|
1 |
|
|
|
y= |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 120- точка минимума на интервале |
|
|
120м, 120м |
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 4 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: -1 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит
ответ: |
1 |
|
|
|
2а |
y ’ = 6х2 -6х |
1 |
|
|
2b |
6х2 - 6х=0 |
1 |
|
|
x=0, x=1 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает: (0;1) |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
108 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(1)=5 |
1 |
|
|
y ’(1)= 3,4 |
1 |
|
|
|
y=3,4x+1,6 |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 60- точка минимума на интервале |
|
|
17м, 17м |
1 |
|
|
|
Итого: |
20 |
|
|
ЗАДАНИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть:
Продолжительность - 40 минут
Количество баллов - 20
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания:
Данные варианты состоят из 4 заданий, включающие вопросы с множественным выбором ответов, и требующие краткого и развернутого ответов.
В заданиях с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.
В заданиях, требующие развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Случайные величины и их числовые характерис-тики |
10.2.1.5 Знать определение дискретной и непрерывной случайной величины и уметь их различать |
Знание и понимание |
1 |
1 |
МВО |
3 |
2 |
20 |
|
10.2.1.6 Составлять таблицу закона распределения некоторых дискретных случайных величин |
Применение |
1 |
2 |
РО |
8 |
3 |
||
|
10.2.1.8 Вычислять математическое ожидание дискретной случайной величины |
Навыки высокого порядка |
1 |
3a |
РО |
8 |
4 |
||
|
10.2.1.9 Вычислять дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины |
Применение |
3b |
7 |
2 |
||||
|
3c |
2 |
2 |
||||||
|
10.2.1.10 Решать задачи с использованием числовых характеристик дискретных случайных величин |
Навыки высокого порядка |
1 |
4 |
РО |
12 |
7 |
||
|
ИТОГО: |
|
|
4 |
|
|
40 минут |
20 |
20 |
ЗАДАНИЯ
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
2 |
3 |
8 |
7 |
|
итого |
20 баллов |
|||
ВАРИАНТ 1.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) количество автомобилей, проехавших за 1 час через некоторый перекресток;
b) скорость течения реки;
c) количество тепловой энергии, потраченной на отопление города за 1 месяц ;
d) количество писем, поступивших в некоторое почтовое отделение за 1 неделю.
2. При организации денежной лотереи выпустили 400 билетов. Из них 60 билетов дают выигрыш 200 тенге, 50 билетов – 500 тенге, 20 билетов – 1000 тенге, 10 билетов – 5000 тенге и 1 билет – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
1 |
3 |
6 |
10 |
|
Р |
0,2 |
0,3 |
0,1 |
k |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до одного знака после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
3 |
4 |
5 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наименее вероятно, если известно, что М(2Х) = 7,6 и D(X) = 0,56 и р1 = р2?
ВАРИАНТ 2.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) температура воздуха, измеренная в течении суток;
b) количество клиентов страховой компании за некоторый месяц;
c) скорость движения велосипедиста за 1час движения;
d) количество подъездов многоэтажного дома.
2. При организации денежной лотереи выпустили 500 билетов. Из них 90 билетов дают выигрыш 100 тенге, 80 билетов – 500 тенге, 50 билетов – 1000 тенге, 15 билетов – 2000 тенге и 1 билет – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
4 |
3 |
5 |
6 |
|
Р |
k |
0,2 |
0,3 |
0,4 |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до двух знаков после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
4 |
5 |
6 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наиболее вероятно, если известно, что М(-3Х) = -15 и D(X) = 0,6 и р1 = р3?
ВАРИАНТ 3.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) количество очков, выпадающих на одной грани при бросании игрального кубика;
b) величина электрического напряжения в городской электросети;
c) количество выстрелов по мишени во время соревнований;
d) атмосферное давление, измеренное в течении суток.
2. При организации денежной лотереи выпустили 500 билетов. Из них 120 билетов дают выигрыш 200 тенге, 80 билетов – 500 тенге, 40 билетов – 1000 тенге, 20 билетов – 5000 тенге и 2 билета – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
5 |
3 |
4 |
9 |
|
Р |
0,2 |
k |
0,2 |
0,3 |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до одного знака после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
5 |
6 |
7 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наименее вероятно, если известно, что М(-2Х) = -11 и D(X) = 0,45 и р1 = 2р2?
ВАРИАНТ 4.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) продолжительность жизни человека;
b) количество людей, участвующих в конференции;
c) количество оценок «5», полученных за контрольную работу;
d) скорость спуска парашютиста.
2. При организации денежной лотереи выпустили 400 билетов. Из них 75 билетов дают выигрыш 100 тенге, 45 билетов – 200 тенге, 10 билетов – 1000 тенге, 2 билета – 5000 тенге и 1 билет – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
4 |
3 |
5 |
8 |
|
Р |
0,2 |
0,1 |
k |
0,4 |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до двух знаков после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
7 |
8 |
9 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наиболее вероятно, если известно, что М(4Х) = 30,4 и D(X) = 0,64 и р1 = 3р3?
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 1.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
a, d |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
400 – (60+50+20+10+1) = 259 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = р5 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
0,2+ 0,3 + 0,1 + k =1 |
1 |
|
|||||||||||||
|
k = 0,4 |
1 |
|
||||||||||||||
|
М(Х) = 1·0,2 + 3·0,3 + 6·0,1 + 10·0,4 |
1 |
|
||||||||||||||
|
М(Х) = 5,7 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 1·0,2 + 9·0,3 + 36·0,1 + 100·0,4 = 46,5 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 46,5 – 32,49 = 14,01 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(2Х) = 2(3·р1 + 4·р2 + 5·р3) = 7,6 |
1 |
|
|||||||||||||
|
М(Х) = 3·р1 + 4·р2 + 5·р3 = 3,8 |
1 |
|
||||||||||||||
|
D(Х) = 9·р1 + 16·р2 + 25·р3 - 3,82= 0,56 |
1 |
|
||||||||||||||
|
|
1 |
или |
||||||||||||||
|
р1 = 0,4 и р3 = 0,2 |
1 |
или р2 = 0,4 и р3 = 0,2 |
||||||||||||||
|
р2 =0,4 |
1 |
или р1 = 0,4 |
||||||||||||||
|
Наименьшая вероятность 5 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 2.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
b, d |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
500 – (90+80+50+15+1) = 264 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = р5 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
k + 0,2+ 0,3 + 0,4=1 |
1 |
|
|||||||||||||
|
k = 0,1 |
1 |
|
||||||||||||||
|
М(Х) = 4·0,1 + 3·0,2 + 5·0,3 + 6·0,4 |
1 |
|
||||||||||||||
|
М(Х) = 4,9 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 16·0,1 + 9·0,2 + 25·0,3 + 36·0,4 = 25,3 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 25,3 – 24,01 = 1,29 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(-3Х) = -3(4·р1 + 5р2 + 6р3) = -15 |
1 |
|
|||||||||||||
|
М(Х) = 4·р1 + 5·р2 + 6·р3 = 5 |
1 |
|
||||||||||||||
|
D(Х) = 16·р1 + 25·р2 + 36·р3 - 52 = 0,6 |
1 |
|
||||||||||||||
|
|
1 |
или |
||||||||||||||
|
р1 = 0,3 и р2 = 0,4 |
1 |
или р2 = 0,4 и р3 = 0,3 |
||||||||||||||
|
р3 =0,3 |
1 |
или р1 = 0,3 |
||||||||||||||
|
Наибольшая вероятность 5 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 3.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
a, c |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
500 – (120+80+40+20+2) = 238 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = р5 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
0,2+ k + 0,2 + 0,3 = 1 |
1 |
|
|||||||||||||
|
k = 0,3 |
1 |
|
||||||||||||||
|
М(Х) = 5·0,2 + 3·0,3 + 4·0,2 + 9·0,3 |
1 |
|
||||||||||||||
|
М(Х) = 5,4 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 25·0,2 + 9·0,3 + 16·0,2 + 81·0,3 = 35,2 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 35,2 – 29,16 = 6,04 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(-2Х) = -2(5·р1 + 6·р2 + 7·р3) = -11 |
1 |
|
|||||||||||||
|
М(Х) = 5·р1 + 6·р2 + 7·р3 = 5,5 |
1 |
|
||||||||||||||
|
D(Х) = 25·р1 + 36·р2 + 49·р3 - 5,52 = 0,45 |
1 |
|
||||||||||||||
|
|
1 |
|
||||||||||||||
|
р2 = 0,3 и р3 = 0,1 |
1 |
|
||||||||||||||
|
р1 =0,6 |
1 |
|
||||||||||||||
|
Наименьшая вероятность 7 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 4.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
b, c |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
400 – (75+45+10+2+1) = 267 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
0,2+ 0,1 + k + 0,4 =1 |
1 |
|
|||||||||||||
|
k = 0,3 |
1 |
|
||||||||||||||
|
М(Х) = 4·0,2 + 3·0,1 + 5·0,3 + 8·0,4 |
1 |
|
||||||||||||||
|
М(Х) = 5,8 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 16·0,2 + 9·0,1 + 25·0,3 + 64·0,4 = 37,2 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 37,2 – 33,64 = 3,56 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(4Х) = 4(7·р1 + 8·р2 + 9·р3) = 30,4 |
1 |
|
|||||||||||||
|
М(Х) = 7·р1 + 8·р2 + 9·р3 = 7,6 |
1 |
|
||||||||||||||
|
D(Х) = 49·р1 + 64·р2 + 81·р3 – 7,62 = 0,64 |
1 |
|
||||||||||||||
|
|
1 |
|
||||||||||||||
|
р3 = 0,2 и р2 = 0,2 |
1 |
|
||||||||||||||
|
р1 =0,6 |
1 |
|
||||||||||||||
|
Наибольшая вероятность 7 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
|
|
1 |
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Сборник работ для суммативного оценивания по алгебре 10 класс
Сборник работ для суммативного оценивания по алгебре 10 класс
|
2020 год |
В помощь учителю математики Сборник работ для суммативного оценивания по алгебре и началам анализа 10 класс общественно-гуманитарное направление |

|
|

|
ТВГ учителей математики |
В помощь учителю математики Сборник работ для суммативного оценивания по алгебре и началам анализа 10 класс общественно-гуманитарное направление |
Содержание
|
Введение |
|
|
Суммативное оценивание за раздел «Функция, ее свойства и график» |
|
|
Суммативное оценивание за раздел «Тригонометрические функции» |
|
|
Суммативное оценивание за раздел «Тригонометрические уравнения и неравенства» |
|
|
Суммативное оценивание за раздел «Вероятность» |
|
|
Суммативное оценивание за раздел «Производная» |
|
|
Суммативное оценивание за раздел «Применение производной» |
|
|
Суммативное оценивание за раздел «Случайные величины и их числовые характеристики» |
|
|
Суммативное оценивание за 1 четверть |
|
|
Суммативное оценивание за 2 четверть |
|
|
Суммативное оценивание за 3 четверть |
|
|
Суммативное оценивание за 4 четверть |
|
Творческая группа авторов-составителей:
Руководитель группы – Середкин В.П. учитель математики, педагог-мастер, Павлодарская область, Павлодарский район, КГУ Чернорецкая СОШ № 1.
Модератор группы – Айтмуханова Ж.А., учитель математики, педагог-эксперт, Акмолинская область, город Кокшетау, КГУ СОШ № 4.
Состав группы - Демец З.Л. - учитель математики, педагог-исследователь, Карагандинская область, Осакаровский район, КГУ СОШ № 25
Цыганов А.Ю. – учитель математики, высшая категория, Акмолинская область, город Кокшетау, КГУ СОШ № 4
Рецензент -
ВВЕДЕНИЕ
Данный сборник составлен в помощь учителю при планировании, организации и проведении суммативного оценивания за раздел и четверть по предмету алгебра общественно-гуманитарного направления для учащихся 10 классов.
Сборник работ по суммативному оцениванию составлен на основе ГОСО, типовой учебной программы и учебного плана. Данные работы позволяют учителю определить уровень достижения учащимися запланированных целей обучения.
Все работы сборника разработаны учителями-практиками на основе своих наблюдений и опыта работы в рамках обновленного содержания образования
В курсе математики 5 класса в соответствии с учебной программой и долгосрочным планом изучаются следующие разделы – «Натуральные числа и нуль», «Делимость натуральных чисел», «Обыкновенные дроби», «Действия над обыкновенными дробями», «Текстовые задачи», «Десятичные дроби и действия над ними», «Множества», «Проценты», «Углы. Многоугольники», «Диаграммы. Развертки пространственных фигур». Каждая из представленных работ для проведения суммативного оценивания за раздел и суммативного оценивание за четверть, состоит из четырех вариантов. Количество вариантов, используемое при проведение суммативного оценивания каждый учитель определяет самостоятельно.
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК»
Тема Свойства функции. Понятие обратой и сложной функции
Цели обучения
10.3.1.4 уметь описывать по заданному графику функции ее свойства:
1) область определения функции;
2)область значений функции;
3) нули функции;
4)промежутки монотонности функции;
7) наибольшее и наименьшее значение функции;
11) экстремумы функции;
10.3.1.5 знать определения обратной функции и уметь находить функцию, обратную заданной и знать свойство расположения графиков взаимно обратных функций
10.3.1.6
уметь
распознавать сложную функцию  и составлять композицию функции;
и составлять композицию функции;
10.3.1.1 - знать определение и способы задания функции;
Критерий оценивания Обучающийся:
-
Исследует свойства функции по ее графику;
-
Применяет алгоритм нахождения обратной функции;
-
Применяет алгоритм нахождения сложной функции;
-
Вычисляет значение функции
Уровень мыслительных навыков Применение
Время выполнения 25 минут
ЗАДАНИЯ
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
5 |
2 |
2 |
3 |
|
итого |
12 баллов |
|||
1 ВАРИАНТ
-
Дан график функции

a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
.
Вычислите: 
-
ВАРИАНТ
-
Дан график функции

a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
.
Вычислите: 
-
ВАРИАНТ
-
Дан график функции

a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
.
Вычислите: 
-
ВАРИАНТ
-
Дан график функции

a) Запишите область определения функции.
b) Найдите множество значений функции.
c) промежутки монотонности функции;
d) промежутки знакопостоянства функции;
e) наибольшее и наименьшее значения функции;
-
Найдите функцию обратную данной
 .
Решите
уравнение
.
Решите
уравнение 

-
Составьте все возможные сложные функции, если


-
Даны функции f(x)=
 .
Вычислите:
.
Вычислите: 
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Исследует свойства функции по ее графику; |
1 |
Определяет область определения функции; |
1 |
|
Определяет множество значений функции; |
1 |
||
|
Определяет промежутки монотонности функции; |
1 |
||
|
Определяет промежутки знакопостоянства функции |
1 |
||
|
Определяет наибольшее и наименьшее значения функции; |
1 |
||
|
Применяет алгоритм нахождения обратной функции; |
2 |
Определяет обратную функцию; |
1 |
|
Находит
корень уравнения |
1 |
||
|
Применяет алгоритм нахождения сложной функции; |
3 |
Составляет
сложную функцию |
1 |
|
Составляет
сложную функцию |
1 |
||
|
Вычисляет значение функции |
4 |
Вычисляет значение первой функции |
1 |
|
Вычисляет значение второй функции |
1 |
||
|
Вычисляет значение выражения |
1 |
||
|
И того: |
12 |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания
за раздел «Функция, ее свойства и график»
ФИ обучающегося :_____________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
|||
|
Низкий |
Средний |
Высокий |
||
|
Исследует свойства функции по ее графику |
Затрудняется в определении свойств функции по ее графику |
Допускает ошибки при определении области определения / промежутков знакопостоянства / максимума / минимума / четности функции |
Oпределяет свойства функции по ее графику |
|
|
Применяет алгоритм нахождения обратной функции |
Затрудняется в использовании алгоритма нахождения обратной функции |
Допускает ошибки при нахождения обратной функции |
Применяет алгоритм и находит обратную функцию |
|
|
Применяет алгоритм нахождения значения сложной функции |
|
Затрудняется нахождения значения сложной функции |
Допускает ошибки в преобразованиях для нахождения значения сложной функции |
Находит значение сложной функции |
|
Вычисляет значение функции |
|
Затрудняется в вычислении значений функций |
Допускает ошибки в вычислении значений функций |
Вычисляет значение функции |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ»
Тема: Тригонометрические функции, их свойства и графики. Арксинус, арккосинус, арктангенс, арккотангенс.
Цели обучения 10.1.3.1 - знать определения, свойства тригонометрических функций и уметь строить их графики;
10.1.3.2 - уметь строить графики тригонометрических функций с помощью преобразований;
10.1.3.4 - находить значения выражений, содержащих обратные тригонометрические функции.
Критерий оценивания Обучающийся:
-
Применяет свойства тригонометрических функций
-
Строит графики тригонометрических функций с помощью преобразований
-
Находит значения выражений, содержащих обратные тригонометрические функции.
Уровень мыслительных навыков Применение
Время выполнения 25 минут
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
8 |
3 |
4 |
|
итого |
15 баллов |
||
1 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=соs x |
y=tg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=sin(x+

-
Вычислите значение выражения:

2 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=sin x |
y=ctg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=cos(x+

-
Вычислите значение выражения:

3 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=cos x |
y=ctg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=cos(x+
 [3
балла]
[3
балла] -
Вычислите значение выражения:

4 ВАРИАНТ
-
Определите свойства функций:
|
Свойства/функция |
y=sin x |
y=tg x |
|
Область определения функции |
|
|
|
Множество значений функции |
|
|
|
Четность/нечетность |
|
|
|
Наименьший положительный период |
|
|
-
Постройте график функции y=sin3x [3 балла]
-
Вычислите значение выражения:

|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Использует свойства тригонометрических функций |
1 |
находит область определения тригонометрической функции cos x \ tg x (sin x\ ctg x); |
2 |
|
находит область значений тригонометрической функции cos x \ tg x (sin x\ ctg x); ; |
2 |
||
|
Определяет четность (нечетность) тригонометрической функции cos x \ tg x (sin x\ ctg x); |
2 |
||
|
определяет периодичность тригонометрической функции cos x \ tg x (sin x\ ctg x); |
2 |
||
|
Строит график тригонометрических функций |
2 |
Строит график функции у= sin x |
1 |
|
Применяет преобразование графика функции у= sin x |
1 |
||
|
Строит
график функции
y=sin(x+ |
1 |
||
|
Находит значения выражений, содержащих обратные тригонометрические функции. |
3 |
Вычисляет первое значение |
1 |
|
Вычисляет второе значение |
1 |
||
|
Вычисляет третье значение |
1 |
||
|
Вычисляет значение выражения |
1 |
||
|
Всего баллов |
15 |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания
за раздел «Тригонометрические функции»
ФИ обучающегося : _____________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Применяет свойства тригонометрических функций |
Затрудняется в использовании свойств тригонометрических функции |
Допускает ошибки при определении четности/ нечетности, использовании монотонности/ нахождении области определения/ периода/ максимального/ минимального значения тригонометрических функций |
Использует свойства тригонометрических функций |
|
Строит график тригонометрических функций |
Затрудняется в построении графиков тригонометрических функций |
Допускает погрешности в построении графиков синуса/ косинуса |
Выполняет построение графиков тригонометрических функций |
|
Находит значения выражений, содержащих обратные тригонометрические функции. |
Затрудняется в вычислении обратных тригонометрических функций |
Допускает ошибки в вычислении обратных тригонометрических функций |
Вычисляет значение обратных тригонометрических функций |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА».
|
Тема |
Простейшие тригонометрические уравнения. Методы решения тригонометрических уравнений. Решение простейших тригонометрических неравенств. |
|
Цели обучения |
10.1.3.5 Уметь решать простейшие тригонометрические уравнения. 10.1.3.8 Уметь решать однородные тригонометрические уравнения. 10.1.3.6 Уметь решать тригонометрические уравнения методом разложения на множители. 10.1.3.9 Уметь решать простейшие тригонометрические неравенства. |
|
Критерии оценивания |
Обучающийся: Находит решение простейших тригонометрических уравнений. Решает однородные тригонометрические уравнения. Использует разложение на множители для решения тригонометрических уравнений. Решает простейшие тригонометрические неравенства. |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
25 мин |
ЗАДАНИЯ.
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
5 |
5 |
3 |
3 |
|
итого |
16 баллов |
|||
ВАРИАНТ 1.
-
Решите уравнение:
-
2sinx =
 ;
; -
ctgx + 3 = 0.
-
Решите уравнение: 2cos2x +
 sin2x – 3sin2x = 0.
sin2x – 3sin2x = 0. -
Решите уравнение: tg2x - 4 tgx = 0.
-
Решите неравенство: 3 cosx < 1,5.
ВАРИАНТ 2.
-
Решите уравнение:
-
– cosx =
 ;
; -
tgx - 12 = 3.
-
Решите уравнение: 3sin2x –sinxcosx -2cos2x = 0.
-
Решите уравнение: 2sin2x + sinx = 0.
-
Решите неравенство: 5ctg x ≤ - 2,5.
ВАРИАНТ 3.
-
Решите уравнение:
-
2sinx =
 ;
; -
21 + ctgx = 0.
-
Решите уравнение: sin2x – 2,5sin2x + 6cos2x = 0.
-
Решите уравнение: 2cos2x -
 cosx = 0.
cosx = 0. -
Решите неравенство: 3tgx ≥
 .
.
ВАРИАНТ 4.
-
Решите уравнение:
-
– 2cosx =
 ;
; -
tgx + 14 = 4.
-
Решите уравнение: - 5cos2x – 4 sinxcosx + sin2x = 0.
-
Решите уравнение: 2ctg2x + 3ctgx = 0.
-
Решите неравенство: 2sinx >
 .
.
Вариант 1.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию sinx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего синус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию ctgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего котангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу синуса двойного аргумента; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители ; |
1 |
|
использует формулы нахождения корней для тангенса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции cosx или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Вариант 2.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию cosx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего косинус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию tgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего тангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу основного тригонометрического тождества; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители; |
1 |
|
использует формулы нахождения корней для синуса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции ctg x или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Вариант 3.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию sinx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего синус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию ctgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего котангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу синуса двойного аргумента; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители; |
1 |
|
использует формулы нахождения корней для косинуса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции tg x или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Вариант 4.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит решение простейших тригонометрических уравнений |
1A |
выражает функцию cosx; |
1 |
|
применяет формулу нахождения корней уравнения, содержащего косинус; |
1 |
||
|
находит решения уравнения. |
1 |
||
|
1B |
выражает функцию tgx; |
1 |
|
|
применяет формулу нахождения корней уравнения, содержащего тангенс. |
1 |
||
|
Решает однородные тригонометрические уравнения |
2 |
применяет формулу основного тригонометрического тождества; |
1 |
|
проверяет, что ???2? ≠ 0 или sin2? ≠ 0 ; |
1 |
||
|
делит обе части уравнения на ???2? или sin2? ; |
1 |
||
|
решает полученное квадратное уравнение относительно tgx или ctgx; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Использует разложение на множители для решения тригонометрических уравнений |
3 |
раскладывает левую часть уравнения на множители; |
1 |
|
использует формулы нахождения корней для котангенса; |
1 |
||
|
находит решение тригонометрического уравнения. |
1 |
||
|
Решает простейшие тригонометрические неравенства |
4 |
приводит тригонометрическое неравенство к простейшему виду |
1 |
|
применяет график функции sinx или единичную окружность; |
1 |
||
|
находит решение неравенства. |
1 |
||
|
Итого |
16 |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Тригонометрические уравнения и неравенства».
ФИ обучающегося : ______________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Находит решение простейших тригонометрических уравнений |
Затрудняется в нахождении решения простейших тригонометрических уравнений |
Допускает ошибки при решении простейших тригонометрических уравнений, содержащих синус / косинус / тангенс / котангенс |
Решает простейшие тригонометрические уравнения |
|
Решает однородные тригонометрические уравнения |
Затрудняется в решении однородных тригонометрических уравнений |
Выбирает метод решения однородного тригонометрического уравнения, допускает ошибки при выполнении преобразований / решении эквивалентного уравнения |
Решает однородные тригонометрические уравнения |
|
Использует разложение на множители для решения тригонометрических уравнений |
Затрудняется в использовании разложения на множители для решения тригонометрических уравнений |
Использует разложение на множители, допускает ошибки при выполнении преобразований / нахождении решения на заданном промежутке |
Использует разложение на множители для решения тригонометрических уравнений |
|
Решает простейшие тригонометрические неравенства |
Затрудняется в нахождении решения простейших тригонометрических неравенств |
Допускает ошибки при решении простейших тригонометрических неравенств, содержащих синус / косинус / тангенс / котангенс |
Решает простейшие тригонометрические неравенства |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ВЕРОЯТНОСТЬ»
|
Тема |
Вероятность события и её свойства. Правила сложения и умножения вероятностей |
|
Цель обучения |
10.2.1.1 - знать понятие случайного события, виды случайных событий и приводить их примеры; 10.2.1.2 - вычислять вероятность случайных событий, применяя свойства вероятностей; 10.2.1.3 - понимать и применять правила сложения и умножения вероятностей * P(A ∙ B) = P(A) ∙ P(B); * P(A + B) = P(A) + P(B); * P(A +B) = P(A)+P(B)–P(A ∙ B); |
|
Критерии оценивания |
Обучающийся: Применяет понятие случайного события, виды случайных событий и приводит их примеры Применяет свойства вероятностей Применяет правила сложения и умножения вероятностей при решении зада |
|
Уровень мыслительных навыков |
Применение |
|
Время для выполнения |
25 минут |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
2 |
5 |
4 |
|
итого |
11 баллов |
||
ВАРИАНТ 1.
-
Установите соответствие:
-
Событие
Вид события
-
«На березе растут яблоки»
1. Равновозможное
-
«При бросании игральной кости выпала цифра 6»
2. Достоверное
-
«За летом наступает осень»
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо..
Б) На тарелке лежат пирожки: 7 с картошкой, 9 с капустой и 4 с вареньем. Сауле наугад выбирает один пирожок. Найдите вероятность того, что он окажется с капустой.
-
Вероятность попадания в цель одним стрелком равна 0,7. Вероятность попадания в цель другим стрелком равна 0,9. Найти вероятность попадания в цель хотя бы одним стрелком.
ВАРИАНТ 2.
-
Установите соответствие:
-
Событие
Вид события
1. После ночи всегда наступает день
1. Равновозможное
2. Новый год отмечают зимой
2. Достоверное
3. В Казахстане всегда лето
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8°C равна 0,87. Найдите вероятность того, что в случайный момент времени у здорового человека температура тела окажется 36,8°C или выше.
Б) В урне 9 красных, 6 жёлтых и 5 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
3. Рабочий обслуживает три станка. Вероятность того, что в течение смены первый станок потребует настройки, равна 0,3, второй – 0,75, третий – 0,4. Найти вероятность того, что в течение смены все станки потребуют настройки.
ВАРИАНТ 3.
-
Установите соответствие:
-
Событие
Вид события
1. Зимой холодно
1. Равновозможное
2. Летом отмечают Наурыз
2. Достоверное
3. В игральном кубике выпало число 5
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) В магазине стоят два платежных автомата. Оба могут быть неисправны с вероятностью 0,0025. Найдите вероятность того, что хотя бы один автомат исправен.
Б) В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
3. Экзаменационный билет состоит из трех вопросов. Вероятность того, что студент ответит на первый вопрос 0,7; на второй – 0,9; на третий – 0,6. Найти вероятность того, что студент, выбрав билет ответит на все вопросы.
ВАРИАНТ 4.
-
Установите соответствие:
-
Событие
Вид события
1. 5+5=11
1. Равновозможное
2. На сосне растут бананы
2. Достоверное
3. Зимой падает снег
-
Невозможное
-
Случайное
-
1________2_____________3______________
-
А) В среднем из 300 шариковых ручек 9 не пишут. Найдите вероятность того, что наугад взятая ручка будет писать.
Б) На семинар приехали 5 ученых из Португалии, 3 из Финляндии и 2 из Болгарии. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что седьмым окажется доклад ученого из Финляндии.
3. Шахматисту в турнире предстоит сыграть с двумя соперниками, вероятность выигрыша у которых равна 0,6 и 0,8 соответственно. Определите вероятность выигрыша хотя бы у одного из них.
|
Критерий оценивания. |
№ задания. |
Дескриптор |
Балл. |
|
Обучающийся. |
|||
|
Применяет понятие случайного события, виды случайных событий и приводит их примеры |
1 |
Находит одно соответствия |
1 |
|
находит все соответствия |
1 |
||
|
Применяет свойства вероятностей
|
2а |
Применяет понятие противоположного события |
1 |
|
Вычисляет вероятность противоположного события. |
1 |
||
|
2б |
находит число всевозможных исходов; |
1 |
|
|
определяет число благоприятствующих исходов по условию; |
1 |
||
|
находит вероятность по формуле. |
1 |
||
|
Применяет правила сложения и умножения вероятностей при решении задач |
3 |
Находит вероятность первого события |
1 |
|
Находит вероятность второго события |
1 |
||
|
Применяет правила сложения и умножения вероятностей |
1 |
||
|
Находит вероятность попадания в цель хотя бы одним стрелком |
1 |
||
|
Итого: |
11 баллов |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Вероятность»
ФИ обучающегося : __________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Применяет понятие случайного события, виды случайных событий и приводит их примеры |
Затрудняется в понятие случайного события, виды случайных событий и приводит их примеры |
Допускает ошибки понятия случайного события, виды случайных событий и приводит их примеры |
Использует понятие случайного события, виды случайных событий и приводит их примеры |
|
Применяет свойства вероятностей |
Затрудняется в применении свойств вероятностей |
Допускает ошибки при применении свойств вероятностей |
Применяет свойства вероятностей |
|
Применяет правила сложения и умножения вероятностей при решении задач |
Затрудняется в применении правил сложения и умножения вероятностей при решении задач |
Допускает ошибки в применении правил сложения и умножения вероятностей при решении задач |
Применяет правила сложения и умножения вероятностей при решении задач |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПРОИЗВОДНАЯ»
|
Тема |
Предел функции в точке и на бесконечности. Правила нахождения производных. Физический и геометрический смысл производной. Уравнение касательной к графику функции. Производная сложной функции. Производные тригонометрических функц |
|
Цель обучения |
10.3.1.7 Знать определение предела функции в точке и на бесконечности 10.3.1.10 Находить производные постоянной функции и степенной функции 10.3.1.11 Знать и применять правила дифференцирования 10.3.3.1 Решать прикладные задачи, опираясь на физический смысл производной 10.3.1.12 Составлять уравнение касательной к графику функции в заданной точке 10.3.1.14 Знать определение сложной функции и находить её производную 10.3.1.13 Находить производные тригонометрических функций |
|
Критерии оценивания |
Обучающийся: Вычисляет предел функции Находит производную степенной функции Решает задачи, используя физический смысл производной Находит производную тригонометрической функции Находит производную сложной функции Составляет уравнение касательной |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время для выполнения |
20 минут |
ЗАДАНИЯ
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
4 |
2 |
4 |
7 |
|
итого |
17 баллов |
|||
1 ВАРИАНТ
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = 3 5
5 -4x
-6
-4x
-6
3.
Материальная точка движется прямолинейно по закону s(t) 19t
3t2 t3 , где s(t) – путь в метрах,
t – время в секундах. Найдите мгновенную скорость  (t) и ускорение g(t) в момент времени t =
5 с.
(t) и ускорение g(t) в момент времени t =
5 с.
4. Дана функция ? = - 3???2?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
2 ВАРИАНТ
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = -4 -6
-6 +2x
+ 9
+2x
+ 9
3.
Материальная точка движется прямолинейно по закону s(t) t3
+4t2 -10t , где s(t) – путь в метрах, t – время в
секундах. Найдите мгновенную скорость  (t) и ускорение g(t) в момент времени t =
4 с.
(t) и ускорение g(t) в момент времени t =
4 с.
4. Дана функция ? = - 3?in3?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
3 ВАРИАНТ
Задания
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = - 10
10 -9x
+8
-9x
+8
3.
Материальная точка движется прямолинейно по закону s(t) 12t
5t2 2t3 , где s(t) – путь в метрах,
t – время в секундах. Найдите мгновенную скорость  (t) и ускорение g(t) в момент времени t =
2 с.
(t) и ускорение g(t) в момент времени t =
2 с.
4. Дана функция ? = -4???4?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
4 ВАРИАНТ
Задания
1.
Вычислите предел функции: a) ;
b)
;
b) 
2.
Найдите производную
функции: fx) = 5 1
1 -12x -12
-12x -12
3.
Материальная точка движется прямолинейно по закону s(t) 10t3 -8t2 -8t, где
s(t) – путь в метрах, t – время в секундах. Найдите мгновенную
скорость  (t) и
ускорение g(t)
в момент времени t = 3 с.
(t) и
ускорение g(t)
в момент времени t = 3 с.
4. Дана функция ? = 5?in5?.
a) Найдите производную функции.
b)
Составьте уравнение касательной в точке ? =  .
.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Вычисляет предел функции |
1a |
выполняет преобразования; |
1 |
|
находит значение предела в точке; |
1 |
||
|
1b |
делит числитель и знаменатель на переменную в старшей степени; |
1 |
|
|
находит предел функции на бесконечности; |
1 |
||
|
Находит производную степенной функции |
2 |
находит производную степени с отрицательным показателем; |
1 |
|
находит производную степени с рациональным показателем; |
1 |
||
|
Решает задачи, используя физический смысл производной |
3 |
находит производную функции; |
1 |
|
вычисляет, мгновенную скорость в момент времени t; |
1 |
||
|
находит производную от скорости |
1 |
||
|
Вычисляет ускорение в момент времени t; |
1 |
||
|
Находит производную тригонометрической функции. Находит производную сложной функции |
4a |
использует формулу производную сложной функции; |
1 |
|
находит производную косинуса (синуса); |
1 |
||
|
находит производную сложной функции; |
1 |
||
|
Составляет уравнение касательной |
4b |
находит значение функции в точке; |
1 |
|
находит значение производной в точке; |
1 |
||
|
использует формулу уравнения касательной; |
1 |
||
|
записывает уравнение касательной. |
1 |
||
|
Итого: |
17 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «ПРОИЗВОДНАЯ»
ФИ обучающегося: _________________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Вычисляет предел функции |
Затрудняется в вычислении предела функции в точке, на бесконечности |
Допускает вычислительные ошибки при нахождении предела функции в точке / на бесконечности |
Вычисляет предел функции в точке, на бесконечности |
|
Находит производную степенной функции |
Затрудняется в нахождении производной степенной функции. |
Допускает ошибки при нахождении производной функции с отрицательным / рациональным показателем |
Находит производную степенной функции. |
|
Решает задачи, используя физический смысл производной |
Затрудняется в применении физического смысла производной при решении задач |
Допускает ошибки в применении физического смысла производной/ вычислительные ошибки при решении задач |
Применяет физический смысл производной при решении задач |
|
Находит производную тригонометрической функции. Находит производную сложной функции |
Затрудняется в нахождении производной тригонометрических функций, сложной функции. |
Допускает ошибки при нахождении производной тригонометрических функций / преобразованиях при нахождении производной сложной функции. |
Находит производную тригонометрических функций и производную сложной функции |
|
Составляет уравнение касательной |
Затрудняется в составлении уравнения касательной |
Допускает ошибки в преобразованиях / вычислениях при составлении уравнения касательной |
Составляет уравнение касательной |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
|
Тема |
Признаки возрастания и убывания функции. Критические точки и точки экстремума. Исследование функции с помощью производной и построение её графика. Наибольшее и наименьшее значения функции на отрезке |
|
Цель обучения |
10.3.1.17 Находить критические точки и точки экстремума функции 10.3.1.15 Знать и применять необходимое и достаточное условие возрастания (убывания) функции на интервале 10.3.1.18 Исследовать свойства функции с помощью производной и строить её график 10.3.1.19 Находить наибольшее и наименьшее значения функции на отрезке 10.3.3.3 Решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции |
|
Критерии оценивания |
Обучающийся: Находит критические точки функции Использует условие возрастания (убывания) функции и находит промежутки монотонности Строит график функции, используя результаты исследования функции Решает задачи на нахождение наибольшего (наименьшего) значения функции |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время для выполнения |
25 минут |
ЗАДАНИЯ
|
Разбаловка заданий работы |
||
|
№ задания |
1 |
2 |
|
Количество баллов |
11 |
6 |
|
итого |
17 баллов |
|
1 ВАРИАНТ
1. Дана
функция f(x) =  х3 – 4х2 + 15х - 7 .
х3 – 4х2 + 15х - 7 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
=  х3 – 4х2 + 15х – 7 при х0 = 1
х3 – 4х2 + 15х – 7 при х0 = 1
d) Для функции f(x) =  х3 – 4х2 + 15х - 7
х3 – 4х2 + 15х - 7
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 80 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
2 ВАРИАНТ
1. Дана
функция f(x) =  х3 –
х3 –  х2 - 5х + 17 .
х2 - 5х + 17 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
=  х3 –
х3 –  х2 - 5х + 17, при х0 = 3
х2 - 5х + 17, при х0 = 3
d) Для функции f(x) =  х3 –
х3 –  х2 - 5х + 17
х2 - 5х + 17
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 96 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
3 ВАРИАНТ
1. Дана
функция f(x) =6
+  х2 –х3 .
х2 –х3 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
= 6 +
 х2 –х3 , при х0 = 0,5
х2 –х3 , при х0 = 0,5
d) Для функции f(x) = 6 +  х2 –х3
х2 –х3
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 102 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
4 ВАРИАНТ
1. Дана
функция f(x) = 4
-  х2 –3х5 .
х2 –3х5 .
a) Найдите критические точки функции.
b)Определите промежутки монотонности.
с) Запишите уравнение касательной функции f(x)
= 4 -
 х2 –3х5 , при х0 = - 0,5
х2 –3х5 , при х0 = - 0,5
d) Для функции f(x) = 4 -  х2 –3х5
х2 –3х5
Найдите область определения и используя результаты пунктов а) и d), постройте схематически график функции.
2. Фермер хочет оградить прямоугольный участок по одну сторону реки, таким образом, что река будет огораживать одну из сторон загона. Общая длина имеющегося штакетника составляет 88 метров. Пусть y метров длина и x метров ширина этого прямоугольного участка соответственно, а S – его площадь.
a) Выразите y через x.
b) Найдите выражение для S через x, указав ограничения для x.
c) При каких размерах площадь участка будет максимальной?
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся Находит критические точки функции |
1а |
Использует правило дифференцирования степенной функции |
1 |
|
Находит производную функции |
1 |
||
|
решает уравнение; |
1 |
||
|
находит критические точки; |
1 |
||
|
Использует условие возрастания (убывания) функции и находит промежутки монотонности |
1b |
определяет знаки производной; |
1 |
|
записывает промежутки монотонности; |
1 |
||
|
Строит график функции, используя результаты исследования функции |
1c |
Находит значение функции в данной точке |
1 |
|
Находит значение производной функции в данной точке |
1 |
||
|
Составляет уравнение касательной в данной точке |
1 |
||
|
1d |
Находит область определения функции |
1 |
|
|
строит эскиз графика функции |
1 |
||
|
Решает задачу на нахождение наибольшего (наименьшего) значения функции |
2 |
выражает одну переменную через другую, используя периметр фигуры |
1 |
|
составляет функцию для нахождения площади |
1 |
||
|
находит производную функции |
1 |
||
|
находит экстремумы функции |
1 |
||
|
находит максимальное значение, учитывая ограничения |
1 |
||
|
находит необходимые размеры |
1 |
||
|
Итого: |
17 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
ФИ обучающегося :_______________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
|||
|
Низкий |
Средний |
Высокий |
||
|
Находит критические точки функции
|
Затрудняется в нахождении критических точек функции |
Допускает ошибки при нахождении критических точек функции |
Находит критические точки функции |
|
|
Использует условие возрастания (убывания) функции и находит промежутки монотонности |
|
Затрудняется в использовании условия возрастания (убывания) функции и нахождения промежутков монотонности |
Допускает ошибки в использовании условия возрастания (убывания) функции и нахождения промежутков монотонности |
Использует условие возрастания (убывания) функции и находит промежутки монотонности |
|
Строит график функции, используя результаты исследования функции |
|
Затрудняется в построении графика функции, используя результаты исследования функции |
Допускает погрешности в построении графика функции, используя результаты исследования функции |
Выполняет построение в построении графика функции, используя результаты исследования функции |
|
Решает задачу на нахождение наибольшего (наименьшего) значения функции |
|
Затрудняется в решении задач на вычисление наибольшего (наименьшего) значения функции |
Допускает ошибки в решении задач на вычисление наибольшего (наименьшего) значения функции |
Решает задачу на нахождение наибольшего(наименьшего) значения функции |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ»».
|
Тема |
Дискретные и непрерывные случайные величины Числовые характеристики дискретных случайных величин. |
|
Цели обучения |
10.2.1.6 Составлять таблицу закона распределения некоторых дискретных случайных величин. 10.2.1.8 Вычислять математическое ожидание дискретной случайной величины. 10.2.1.9 Вычислять дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины. |
|
Критерии оценивания |
Обучающийся: Использует закон распределения дискретных случайных величин. Использует свойства математического ожидания дискретной случайной величины. Вычисляет дисперсию и стандартное отклонение дискретной случайной величины. |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
25 мин |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
2 |
6 |
6 |
|
итого |
14 баллов |
||
ВАРИАНТ 1
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 9; 8; 10; 12; 11. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
12
10
-5
11
6
р
֍
0,3
֍
֍
0,1
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны числам 1 : 3 : 2 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(-4Х+2).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
5
8
-5
х4
р
0,2
0,3
0,4
0,1
-
-
Найдите х4, зная, что М(Х) = 2.
-
Найдите дисперсию и среднее квадратическое (стандартное ) отклонение дискретной случайной величины.
ВАРИАНТ 2.
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 13; 5; 7; 6; 9. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
15
12
8
-11
9
р
0,2
֍
֍
֍
0,3
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны числам 2 : 1: 2 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(6Х -1).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
4
х2
-5
2
р
0,1
0,3
0,2
0,4
-
-
Найдите х2, зная, что М(Х) = 2,3.
-
Найдите дисперсию и среднее квадратическое (стандартное ) отклонение дискретной случайной величины.
ВАРИАНТ 3.
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 4; 13; 15; 10; 8. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
9
-13
6
10
7
р
֍
0,05
֍
0,15
֍
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны числам 2 :3: 3 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(-3Х + 4).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
10
-6
х3
4
р
0,1
0,3
0,4
0,2
-
-
Найдите х3, зная, что М(Х) = 4.
-
Найдите дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины.
ВАРИАНТ 4.
-
Дискретная случайная величина Х в результате проведения опытов принимает следующие значения: 9; 7; 11; 5; 8. Составьте закон распределения этой случайной величины.
-
Закон распределения дискретной случайной величины представлен в таблице:
-
-
Х
-8
15
-4
12
6
р
֍
֍
0,25
֍
0,15
-
-
Заполните таблицу распределения, если доли неизвестных вероятностей пропорциональны
числам 1:2: 3 соответственно.
-
Вычислите математическое ожидание дискретной случайной величины.
-
Вычислите М(10Х - 6).
-
Дискретная случайная величина задана законом распределения:
-
-
Х
х1
10
-5
5
р
0,2
0,1
0,4
0,3
-
-
Найдите х1, зная, что М(Х) = 2,7.
-
Найдите дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Использует закон распределения дискретных случайных величин |
1 |
находит вероятности значений дискретной случайной величины; |
1 |
|
составляет закон распределения дискретной случайной величины; |
1 |
||
|
2А |
составляет выражение для вычисления долей неизвестных вероятностей; |
1 |
|
|
находит неизвестную переменную; |
1 |
||
|
находит доли неизвестных вероятностей; |
1 |
||
|
Использует свойства математического ожидания дискретной случайной величины |
2В |
использует формулу математического ожидания дискретной случайной величины; |
1 |
|
вычисляет математическое ожидание дискретной случайной величины; |
1 |
||
|
2С |
применяет свойства математического ожидания дискретной случайной величины; |
1 |
|
|
3А |
составляет выражение, для нахождения неизвестного значения случайной величины, используя формулу математического ожидания; |
1 |
|
|
находит неизвестное значение дискретной случайной величины; |
1 |
||
|
Вычисляет дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины |
3В |
использует формулу дисперсии дискретной случайной величины; |
1 |
|
вычисляет дисперсию дискретной случайной величины; |
1 |
||
|
использует формулу среднего квадратического (стандартного) отклонения дискретной случайной величины; |
1 |
||
|
вычисляет среднее квадратическое (стандартное) отклонение дискретной случайной величины. |
1 |
||
|
Общий балл |
14 баллов |
||
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Случайные величины и их числовые характеристики».
ФИ обучающегося : ______________________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Использует закон распределения дискретных случайных величин |
Затрудняется в составлении и использовании закона распределения дискретных случайных величин |
Допускает вычислительные ошибки при составлении / использовании закона распределения дискретных случайных величин |
Составляет и использует закон распределения дискретных случайных величин |
|
Использует свойства математического ожидания дискретной случайной величины |
Затрудняется в нахождении математического ожидания дискретной случайной величины |
Допускает вычислительные ошибки при нахождении математического ожидания дискретной случайной величины |
Находит математическое ожидание дискретной случайной величины |
|
Вычисляет дисперсию и стандартное отклонение случайной величины |
Затрудняется в вычислении дисперсии и стандартного отклонения дискретной случайной величины |
Допускает вычислительные ошибки при нахождении дисперсии / стандартного отклонения дискретной случайной величины |
Вычисляет дисперсию и стандартное отклонение дискретной случайной величины |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 1 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 7 заданий, включающих вопросы с множественным выбором ответов, с кратким и развернутым ответом.
В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде
численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла.
Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов.
Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол.заданий |
№ задания |
Тип задания |
Время выполн. |
балл |
Балл за раздел |
|
Функция, её свойства и график |
10.3.1.1 Знать определение и способы задания функции |
Знание и понимание |
1 |
1 |
КО |
2 |
1 |
10 |
|
10.3.1.2 Уметь выполнять преобразования графика функции (параллельный перенос, сжатие и растяжение) |
Применение |
1 |
2 |
РО |
7 |
2 |
||
|
10.3.1.5 Знать определение обратной функции и уметь находить функцию, обратную заданной и знать свойство расположения графиков взаимно обратных функций |
Применение |
1 |
3 |
РО |
7 |
4 |
||
|
10.3.1.6 Уметь распознавать сложную функцию f(g(x)) и составлять композицию функций |
Применение |
1 |
4 |
РО |
6 |
3 |
||
|
Тригонометрические функции |
10.1.3.2 Уметь строить графики тригонометрических функций с помощью преобразований |
Применение |
1 |
5 |
РО |
7 |
4 |
10 |
|
10.1.3.3 Знать определения арксинуса, арккосинуса, арктангенса, арккотангенса и уметь находить их значения |
Знание и понимание |
1 |
6 |
КО |
3 |
2 |
||
|
10.1.3.4 Находить значения выражений, содержащих обратные тригонометрические функции |
Применение |
1 |
7 |
РО |
7 |
4 |
||
|
итого |
|
|
|
|
|
|
40 |
20 |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
1 ВАРИАНТ
-
Из указанных функций выберите линейную:
-
2х+у-4=0
-
У=(х-2)2
-

-

-

2. Используя график функции у=х2, постройте график функции у=х2+2
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=5x-125, g(x)=x2. Решите уравнение f(g(x))=0
5. Постройте график функции y=sin x+1. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 1.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
1 |
1 |
|
|
2 |
Строит график функции у=х2 |
1 |
|
|
Строит график функции у=х2+2 |
1 |
|
|
|
3 |
(2х-5)у=4х-3 |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=5х2-125 |
1 |
|
|
5х2-125=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y=sin x |
1 |
|
|
Определяет перемещение графика функции y=sin x |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[0;2] |
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Всего: |
20 |
|
|
2 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
-
1. Из указанных функций выберите квадратичную:
-
2х+у-4=0
-
у=(х-2)2
-

-

-

2. Используя график функции у=х2, постройте график функции у=(х+3)2
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=х2, g(x)=2х-4. Решите уравнение f(g(x))=0
5. Постройте график функции y=cos x-2. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 2.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
2 |
|
|
|
2 |
Строит график функции у=х2 |
1 |
|
|
Строит график функции у=(х+3)2 |
|
|
|
|
3 |
y(x-4)=3x-2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=(2x-4)2 |
1 |
|
|
2x-4=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y=cosx |
1 |
|
|
Определяет перемещение графика функции y= cosx |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[-2;-1] |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
Всего: |
20 |
|
|
3 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
-
1. Из указанных функций выберите обратно-пропорциональную:
-
2х+у-4=0
-
У=(х-2)2
-

-

-

2. Используя график функции у=-х2, постройте график функции у=-х2+2
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=2х+3, g(x)=-6х+9. Решите уравнение f(g(x))=0
5. Постройте график функции y=sin x+1. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 3.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
5 |
|
|
|
2 |
Строит график функции у=-х2 |
1 |
|
|
Строит график функции у=-х2+2 |
|
|
|
|
3 |
y(2x-3)=4x+5 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=-12х+21 |
1 |
|
|
-12х+21=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y=sinx |
1 |
|
|
Определяет перемещение графика функции y=sinx |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[0;2] |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
Всего: |
20 |
|
|
4 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
4 |
3 |
4 |
2 |
4 |
|
итого |
20 баллов |
||||||
-
1. Из указанных функций выберите степенную:
-
2х+у-4=0
-
У=(х-2)2
-

-

-

2. Используя график функции у=-х2, постройте график функции у=-х2-3
3.
Найдите функцию, обратную данной  . Запишите область определения полученной
функции.
. Запишите область определения полученной
функции.
4. Пусть f(x)=2х-5, g(x)=5х+7. Решите уравнение f(g(x))=0
5. Постройте график функции y=cos x+1. Укажите область значения функции.
6.
Вычислите: а) 
7.
Вычислите значение выражения: 
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 4.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
4 |
|
|
|
2 |
Строит график функции у=-х2 |
1 |
|
|
Строит график функции у=-х2-3 |
|
|
|
|
3 |
y(x-4)=3x-2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4 |
f(g(x))=10х+9 |
1 |
|
|
10х+9=0 |
1 |
|
|
|
|
1 |
|
|
|
5 |
Строит график функции y= cos x |
1 |
|
|
Определяет перемещение графика функции y= cos x |
1 |
|
|
|
|
1 |
|
|
|
Е(у)ꞓ[0;2] |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
6 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
Всего: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 2 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 7 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла.
Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных
частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Тригонометрические уравнения и неравенства |
10.1.3.5 Уметь решать простейшие тригонометрические уравнения |
Применение |
1 |
5а |
КО |
5 |
2 |
10 |
|
10.1.3.7 Уметь решать тригонометрические уравнения, приводимые к квадратному уравнению |
Применение |
5b |
РО |
10 |
5 |
|||
|
10.1.3.9 Уметь решать простейшие тригонометрические неравенства |
Применение |
1 |
4 |
КО |
5 |
3 |
||
|
Вероятность |
10.2.1.2 Вычислять вероятность случайных событий, применяя свойства вероятностей * P(A ∙ B) = P(A) ∙ P(B); * P(A + B) = P(A) + P(B); * P(A +B) = P(A)+P(B)–P(A ∙ B) |
Применение |
3 |
1 |
КО |
2 |
1 |
10 |
|
2 |
КО |
3 |
2 |
|||||
|
3 |
КО |
5 |
2 |
|||||
|
Применение |
2 |
6 |
КО |
5 |
2 |
|||
|
7 |
РО |
5 |
3 |
|||||
|
ИТОГО: |
|
|
7 |
|
|
40 |
20 |
20 |
ЗАДАНИЯ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1 ВАРИАНТ
1. Вероятность того, что Асхат опоздает на работу равна 0,3. Какова вероятность того, что Асхат не опоздает на работу?
2. В
коробке лежат маленькие кубики разных цветов: белые и синие. Всего
21 кубик. Вероятность того, что случайным образом из коробки
достанут синий кубик равна  . Сколько белых
кубиков в коробке?
. Сколько белых
кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство: 3tg( x +
x +
 )
)
 .
.
5. a) Определите, имеют ли решения следующие тригонометрические уравнения:
1) cos x 3 2) cos x 1.
Поясните ответ и найдите решение, если оно существует.
b) Решите
уравнение 4sin2x+8sinx= 8 sin60o
, на отрезке
2;
sin60o
, на отрезке
2;
6. В двух коробках лежат ручки. В коробке А – 15 ручек: 6 красных, 7 синих и 2 зелёных.
В коробке В – 21 ручка: n синих и остальные красные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно,
что вероятность того, что Рамазан и Асель достанут обе синие ручки,
равна  Сколько синих ручек в коробке
В?
Сколько синих ручек в коробке
В?
7. Имеется девять карточек с числами
1
2
2
2
2
3
3
3
4
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
2 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1.
Вероятность того, что Артур опоздает на работу равна 0,1. Какова
вероятность того, что Артур не опоздает на работу? 2. В коробке
лежат маленькие кубики разных цветов: белые и чёрные. Всего 24
кубика. Вероятность того, что случайным образом из коробки достанут
белый кубик равна  . Сколько
чёрных кубиков в коробке?
. Сколько
чёрных кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство:  tg
(
tg
( x -
x -  ) >
1.
) >
1.
5. a) Определите, имеют ли решения, следующие тригонометрические уравнения:
1) sin x 3 2) cos x -1.
Поясните ответ и найдите решение, если оно существует.
b) Решите уравнение 4 cos2x + 4 cos x = 16 cos 60o , на отрезке ; 2
6. В двух коробках лежат ручки. В коробке А – 9 ручек: 2 красных, 6 синих и 1 зелёная.
В коробке В – 14 ручек: n синих и остальные зелёные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно,
что вероятность того, что Рамазан и Асель достанут обе синие ручки,
равна  Сколько синих ручек в коробке
В?
Сколько синих ручек в коробке
В?
7. Имеется восемь карточек с числами
1
2
2
3
3
3
3
4
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
3 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1.
Вероятность того, что Асхат опоздает на работу равна 0,16. Какова
вероятность того, что Асхат не опоздает на работу? 2. В коробке
лежат маленькие кубики разных цветов: белые и синие. Всего 27
кубик. Вероятность того, что случайным образом из коробки достанут
синий кубик равна  . Сколько белых
кубиков в коробке?
. Сколько белых
кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство:  tg
(
tg
( x -
x -  )
)
 .
.
5. a) Определите, имеют ли решения следующие тригонометрические уравнения:
1)
sin x  2)
sin x - 1.
2)
sin x - 1.
Поясните ответ и найдите решение, если оно существует.
b) Решите уравнение 2sin2x – 10 sinx= -8 sin 90o , на отрезке 2;
6. В двух коробках лежат ручки. В коробке А – 18 ручек: 7 красных, 8 синих и 3 зелёных.
В коробке В – 8 ручек: n зелёных и остальные красные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно,
что вероятность того, что Рамазан и Асель достанут обе зелёные
ручки, равна  Сколько зелёных
ручек в коробке В?
Сколько зелёных
ручек в коробке В?
7. Имеется одиннадцать карточек с числами
1
2
2
2
2
3
3
3
4
3
3
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
4 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
1 |
2 |
2 |
3 |
7 |
2 |
3 |
|
итого |
20 баллов |
||||||
1.
Вероятность того, что Артур опоздает на работу равна 0,25. Какова
вероятность того, что Артур не опоздает на работу? 2. В коробке
лежат маленькие кубики разных цветов: белые и чёрные. Всего 18
кубиков. Вероятность того, что случайным образом из коробки
достанут белый кубик равна  . Сколько
чёрных кубиков в коробке?
. Сколько
чёрных кубиков в коробке?
3.
Покажите, являются ли события А и В зависимыми или независимыми,
если P(A)  , P(B)
, P(B)
 ,
P(A
,
P(A B)
B)  .
.
4. Решите
неравенство:  tg
(
tg
( x -
x -  )>
)> .
.
5. a) Определите, имеют ли решения следующие тригонометрические уравнения:
1)
cos
x  2)
cos
x 0.
2)
cos
x 0.
Поясните ответ и найдите решение, если оно существует.
b) Решите уравнение 6 cos2x + 9 cos x = 12 cos 60o, на отрезке 2; 2
6. В двух коробках лежат ручки. В коробке А – 12 ручек: 5 красных, 4 синих и 3 зелёная.
В коробке В – 9 ручек: n красных и остальные зелёные. Рамазан достает случайным образом ручку из коробки А, Асель достает случайным образом ручку из коробки В.
Известно, что вероятность того, что Рамазан и Асель достанут обе красные ручки,
равна  Сколько красных
ручек в коробке В?
Сколько красных
ручек в коробке В?
7. Имеется семь карточек с числами:
1
2
2
2
3
3
4
Последовательно случайным образом выбирают две карточки.
Найдите вероятность того, что на двух карточках числа окажутся одинаковыми.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 1 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,7 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не имеет решения, т.к. 31;1 |
1 |
|
|
2) имеет
решение и x 2 |
1 |
|
|
|
5b |
sin2 x + 2 sin x – 3 = 0 |
1 |
|
|
t2 2t 3 0 |
1 |
Использует метод замены переменной |
|
|
t1 3, t2 1 |
1 |
|
|
|
x = |
1 |
Принимать решения только в радианной мере |
|
|
x = - |
1 |
||
|
6 |
|
1 |
|
|
12 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 2 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,9 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не имеет решения, т.к. - 31;1 |
1 |
|
|
2) имеет
решение и x |
1 |
|
|
|
5b |
cos2 x + cos x – 2 = 0 |
1 |
|
|
t2 t 2 0 |
1 |
Использует метод замены переменной |
|
|
t1 2, t2 1 |
1 |
|
|
|
x = 0 |
1 |
Принимать решения только в радианной мере |
|
|
x = 2 |
1 |
||
|
6 |
|
1 |
|
|
6 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 3 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,84 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не
имеет решения, т.к. |
1 |
|
|
2) имеет
решение и x |
1 |
|
|
|
5b |
sin2 x - 5 sin x + 4 = 0 |
1 |
|
|
t2 - 5t + 4 0 |
1 |
Использует метод замены переменной |
|
|
t1 4, t2 1 |
1 |
|
|
|
x = |
1 |
Принимать решения только в радианной мере |
|
|
x = - |
1 |
||
|
6 |
|
1 |
|
|
2 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 4 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
0,75 |
1 |
Принимается альтернативное решение |
|
2 |
|
1 |
|
|
|
1 |
||
|
3 |
P(A) P(B)= |
1 |
|
|
P(A) P(B) |
1 |
|
|
|
4 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5а |
1) не
имеет решения, т.к.- |
1 |
|
|
2) имеет
решение и x |
1 |
|
|
|
5b |
2cos2 x + 3 cos x – 2 = 0 |
1 |
|
|
2t2 3t 2 0 |
1 |
Использует метод замены переменной |
|
|
t1
2, t2
|
1 |
|
|
|
x = |
1 |
Принимать решения только в радианной мере |
|
|
x = |
1 |
||
|
6 |
|
1 |
|
|
2 |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответом.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов.
Характеристика заданий суммативного оценивания за 3 четверть
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Производная |
10.3.1.7 Знать определение предела функции в точке и на бесконечности |
Знание и понимание |
1 |
1 |
КО |
2 |
3 |
11 |
|
10.3.3.1 Решать прикладные задачи, опираясь на физический смысл производной |
Применение |
1 |
3 |
КО |
5 |
2 |
||
|
10.3.1.14 Знать определение сложной функции и находить её производную |
Применение |
1 |
4а |
РО |
|
2 |
||
|
10.3.1.12 Составлять уравнение касательной к графику функции в заданной точке |
Применение |
4b |
РО |
|
3 |
|||
|
10.3.1.11 Знать и применять правила дифференцирования |
Применение |
1 |
2a |
РО |
12 |
1 |
||
|
Применение производной |
10.3.1.17 Находить критические точки и точки экстремума функции |
Применение |
2b |
РО |
2 |
9 |
||
|
10.3.1.15 Знать и применять необходимое и достаточное условие возрастания (убывания) функции на интервале |
Применение |
2c |
КО |
2 |
||||
|
10.3.3.3 Решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции |
Навыки высокого порядка |
1 |
5 |
РО |
10 |
5 |
||
|
ИТОГО: |
|
|
5 |
|
|
40 |
20 |
20 |
ЗАДАНИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ
1 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = х3 -3х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 7t3 +6t2 +1, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 2 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке (2;1)
.
в точке (2;1)
.
5. Прямоугольный участок площадью 4900 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
2 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = 5х3 -15х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 12t3 +5t2 +11, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 4 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке
(1;2).
в точке
(1;2).
5. Прямоугольный участок площадью 8100 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
3 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = 7х3 -14х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 7t3 - t2 +2, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 3 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке
(1;3).
в точке
(1;3).
5. Прямоугольный участок площадью 14400 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
4 ВАРИАНТ
|
Разбаловка заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
|
|
Количество баллов |
4 |
5 |
2 |
4 |
5 |
|
|
|
итого |
20 баллов |
||||||
1.
Определите значение предела: a)![]() ; b)
; b) ![]() .
.
2. Дана функция y = 2х3 -3х2 Найдите:
a) производную функции;
b) критические точки функции;
c) промежутки возрастания и убывания функции.
3. Закон движения точки по прямой задается формулой S(t) = 6t3 - 9 t2 +6, где t – время (в секундах), S – путь (в метрах). Вычислите мгновенную скорость точки в момент t 3 с.
4.
а) Найдите производную функции у =
![]() ; .
; .
b) Запишите уравнение касательной к графику функции
у = ![]() в точке
(1;2).
в точке
(1;2).
5. Прямоугольный участок площадью 289 м2 огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с помощью производной.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 1 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: -2 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит
ответ: |
1 |
|
|
|
2а |
y ’ = 3х2 -6х |
1 |
|
|
2b |
3х2 - 6х=0 |
1 |
|
|
x=0, x= 2 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает: (0; 2) |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
108 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(2)= 2 |
1 |
|
|
y ’(2)=1 |
1 |
|
|
|
y=1 |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 70- точка минимума на интервале |
|
|
70м, 70м |
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 2 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: 1 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит
ответ: |
1 |
|
|
|
2а |
y ’ = 15х2 -30х |
1 |
|
|
2b |
15х2 - 30х=0 |
1 |
|
|
x=0, x= 2 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает: (0; 2) |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
616 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(1)= 4 |
1 |
|
|
y
’(1)=1 |
1 |
|
|
|
y=1 |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 81- точка минимума на интервале |
|
|
81м, 81м |
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 3 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: -20 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит ответ: -2 |
1 |
|
|
|
2а |
y ’ = 21х2 -28х |
1 |
|
|
2b |
21х2 - 28х=0 |
1 |
|
|
x=0,
x=1 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает:
(0; 1 |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
183 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(1)=3 |
1 |
|
|
y ’(1)=
|
1 |
|
|
|
y= |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 120- точка минимума на интервале |
|
|
120м, 120м |
1 |
|
|
|
Итого: |
20 |
|
|
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ 4 ВАРИАНТ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1а |
Упрощает
выражение: |
1 |
|
|
Ответ: -1 |
1 |
|
|
|
1b |
Упрощает
выражение: делит и числитель и знаменатель на х в наибольшей
степени: |
1 |
|
|
Находит
ответ: |
1 |
|
|
|
2а |
y ’ = 6х2 -6х |
1 |
|
|
2b |
6х2 - 6х=0 |
1 |
|
|
x=0, x=1 |
1 |
|
|
|
2c |
Возрастает
(- |
1 |
|
|
Убывает: (0;1) |
1 |
|
|
|
3 |
S’(t) =
|
1 |
|
|
108 м/с |
1 |
|
|
|
4a |
y ’ = |
1 |
|
|
4b |
y(1)=5 |
1 |
|
|
y ’(1)= 3,4 |
1 |
|
|
|
y=3,4x+1,6 |
1 |
|
|
|
5 |
S(x)=2 |
1 |
|
|
S
“(x)=2 |
1 |
|
|
|
|
1 |
|
|
|
S “(x) - +
|
1 |
Доказывает, что x 60- точка минимума на интервале |
|
|
17м, 17м |
1 |
|
|
|
Итого: |
20 |
|
|
ЗАДАНИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть:
Продолжительность - 40 минут
Количество баллов - 20
Типы заданий:
МВО – задания с множественным выбором ответов;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания:
Данные варианты состоят из 4 заданий, включающие вопросы с множественным выбором ответов, и требующие краткого и развернутого ответов.
В заданиях с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.
В заданиях, требующие развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Случайные величины и их числовые характерис-тики |
10.2.1.5 Знать определение дискретной и непрерывной случайной величины и уметь их различать |
Знание и понимание |
1 |
1 |
МВО |
3 |
2 |
20 |
|
10.2.1.6 Составлять таблицу закона распределения некоторых дискретных случайных величин |
Применение |
1 |
2 |
РО |
8 |
3 |
||
|
10.2.1.8 Вычислять математическое ожидание дискретной случайной величины |
Навыки высокого порядка |
1 |
3a |
РО |
8 |
4 |
||
|
10.2.1.9 Вычислять дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины |
Применение |
3b |
7 |
2 |
||||
|
3c |
2 |
2 |
||||||
|
10.2.1.10 Решать задачи с использованием числовых характеристик дискретных случайных величин |
Навыки высокого порядка |
1 |
4 |
РО |
12 |
7 |
||
|
ИТОГО: |
|
|
4 |
|
|
40 минут |
20 |
20 |
ЗАДАНИЯ
|
Разбаловка заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
2 |
3 |
8 |
7 |
|
итого |
20 баллов |
|||
ВАРИАНТ 1.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) количество автомобилей, проехавших за 1 час через некоторый перекресток;
b) скорость течения реки;
c) количество тепловой энергии, потраченной на отопление города за 1 месяц ;
d) количество писем, поступивших в некоторое почтовое отделение за 1 неделю.
2. При организации денежной лотереи выпустили 400 билетов. Из них 60 билетов дают выигрыш 200 тенге, 50 билетов – 500 тенге, 20 билетов – 1000 тенге, 10 билетов – 5000 тенге и 1 билет – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
1 |
3 |
6 |
10 |
|
Р |
0,2 |
0,3 |
0,1 |
k |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до одного знака после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
3 |
4 |
5 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наименее вероятно, если известно, что М(2Х) = 7,6 и D(X) = 0,56 и р1 = р2?
ВАРИАНТ 2.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) температура воздуха, измеренная в течении суток;
b) количество клиентов страховой компании за некоторый месяц;
c) скорость движения велосипедиста за 1час движения;
d) количество подъездов многоэтажного дома.
2. При организации денежной лотереи выпустили 500 билетов. Из них 90 билетов дают выигрыш 100 тенге, 80 билетов – 500 тенге, 50 билетов – 1000 тенге, 15 билетов – 2000 тенге и 1 билет – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
4 |
3 |
5 |
6 |
|
Р |
k |
0,2 |
0,3 |
0,4 |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до двух знаков после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
4 |
5 |
6 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наиболее вероятно, если известно, что М(-3Х) = -15 и D(X) = 0,6 и р1 = р3?
ВАРИАНТ 3.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) количество очков, выпадающих на одной грани при бросании игрального кубика;
b) величина электрического напряжения в городской электросети;
c) количество выстрелов по мишени во время соревнований;
d) атмосферное давление, измеренное в течении суток.
2. При организации денежной лотереи выпустили 500 билетов. Из них 120 билетов дают выигрыш 200 тенге, 80 билетов – 500 тенге, 40 билетов – 1000 тенге, 20 билетов – 5000 тенге и 2 билета – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
5 |
3 |
4 |
9 |
|
Р |
0,2 |
k |
0,2 |
0,3 |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до одного знака после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
5 |
6 |
7 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наименее вероятно, если известно, что М(-2Х) = -11 и D(X) = 0,45 и р1 = 2р2?
ВАРИАНТ 4.
1. Из приведенных ниже примеров выберите все примеры дискретных случайных величин:
а) продолжительность жизни человека;
b) количество людей, участвующих в конференции;
c) количество оценок «5», полученных за контрольную работу;
d) скорость спуска парашютиста.
2. При организации денежной лотереи выпустили 400 билетов. Из них 75 билетов дают выигрыш 100 тенге, 45 билетов – 200 тенге, 10 билетов – 1000 тенге, 2 билета – 5000 тенге и 1 билет – 10000 тенге. Покупка участником лотереи билета с любой суммой выигрыша - случайная величина Х. Составьте закон распределения случайной величины Х.
3. Распределение дискретной случайной величины представлено в таблице:
|
Х |
4 |
3 |
5 |
8 |
|
Р |
0,2 |
0,1 |
k |
0,4 |
-
Найдите математическое ожидание дискретной случайной величины.
-
Найдите дисперсию дискретной случайной величины.
-
Найдите среднее квадратическое (стандартное) отклонение дискретной случайной величины. Результат округлите до двух знаков после запятой.
4. Закон распределения количества точных попаданий стрелка в мишень представлен в таблице.
|
Х |
7 |
8 |
9 |
|
Р |
р1 |
р2 |
p3 |
Какое количество точных попаданий наиболее вероятно, если известно, что М(4Х) = 30,4 и D(X) = 0,64 и р1 = 3р3?
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 1.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
a, d |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
400 – (60+50+20+10+1) = 259 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = р5 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
0,2+ 0,3 + 0,1 + k =1 |
1 |
|
|||||||||||||
|
k = 0,4 |
1 |
|
||||||||||||||
|
М(Х) = 1·0,2 + 3·0,3 + 6·0,1 + 10·0,4 |
1 |
|
||||||||||||||
|
М(Х) = 5,7 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 1·0,2 + 9·0,3 + 36·0,1 + 100·0,4 = 46,5 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 46,5 – 32,49 = 14,01 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(2Х) = 2(3·р1 + 4·р2 + 5·р3) = 7,6 |
1 |
|
|||||||||||||
|
М(Х) = 3·р1 + 4·р2 + 5·р3 = 3,8 |
1 |
|
||||||||||||||
|
D(Х) = 9·р1 + 16·р2 + 25·р3 - 3,82= 0,56 |
1 |
|
||||||||||||||
|
|
1 |
или |
||||||||||||||
|
р1 = 0,4 и р3 = 0,2 |
1 |
или р2 = 0,4 и р3 = 0,2 |
||||||||||||||
|
р2 =0,4 |
1 |
или р1 = 0,4 |
||||||||||||||
|
Наименьшая вероятность 5 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 2.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
b, d |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
500 – (90+80+50+15+1) = 264 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = р5 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
k + 0,2+ 0,3 + 0,4=1 |
1 |
|
|||||||||||||
|
k = 0,1 |
1 |
|
||||||||||||||
|
М(Х) = 4·0,1 + 3·0,2 + 5·0,3 + 6·0,4 |
1 |
|
||||||||||||||
|
М(Х) = 4,9 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 16·0,1 + 9·0,2 + 25·0,3 + 36·0,4 = 25,3 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 25,3 – 24,01 = 1,29 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(-3Х) = -3(4·р1 + 5р2 + 6р3) = -15 |
1 |
|
|||||||||||||
|
М(Х) = 4·р1 + 5·р2 + 6·р3 = 5 |
1 |
|
||||||||||||||
|
D(Х) = 16·р1 + 25·р2 + 36·р3 - 52 = 0,6 |
1 |
|
||||||||||||||
|
|
1 |
или |
||||||||||||||
|
р1 = 0,3 и р2 = 0,4 |
1 |
или р2 = 0,4 и р3 = 0,3 |
||||||||||||||
|
р3 =0,3 |
1 |
или р1 = 0,3 |
||||||||||||||
|
Наибольшая вероятность 5 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 3.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
a, c |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
500 – (120+80+40+20+2) = 238 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = р5 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
0,2+ k + 0,2 + 0,3 = 1 |
1 |
|
|||||||||||||
|
k = 0,3 |
1 |
|
||||||||||||||
|
М(Х) = 5·0,2 + 3·0,3 + 4·0,2 + 9·0,3 |
1 |
|
||||||||||||||
|
М(Х) = 5,4 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 25·0,2 + 9·0,3 + 16·0,2 + 81·0,3 = 35,2 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 35,2 – 29,16 = 6,04 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(-2Х) = -2(5·р1 + 6·р2 + 7·р3) = -11 |
1 |
|
|||||||||||||
|
М(Х) = 5·р1 + 6·р2 + 7·р3 = 5,5 |
1 |
|
||||||||||||||
|
D(Х) = 25·р1 + 36·р2 + 49·р3 - 5,52 = 0,45 |
1 |
|
||||||||||||||
|
|
1 |
|
||||||||||||||
|
р2 = 0,3 и р3 = 0,1 |
1 |
|
||||||||||||||
|
р1 =0,6 |
1 |
|
||||||||||||||
|
Наименьшая вероятность 7 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ ВАРИАНТ 4.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||
|
1 |
b, c |
2 |
Балл ставится за каждый правильный ответ |
|||||||||||||
|
2 |
400 – (75+45+10+2+1) = 267 |
1 |
Определяет количество невыигрышных билетов |
|||||||||||||
|
р1 = |
1 |
|
||||||||||||||
|
1 |
|
||||||||||||||
|
3a |
0,2+ 0,1 + k + 0,4 =1 |
1 |
|
|||||||||||||
|
k = 0,3 |
1 |
|
||||||||||||||
|
М(Х) = 4·0,2 + 3·0,1 + 5·0,3 + 8·0,4 |
1 |
|
||||||||||||||
|
М(Х) = 5,8 |
1 |
|
||||||||||||||
|
3b |
M(X2) = 16·0,2 + 9·0,1 + 25·0,3 + 64·0,4 = 37,2 |
1 |
|
|||||||||||||
|
D(X) = M(X2) – M2(X) = 37,2 – 33,64 = 3,56 |
1 |
|
||||||||||||||
|
3c |
|
1 |
|
|||||||||||||
|
σ
|
1 |
|
||||||||||||||
|
4 |
М(4Х) = 4(7·р1 + 8·р2 + 9·р3) = 30,4 |
1 |
|
|||||||||||||
|
М(Х) = 7·р1 + 8·р2 + 9·р3 = 7,6 |
1 |
|
||||||||||||||
|
D(Х) = 49·р1 + 64·р2 + 81·р3 – 7,62 = 0,64 |
1 |
|
||||||||||||||
|
|
1 |
|
||||||||||||||
|
р3 = 0,2 и р2 = 0,2 |
1 |
|
||||||||||||||
|
р1 =0,6 |
1 |
|
||||||||||||||
|
Наибольшая вероятность 7 точных попаданий |
1 |
|
||||||||||||||
|
Всего: |
20 |
|
||||||||||||||
|
|
1 |

шағым қалдыра аласыз


















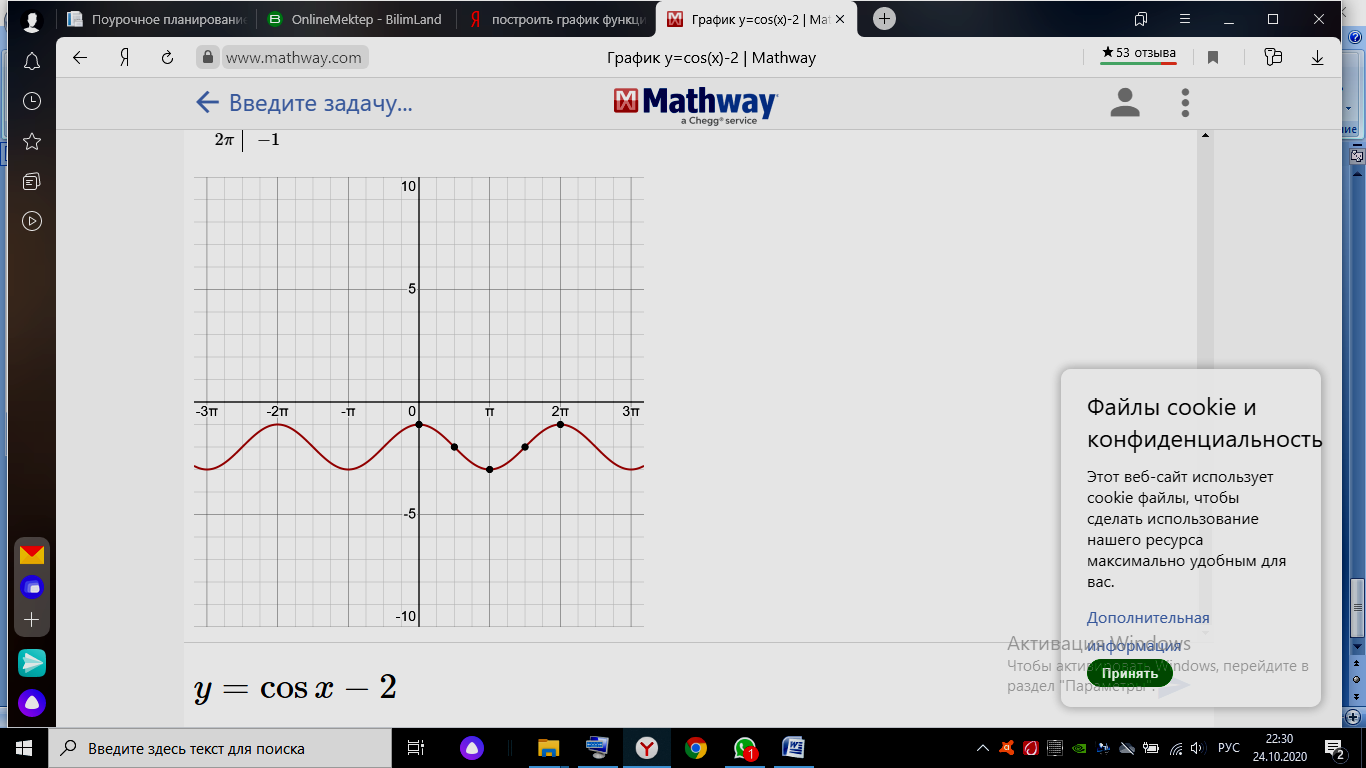

















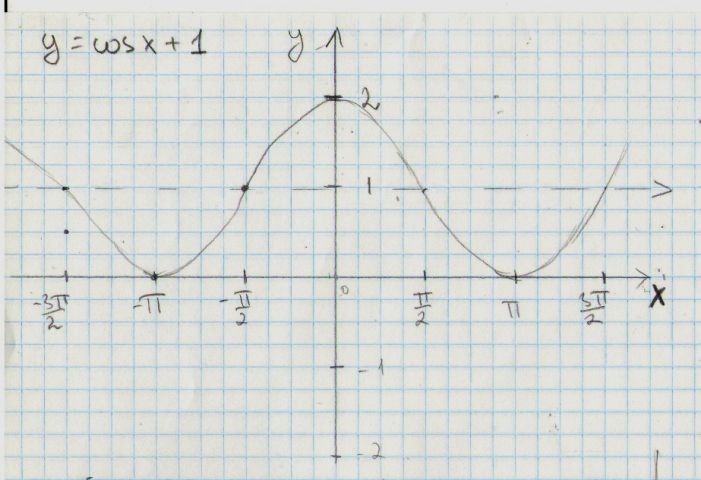













 n,
n Z
n,
n Z




 или
или 






 2
2









 +2
+2















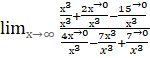
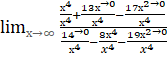
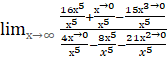
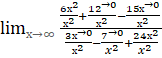
 = 0,15;
р2
=
= 0,15;
р2
=  = 0,125;
р3
=
= 0,125;
р3
=  = 0,05;
р4
=
= 0,05;
р4
=  =
0,025;
=
0,025; = 0,0025;
р6
=
= 0,0025;
р6
=  =
0,6475
=
0,6475
 3,7
3,7

 = 0,18;
р2
=
= 0,18;
р2
=  = 0,16;
р3
=
= 0,16;
р3
=  = 0,1;
р4
=
= 0,1;
р4
=  =
0,03;
=
0,03; = 0,002;
р6
=
= 0,002;
р6
=  =
0,528
=
0,528


 = 0,24;
р2
=
= 0,24;
р2
=  = 0,08;
р4
=
= 0,08;
р4
=  =
0,04;
=
0,04; = 0,004;
р6
=
= 0,004;
р6
=  =
0,476
=
0,476

 = 0,1875;
р2
=
= 0,1875;
р2
=  = 0,1125;
р3
=
= 0,1125;
р3
=  = 0,005;
р5
=
= 0,005;
р5
=  =
0,6675
=
0,6675














