Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз

Бонусты жинап картаңызға (kaspi Gold, Halyk bank) шығарып аласыз
Сборник суммативного оценивания по алгебре и геометрии 7 класс 1.doc

|
2022 год |
В помощь учителю математики Сборник работ для суммативного оценивания по алгебре и геометрии 7 класс |
 2022 год
2022 год
|
|
|
ТВГ учителей математики |
В помощь учителю математики Сборник работ для суммативного оценивания по алгебре и геометрии 7 класс |
Содержание
|
Вступление |
|
Алгебра |
|
Суммативное оценивание за раздел «Степень с целым показателем» |
|
Суммативное оценивание за раздел «Многочлены » |
|
Суммативное оценивание за раздел «Функция. График функции» |
|
Суммативное оценивание за раздел «Элементы статистики» |
|
Суммативное оценивание за раздел «Формулы сокращенного умножения» |
|
Суммативное оценивание за раздел «Алгебраические дроби» |
|
Суммативное оценивание за 1 четверть |
|
Суммативное оценивание за 2 четверть |
|
Суммативное оценивание за 3 четверть |
|
Суммативное оценивание за 4 четверть |
|
Геометрия |
|
Суммативное оценивание за раздел «Начальные геометрические сведения» |
|
Суммативное оценивание за раздел «Треугольники » |
|
Суммативное оценивание за раздел «Взаимное расположение прямых» |
|
Суммативное оценивание за раздел «Окружность. Геометрические построения» |
|
Суммативное оценивание за 1 четверть |
|
Суммативное оценивание за 2 четверть |
|
Суммативное оценивание за 3 четверть |
|
Суммативное оценивание за 4 четверть |
|
Форма анализа суммативного оценивания за учебный период |
|
Литература |
|
Рецензия |
Рецензент - Даниярова Ж.К. кандидат педагогических наук, доцент кафедры ЭМиИТ ИнЕУ
Авторы составители суммативного оценивания :
Руководитель группы – Середкин В.П. учитель математики, педагог-мастер, Павлодарская область, Павлодарский район, КГУ Чернорецкая СОШ № 1.
Белгибаева Н.Б. - учитель математики, высшая категория, г.Кызылорда, КГУ СОШ № 6 им. М.А. Сужикова
Стурова О.А. – учитель математики, высшая категория, Жамбылская область, Таласский район, г.Каратау, КГУ школа-лицей № 1
Кузьмина И.В. - учитель математики, педагог-исследователь, Костанайская область, Карасуский район, ГУ Новоселовская ООШ
Арютина С.И. – учитель математики, педагог-эксперт, КГУ "Заградовская средняя школа "КГУ "Отдел образования Есильского района" КГУ "Управление образования акимата Северо-Казахстанской области"
Иванова И.Е. - учитель математики, вторая категория, КГУ «Школа-лицей города Алтай» отдела образования по району Алтай Управления образования Восточно-Казахстанской области
Жунусова Г.С. – учитель математики, педагог-модератор, Павлодарская область, Щербактинский район, КГУ Чигириновская СОШ
Корсак А.С. – учитель математики, педагог-модератор, КГУ "Заградовская средняя школа" КГУ "Отдел образования Есильского района"КГУ "Управление образования акимата Северо-Казахстанской области"
ВВЕДЕНИЕ
Данный сборник составлен в помощь учителю при планировании, организации и проведении суммативного оценивания за раздел и четверть по предметам алгебра и геометрия для учащихся 7 классов.
Сборник работ по суммативному оцениванию составлен на основе ГОСО, типовой учебной программы и учебного плана. Данные работы позволяют учителю определить уровень достижения учащимися запланированных целей обучения.
Все работы сборника разработаны учителями-практиками на основе своих наблюдений и опыта работы в рамках обновленного содержания образования
В курсе алгебры 7 класса в соответствии с учебной программой и долгосрочным планом изучаются следующие разделы – «Степень с целым показателем», «Многочлены», «Функция. График функции», «Элементы статистики», «Формулы сокращенного умножения», «Алгебраические дроби» и в курсе геометрии 7 класса изучаются разделы – «Начальные геометрические сведения», «Треугольники», «Взаимное расположение прямых», «Окружность. Геометрические построения». Каждая из представленных работ для проведения суммативного оценивания за раздел и суммативного оценивание за четверть, состоит из четырех вариантов. Количество вариантов, используемое при проведение суммативного оценивания каждый учитель определяет самостоятельно.
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ»
|
Тема |
|
|
Цель обучения |
7.1.1.1 записывать числа в стандартном виде 7.1.2.5 применять свойства степеней для упрощения алгебраических выражений 7.2.1.1 применять свойства степени с целым показателем при нахождении значений числовых выражений 7.1.2.9 сравнивать числа, записанные в стандартном виде 7.1.2.10 переводить величины из одних единиц измерения в другие и записывать результаты в стандартном виде |
|
Критерий оценивания |
Обучающийся Представляет число в стандартном виде Применяет свойства степени для преобразования алгебраических выражений Находит значение числовых выражений, используя свойства степени Сравнивает числа, записанные в стандартном виде Переводит величину из одних единиц измерения в другие и записывает результат в стандартном виде |
|
Уровень мыслительных навыков |
Применение |
|
Время выполнения |
20 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
|||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Количество баллов |
1 |
3 |
1 |
5 |
5 |
|
Всего баллов |
15 баллов |
||||
1 ВАРИАНТ
-
Запишите число 4350000 в стандартном виде.
-
Сравните числа:
-
5,6∙
 и 6,5∙
и 6,5∙ 
-
1,7∙
 и 1,7∙
и 1,7∙ 
-
4,2∙
 и 4,1∙
и 4,1∙
-
Представьте: 2,85 • 108 см в километрах
-
Выполните действия:
-
Вычислите:

2 ВАРИАНТ
-
Запишите число 2180000 в стандартном виде.
-
Сравните числа:
-
4,11∙
 и 3,5∙
и 3,5∙ 
-
8,2∙
 и 8,2∙
и 8,2∙ 
-
3,3∙
 и 2,6∙
и 2,6∙
-
Представьте: 6,75 • 1015 г в тоннах;
-
Выполните действия:
-
Вычислите:

3 ВАРИАНТ
-
Запишите число 5680000 в стандартном виде.
-
Сравните числа:
-
3,8∙
 и 2,5∙
и 2,5∙ 
-
5,4∙
 и 5,4∙
и 5,4∙ 
-
7,3∙
 и 2,8∙
и 2,8∙
-
Представьте: 4,6۰10-2 м в миллиметрах;
-
Выполните действия:
-
Вычислите:

4 ВАРИАНТ
-
Запишите число 6750000 в стандартном виде.
-
Сравните числа:
-
2,14∙
 и 3,5∙
и 3,5∙ 
-
4,8∙
 и 4,8∙
и 4,8∙ 
-
7,3∙
 и 4,6∙
и 4,6∙
-
Представьте: 1,9۰10-2 т в килограммах
-
Выполните действия:
-
Вычислите:

|
Критерий оценивания |
№ задания |
Дескриптор (Обучающийся) |
Балл |
|
Представляет число в стандартном виде |
1 |
указывает стандартный вид числа |
1 |
|
Сравнивает числа, записанные в стандартном виде |
2 |
выполняет сравнение чисел по их значащей части при одинаковом порядке |
1 |
|
выполняет сравнение чисел с одинаковой значащей частью, анализируя порядок числа |
1 |
||
|
сравнивает числа |
1 |
||
|
Переводит величину из одних единиц измерения в другие и записывает результат в стандартном виде |
3 |
переводит: см в км / г в т/ м в мм / т в кг |
1 |
|
Вычислите, используя свойства корня |
4 |
Умножение степеней с одинаковыми основаниями. |
1 |
|
Возведение степени в степень |
1 |
||
|
Возведение в степень. произведение |
1 |
||
|
Возведение в степень частного |
1 |
||
|
Деление степеней с одинаковыми основаниями |
1 |
||
|
Находит значение числовых выражений, используя свойства степени |
5 |
переходит к одному основанию |
1 |
|
находит значение нулевой степени числа |
1 |
||
|
использует свойство возведение степени в степень |
1 |
||
|
Применяет свойство произведения степени |
1 |
||
|
применяет свойство частного степеней и записывает ответ |
1 |
||
|
Итого: |
15 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ»
ФИО ОБУЧАЮЩЕГОСЯ _______________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
низкий |
средний |
высокий |
|
|
Представляет число в стандартном виде |
Затрудняется в представлении числа в стандартном виде. |
Допускает ошибки при определении значащей части / порядка числа. |
Верно, представляет число в стандартном виде. |
|
Сравнивает числа, записанные в стандартном виде |
Затрудняется в сравнении чисел, представленных в стандартном виде |
Допускает ошибки при сравнении чисел с одинаковой порядковой частью / с одинаковой значащей частью / с разными порядковой и значащей частями. |
Верно, выполняет сравнение чисел, записанных в стандартном виде |
|
Переводит величину из одних единиц измерения в другие и записывает результат в стандартном виде |
Затрудняется в переводе величины из одних единиц измерения в другие |
Приступает к решению, но допускает ошибки при переводе единиц измерения (вычислительные ошибки). |
Верно, переводит единицы измерения, показывая полное решение, записывает ответ в стандартном виде. |
|
Находит значение числовых выражений, используя свойства степени |
Затрудняется в нахождении значения выражения |
Приводит числа к одному основанию, допускает ошибки при использовании одного из свойств степени вычислительные ошибки. |
Осуществляет выбор рационального способа решения, использует свойства степени, выполняет арифметические действия и находит значение выражения |
|
Применяет свойства степени для преобразования алгебраических выражений |
Использует одно из свойств степени, затрудняется в дальнейшем выполнении задания |
Допускает ошибки при использовании одного из свойств степени ошибки вычислительного характера нахождении коэффициента выражения |
Верно, использует свойства степени, упрощает выражение. |
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ «МНОГОЧЛЕНЫ»
|
Тема |
Одночлены и действия над ними. Степень и стандартный вид одночлена. Многочлены. Степень и стандартный вид многочлена. Действия над многочленами. Тождественные преобразования выражений |
|
Цель обучения |
7.2.1.3 записать одночлен в стандартном виде 7.2.1.4 выполнять умножение одночленов и представлять одночлен в виде произведения множителей 7.2.1.7 выполнять сложение и вычитание многочленов 7.2.1.13 выполнять тождественные преобразования алгебраических выражений с помощью действий над многочленами, разложение многочлена на множители |
|
Критерий оценивания |
Обучающийся Приводит одночлен к стандартному виду Использует правила умножения одночленов при решении задач Выполняет операции сложения и вычитания многочленов Применять умножение одночленов и многочленов для решения задач Раскладывает алгебраические выражения на множители? Используя различные способы |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
20 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
|||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Количество баллов |
3 |
2 |
2 |
5 |
4 |
|
Всего баллов |
16 баллов |
||||
1 ВАРИАНТ
-
Дан одночлен

-
приведите одночлен к стандартному виду
-
укажите его коэффициент
-
укажите степень одночлена
-
Составьте выражение для нахождения площади прямоугольника, ответ запишите в стандартном виде, если его измерения выражены следующими величинами: длина = 3а2b3, ширина = 4ab4.
-
Даны многочлены p1(а)=2a+5 и p2(а)=3a – 7. Найдите:
-
p(а) = p1(а) + p2(а)
-
p(а) = p1(а) – p2(а)
-
Разложите многочлен на множители: 4ab2 – 3b2 + 8a2b – 6ab
-
Упростите выражение и найдите его значение: 5х(2х – 3) – 2,5х(4х – 2) при х = – 0,01
2 ВАРИАНТ
-
Дан одночлен

-
приведите одночлен к стандартному виду
-
укажите его коэффициент
-
укажите степень одночлена
-
Составьте выражение для нахождения площади прямоугольника, ответ запишите в стандартном виде, если его измерения выражены следующими величинами: длина = 4а5b2, ширина = 6ab3.
-
Даны многочлены p1(а)=7 – 2a и p2(а)= –1 – 5a. Найдите:
-
p(а) = p1(а) + p2(а)
-
p(а) = p1(а) – p2(а)
-
Разложите многочлен на множители: 6a2c – 3a2 + 2ac2 – ac
-
Упростите выражение и найдите его значение: 12(2 – p) + 29p – 9(p + 1) при p =

3 ВАРИАНТ
-
Дан одночлен

-
приведите одночлен к стандартному виду
-
укажите его коэффициент
-
укажите степень одночлена
-
Составьте выражение для нахождения площади прямоугольника, ответ запишите в стандартном виде, если его измерения выражены следующими величинами: длина = 5а6b, ширина = 7ab7.
-
Даны многочлены p1(а)=3a – 4 и p2(а)= 11 – 3a. Найдите:
-
p(а) = p1(а) + p2(а)
-
p(а) = p1(а) – p2(а)
-
Разложите многочлен на множители: 3b2 – a2b – 6ab + 2a3
-
Упростите выражение и найдите его значение: 5a(a2 – 4a) – 4a(a2 – 5a) при a = –3
4 ВАРИАНТ
-
Дан одночлен

-
приведите одночлен к стандартному виду
-
укажите его коэффициент
-
укажите степень одночлена
-
Составьте выражение для нахождения площади прямоугольника, ответ запишите в стандартном виде, если его измерения выражены следующими величинами: длина = 8а3b5, ширина = 5a2b3.
-
Даны многочлены p1(а)= – 4 – 3a и p2(а)= 7 – 8a. Найдите:
-
p(а) = p1(а) + p2(а)
-
p(а) = p1(а) – p2(а)
-
Разложите многочлен на множители: 2x3 – 8xy – x2y + 4y2
-
Упростите выражение и найдите его значение: 3(3d – 1) + 7(2d +1) при d =

|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Приводит одночлен к стандартному виду |
1 |
записывает ответ в стандартном виде |
1 |
|
указывает коэффициент одночлена |
1 |
||
|
указывают степень одночлена |
1 |
||
|
Использует правила умножения одночленов при решении задач |
2 |
использует формулу площади прямоугольника для составления выражения |
1 |
|
выполняет умножение и записывает ответ в стандартном виде |
1 |
||
|
Выполняет операции сложения и вычитания многочленов |
3 |
находит сумму многочленов |
1 |
|
находит разность многочленов |
1 |
||
|
Раскладывает алгебраические выражения на множители, используя различные способы |
4 |
определяет общий множитель |
1 |
|
выполняет разложение на множители |
1 |
||
|
использует метод группировки |
1 |
||
|
выносит общий множитель за скобки |
1 |
||
|
выполняет разложение на множители |
1 |
||
|
Применяет умножение одночленов и многочленов для решения задач |
5 |
умножает одночлен на многочлен |
1 |
|
приводит подобные множители |
1 |
||
|
упрощает выражение |
1 |
||
|
находит его значение |
1 |
||
|
Всего баллов |
16 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «МНОГОЧЛЕНЫ»
ФИО обучающегося _______________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
низкий |
средний |
высокий |
|
|
Приводит одночлен к стандартному виду |
Затрудняется в приведении одночлена к стандартному виду |
Допускает ошибки при определении коэффициента и степени |
Верно, приводит одночлен к стандартному виду |
|
Использует правила умножения одночленов при решении задач |
Затрудняется в составлении выражения для нахождения площади прямоугольника |
Допускает ошибки при умножении одночленов |
Верно, выполняет умножение одночленов при решении задач |
|
Выполняет операции сложения и вычитания многочленов |
Затрудняется в выполнении операции сложения и вычитания многочленов |
Допускает ошибки при выполнении операции сложения / вычитания многочленов |
Верно, выполняет операции сложения и вычитания многочленов |
|
Раскладывает алгебраические выражения на множители, используя различные способы |
Затрудняется в нахождении общего множителя |
Допускает ошибки при вынесении общего множителя за скобку |
Верно, раскладывает алгебраические выражения на множители |
|
Применяет умножение одночленов и многочленов для решения задач |
Затрудняется при умножении одночленов на многочлен |
Допускает ошибки при упрощении выражения |
Верно, выполняет умножение одночлена на многочлен и находит его значение |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ФУНКЦИЯ. ГРАФИК ФУНКЦИИ»
|
Тема |
Функция и график функции. Линейная
функция и ее график. Взаимное расположение графиков линейных
функций. Решение систем линейных уравнений с двумя переменными
графическим методом. Функция вида
у=ах2,
у=ах3,
у= |
|
Цель обучения |
7.4.1.8 обосновывать взаимное расположение графиков линейных функций в зависимости от значений их коэффициентов 7.4.1.10 строить графики функции у=ах2 (а≠0) и знать ее свойства 7.4.1.5 знать определение линейной функции у= kx+b, строить ее график и устанавливать его расположение в зависимости от значений k и b 7.4.2.4 решать системы линейных уравнений графическим способом 7.4.1.3 находить область определения и множество значений функции |
|
Критерии оценивания |
Обучающийся Определяет расположение графиков функций, соответствующее заданному условию параллельности / пересечения в одной точке Определяет график функции у=ах2 Устанавливает расположение графика линейной функции по ее уравнению Использует графики функций для решения систем уравнений Находит область определения и множество значений функции |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
20 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
|||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Количество баллов |
2 |
1 |
2 |
5 |
4 |
|
Всего баллов |
14 баллов |
||||
1 ВАРИАНТ
1.Выберите функции, графики которых параллельны, ответ обоснуйте:
-
у=4 и у=х-4
-
у=х-6 и у=2х-6
-
у= -5х-5 и у= -6х+7
-
у= -2х+6 и у= -2х+2
-
у=1,5х-3 и у=4х+2
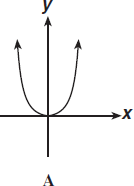
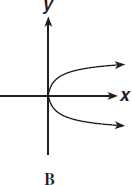
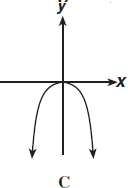
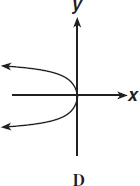
2.Укажите график функции у= х2:
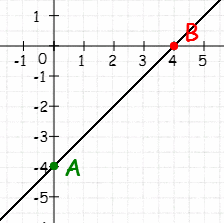
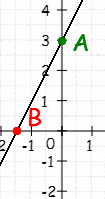
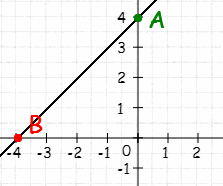
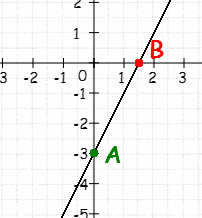
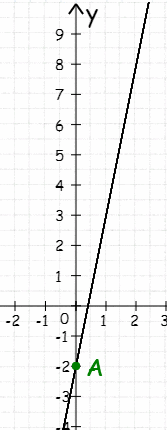
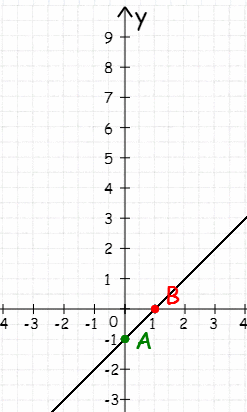
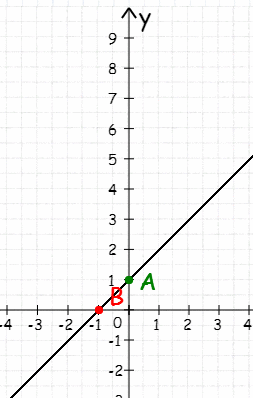
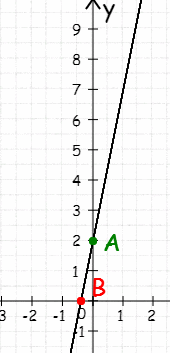
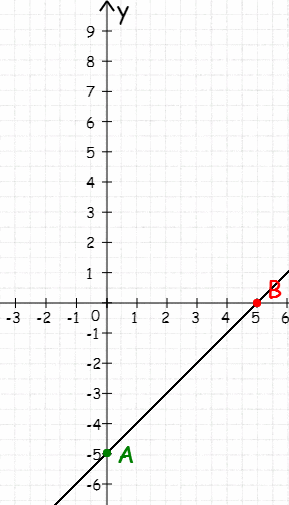
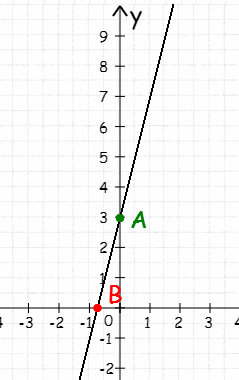
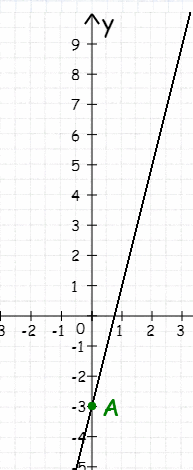
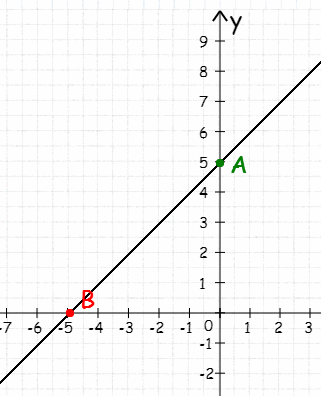
3.Установите соответствие между функциями и их графиками:
-
у= 3х-2
-
у= х+3
-
у=3х+2
-
у=х-3
|
|
|
|
|
a) b) c) d)
4.Решите систему уравнений графическим способом:
![]()
5.Найдите:
а) область определения функции, заданной формулой:
1) у=7-3х 2)
![]()
б) область значений
функции ![]() ,
на отрезке -3≤х
,
на отрезке -3≤х![]()
2 ВАРИАНТ
1.Выберите функции, графики которых параллельны, ответ обоснуйте:
-
у=-3х+2 и у=-3х+1
-
у=5х+3 и у=2х+1
-
у= -5х+6 и у= -3х+11
-
у= -х+6 и у= -4х+2
-
у=2,5х+1 и у=1,5х+4
2.Укажите график функции у= 3х2:
3.Установите соответствие между функциями и их графиками:
-
у= 2х+3
-
у= х+4
-
у=х-4
-
у=2х-3
|
|
|
|
|
a) b) c) d)
4.Решите систему уравнений графическим способом:
![]()
5.Найдите:
а) область определения функции, заданной формулой:
1) у=9-2x 2)
![]()
б) область значений
функции ![]() ,
на отрезке -3≤х
,
на отрезке -3≤х![]()
3 ВАРИАНТ
1.Выберите функции, графики которых параллельны, ответ обоснуйте:
-
у=0,5х+4 и у=-2,5х-2
-
у=2х+3 и у=2х-4
-
у= -х+4 и у= -3х-1
-
у= 2х+1 и у=1,5х
-
у=2,5х+6 и у=2х-1
2.Укажите график функции у= -2х2:
3.Установите соответствие между функциями и их графиками:
-
у= 5х+2
-
у= х+1
-
у=5х-2
-
у=х-1
|
|
|
|
|
a) b) c) d)
4.Решите систему уравнений графическим способом:
![]()
5.Найдите:
а) область определения функции, заданной формулой:
1) у=6+4х 2)
![]()
б) область значений
функции ![]() ,
на отрезке -2≤х
,
на отрезке -2≤х![]()
4 ВАРИАНТ
1.Выберите функции, графики которых параллельны, ответ обоснуйте:
-
у=2х+4 и у=2х+1
-
у=-2х и у= -4+3х
-
у= -х+6 и у= -3х+2
-
у= 3х-1 и у=1,5х+3
-
у=2х-6 и у=-2х+8
2.Укажите график функции у= -4х2:
3.Установите соответствие между функциями и их графиками:
-
у= 4х+3
-
у= х-5
-
у=4х-3
-
у=х+5
|
|
|
|
|
a) b) c) d)
4.Решите систему уравнений графическим способом:
![]()
5.Найдите:
а) область определения функции, заданной формулой:
1) у=5+6х 2)
![]()
б) область значений
функции ![]() ,
на отрезке -1≤х
,
на отрезке -1≤х![]()
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Определяет расположение графиков функций соответствующее заданному условию параллельности/ пересечения в одной точке |
1 |
Указывает функции, графики которых параллельны |
1 |
|
Обосновывает ответ, используя условие параллельности |
1 |
||
|
Определяет график функции у= ах2 |
2 |
Выбирает график заданной функции |
1 |
|
Устанавливает расположение графика линейной функции по ее уравнению |
3 |
Устанавливает соответствие между функциями и их графиками в двух случаях |
1 |
|
Устанавливает соответствие между функциями и их графиками в оставшихся случаях |
1 |
||
|
Использует графики функций для решения систем уравнений |
4 |
Приводит уравнения функций к виду у= kx+b |
1 |
|
Выполняет построение графика первого уравнения |
1 |
||
|
Выполняет построение графика второго уравнения |
1 |
||
|
Определяет точку пересечения графиков на плоскости |
1 |
||
|
Записывает ответ решения системы уравнений |
1 |
||
|
Находит область определения и множество значений функции |
5 |
Находит область определения первой функции |
1 |
|
Находит область определения второй функции |
1 |
||
|
Находит значение функции на концах отрезка области определения |
1 |
||
|
Записывает в ответ область значений функции, используя математический язык |
1 |
||
|
Всего баллов |
14 |
||
РУБРИКА ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ФУНКЦИЯ. ГРАФИК ФУНКЦИИ»
ФИ обучающегося_________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Определяет расположение графиков функций соответствующее заданному условию параллельности/пересечения в одной точке |
Затрудняется в определении взаимного расположения прямых |
Выбирает функции, графики которых параллельны, допускает ошибки при обосновании |
Определяет линейные функции, графики которых параллельны, верно обосновывает ответ |
|
Определяет график функции у=ах2 |
Затрудняется в определении графика функции у=ах2 |
Выбирает параболу, ветви которой симметричны относительно Оу, допускает ошибку при анализе коэффициента (а=-1, значит ветви направлены вниз) |
Верно определяет график функции у=ах2 |
|
Устанавливает расположение графика линейной функции по ее уравнению |
Затрудняется в определении графика линейной функции по ее уравнению |
Оценивает расположение графика функции по значениям коэффициентов k и b, однако, допускает ошибки при соотнесении графика функции с ее уравнением |
Верно использует свойства коэффициентов k и b, соотносит графики с уравнениями функций |
|
Использует графики функций для решения систем уравнений |
Затрудняется в решении систем линейных уравнений графическим способом |
Понимает, что решением систем является точка пересечения графиков функций (находит точки пересечения графиков), однако, допускает ошибки при построении одного их графиков или находит только абсциссу/ординату точки пересечения |
В одной системе координат выполняет построение графиков функций, находит точку пересечения графиков, интерпретирует ее как ответ решения системы уравнений |
|
Находит область определения и множество значений функции |
Затрудняется в нахождении области определения и множества значений функции |
Допускает ошибки при нахождении области определения одной из функций/множества значений функции |
Верно находит область определения и множество значений функции |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ЭЛЕМЕНТЫ СТАТИСТИКИ»
|
Тема |
Вариационные ряды. Абсолютная частота и относительная частота. Таблица частот. Полигон частот. |
|
Цель обучения |
7.3.3.2 вычислять абсолютную и относительную частоты варианты 7.3.3.4 представлять выборку в виде частотной таблицы. |
|
Критерии оценивания |
Обучающийся Находит абсолютную частоту и относительную частоты выборки Представляет выборку в виде частотной таблицы |
|
Уровень мыслительных навыков |
Применение
|
|
Время выполнения |
15 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
4 |
4 |
|
|
Всего баллов |
8 баллов |
||
1 ВАРИАНТ
-
Для итоговой контрольной работы был создан тест из 10 заданий. Количество верных ответов, полученных каждым из 40 учащихся, было представлено в виде таблицы частот. Найдите пропущенное значение частоты.
|
Число верных ответов |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Частота |
1 |
2 |
|
1 |
1 |
5 |
14 |
3 |
6 |
3 |
2 |
-
Для определения оптимального плана выпуска мужской обуви фиксировалась относительная частота (в процентах) размеров проданной в течение месяца обуви. Найдите пропущенное значение относительной частоты.
|
Размер обуви |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
|
Относительная частота, % |
19 |
12 |
19 |
|
17 |
12 |
8 |
3 |
-
На выборах акима города будут баллотироваться три кандидата: Иванов, Петров, Сидоров (обозначим из букв И, П, С). Проведя опрос 30 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:
С, П, П, П, И, С, П, П, И, С, П, П, П, И, И,
П, С, С, И, И, С, И, П, С, И, П, И, С, И, И.
-
Представьте эти данные в виде таблицы абсолютной и относительной частот.
-
Проверьте данные таблицы на непротиворечивость.
2 ВАРИАНТ
-
Для итоговой контрольной работы был создан тест из 9 заданий. Количество верных ответов, полученных каждым из 30 учащихся, было представлено в виде таблицы частот. Найдите пропущенное значение частоты.
-
Число верных ответов
0
1
2
3
4
5
6
7
8
9
Частота
2
4
3
1
6
3
5
1
4
-
Для определения оптимального плана выпуска мужской обуви фиксировалась относительная частота (в процентах) размеров проданной в течение месяца обуви. Найдите пропущенное значение относительной частоты.
|
Размер обуви |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
Относительная частота, % |
13 |
19 |
12 |
19 |
|
17 |
12 |
-
На выборах акима города будут баллотироваться три кандидата: Ахметов, Нигметов, Садвокасов (обозначим из букв А, Н, С). Проведя опрос 25 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:
А, А, Н, С, С, С, Н, А, А, С, А, Н, С, Н, Н, А, С, Н, Н, С, С, С, А, Н, Н.
-
Представьте эти данные в виде таблицы абсолютной и относительной частот.
-
Проверьте данные таблицы на непротиворечивость.
3 ВАРИАНТ
-
Для итоговой контрольной работы был создан тест из 7 заданий. Количество верных ответов, полученных каждым из 35 учащихся, было представлено в виде таблицы частот. Найдите пропущенное значение частоты.
|
Число верных ответов |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Частота |
1 |
3 |
3 |
|
6 |
6 |
8 |
4 |
-
Для определения оптимального плана выпуска мужской обуви фиксировалась относительная частота (в процентах) размеров проданной в течение месяца обуви. Найдите пропущенное значение относительной частоты.
|
Размер обуви |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
Относительная частота, % |
13 |
19 |
19 |
|
12 |
21 |
8 |
-
На выборах акима города будут баллотироваться три кандидата: Ашимов, Ильясов, Жумабаев (обозначим из букв А, И, Ж). Проведя опрос 20 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:
А, А, Ж, Ж, И, И, Ж, А, А, И, А, Ж, Ж, И, И, Ж, Ж, А, И, Ж.
-
Представьте эти данные в виде таблицы абсолютной и относительной частот.
-
Проверьте данные таблицы на непротиворечивость.
4 ВАРИАНТ
-
Для итоговой контрольной работы был создан тест из 12 заданий. Количество верных ответов, полученных каждым из 40 учащихся, было представлено в виде таблицы частот. Найдите пропущенное значение частоты.
|
Число верных ответов |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Частота |
2 |
1 |
1 |
4 |
6 |
5 |
|
1 |
4 |
3 |
8 |
2 |
1 |
-
Для определения оптимального плана выпуска мужской обуви фиксировалась относительная частота (в процентах) размеров проданной в течение месяца обуви. Найдите пропущенное значение относительной частоты.
|
Размер обуви |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|
Относительная частота, % |
13 |
19 |
10 |
|
12 |
21 |
8 |
8 |
-
На выборах акима города будут баллотироваться три кандидата: Архипов, Исамуддинов, Жакбаев (обозначим из букв А, И, Ж). Проведя опрос 30 избирателей, выяснили, за кого из кандидатов они собираются голосовать. Получили следующие данные:
А, А, Ж, Ж, И, И, Ж, А, А, И, А, Ж, Ж, И, И, Ж, Ж, А, И, Ж, И, А, А, А, Ж, И, А, Ж, И, И.
-
Представьте эти данные в виде таблицы абсолютной и относительной частот.
-
Проверьте данные таблицы на непротиворечивость.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Находит абсолютную и относительную частоты варианты |
1,2 |
Составляет выражение, используя значение суммы частот |
1 |
|
Вычисляет абсолютную частоту варианты |
1 |
||
|
Составляет выражение, используя значение суммы частот |
1 |
||
|
Вычисляет относительную частоту варианты |
1 |
||
|
Представляет выборку в виде таблицы частот |
3 |
Определяет варианту |
1 |
|
Записывает абсолютные частоты |
1 |
||
|
Записывает относительные частоты |
1 |
||
|
Проверяет данные таблицы на непротиворечивость |
1 |
||
|
Всего баллов |
|
|
8 |
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ЭЛЕМЕНТЫ СТАТИСТИКИ»
ФИО ОБУЧАЮЩЕГОСЯ______________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Находит абсолютную и относительную частоты варианты |
Затрудняется в нахождении абсолютной и относительной частоты |
Использует значение сумм частот, допускает ошибки вычислительного характера при вычислении абсолютной/относительной частоты. |
Использует значение сумм частот, проводит вычисления и находит верный ответ |
|
Представляет выборку в виде таблиц частот |
Определяет варианты. Затрудняется в заполнении остальных таблицы частот. |
Представляет выборку в виде таблицы частот, составляет строку абсолютных частот. Допускает ошибки при вычислениях относительной частоты/ при осуществлении проверки на непротиворечивость |
Определяет варианты, составляет строку абсолютных частот, находит значение относительных частот. Осуществляет проверку на непротиворечивость, используя значение сумм частот. |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ»
|
Подраздел |
Формулы сокращённого умножения. Преобразования выражений с помощью формул сокращённого умножения. Решение текстовых задач |
|
Цели обучения |
7.2.1.14 Раскладывать алгебраические выражения на множители с помощью формул сокращенного умножения 7.2.1.10 Знать и применять формулы сокращённого умножения
7.2.1.11 Знать и применять формулы сокращённого умножения
7.1.2.14 Использовать формулы сокращённого умножения для рационального счёта 7.4.2.2 Решать текстовые задачи, с помощью составления уравнений и неравенств |
|
Критерии оценивания |
Обучающийся Использует формулы сокращенного умножения для разложения алгебраических выражений на множители Применяет формулы сокращенного умножения для решения задач Использует формулы сокращенного умножения для рационального счета Решает текстовые задачи, с помощью составления уравнения / неравенства |
|
Уровень мыслительных навыков |
применение навыки высокого порядка |
|
Время выполнения |
25 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
2 |
3 |
5 |
5 |
|
Всего баллов |
15 баллов |
|||
-
ВАРИАНТ
1. Разложите на множители:
-
Докажите, что значение выражения: 413+193 делится на 60
3. Вычислите: ![]()
4. Решите задачу с помощью составления уравнения: Разность двух чисел равна 9, а разность их квадратов 369. Найдите эти числа.
-
ВАРИАНТ
1. Разложите на множители:
2. Докажите, что значение выражения: 793 – 293 делится на 50
3.
Вычислите: ![]()
4. Решите задачу с помощью составления уравнения:
Сумма двух чисел равна 26, а разность их квадратов составляет 52. Найдите эти числа.
3 ВАРИАНТ
1. Разложите на множители:
2. Докажите, что значение выражения: 4663+343 делится на 500
3. Вычислите: ![]()
4. Решите задачу с помощью составления уравнения:
Разность двух чисел равна 17, а разность их квадратов 799. Найдите эти числа.
4 ВАРИАНТ
1. Разложите на множители:
2. Докажите, что значение выражения: 543 – 243 делится на 30
3.
Вычислите: ![]()
4. Решите задачу с помощью составления уравнения: Сумма двух чисел равна 32, а разность их квадратов составляет 64. Найдите эти числа.
|
Критерий оценивания |
№ |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Использует формулы сокращенного умножения для разложения алгебраических выражений на множители |
1 |
раскладывает на множители первое выражение |
1 |
|
раскладывает на множители второе выражение |
1 |
||
|
Доказывает делимость значения выражения на число |
2 |
Упрощает выражение |
1 |
|
Получает результат |
1 |
||
|
Делает вывод |
1 |
||
|
Использует формулы сокращенного умножения для рационального счета |
3 |
использует формулу квадрата разности (квадрата суммы); |
1 |
|
использует формулу разности квадратов; |
1 |
||
|
находит значение числителя |
1 |
||
|
находит значение знаменателя |
1 |
||
|
выполняет сокращение дроби; |
1 |
||
|
Решает текстовые задачи, с помощью составления уравнения / неравенства |
4 |
вводит переменную; |
1 |
|
составляет уравнение по условию задачи; |
1 |
||
|
применяет формулу разности квадратов; |
1 |
||
|
решает уравнение; |
1 |
||
|
находит ответ. |
1 |
||
|
Итого: |
15 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ»
ФИ ОБУЧАЮЩЕГОСЯ_______________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Использует формулы сокращенного умножения для разложения алгебраических выражений на множители. |
Затрудняется в разложении алгебраического выражения на множители. |
Выносит множитель за скобку, допускает ошибки в знаках при использовании ФСУ. |
|
|
Доказывает делимость значения выражения на число |
Затрудняется в применении формул сокращенного умножения. |
Выполняет задание, не используя ФСУ / допускает ошибки при использовании ФСУ при упрощении выражения |
|
|
Использует формулы сокращенного умножения для рационального счета. |
Затрудняется в применении формул сокращенного умножения /выбирает нерациональный путь счета. |
Использует ФСУ, допускает ошибки вычислительного характера в одном из случаев / при сокращении дроби. |
Осуществляет выбор ФСУ, использует формулу для
рационального счета, находит значение
выражения. |
|
Решает текстовые задачи, с помощью составления уравнения / неравенства. |
Демонстрирует основы математического моделирования условия задачи, однако, затрудняется при составлении уравнения. |
Составляет уравнение по условию задачи, применяет ФСУ, допускает ошибки при решении уравнения / находит только одно число. |
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ «АЛГЕБРАИЧЕСКИЕ ДРОБИ»
|
Подраздел |
Алгебраическая дробь и ее основное свойство. Действия над алгебраическими дробями. Тождественные преобразования алгебраических выражений |
|
Цели обучения |
7.2.1.18
применять основное свойство алгебраической дроби
7.2.1.19 выполнять сложение и вычитание алгебраических дробей 7.2.1.20 выполнять умножение и деление, возведение в степень алгебраических дробей 7.2.1.21 выполнять преобразования алгебраических выражений |
|
Критерии оценивания |
Обучающийся Сокращает алгебраические дроби Выполняет сложение и вычитание алгебраических дробей Выполняет деление алгебраических дробей Преобразовывает выражения, содержащие алгебраические дроби |
|
Уровень мыслительных навыков |
применение навыки высокого порядка |
|
Время выполнения |
25 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
3 |
3 |
4 |
3 |
|
Всего баллов |
13 баллов |
|||
1 ВАРИАНТ
1. Сократить дробь:
а) ![]() ; б)
; б) ![]() ;
;
2. Выполните действия:
а)![]()
3. Найдите значение выражения:
![]()
4. Если
![]() = в,
= в, ![]() =
=
![]() , то чему
равно
, то чему
равно ![]() ?
?
2 ВАРИАНТ
1. Сократить дробь:
а) ![]() ; б)
; б) ![]() ;
;
2. Выполните действия:
а)![]() б)
б)![]()
3. Найдите значение выражения:
![]() ;
;
4. Если
![]() = с,
= с, ![]() =
=
![]() , то чему
равно
, то чему
равно ![]() ?
?
3 ВАРИАНТ
1. Сократить дробь:
а) ![]() ; б)
; б) ![]() ;
;
2. Выполните действия:
а)![]() б)
б)![]()
3. Найдите значение выражения:
![]() ;
;
4. Если
![]() = d,
= d,
![]() =
= ![]() , то чему
равно
, то чему
равно ![]() ?
?
4 ВАРИАНТ
1. Сократить дробь:
а) ![]() ; б)
; б) ![]() ;
;
2. Выполните действия:
а)![]() б)
б)![]()
3. Найдите значение выражения:
![]()
4. Если
![]() =
f,
=
f, ![]() =
=
![]() , то чему равно
, то чему равно
![]() ?
?
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Сокращает алгебраические дроби |
1 |
Использует вынесение общего множителя |
1 |
|
использует ФСУ для разложения на множители |
1 |
||
|
сокращает дроби |
1 |
||
|
Выполняет сложение и вычитание алгебраических дробей |
2 |
определяет общий знаменатель дробей |
1 |
|
выполняет сложение дробей |
1 |
||
|
выполняет вычитание дробей |
1 |
||
|
Выполняет деление алгебраических дробей
|
3 |
использует ФСУ для разложения на множители |
1 |
|
выносит общий множитель за скобки |
1 |
||
|
выполняет деление дробей |
1 |
||
|
находит значение выражения |
1 |
||
|
Преобразовывает выражения, содержащие алгебраические дроби
|
4 |
выражает переменную у во втором выражении / выражает x через у в первом выражении |
1 |
|
Подставляет выраженное значение в первое выражение / выражает z через y во втором выражении |
1 |
||
|
определяет значение выражения |
1 |
||
|
Всего баллов: |
13 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «АЛГЕБРАИЧЕСКИЕ ДРОБИ»
ФИ ОБУЧАЮЩЕГОСЯ ___________________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Сокращает алгебраические дроби |
Сокращает дробь, не выполняя разложение на множители |
Допускает ошибки при сокращении одной из дробей /вынесение общего множителя/ применении ФСУ |
Выполняет разложение на множители, сокращает дроби |
|
Выполняет сложение и вычитание алгебраических дробей |
Затрудняется при сложении и вычитании алгебраических дробей |
Определяет алгоритм выполнения действий, приводит дроби к общему знаменателю, однако, допускает ошибки при сложении / вычитании дробей |
Определяет алгоритм выполнения действий, находит общий знаменатель, дополнительные множители к каждой дроби, получает верный ответ |
|
Выполняет деление алгебраических дробей |
Затрудняется при делении алгебраических дробей |
Определяет алгоритм выполнения действий, однако, совершает ошибки в выполнении преобразований при делении / ошибки вычислительного характера |
Определяет алгоритм выполнения действий, выполняет разложение на множители числителя и знаменателя, сокращает дробь, находит значение выражения при заданном значении переменной |
|
Преобразовывает выражения, содержащие алгебраические дроби |
Затрудняется в выборе алгоритма действий для ответа на вопрос |
Допускает ошибки при выражении переменных в исходных выражениях / получает неверный ответ |
Выбирает рациональный способ решения, выполняет преобразование выражения, находит значение выражения |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
ОБЗОР СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Продолжительность – 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с множественным выбором ответов, кратким и развернутым ответом.
В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Характеристика заданий суммативного оценивания
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Степень с целым показателем |
7.4.2.3 оценивать, как изменяются площадь квадрата и объём куба при изменении их линейных размеров |
Навыки высокого порядка |
1 |
6 |
РО |
12 |
6 |
13 |
|
7.2.1.1 применять свойства степени с целым показателем при нахождении значений числовых выражений |
Применение |
1 |
5 |
РО |
8 |
4 |
||
|
7.1.1.1 записывать числа в стандартном виде |
Применение |
1 |
4 |
КО |
6 |
3 |
||
|
7.1.2.7 выполнять арифметические действия над числами, записанными в стандартном виде |
Применение |
|||||||
|
Многочлены |
7.2.1.2 знать определение одночлена, находить его коэффициент и степень |
Знание и понимание |
1 |
1 |
МВО |
2 |
1 |
7 |
|
7.2.1.6 приводить многочлен к стандартному виду |
Применение |
1 |
2 |
КО |
6 |
3 |
||
|
7.2.1.7 выполнять сложение и вычитание многочленов |
Применение |
|||||||
|
7.2.1.5 знать определение многочлена и находить его степень |
Знание и понимание |
|||||||
|
7.2.1.12 раскладывать алгебраические выражения на множители вынесением общего множителя за скобки и способом группировки |
Применение |
1 |
3 |
РО |
6 |
3 |
||
|
7.2.1.13 выполнять тождественные преобразования алгебраических выражений с помощью действий над многочленами, разложения многочлена на множители |
Применение |
|||||||
|
ИТОГО: |
|
|
6 |
|
|
40 |
20 |
20 |
|
Примечание: * - разделы, в которые можно вносить изменения |
||||||||
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
1 |
3 |
3 |
3 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
1 ВАРИАНТ
1. Определите коэффициент и степень
одночлена ![]()
-
 и
4
и
4 -
 и
3
и
3 -
 и
4
и
4 -
 и
3
и
3 -
7 и 4
2. Найдите периметр фигуры. Ответ запишите в виде многочлена стандартного вида и укажите его степень.
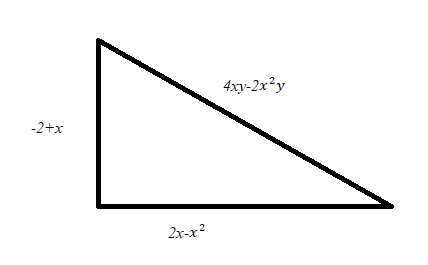
3.
Разложите
на множители:![]() .
.
4. Запишите числа а= 2100000 и в=0,0007 в стандартном виде и найдите их произведение.
5. Вычислите: ![]()
6. Если ребро куба увеличить в 4 раза, то как изменится объем куба и площадь его основания ?
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
Вопрос № |
Ответ |
Балл |
Дополнительная информация |
|
1 |
С |
1 |
указан верный ответ |
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 |
1 |
|
|
|
3 |
(2x- |
1 |
|
|
x(2-x)+2xy(2-x)-(2-x) |
1 |
|
|
|
(2-x)(x+2xy-1) |
1 |
|
|
|
4 |
2100000 |
1 |
|
|
0,0007=0,7 |
1 |
|
|
|
1,47 |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
5-1+ |
1 |
|
|
|
6 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Принимать другие правильные альтернативные решения |
|
|
Итого: |
20 |
|
|
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
1 |
3 |
3 |
3 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
2 ВАРИАНТ
1. Определите коэффициент и степень
одночлена ![]()
A) ![]() и 5
и 5
![]() и
3
и
3
![]() и
5
и
5
![]() и
2
и
2
E) 9 и 3
2. Найдите периметр фигуры. Ответ запишите в виде многочлена стандартного вида и укажите его степень.
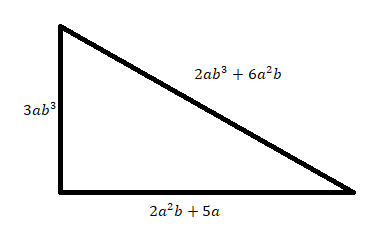
3.
Разложите
на множители:![]() a-1
a-1
4. Запишите числа а= 625000000 и в=0,000003 в стандартном виде и найдите их произведение.
5. Вычислите: ![]()
6. Если ребро куба увеличить в 5 раза, то как изменится объем куба и площадь его основания ?
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
Вопрос № |
Ответ |
Балл |
Дополнительная информация |
|
1 |
С |
1 |
указан верный ответ |
|
2 |
|
1 |
|
|
5 |
1 |
|
|
|
4 |
1 |
|
|
|
3 |
(2 |
1 |
|
|
2 |
|
|
|
|
(a+1)(2 |
|
|
|
|
4 |
625000000 |
1 |
|
|
0,000003=0,3 |
1 |
|
|
|
1,875 |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
16-1+ |
1 |
|
|
|
6 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Принимать другие правильные альтернативные решения |
|
|
Итого: |
20 |
|
|
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
1 |
3 |
3 |
3 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
3 ВАРИАНТ
1. Определите коэффициент и степень
одночлена ![]()
A ) ![]() и 4
и 4
![]() и
5
и
5
![]() и
5
и
5
![]() и
4
и
4
E)13 и 5
2. Найдите периметр фигуры. Ответ запишите в виде многочлена стандартного вида и укажите его степень.
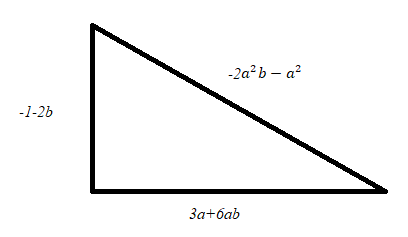
3.
Разложите
на множители:![]() .
.
4. Запишите числа а= 1600000 и в=0,00012 в стандартном виде и найдите их произведение.
5. Вычислите: ![]()
6. Если ребро куба увеличить в 6 раза, то как изменится объем куба и площадь его основания ?
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
Вопрос № |
Ответ |
Балл |
Дополнительная информация |
|
1 |
С |
1 |
указан верный ответ |
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 |
1 |
|
|
|
3 |
(3a+6ab |
1 |
|
|
3a(1+2b)- |
1 |
|
|
|
(1+2b)(3a |
1 |
|
|
|
4 |
1600000 |
1 |
|
|
0,00012=1,2 |
1 |
|
|
|
1,92 |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
7-1+ |
1 |
|
|
|
6 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Принимать другие правильные альтернативные решения |
|
|
Итого: |
20 |
|
|
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
1 |
3 |
3 |
3 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
4 ВАРИАНТ
1. Определите коэффициент и степень
одночлена ![]()
A) ![]() и 5
и 5
![]() и
3
и
3
![]() и
8
и
8
![]() и
8
и
8
E) 9 и 8
2. Найдите периметр фигуры. Ответ запишите в виде многочлена стандартного вида и укажите его степень.
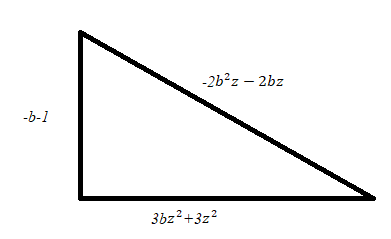
3.
Разложите
на множители:![]() b
b![]() 1
1
4. Запишите числа а= 324000000 и в=0,000005 в стандартном виде и найдите их произведение.
5. Вычислите: ![]()
6. Если ребро куба увеличить в 7 раза, то как изменится объем куба и площадь его основания ?
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
Вопрос № |
Ответ |
Балл |
Дополнительная информация |
|
1 |
С |
1 |
указан верный ответ |
|
2 |
|
1 |
|
|
7 |
1 |
|
|
|
4 |
1 |
|
|
|
3 |
(3b |
1 |
|
|
3 |
1 |
|
|
|
(b+1)(3 |
1 |
|
|
|
4 |
324000000 |
1 |
|
|
0,000005=0,5 |
1 |
|
|
|
1,62 |
1 |
|
|
|
5 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2 |
1 |
|
|
|
6 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Принимать другие правильные альтернативные решения |
|
|
Итого: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
ОБЗОР СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 2 ЧЕТВЕРТЬ
Продолжительность - 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
СТРУКТУРА СУММАТИВНОГО ОЦЕНИВАНИЯ
Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответом.
В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков
|
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Функция. График функции |
7.4.1.5знать определение линейной функции y=kx+b, строить её график и устанавливать его расположение в зависимости от значений k и b |
Применение |
1 |
1 |
МВО |
2 |
1 |
12 |
|
7.4.1.7 определять знаки k и b линейной функции y=kx+b, заданной графиком |
Применение |
|||||||
|
7.4.1.12 строить график функции у=кх (k≠0) и знать её свойства |
Применение
|
1 |
|
МВО |
2 |
1 |
||
|
7.4.1.9 задавать формулой линейную функцию, график которой параллелен графику данной функции или пересекает его |
Применение
|
1 |
3 |
КО |
6 |
3 |
||
|
7.4.1.4 знать определение функции y=kx, строить её график и устанавливать его расположение в зависимости от k |
Применение
|
|
|
|
|
|
||
|
7.4.2.4 решать системы линейных уравнений графическим способом |
Применение
|
1 |
4 |
РО |
6 |
3 |
||
|
7.4.1.6 находить точки пересечения графика линейной функции с осями координат (без построения графика) |
Применение
|
1 |
2 |
РО |
2 |
4 |
||
|
7.4.1.5 знать определение линейной функции y=kx+b, строить её график и устанавливать его расположение в зависимости от значений k и b |
Применение
|
|||||||
|
7.4.1.8обосновывать взаимное расположение графиков линейных функций в зависимости от значений их коэффициентов |
Навыки высокого порядка
|
|||||||
|
Элементы статистики
|
7.3.3.2 вычислять абсолютную и относительную частоты варианты |
Применение |
1 |
5 |
РО |
8 |
4 |
8 |
|
7.3.3.5 проверять данные таблицы на непротиворечивость |
Применение |
|||||||
|
7.3.3.7 анализировать статистическую информацию, представленную в виде таблицы или полигона частот |
Навыки высокого порядка
|
1 |
КО |
8 |
4 |
|||
|
ИТОГО: |
|
|
7 |
|
|
40 |
20 |
20 |
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
3 |
3 |
4 |
4 |
4 |
|
Всего баллов |
20 баллов |
|||||
1 ВАРИАНТ
-
Найдите значение коэффициента k, если известно, что график функции
 проходит через точку с координатами А(1;
-6).
проходит через точку с координатами А(1;
-6).
-
-6
-
1
-
-1
-
6
-
Найдите координаты точки пересечения функции
 с
осью абсцисс:
с
осью абсцисс:
-
(0; 8)
-
(

-
(

-
(-8; 0)
-
Задайте формулой функцию, график которой проходит через точку (0; 5) и параллелен графику функции у=-2х.
-
Решите графическим способом систему уравнений:
![]()
-
Социологи опросили 20 школьников, выясняя, сколько книг каждый из них прочел за прошедший месяц. Были получены следующие данные:
0,4,6,2,1,1,1,0,3,5,1,3,2,2,3,4,6,7,2,3.
а) постройте таблицу абсолютных частот и таблицу относительных частот;
б) укажите самое распространенное число прочитанных книг;
в) проверьте таблицу относительных частот на непротиворечивость.
6. График функции, заданной уравнением у=(a +1)x+a-1 пересекает ось абсцисс в точке с координатами (-3; 0).
-
Найдите значение а;
-
Запишите функцию в виде у=kx+b;
-
Не выполняя построения графика функции, определите, через какую четверть график не проходит.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||||||||||||||||||||||||
|
1 |
Использует свойство принадлежности точки к графику функции |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Верно, выполняет вычисления. Ответ А |
1 |
|
||||||||||||||||||||||||||||||||||||
|
2 |
Использует свойство пересечения с осями координат |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Верно подставляет значения координат |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Верно выполняет вычисления Ответ: D |
1 |
|
||||||||||||||||||||||||||||||||||||
|
3 |
|
1 |
|
|||||||||||||||||||||||||||||||||||
|
b = 5 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
|
1 |
|
||||||||||||||||||||||||||||||||||||
|
4 |
Изображает
график функции |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Изображает
график функции |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Находит координаты точки пересечения графиков: |
1 |
(4; 6) |
||||||||||||||||||||||||||||||||||||
|
Записывают ответ x = 4; y = 6 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
5 |
|
1 |
|
|||||||||||||||||||||||||||||||||||
или
|
1 |
Принимать любой альтернативный вариант |
||||||||||||||||||||||||||||||||||||
|
Самое распространенное число: 1, 2, 3 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
или 10% + 20% + 20% + 20%+10% + 5% +10% + 5% = 100% |
1 |
|
||||||||||||||||||||||||||||||||||||
|
6 |
Для нахождения значения а, в заданное уравнение подставляет координаты точки, через которую проходит график функции а = -2 |
1 |
|
|||||||||||||||||||||||||||||||||||
|
к=-1, b=-3 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
у=-х - 3 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Не проходит через I четверть |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Всего баллов: |
20 |
|
||||||||||||||||||||||||||||||||||||
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
3 |
3 |
4 |
4 |
4 |
|
Всего баллов |
20 баллов |
|||||
2 ВАРИАНТ
-
Найдите значение коэффициента k, если известно, что график функции
 проходит через точку с координатами А(1;
-4).
проходит через точку с координатами А(1;
-4).
-
-4
-
1
-
-1
-
4
-
Найдите координаты точки пересечения функции
 с
осью абсцисс:
с
осью абсцисс:
-
(0; 18)
-
(

-
(

-
(-18; 0)
-
Задайте формулой функцию, график которой проходит через точку (0; 3) и параллелен графику функции у=-4х.
-
Решите графическим способом систему уравнений:
![]()
-
Социологи опросили 20 школьников, выясняя, сколько книг каждый из них прочел за прошедший месяц. Были получены следующие данные:
0,2,1,7,1,3,1,0,3,5,1,3,2,2,3,4,6,0,2,0.
а) постройте таблицу абсолютных частот и таблицу относительных частот;
б) укажите самое распространенное число прочитанных книг;
в) проверьте таблицу относительных частот на непротиворечивость.
-
График функции, заданной уравнением у=(a +1)x+a-1 пересекает ось абсцисс в точке с координатами
(-2; 0).
-
Найдите значение а;
-
Запишите функцию в виде у=kx+b;
-
Не выполняя построения графика функции, определите, через какую четверть график не проходит.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||||||||||||||||||||||||
|
1 |
Использует свойство принадлежности точки к графику функции |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Верно, выполняет вычисления. Ответ А |
1 |
|
||||||||||||||||||||||||||||||||||||
|
2 |
Использует свойство пересечения с осями координат |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Верно подставляет значения координат |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Верно выполняет вычисления Ответ: D |
1 |
|
||||||||||||||||||||||||||||||||||||
|
3 |
|
1 |
|
|||||||||||||||||||||||||||||||||||
|
b = 3 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
|
1 |
|
||||||||||||||||||||||||||||||||||||
|
4 |
Изображает
график функции |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Изображает
график функции |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Находит координаты точки пересечения графиков |
1 |
(4; -1) |
||||||||||||||||||||||||||||||||||||
|
Записывают ответ x = 4; y = -1 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
5 |
|
1 |
|
|||||||||||||||||||||||||||||||||||
или
|
1 |
Принимать любой альтернативный вариант |
||||||||||||||||||||||||||||||||||||
|
Самое распространенное число: 0, 1, 2, 3 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
или 20% + 20% + 20% + 20%+5% + 5% +5% + 5% = 100% |
1 |
|
||||||||||||||||||||||||||||||||||||
|
6 |
Для нахождения значения а, в заданное уравнение подставляет координаты точки, через которую проходит график функции а = - 3 |
1 |
|
|||||||||||||||||||||||||||||||||||
|
к= - 2, b= - 4 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
у= - 2 х - 4 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Не проходит через I четверть |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Всего баллов: |
20 |
|
||||||||||||||||||||||||||||||||||||
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
3 |
3 |
4 |
4 |
4 |
|
Всего баллов |
20 баллов |
|||||
3 ВАРИАНТ
-
Найдите значение коэффициента k, если известно, что график функции
 проходит через точку с координатами А(1;
-7).
проходит через точку с координатами А(1;
-7).
-
-7
-
1
-
-1
-
7
-
Найдите координаты точки пересечения функции
 с
осью абсцисс:
с
осью абсцисс:
-
(0; 12)
-
(

-
(

-
(-12; 0)
-
Задайте формулой функцию, график которой проходит через точку (0; 6) и параллелен графику функции у=-3х.
-
Решите графическим способом систему уравнений:
![]()
-
Социологи опросили 20 школьников, выясняя, сколько книг каждый из них прочел за прошедший месяц. Были получены следующие данные:
2,2,1,1,7,3,1,0,2,5,1,3,2,2,3,4,5,0,2,4.
а) постройте таблицу абсолютных частот и таблицу относительных частот;
б) укажите самое распространенное число прочитанных книг;
в) проверьте таблицу относительных частот на непротиворечивость.
6. График функции, заданной уравнением у=(a +1)x+a-1 пересекает ось абсцисс в точке с координатами
(-5; 0).
-
Найдите значение а;
-
Запишите функцию в виде у=kx+b;
-
Не выполняя построения графика функции, определите, через какую четверть график не проходит.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||||||||||||||||||||
|
1 |
Использует свойство принадлежности точки к графику функции |
1 |
|
|||||||||||||||||||||||||||||||
|
Верно, выполняет вычисления. Ответ А |
1 |
|
||||||||||||||||||||||||||||||||
|
2 |
Использует свойство пересечения с осями координат |
1 |
|
|||||||||||||||||||||||||||||||
|
Верно подставляет значения координат |
1 |
|
||||||||||||||||||||||||||||||||
|
Верно выполняет вычисления Ответ: С |
1 |
|
||||||||||||||||||||||||||||||||
|
3 |
|
1 |
|
|||||||||||||||||||||||||||||||
|
b = 6 |
1 |
|
||||||||||||||||||||||||||||||||
|
|
1 |
|
||||||||||||||||||||||||||||||||
|
4 |
Изображает
график функции |
1 |
|
|||||||||||||||||||||||||||||||
|
Изображает
график функции |
1 |
|
||||||||||||||||||||||||||||||||
|
Находит координаты точки пересечения графиков |
1 |
(-3; 3) |
||||||||||||||||||||||||||||||||
|
Записывают ответ x = -3; y = 3 |
1 |
|
||||||||||||||||||||||||||||||||
|
5 |
|
1 |
|
|||||||||||||||||||||||||||||||
или
|
1 |
Принимать любой альтернативный вариант |
||||||||||||||||||||||||||||||||
|
Самое распространенное число: 2 |
1 |
|
||||||||||||||||||||||||||||||||
|
или 10% + 20% + 30% + 15%+10% + 10% + 5%= 100% |
1 |
|
||||||||||||||||||||||||||||||||
|
6 |
Для нахождения значения а, в заданное уравнение подставляет координаты точки, через которую проходит график функции а = - 1,5 |
1 |
|
|||||||||||||||||||||||||||||||
|
к= - 0,5, b= - 2,5 |
1 |
|
||||||||||||||||||||||||||||||||
|
у= - 0,5x - 2,5 |
1 |
|
||||||||||||||||||||||||||||||||
|
Не проходит через I четверть |
1 |
|
||||||||||||||||||||||||||||||||
|
Всего баллов: |
20 |
|
||||||||||||||||||||||||||||||||
ЗАДАНИЯ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
3 |
3 |
4 |
4 |
4 |
|
Всего баллов |
20 баллов |
|||||
4 ВАРИАНТ
-
Найдите значение коэффициента k, если известно, что график функции
 проходит через точку с координатами А(1;
-2).
проходит через точку с координатами А(1;
-2).
-
-2
-
1
-
-1
-
2
-
Найдите координаты точки пересечения функции
 с
осью абсцисс:
с
осью абсцисс:
-
(0; 24)
-
(

-
(

-
(-24; 0)
-
Задайте формулой функцию, график которой проходит через точку (0; 5) и параллелен графику функции у=-х.
-
Решите графическим способом систему уравнений:
![]()
-
Социологи опросили 20 школьников, выясняя, сколько книг каждый из них прочел за прошедший месяц. Были получены следующие данные:
3,7,2,1,6,1,1,0,2,7,1,3,0,0,3,4,5,0,2,0.
а) постройте таблицу абсолютных частот и таблицу относительных частот;
б) укажите самое распространенное число прочитанных книг;
в) проверьте таблицу относительных частот на непротиворечивость.
6. График функции, заданной уравнением у=(a +1)x+a-1 пересекает ось абсцисс в точке с координатами
(-6; 0).
-
Найдите значение а;
-
Запишите функцию в виде у=kx+b;
-
Не выполняя построения графика функции, определите, через какую четверть график не проходит.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|||||||||||||||||||||||||||||||||||
|
1 |
Использует свойство принадлежности точки к графику функции |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Верно, выполняет вычисления. Ответ A |
1 |
|
||||||||||||||||||||||||||||||||||||
|
2 |
Использует свойство пересечения с осями координат |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Верно подставляет значения координат |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Верно выполняет вычисления Ответ: D |
1 |
|
||||||||||||||||||||||||||||||||||||
|
3 |
|
1 |
|
|||||||||||||||||||||||||||||||||||
|
b = 5 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
|
1 |
|
||||||||||||||||||||||||||||||||||||
|
4 |
Изображает
график функции |
1 |
|
|||||||||||||||||||||||||||||||||||
|
Изображает
график функции |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Находит координаты точки пересечения графиков |
1 |
(-2; 7) |
||||||||||||||||||||||||||||||||||||
|
Записывают ответ x = -2; y = 7 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
5 |
|
1 |
|
|||||||||||||||||||||||||||||||||||
или
|
1 |
Принимать любой альтернативный вариант |
||||||||||||||||||||||||||||||||||||
|
Самое распространенное число: 0 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
или 25% + 20% + 15% + 15%+5% + 5% +5% + 10% = 100% |
1 |
|
||||||||||||||||||||||||||||||||||||
|
6 |
Для нахождения значения а, в заданное уравнение подставляет координаты точки, через которую проходит график функции а = - 1,4 |
1 |
|
|||||||||||||||||||||||||||||||||||
|
к= - 0,4, b= - 2,4 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
у= - 0,4х - 2,4 |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Не проходит через I четверть |
1 |
|
||||||||||||||||||||||||||||||||||||
|
Всего баллов: |
20 |
|
||||||||||||||||||||||||||||||||||||
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 3 четверть
Продолжительность суммативной работы – 40 минут
Количество баллов – 20
Типы заданий:
КО – вопросы, требующие краткого ответа;
РО – вопросы, требующие развернутого ответа.
Структура суммативной работы
Данный вариант состоит из 4 заданий, включающих вопросы с кратким и развернутым ответом.
В заданиях, требующих краткого ответа, учащийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующих развернутого ответа, учащийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность учащегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Формулы сокращённого умножения |
7.1.2.14 использовать формулы сокращённого умножения для рационального счёта |
Применение |
1 |
1 |
КО |
6 |
4 |
20 |
|
7.2.1.15 выполнять тождественные преобразования алгебраических выражений с помощью формул сокращённого умножения |
Применение |
1 |
3 |
КО |
7 |
5 |
||
|
7.2.1.10 знать и применять формулы сокращённого умножения
|
Применение |
1 |
2 |
КО |
12 |
5 |
||
|
7.2.1.11 знать и применять формулы сокращённого умножения |
Применение |
|||||||
|
7.2.1.14 раскладывать алгебраические выражения на множители с помощью формул сокращённого умножения |
Применение |
|||||||
|
7.4.2.2 решать текстовые задачи, с помощью составления уравнений и неравенств |
Навыки высокого порядка |
1 |
4 |
РО |
15 |
6 |
||
|
ИТОГО: |
|
|
4 |
|
|
40 мин |
20 |
20 |
|
Примечание: * - разделы, в которые можно вносить изменения |
||||||||
ЗАДАНИЯ
|
Оценивание заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
4 |
5 |
5 |
6 |
|
Всего баллов |
20 баллов |
|||
1 ВАРИАНТ
-
Вычислите наиболее рациональным способом:
![]()
2) Разложите многочлен на множители:
a) ![]() ;
;
b) ![]()
3)
а) Упростите выражение: ![]()
b) Покажите, что значение выражения
![]() при
при ![]() равно
равно ![]() .
.
4) Разность квадратов двух чисел равна 52, а сумма этих чисел равна 26. Найдите эти числа.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2a |
|
1 |
|
|
|
1 |
|
|
|
2b |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3a |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3b |
|
1 |
|
|
|
1 |
|
|
|
4 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
Принимается альтернативный способ решения |
|
|
|
1 |
||
|
|
1 |
|
|
|
x=14 |
1 |
|
|
|
y=12 |
1 |
|
|
|
Всего баллов: |
20 |
|
|
ЗАДАНИЯ
|
Оценивание заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
4 |
5 |
5 |
6 |
|
Всего баллов |
20 баллов |
|||
2 ВАРИАНТ
-
Вычислите наиболее рациональным способом:
![]()
2) Разложите многочлен на множители:
a) ![]() ;
;
b) ![]()
3)
а) Упростите выражение: ![]()
b) Покажите, что значение выражения
![]() при
при ![]() равно
равно ![]() .
.
4) Разность квадратов двух чисел равна 87, а разность этих чисел равна 3. Найдите эти числа.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2a |
|
1 |
|
|
|
1 |
|
|
|
2b |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3a |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3b |
|
1 |
|
|
|
1 |
|
|
|
4 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
Принимается альтернативный способ решения |
|
|
|
1 |
||
|
|
1 |
|
|
|
x=16 |
1 |
|
|
|
y=13 |
1 |
|
|
|
Всего баллов: |
20 |
|
|
ЗАДАНИЯ
|
Оценивание заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
4 |
5 |
5 |
6 |
|
Всего баллов |
20 баллов |
|||
3 ВАРИАНТ
-
Вычислите наиболее рациональным способом:
![]()
2) Разложите многочлен на множители:
a) ![]() ;
;
b) ![]()
3)
а) Упростите выражение: ![]()
b) Покажите, что значение выражения
![]() при
при ![]() равно 5.
равно 5.
4) Разность квадратов двух чисел равна 48, а сумма этих чисел равна 24. Найдите эти числа.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2a |
|
1 |
|
|
|
1 |
|
|
|
2b |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3a |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3b |
|
1 |
|
|
6 – 1 = 5 |
1 |
|
|
|
4 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
Принимается альтернативный способ решения |
|
|
|
1 |
||
|
|
1 |
|
|
|
x=13 |
1 |
|
|
|
y=11 |
1 |
|
|
|
Всего баллов: |
20 |
|
|
ЗАДАНИЯ
|
Оценивание заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
4 |
5 |
5 |
6 |
|
Всего баллов |
20 баллов |
|||
4 ВАРИАНТ
-
Вычислите наиболее рациональным способом:
![]()
2) Разложите многочлен на множители:
a) ![]() ;
;
b) ![]()
3)
а) Упростите выражение: ![]()
b) Покажите, что значение выражения
![]() при
при ![]() равно 26.
равно 26.
4) Разность квадратов двух чисел равна 81, а разность этих чисел равна 3. Найдите эти числа.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
2a |
|
1 |
|
|
|
1 |
|
|
|
2b |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3a |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3b |
|
1 |
|
|
27 – 1 = 26 |
1 |
|
|
|
4 |
|
1 |
Принимать любые буквенные обозначения |
|
|
1 |
Принимается альтернативный способ решения |
|
|
|
1 |
||
|
|
1 |
|
|
|
x=15 |
1 |
|
|
|
y=12 |
1 |
|
|
|
Всего баллов: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания за 4 четверть
Продолжительность суммативной работы – 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативной работы
Данный вариант состоит из 6 заданий, включающие вопросы с множественным выбором ответов, требующие краткого и развернутого ответов.
В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В вопросах, требующие развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Алгебраические дроби |
7.2.1.17 находить область допустимых значений переменных в алгебраической дроби |
Применение |
1 |
1 |
КО |
4 |
2 |
20 |
|
7.2.1.18 применять основное свойство алгебраической
дроби |
Применение |
1 |
2 |
КО |
2 |
1 |
||
|
7.2.1.21 выполнять преобразования алгебраических выражений |
Применение |
2 |
3, 6 |
РО |
18 |
9 |
||
|
7.2.1.19 выполнять сложение и вычитание алгебраических дробей |
Применение |
1 |
4 |
РО |
8 |
4 |
||
|
7.2.1.20 выполнять умножение и деление, возведение в степень алгебраических дробей |
Применение |
1 |
5 |
РО |
8 |
4 |
||
|
ИТОГО: |
|
|
6 |
|
|
40 минут |
20 |
20 |
|
Примечание: * - разделы, в которые можно вносить изменения |
||||||||
ЗАДАНИЯ
1 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
1 |
3 |
4 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
1. При каких значениях переменной,
алгебраическая дробь ![]()
имеет смысл?
2. Сократите дробь:
![]()
3. Упростите дробь:
![]()
Найдите значение дроби при c = 5
4. Выполните сложение и вычитание дробей:
a)
![]()
b)
![]()
5. Выполните умножение и деление алгебраических дробей:
a)
![]()
b)
![]()
6. Упростите выражение:
-
 +
+

-
 -
-

СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
d – 3 ≠ 0 |
1 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
3 |
|
1 |
|
|
|
1 |
|
|
|
2
|
1 |
|
|
|
4a |
|
1 |
|
|
4b |
|
1 |
|
|
|
1 |
Приводит к общему знаменателю |
|
|
|
1 |
|
|
|
5a |
|
1 |
|
|
5b |
|
1 |
Принимается любой вариант записи |
|
= |
1 |
||
|
= |
1 |
||
|
6a |
|
1 |
|
|
= |
1 |
|
|
|
=
|
1 |
|
|
|
6b |
|
1 |
|
|
|
1 |
|
|
|
= |
1 |
|
|
|
Итого: |
20 |
|
|
2 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
1 |
3 |
4 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
1. При каких значениях переменной,
алгебраическая дробь ![]()
имеет смысл?
2. Сократите дробь:
![]()
3. Упростите дробь:
![]()
Найдите значение дроби при a = 7
4. Выполните сложение и вычитание дробей:
a)
![]()
b)
![]()
5. Выполните умножение и деление алгебраических дробей:
a)
![]()
b)
![]()
6. Упростите выражение:
-
 : (
: (
 )
)
![]() -
-
![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
(x-4)(x+4)≠0 |
1 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
3 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
2,5 или |
|
|
4a |
|
1 |
|
|
4b |
|
1 |
|
|
|
1 |
Приводит к общему знаменателю |
|
|
|
1 |
|
|
|
5a |
|
1 |
|
|
5b |
|
1 |
|
|
= |
1 |
|
|
|
= |
1 |
|
|
|
6a |
|
1 |
|
|
= |
1 |
|
|
|
= -
|
1 |
|
|
|
6b |
|
1 |
|
|
= |
1 |
|
|
|
x-y |
1 |
|
|
|
Итого: |
20 |
|
|
3 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
1 |
3 |
4 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
1. При каких значениях переменной,
алгебраическая дробь ![]()
имеет смысл?
2. Сократите дробь:
![]()
3. Упростите дробь:
![]()
Найдите значение дроби при x= -1, y=3
4. Выполните сложение и вычитание дробей:
a)
![]()
b)
![]()
5. Выполните умножение и деление алгебраических дробей:
a)
![]()
b)
![]()
6. Упростите выражение:
a)![]()
b)
![]() +
+ ![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
(2-b)(2+b) |
1 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
3 |
|
1 |
|
|
|
1 |
|
|
|
- |
1 |
-0,3 |
|
|
4a |
|
1 |
|
|
4b |
|
1 |
|
|
|
1 |
Приводит к общему знаменателю |
|
|
|
1 |
|
|
|
5a |
|
1 |
|
|
5b |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
6a |
|
1 |
|
|
|
1 |
|
|
|
0 |
1 |
|
|
|
6b |
|
1 |
|
|
|
1 |
|
|
|
- |
1 |
|
|
|
Итого: |
20 |
|
|
4 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
1 |
3 |
4 |
4 |
6 |
|
Всего баллов |
20 баллов |
|||||
1. При каких значениях переменной,
алгебраическая дробь ![]()
имеет смысл?
2. Сократите дробь:
![]()
3. Упростите дробь:
![]()
Найдите значение дроби при x = 2, y = - 6
4. Выполните сложение и вычитание дробей:
a)
![]()
b)
![]()
5. Выполните умножение и деление алгебраических дробей:
a)
![]()
b)
![]()
6. Упростите выражение:
-
(x + 1) -

СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
(x+1)(2x-6)≠0 |
1 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
3 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
4a |
|
1 |
|
|
4b |
|
1 |
|
|
|
1 |
Приводит к общему знаменателю |
|
|
|
1 |
|
|
|
5a |
|
1 |
|
|
5b |
|
1 |
|
|
|
1 |
|
|
|
= |
1 |
|
|
|
6a |
|
1 |
|
|
= |
1 |
|
|
|
= |
1 |
|
|
|
6b |
|
1 |
|
|
= |
1 |
|
|
|
|
1 |
|
|
|
Итого: |
20 |
|
|
ГЕОМЕТРИЯ
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ
«НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ».
|
Тема |
Основные понятия геометрии. Аксиомы. Теоремы. Смежные и вертикальные углы, их свойства. |
|
Цели обучения |
7.1.1.2 знать и применять аксиомы принадлежности точек и прямых; 7.1.1.5 знать определения отрезка, луча, угла, треугольника, полуплоскости; 7.1.1.6 знать и применять аксиомы измерения отрезков и углов;
7.1.1.9 знать определения
смежных и вертикальных углов; |
|
Критерии оценивания |
Обучающийся Выполняет построение, применяя аксиомы принадлежности точек и прямых, и определения отрезка, луча, полуплоскости; Применяет аксиомы измерения отрезков для решения задач; Решает задачи на определение смежных, вертикальных углов и на применение их свойств. |
|
Уровень мыслительных навыков |
Знание и понимание. Применение. |
|
Время выполнения |
20 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
4 |
4 |
7 |
|
итого |
15 баллов |
||
1 ВАРИАНТ
-
Выполните построение, следуя инструкции:
-
начертите прямую n;
-
отметьте точки B, D, К, при условии, что точка К принадлежит прямой n, а точки B и D не принадлежат прямой n и лежат в разных полуплоскостях;
-
проведите отрезок КD:
-
проведите луч КB.
-
Дан отрезок CN. Точка M принадлежит отрезку СN, причем СM: MN=1:4. Найдите СM и MN, если СN=24,5 см.
-
Прямые АВ и СД пересекаются в точке К.
-
назовите образованные углы;
-
определите пары смежных и вертикальных углов;
-
найдите значения всех образованных углов, если один из них равен 1340.
2 ВАРИАНТ
-
Выполните построение, следуя инструкции:
-
начертите прямую m;
-
отметьте точки A, O, P, при условии, что точка O принадлежит прямой m, а точки A и P не принадлежат прямой m и лежат в разных полуплоскостях;
-
проведите отрезок OA:
-
проведите луч OP.
-
Дан отрезок LM. Точка K принадлежит отрезку LМ, причем LK: KМ=2:7. Найдите LK и KМ, если LМ=32.4 см.
-
Прямые OX и YZ пересекаются в точке H.
-
назовите образованные углы;
-
определите пары смежных и вертикальных углов;
-
найдите значения всех образованных углов, если один из них равен 1020.
3 ВАРИАНТ
-
Выполните построение, следуя инструкции:
-
начертите прямую p;
-
отметьте точки G, K, S, при условии, что точка G принадлежит прямой p, а точки K и S не принадлежат прямой p и лежат в разных полуплоскостях;
-
проведите отрезок GS:
-
проведите луч GK.
-
Дан отрезок QJ. Точка Z принадлежит отрезку QJ, причем QZ: ZJ=3:1. Найдите QZ и ZJ, если QJ=28,8 см.
-
Прямые CD и AF пересекаются в точке O.
-
назовите образованные углы;
-
определите пары смежных и вертикальных углов;
-
найдите значения всех образованных углов, если один из них равен 270.
4 ВАРИАНТ
-
Выполните построение, следуя инструкции:
-
начертите прямую f;
-
отметьте точки O, M, К, при условии, что точка O принадлежит прямой f, а точки M и K не принадлежат прямой f и лежат в разных полуплоскостях;
-
проведите отрезок MK:
-
проведите луч OM.
-
Дан отрезок UV. Точка S принадлежит отрезку UV, причем US: SV=2:5. Найдите US и SV, если UV=16,8 см.
-
Прямые OP и MN пересекаются в точке X.
-
назовите образованные углы;
-
определите пары смежных и вертикальных углов;
-
найдите значения всех образованных углов, если один из них равен 480.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Выполняет построение, применяя аксиомы принадлежности точек и прямых, и определения отрезка, луча, полуплоскости |
1 |
Чертит прямую |
1 |
|
Отмечает точки по условию задачи |
1 |
||
|
Проводит отрезок |
1 |
||
|
Проводит луч |
1 |
||
|
Применяет аксиомы измерения отрезков для решения задач |
2 |
Выполняет чертеж по условию задачи |
1 |
|
Составляет уравнение по условию задачи |
1 |
||
|
Находит длину первого отрезка |
1 |
||
|
Находит длину второго отрезка |
1 |
||
|
Решает задачи на определение смежных, вертикальных углов и на применение их свойств |
3 |
Выполняет чертеж по условию задачи |
1 |
|
Называет образованные углы |
1 |
||
|
Определяет пары вертикальных углов |
1 |
||
|
Определяет пары смежных углов |
1 |
||
|
Применяет свойство вертикальных углов |
1 |
||
|
Применяет свойство смежных углов |
1 |
||
|
Выполняет вычисления и записывает ответ |
1 |
||
|
Всего баллов |
15 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ
РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «НАЧАЛЬНЫЕ
ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ»
ФИО
ОБУЧАЮЩЕГОСЯ_____________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
|||
|
Низкий |
Средний |
Высокий |
||
|
Выполняет построение, применяя аксиомы принадлежности точек и прямых, и определения отрезка, луча, полуплоскости |
Затрудняется в применении аксиом принадлежности и определений отрезка, луча, полуплоскости при построении |
Допускает ошибки в применении аксиом принадлежности/ определений отрезка/ луча/ полуплоскости при построении |
Верно выполняет построение, применяя аксиомы принадлежности и определений отрезка, луча, полуплоскости |
|
|
Применяет аксиомы измерения отрезков для решения задач |
Затрудняется в применении аксиомы измерения отрезков для решения задач |
Допускает ошибки при построении/ при составлении уравнения по условию задачи/ при нахождении длин отрезков/ при вычислениях |
Верно применяет аксиомы измерения отрезков для решения задач |
|
|
Решает задачи на определение смежных, вертикальных углов и на применение их свойств |
Затрудняется в решении задачи на определение смежных, вертикальных углов и на применение их свойств |
Допускает ошибки при построении/ при определении углов/ при применении свойств смежных и вертикальных углов |
Верно решает задачи на определение смежных, вертикальных углов и на применение их свойств |
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТРЕУГОЛЬНИКИ»
|
Тема |
Медианы, биссектрисы, высоты и средние линии треугольника Признаки равенства треугольников Равнобедренный треугольник, его свойства и признаки |
|
Цели обучения |
7.1.1.12 Знать определение медианы, биссектрисы, высоты, серединного перпендикуляра и средней линии треугольника и изображать их 7.1.1.21 Знать и доказывать признаки равенства треугольников 7.1.1.23 Применять свойства и признаки равнобедренного треугольника 7.1.1.22 Применять признаки равенства треугольников при решении задач на вычисление и на доказательство |
|
Критерии оценивания |
Обучающийся Определяет медиану, биссектрису, высоту треугольника по чертежу Распознает равные элементы фигур и определяет соответствующий признак равенства треугольников Использует свойства равнобедренного треугольника для решения задач Применяет признаки равенства треугольников при решении задач на доказательство |
|
Уровень мыслительных навыков |
Знание и понимание Применение |
|
Время выполнения |
25 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
||||
|
№ задания |
1 |
2 |
3 |
4 |
|
Количество баллов |
3 |
3 |
3 |
4 |
|
итого |
13 баллов |
|||
1 ВАРИАНТ
1. Используя рисунок, укажите верные утверждения:
|
|
|
|
1)RH-высота треугольника СRS,
2)ТМ-биссектриса треугольника NFT,
3)AD-биссектриса треугольника AFN,
4)ТМ-медиана треугольника NFT,
5) RH-медиана треугольника СRS.
2. Используя рисунок, выясните, по каким элементам треугольник АДВ равен треугольнику АСВ.
а ) по трем
сторонам
) по трем
сторонам
б) по стороне и двум прилежащим к ней углам
в) по двум сторонам и углу между ними.
3. Докажите, что треугольник АВС равнобедренный и найдите все его углы.

4. Докажите, что треугольники ABC и CDA равны. Найдите периметр треугольника АДС, если АВ=15 см, АС= 19 см и ВС= 17 см
2 ВАРИАНТ
1. Используя рисунок, укажите верные утверждения:

|
|
|
|
1) ТМ-медиана треугольника NFT,
2) RH-высота треугольника LRS,
3)TM- высота треугольника NFT,
4) AК-биссектриса треугольника AFN,
5) ТМ-биссектриса треугольника NFT.
2. Используя рисунок, выясните, по каким элементам треугольник АВС равен треугольнику СДА.
а ) по трем
сторонам
) по трем
сторонам
б) по стороне и двум прилежащим к ней углам
в) по двум сторонам и углу между ними.
3.Докажите, что треугольник АВС равнобедренный и найдите все его углы.
4. Докажите, что треугольники MFE и DCE равны. Найдите периметр треугольника ЕСД, если МЕ=4 см, MF= 8 см, FЕ= 7 см.
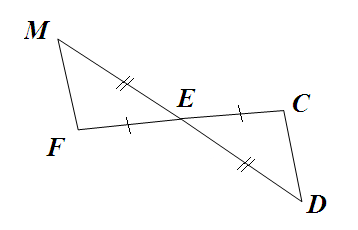
3 ВАРИАНТ
1. Используя рисунок, укажите верные утверждения:
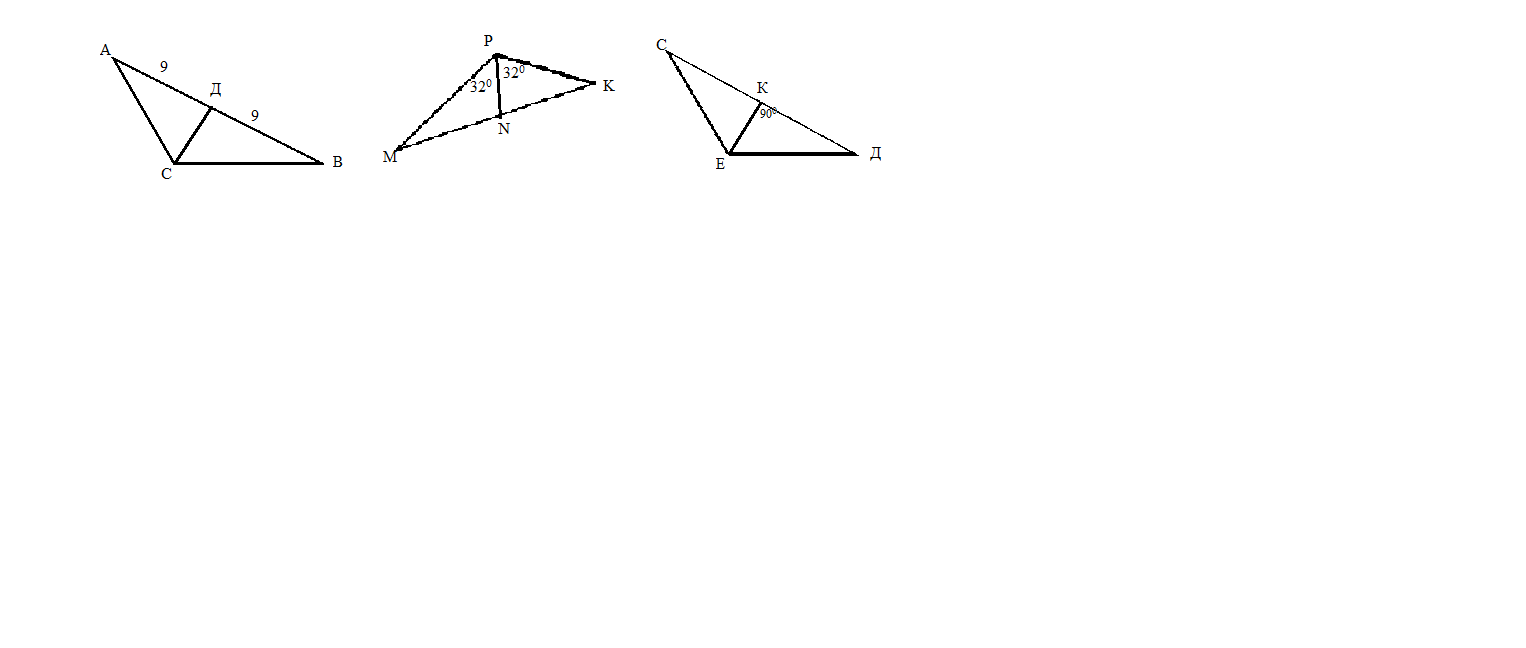
1) СД - высота треугольника АВС,
2) СД - медиана треугольника АВС,
3) PN-биссектриса треугольника MPK,
4) NP-медиана треугольника MPK,
5) KE-высота треугольника СДЕ.
2. Используя рисунок, выясните, по каким элементам треугольник АСО равен треугольнику ВДО.
А) по трем сторонам
б) по трём углам
в) по стороне и прилежащим к ней углам.

3. Докажите, что треугольник PMD равнобедренный, если <1=1120, <D=680 и найдите все его углы.
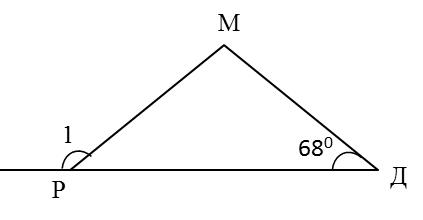
4. AD=AB и BC=DC. Докажите, что ΔВАС=ΔDAC . Найдите периметр треугольника ВАС, если АД=11 см, СД=9 см, АС=7 см

4 ВАРИАНТ
-
Используя рисунок, укажите верные утверждения:

1) ВК-высота треугольника АВС,
2) KS-медиана треугольника KLM,
3) KS-биссектриса треугольника KLM,
4) CN-медиана треугольника CFB,
5) CN- биссектриса треугольника СFB.
2. Используя рисунок, выясните, по каким элементам треугольник АДВ равен треугольнику СДВ.
а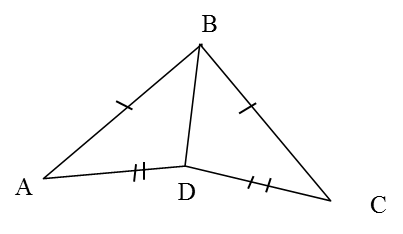 ) по трем
сторонам
) по трем
сторонам
б) по стороне и двум прилежащим к ней углам
в) по двум сторонам и углу между ними.
3. Доказать, что треугольник АВС равнобедренный, если <1=1300, <С=500 и найдите все его углы.
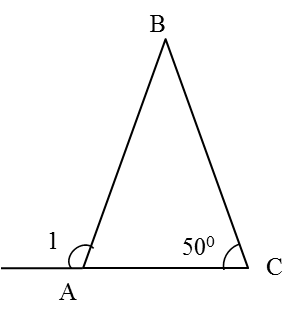
4. АС - биссектриса < ВАD и AB =AD. Докажите, что ΔBAC =ΔDAC. Найдите периметр треугольника АДС, если АВ=2,5 см, ВС=1,7 см, АС= 0,9 см
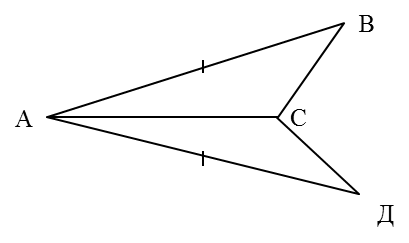
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Определяет медиану, биссектрису, высоту треугольника по чертежу |
1 |
Находит медиану треугольника |
1 |
|
Находит высоту треугольника |
1 |
||
|
Находит биссектрису треугольника |
1 |
||
|
Распознает равные элементы фигур и определяет соответствующий признак равенства треугольников |
2 |
указывает равные стороны треугольников; |
1 |
|
Указывает равные углы треугольников |
1 |
||
|
указывает соответствующий признак равенства треугольников; |
1 |
||
|
Использует свойства равнобедренного треугольника для решения задач |
3 |
Находит грусную меру углов при основании треугольника |
1 |
|
Применяет свойства углов равнобедренного треугольника |
1 |
||
|
Находит угол при вершине |
1 |
||
|
Применяет признаки равенства треугольников при решении задач на доказательство |
4 |
Определяет равные элементы треугольника |
1 |
|
Указывает признак равенства треугольников |
1 |
||
|
Определяет стороны треугольника |
1 |
||
|
Вычисляет периметр треугольника |
1 |
||
|
Общий балл |
13 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «ТРЕУГОЛЬНИКИ»
ФИ ОБУЧАЮЩЕГОСЯ ______________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Определяет медиану, биссектрису, высоту треугольника по чертежу |
Затрудняется в определении медианы, биссектрисы, высоты треугольника. |
Допускает ошибки при определении медианы / биссектрисы/ высоты треугольника. |
Верно определяет медиану, биссектрису, высоту треугольника по чертежу. |
|
Распознает равные элементы фигур и определяет соответствующий признак равенства треугольников |
Затрудняется в определении равных элементов треугольников и соответствующего признака равенства треугольников. |
Допускает ошибки в определении равных элементов треугольников или соответствующего признака равенства треугольников. |
Распознаёт равные элементы треугольников, верно определяет соответствующий признак равенства треугольников. |
|
Использует свойства равнобедренного треугольника для решения задач |
Затрудняется в использовании свойств равнобедренного треугольника. |
Применяет свойства равнобедренного треугольника, допускает ошибки при нахождении угла. |
Использует свойства равнобедренного треугольника, верно находит все искомые углы. |
|
Применяет признаки равенства треугольников при решении задач на доказательство |
Затрудняется в применении признаков равенства треугольников и вычислении периметра треугольника |
Доказывает равенство треугольников, но не делает вывод о равенстве отрезков/ допускает ошибки при указании длин сторон |
Верно применяет признаки равенства треугольников при решении задач на доказательство и определяет периметр треугольника |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ»
|
Тема |
Параллельные прямые, их признаки и свойства. Сумма углов треугольника. Внешний угол треугольника. Признаки равенства прямоугольных треугольников. Свойства прямоугольного треугольника . |
|
Цели обучения |
7.1.2.5 Применять признаки параллельности прямых при решении задач 7.1.1.17 Применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач 7.1.1.19 Применять теорему о внешнем угле треугольника 7.1.1.27 Применять свойства прямоугольного треугольника |
|
Критерии оценивания |
Обучающийся Определяет параллельность прямых, используя признаки параллельности Использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника при решении задач Применяет свойства прямоугольного треугольника при решении задач |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
25 минут |
ЗАДАНИЯ
|
Оценивание заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
3 |
5 |
3 |
|
итого |
12 баллов |
||
1 ВАРИАНТ
-
Верны ли утверждения ? Прямые а и b параллельны, если
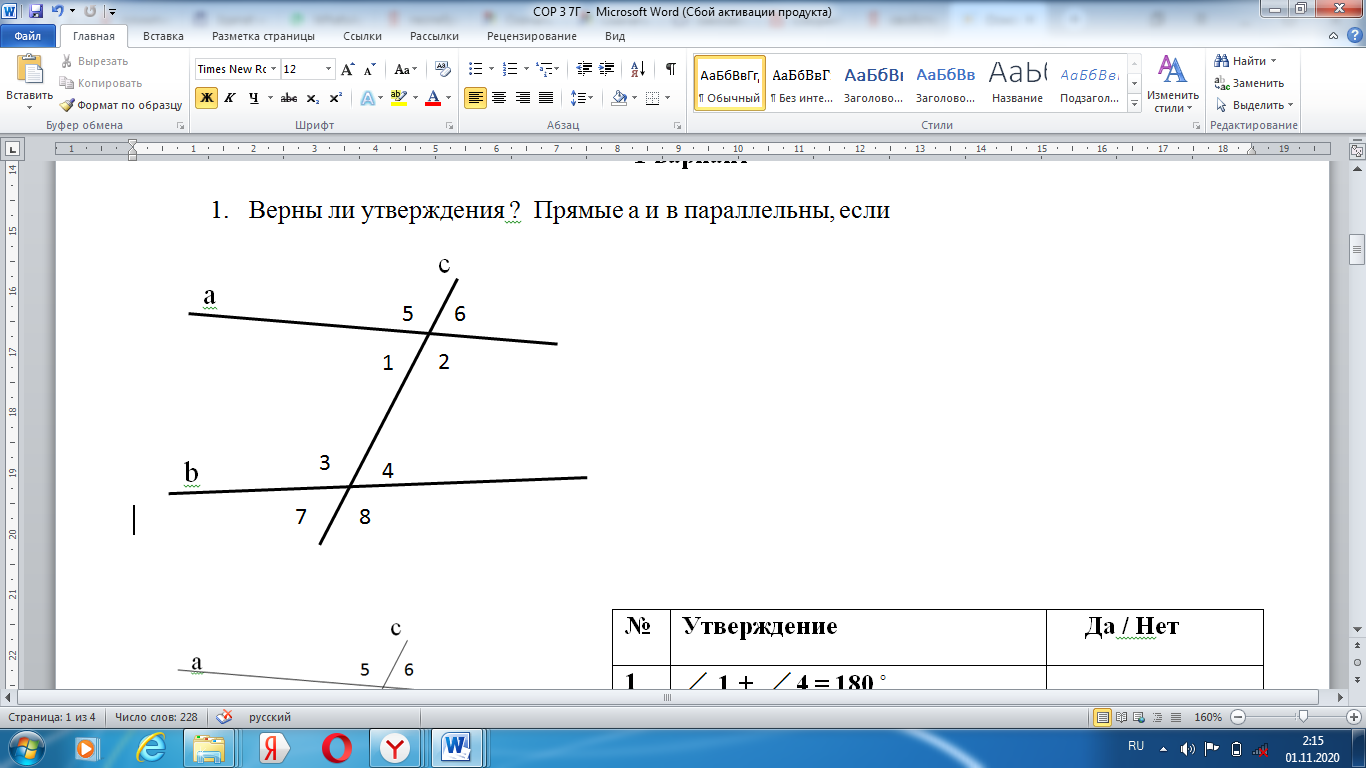
|
№ |
Утверждение |
Да / Нет |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
-
а) По данным рисунка найдите углы треугольника АВС
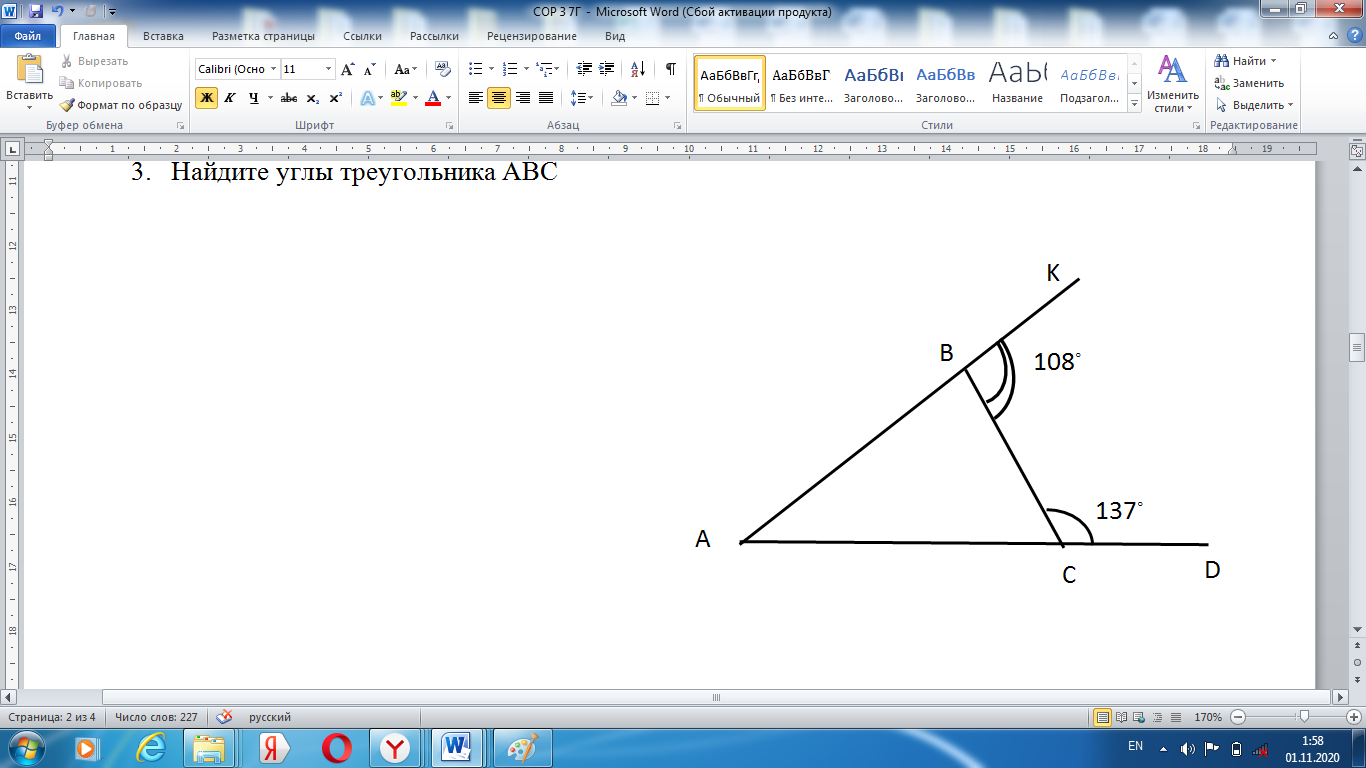
б)
Используя теорему о внешнем угле треугольника, найдите
![]() А
А ![]() АВС.
АВС.
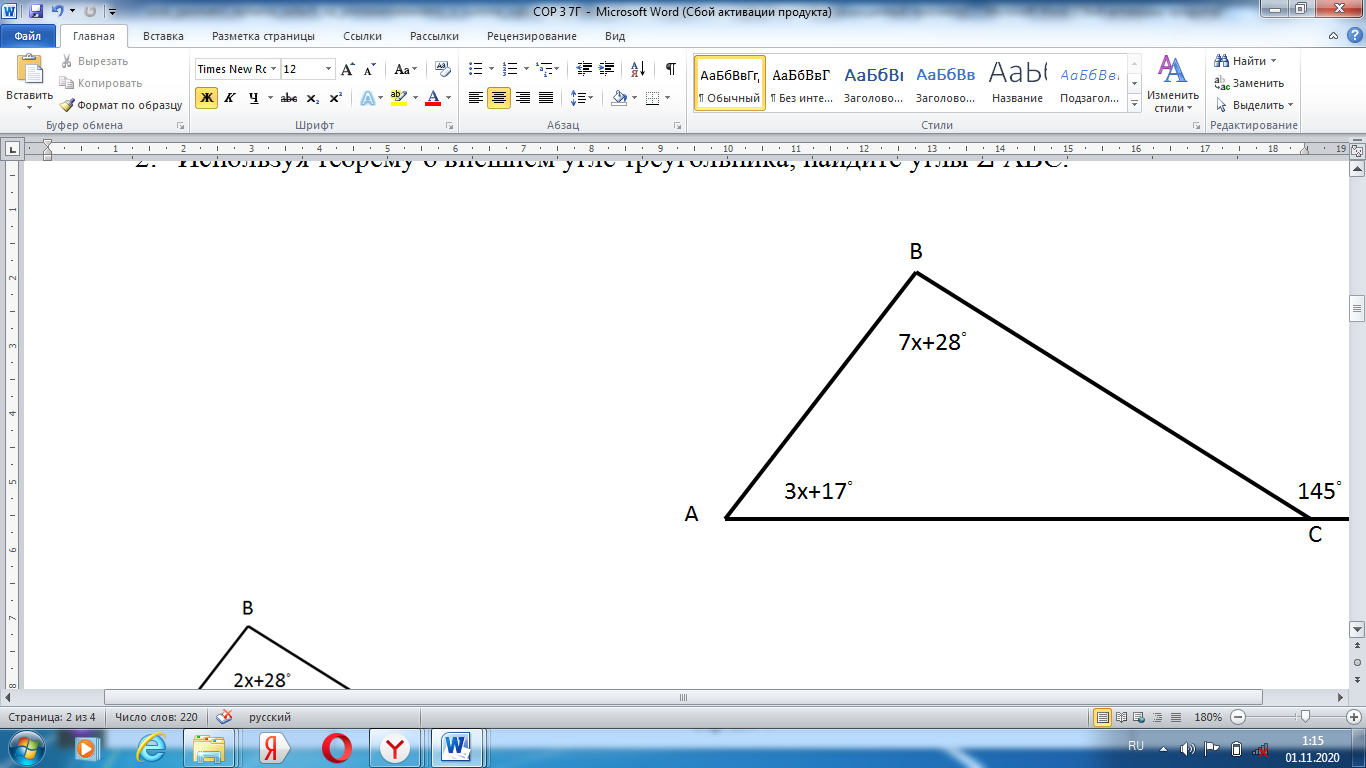
-
Найти: 1) острые углы ΔАВС;
2) высоту СК, если ВС= 7,8 см.
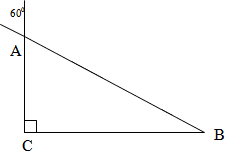
2 ВАРИАНТ
-
Верны ли утверждения? Прямые а и b параллельны, если
|
№ |
Утверждение |
Да / Нет |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
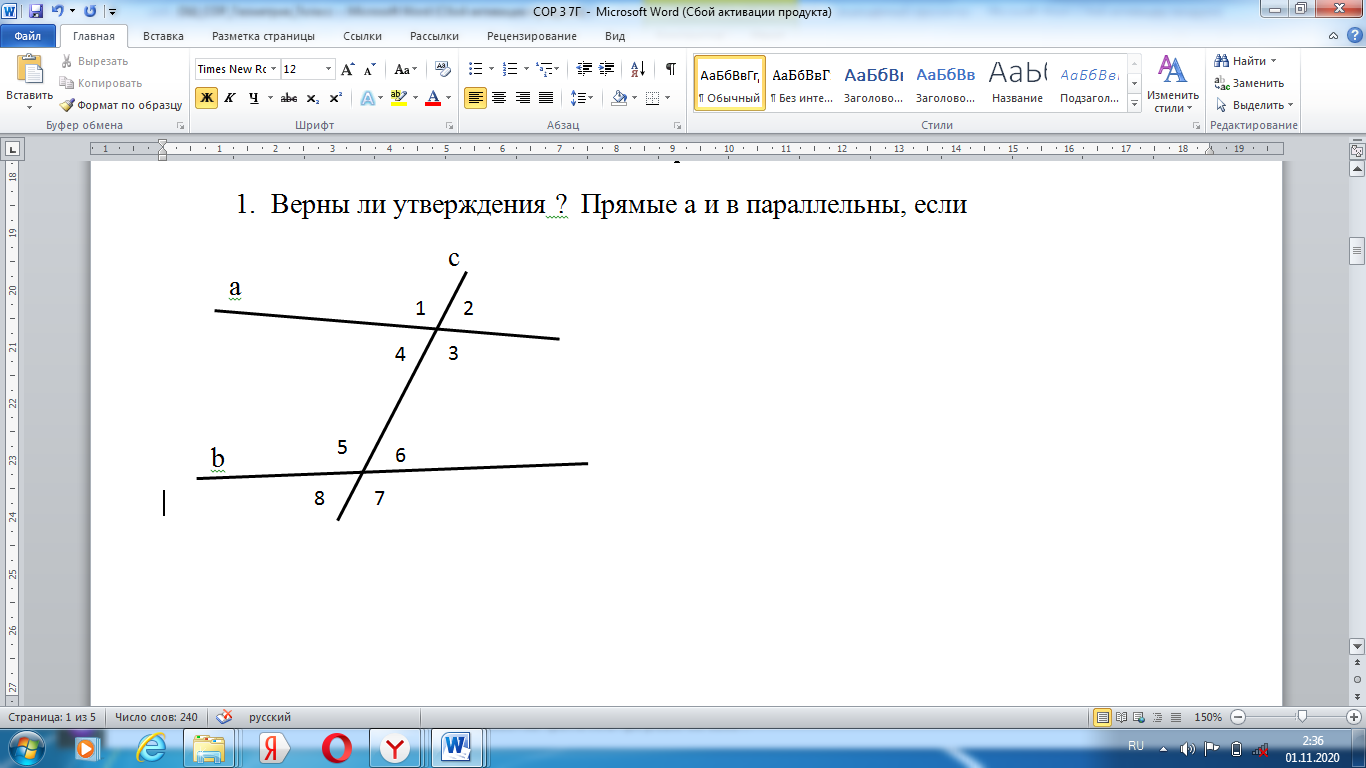
-
а
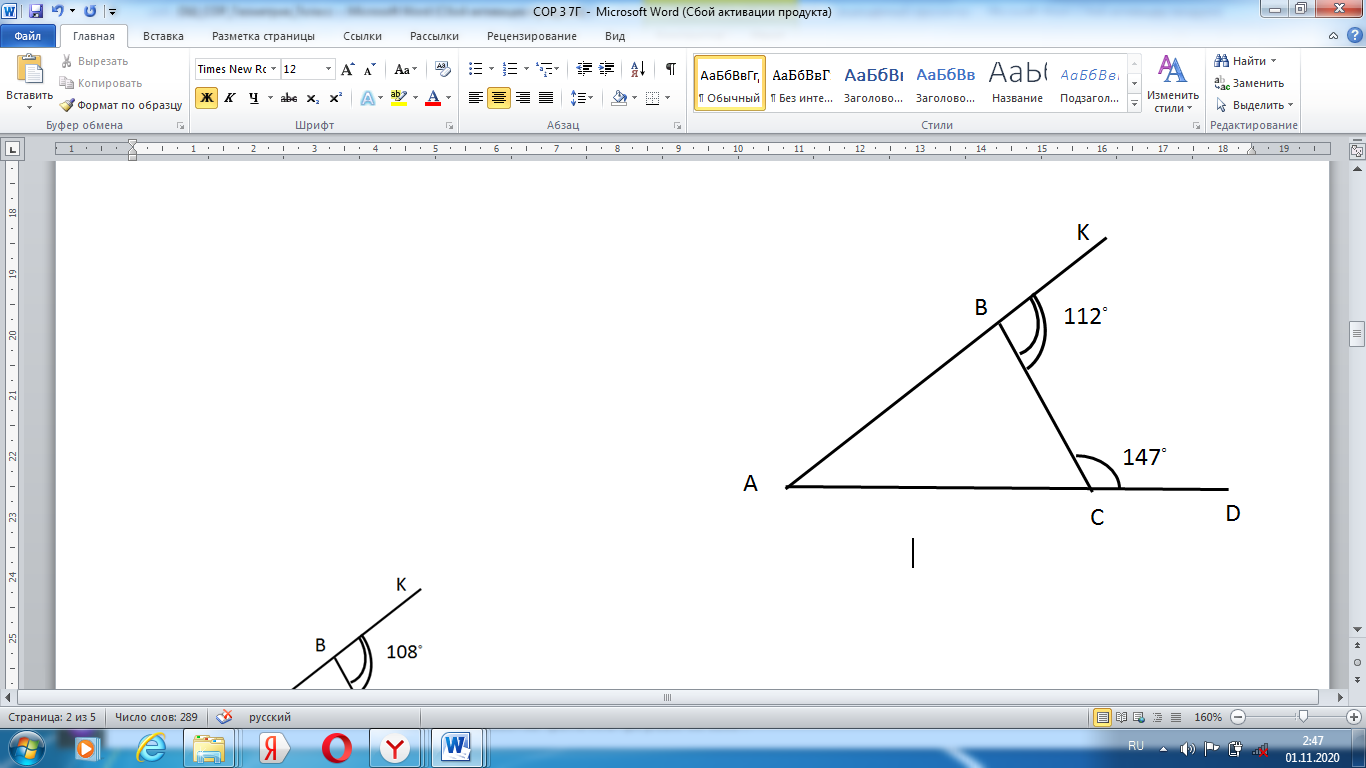 ) По данным
рисунка найдите углы треугольника АВС
) По данным
рисунка найдите углы треугольника АВС
б)
Используя теорему о внешнем угле треугольника, найдите
![]() В
В ![]() АВС.
АВС.
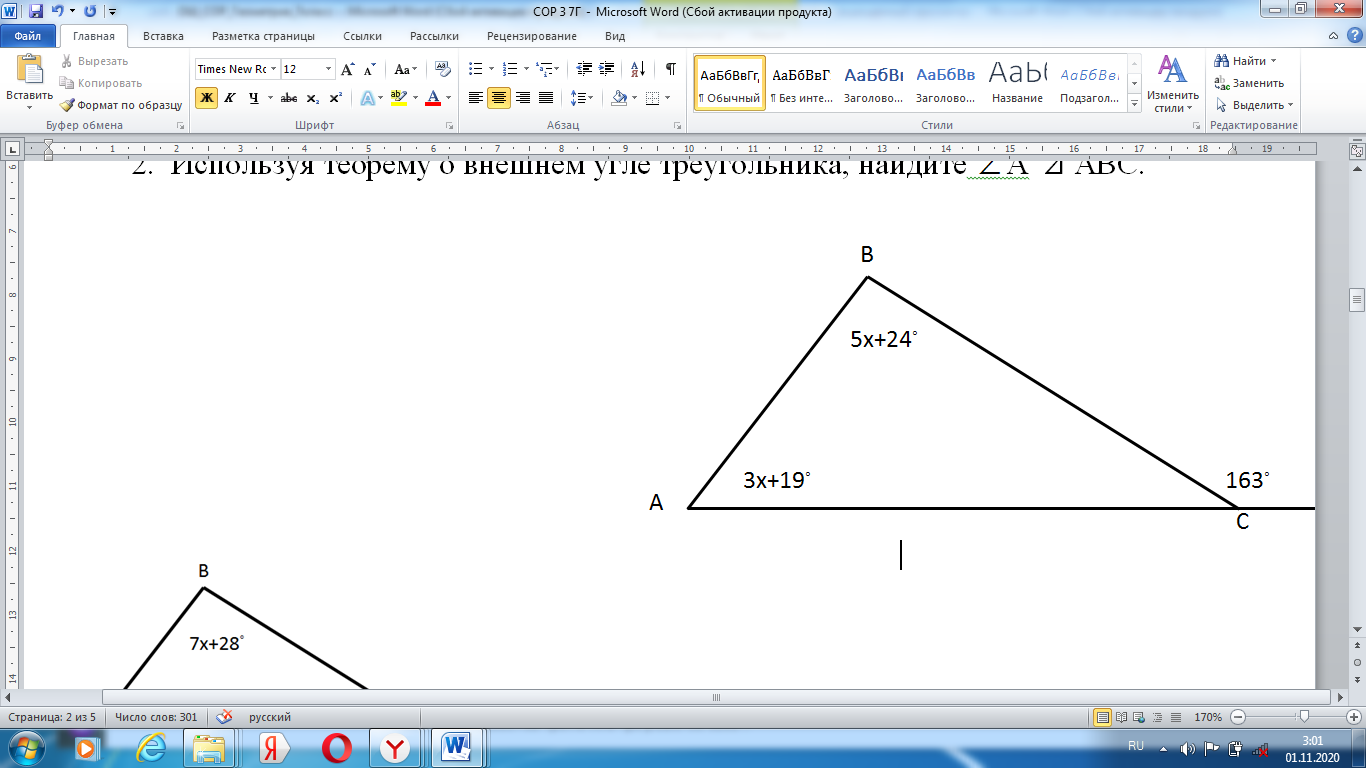
-
Найти: 1) острые углы ΔАВС;
2) высоту СК, если ВС= 14,7 см.
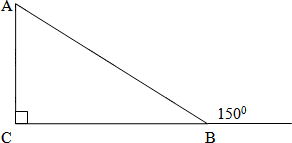
3 ВАРИАНТ
-
В
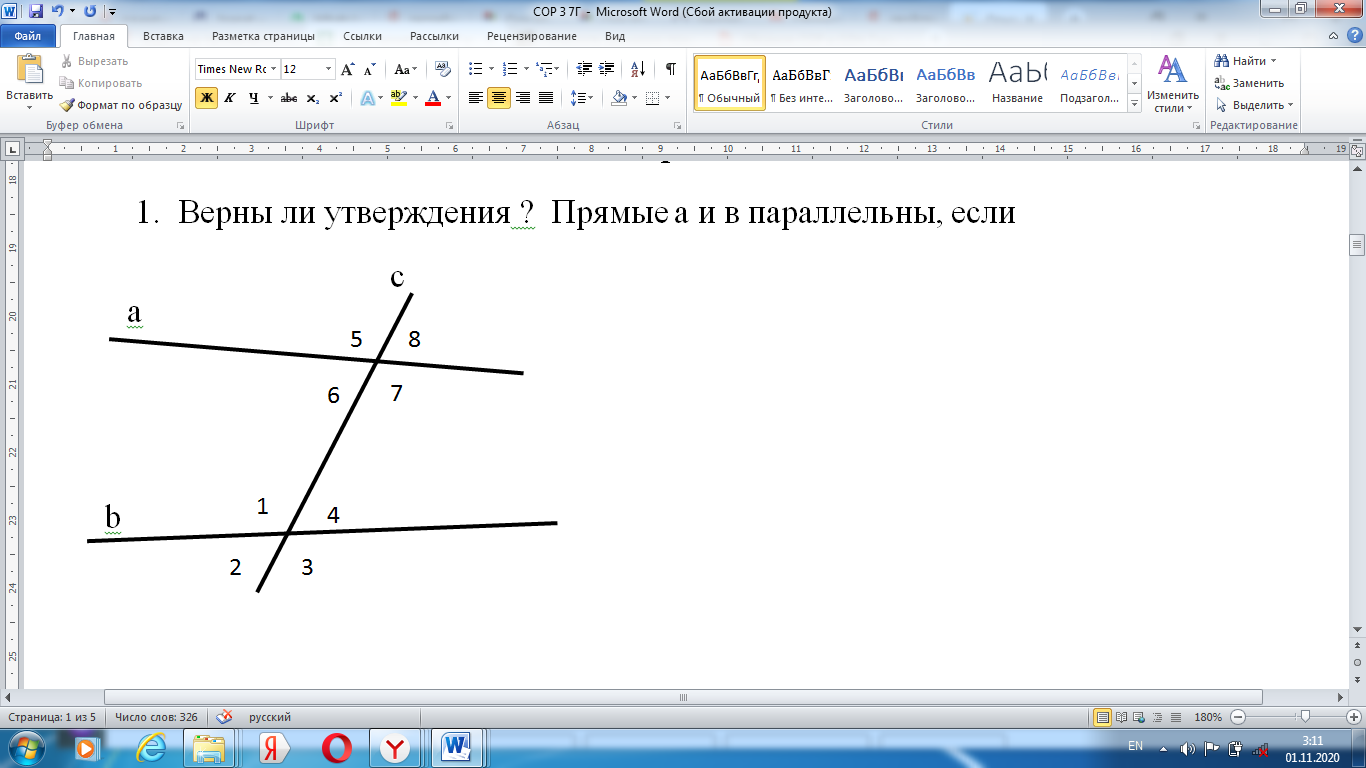 ерны ли
утверждения ? Прямые а и в параллельны, если
ерны ли
утверждения ? Прямые а и в параллельны, если
|
№ |
Утверждение |
Да / Нет |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
-
а) По данным рисунка найдите углы треугольника АВС
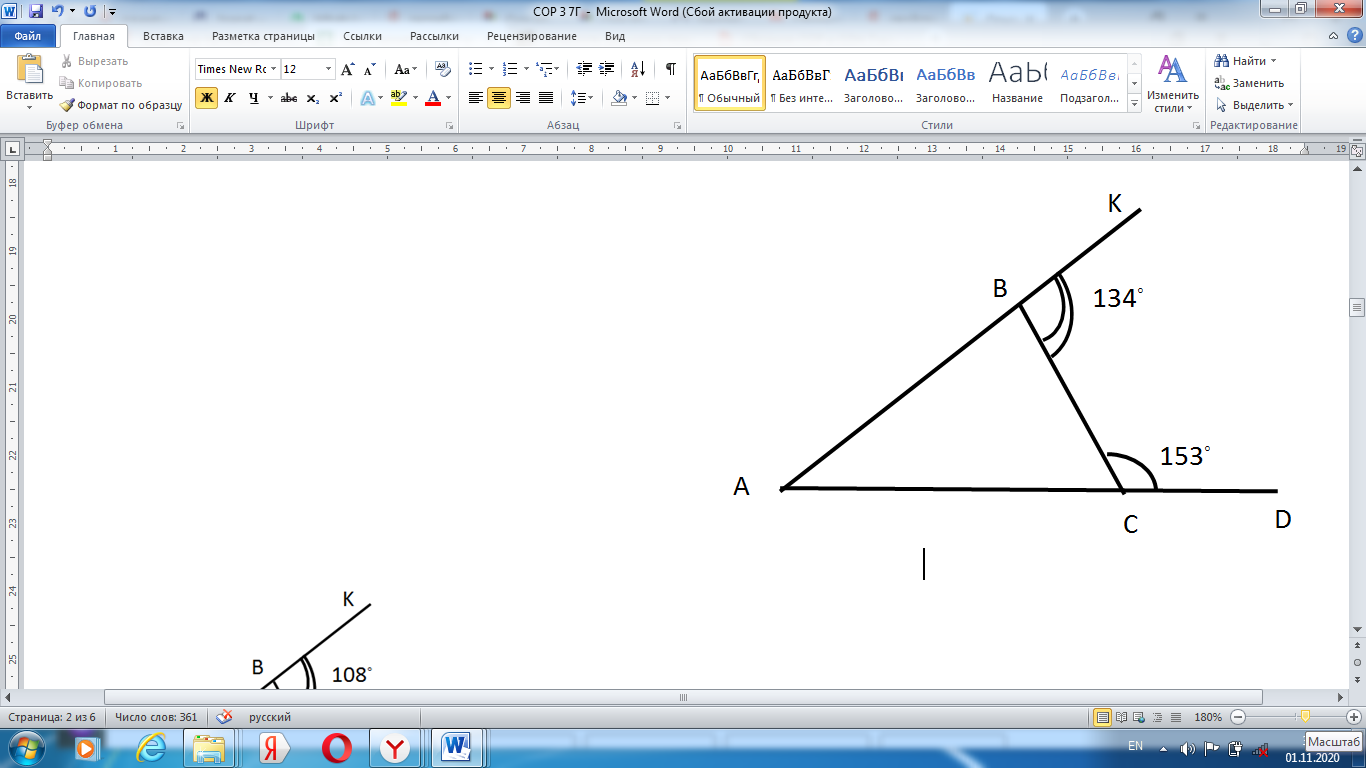
]
б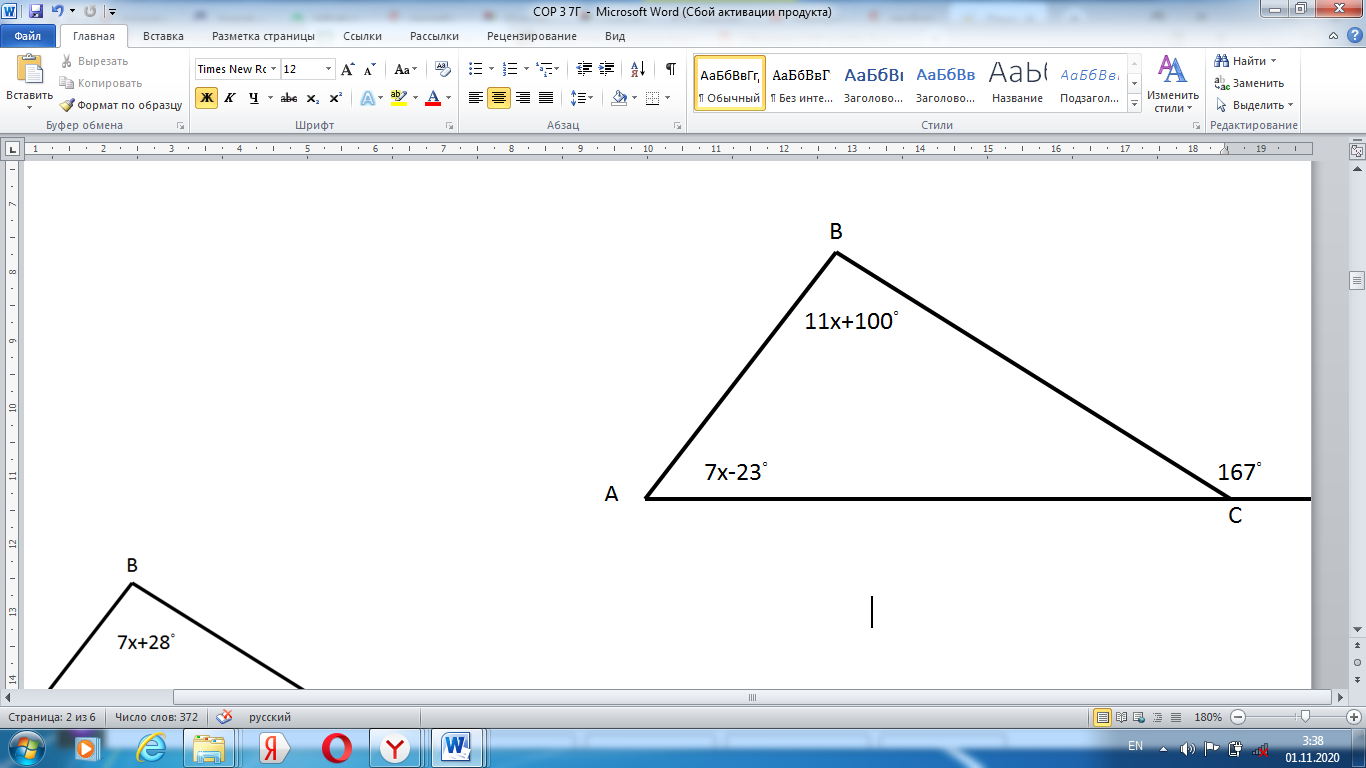 ) Используя
теорему о внешнем угле треугольника, найдите
) Используя
теорему о внешнем угле треугольника, найдите ![]() A
A
![]() АВС
АВС
-
Найти: 1) острые углы ΔАВС;
2) высоту СК, если ВС= 9,5 см.

4 ВАРИАНТ
-
В
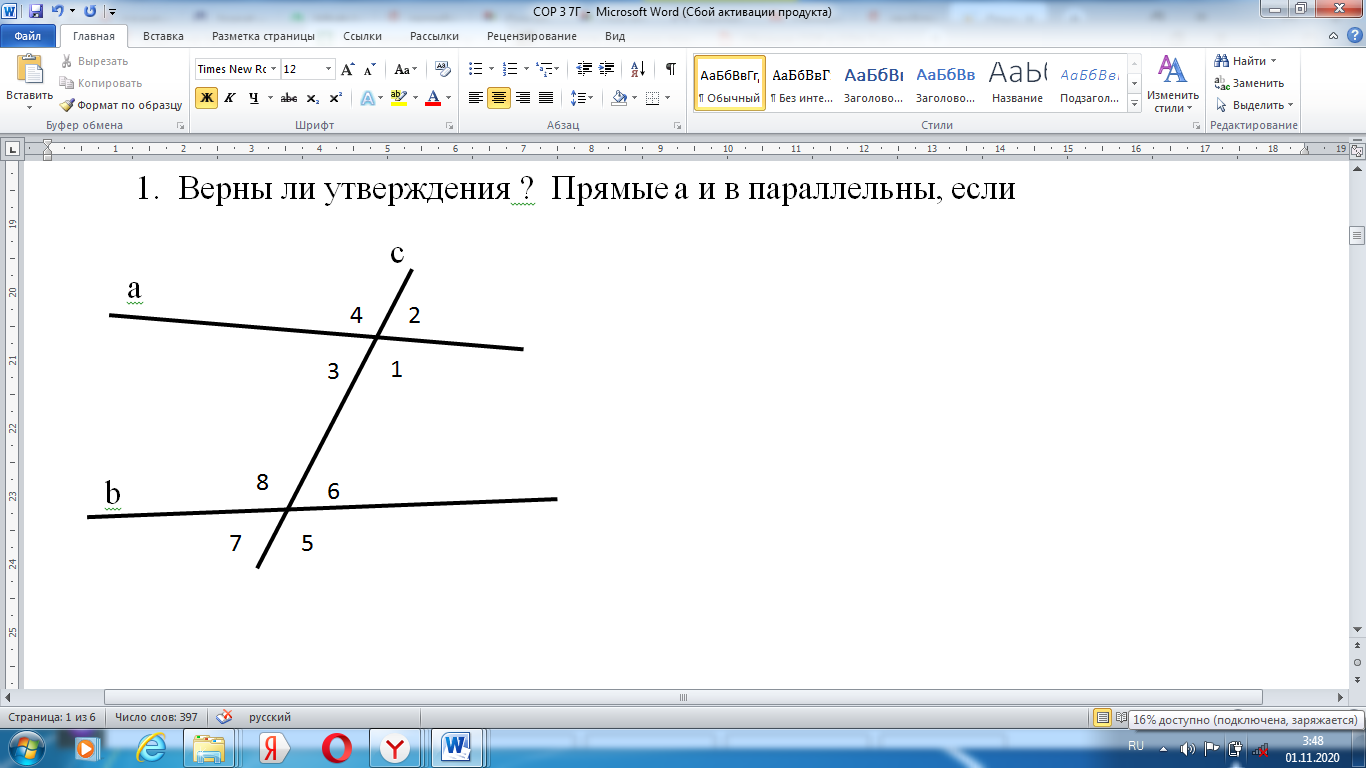 ерны ли
утверждения ? Прямые а и b параллельны, если
ерны ли
утверждения ? Прямые а и b параллельны, если
|
№ |
Утверждение |
Да / Нет |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
-
а) По данным рисунка найдите углы треугольника АВС
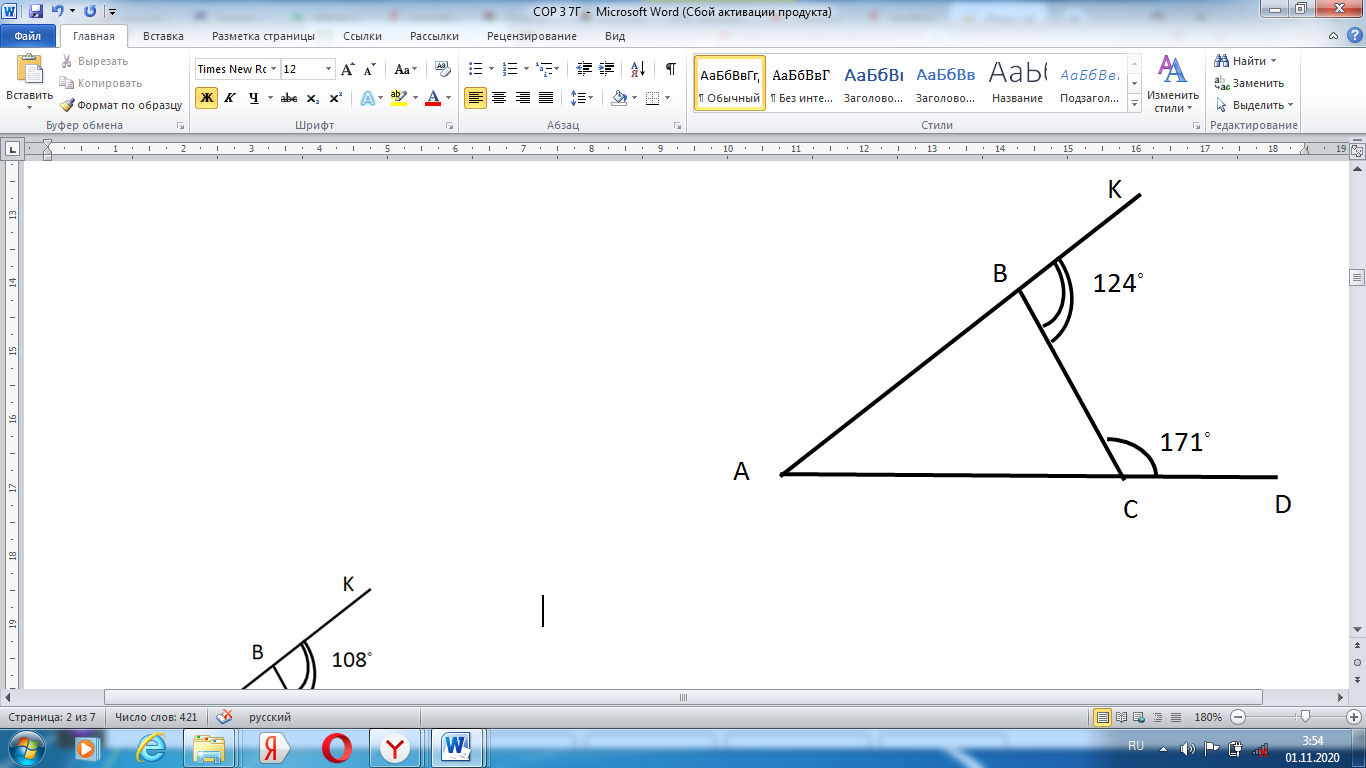
б)
Используя теорему о внешнем угле треугольника, найдите
![]() В
В ![]() АВС
АВС
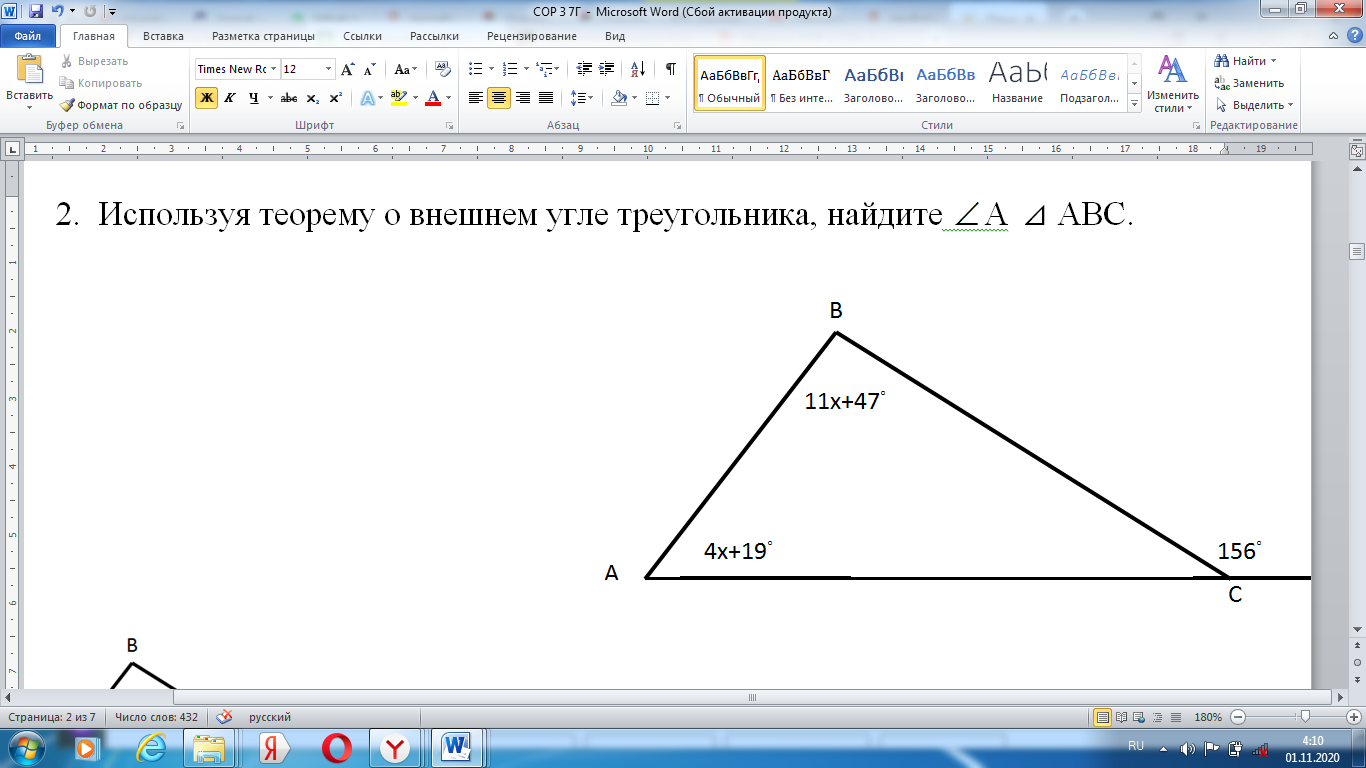
]
-
Найти: 1) острые углы ΔАВС;
2) высоту СК, если ВС= 16,3 см.

|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Определяет верные утверждения, используя признаки параллельности |
1 |
выбирает одно верное утверждение, используя признаки параллельности прямых; |
1 |
|
выбирает все верные утверждения, используя признаки параллельности прямых; |
2 |
||
|
Использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника при решении задач |
2 а) |
использует
определение внешнего угла треугольника, находит
|
1 |
|
использует
теорему о сумме внутренних углов треугольника, находит
|
1 |
||
|
2 б) |
использует теорему о внешнем угле треугольника; |
1 |
|
|
находит значение х; |
1 |
||
|
находит |
1 |
||
|
Применяет свойства прямоугольного треугольника при решении задач |
3 |
находит |
1 |
|
находит |
1 |
||
|
использует свойство прямоугольного треугольника, находит длину высоты СК |
1 |
||
|
Итого: |
11 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА РАЗДЕЛ «ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ»
ФИ ОБУЧАЮЩЕГОСЯ ________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Определяет параллельность прямых, используя признаки параллельности |
Затрудняется в выборе правильных ответов, не знает признаки параллельности прямых |
Выбирает не все правильные ответы, используя признаки параллельности |
Выбирает все правильные ответы, используя соответствующий признак параллельности прямых |
|
Использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника при решении задач |
Затрудняется в использовании теорем при решении задач. |
Допускает ошибки вычислительного характера при использовании теоремы о сумме углов треугольника / теоремы о внешнем угле треугольника |
Решает задачи, применяя теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника, находит углы треугольника |
|
Применяет свойства прямоугольного треугольника при решении задач |
Затрудняется в использовании свойства катета, против угла в 30 градусов, что затрудняет решение задачи в целом |
Использует свойство катета в прямоугольном треугольнике, равного половине гипотенузы, но не находит углы, которые образует высота с катетами треугольника |
Использует свойство катета в прямоугольном треугольнике, равного половине гипотенузы, находит углы, которые образует высота с катетами треугольника |
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ОКРУЖНОСТЬ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ»
|
Тема |
Окружность, круг, их элементы и части. Центральный угол. Касательная к окружности. Свойства касательных к окружности. Задачи на построение |
|
Цели обучения |
7.1.2.13 Знать и применять свойства касательной к окружности при решении задач 7.1.1.30 Доказывать и применять теоремы о перпендикулярности диаметра и хорды 7.1.2.18 Строить треугольник по заданным элементам 7.1.2.17 Строить серединный перпендикуляр к отрезку, прямую, перпендикулярную к данной прямой |
|
Критерии оценивания |
Обучающийся Применяет свойство касательной к окружности при решении задач Применяет теоремы о перпендикулярности диаметра и хорды при решении задач Выполняет построение треугольника, прямой, перпендикулярной к данной прямой |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
25 мин |
ЗАДАНИЯ
|
Оценивание заданий работы |
|||
|
№ задания |
1 |
2 |
3 |
|
Количество баллов |
3 |
4 |
4 |
|
итого |
11 баллов |
||
1 ВАРИАНТ
1. Прямая BC касается окружности, с центром О и радиусом
ОВ=1,6см, в точке В. Чему равна длина отрезка ОС,
если ![]() ВОС=
ВОС=![]() ?
?

2. В
окружности с центром О, диаметр АВ проходит через середину
хорды СD. Найдите все внутренние углы
![]() , если
, если ![]() САК на
САК на ![]() больше
больше ![]() КСА.
КСА.

3. a) Постройте треугольник KLM,
по стороне KL=5см, ![]()
![]()
![]()
![]()
b) Постройте высоту, проведенную к стороне LM.
2 ВАРИАНТ
1. Прямая DB касается окружности, с центром О и радиусом
ОD=1,8см, в точке
D. Чему равна длина отрезка
ОB, если ![]() DОB=
DОB=![]() ?
?

2. В
окружности с центром О, диаметр АD проходит через середину хорды
KM.
Найдите все внутренние углы ![]() , если
, если ![]() KАS на
KАS на ![]() больше
больше ![]() SKA.
SKA.

3. a)Постройте треугольник АВС, по стороне
АВ=4см, ![]()
![]()
![]()
![]()
b) Постройте высоту, проведенную к стороне ВС.
3 ВАРИАНТ
1. Прямая SR касается окружности, с центром О и радиусом
ОR=2,3см, в точке
R. Чему равна длина отрезка
ОS, если ![]() SОR=
SОR=![]() ?
?

2. В
окружности с центром О, диаметр EF проходит через середину хорды
KM.
Найдите все внутренние углы ![]() , если
, если ![]() EKB
на
EKB
на ![]() больше
больше ![]() BEK.
BEK.

3. a)Постройте треугольник BDC,
по стороне BD=4см, ![]()
![]()
![]()
![]()
b) Постройте высоту, проведенную к стороне ВD.
4 ВАРИАНТ
1. Прямая BK касается окружности, с центром О и радиусом
ОB=2,4см, в точке
B. Чему равна длина отрезка
ОK, если ![]() KОB=
KОB=![]() ?
?

2. В
окружности с центром О, диаметр EK проходит через середину хорды
AB.
Найдите все внутренние углы ![]() , если
, если ![]() EAD
на
EAD
на ![]() больше
больше ![]() DEA.
DEA.

3. a)Постройте треугольник EKF,
по стороне EK=5см, ![]()
![]()
![]()
![]()
b) Постройте высоту, проведенную к стороне EF.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Применяет свойство касательной к окружности при решении задач |
1 |
Применяет свойство касательной к окружности (перпендикулярна радиусу) и определяет вид треугольника |
1 |
|
Находит градусную меру угла |
1 |
||
|
Применяет свойство катета лежащего против
угла |
1 |
||
|
Применяет теоремы о перпендикулярности диаметра и хорды при решении задач |
2 |
Применяет теорему о перпендикулярности диаметра и хорды, находит градусную меру угла треугольника |
1 |
|
Составляет уравнение по условию задачи |
1 |
||
|
Вычисляет градусную меру второго угла треугольника |
1 |
||
|
Вычисляет градусную меру третьего угла треугольника |
1 |
||
|
Выполняет построение треугольника, прямой, перпендикулярной к данной прямой |
3 |
Выполняет построение отрезка |
1 |
|
Выполняет построение угла первого угла |
1 |
||
|
Выполняет построение угла второго угла |
1 |
||
|
Выполняет построение высоты |
1 |
||
|
Общий балл |
11 |
||
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ОКРУЖНОСТЬ. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ»
ФИ ОБУЧАЮЩЕГОСЯ ______________________________________________________
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Применяет свойство касательной при решении задачи |
Затрудняется в использовании свойств касательной |
Использует перпендикулярность касательной и радиуса, допускает ошибки при нахождении длины искомого отрезка |
Использует
свойство касательной, использует свойство катета лежащего против
угла |
|
Применяет теоремы о перпендикулярности диаметра и хорды при решении задач |
Затрудняется в использовании теоремы |
Использует теорему о перпендикулярности диаметра и хорды, допускает ошибки при составлении уравнения / нахождении искомых углов |
Использует теорему о перпендикулярности диаметра и хорды, находит искомые углы |
|
Выполняет построение треугольника, прямой, перпендикулярной к данной прямой |
Затрудняется в построении треугольника, высоты |
Допускает погрешности в построении треугольника /высоты |
Выполняет построение треугольника по стороне и двум углам Выполняет построение высоты. |
-
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 1 ЧЕТВЕРТЬ
Продолжительность - 40 минут
Количество баллов - 20
Типы заданий
КО – задания, требующие краткого ответа
РО – задания, требующие развернутого ответа
-
-
Структура суммативного оценивания
Данный вариант состоит из 7 заданий, включающих вопросы с кратким и развернутым ответом.
В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
-
Характеристика заданий суммативного оценивания
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков
|
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Начальные геометрические сведения |
7.1.1.2 знать и применять аксиомы принадлежности точек и прямых |
Применение |
1 |
1 |
КО |
4 |
2 |
20 |
|
7.1.2.1 знать и применять аксиомы расположения точек на прямой и на плоскости (аксиома порядка) |
Применение |
|||||||
|
7.1.1.9 знать определения смежных и вертикальных углов |
Знание и понимание |
1 |
2 |
РО |
4 |
3 |
||
|
7.1.1.10 доказывать и применять свойства вертикальных и смежных углов |
Применение |
|||||||
|
7.1.1.6 знать и применять аксиомы измерения отрезков и углов |
Применение |
1 |
3 |
КО |
4 |
2 |
||
|
7.1.2.1 знать и применять аксиомы расположения точек на прямой и на плоскости (аксиома порядка) |
Применение |
|||||||
|
7.1.1.8 знать и применять аксиомы откладывания отрезков и углов |
Применение |
|||||||
|
7.1.1.5 знать определения отрезка, луча, угла, треугольника, полуплоскости |
Знание и понимание |
1 |
4 |
РО |
7 |
4 |
||
|
7.1.1.8 знать и применять аксиомы откладывания отрезков и углов |
Применение |
|||||||
|
7.1.1.9 знать определения смежных и вертикальных углов |
Знание и понимание |
1 |
5 |
РО |
7 |
3 |
||
|
7.1.1.32 знать понятие о перпендикуляре |
Знание и понимание |
|||||||
|
7.1.1.10 доказывать и применять свойства вертикальных и смежных углов |
Применение Применение |
|||||||
|
7.1.1.6 знать и применять аксиомы измерения отрезков и углов |
|
1 |
6 |
РО |
7 |
3 |
||
|
7.1.1.8 знать и применять аксиомы откладывания отрезков и углов |
Применение |
|||||||
|
7.1.1.6 знать и применять аксиомы измерения отрезков и углов |
Применение |
1 |
7 |
РО |
7 |
3 |
||
|
7.1.1.8 знать и применять аксиомы откладывания отрезков и углов |
Применение |
|||||||
|
7.1.1.32 знать понятие о перпендикуляре |
Знание и понимание |
|||||||
|
Итого: |
|
|
7 |
|
|
40 |
20 |
20 |
|
Примечание: * - разделы, в которые можно вносить изменения |
||||||||
1 ВАРИАНТ
|
Оценивание заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
2 |
3 |
2 |
4 |
3 |
3 |
3 |
|
итого |
20 баллов |
||||||
-
а) Выполните построение:
В плоскости α проведите прямую n. Отметьте точки B, D, К, Х при условии, что точки В и К принадлежат прямой n, а точки Х и D не принадлежат прямой n и лежат в разных полуплоскостях относительно прямой n. Через точки Х, В проведите прямую m.
б) Определите верность утверждений:
|
|
Утверждение |
Верно/неверно |
|
1 |
К ∈ n |
|
|
2 |
n |
|
|
3 |
D ∉m |
|
-
И
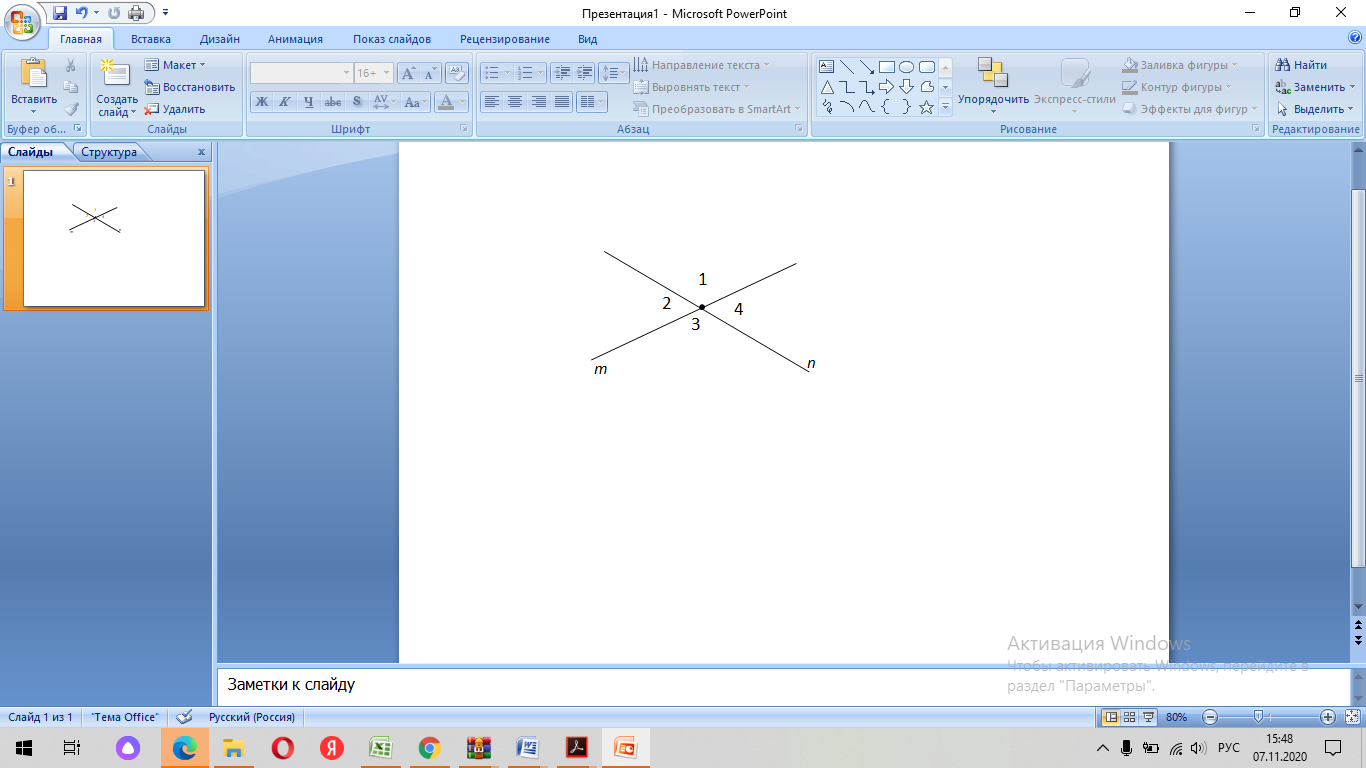 спользуя
рисунок, найдите градусную меру
спользуя
рисунок, найдите градусную меру
-
Точки В, С, К принадлежат прямой l. Если известно, что СК=16см, ВС=6,4см, ВК=9,6 см, то определите какая из точек В,С,К лежит между двумя другими?
-
 300 и
300 и  в 4 раза больше
в 4 раза больше  . Чему рана градусная мера
. Чему рана градусная мера
 если луч ОК является
биссектрисой
если луч ОК является
биссектрисой 
-
Прямые АВ и СD пересекаются в точке О. Через точку О проведена прямая КТ перпендикулярная АВ. Чему равна градусная мера
 ?
?
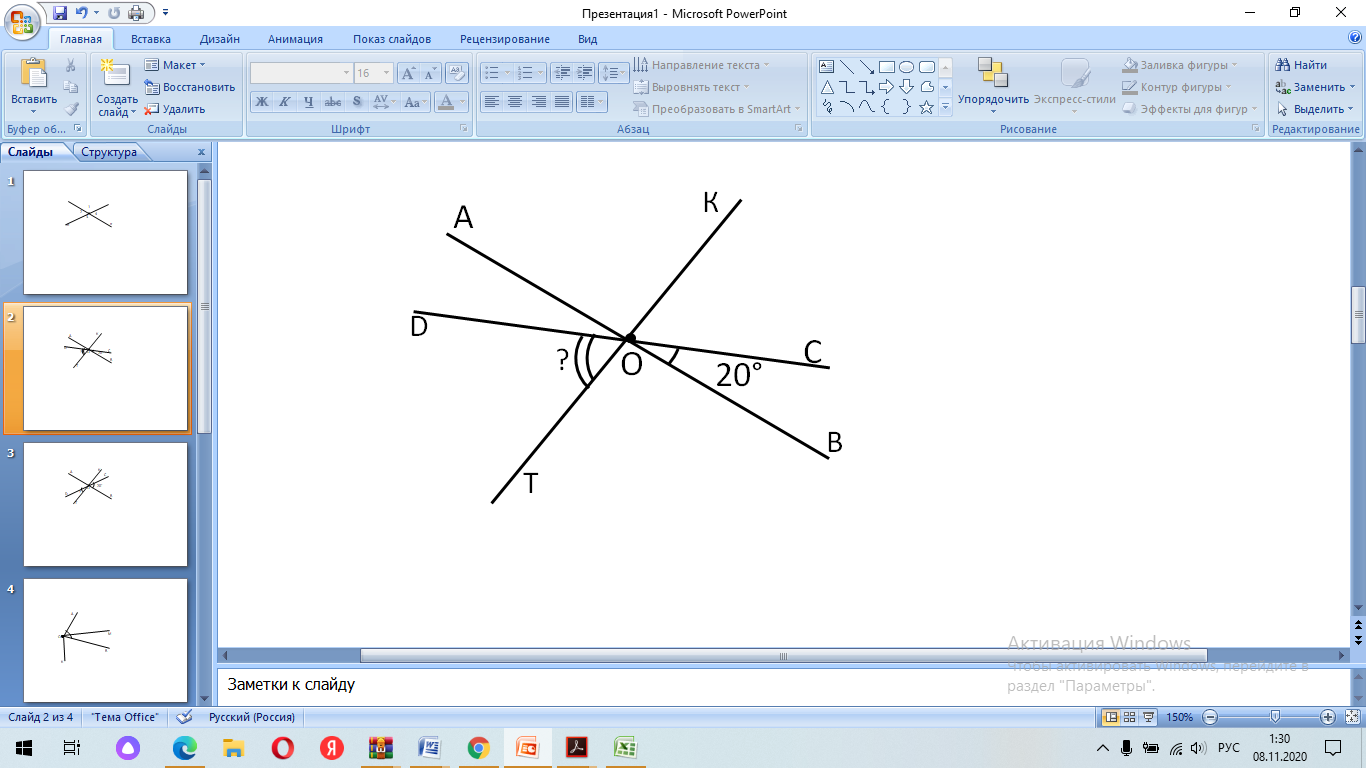
-
Отложите на прямой а отрезки ВМ и ОМ, причем ВМ в 6 раз больше ОМ. Найдите длину отрезков ОМ и ВО, если длина отрезка ВМ равна 24 см.
-
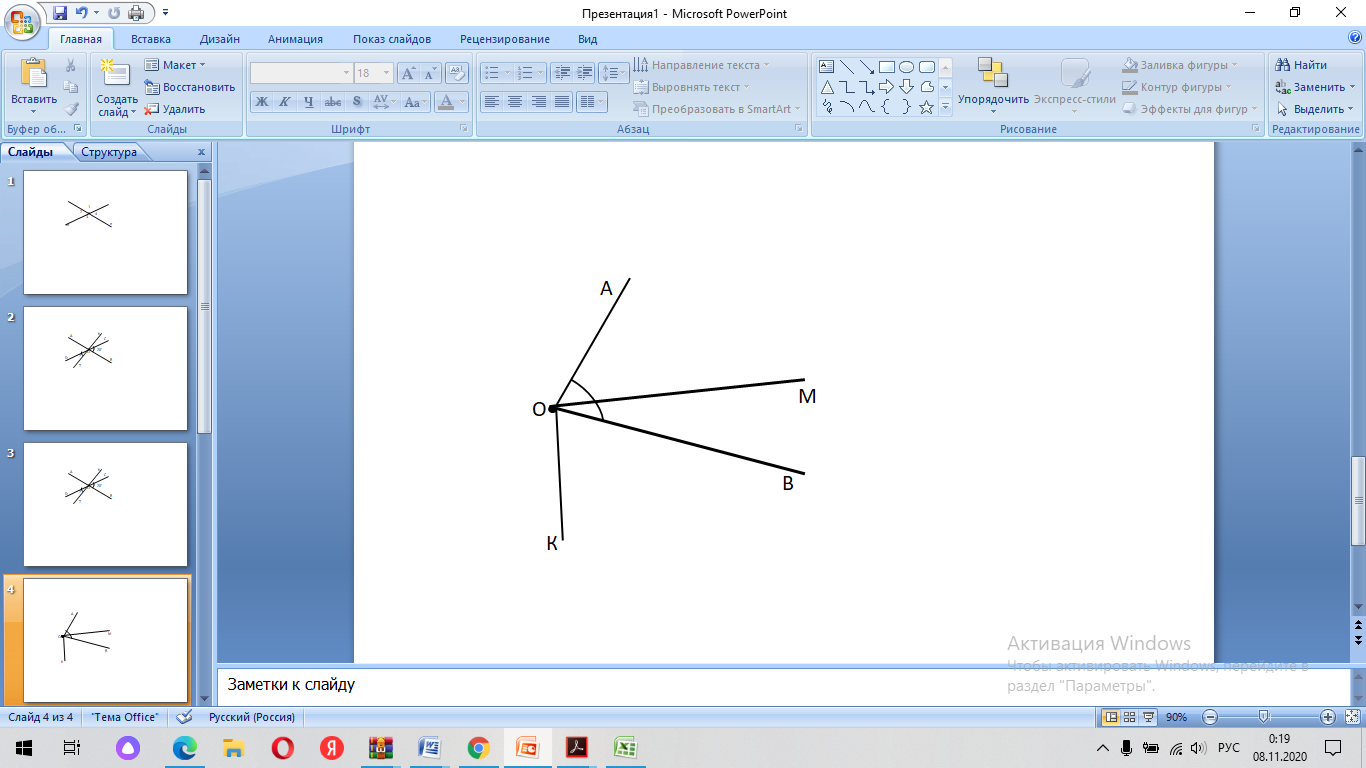
 =800, ОМ – внутренний луч
=800, ОМ – внутренний луч  . Если
. Если  меньше
меньше  на 350, то чему равна градусная мера
на 350, то чему равна градусная мера

-
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
Выполнен чертеж по условию задачи |
1 |
|
|
Да. Да. Да. |
1 |
Принимается ответ в знаковой форме: «+», «-». |
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3 |
Выполнен чертеж по условию задачи |
1 |
|
|
Точка В лежит между точками С,К |
1 |
|
|
|
4 |
Выполнен чертеж по условию задачи |
1 |
|
|
Применяет
определение биссектрисы угла: |
1 |
|
|
|
1
случай: |
1 |
|
|
|
2
случай: |
1 |
|
|
|
5 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
6 |
Выполнен чертеж по условию задачи |
1 |
|
|
1 случай: 4 см и 28 см |
1 |
|
|
|
1 случай: 4 см и 20 см |
1 |
|
|
|
7 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
Всего баллов |
20 |
|
|
2 ВАРИАНТ
|
Оценивание заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
2 |
3 |
2 |
4 |
3 |
3 |
3 |
|
итого |
20 баллов |
||||||
-
а) Выполните построение:
В плоскости γ проведите прямую а. Отметьте точки А, В, С, Е при условии, что точки В и С принадлежат прямой а, а точки А и Е не принадлежат прямой а и лежат в разных полуплоскостях относительно прямой а. Через точки А, В проведите прямую b.
б) Определите верность утверждений:
|
|
Утверждение |
Верно/неверно |
|
1 |
E ∈ a |
|
|
2 |
a |
|
|
3 |
C ∉b |
|
-
И
 спользуя
рисунок, найдите градусную меру
спользуя
рисунок, найдите градусную меру
-
Точки M, N, R принадлежат прямой x. Если известно, что MR=15см, NR=8,5см, MN=6,5 см, то определите какая из точек M, N, R лежит между двумя другими?

-
 400 и
400 и  в 3 раза больше
в 3 раза больше  . Чему рана градусная мера
. Чему рана градусная мера
 если луч LO
является биссектрисой
если луч LO
является биссектрисой

-
Прямые АВ и KM пересекаются в точке О. Через точку О проведена прямая CD перпендикулярная KM. Чему равна градусная мера
 ?
?
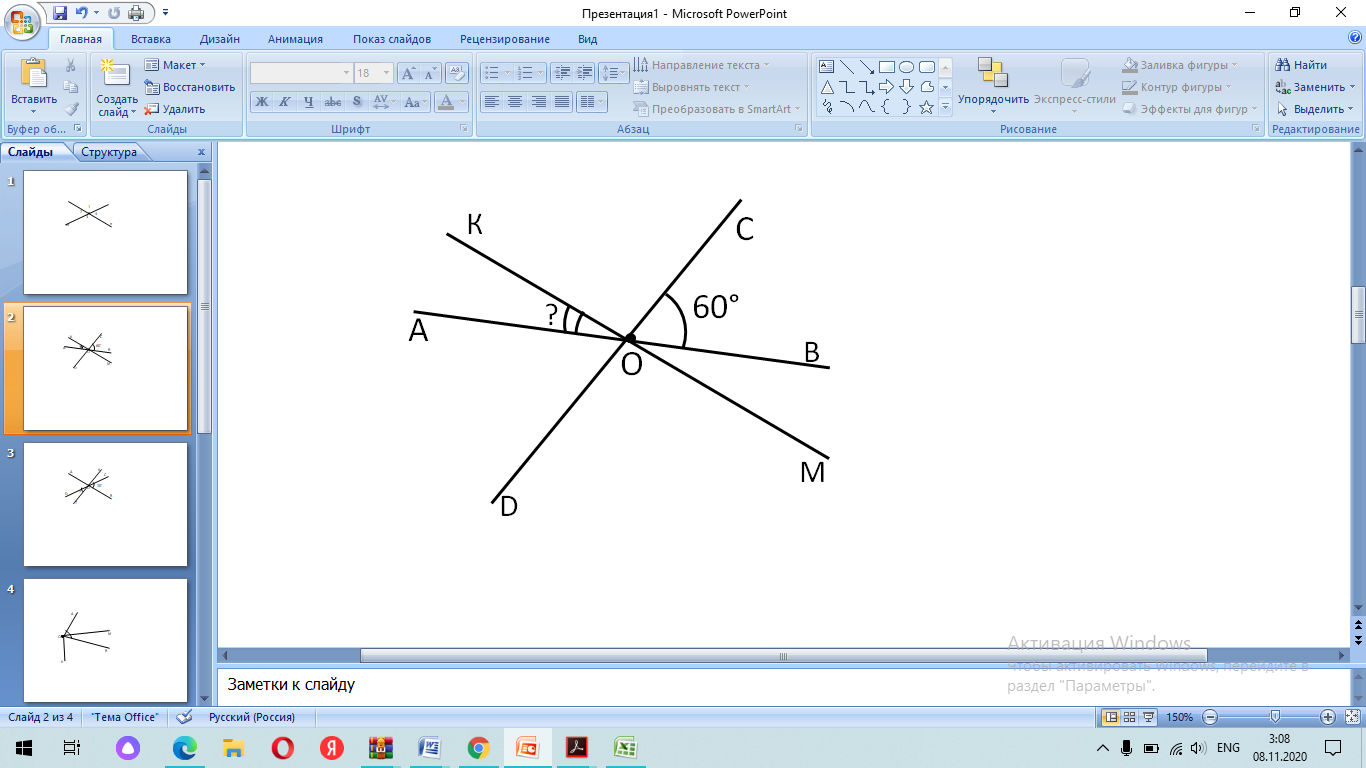
-
Отложите на прямой p отрезки AB и BC, причем AC в 5 раз больше BC. Найдите длину отрезков AB и ВC, если длина отрезка AC равна 25 см.
-
 =700, ОМ – внутренний луч
=700, ОМ – внутренний луч  . Если
. Если  в 2 раза меньше
в 2 раза меньше  , то чему равна градусная мера
, то чему равна градусная мера

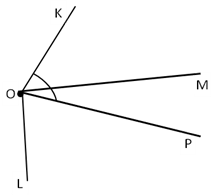
-
-
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
Выполнен чертеж по условию задачи |
1 |
|
|
Нет. Да. Да. |
1 |
Принимается ответ в знаковой форме: «+», «-». |
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3 |
Выполнен чертеж по условию задачи |
1 |
|
|
Точка N лежит между точками M, R |
1 |
|
|
|
4 |
Выполнен чертеж по условию задачи |
1 |
|
|
Применяет
определение биссектрисы угла: |
1 |
|
|
|
1
случай: |
1 |
Принимается альтернативный вариант решения |
|
|
2
случай: |
1 |
||
|
5 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
6 |
Выполнен чертеж по условию задачи |
1 |
|
|
1 случай: 5 см и 20 см |
1 |
|
|
|
1 случай: 5 см и 30 см |
1 |
|
|
|
7 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
Всего баллов |
20 |
|
|
3 ВАРИАНТ
|
Оценивание заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
2 |
3 |
2 |
4 |
3 |
3 |
3 |
|
итого |
20 баллов |
||||||
-
а) Выполните построение:
В плоскости β проведите прямую f. Отметьте точки K, L, M, N при условии, что точки L и M принадлежат прямой f, а точки K и N не принадлежат прямой f и лежат в разных полуплоскостях относительно прямой f. Через точки K, M проведите прямую m.
б) Определите верность утверждений:
|
|
Утверждение |
Верно/неверно |
|
1 |
K ∈ f |
|
|
2 |
f |
|
|
3 |
N ∉m |
|
-
И
 спользуя
рисунок, найдите градусную меру
спользуя
рисунок, найдите градусную меру
-
Точки A, B, D принадлежат прямой n. Если известно, что AD=16,3см, AB=20 см, BD=3,7см, то определите какая из точек A, B, D лежит между двумя другими?

-
 200 и
200 и  в 4 раза больше
в 4 раза больше  . Чему рана градусная мера
. Чему рана градусная мера
 если луч ОC
является биссектрисой
если луч ОC
является биссектрисой

-
Прямые KN и LM пересекаются в точке О. Через точку О проведена прямая AP перпендикулярная LM. Чему равна градусная мера
 ?
?
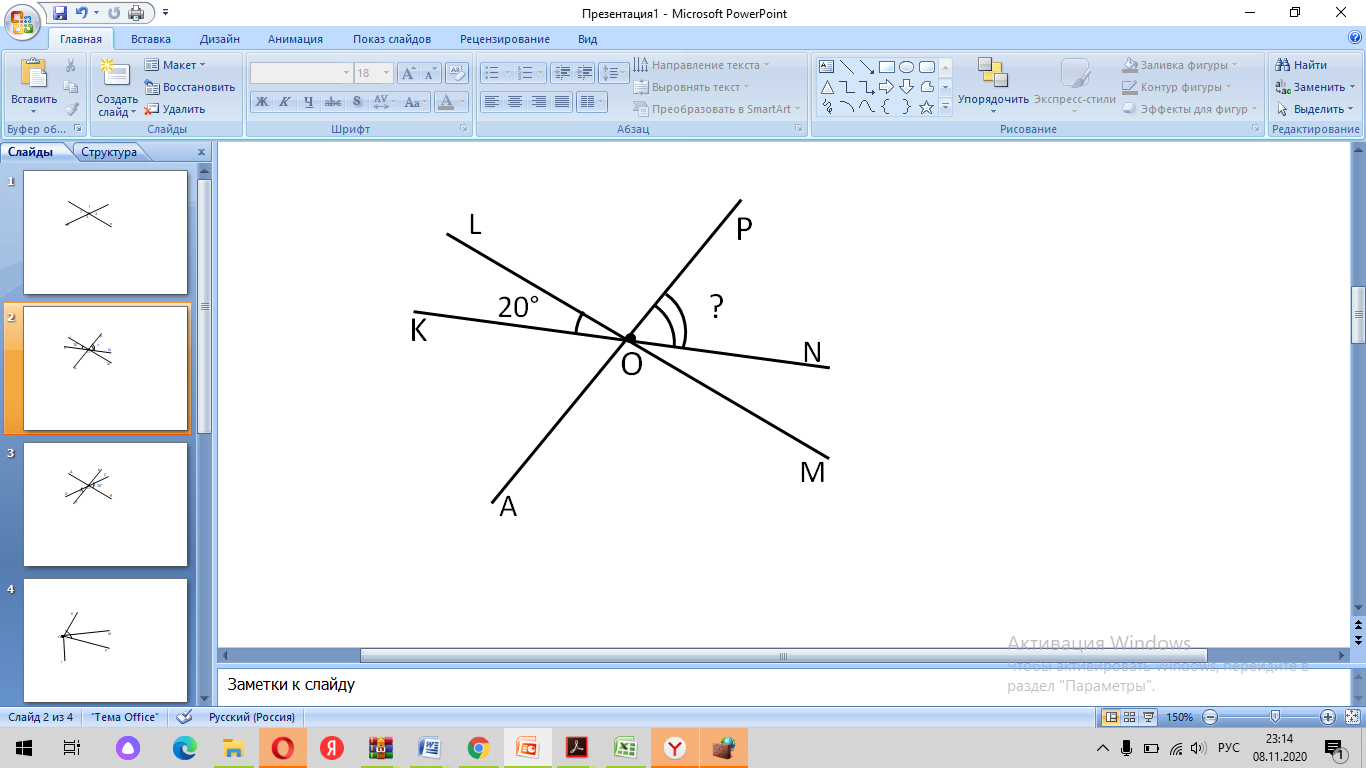
-
Отложите на прямой a отрезки XY и YZ, причем XZ в 6 раз больше YZ. Найдите длину отрезков XY и YZ, если длина отрезка XZ равна 42 см.
-
 =820, AB – внутренний луч
=820, AB – внутренний луч  . Если
. Если  на 200 меньше
на 200 меньше  , то чему равна градусная мера
, то чему равна градусная мера

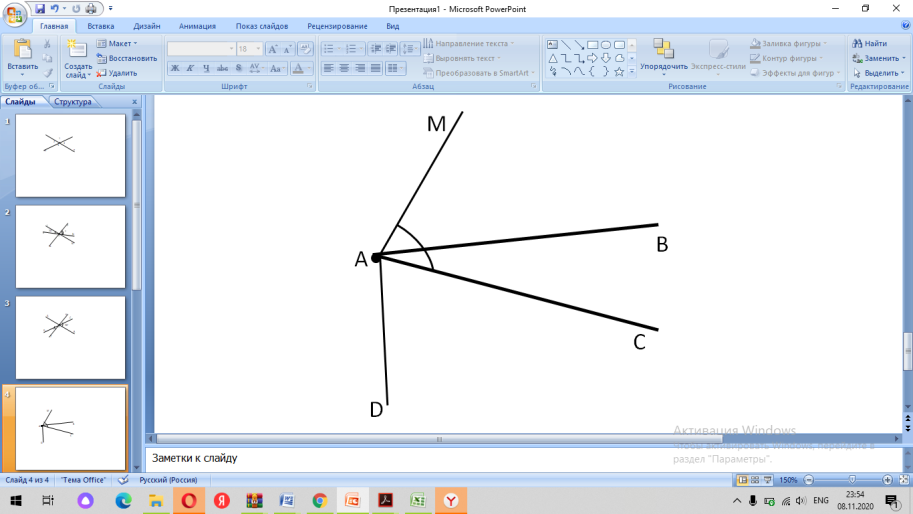
-
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
Выполнен чертеж по условию задачи |
1 |
|
|
Нет. Да. Да. |
1 |
Принимается ответ в знаковой форме: «+», «-». |
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3 |
Выполнен чертеж по условию задачи |
1 |
|
|
Точка D лежит между точками A, B |
1 |
|
|
|
4 |
Выполнен чертеж по условию задачи |
1 |
|
|
Применяет
определение биссектрисы угла: |
1 |
|
|
|
1
случай: |
1 |
Принимается альтернативный вариант решения |
|
|
2
случай: |
1 |
||
|
5 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
6 |
Выполнен чертеж по условию задачи |
1 |
|
|
1 случай: 7 см и 35 см |
1 |
|
|
|
1 случай: 7 см и 49 см |
1 |
|
|
|
7 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
Всего баллов |
20 |
|
|
4 ВАРИАНТ.
|
Оценивание заданий работы |
|||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Количество баллов |
2 |
3 |
2 |
4 |
3 |
3 |
3 |
|
итого |
20 баллов |
||||||
-
а) Выполните построение:
В плоскости α проведите прямую b. Отметьте точки A, B, C, L при условии, что точки L и B принадлежат прямой b, а точки A и C не принадлежат прямой b и лежат в разных полуплоскостях относительно прямой b. Через точки C, L проведите прямую m.
б) Определите верность утверждений:
|
|
Утверждение |
Верно/неверно |
|
1 |
B ∈ m |
|
|
2 |
b |
|
|
3 |
A ∉ m |
|
-
И
 спользуя
рисунок, найдите градусную меру
спользуя
рисунок, найдите градусную меру
-
Точки Q, R, W принадлежат прямой a. Если известно, что QR=10.5 см, QW=18 см, RW=7,5см, то определите какая из точек Q, R, W лежит между двумя другими?

-
 600 и
600 и  в 2 раза больше
в 2 раза больше  . Чему рана градусная мера
. Чему рана градусная мера
 если луч BO
является биссектрисой
если луч BO
является биссектрисой

-
Прямые OP и RN пересекаются в точке A. Через точку A проведена прямая ET перпендикулярная RN. Чему равна градусная мера
 ?
?
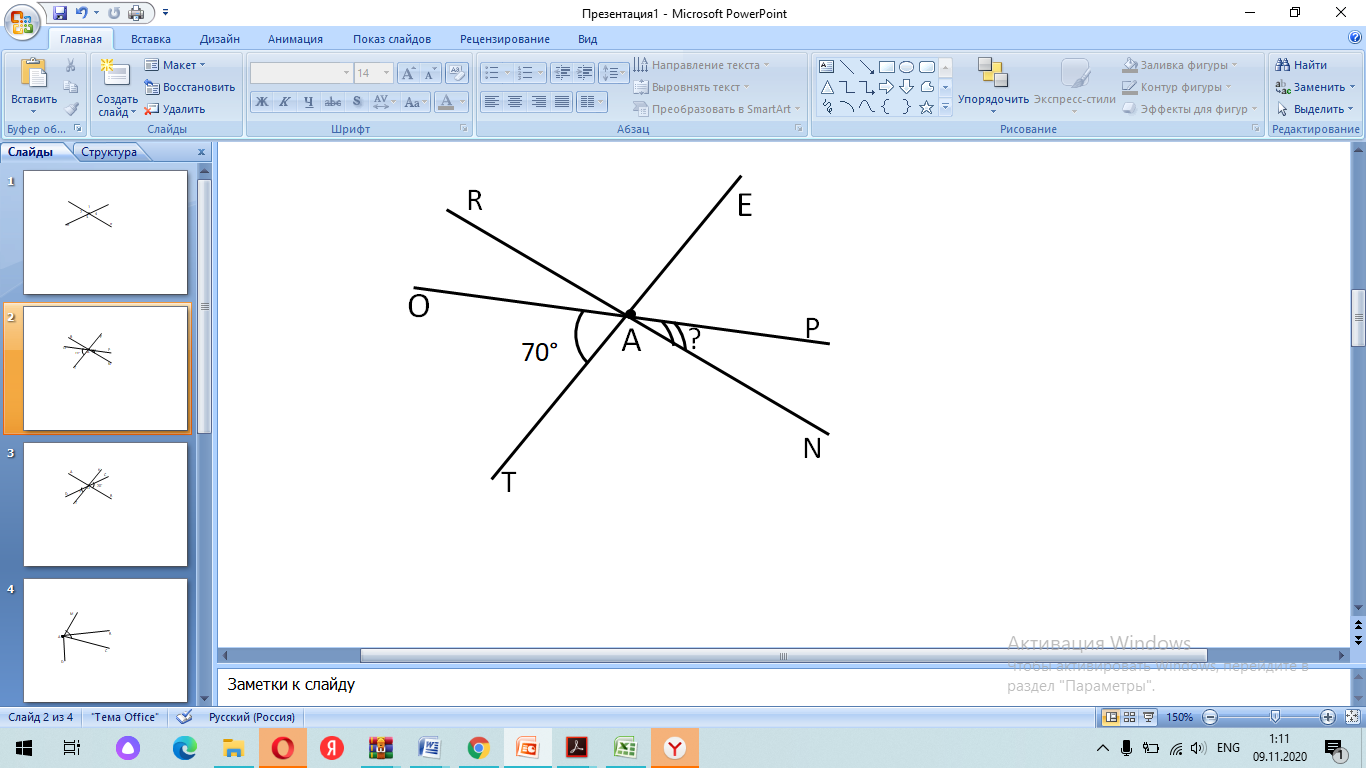
-
Отложите на прямой b отрезки KL и LM, причем KL в 4 раз меньше KM. Найдите длину отрезков KL и LM, если длина отрезка KM равна 24 см.
-
 =870, KB – внутренний луч
=870, KB – внутренний луч  . Если
. Если  на 300 меньше
на 300 меньше  , то чему равна градусная мера
, то чему равна градусная мера

-
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ.
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
Выполнен чертеж по условию задачи |
1 |
|
|
Нет. Да. Да. |
1 |
Принимается ответ в знаковой форме: «+», «-». |
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
3 |
Выполнен чертеж по условию задачи |
1 |
|
|
Точка R лежит между точками Q, W |
1 |
|
|
|
4 |
Выполнен чертеж по условию задачи |
1 |
|
|
Применяет
определение биссектрисы угла: |
1 |
|
|
|
1
случай: |
1 |
Принимается альтернативный вариант решения |
|
|
2
случай: |
1 |
||
|
5 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
6 |
Выполнен чертеж по условию задачи |
1 |
|
|
1 случай: 6 см и 18 см |
1 |
|
|
|
1 случай: 6 см и 30 см |
1 |
|
|
|
7 |
|
1 |
Принимается альтернативный вариант решения |
|
|
1 |
||
|
|
1 |
||
|
Всего баллов |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА 2 ЧЕТВЕРТЬ
Продолжительность - 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответом.
В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков
|
Кол. заданий* |
№ заданя* |
Тип задани я* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Треугольники |
7.1.1.21 знать и доказывать признаки равенства треугольников |
Применение |
1 |
1 |
КО |
5 |
2 |
20 |
|
7.1.1.22 применять признаки равенства треугольников при решении задач на вычисление и на доказательство |
Применение |
|||||||
|
7.1.1.13 различать виды треугольников |
Знание и понимание |
1 |
2 |
КО |
5 |
2 |
||
|
7.1.1.23 применять свойства и признаки равнобедренного треугольника |
Применение |
|||||||
|
7.1.1.21 знать и доказывать признаки равенства треугольников |
Применение |
1 |
3 |
РО |
7 |
4 |
||
|
7.1.1.23 применять свойства и признаки равнобедренного треугольника |
Применение |
|||||||
|
7.1.1.22 применять признаки равенства треугольников при решении задач на вычисление и на доказательство |
Навыки высокого порядка |
1 |
4 |
РО |
8 |
5 |
||
|
7.1.1.23 применять свойства и признаки равнобедренного треугольника |
Применение |
1 |
5 |
РО |
5 |
2 |
||
|
7.1.1.12 знать определение медианы, биссектрисы, высоты, серединного перпендикуляра и средней линии треугольника и изображать их |
Знание и понимание |
1 |
6 |
РО |
10 |
5 |
||
|
7.1.1.23 применять свойства и признаки равнобедренного треугольника |
Навыки высокого порядка |
|||||||
|
Итого: |
|
|
6 |
|
|
40 |
20 |
20 |
|
Примечание: * - разделы, в которые можно вносить изменения |
||||||||
1 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
4 |
5 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
Для доказательства равенства треугольников АВС и NКМ достаточно доказать, что…

а) ![]() С =
С = ![]() К; б)
К; б) ![]() С =
С = ![]() М; в)
М; в) ![]() В =
В = ![]() М.
М.
Укажите, по какому признаку равны треугольники.
-
Найдите основание равнобедренного треугольника, у которого боковая сторона равна 17 см, а периметр равен 45 см.
-
Равные отрезки АВ и СД пересекаются в точке О. Точка О является серединой отрезков АВ и СД. Проведены отрезки ВС и АД. Чему равен угол ВСО, если <ДАО= 400
-
В равнобедренном треугольнике АВС с основанием АС проведена биссектриса ВД. На отрезке ВД отмечена любая точка К. Докажите равенство треугольников АВК и СВК.
-
АВ – основание равнобедренного треугольника АВС.<C=500 . Найдите остальные углы треугольника.
-
ВТ – медиана равнобедренного треугольника АВС. АС – основание. Перимерт треугольника АВС равен 60 м, а периметр треугольника АВТ – 45 м. Найдите длину медианы ВТ.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
б)
|
1 |
|
|
Указывает признак равенства треугольников: По стороне и двум прилежащим к ней углам |
1 |
|
|
|
2 |
Указывает длину второй боковой стороны, используя свойство равнобедренного треугольника. Боковая сторона равна 17 см |
1 |
|
|
Находит основание треугольника 45-(17+17)= 11 см |
1 |
Принимается любой альтернативный вариант |
|
|
3 |
Изображен чертеж по условию задачи и введены соответствующие обозначения АВ=СД, АО=ОВ, СО=ОД, <АОД = < ВОС (вертикальные углы) |
1 |
|
|
|
1 |
1 признак равенства треугольников |
|
|
Так как по
условию АО=ОВ, СО=ОД, то |
1 |
|
|
|
Следовательно <ВСО = < ДАО= 400 . |
1 |
|
|
|
4 |
Изображен чертеж по условию задачи |
1 |
|
|
Треугольник АВС равнобедренный: АВ=ВС |
1 |
|
|
|
Так как ВД – биссектриса, то <АВД=<СВД |
1 |
|
|
|
ВК – общая сторона |
1 |
|
|
|
|
1 |
1 признак |
|
|
5 |
<А =<В – углы при основании |
1 |
|
|
(1800 – < С):2 = 650 Или (1800 – < С):2 = 650 |
1 |
|
|
|
6 |
ВТ – медиана треугольника: АС= 2 АТ и Р(АВС)= АВ+ВС+АС= 2АВ+АС= 2 АВ+2АТ |
1 |
Принимается любой альтернативный вариант решения |
|
2АВ + 2 АТ=60 АВ+АТ=30 м |
1 |
||
|
Р(АВТ)=АВ+ВТ+АТ АВ+ВТ+АТ=45 м |
1 |
||
|
30+ВТ=45 |
1 |
||
|
ВТ= 15 м |
1 |
||
|
Итого: |
20 |
|
|
2 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
4 |
5 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
Для доказательства равенства треугольников АPK и DCE достаточно доказать, что…

а) АР = CD; б) AP = DE; в) AP = CE.
Укажите, по какому признаку равны треугольники.
-
Найдите основание равнобедренного треугольника, у которого боковая сторона равна 15 см, а периметр равен 48 см.
-
Равные отрезки АС и ВД пересекаются в точке О. Точка О делит эти отрезки пополам. Проведены отрезки АВ и ДС. Чему равен угол ВАО, если <СДО= 600
-
В равнобедренном треугольнике КРН с основанием КН проведена биссектриса РД. На отрезке РД отмечена любая точка А. Докажите равенство треугольников РАК и РАН.
-
ОА – основание равнобедренного треугольника ОАВ. .<В=400 . Найдите остальные углы треугольника.
-
ВТ – медиана равнобедренного треугольника LВN. LN – основание. Перимерт треугольника LBN равен 50 м, а периметр треугольника LВТ – 40 м. Найдите длину медианы ВТ.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
А) АР= СД |
1 |
|
|
Указывает признак равенства треугольников: По стороне и двум прилежащим к ней углам |
1 |
|
|
|
2 |
Указывает длину второй боковой стороны, используя свойство равнобедренного треугольника. Боковая сторона равна 15 см |
1 |
|
|
Находит основание треугольника 48-(15+15)= 18 см |
1 |
Принимается любой альтернативный вариант |
|
|
3 |
Изображен чертеж по условию задачи и введены соответствующие обозначения АС=ВД, АО=ОС, ВО=ОД, <АОВ = < СОД (вертикальные углы) |
1 |
|
|
|
1 |
1 признак равенства треугольников |
|
|
Так как по
условию АО=ОС, ВО=ОД, то |
1 |
|
|
|
Следовательно <ВАО = < СДО= 600 . |
1 |
|
|
|
4 |
Изображен чертеж по условию задачи |
1 |
|
|
Треугольник КРН равнобедренный: 1) РК=РН 2) Так как РД – биссектриса, то <КРД=<НРД |
1 |
|
|
|
РА – общая сторона |
1 |
|
|
|
|
1 |
1 признак |
|
|
5 |
<А =<О – углы при основании |
1 |
|
|
(1800 – < В):2 = 700 Или (1800 – < В):2 = 700 |
1 |
|
|
|
6 |
ВТ – медиана треугольника: LN= 2 LТ и Р(LBN)= LВ+ВN+LN= 2ВN+LN= 2 ВN+2LТ |
1 |
Принимается любой альтернативный вариант решения |
|
2 ВN+2LТ =50 ВN+LТ = 25 м |
1 |
||
|
Р(LВТ)=LВ+ВТ+LТ LВ+ВТ+LТ =40 м |
1 |
||
|
25+ВТ=40 |
1 |
||
|
ВТ= 15 м |
1 |
||
|
Итого: |
20 |
|
|
3 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
4 |
5 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
Для доказательства равенства треугольников АВС и КМР достаточно доказать, что…
а) ВС = МР; б) ВС = РК; в) МК = ВС.
Укажите, по какому признаку равны треугольники.
-
Найдите основание равнобедренного треугольника, у которого боковая сторона равна 11 дм, а периметр равен 29 дм.
-
Равные отрезки АС и ВД пересекаются в точке О. Точка О делит эти отрезки пополам. Точки С и В и А и Д соеденены. Чему равен угол ВСО, если <АДО= 700
-
В равнобедренном треугольнике АВС с основанием АС проведена медиана ВД. Точка Р - середина стороны ВА, точка К – середина стороны ВС. Докажите равенство треугольников ВДР и ВДК.
-
АВС – равнобедренный треугольник, ВС – основание. <А=700 . Найдите остальные углы треугольника.
-
SQ – медиана равнобедренного треугольника FST. FT – основание. Перимерт треугольника FST равен 70 м, а периметр треугольника FSQ – 50 м. Найдите длину медианы SQ.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
а) ВС = МР; |
1 |
|
|
Указывает признак равенства треугольников: По стороне и двум прилежащим к ней углам |
1 |
|
|
|
2 |
Указывает длину второй боковой стороны, используя свойство равнобедренного треугольника. Боковая сторона равна 11 дм |
1 |
|
|
Находит основание треугольника 29-(11+11)=7 дм |
1 |
Принимается любой альтернативный вариант |
|
|
3 |
Изображен чертеж по условию задачи и введены соответствующие обозначения АС=ВД, АО=ОВ, СО=ОД, <АОД = < ВОС (вертикальные углы) |
1 |
|
|
|
1 |
1 признак равенства треугольников |
|
|
Так как по
условию АО=ОС, ВО=ОД, то |
1 |
|
|
|
<СВО = < АДО= 700 . |
1 |
|
|
|
4 |
Изображен чертеж по условию задачи |
1 |
|
|
Треугольник АВС равнобедренный: АВ=ВС, так как Р и К середины боковых сторон, то ВР=ВК |
1 |
|
|
|
Так как ВД – медиана, то она является и биссектрисой <АВД=<СВД ВД – общая сторона |
1 |
|
|
|
|
1 |
1 признак |
|
|
5 |
<С =<В – углы при основании |
1 |
|
|
(1800 – < А):2 = 550 Или (1800 – < А):2 = 550 |
1 |
|
|
|
6 |
SQ – медиана треугольника: FT= 2 FQ и Р(FST)= SF+ST+FT= 2 FS+FT= 2 FS+2 FQ |
1 |
Принимается любой альтернативный вариант решения |
|
2 FS+2 FQ =70 FS+ FQ = 35 м |
1 |
||
|
Р(FSQ)= FS+SQ+FQ FS+SQ+FQ = 50 м |
1 |
||
|
35+SQ = 50 |
1 |
||
|
SQ = 15 м |
1 |
||
|
Итого: |
20 |
|
|
4 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
4 |
5 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
Для доказательства равенства треугольников АВС и РEК достаточно доказать, что…
а) ![]() В =
В = ![]() Е; б)
Е; б) ![]() В =
В = ![]() К; в)
К; в) ![]() В =
В = ![]() Р.
Р.
Укажите, по какому признаку равны треугольники.
-
Найдите основание равнобедренного треугольника, у которого боковая сторона равна 12 дм, а периметр равен 28 дм.
-
Равные отрезки MN и AK пересекаются в точке О. Точка О делит эти отрезки пополам. Точки A и M, N и K соединены. Чему равен угол ОКN, если <ОMA= 350
-
В равнобедренном треугольнике КРН с основанием КН проведена медиана РД. Точка А - середина стороны РК, точка В – середина стороны РН. Докажите равенство треугольников РДА и РДВ.
-
ДОС – равнобедренный треугольник с основанием ДС, <О = 800 . Найдите остальные углы треугольника
-
ВМ – медиана равнобедренного треугольника РВК. РК – основание. Перимерт треугольника РВК равен 80 м, а периметр треугольника РВМ – 50 м. Найдите длину медианы ВМ.
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
а)
|
1 |
|
|
Указывает признак равенства треугольников: По стороне и двум прилежащим к ней углам |
1 |
|
|
|
2 |
Указывает длину второй боковой стороны, используя свойство равнобедренного треугольника. Боковая сторона равна 12 дм |
1 |
|
|
Находит основание треугольника 28-(12+12) = 4 дм |
1 |
Принимается любой альтернативный способ |
|
|
3 |
Изображен чертеж по условию задачи и введены соответствующие обозначения MN=AK, MO=ОN, AО=ОK, <АОM = < KОN (вертикальные углы) |
1 |
|
|
|
1 |
1 признак равенства треугольников |
|
|
Так как по
условию MO=ОN, AО=ОK, то |
1 |
|
|
|
< OKN = < OMA = 350 . |
1 |
|
|
|
4 |
Изображен чертеж по условию задачи |
1 |
|
|
Треугольник АВС равнобедренный: РК=РН Так как А и В середины боковых сторон, то РА=РВ |
1 |
|
|
|
Так как РД – медиана, то она является и биссектрисой <КРД=<НРД РД – общая сторона |
1 |
|
|
|
|
1 |
1 признак |
|
|
5 |
<С =<Д – углы при основании |
1 |
|
|
(1800 – < О):2 = 500 Или (1800 – < О):2 = 500 |
1 |
|
|
|
6 |
ВМ – медиана треугольника: РК= 2 РМ и Р(РВК)= РВ+ВК+РК= 2РВ+РК= 2 РВ+2 РМ |
1 |
Принимается любой альтернативный вариант решения |
|
2РВ + 2 РМ= 80 РВ+ РМ=40 м |
1 |
||
|
Р(РВМ)= РВ+ВМ+РМ РВ+ВМ+РМ =50 м |
1 |
||
|
40+ВМ= 50 |
1 |
||
|
ВМ= 10 м |
1 |
||
|
Итого: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬ
Продолжительность - 40 минут
Количество баллов – 20
Типы заданий:
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым ответом.
В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения.
В заданиях, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выолнение, мин* |
Балл* |
Балл за раздел |
|
Взаимное расположение прямых |
7.1.2.3 распознавать углы, образованные при пересечении двух прямых секущей |
Знание и понимание |
1 |
1 |
КО |
5 |
2 |
20 |
|
7.1.2.7 применять свойства параллельных прямых при решении задач |
Применение |
|||||||
|
7.1.1.19 применять теорему о внешнем угле треугольника |
Применение |
1 |
2 |
КО |
5 |
2 |
||
|
7.1.1.17 применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач |
Навыки высокого порядка |
1 |
3 |
РО |
8 |
5 |
||
|
7.1.1.20 знать соотношение между сторонами и углами треугольника и применять его при решении задач |
Применение |
|||||||
|
7.1.3.1 знать и применять неравенство треугольника |
Применение |
1 |
4 |
РО |
5 |
4 |
||
|
7.1.1.27 применять свойства прямоугольного треугольника |
Применение |
1 |
5 |
РО |
5 |
2 |
||
|
7.1.2.5 применять признаки параллельности прямых при решении задач |
Применение |
1 |
6 |
РО |
12 |
5 |
||
|
7.1.1.17 применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач |
Навыки высокого порядка |
|||||||
|
ИТОГО: |
|
|
6 |
|
|
40 мин |
20 |
20 |
|
Примечание: * - разделы, в которые можно вносить изменения |
||||||||
1 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
5 |
4 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
По данным рисунка найдите
 , если
a || b
и
, если
a || b
и  = 63 ◦.
= 63 ◦.
-
В треугольнике АКМ внешний угол при вершине А равен 112 ◦, а внутренний при вершине М равен 56 ◦.Найдите внешний угол при вершине К.
-
Найдите угла треугольника АВС, если
 .
.
-
Определите вид треугольника АВС.
-
Укажите самую длинную сторону треугольника, обоснуйте свой ответ.
-
Найдите боковую сторону и основание равнобедренного треугольника, если две его стороны равны 3,5 см и 8,3 см.
-
В треугольнике АВС известно , что
 А=60 ◦,
А=60 ◦,  С=90 ◦, ВС= 7,5 см и проведена высота СМ. Найдите длину
высоты СМ.
С=90 ◦, ВС= 7,5 см и проведена высота СМ. Найдите длину
высоты СМ. -
На рисунке дано
 СВМ больше
СВМ больше
 АВМ на
63
АВМ на
63 . Найдите углы
треугольника АВС.
. Найдите углы
треугольника АВС.
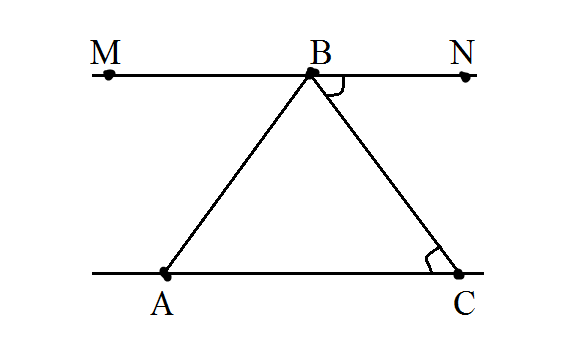
72![]()
72![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
||
|
2 |
|
1 |
Принимается альтернативный вариант |
|
124 |
1 |
|
|
|
3 |
Обозначает
углы через х, |
1 |
Применение теоремы о сумме внутренних углов треугольника |
|
Составляет
уравнение 2х+3х+5х=180 находит
х=18 |
1 |
||
|
Находит
углы треугольника : 36 |
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Применяет соотношение между сторонами и углами треугольника |
|
|
4 |
|
1 |
Применяет определение равнобедренного треугольника Применяет неравенство треугольника |
|
АВ+ВС >
АС |
1 |
||
|
В
|
1 |
||
|
|
1 |
||
|
5 |
|
1 |
|
|
|
1 |
Применяет свойства прямоугольного треугольника |
|
|
6 |
|
1 |
Принимается альтернативный вариант |
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
Итого: |
20 |
|
|
2 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
5 |
4 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
По данным рисунка найдите
 , если
a || b
и
, если
a || b
и  = 59 ◦.
= 59 ◦.

-
В треугольнике АКМ внешний угол при вершине А равен 109 ◦, а внутренний при вершине М равен 63 ◦.Найдите внешний угол при вершине К.
-
Найдите угла треугольника АВС, если
 .
.
-
Определите вид треугольника АВС.
-
Укажите самую длинную сторону треугольника, обоснуйте свой ответ.
-
Найдите боковую сторону и основание равнобедренного треугольника, если две его стороны равны 2,7 см и 6,5 см.
-
В треугольнике АВС известно , что
 А=60 ◦,
А=60 ◦,  С=90 ◦, ВС= 9,4 см и проведена высота СМ. Найдите длину
высоты СМ.
С=90 ◦, ВС= 9,4 см и проведена высота СМ. Найдите длину
высоты СМ. -
На рисунке дано
 СВМ больше
СВМ больше
 АВМ на
54
АВМ на
54 . Найдите углы
треугольника АВС.
. Найдите углы
треугольника АВС.

68![]()
68![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
||
|
2 |
|
1 |
Принимается альтернативный вариант |
|
134 |
1 |
|
|
|
3 |
Обозначает
углы через х, |
1 |
Применение теоремы о сумме внутренних углов треугольника |
|
Составляет
уравнение 13х+17х+6х=180 находит
х=5 |
1 |
||
|
Находит
углы треугольника : 65 |
1 |
|
|
|
Все углы
острые, следовательно |
1 |
|
|
|
|
1 |
Применяет соотношение между сторонами и углами треугольника |
|
|
4 |
|
1 |
Применяет определение равнобедренного треугольника Применяет неравенство треугольника |
|
АВ+ВС >
АС |
1 |
||
|
В
|
1 |
||
|
|
1 |
||
|
5 |
|
1 |
|
|
|
1 |
Применяет свойства прямоугольного треугольника |
|
|
6 |
|
1 |
Принимается альтернативный вариант |
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
Итого: |
20 |
|
|
3 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
5 |
4 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
По данным рисунка найдите
 , если
a || b
и
, если
a || b
и  = 43 ◦.
= 43 ◦.

-
В треугольнике АКМ внешний угол при вершине А равен 117 ◦, а внутренний при вершине М равен 74 ◦.Найдите внешний угол при вершине К.
-
Найдите угла треугольника АВС, если
 .
.
-
Определите вид треугольника АВС.
-
Укажите самую длинную сторону треугольника, обоснуйте свой ответ.
-
Найдите боковую сторону и основание равнобедренного треугольника, если две его стороны равны 3,83 см и 7,91 см.
-
В треугольнике АВС известно , что
 А=60 ◦,
А=60 ◦,  С=90 ◦, ВС= 8,7 см и проведена высота СМ. Найдите длину
высоты СМ.
С=90 ◦, ВС= 8,7 см и проведена высота СМ. Найдите длину
высоты СМ.
-
На рисунке дано
 СВМ больше
СВМ больше
 АВМ на
27
АВМ на
27 . Найдите углы
треугольника АВС.
. Найдите углы
треугольника АВС.
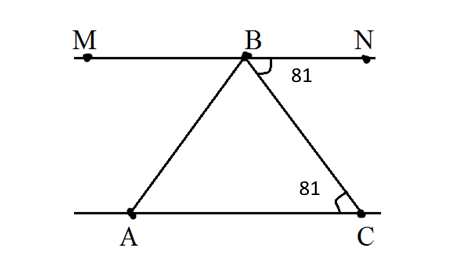
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
||
|
2 |
|
1 |
Принимается альтернативный вариант |
|
137 |
1 |
|
|
|
3 |
Обозначает
углы через х, |
1 |
Применение теоремы о сумме внутренних углов треугольника |
|
Составляет
уравнение 2х+3х+5х=180 находит
х=15 |
1 |
||
|
Находит
углы треугольника : 75 |
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Применяет соотношение между сторонами и углами треугольника |
|
|
4 |
|
1 |
Применяет определение равнобедренного треугольника Применяет неравенство треугольника |
|
АВ+ВС >
АС |
1 |
||
|
В
|
1 |
||
|
|
1 |
||
|
5 |
|
1 |
|
|
|
1 |
Применяет свойства прямоугольного треугольника |
|
|
6 |
|
1 |
Принимается альтернативный вариант |
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
Итого: |
20 |
|
|
4 ВАРИАНТ
|
Оценивание заданий работы |
||||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
|
Количество баллов |
2 |
2 |
5 |
4 |
2 |
5 |
|
итого |
20 баллов |
|||||
-
По данным рисунка найдите
 , если
a || b
и
, если
a || b
и  = 74 ◦.
= 74 ◦.

-
В треугольнике АКМ внешний угол при вершине А равен 123 ◦, а внутренний при вершине М равен 85 ◦.Найдите внешний угол при вершине К.
-
Найдите угла треугольника АВС, если
 .
.
-
Определите вид треугольника АВС.
-
Укажите самую длинную сторону треугольника, обоснуйте свой ответ.
-
Найдите боковую сторону и основание равнобедренного треугольника, если две его стороны равны 4,21 см и 9,01 см.
-
В треугольнике АВС известно , что
 А=60 ◦,
А=60 ◦,  С=90 ◦, ВС= 11,3 см и проведена высота СМ. Найдите
длину высоты СМ.
С=90 ◦, ВС= 11,3 см и проведена высота СМ. Найдите
длину высоты СМ. -
На рисунке дано
 СВМ больше
СВМ больше
 АВМ на
67
АВМ на
67 . Найдите углы
треугольника АВС.
. Найдите углы
треугольника АВС.
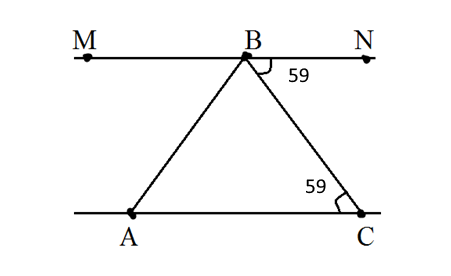
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
|
|
|
1 |
||
|
2 |
|
1 |
Принимается альтернативный вариант |
|
142 |
1 |
|
|
|
3 |
Обозначает
углы через х, |
1 |
Применение теоремы о сумме внутренних углов треугольника |
|
Составляет
уравнение 12х+5х+х=180 находит
х=10 |
1 |
||
|
Находит
углы треугольника : 120 |
1 |
|
|
|
|
1 |
|
|
|
|
1 |
Применяет соотношение между сторонами и углами треугольника |
|
|
4 |
|
1 |
Применяет определение равнобедренного треугольника Применяет неравенство треугольника |
|
АВ+ВС >
АС |
1 |
||
|
В
|
1 |
||
|
|
1 |
||
|
5 |
|
1 |
|
|
|
1 |
Применяет свойства прямоугольного треугольника |
|
|
6 |
|
1 |
Принимается альтернативный вариант |
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
Итого: |
20 |
|
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА 4 ЧЕТВЕРТЬ
Продолжительность - 40 минут
Количество баллов – 20
Типы заданий:
МВО – задания с множественным выбором ответов;
КО – задания, требующие краткого ответа;
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 5 заданий, включающих вопросы с кратким и развернутым ответом. В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения. В заданиях, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
|
Раздел |
Проверяемая цель |
Уровень мыслительных навыков |
Кол. заданий* |
№ задания* |
Тип задания* |
Время на выполнение, мин* |
Балл* |
Балл за раздел |
|
Окружность. Геометрические построения |
7.1.2.13 знать и применять свойства касательной к окружности при решении задач |
Применение |
1 |
1 |
КО |
4 |
3 |
20 |
|
7.1.2.14 знать определения окружностей, вписанной в треугольник и описанной около треугольника |
Знание и понимание |
1 |
2 |
РО |
8 |
4 |
||
|
7.1.1.29 знать и применять определение и свойства центрального угла |
Применение |
|||||||
|
7.1.1.28 знать определения окружности и круга, их элементов (центр, радиус, диаметр, хорда) |
Знание и понимание |
1 |
3 |
РО |
8 |
4 |
||
|
7.1.1.30 доказывать и применять теоремы о перпендикулярности диаметра и хорды |
Применение |
|||||||
|
7.1.2.12 анализировать случаи взаимного расположения прямой и окружности, двух окружностей |
Применение |
1 |
4 |
РО |
8 |
4 |
||
|
7.1.2.18 строить треугольник по заданным элементам |
Навыки высокого порядка |
1 |
5 |
РО |
12 |
5 |
||
|
7.1.2.16 строить угол, равный данному, биссектрису угла, делить отрезок пополам |
Применение |
|||||||
|
ИТОГО: |
|
|
|
|
|
40 |
20 |
20 |
|
Примечание: * - разделы, в которые можно вносить изменения |
||||||||
1 ВАРИАНТ
|
Оценивание заданий работы |
|||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Количество баллов |
3 |
4 |
4 |
4 |
5 |
|
итого |
20 баллов |
||||
1. Через точку С окружности, проведена
касательная MN и хорда СD. Чему равна градусная
мера ![]() , если
, если ![]() ?
?

2. В окружность
с центром О, вписан ![]() так, что
так, что ![]() ,
, ![]() . Найдите величину дуги
АВ.
. Найдите величину дуги
АВ.
3. В окружности с центром О проведен диаметр
АВ=8,4см, пересекающий хорду CD в точке К, причем К середина хорды.
Угол между диаметром и радиусом равен
![]() .Найдите длину
хорды CD и периметр
.Найдите длину
хорды CD и периметр ![]() .
.
4. Начертите окружность радиуса 3см. с центром О.Проведите луч с началом в точке О и отметьте на нем точку В, удаленную от точки О на 5см. Проведите окружность с центром в точке В, радиус которой:
а)2см; b)3см 5мм.; c)1см 5мм
Сколько общих точек имеют окружности в каждом из этих случаев?
5. а)Постройте треугольник АВС по сторонам
АС=5см, АВ=4см, ![]() ;
;
b) В полученном
треугольнике постройте биссектрису
![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
Принимается альтернативная запись решения |
|
|
1 |
||
|
|
1 |
||
|
2 |
Выполнен чертеж по условию задачи |
1 |
|
|
|
1 |
Принимается альтернативное решение |
|
|
2х+3х+ |
1 |
||
|
|
1 |
||
|
3 |
OD=4,2см |
1 |
|
|
KD=2,1см (по свойству катета лежащего против
угла |
1 |
|
|
|
СD=4,2см |
1 |
|
|
|
P |
1 |
|
|
|
4 |
а) Одна
общая точка, т.к. |
1 |
Принимается альтернативная запись решения |
|
b) Две общие точки,
т.к. |
1 |
||
|
с) нет
общих точек, т.к. |
1 |
||
|
Выполнен чертеж для каждого случая |
1 |
|
|
|
5а |
Построен отрезок равный 5см/4см |
1 |
|
|
Построен
угол |
1 |
|
|
|
Построен отрезок равный 4см/5см |
1 |
|
|
|
Построен треугольник и записан ход построения |
1 |
|
|
|
5b |
Построена биссектриса угла |
1 |
|
|
Итого: |
20 |
|
|
2 ВАРИАНТ
|
Оценивание заданий работы |
|||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Количество баллов |
3 |
4 |
4 |
4 |
5 |
|
итого |
20 баллов |
||||
1. Через точку В окружности, проведена
касательная КN и хорда ВD. Чему равна градусная
мера ![]() , если
, если ![]() ?
?

2. В окружность с центром О,
вписан ![]() так, что
так, что ![]() ,
, ![]() . Найдите величину дуги
KL.
. Найдите величину дуги
KL.
3. В окружности с центром О проведен диаметр
КС=10,4см, пересекающий хорду АВ в точке Р, причем Р середина
хорды. Угол между диаметром и радиусом равен
![]() .Найдите длину
хорды АВ и периметр
.Найдите длину
хорды АВ и периметр ![]() .
.
4. Начертите окружность радиуса 4см. с центром О.Проведите луч с началом в точке О и отметьте на нем точку К, удаленную от точки О на 7см. Проведите окружность с центром в точке В, радиус которой:
а)3см; b)4см 5мм.; c)2см 5мм
Сколько общих точек имеют окружности в каждом из этих случаев?
5. а)Постройте треугольник КВО по сторонам
КВ=3см, КО=4см, ![]() ;
;
b) В полученном
треугольнике постройте биссектрису
![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
Принимается альтернативная запись решения |
|
|
1 |
||
|
|
1 |
||
|
2 |
Выполнен чертеж по условию задачи |
1 |
|
|
|
1 |
Принимается альтернативное решение |
|
|
3х+2х+ |
1 |
||
|
|
1 |
||
|
3 |
OВ=5,2см |
1 |
|
|
РD=2,6см (по свойству катета лежащего против
угла |
1 |
|
|
|
АВ=5,2см |
1 |
|
|
|
P |
1 |
|
|
|
4 |
а) Одна
общая точка, т.к. |
1 |
Принимается альтернативная запись решения |
|
b) Две общие точки, т.к.
|
1 |
||
|
с) нет
общих точек, т.к. |
1 |
||
|
Выполнен чертеж для каждого случая |
1 |
|
|
|
5а |
Построен отрезок равный 3см/4см |
1 |
|
|
Построен
угол |
1 |
|
|
|
Построен отрезок равный 4см/3см |
1 |
|
|
|
Построен треугольник и записан ход построения |
1 |
|
|
|
5b |
Построена биссектриса угла |
1 |
|
|
Итого: |
20 |
|
|
3 ВАРИАНТ
|
Оценивание заданий работы |
|||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Количество баллов |
3 |
4 |
4 |
4 |
5 |
|
итого |
20 баллов |
||||
1. Через точку К окружности, проведена
касательная TS и хорда KD. Чему равна градусная
мера ![]() , если
, если ![]() ?
?

2. В окружность с центром О,
вписан ![]() так, что
так, что ![]() ,
, ![]() . Найдите величину дуги
BC.
. Найдите величину дуги
BC.
3. В окружности с центром О проведен диаметр
NM=12,4см, пересекающий хорду CD в точке E, причем E середина
хорды. Угол между диаметром и радиусом равен
![]() .Найдите длину
хорды CD и периметр
.Найдите длину
хорды CD и периметр ![]() .
.
4. Начертите окружность радиуса 2см. с центром О.Проведите луч с началом в точке О и отметьте на нем точку D, удаленную от точки О на 6см. Проведите окружность с центром в точке D, радиус которой:
а)4см; b)4см 5мм.; c)1см 5мм
Сколько общих точек имеют окружности в каждом из этих случаев?
5. а)Постройте
треугольник BCD по сторонам BC=4см, BD=6см,
![]() ;
;
b) В полученном
треугольнике постройте биссектрису
![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
Принимается альтернативная запись решения |
|
|
1 |
||
|
|
1 |
||
|
2 |
Выполнен чертеж по условию задачи |
1 |
|
|
|
1 |
Принимается альтернативное решение |
|
|
2х+4х+ |
1 |
||
|
|
1 |
||
|
3 |
OD=6,2см |
1 |
|
|
ED=3,1см (по свойству катета лежащего против
угла |
1 |
|
|
|
CD=6,2см |
1 |
|
|
|
P |
1 |
|
|
|
4 |
а)
Одна общая точка, т.к. |
1 |
Принимается альтернативная запись решения |
|
b) Две общие точки, т.к.
|
1 |
||
|
с)
нет общих точек, т.к. |
1 |
||
|
Выполнен чертеж для каждого случая |
1 |
|
|
|
5a |
Построен отрезок равный 4см/6см |
1 |
|
|
Построен угол |
1 |
|
|
|
Построен отрезок равный 6см/4см |
1 |
|
|
|
Построен треугольник и записан ход построения |
1 |
|
|
|
5b |
Построена биссектриса угла |
1 |
|
|
Итого: |
20 |
|
|
4 ВАРИАНТ
|
Оценивание заданий работы |
|||||
|
№ задания |
1 |
2 |
3 |
4 |
5 |
|
Количество баллов |
3 |
4 |
4 |
4 |
5 |
|
итого |
20 баллов |
||||
1. Через точку A окружности, проведена
касательная KM и хорда AB. Чему равна градусная
мера ![]() , если
, если ![]() ?
?

2. В окружность с центром О,
вписан ![]() так, что
так, что ![]() ,
, ![]() . Найдите величину дуги
KL.
. Найдите величину дуги
KL.
3. В окружности с центром О проведен диаметр
KM=14,4см, пересекающий хорду BD в точке A, причем A середина
хорды. Угол между диаметром и радиусом равен
![]() .Найдите длину
хорды BD и периметр
.Найдите длину
хорды BD и периметр ![]() .
.
4. Начертите окружность радиуса 3см. с центром О.Проведите луч с началом в точке О и отметьте на нем точку E, удаленную от точки О на 7см. Проведите окружность с центром в точке E, радиус которой:
а)4см; b)5см 5мм.; c)2см 5мм
Сколько общих точек имеют окружности в каждом из этих случаев?
5. а)Постройте
треугольник KMN по сторонам KM=5см, KN=6см,
![]() ;
;
b) В полученном
треугольнике постройте биссектрису
![]()
СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
|
№ |
Ответ |
Балл |
Дополнительная информация |
|
1 |
|
1 |
Принимается альтернативная запись решения |
|
|
1 |
||
|
|
1 |
||
|
2 |
Выполнен чертеж по условию задачи |
1 |
|
|
|
1 |
Принимается альтернативное решение |
|
|
2х+3х+ |
1 |
||
|
|
1 |
||
|
3 |
OD=7,2см |
1 |
|
|
AD=3,6см (по свойству катета лежащего против
угла |
1 |
|
|
|
BD=7,2см |
1 |
|
|
|
P |
1 |
|
|
|
4 |
а) Одна
общая точка, т.к. |
1 |
Принимается альтернативная запись решения |
|
b) Две общие точки, т.к.
|
1 |
||
|
с) нет
общих точек, т.к. |
1 |
||
|
Выполнен чертеж для каждого случая |
1 |
|
|
|
5a |
Построен отрезок равный 5см/6см |
1 |
|
|
Построен
угол |
1 |
|
|
|
Построен отрезок равный 6см/5см |
1 |
|
|
|
Построен треугольник и записан ход построения |
1 |
|
|
|
5b |
Построена биссектриса угла |
1 |
|
|
Итого: |
20 |
|
|
Форма анализа суммативного оценивания за учебный период (четверть)
_________________________________________________
(наименование организации образования)
Сведения об анализе по итогам проведения суммативного оценивания
за ______ четверть по предмету _______________
Класс: __________
Количество учащихся: __________________
Педагог: ____________________________________________________________________
Цель: Анализ результатов СОР и СОЧ
|
Предмет |
Писал |
Макс балл |
Процентное содержание баллов суммативного оценивания |
% качества |
|||
|
низкий |
средний |
высокий |
|||||
|
0-39% |
40-84% |
85-100% |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
Количество учеников |
|
|||
|
СОР 1 |
|
|
|
|
|
|
|
|
СОР 2 |
|
|
|
|
|
|
|
|
СОЧ |
|
|
|
|
|
|
|
|
|
Достигнутые цели |
Цели, вызвавшие затруднения |
|||||
|
СОР 1 |
|
|
|||||
|
СОР 2 |
|
|
|||||
|
СОЧ |
|
|
|||||
1.Анализ СОР и СОЧ показал следующий уровень знаний у обучающихся:
высокий (В): 85-100% (перечисляем ФИ обучающихся) –
средний (С): 40-84% (перечисляем ФИ обучающихся) -
низкий (Н): 0-39% (перечисляем ФИ обучающихся) –
2.Перечень затруднений, которые возникли у обучающихся при выполнении заданий
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3.Причины, указанных выше затруднений у обучающихся при выполнении заданий
__________________________________________________________________________________________________________________________________________________________
4.Планируемая коррекционная работа: ______________________________________________________________________________
Дата_______________ФИО(при наличии) педагога ____________________
Список литературы
-
Сборник заданий по суммативному оцениванию по учебным предметам основного среднего уровня. Сборник заданий. Вторая часть – Нур-Султан: АО имени И. Алтынсарина, 2019. – 300 с.
-
Методические рекомендации по составлению рубрик согласно целям обучения по учебным предметам 5-9 классов для предоставления обратной связи. - г.Нур-Султан: НАО имени И. Алтынсарина, 2019. - 204 с.
-
Методические рекомендации по составлению дифференцированных заданий СОР и СОЧ по учебным предметам естественно-математического направления 5-9 классов в условиях инклюзии. Методические рекомендации – Нур-Султан: НАО имени И. Алтынсарина, 2020. – 144 с.
-
Методические рекомендации по изучению учебного предмета "математика" (5-9классы) в рамках обновления содержания образования.-Астана, НАО имени И. Алтынсарина, 2017
-
Руководство по критериальному оцениванию для учителей основной и общей средней школ:Учебно-методическое пособие под ред. О.И. Можаевой, А.С. Шилибековой- Астана, АОО "Назарбаев Интеллектуальные школы", 2016
-
Руководство для учителя, ЦПМ АОО " Назарбаев Интеллектуальные школы" 2018
-
Сборник заданий и упражнений. Учебные цели согласно таксономии Блума / А.Е. Мурзагалиева, Б.М. Утегенова. – Астана: АОО «Назарбаев Интеллектуальные школы» Центр педагогического мастерства, 2015. – 54 с.
-
Алгебра: Учебная программа для 7-9 классов уровня основного среднего образования. – Астана: НАО им. И.Алтынсарина, 2013. – 18 с.
-
Геометрия: Учебная программа для 7-9 классов уровня основного среднего образования. – Астана: НАО им. И.Алтынсарина, 2013. – 20 с.


|
|
1 |