
ШЕКТЕУСІЗ АРАЛАС ПЕРИОДТЫ ОНДЫҚ БӨЛШЕКТІ ЖАЙ БӨЛШЕККЕ АЙНАЛДЫРУДЫҢ АНЫҚТАЛМАҒАН ЕРЕЖЕСІ
Шақарбекқызы А.
Жаратылыстану ғылымдарының магистрі,
математика пәнінің мұғалімі.
“АйСаф жеке қыздар мектебі”
Күнделікті өмірде барлық адамдар натурал сандарды (оң бүтін сандар) жиі қолданады. Мысалы: үйден жұмысқа баратын кезде, міндетті түрде кешігіп қалмауы үшін, уақытқа қарайды. Бұл үшін санды білу керек болады. Дәл солай, жолақы төлеу үшін, кез келген өзіне қажетті затты сатып алу үшін, кейбір заттарды өлшеу үшін (жеміс-жидек, көкеніс, т.б.) немесе өлшемін білу үшін (аяқ киім размері, пальто өлшемі т.б.) сандарды білу және қолдану маңызды екенін түсінуге болады.
Жалпы сандарды бес топқа жіктеп қарастыруға болады.
-
НАТУРАЛ САНДАР - өмірде санауда қолданылатын оң үтін сандар жиыны.
Математикада оны N арқылы белгілейді.
-
БҮТІН САНДАР- натурал сандармен бірге, теріс бүтін сандар және нөл санын айтады. Математикада оны Z арқылы белгілейді.
-
РАЦИОНАЛ САНДАР- бүтін сандармен бірге оң және теріс бөлшек сандарды айтады. Математикада оны Q арқылы белгілейді.
-
ИРРАЦИОНАЛ САНДАР- шектеусіз, периодсыз, ондық бөлшектерді айтады.Математикада оны I арқылы белгілейді.
-
НАҚТЫ САНДАР – жоғарыда аталған сандардың барлығы бірге нақты сандар деп аталады. Математикада оны R арқылы белгілейді.

Жоғарыда айтылған сандар жиынын Эйлер дөңгелегі арқылы төмендегідей көрсетуге болады.

Бұл ғылыми жұмыста аталған сандар тобындағы рационалсандар жиынына жатқызуға болатын шектеусіз периодты ондық бөлшектерді, жай бөлшек түрінде жазудың оңай тәсілдерін қарастырып, сол әдіс тәсіл арқылы жаттығу есептерін жылдам әрі дұрыс шығаратын заңдылықты қортындалаймыз.
Осы тақырып жалпы мектеп қабырғасындағы оқушылар үшін 6-сыныпта және
9-сыныпта қарастырылады. Осы екі сыныпта бұл тақырыпты екі бөлек қарастырудың қандай айырмашылығы бар? Бұл тақырыпқа арналған жаттығу есептерін оқулықта көрсетілген әдістерден тыс, оңай әрі дұрыс шығару тәсілдері бар ма? Осы сауалдар төңірегінде нақты бір есепті мысалға ала отыры түсіндіреміз.
6-сыныпта, шектеусіз периодты ондық бөлшекті жай бөлшек айналдыру деген тақырыпта, периодты ондық бөлшектер, таза периодты ондық бөлшек және аралас периодты ондық бөлшек деп екіге бөлініп қарастырылған.
Берілген есептің таза немесе аралас периодты ондық бөлшек екенін ажырату үшін, олардың анықтамасына қысқаша тоқталып өтуді жөн көрдік.
Егер периодты ондық бөлшектің периоды үтірден кейін басталса, оны таза периодты ондық бөлшек деп атайды.
Мысалы,2/3=0,(6)
-2/11=-0,(18)
1/9= 0,(1)
1/99= 0,(01)
1/999= 0,(001)
Егер периодты ондық бөлшектің үтірі мен бірінші периодының аралығында бір немесе бірнеше қайталанбайтын цифрлар тобы болса, оны аралас периодты ондық бөлшек деп атайды.
Мысалы,7/15= 0,4(6)
-5/12=- 0,41(6)
Таза периодты ондық бөлшекті жай бөлшекке айналдырғанда, жай бөлшектің алымына периодтағы санды жазып, бөліміне периодта неше цифр болса, 9 цифрын сонша рет жазу керек. Бұл айтылған тұжырымға төменде көрсетілген есептерден анық көз жеткізуге болады.
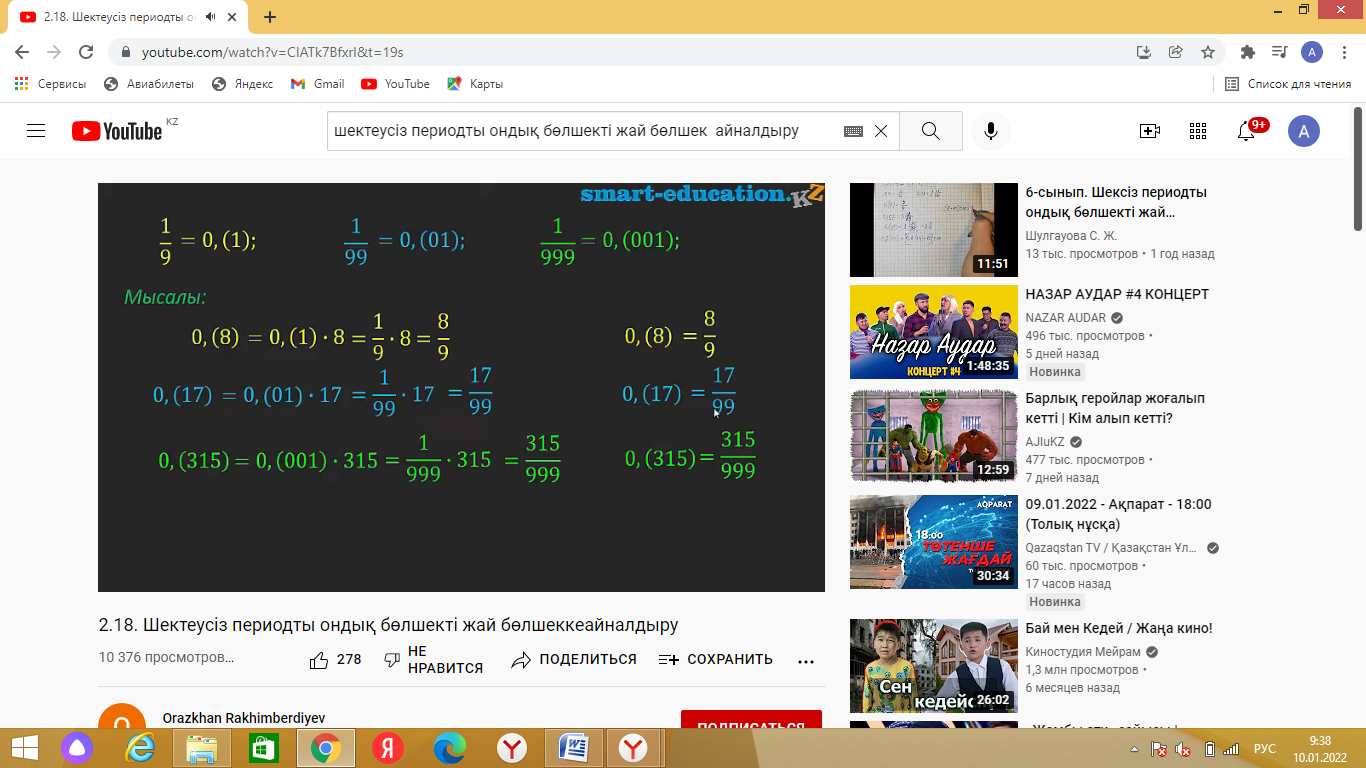
Аралас периодты ондық бөлшекті жай бөлшекке айналдыру үшін:
1) аралас периодты ондық бөлшектің бөлшек бөлігін қажетінше разрядтық бірліктерге (10-ға, 100-ге, 1000-ға) көбейтіп таза периодты ондық бөлшекке айналдыру керек;
2) таза периодты ондық бөлшекті жай бөлшекке айналдыру керек;
3) алғашқы аралас периодты ондық бөлшек қандай разрядтық бірліктеріне көбейтілсе, шыққан жай бөлшекті сонша разрядтық бірліктеріне бөлу керек.
Мысыалы: санын жай бөлшек түрінде
жазу керек.
санын жай бөлшек түрінде
жазу керек.


Ал ендіосы мысалдағы есепті, 9-сынып оқулығында келген есепті шығару әдісімен қарастырайық.
Мысалы:
 санын жай бөлшек
түрінде жазу керек.
санын жай бөлшек
түрінде жазу керек.


 қатары _
еселігі
қатары _
еселігі  болатын шексіз кемімелі
геометриялық прогрессия мүшелерінің қосындысы.
болатын шексіз кемімелі
геометриялық прогрессия мүшелерінің қосындысы.
 формула
бойынша
формула
бойынша

Сондықтан

Жоғардағы мысалдан көріп отырғандарыңыздай, есептің нәтижесі бірдей, бірақ шығарылу жолдары әр түрлі.
Аралас периодты ондық бөлшекті жай бөлшекке айналдырғанда, жай бөлшектің алымына үтір белгісімен жақшаны ескермей, қанша цифр болса, толық жазып, сол саннан периодтағы саннан басқа сандарды азайтамыз. Бөліміне периодта неше цифр болса, 9 цифрын сонша рет жазып, үтір мен периодтағы санға дейін қанша цифр болса, сонша 0 цифрын тіркеп жазу керек. Бұл айтылған тұжырымға жоғарыдағы есепті шығару арқылы анық көз жеткізуге болады.
Мысалы:
 санын жай бөлшек
түрінде жазу керек.
санын жай бөлшек
түрінде жазу керек.

Соңғы әдістің өте аз уақытта, есепті оңай әрі жылдам және дұрыс есептеуге мүмкіндік беретіндігіне көз жеткізуге болады.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Шектеусіз аралас периодты ондық бөлшекті жай бөлшекке айналдырудың анықталмаған ережесі
Шектеусіз аралас периодты ондық бөлшекті жай бөлшекке айналдырудың анықталмаған ережесі
ШЕКТЕУСІЗ АРАЛАС ПЕРИОДТЫ ОНДЫҚ БӨЛШЕКТІ ЖАЙ БӨЛШЕККЕ АЙНАЛДЫРУДЫҢ АНЫҚТАЛМАҒАН ЕРЕЖЕСІ
Шақарбекқызы А.
Жаратылыстану ғылымдарының магистрі,
математика пәнінің мұғалімі.
“АйСаф жеке қыздар мектебі”
Күнделікті өмірде барлық адамдар натурал сандарды (оң бүтін сандар) жиі қолданады. Мысалы: үйден жұмысқа баратын кезде, міндетті түрде кешігіп қалмауы үшін, уақытқа қарайды. Бұл үшін санды білу керек болады. Дәл солай, жолақы төлеу үшін, кез келген өзіне қажетті затты сатып алу үшін, кейбір заттарды өлшеу үшін (жеміс-жидек, көкеніс, т.б.) немесе өлшемін білу үшін (аяқ киім размері, пальто өлшемі т.б.) сандарды білу және қолдану маңызды екенін түсінуге болады.
Жалпы сандарды бес топқа жіктеп қарастыруға болады.
-
НАТУРАЛ САНДАР - өмірде санауда қолданылатын оң үтін сандар жиыны.
Математикада оны N арқылы белгілейді.
-
БҮТІН САНДАР- натурал сандармен бірге, теріс бүтін сандар және нөл санын айтады. Математикада оны Z арқылы белгілейді.
-
РАЦИОНАЛ САНДАР- бүтін сандармен бірге оң және теріс бөлшек сандарды айтады. Математикада оны Q арқылы белгілейді.
-
ИРРАЦИОНАЛ САНДАР- шектеусіз, периодсыз, ондық бөлшектерді айтады.Математикада оны I арқылы белгілейді.
-
НАҚТЫ САНДАР – жоғарыда аталған сандардың барлығы бірге нақты сандар деп аталады. Математикада оны R арқылы белгілейді.

Жоғарыда айтылған сандар жиынын Эйлер дөңгелегі арқылы төмендегідей көрсетуге болады.

Бұл ғылыми жұмыста аталған сандар тобындағы рационалсандар жиынына жатқызуға болатын шектеусіз периодты ондық бөлшектерді, жай бөлшек түрінде жазудың оңай тәсілдерін қарастырып, сол әдіс тәсіл арқылы жаттығу есептерін жылдам әрі дұрыс шығаратын заңдылықты қортындалаймыз.
Осы тақырып жалпы мектеп қабырғасындағы оқушылар үшін 6-сыныпта және
9-сыныпта қарастырылады. Осы екі сыныпта бұл тақырыпты екі бөлек қарастырудың қандай айырмашылығы бар? Бұл тақырыпқа арналған жаттығу есептерін оқулықта көрсетілген әдістерден тыс, оңай әрі дұрыс шығару тәсілдері бар ма? Осы сауалдар төңірегінде нақты бір есепті мысалға ала отыры түсіндіреміз.
6-сыныпта, шектеусіз периодты ондық бөлшекті жай бөлшек айналдыру деген тақырыпта, периодты ондық бөлшектер, таза периодты ондық бөлшек және аралас периодты ондық бөлшек деп екіге бөлініп қарастырылған.
Берілген есептің таза немесе аралас периодты ондық бөлшек екенін ажырату үшін, олардың анықтамасына қысқаша тоқталып өтуді жөн көрдік.
Егер периодты ондық бөлшектің периоды үтірден кейін басталса, оны таза периодты ондық бөлшек деп атайды.
Мысалы,2/3=0,(6)
-2/11=-0,(18)
1/9= 0,(1)
1/99= 0,(01)
1/999= 0,(001)
Егер периодты ондық бөлшектің үтірі мен бірінші периодының аралығында бір немесе бірнеше қайталанбайтын цифрлар тобы болса, оны аралас периодты ондық бөлшек деп атайды.
Мысалы,7/15= 0,4(6)
-5/12=- 0,41(6)
Таза периодты ондық бөлшекті жай бөлшекке айналдырғанда, жай бөлшектің алымына периодтағы санды жазып, бөліміне периодта неше цифр болса, 9 цифрын сонша рет жазу керек. Бұл айтылған тұжырымға төменде көрсетілген есептерден анық көз жеткізуге болады.

Аралас периодты ондық бөлшекті жай бөлшекке айналдыру үшін:
1) аралас периодты ондық бөлшектің бөлшек бөлігін қажетінше разрядтық бірліктерге (10-ға, 100-ге, 1000-ға) көбейтіп таза периодты ондық бөлшекке айналдыру керек;
2) таза периодты ондық бөлшекті жай бөлшекке айналдыру керек;
3) алғашқы аралас периодты ондық бөлшек қандай разрядтық бірліктеріне көбейтілсе, шыққан жай бөлшекті сонша разрядтық бірліктеріне бөлу керек.
Мысыалы: санын жай бөлшек түрінде
жазу керек.
санын жай бөлшек түрінде
жазу керек.


Ал ендіосы мысалдағы есепті, 9-сынып оқулығында келген есепті шығару әдісімен қарастырайық.
Мысалы:
 санын жай бөлшек
түрінде жазу керек.
санын жай бөлшек
түрінде жазу керек.


 қатары _
еселігі
қатары _
еселігі  болатын шексіз кемімелі
геометриялық прогрессия мүшелерінің қосындысы.
болатын шексіз кемімелі
геометриялық прогрессия мүшелерінің қосындысы.
 формула
бойынша
формула
бойынша

Сондықтан

Жоғардағы мысалдан көріп отырғандарыңыздай, есептің нәтижесі бірдей, бірақ шығарылу жолдары әр түрлі.
Аралас периодты ондық бөлшекті жай бөлшекке айналдырғанда, жай бөлшектің алымына үтір белгісімен жақшаны ескермей, қанша цифр болса, толық жазып, сол саннан периодтағы саннан басқа сандарды азайтамыз. Бөліміне периодта неше цифр болса, 9 цифрын сонша рет жазып, үтір мен периодтағы санға дейін қанша цифр болса, сонша 0 цифрын тіркеп жазу керек. Бұл айтылған тұжырымға жоғарыдағы есепті шығару арқылы анық көз жеткізуге болады.
Мысалы:
 санын жай бөлшек
түрінде жазу керек.
санын жай бөлшек
түрінде жазу керек.

Соңғы әдістің өте аз уақытта, есепті оңай әрі жылдам және дұрыс есептеуге мүмкіндік беретіндігіне көз жеткізуге болады.

шағым қалдыра аласыз















