Мазмұны

Кіріспе

Ғылыми математикалық жұмыс үшін тақырыпты таңдау зерттеудің қызықты кезеңі болып табылады. Біз "сиқырлы» шаршы тақырыбына тоқталдық. "Сиқырлы шаршылар" ұғымы құпияны, жұмбақты қамтиды және осы квадраттардың тарихымен және кейбір қасиеттерімен танысқаннан кейін зерттеуді жалғастыруға ниет бар.

Біздің жұмысымызда біз сиқырлы шаршыларды құрастырудың теориясы мен тәжірибесінен ең тиімді, маңызды, қызықты фактілерді көрсетуге тырыстық. Сонымен бірге зерттеу тақырыбының қызықты математикалық қасиеттері ашылды.

Міне, біздің жұмысымыздың негізгі міндеттері: "сиқырлы шаршылар" ұғымының пайда болуы және олардың ғылымда да, өмірде де танымалдылығының өсуі туралы айту, құрастыру тәсілдерін қарастыру, негізгі ерекшеліктерді көрсету.

Сонымен қатар, біз сынып оқушылары арасында зерттеу жүргіздік. Біз бұрын осы тақырыпқа тап болмаған адамдар бұл мәселені қысқаша түсініктеме негізінде қаншалықты тез шеше алатынын көргіміз келді:. Бұл зерттеудің нәтижелері біздің жұмысымызда да келтіріледі.

Зерттеу мақсаты. Кез-келген мөлшердегі шаршыны толтыруға болатын сиқырлы шаршыларды құрудың әртүрлі нұсқаларын анықтай отырып, құпиясын ашу. Сонымен қатар оларды қолданудың мүмкін бағыттарын қарастыру.

Зерттеу міндеті. 

• сиқырлы квадраттардың пайда болу және даму тарихын зерттеу;

• сиқырлы квадраттардың қасиеттерін зерттеу;

• сиқырлы квадраттарды құрудың негізгі әдістерімен танысу;

• кез-келген тәртіптің сиқырлы квадраттарын құруды үйрену;

• зерттеу нәтижелерін жобалау

Тақырыптың өзектілігі. Зерттеу жұмысында шаршыдағы сандардың бір заңдылықтарын зерттей білу. Хабарланып отырған материалға тарихи бағдар беру, ілімнің практикалық мәнін ашып көрсету.

Зерттеудің болжамы. Сиқырлы шаршыны толтыру үшін оны тез және әр түрлі жасауға мүмкіндік беретін арнайы әдістер бар. Оқу материалдарын игеру барысында зерттеу әдісін жетілдіріп, деректерді тиімді әрі жүйелі пайдалансақ, онда оқушылардың зерттеу құзіреттілігі және коммуникативтік, ақпараттық құзіреттілігі өз мәнінде дамып, сонымен қоса оқушылардың математикаға деген қызығушылығы артады деген ойдамын.

Зерттеу кезеңдері. Мен өзімнің ғылыми жұмысымды 5 кезеңге бөлдім.

І кезең-мәселені зерттеу ;

ІІ кезең – мәселе бойынша ақпарат жинау ;

ІІІ кезең – ақпаратты өңдеу және талдау ;

ІV кезең – құжаттаманы рәсімдеу;

V кезең- оқу жобасын таныстыру .

Зерттеу құралдары. Зерттеу құралдары: математикалық кітаптар, бұқаралық ақпарат, интернет желісі.

Зерттеу әдісі: Анализ, синтез, жобалау әдісі.

1. Сиқырлы шаршы ұғымының пайда болу тарихы

  Натурал сандардың бірталай қасиеттерін ежелгі грек математиктері тағайындаған . Бізге жеткен аңыз бойынша Пифагор мен оның шәкірттері сандарды жұп және тақ , жай және құрама сандар деп  топтарға бөлген. Алайда пифагоршылар, арифметикаға елеулі жаңалықтар енгізе  отырып, сандардың табиғатын қате түсінген. Олар еш бір  дәлелсіз, негізсіз «бір - ақылдың немесе сананың  белгісі, бес - махаббаттың белгісі. 666 - айуандықтың  белгісі» т.с.с деп, былшыл уағыздар таратқан. Бұл уағыздар беретін әр түрлі сұмпайылар мен балгерлердің қарта ашу, құмалақ тарту, сәуегейлік жасау сияқты әрекеттеріне арқау болған.

Орта ғасырлар математикасында «керемет «квадраттар» елеулі орын алған. Жолдарындағы, бағандағыларды және үлкен диагональдарындағы сандардың қосындылары өз ара тең болып отыратын квадрат таблица керемет квадрат деп аталып кеткен (орыс тілінде «магический квадраты», мұндағы «магический» сөзі араб тілінің «маги» сөзінен шыққан, мағынасы –«сиқыр»)

Сиқырлы немесе сиқырлы квадрат-бұл әр жолдағы, әр бағандағы және екі диагональдағы сандардың қосындысы бірдей болатындай сандармен толтырылған квадрат кесте. Онда кез-келген жол, кез-келген баған және екі негізгі диагоналдың кез-келгені бірдей санға тең болады.

Сиқырлы шаршыны алғаш ойлап табылған ел дәл белгісіз, ғасыр белгісіз, тіпті мыңжылдықты дәл анықтау мүмкін емес. Сиқырлы шаршылар туралы алғашқы ескерту ежелгі қытайларда болған. Бізге жеткен сиқырлы квадраттардың ішіндегі ең көнесі-Ло Шу кестесі. Ол 3*3 өлшеміне ие және 1-ден 9-ға дейінгі натурал сандармен толтырылған. Бұл сиқырлы квадратта әр жолдағы, бағандағы және диагональдағы сандардың қосындысы 15-ке тең. Аңыздардың біріне сәйкес, Ло Шудың прототипі Сары өзен суларынан пайда болған үлкен қасиетті тасбақаның қабығын безендірген қара және ақ нүктелердің үлгісі болды.

Қытайдан сиқырлы шаршылар алдымен Үндістанға, содан кейін басқа елдерге таралды. XVI ғасырдың басында әйгілі неміс суретшісі Альбрехт Дюрер өнердегі сиқырлы шаршыны мәңгі қалдырды, оны "Меланхолия" гравюрасында суреттеді. Гравюраның жасалған күні (1514 жыл) төменгі жолдың екі орталық торында тұрған сандармен көрсетілген.

IX ғасырда. сиқырлы шаршыларға деген қызығушылық жаңа күшпен басталды. Олар жоғары алгебра әдістерінің көмегімен зерттеле бастады. Сиқырлы квадраттарды алу математиктер арасында танымал ойын-сауық болып саналды. Олар үлкен квадраттар жасады, мысалы, 1-ден 2025-ке дейінгі сандардан тұратын 45*45, кез-келген мөлшердегі сиқырлы квадраттарды салу тәсілдері ойлап табылды, бірақ осы мөлшердегі сиқырлы квадраттардың санын табуға болатын формула әлі табылған жоқ.

Қазіргі уақытта сиқырлы шаршылар тек мамандардың ғана емес, сонымен қатар математикалық ойындар мен ойын-сауық әуесқойларының назарын аударуда. Өткен ғасырда ерекше квадраттармен байланысты жұмбақтар мен тапсырмаларды қамтитын ойын-сауық математикасы бойынша кітаптар саны едәуір өсті.

2. «Сиқырлы» шаршының түрлері

1. Үшінші ретті «сиқырлы» шаршы

3×3 Сиқырлы шаршы қарапайым көрінеді, бірақ оның бір ерекшелігі бар, ол басқа үлкен сиқырлы шаршыға ие емес. Бұл ерекшелігі-бұл сиқырлы шаршы бір ғана нұсқада бар.

Бұл сиқырлы шаршыны табудың бір тәсілі-n сандарының әр тобындағы қатардағы сандардан топтар таңдалады (біздің жағдайда 3 Сан), осы топтардың қосындылары бір-біріне тең болуы керек. Біздің жағдайда m={1,2,3,4,5,6,7,8,9} жиынтығы бар. Бұл қосынды 15 = (1+2+3+4+5+6+7+8+9)/3 болатыны анық.

1)    1+5+9=15

2)    1+6+8=15

3)    2+4+9=15

4)    2+5+8=15

5)    2+6+7=15

6)    3+4+8=15

7)    3+5+7=15

8)    4+5+6=15

Бұл кесте дайын болғаннан кейін, ол сандарды сиқырлы шаршыға орналастыру ережелерін жаза бастайды.

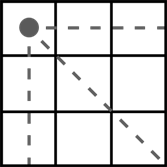
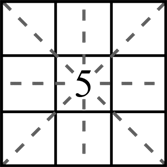
5 саны төрт топқа жатады, яғни 5 саны бар ұяшық төрт қатардың қиылысында тұр, мұндай ұяшық тек біреу және ол квадраттың ортасында орналасқан. Бір топта және 5 санымен бір қатарда орналасқан әр екі Сан жұпты құрайды. Бұл жұптар шаршының ортасына қатысты симметриялы орналасқан. Сондықтан ішкі құрылым толық симметрияға ие болады.

Әр қатардың жұп саны үш топта кездеседі. Бұл жұп сандар үш түзу жолдың қиылысында, яғни бұрыштық торларда болатындығын білдіреді.

Төрт тақ санның әрқайсысы тек 2 топқа енеді. Олардың шаршының жиектеріндегі орташа ұяшықтардағы орны.

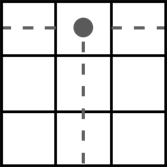
	1				1			6	1	8		6	1	8		6	1	8
	5		Жүктеу ЖИ арқылы жасау ЖИ арқылы жасау Бөлісу 1 - айлық Материал тарифі -96% жеңілдік 00 05 00 ҚМЖ Ашық сабақ Тәрбие сағаты Презентация БЖБ, ТЖБ тесттер Көрнекіліктер Балабақшаға арнарлған құжаттар Мақала, Эссе Дидактикалық ойындар және тағы басқа 400 000 материал Барлық 400 000 материалдарды шексіз жүктеу мүмкіндігіне ие боласыз 1 990 ₸ 49 000₸ 1 айға қосылу Таңдау Материалға шағымдану Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз Жариялаған: Токанова Назерке Оразбековна 07 Ақпан 2024 736 Шағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз Шағымды қалдыру Сиқырлы шаршылар Тақырып бойынша 11 материал табылды Сиқырлы шаршылар Материал туралы қысқаша түсінік Сиқырлы шаршы ұғымы Материалды жүктеу Материалдың қысқаша нұсқасы Мазмұны Аннотация ........................................................... Кіріспе ........................................................... 3 Негізгі бөлім: І. «Сиқырлы» шаршы ұғымының пайда болу тарихы ........................................................... 5 ІІ. «Сиқырлы» шаршының түрлері және оның шешу жолдары 2.1. Үшінші ретті сиқырлы шаршы ........................................................... 7 2.2. Төртінші сиқырлы шаршы ........................................................... 9 2.3. Бесінші ретті сиқырлы шаршы ........................................................... 11 ІІІ. «Сиқырлы» шаршыны шешу кейбір тәсілдері 3.1. Үнді тәсілі ........................................................... 13 3.2. А. Дюрердің «сиқырлы» шаршысы ........................................................... 14 ІV. Практикалық жұмыс ........................................................... 16 Қорытынды ........................................................... 18 Пайдаланған әдебиеттер ........................................................... 19 Кіріспе Ғылыми математикалық жұмыс үшін тақырыпты таңдау зерттеудің қызықты кезеңі болып табылады. Біз "сиқырлы» шаршы тақырыбына тоқталдық. "Сиқырлы шаршылар" ұғымы құпияны, жұмбақты қамтиды және осы квадраттардың тарихымен және кейбір қасиеттерімен танысқаннан кейін зерттеуді жалғастыруға ниет бар. Біздің жұмысымызда біз сиқырлы шаршыларды құрастырудың теориясы мен тәжірибесінен ең тиімді, маңызды, қызықты фактілерді көрсетуге тырыстық. Сонымен бірге зерттеу тақырыбының қызықты математикалық қасиеттері ашылды. Міне, біздің жұмысымыздың негізгі міндеттері: "сиқырлы шаршылар" ұғымының пайда болуы және олардың ғылымда да, өмірде де танымалдылығының өсуі туралы айту, құрастыру тәсілдерін қарастыру, негізгі ерекшеліктерді көрсету. Сонымен қатар, біз сынып оқушылары арасында зерттеу жүргіздік. Біз бұрын осы тақырыпқа тап болмаған адамдар бұл мәселені қысқаша түсініктеме негізінде қаншалықты тез шеше алатынын көргіміз келді:. Бұл зерттеудің нәтижелері біздің жұмысымызда да келтіріледі. Зерттеу мақсаты. Кез-келген мөлшердегі шаршыны толтыруға болатын сиқырлы шаршыларды құрудың әртүрлі нұсқаларын анықтай отырып, құпиясын ашу. Сонымен қатар оларды қолданудың мүмкін бағыттарын қарастыру. Зерттеу міндеті.  сиқырлы квадраттардың пайда болу және даму тарихын зерттеу; сиқырлы квадраттардың қасиеттерін зерттеу; сиқырлы квадраттарды құрудың негізгі әдістерімен танысу; кез-келген тәртіптің сиқырлы квадраттарын құруды үйрену; зерттеу нәтижелерін жобалау Тақырыптың өзектілігі. Зерттеу жұмысында шаршыдағы сандардың бір заңдылықтарын зерттей білу. Хабарланып отырған материалға тарихи бағдар беру, ілімнің практикалық мәнін ашып көрсету. Зерттеудің болжамы. Сиқырлы шаршыны толтыру үшін оны тез және әр түрлі жасауға мүмкіндік беретін арнайы әдістер бар. Оқу материалдарын игеру барысында зерттеу әдісін жетілдіріп, деректерді тиімді әрі жүйелі пайдалансақ, онда оқушылардың зерттеу құзіреттілігі және коммуникативтік, ақпараттық құзіреттілігі өз мәнінде дамып, сонымен қоса оқушылардың математикаға деген қызығушылығы артады деген ойдамын. Зерттеу кезеңдері. Мен өзімнің ғылыми жұмысымды 5 кезеңге бөлдім. І кезең-мәселені зерттеу ; ІІ кезең – мәселе бойынша ақпарат жинау ; ІІІ кезең – ақпаратты өңдеу және талдау ; ІV кезең – құжаттаманы рәсімдеу; V кезең- оқу жобасын таныстыру . Зерттеу құралдары. Зерттеу құралдары: математикалық кітаптар, бұқаралық ақпарат, интернет желісі. Зерттеу әдісі: Анализ, синтез, жобалау әдісі. Сиқырлы шаршы ұғымының пайда болу тарихы   Натурал сандардың бірталай қасиеттерін ежелгі грек математиктері тағайындаған . Бізге жеткен аңыз бойынша Пифагор мен оның шәкірттері сандарды жұп және тақ , жай және құрама сандар деп  топтарға бөлген. Алайда пифагоршылар, арифметикаға елеулі жаңалықтар енгізе  отырып, сандардың табиғатын қате түсінген. Олар еш бір  дәлелсіз, негізсіз «бір - ақылдың немесе сананың  белгісі, бес - махаббаттың белгісі. 666 - айуандықтың  белгісі» т.с.с деп, былшыл уағыздар таратқан. Бұл уағыздар беретін әр түрлі сұмпайылар мен балгерлердің қарта ашу, құмалақ тарту, сәуегейлік жасау сияқты әрекеттеріне арқау болған. Орта ғасырлар математикасында «керемет «квадраттар» елеулі орын алған. Жолдарындағы, бағандағыларды және үлкен диагональдарындағы сандардың қосындылары өз ара тең болып отыратын квадрат таблица керемет квадрат деп аталып кеткен (орыс тілінде «магический квадраты», мұндағы «магический» сөзі араб тілінің «маги» сөзінен шыққан, мағынасы –«сиқыр») Сиқырлы немесе сиқырлы квадрат-бұл әр жолдағы, әр бағандағы және екі диагональдағы сандардың қосындысы бірдей болатындай сандармен толтырылған квадрат кесте. Онда кез-келген жол, кез-келген баған және екі негізгі диагоналдың кез-келгені бірдей санға тең болады. Сиқырлы шаршыны алғаш ойлап табылған ел дәл белгісіз, ғасыр белгісіз, тіпті мыңжылдықты дәл анықтау мүмкін емес. Сиқырлы шаршылар туралы алғашқы ескерту ежелгі қытайларда болған. Бізге жеткен сиқырлы квадраттардың ішіндегі ең көнесі-Ло Шу кестесі. Ол 3*3 өлшеміне ие және 1-ден 9-ға дейінгі натурал сандармен толтырылған. Бұл сиқырлы квадратта әр жолдағы, бағандағы және диагональдағы сандардың қосындысы 15-ке тең. Аңыздардың біріне сәйкес, Ло Шудың прототипі Сары өзен суларынан пайда болған үлкен қасиетті тасбақаның қабығын безендірген қара және ақ нүктелердің үлгісі болды. Қытайдан сиқырлы шаршылар алдымен Үндістанға, содан кейін басқа елдерге таралды. XVI ғасырдың басында әйгілі неміс суретшісі Альбрехт Дюрер өнердегі сиқырлы шаршыны мәңгі қалдырды, оны "Меланхолия" гравюрасында суреттеді. Гравюраның жасалған күні (1514 жыл) төменгі жолдың екі орталық торында тұрған сандармен көрсетілген. IX ғасырда. сиқырлы шаршыларға деген қызығушылық жаңа күшпен басталды. Олар жоғары алгебра әдістерінің көмегімен зерттеле бастады. Сиқырлы квадраттарды алу математиктер арасында танымал ойын-сауық болып саналды. Олар үлкен квадраттар жасады, мысалы, 1-ден 2025-ке дейінгі сандардан тұратын 45*45, кез-келген мөлшердегі сиқырлы квадраттарды салу тәсілдері ойлап табылды, бірақ осы мөлшердегі сиқырлы квадраттардың санын табуға болатын формула әлі табылған жоқ. Қазіргі уақытта сиқырлы шаршылар тек мамандардың ғана емес, сонымен қатар математикалық ойындар мен ойын-сауық әуесқойларының назарын аударуда. Өткен ғасырда ерекше квадраттармен байланысты жұмбақтар мен тапсырмаларды қамтитын ойын-сауық математикасы бойынша кітаптар саны едәуір өсті. «Сиқырлы» шаршының түрлері Үшінші ретті «сиқырлы» шаршы 6 1 8 7 5 3 2 9 4 3×3 Сиқырлы шаршы қарапайым көрінеді, бірақ оның бір ерекшелігі бар, ол басқа үлкен сиқырлы шаршыға ие емес. Бұл ерекшелігі-бұл сиқырлы шаршы бір ғана нұсқада бар. Бұл сиқырлы шаршыны табудың бір тәсілі-n сандарының әр тобындағы қатардағы сандардан топтар таңдалады (біздің жағдайда 3 Сан), осы топтардың қосындылары бір-біріне тең болуы керек. Біздің жағдайда m={1,2,3,4,5,6,7,8,9} жиынтығы бар. Бұл қосынды 15 = (1+2+3+4+5+6+7+8+9)/3 болатыны анық. 1)    1+5+9=15 2)    1+6+8=15 3)    2+4+9=15 4)    2+5+8=15 5)    2+6+7=15 6)    3+4+8=15 7)    3+5+7=15 8)    4+5+6=15 Бұл кесте дайын болғаннан кейін, ол сандарды сиқырлы шаршыға орналастыру ережелерін жаза бастайды. 5 саны төрт топқа жатады, яғни 5 саны бар ұяшық төрт қатардың қиылысында тұр, мұндай ұяшық тек біреу және ол квадраттың ортасында орналасқан. Бір топта және 5 санымен бір қатарда орналасқан әр екі Сан жұпты құрайды. Бұл жұптар шаршының ортасына қатысты симметриялы орналасқан. Сондықтан ішкі құрылым толық симметрияға ие болады. Әр қатардың жұп саны үш топта кездеседі. Бұл жұп сандар үш түзу жолдың қиылысында, яғни бұрыштық торларда болатындығын білдіреді. Төрт тақ санның әрқайсысы тек 2 топқа енеді. Олардың шаршының жиектеріндегі орташа ұяшықтардағы орны. 1 1 6 1 8 6 1 8 6 1 8 5 Материалды жүктеу Жүктеу Сақтау Бөлісу ЖИ арқылы жасау Файл форматы: docx Математика Сабақ жоспары Барлық сыныптар 07.02.2024 736 Жүктеу Сақтау ЖИ арқылы жасау Жариялаған: Токанова Назерке Оразбековна Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз, шағым қалдыра аласыз Қазақстандағы ең үлкен материалдар базасынан іздеу Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз Іздеу Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз! Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі. Толығырақ Оқу-ағарту министірлігінің ресми жауабы Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз! Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз! Жариялау Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз! Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз! Жариялау Министірлікпен келісілген курстар тізімі Химия пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Тарих пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Биология пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Ағылшын тілі пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ География пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Информатика пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Мектепке дейінгі білім беру бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ «Қазақ тілі» жəне «Қазақ əдебиеті» бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Дене шынықтыру пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Білім алушылардың білім сапасын арттыру мақсатында сабақта цифрлық технологияларды қолдану 80/108 сағат Толығырақ Инклюзивті білім беру жүйесінде ерекше білім беру қажеттілігі бар білім алушыға психологиялық-педагогикалық қолдау көрсету бойынша педагогтердің кәсіби және пәндік құзыреттіліктерін дамыту 80/108 сағат Толығырақ