СОЧ 3-четверть 9 класс Геометрия

400 000+ дайын материалды шексіз жүктеңіз

ҚМЖ, БЖБ, ТЖБ, презентациялар, көрнекіліктер және авторлық материалдар - 690 тг-ден бастап

Тақырып бойынша 24 материал табылды

Оценивание заданий работы

№ задания

Количество баллов

Всего баллов

20 баллов

Материал туралы қысқаша түсінік

Суммативное оценивание за 3-четверть за раздел «Решение треугольников». Работа состоит из 6х заданий на определения критерий оценивания, знание и применение задачи на нахождение радиусов вписанной в треугольник и описанной около треугольника окружностей.

Материалдың қысқаша нұсқасы

Геометрия 9 класс 3 четверть

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ

ЗА 3 ЧЕТВЕРТЬ

Обзор суммативного оценивания за 3 четверть

Продолжительность – 45 минут

Количество баллов – 20

Типы заданий:

МВО – задания с множественным выбором ответов;

КО – задания, требующие краткого ответа;

РО – задания, требующие развернутого ответа.

Структура суммативного оценивания

Данный вариант состоит из 6 заданий, включающих вопросы с множественным выбором ответов,с кратким и развернутым ответами.

В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов.

В вопросах, требующих краткого ответа, обучащийся записывает ответ в виде численного значения, слова или короткого предложения.

В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/ вопросов

Характеристика заданий суммативного оценивания за 3 четверть

Раздел	Проверяемая цель	Уровень мыслительных навыков	Кол. заданий*	№ задания*	Тип задания*	Время на выполнение, мин*	Балл*	Балл за раздел
Решение треугольников	9.1.3.8 Знать и применять формулы площади вписанного треугольника (S = ^abc , где a, b, c- 4R стороны треугольника, R-радиус описанной окружности), площади описанного многоугольника (S = p ∙ r, где r – радиус вписанной окружности, p - полупериметр многоугольника)	Применение	1	1	КО	3	2	20
	9.1.3.7 Знать и применять теорему синусов	Применение	1	3	КО	4	2
	9.1.3.6 Знать и применять теорему косинусов	Применение	1	2	КО	6	3
	9.1.3.9 Знать и применять формулы для нахождения радиуса окружности, используя площади вписанных и описанных треугольников	Применение	1	4	РО	7	6
	9.1.3.10 применять теоремы синусов и косинусов для решения треугольников и прикладных задач	Навыки высокого порядка	2	5	РО	10	3
		Навыки высокого порядка	2	6	РО	10	4
ИТОГО:			6			40	20	20
Примечание: - разделы, в которые можно вносить изменения*

СУММАТИВНОЕ ОЦЕНИВАНИЕ

ЗА 3 ЧЕТВЕРТЬ

ДАТА _____________ ФИ учащегося_________________________________

1 ВАРИАНТ

1. Радиус окружности, вписанной в треугольник, равен 12, а периметр треугольника равен 56. Найдите площадь треугольника.

2. Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны:

а) 3; 5 и 6; b) 4; 5и 6; с) 3; 4 и 5.

3. В треугольнике АВС известно, что АВ = 14 см, ВС = 10 см, sin A = 0,2. Найдите синус угла С треугольника.

4. Основания равнобокой трапеции ABCD равны 8 см и 20 см, а высота – 8 см. Найдите:

диагональ трапеции АС;
радиус окружности, описанной около трапеции.

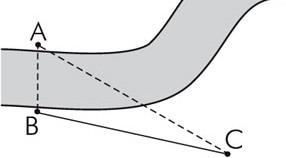
5. Определите ширину реки AB для геодезических измерений как показано на рисунке:

В 105⁰ ,

С  30⁰ ,

ВС  230 м.

^{6. К
одной точке приложили две силы:} ^F1 ^{= 13 H и} ^F2 ^{= 20 H под углом 60°. Найдите} равнодействующую этих двух сил. Выполните рисунок.

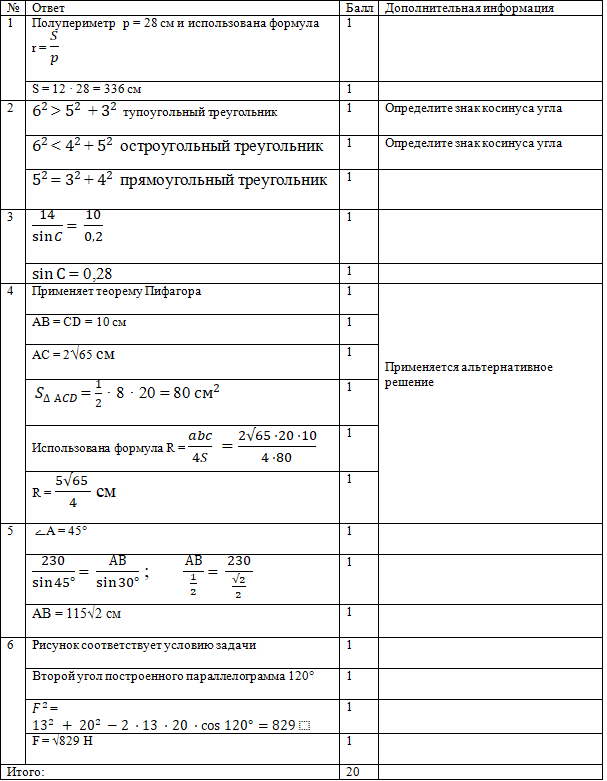
Схема выставления баллов

1 вариант

СУММАТИВНОЕ ОЦЕНИВАНИЕ

ЗА 3 ЧЕТВЕРТЬ

ДАТА _____________ ФИ учащегося_________________________________

2 ВАРИАНТ

1. Радиус окружности, вписанной в треугольник, равен 14, а периметр треугольника 58. Найдите площадь треугольника.

2. Не вычисляя углов треугольника, определите его вид (по величине углов), если стороны треугольника равны:

а) 5; 7 и 9; b) 5; 6 и 7; с) 6; 8 и 10.

[3]

3. В треугольнике АВС известно, что АВ = 14 см, ВС = 10 см, sin A = 0,3. Найдите синус угла С треугольника.

4. Основания равнобокой трапеции ABCD равны 10 см и 22 см, а высота – 8 см. Найдите:

диагональ трапеции АС;
радиус окружности, описанной около трапеции.

5. Определите ширину реки AB для геодезических измерений как показано на рисунке:

В 105⁰ ,

С  30⁰ ,

ВС  240 м.

^6. ^{К одной точке приложили две силы:} ^F1 ^{= 12 H и} ^F2 ^{= 20 H под углом 60°. Найдите} равнодействующую этих двух сил. Выполните рисунок.

Материалды Word форматында жүктеп аласыз

Тарифке кіреді

14 ұстаз жүктеп алған

16.05.2022

2349

Бұл материалды қолданушы жариялаған. UstazTilegi материалдың мазмұны мен авторлық құқықтарына жауап бермейді. Авторлық құқық бұзылған жағдайда шағым қалдыра аласыз

"Ұстаз" платформасында тіркелген пәндік олимпиадалар

Аттестацияға жарамды екенін көру үшін "Ұстаз" платформасында "Жарыстар, олимпиадалар тізімінен "Ustaz tilegi" деп іздесеңіз шығады

Ұстаздарға арналған олимпиадалар

Оқушыларға арналған олимпиадалар

Тәрбиешілерге арналған олимпиадалар

Қазақстандағы ең үлкен материалдар базасынан іздеу

Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз

Осы тақырыпта
көрнекілік керек па?

10 000 астам көрнекіліктерді жинап қойдық.

Көрнекілік бөліміне өтіп тақырыбын жазып жүктеп алыңыз!