
Мазмұны
Кіріспе.................................................................................................
Негізгі бөлім
І. Арифметикалық амалдар
1.1 Сандарды жылдам көбейту әдістері...............................................
1.2 Сандардың бөлінгіштік белгілері..................................................
ІІ. Күрделі есептерді шығару
2.1 Есептерді түрлендіру арқылы табу.............................................
2.2 Кейбір есептерді шығарудың тиімді әдістері.................................
Қорытынды...............................................
Ұсыныстар.................................................
Пайдаланылған әдебиеттер тізімі.............................................
Кіріспе
«Арифметика математиканың, ал
математика ғылымдардың патшасы»
К.Гаусс
Математика өмірді сан арқылы бейнелейді. Адамзат баласы ең алғаш рет жазу-сызудан бұрын санауды үйренгені хақ. Осылайша, бертін келе адамдар қарапайым арифметикалық амалдарды қолдануды үйреніп, олардың негізгі қасиеттерін сараптап, тағы басқа да математикалық білімдерін дамыта түседі. Әуел баста адамдар саусақтармен амалдар қолданып, кейіннен есептеудің өзге де тәсілдерін ашқан. Сондай-ақ жылдам есептеу әдістеріне талдау жасап, оны келешек ұрпаққа таратып отырған. Ал біздің заманымыз ғылым мен техниканың қарқынды дамуымен ерекшеленеді. Қазіргі кезде ғылым мен техниканың даму деңгейі әрбір адамға сапалы және терең білімнің, іскерліктің және жылдамдықтың болуын қажет етеді.
Сондай-ақ жастардың белсенді шығармашылықпен жұмыс істеуін де талап етеді. Сол себепті әрбір адам өз бойындағы туғаннан пайда болған интуициясын әрі қарай дамытуға, табиғи қасиеттерін, математикалық білім деңгейін тереңдету үшін өз бетінше білім алуға қадам басып, алға қарай ұмтылу қажет. Соңғы жылдардағы компьютер, калькулятордың өмірге көптеп енуі – оқушылардың шапшаң есептеу дағдыларына, ойлау қабілетінің тежелуіне әсер етуде. Осындай жайттарды ескерген әрбір оқушы өз бетінше шапшаң есептеуге, ауызша жаттығуларға көп уақыт бөліп отырғаны жөн. Cебебі тез есептеу әдістері есептеуді жеңілдетуге, математикалық терең ойлауды дамытуға және ең бастысы әр адамның интуициясын дамытуға өз үлесін қосады.
Математикалық логика ақыл-ой еңбегін техникаландырудың құралы болып табылады және ойлау процесін арнаулы математикалық әдістер, символдық аппараттар арқылы зерттейді. Бірақ дәстүрлі математикалық логика пәнін білмейінше, оны ойдағыдай меңгеру қиын. Өйткені бүгінгі күнде ғылыми технологияның дамуына байланысты адамзат баласы ой және дене еңбегін жеңілдететін техникалық құрылғылардың түр-түрін ойлап табуда. Мысалы, қазіргі кезде электронды есептеу машинасын қолдана отырып, кез-келген күрделі есептің шешімін аз ғана уақыт аралығында табуға болады. Тіпті, қарапайым есептеу құралы – калькуляторлардың өзі бүгінгідей нарық заманында қарапайым халық үшін аса тиімді. Әрине, мұның бәрі адамның ойлау қабілетінің ең ірі жетістіктері болып табылады. Алайда, қалыптасқан жағдайдың пайдасымен қатар зияны да жоқ емес. Атап айтқанда, бүгінде кез-келген оқушының қарапайым көбейту кестесін біле бермеуі мүмкін. Сол себепті де, баланың логикалық ойлау қабілетін дамыту бүгінгі күннің өзекті мәселелерінің бірі деуге болады. Осы жайды ескеріп, мен бұл ғылыми жұмыста логикалық ойлау қабілетін дамытатын шапшаң есептеудің кейбір әдістерін мейілінше қарастырдым. Ендеше, мен секілді математиканың ғылымилығын жаңа бастаған оқушы үшін бұл маңызды тақырып.
Бұл жобаны қорғаудағы басты мақсат: тез есептеу әдістерін үйрене отырып, есептеуді ойша шешіп, есеп нәтижесін табуды жылдамдату және тез есептеу әдістері арқылы болашақта математика ғылымының дамуына өз үлесімді қосу болып табылады. Cодай-ақ бұл жоба арқылы әр оқырманның математикалық қызығушылығын дамытып, өмірге деген ой толғанысын тудыру және білімін шыңдай түсу саналады. Осындай шараларды жүзеге асырып, қазіргі таңдағы негізгі проблема – оқушының пәнге деген қызығушылығын, есепке деген құштарлығын оятып, математикалық және логикалық білімін арттыруды мен өзімнің азаматтық борышым деп білемін.
Негізгі бөлім
І. Арифметикалық амалдар
1.1 Сандарды жылдам көбейту әдістері
Көбейту кестесін жаттаудың оңай жолы. Математикаға кіріспе көбейту кестесін жаттаудан басталатыны баршаға аян. Оны жаттамаған бүлдіршін математиканы оқып үйрене алмайды. Алайда, көбейту кестесін жаттаудың да оңай тәсілі бар. Мәселен, 9 санына байланысты көбейту кестесін оп-оңай жаттауға болады. Ол үшін әуелі, 9 санын 1-ге көбейтуден бастап 1-ден 9-ға дейінгі сандарды ретімен жоғарыдан төмен қарай жазып шығамыз (1).
Кейін дәл осылай 1-ден 9-ға дейінгі сандарды ретімен төменнен жоғары қарай жазып шығамыз (2). Міне, осылай дайын көбейту кестесі шыға келеді (төмендегі кесте).
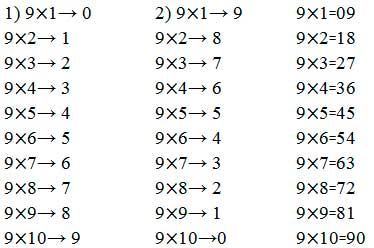
Саусақпен шапшаң көбейту әдісі. Саусақтарды бүгіп санау ерте заманда кең қолданылып келді. Адамның саусақтары мен олардың буындары, сондай-ақ саусақтарын бүгу және жазу, қолдарын бүгу мен жазу олардың ондаған және жүздеген мыңға дейін санай алуына ғана емес, сол сияқты кейбір арифметикалық амалдарды орындауына да мүмкіндік берді. Мысалы, ежелгі римдіктер 5 пен 10 сандарының арасындағы сандарды саусақпен былайша көбейткен.
Айталық, 6-ны 7-ге көбейту керек болсын. Сол қолымыздың жұдырығын жазбастан, бір-бірлеп саусағымызды жаза отырып, 6-ға дейін санаймыз. Ал оң қолымыздың саусақтарымен дәл соны қайталап, 7-ге дейін санаймыз. Оң қолдың жазылған екі саусағын сол қолдың жазылған бір саусағынан үстіне саламыз. Жазылған саусақ небары 3-еу болады, бұл – 3 ондық, яғни, 30 болады. Қалған төртеуі (сол қолдың бүгілулі тұрған саусақтары) 3-ке (оң қолдын бүгілулі саусақтарына ) көбейтіледі, сонда 12 шығады. Сөйтіп, 6•7=42 мәнін аламыз.
Осылайша:
6•8=(1+3)•10+4•2=48
6•9=(1+4)•10+4•1=54
7•7=(2+2)•10+3•3=49
7•8=(2+3)•10+3•2=56
7•9=(2+4)•10+3•1=63
8•8=(3+3)•10+2•2=64
8•9=(3+4)•10+2•1=72
9•9=(4+4)•10+1•1=81
cандарының мәндерін ойша табуға болады..
Екі таңбалы санды бір таңбалы санға ойша көбейту үшін, бұл санның ондық бөлігін бірінші көбейтіп, артынан бірлік бөлігін көбейту керек. Нәтижесінде шыққан екі санды бір біріне қосу керек. Мысалы келтірсек:




99 санына шапшаң көбейту әдістері. Екі таңбалы сандарды 99 санына шапшаң көбейтудің ең тамаша әдісі. Мысалы: 73 санын 99 – ға көбейту үшін, ең алдымен 72 санынан 1 – ді азайтын, 100 – санынан 73 ті азайтқан санды бір – біріне тіркеп жазу керек.


11 санына шапшаң көбейту әдісі. Есептеуді тездетудің өзгеше бір әдісі – санды 11-ге көбейту әдісімен танысайық. Мысалы, 26-ны 11-ге көбейту керек болсын. Oл үшін әуелі 26 санын құрайтын 2 және 6 цифрларын қосып, 2 шыққан қосындыны 2 және 6 цифрларының арасына «сыналап» енгізіп жазамыз, сонда 286 саны пайда болады.
Cанды құрайтын цифрлардың қосындысы екі таңбалы сан болуы да мүмкін, алғашқы цифры 1 болмақ. Осы 1-ді санның ондық орында жазылған цифрына қосу керек те, цифрлардың арасына қосындының бірлік орындағы цифрын «сыналап» енгізу шарт. Мысалы, 75-ті 11-ге көбейткен кезде 75 санын құрайтын цифрларды қосып, (7+5=12) пайда болған нәтиженің алдыңғы цифрын 7-ге қосамыз. Сонда 85 саны, ал 2 цифрын жаңадан пайда болған 85 санының 8 бен 5 цифрларының арасына «сыналап» ендіріп жазамыз.
Cанды лезде 1001-ге көбейту. 1001 – даңқы шыққан Шахеризада саны 7, 11 және 13 сандарына қалдықсыз бөлінеді немесе 1001=7 11 13 болады, бірақ бұл санның ерекшелігі бұл емес. Кез келген үш таңбалы санды 1001-ге көбейткенде шығатын көбейтіндіні осы үш таңбалы санды екі рет қайталап жазғанға тең. Яғни, есептеу барысында жоғарыдағы ережені пайдаланып, есептің нәтижесін әп-сәтте табуға болады. Мәселен:
873* 1001=873873
236* 1001=236236
Мұның ешқандай құпияcы жоқ. Үш таңбалы бір сан ойлап, оны 1001-ге көбейтіп, қайта 1001-ге бөлдік. Нәтижесінде ойлаған санның өзі шықты. Бұл саннан басқа да үш таңбалы кез келген сан ойлап, ойынды жалғастыруға болады.
Енді 1001 санын 2 таңбалы санға көбейтелік: 47х1001=47047; 68х1001=68068. Бұдан кез келген екі таңбалы санды 1001-ге көбейтсек, нәтиже сол санды екі рет тіркеп, арасына 0 санын тіркегендегі мәнге тең болады.
Келесі кезекте 1001 санын төрт таңбалы санға көбейтелік: 5628х1001=5633628 саны шығады.
Бұдан байқағанымыз: 5628х1000+5628=562800+5628=5633628 шығады.
Дәл осылай санды түрлендіру арқылы есепті шешуді жеңілдетуге болады.
Сандардың квадраттарын табудың оңай әдісі
10 – 20 ға дейінгі сандардың квадраттарын табу әдісі. Көбейтіндінің мәніне алдымен ондықтарын көбейтіп, бірліктерін қосып, бірліктерін көбейтіп тіркеп жазсақ жеткілікті






16 – дан басталған сандардың квадратын табу үшін бірліктерін көбейтіп, шыққан екі таңбалы санның бірлігін жазып, ондығын осы бірліктердің қосындысына қосамыз





5 пен аяқталатын сандардың екінші дәрежесін есептеу үшін 25- ті соңына жазып, ондықты өзінен кейінгі санға көбейтіп шыққан нәтижені жазамыз.








Көбейту, бөлу таблицасын білгеннен кейін сандарды көбейтудің, бөлудің, дәрежелеудің оң тәсілдерін үйрену мақсат. Әдетте 10, 20, 30, 40, 50, ... ..., 100 оңай есептеледі. Ал 192, 292, 392, 492, ... ..., 992 – ын табу бір жаңа есептеуді қажет етеді. Сол әдістерге тоқталайық.
192 = 361 шығару үшін 9 х 19 көбейтіндісінің 202 – нан 20+19=39 – ды шегеру жеткілікті 400-39=361

Ал 182, 282, 382, 482, ... ... 172, 272, 372, есептеп табу үшін

1.2 Сандардың бөлінгіштік белгілері
4-ке бөлінгіштік белгісі: тек соңғы екі цифрымен таңбаланған сан 4-ке бөлінетін сандар ғана, тек сол сандар ғана, 4-ке бөлінеді. Мысалы, 83745656 саны 4-ке бөлінеді, өйткені, 56 саны 4-ке бөлінеді; 5349741414 саны 4-ке бөлінбейді, өйткені, 14 саны 4-ке бөлінбейді.
8-ге бөлінгіштік белгісі: тек саны 8-ге бөлінетін сандар ғана, тек сондай сандар ғана 8-ге бөлінеді. Мысалы, 437258112 саны 8-ге бөлінеді, өйткені, 112 саны 8-ге бөлінеді, ал 256124 саны 8-ге бөлінбейді, өйткені, 124 саны 8-ге бөлінбейді
11-ге бөлінгіштік белгісі. Берілген сан 11-ге бөліну үшін ол санның жұп орындағы цифрларының қосындысы мен тақ орындағы цифрларының қосындысының айырмасы не нөл немесе 11-ге бөлінетін сан болуы керек.
Мысалы үшін 92637294 санын 11- ге бөлінгіштік белгісін дәлелдейік.
92637294 санын тез есептеу әдісін қолданайық. Ол үшін бірінші
2+1+2+4=9
9+6+7+9=31
31-9=22
22![]() 11=2
11=2
Яғни бұл сан 11-ге қалдықсыз бөлінетінің дәлелдедім.
13-ке бөлінгіштік белгісі. Берілген санды солдан оңға қарай сызықшамен үш орынды сандарға бөлеміз. Бірінші, үшінші, бесінші орындағы бөліктердің қосындысын тауып, сол қосындылардың айырмасы 13- ке бөлінсе, онда берілген сан 13-ке бөлінеді.
Мысалы, 91182091 санын тексерейік: 911/820/91, бұдан 911+91=1002 , 1002-820=182 , 182 13-ке бөлінеді, ендеше 91182091 саны да 13-ке бөлінеді.
999-ға, 333-ке, 111-ге, 37-ге, 27-ге бөлінгіштік белгілері.
Берілген сан 999-ға, 333-ке, 111-ге 37-ге, 27-ге бөлінуі үшін оңнан солға қарай үш- үштен санағанда алғашқы үш бөліктің қосындысы, одан кейінгі үш бөліктің қосындысына тең болса және олар 999,333,111,37, 27-ге бөлінетін болса, ол осы сандарға бөлінеді.
Мысалы 776223-ті тексеріп
көрейік: 223+776=999; 999=3![]() = 9
= 9![]() 111=
111=![]() демек, берілген сан 999-ға да, 333-ке де, 11-ге де, 27-ге
де бөлінеді.
демек, берілген сан 999-ға да, 333-ке де, 11-ге де, 27-ге
де бөлінеді.
25-ке бөлінгіштік белгісі: тек соңғы екі цифрларымен таңбаланған сан 25-ке бөлінсе немесе сан екі нольмен аяқталса, тек сол сандар ғана 25-ке бөлінеді. Мысалы, 4381997550 саны 25-ке бөлінеді, өйткені, 50 саны 25-ке бөлінеді, ал 1112221740 саны 25-ке бөлінбейді, себебі, 40 саны 25-ке бөлінбейді.
ІІ. Күрделі есептерді шығару
2.1 Есептерді түрлендіру арқылы табу
Алгебралық есептерді шешкенде оңай әрі тиімді тәсілдер қолданылады. Асқан шебер есептеушілер көптеген жағдайларда онша күрделі емес алгебралық түрлендірулерге сүйене отырып, өздерінің есептеу жұмыстарын оңайлатады. Мысалы, есептеу былайша іске асырылады:
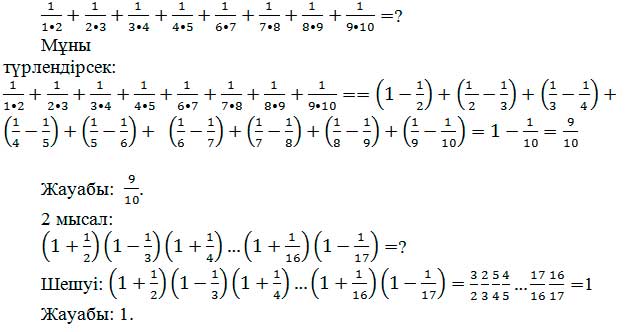
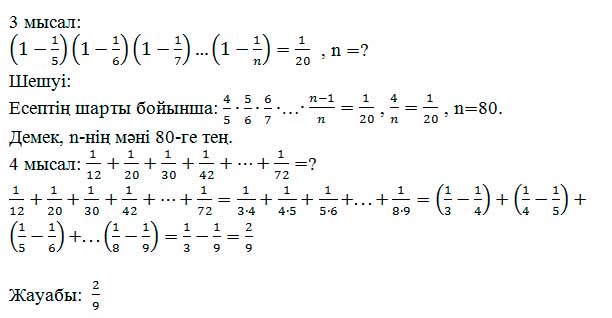
Күрделі радикалы бар өрнекті түрлендіру
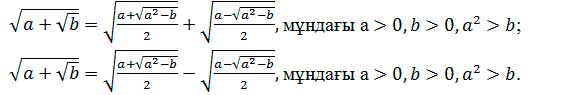
Күрделі радикалы бар
өрнектерді түрлендіргенде көбінесе қос радикалды ішкі радикалдан
құтқарып алған тиімді.
Егер түбір астында тұрған өрнек толық квадрат болса, онда оны мына
тепе-теңдікті қолдану арқылы сыртқы радикалдан құтқаруға
болады.
1
мысал: 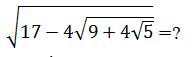
Шешуі: арифметикалық квадрат түбірдің қасиетін пайдаланып табатынымыз:


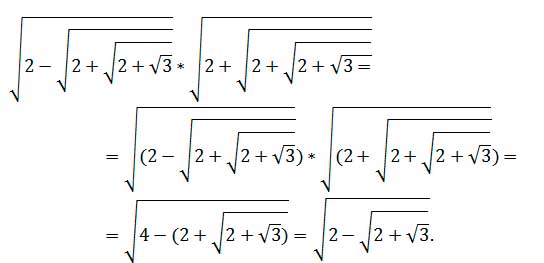

2.2 Кейбір есептерді шығарудың тиімді әдістері.
Кейде есеп барысында мынадай есептер жиі кездеседі:
a) 100! саны неше нөлмен аяқталады: (100)!= 1*2*3*...*100).
ә) 19821982 саны қай цифрмен аяқталады?
б) Қай сан үлкен: 1020 немесе 2010? 10020 немесе 90010?
в) (2*57 – 5*27)83 – [(2*57)83 – (5*27)83] өрнегі 83-ке бөліне ме?
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Стандартты емес теңсіздіктерді шешу
Стандартты емес теңсіздіктерді шешу
Мазмұны
Кіріспе.................................................................................................
Негізгі бөлім
І. Арифметикалық амалдар
1.1 Сандарды жылдам көбейту әдістері...............................................
1.2 Сандардың бөлінгіштік белгілері..................................................
ІІ. Күрделі есептерді шығару
2.1 Есептерді түрлендіру арқылы табу.............................................
2.2 Кейбір есептерді шығарудың тиімді әдістері.................................
Қорытынды...............................................
Ұсыныстар.................................................
Пайдаланылған әдебиеттер тізімі.............................................
Кіріспе
«Арифметика математиканың, ал
математика ғылымдардың патшасы»
К.Гаусс
Математика өмірді сан арқылы бейнелейді. Адамзат баласы ең алғаш рет жазу-сызудан бұрын санауды үйренгені хақ. Осылайша, бертін келе адамдар қарапайым арифметикалық амалдарды қолдануды үйреніп, олардың негізгі қасиеттерін сараптап, тағы басқа да математикалық білімдерін дамыта түседі. Әуел баста адамдар саусақтармен амалдар қолданып, кейіннен есептеудің өзге де тәсілдерін ашқан. Сондай-ақ жылдам есептеу әдістеріне талдау жасап, оны келешек ұрпаққа таратып отырған. Ал біздің заманымыз ғылым мен техниканың қарқынды дамуымен ерекшеленеді. Қазіргі кезде ғылым мен техниканың даму деңгейі әрбір адамға сапалы және терең білімнің, іскерліктің және жылдамдықтың болуын қажет етеді.
Сондай-ақ жастардың белсенді шығармашылықпен жұмыс істеуін де талап етеді. Сол себепті әрбір адам өз бойындағы туғаннан пайда болған интуициясын әрі қарай дамытуға, табиғи қасиеттерін, математикалық білім деңгейін тереңдету үшін өз бетінше білім алуға қадам басып, алға қарай ұмтылу қажет. Соңғы жылдардағы компьютер, калькулятордың өмірге көптеп енуі – оқушылардың шапшаң есептеу дағдыларына, ойлау қабілетінің тежелуіне әсер етуде. Осындай жайттарды ескерген әрбір оқушы өз бетінше шапшаң есептеуге, ауызша жаттығуларға көп уақыт бөліп отырғаны жөн. Cебебі тез есептеу әдістері есептеуді жеңілдетуге, математикалық терең ойлауды дамытуға және ең бастысы әр адамның интуициясын дамытуға өз үлесін қосады.
Математикалық логика ақыл-ой еңбегін техникаландырудың құралы болып табылады және ойлау процесін арнаулы математикалық әдістер, символдық аппараттар арқылы зерттейді. Бірақ дәстүрлі математикалық логика пәнін білмейінше, оны ойдағыдай меңгеру қиын. Өйткені бүгінгі күнде ғылыми технологияның дамуына байланысты адамзат баласы ой және дене еңбегін жеңілдететін техникалық құрылғылардың түр-түрін ойлап табуда. Мысалы, қазіргі кезде электронды есептеу машинасын қолдана отырып, кез-келген күрделі есептің шешімін аз ғана уақыт аралығында табуға болады. Тіпті, қарапайым есептеу құралы – калькуляторлардың өзі бүгінгідей нарық заманында қарапайым халық үшін аса тиімді. Әрине, мұның бәрі адамның ойлау қабілетінің ең ірі жетістіктері болып табылады. Алайда, қалыптасқан жағдайдың пайдасымен қатар зияны да жоқ емес. Атап айтқанда, бүгінде кез-келген оқушының қарапайым көбейту кестесін біле бермеуі мүмкін. Сол себепті де, баланың логикалық ойлау қабілетін дамыту бүгінгі күннің өзекті мәселелерінің бірі деуге болады. Осы жайды ескеріп, мен бұл ғылыми жұмыста логикалық ойлау қабілетін дамытатын шапшаң есептеудің кейбір әдістерін мейілінше қарастырдым. Ендеше, мен секілді математиканың ғылымилығын жаңа бастаған оқушы үшін бұл маңызды тақырып.
Бұл жобаны қорғаудағы басты мақсат: тез есептеу әдістерін үйрене отырып, есептеуді ойша шешіп, есеп нәтижесін табуды жылдамдату және тез есептеу әдістері арқылы болашақта математика ғылымының дамуына өз үлесімді қосу болып табылады. Cодай-ақ бұл жоба арқылы әр оқырманның математикалық қызығушылығын дамытып, өмірге деген ой толғанысын тудыру және білімін шыңдай түсу саналады. Осындай шараларды жүзеге асырып, қазіргі таңдағы негізгі проблема – оқушының пәнге деген қызығушылығын, есепке деген құштарлығын оятып, математикалық және логикалық білімін арттыруды мен өзімнің азаматтық борышым деп білемін.
Негізгі бөлім
І. Арифметикалық амалдар
1.1 Сандарды жылдам көбейту әдістері
Көбейту кестесін жаттаудың оңай жолы. Математикаға кіріспе көбейту кестесін жаттаудан басталатыны баршаға аян. Оны жаттамаған бүлдіршін математиканы оқып үйрене алмайды. Алайда, көбейту кестесін жаттаудың да оңай тәсілі бар. Мәселен, 9 санына байланысты көбейту кестесін оп-оңай жаттауға болады. Ол үшін әуелі, 9 санын 1-ге көбейтуден бастап 1-ден 9-ға дейінгі сандарды ретімен жоғарыдан төмен қарай жазып шығамыз (1).
Кейін дәл осылай 1-ден 9-ға дейінгі сандарды ретімен төменнен жоғары қарай жазып шығамыз (2). Міне, осылай дайын көбейту кестесі шыға келеді (төмендегі кесте).
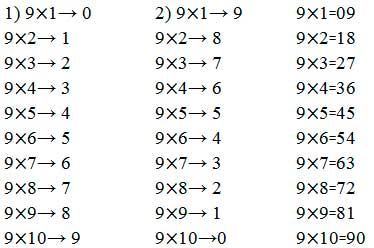
Саусақпен шапшаң көбейту әдісі. Саусақтарды бүгіп санау ерте заманда кең қолданылып келді. Адамның саусақтары мен олардың буындары, сондай-ақ саусақтарын бүгу және жазу, қолдарын бүгу мен жазу олардың ондаған және жүздеген мыңға дейін санай алуына ғана емес, сол сияқты кейбір арифметикалық амалдарды орындауына да мүмкіндік берді. Мысалы, ежелгі римдіктер 5 пен 10 сандарының арасындағы сандарды саусақпен былайша көбейткен.
Айталық, 6-ны 7-ге көбейту керек болсын. Сол қолымыздың жұдырығын жазбастан, бір-бірлеп саусағымызды жаза отырып, 6-ға дейін санаймыз. Ал оң қолымыздың саусақтарымен дәл соны қайталап, 7-ге дейін санаймыз. Оң қолдың жазылған екі саусағын сол қолдың жазылған бір саусағынан үстіне саламыз. Жазылған саусақ небары 3-еу болады, бұл – 3 ондық, яғни, 30 болады. Қалған төртеуі (сол қолдың бүгілулі тұрған саусақтары) 3-ке (оң қолдын бүгілулі саусақтарына ) көбейтіледі, сонда 12 шығады. Сөйтіп, 6•7=42 мәнін аламыз.
Осылайша:
6•8=(1+3)•10+4•2=48
6•9=(1+4)•10+4•1=54
7•7=(2+2)•10+3•3=49
7•8=(2+3)•10+3•2=56
7•9=(2+4)•10+3•1=63
8•8=(3+3)•10+2•2=64
8•9=(3+4)•10+2•1=72
9•9=(4+4)•10+1•1=81
cандарының мәндерін ойша табуға болады..
Екі таңбалы санды бір таңбалы санға ойша көбейту үшін, бұл санның ондық бөлігін бірінші көбейтіп, артынан бірлік бөлігін көбейту керек. Нәтижесінде шыққан екі санды бір біріне қосу керек. Мысалы келтірсек:




99 санына шапшаң көбейту әдістері. Екі таңбалы сандарды 99 санына шапшаң көбейтудің ең тамаша әдісі. Мысалы: 73 санын 99 – ға көбейту үшін, ең алдымен 72 санынан 1 – ді азайтын, 100 – санынан 73 ті азайтқан санды бір – біріне тіркеп жазу керек.


11 санына шапшаң көбейту әдісі. Есептеуді тездетудің өзгеше бір әдісі – санды 11-ге көбейту әдісімен танысайық. Мысалы, 26-ны 11-ге көбейту керек болсын. Oл үшін әуелі 26 санын құрайтын 2 және 6 цифрларын қосып, 2 шыққан қосындыны 2 және 6 цифрларының арасына «сыналап» енгізіп жазамыз, сонда 286 саны пайда болады.
Cанды құрайтын цифрлардың қосындысы екі таңбалы сан болуы да мүмкін, алғашқы цифры 1 болмақ. Осы 1-ді санның ондық орында жазылған цифрына қосу керек те, цифрлардың арасына қосындының бірлік орындағы цифрын «сыналап» енгізу шарт. Мысалы, 75-ті 11-ге көбейткен кезде 75 санын құрайтын цифрларды қосып, (7+5=12) пайда болған нәтиженің алдыңғы цифрын 7-ге қосамыз. Сонда 85 саны, ал 2 цифрын жаңадан пайда болған 85 санының 8 бен 5 цифрларының арасына «сыналап» ендіріп жазамыз.
Cанды лезде 1001-ге көбейту. 1001 – даңқы шыққан Шахеризада саны 7, 11 және 13 сандарына қалдықсыз бөлінеді немесе 1001=7 11 13 болады, бірақ бұл санның ерекшелігі бұл емес. Кез келген үш таңбалы санды 1001-ге көбейткенде шығатын көбейтіндіні осы үш таңбалы санды екі рет қайталап жазғанға тең. Яғни, есептеу барысында жоғарыдағы ережені пайдаланып, есептің нәтижесін әп-сәтте табуға болады. Мәселен:
873* 1001=873873
236* 1001=236236
Мұның ешқандай құпияcы жоқ. Үш таңбалы бір сан ойлап, оны 1001-ге көбейтіп, қайта 1001-ге бөлдік. Нәтижесінде ойлаған санның өзі шықты. Бұл саннан басқа да үш таңбалы кез келген сан ойлап, ойынды жалғастыруға болады.
Енді 1001 санын 2 таңбалы санға көбейтелік: 47х1001=47047; 68х1001=68068. Бұдан кез келген екі таңбалы санды 1001-ге көбейтсек, нәтиже сол санды екі рет тіркеп, арасына 0 санын тіркегендегі мәнге тең болады.
Келесі кезекте 1001 санын төрт таңбалы санға көбейтелік: 5628х1001=5633628 саны шығады.
Бұдан байқағанымыз: 5628х1000+5628=562800+5628=5633628 шығады.
Дәл осылай санды түрлендіру арқылы есепті шешуді жеңілдетуге болады.
Сандардың квадраттарын табудың оңай әдісі
10 – 20 ға дейінгі сандардың квадраттарын табу әдісі. Көбейтіндінің мәніне алдымен ондықтарын көбейтіп, бірліктерін қосып, бірліктерін көбейтіп тіркеп жазсақ жеткілікті






16 – дан басталған сандардың квадратын табу үшін бірліктерін көбейтіп, шыққан екі таңбалы санның бірлігін жазып, ондығын осы бірліктердің қосындысына қосамыз





5 пен аяқталатын сандардың екінші дәрежесін есептеу үшін 25- ті соңына жазып, ондықты өзінен кейінгі санға көбейтіп шыққан нәтижені жазамыз.








Көбейту, бөлу таблицасын білгеннен кейін сандарды көбейтудің, бөлудің, дәрежелеудің оң тәсілдерін үйрену мақсат. Әдетте 10, 20, 30, 40, 50, ... ..., 100 оңай есептеледі. Ал 192, 292, 392, 492, ... ..., 992 – ын табу бір жаңа есептеуді қажет етеді. Сол әдістерге тоқталайық.
192 = 361 шығару үшін 9 х 19 көбейтіндісінің 202 – нан 20+19=39 – ды шегеру жеткілікті 400-39=361

Ал 182, 282, 382, 482, ... ... 172, 272, 372, есептеп табу үшін

1.2 Сандардың бөлінгіштік белгілері
4-ке бөлінгіштік белгісі: тек соңғы екі цифрымен таңбаланған сан 4-ке бөлінетін сандар ғана, тек сол сандар ғана, 4-ке бөлінеді. Мысалы, 83745656 саны 4-ке бөлінеді, өйткені, 56 саны 4-ке бөлінеді; 5349741414 саны 4-ке бөлінбейді, өйткені, 14 саны 4-ке бөлінбейді.
8-ге бөлінгіштік белгісі: тек саны 8-ге бөлінетін сандар ғана, тек сондай сандар ғана 8-ге бөлінеді. Мысалы, 437258112 саны 8-ге бөлінеді, өйткені, 112 саны 8-ге бөлінеді, ал 256124 саны 8-ге бөлінбейді, өйткені, 124 саны 8-ге бөлінбейді
11-ге бөлінгіштік белгісі. Берілген сан 11-ге бөліну үшін ол санның жұп орындағы цифрларының қосындысы мен тақ орындағы цифрларының қосындысының айырмасы не нөл немесе 11-ге бөлінетін сан болуы керек.
Мысалы үшін 92637294 санын 11- ге бөлінгіштік белгісін дәлелдейік.
92637294 санын тез есептеу әдісін қолданайық. Ол үшін бірінші
2+1+2+4=9
9+6+7+9=31
31-9=22
22![]() 11=2
11=2
Яғни бұл сан 11-ге қалдықсыз бөлінетінің дәлелдедім.
13-ке бөлінгіштік белгісі. Берілген санды солдан оңға қарай сызықшамен үш орынды сандарға бөлеміз. Бірінші, үшінші, бесінші орындағы бөліктердің қосындысын тауып, сол қосындылардың айырмасы 13- ке бөлінсе, онда берілген сан 13-ке бөлінеді.
Мысалы, 91182091 санын тексерейік: 911/820/91, бұдан 911+91=1002 , 1002-820=182 , 182 13-ке бөлінеді, ендеше 91182091 саны да 13-ке бөлінеді.
999-ға, 333-ке, 111-ге, 37-ге, 27-ге бөлінгіштік белгілері.
Берілген сан 999-ға, 333-ке, 111-ге 37-ге, 27-ге бөлінуі үшін оңнан солға қарай үш- үштен санағанда алғашқы үш бөліктің қосындысы, одан кейінгі үш бөліктің қосындысына тең болса және олар 999,333,111,37, 27-ге бөлінетін болса, ол осы сандарға бөлінеді.
Мысалы 776223-ті тексеріп
көрейік: 223+776=999; 999=3![]() = 9
= 9![]() 111=
111=![]() демек, берілген сан 999-ға да, 333-ке де, 11-ге де, 27-ге
де бөлінеді.
демек, берілген сан 999-ға да, 333-ке де, 11-ге де, 27-ге
де бөлінеді.
25-ке бөлінгіштік белгісі: тек соңғы екі цифрларымен таңбаланған сан 25-ке бөлінсе немесе сан екі нольмен аяқталса, тек сол сандар ғана 25-ке бөлінеді. Мысалы, 4381997550 саны 25-ке бөлінеді, өйткені, 50 саны 25-ке бөлінеді, ал 1112221740 саны 25-ке бөлінбейді, себебі, 40 саны 25-ке бөлінбейді.
ІІ. Күрделі есептерді шығару
2.1 Есептерді түрлендіру арқылы табу
Алгебралық есептерді шешкенде оңай әрі тиімді тәсілдер қолданылады. Асқан шебер есептеушілер көптеген жағдайларда онша күрделі емес алгебралық түрлендірулерге сүйене отырып, өздерінің есептеу жұмыстарын оңайлатады. Мысалы, есептеу былайша іске асырылады:
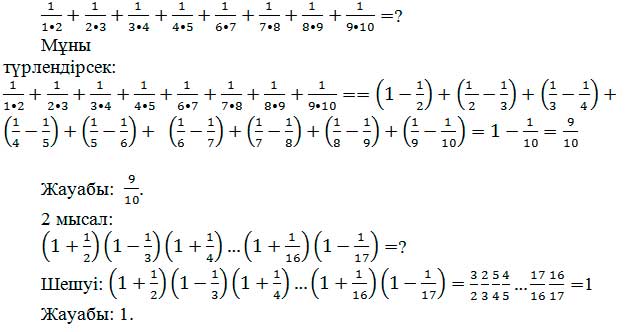
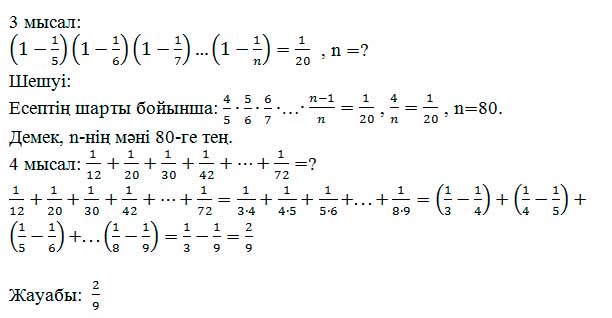
Күрделі радикалы бар өрнекті түрлендіру
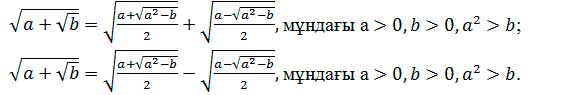
Күрделі радикалы бар
өрнектерді түрлендіргенде көбінесе қос радикалды ішкі радикалдан
құтқарып алған тиімді.
Егер түбір астында тұрған өрнек толық квадрат болса, онда оны мына
тепе-теңдікті қолдану арқылы сыртқы радикалдан құтқаруға
болады.
1
мысал: 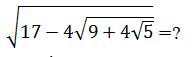
Шешуі: арифметикалық квадрат түбірдің қасиетін пайдаланып табатынымыз:


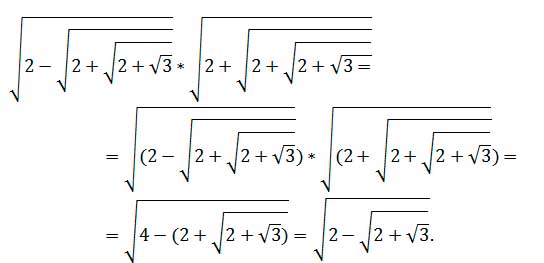

2.2 Кейбір есептерді шығарудың тиімді әдістері.
Кейде есеп барысында мынадай есептер жиі кездеседі:
a) 100! саны неше нөлмен аяқталады: (100)!= 1*2*3*...*100).
ә) 19821982 саны қай цифрмен аяқталады?
б) Қай сан үлкен: 1020 немесе 2010? 10020 немесе 90010?
в) (2*57 – 5*27)83 – [(2*57)83 – (5*27)83] өрнегі 83-ке бөліне ме?

шағым қалдыра аласыз















