Ұзақ мерзімді жоспардың бөлімі:

7.2А Функция. Функцияның графигі.

Мектеп:

Күні:

Мұғалімнің аты-жөні:

Сынып:

Қатысқандар саны:

Қатысқандар саны:

Сабақтың тақырыбы

Cызықтық функциялардың графиктерінің өзара орналасуы

Сабақтың түрі

Жаңа тақырыпты оқып білу

Осы сабақта қолжеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)

7.5.1.8 сызықтық функция графиктерінің өзара орналасуы олардың қоэффициенттеріне тәуелді болатынын негіздеу;

Сабақтың мақсаты

Оқушылар сызықтық функциялардың графиктерінің өзара орналасуын зерттей алады

Бағалау критерийі

Оқушы:

Тілдік мақсаттар

Тілдік оқыту мақсаттары:

Оқушылар:

• сызықтық функциялардың графиктерін салу алгоритмін сипаттайды;

• сызықтық функциялардың коэффициенттердің арасындағы тәуелділікке және олардың графиктерінің өзара орналасуының ерекшеліктеріне түсінік береді;

Пәндік лексика және терминология:

– функция графигі;

– сызықтық функция;

– сызықтық функцияның бұрыштық коэффициенті;

– түзулер параллель;

– түзулер қиылысады

– түзулер қиылыспайды

Құндылықтарды дарыту

Оқуға ептілігін, өзбетінше ақпаратты жинау дағдыларын арттыру, жағдайды талдау және жаңа ситуацияға бейімделу, мәселелерді қою және шешім қабылдау, өз және топтың жұмысының сапасына жауапты болу, өз уақытын тиімді ұйымдастыру, сабақтарда көпмәдениеттілікті және басқалардың пікірін сыйлау білу.

Құндылықтарды дарыту сабақта барлық жоспарлаған іс- әрекеттердің кезеңдері арқылы жүзеге асырылады.

Пәнаралық байланыстар

АКТ қолдану дағдылары

АКТ тиімді қолдану үшін оқуға қажет пайдаланушылардың дағдылары. «GeoGebra», «Математический конструктор» немесе «Рисование графиков онлайн» бағдарламалық жасақтамаларды қолдану.

Бастапқы білім

Шамалар арасындағы тәуелділіктерді білу; тура және кері пропорционалдық ұғымдарын білу; тура пропорционалдық тәуелділіктің графигін сала алу. Айнымалылары бар өрнектерді түрлендірулерді орындай алу. Формулалармен жұмыс істей алу.

Сабақ барысы

Сабақтың жоспарланған кезеңдері

Сабақтағы жоспарланған іс-әрекет

Ресурс

тар

Сабақтың басы

3 мин

Сабақтың басында мұғалім ерекше көңіл аударады:

- оқушылардың зейін қоюына

- оқушылармен бірге сабақтың мақсаттарын анықтайды

- оқушылардың «жақын даму аймағын» анықтайды - деңгейлер бойынша (А, В және С) өзіндік және үй жұмысын орындау

- сабақтың аяғындағы күтілетін нәтижелер

Сабақтың ортасы

40 мин

Сабақта оқушылар білетін ұғымдар қолданылады және жаңа ұғымдар енгізіледі. Сондықтан материалмен танысу барысында сөздікке жаңа терминдер енгізіледі.

Әртүрлі іс-әрекеттер жасау барысында оқушылар бағалау парағын толтырады. Сабақтың соңында қорытынды жасалады және мұғалімнің жұрналында белгіленеді.

1. Ой қозғау – 4 мин.

Бұл кезеңде оқушыларда өмір бойы білім алуға бейімделу және сабақтарда көпмәдениеттілікті және басқалардың пікірін сыйлау білу құндылықтар дамиды.

Презентация бойынша ауызша жұмыс:

1. Функциялардың қайсылары сызықтық болатынын анықтаңыз:

2. Қандай суретте сызықтық функцияның графигі көрсетілген?

3. функциясының k және b коэффициенттерінің таңбалары қандай?

_{1-сурет 2-сурет 3-сурет}

_{4-сурет 5-сурет 6-сурет}

Критерийлер бойынша өзін-өзі бағалау:

1. Сызықтық функцияның формуласын біледі – 1 б;

2. Сызықтық функцияның графикті анықтай алады – 1 б;

3. Функцияның графигі бойынша k және b коэффициенттерінің таңбаларын анықтайды - 1б.

3 балл – 100%

2 балл – 67 %

1 балл – 33%

0 балл – 0%

2. Жаңа материалмен жұмыс – 15 мин:

Бұл кезеңде оқушыларда өмір бойы білім алуға бейімделу құндылығы дамиды. Сонымен қатар жұптасып бекітуге тапсырмаларды орындау барысында оқушыларда оқуға бейімділігі, ақпаратты өзбетінше табу, жағдайды талдау дағдылары дамиды.

Оқушылар «GeoGebra», «Математический конструктор» немесе «Рисование графиков онлайн» бағдарламалрында келесі функциялардың графиктерін салады , , , және салынған түзулердің өзара орналасуын сипаттайды (егер мұндай мүмкіндік болмаса, салуларды постерлерде орындайды):

1) және функциялардың графиктері параллель;

2) және қиылысады және т.с.с.

Содан соң оқушылар графиктердің өзара орналасуын коэффициенттерге тәуелділігін талдайды және қорытынды жасайды.

Қорытынды: k-ның бірдей мәндерінде сызықтық функциялардың графиктері параллель түзулер болады, ал әртүрлі мәндерінде – графиктер қиылысады.

Мұғалім: Қарастырылған мысалдар негізінде қорытындыларды дәлелдейік. Екі сызықтық функция берілсін және Олар координаталары С нүктесінде қиылысады деп ұйғарайық. Бұл кезде нүкте әрбір түзудің бойында жатады және оның координаталары әрбір түзудің теңдеуін қанағаттандырады. Сондықтан теңдеуге және

Жүктеу

ЖИ арқылы жасау

ЖИ арқылы жасау

Бөлісу

1 - айлық

Материал тарифі

-96% жеңілдік

00

05

00

ҚМЖ

Ашық сабақ

Тәрбие сағаты

Презентация

БЖБ, ТЖБ тесттер

Көрнекіліктер

Балабақшаға арнарлған құжаттар

Мақала, Эссе

Дидактикалық ойындар

және тағы басқа 400 000 материал

Барлық 400 000 материалдарды шексіз
жүктеу мүмкіндігіне ие боласыз

1 990 ₸ 49 000₸

1 айға қосылу

Таңдау

Материалға шағымдану

Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз

Жариялаған:

Арипбай Мақсат Шаншарханұлы

26 Қараша 2021

441

Шағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз

Шағымды қалдыру

Сызықтық функциялардың графиктерінің өзара орналасуы

Тақырып бойынша 31 материал табылды

Сызықтық функциялардың графиктерінің өзара орналасуы

Материал туралы қысқаша түсінік

жаңартылған бағдарлама бойынша жасалған.Оқушыларға сызықтық функциялардың графиктерінің орналасуын үйрету,егер коэфицциенттері тең болса,параллель болады.

Материалды жүктеу

Материалдың қысқаша нұсқасы

Қысқа мерзімді жоспар

Сабақ жоспары

Ұзақ мерзімді жоспардың бөлімі: 7.2А Функция. Функцияның графигі.		Мектеп:
Күні:		Мұғалімнің аты-жөні:
Сынып:		Қатысқандар саны:		Қатысқандар саны:
Сабақтың тақырыбы		Cызықтық функциялардың графиктерінің өзара орналасуы
Сабақтың түрі		Жаңа тақырыпты оқып білу
Осы сабақта қолжеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)		7.5.1.8 сызықтық функция графиктерінің өзара орналасуы олардың қоэффициенттеріне тәуелді болатынын негіздеу;
Сабақтың мақсаты		Оқушылар сызықтық функциялардың графиктерінің өзара орналасуын зерттей алады
Бағалау критерийі		Оқушы: Білу және түсіну k мен b-ға байланысты сызықтық функциялардың графиктері қалай орналасатынын біледі (параллель, қиылысады, қиылыспайды) Жоғары деңгейдегі дағдылар Координаталық жазықтықта екі түзудің салыстырмалық орналасуын зерттейді
Тілдік мақсаттар		Тілдік оқыту мақсаттары: Оқушылар: сызықтық функциялардың графиктерін салу алгоритмін сипаттайды; сызықтық функциялардың коэффициенттердің арасындағы тәуелділікке және олардың графиктерінің өзара орналасуының ерекшеліктеріне түсінік береді; Пәндік лексика және терминология: – функция графигі; – сызықтық функция; – сызықтық функцияның бұрыштық коэффициенті; – түзулер параллель; – түзулер қиылысады – түзулер қиылыспайды
Құндылықтарды дарыту		Оқуға ептілігін, өзбетінше ақпаратты жинау дағдыларын арттыру, жағдайды талдау және жаңа ситуацияға бейімделу, мәселелерді қою және шешім қабылдау, өз және топтың жұмысының сапасына жауапты болу, өз уақытын тиімді ұйымдастыру, сабақтарда көпмәдениеттілікті және басқалардың пікірін сыйлау білу. Құндылықтарды дарыту сабақта барлық жоспарлаған іс- әрекеттердің кезеңдері арқылы жүзеге асырылады.
Пәнаралық байланыстар
АКТ қолдану дағдылары		АКТ тиімді қолдану үшін оқуға қажет пайдаланушылардың дағдылары. «GeoGebra», «Математический конструктор» немесе «Рисование графиков онлайн» бағдарламалық жасақтамаларды қолдану.
Бастапқы білім		Шамалар арасындағы тәуелділіктерді білу; тура және кері пропорционалдық ұғымдарын білу; тура пропорционалдық тәуелділіктің графигін сала алу. Айнымалылары бар өрнектерді түрлендірулерді орындай алу. Формулалармен жұмыс істей алу.
Сабақ барысы
Сабақтың жоспарланған кезеңдері	Сабақтағы жоспарланған іс-әрекет				Ресурс тар
Сабақтың басы 3 мин	Сабақтың басында мұғалім ерекше көңіл аударады: - оқушылардың зейін қоюына - оқушылармен бірге сабақтың мақсаттарын анықтайды - оқушылардың «жақын даму аймағын» анықтайды - деңгейлер бойынша (А, В және С) өзіндік және үй жұмысын орындау - сабақтың аяғындағы күтілетін нәтижелер
Сабақтың ортасы 40 мин	Сабақта оқушылар білетін ұғымдар қолданылады және жаңа ұғымдар енгізіледі. Сондықтан материалмен танысу барысында сөздікке жаңа терминдер енгізіледі. Әртүрлі іс-әрекеттер жасау барысында оқушылар бағалау парағын толтырады. Сабақтың соңында қорытынды жасалады және мұғалімнің жұрналында белгіленеді. Ой қозғау – 4 мин. Бұл кезеңде оқушыларда өмір бойы білім алуға бейімделу және сабақтарда көпмәдениеттілікті және басқалардың пікірін сыйлау білу құндылықтар дамиды. 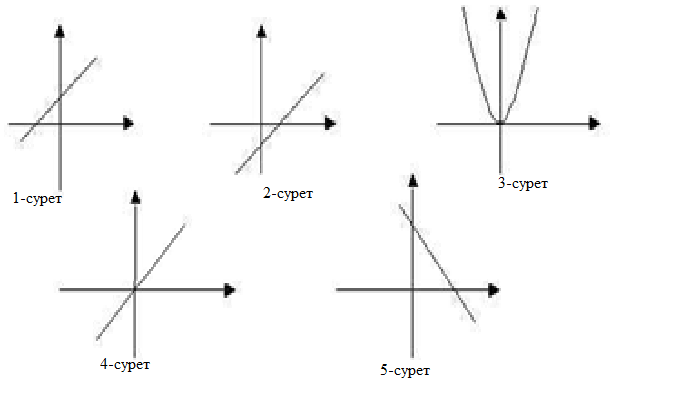Презентация бойынша ауызша жұмыс: Функциялардың қайсылары сызықтық болатынын анықтаңыз: Қандай суретте сызықтық функцияның графигі көрсетілген? функциясының k және b коэффициенттерінің таңбалары қандай? 1-сурет 2-сурет 3-сурет 4-сурет 5-сурет 6-сурет Критерийлер бойынша өзін-өзі бағалау: 1. Сызықтық функцияның формуласын біледі – 1 б; 2. Сызықтық функцияның графикті анықтай алады – 1 б; 3. Функцияның графигі бойынша k және b коэффициенттерінің таңбаларын анықтайды - 1б. 3 балл – 100% 2 балл – 67 % 1 балл – 33% 0 балл – 0% Жаңа материалмен жұмыс – 15 мин: Бұл кезеңде оқушыларда өмір бойы білім алуға бейімделу құндылығы дамиды. Сонымен қатар жұптасып бекітуге тапсырмаларды орындау барысында оқушыларда оқуға бейімділігі, ақпаратты өзбетінше табу, жағдайды талдау дағдылары дамиды. Оқушылар «GeoGebra», «Математический конструктор» немесе «Рисование графиков онлайн» бағдарламалрында келесі функциялардың графиктерін салады , , , және салынған түзулердің өзара орналасуын сипаттайды (егер мұндай мүмкіндік болмаса, салуларды постерлерде орындайды): 1) және функциялардың графиктері параллель; 2) және қиылысады және т.с.с. Содан соң оқушылар графиктердің өзара орналасуын коэффициенттерге тәуелділігін талдайды және қорытынды жасайды. Қорытынды: k-ның бірдей мәндерінде сызықтық функциялардың графиктері параллель түзулер болады, ал әртүрлі мәндерінде – графиктер қиылысады. Мұғалім: Қарастырылған мысалдар негізінде қорытындыларды дәлелдейік. Екі сызықтық функция берілсін және Олар координаталары С нүктесінде қиылысады деп ұйғарайық. Бұл кезде нүкте әрбір түзудің бойында жатады және оның координаталары әрбір түзудің теңдеуін қанағаттандырады. Сондықтан теңдеуге және Материалды жүктеу Жүктеу Сақтау Бөлісу ЖИ арқылы жасау Файл форматы: docx Алгебра Ашық сабақ 7 сынып 26.11.2021 441 Жүктеу Сақтау ЖИ арқылы жасау Жариялаған: Арипбай Мақсат Шаншарханұлы Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз, шағым қалдыра аласыз Қазақстандағы ең үлкен материалдар базасынан іздеу Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз Іздеу Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз! Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі. Толығырақ Оқу-ағарту министірлігінің ресми жауабы Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз! Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз! Жариялау Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз! Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз! Жариялау Министірлікпен келісілген курстар тізімі Химия пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Тарих пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Биология пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Ағылшын тілі пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ География пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Информатика пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Мектепке дейінгі білім беру бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ «Қазақ тілі» жəне «Қазақ əдебиеті» бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Дене шынықтыру пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Білім алушылардың білім сапасын арттыру мақсатында сабақта цифрлық технологияларды қолдану 80/108 сағат Толығырақ Инклюзивті білім беру жүйесінде ерекше білім беру қажеттілігі бар білім алушыға психологиялық-педагогикалық қолдау көрсету бойынша педагогтердің кәсіби және пәндік құзыреттіліктерін дамыту 80/108 сағат Толығырақ