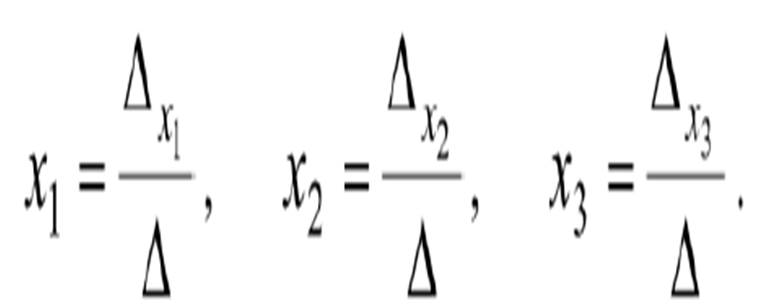СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДЕ КРАМЕР ӘДІСІ АРҚЫЛЫ ЭКОНОМИКАЛЫҚ ЕСЕПТЕРДІ ШЫҒАРУ

СЫЗЫҚТЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДЕ КРАМЕР ӘДІСІ АРҚЫЛЫ ЭКОНОМИКАЛЫҚ ЕСЕПТЕРДІ ШЫҒАРУ

Аңдатпа: Бұл зерттеу еңбегі жоғарғы оқу орнындағы экономикалық математика пәніндегі сызықтық теңдеулер жүйесін шешуде Крамер әдісі арқылы экономикалық есептерді шығару, математикалық формулаларды дұрыс қолдана білу, мәтін есептерді шығаруда теңдеулер жүйесін құру және шешімдерін Крамер әдісімен өрнектеу қарастырылады.

Кілт сөздер: экономикалық математика, сызықтыұ теңдеулер жүйесі, Крамер әдісі, экономикалық есеп.

«Төртінші өнеркәсіптік революция жағдайындағы дамудың жаңа мүмкіндіктері» атты жолдауда білім берудің барлық жағдайында математика және жаратылыстану ғылымдарын оқыту сапасын жандандыру қажеттілігі және жоғары оқу орындарында ақпараттық технологиялар бойынша білім алатын түлектер санын ұлғайту керектігін Елбасы Н.Ә.Назарбаев атап көрсетті. Сол себепті жоғары оқу орнында математика пәні оқытушылары қазіргі заман талабына сай білім беріп, математикалық ойлауы жоғары қалыптасқан, жеке дара нақ шешім қабылдайтын, бәсекеге қабілетті, білімді студенттерді даярлап шығаруға зор үлес қосуы тиіс. Мақалаға қатысты терминология: 1.Матрица-матрица-matrix.

2.Аудан-площадь –area,space.

3.Анықтауыш-определитель-determinant.

4.Теңдеу-уравнение-equation.

5.Теңдеулер жүйесі-системы уравнений- system of equarions.

6.Сызықтық теңдеулер жүйесін Крамер әдісімен шешу-решение систем линейных уравнений-solving systems of linear equations by Cramer`s method.

Крамер әдісін ғылымға кім енгізді?

Габриэль Крамер(1704-1752) - швейцариялық математик,Иоганн Бернуллидің досы, сызықтық алгебраның дамуына өз үлесін қосқан ғалым. Француз тілді дәрігерлер отбасында дүниеге келген Крамер кішкентайынан математикаға бейімді болды. Ол өзінің 18 жасында диссертация қорғап, 20 жасында Женева университетінің философия кафедрасында жұмыс жасайды. Университет қабырғасында өткізген 2 жылында ол Европа елдеріне саяхат жасап, Базель қаласында Бернулли мен Эйлерді, Лондонда Галлей мен Муаврды, Парижде Мопертюи мен Клеро сынды математикатермен кездесіп, хат алмасып тұрады. Бос уақытында геометрия, тарих, математика, философия салаларында мақала жазған .

Крамер әдісі қолданысқа қалай енді?

Крамер әдісі сызықтық теңдеулер жүйесін шешуде детерминанттарды қолдануға негізделген. Бұл шешім процесін едәуір жылдамдатады. Крамер әдісін көптеген сызықтық теңдеулер жүйесін шешу үшін қолдануға болады.

Әдіс Габриэль Крамердің есімімен аталады, ол 1750 жылы өзінің атақты «Алгебралық қисықтарды талдауға кіріспе» трактатын жарыққа шығарып, бұл еңбегінде сызықтық теңдеулер жүйесін құрып, алгоритм бойынша есептеп, дәлелдеген. Бірақ Крамерден бұрын 1748 жылы бұл ереженің ерекше жағдайларын қарастыра сипаттаған шотландық математик Колин Маклорен болды.

Формуланың негізгі сипаты:

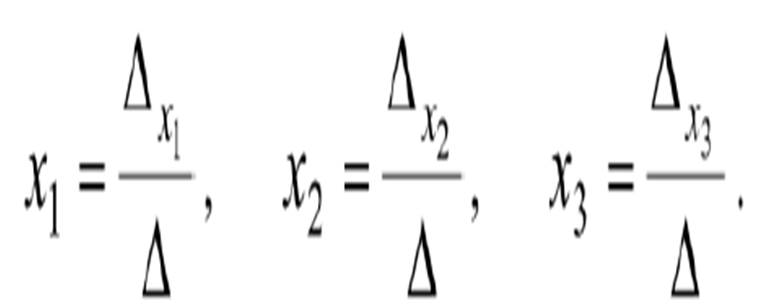
1750 жылы өз есімімен формуланы(ережені) ғылымға енгізген Крамермен қатар сол жылдары ғылымға Гаусста өз есімімен ережесін жарыққа шығарды. Байқайтынымыздай, «Крамер әдісі» сызықтық алгебрада анықтауышы нөлге тең емес болмайтын есептерде қолданылады. Ал Гаусс әдісі сызықтық алгебраның барлық мүмкін болған жағдайларында қолданылады.

Кейін осы ғалымдардың ықпалымен XVIII ғасырда ирландық математик У.Гамильтон, ағылшындық математик А.Кэли, неміс математигі К.Вейерштрасс және Ф.Фробениус, француздық Жордан сызықтық алгебраны одан әдісі дамытты. 1850 жылы ағылшындық Джеймс Сильвестр матрицаның заманауи тұжырымдамасын енгізді.

Экономикадағы Крамер әдісі:

Осы ұлы ғалымдардың математика саласына қосқан үлесі арқылы “матрицалық алгебра” деп аталатын жаңа бөлім пайда болды. Матрицалық алгебра ғылымда, оның ішінде экономикада өте маңызды.

Матрицаларды қолдану арқылы экономикалық мәселелердің шешуін Крамер формуласын қолдана отырып, есептеді. Матрица арқылы біз кез келген өнімнің өндірістегі шығыны, бір күндік шығын көлемі, өзіндік құны және өнімділігі туралы ақпарат ала аламыз.

Мысал қарастырайық:

1. Баспа типографияның үш түрін шығарады: газет, журнал, кітап. Оларды өндіру үшін шикізаттың үш түрі қолданылады: қағаз 297 × 420 мм, баспаға арналған сия 1 литр, бумвинил 1 м². Олардың әрқайсысының бір өнімге кеткен шығын нормалары және бір күндегі шикізатты тұтыну көлемі кестеде келтірілген.

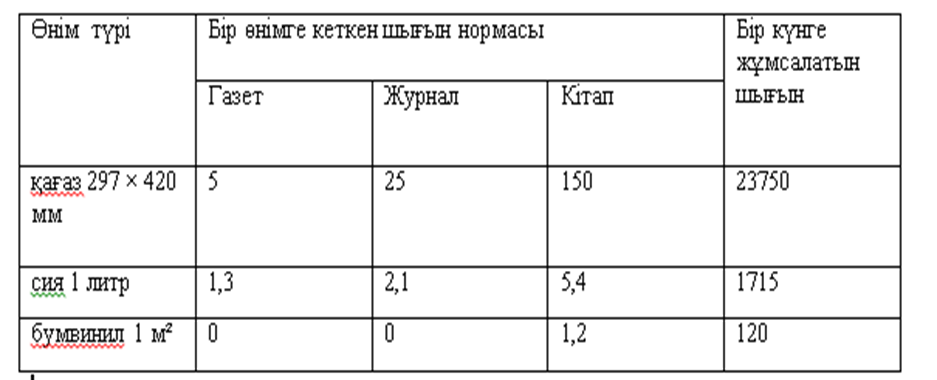
Шешімі:

Әр күні типография х1 газет,х2 журнал,х3 кітап шығарсын.Осыған сай біз жүйе қарастырамыз:

5x₁ + 25x₂ + 150x₃ = 23750

1,3x₁ + 2,1x₂ + 5,4x₃ = 1715

1,2x₃ = 120

∆ = -26,4

∆₁ = -13200 x₁ = -13200/(-26,4) = 500

∆₂ = -6600 x₂ = -6600/(-26,4) = 250

∆₃ = -2640 x₃ = -2640/(-26,4) = 100

Жауабы: типография күніне 500 газет, 250 журнал және 100 кітап шығарған.

2. Кондитер фабрикасы өнімнің үш түрін шығарады: торт, тоқаш және рулет. Оларды өндіру үшін үш түрлі шикізат қолданылады: ұн 1 кг, сүт 1 л, қант 1 кг. Олардың әрқайсысының бір өнімге шығын нормалары және бір күндегі шикізатты тұтыну көлемі кестеде келтірілген:

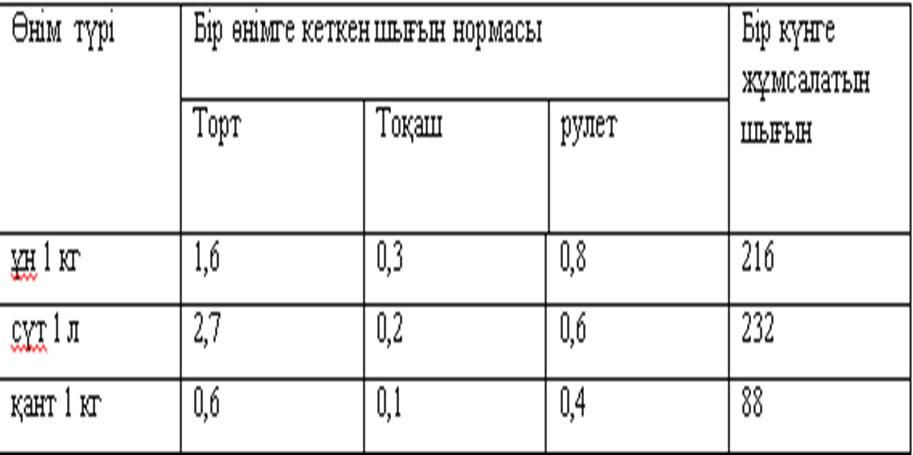
Шешімі:

Әр күні кондитерлік фабрика x₁ торт, x₂ тоқаш, x₃ рулет дайындасын. Осыған сай біз жүйе қарастырамыз:

1,6x₁ + 0,3x₂ + 0,8x₃ = 216

2,7x₁ + 0,2x₂ + 0,6x₃ = 232

0,6x₁ + 0,1x₂ + 0,4x₃ = 88

∆ = -0,064

∆₁ = -3,2 x₁ = -3,2/-0,064= 50

∆₂ = -12,8 x₂ = -12,8/-0,064 = 200

∆₃ = -6,08 x₃ = -6,08/-0,064 = 95

Жауабы: кондитерлік фабрика күніне 50 торт, 200 тоқаш и 95 рулет жасаған.

Математикада теңдеулер жүйесін қолдану арқылы шешуді қажет ететін есептер жетерлік. Мектеп қабырғасында екі айнымалысы бар теңдеулер жүйесін шешіп, ЖОО қабырғасында үш, төрт т.б. айнымалысы бар теңдеулер жүйесімен таныстып, сабақ барысында мамандығыма сай келетін, яғни экономика (қаржы,есеп және аудит) саласында да теңдеулер жүйесімен шығарылатын есептер барын білдім.

Математика – тарихы терең ғылым патшасы. Болашақта бұл ғылым саласында жақсы жаңалықтар көп болуына, бетке ұстар жас ғалымдар шығатынына сенімдімін!

ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР:

1.Мальцев И. А. Основы линейной алгебры. — Изд. 3-е, перераб., М.: «Наука», 1970. — 400 c

2.История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.

3.Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Крамер, Габриэль — биография в архиве MacTutor.

4.Том 3 Математика XVIII столетия. Под редакцией А.П.Юшкевича.М., Наука, 1972 — 496 с.