
Сабақтың тақырыбы: «Анықталған интегралдың негізгі қасиеттері және оны есептеу»
Мақсаты
Білімділік: Студенттерге анықталған интеграл ұғымы мен қасиеттерін және интегралды есептеу үшін Ньютон-Лейбниц формуласын қолдану бойынша білік, дағдыларын қалыптастырып, білімдерін нақтылау.
Дамытушылық: интегралдарды есептеу кестелерін есте сақтау және оларды есептер шығаруда қолдана білуге дағдыландыру, логикалық ойлау қабілетін дамыту;
Тәрбиелік: Соңғы нәтижеге жету жолында табандылық пен жігерлілік көрсете білуге, өзін-өзі бағалай білуге тәрбиелеу.
Түрі: Жаңа сабақты меңгерту
Оқыту әдісі: Түсіндіру, сұрақ-жауап, жүйелеу, есеп шығарту
Әдістемелік қамтамасыз етілуі:
Көрнекіліктер: Таратпа материалдары, слайдтар, плакаттар.ОТҚ: Интерактивті тақта
Пән аралық байланыс: Физика, информатика
Сабақ құрылымы мен мазмұны
І. Ұйымдастыру кезеңі:
1. Түгелдеу, сабаққа дайындықты бақылай отырып, зейінін сабаққа аудару.
2. Өткен білімдерге сүйене отырып, оқу әрекетін дамыту
ІІ. Үй тапсырмасын сұрау: Интегралдарды есептеудің негізгі әдістері.
![]() Анықтама: Берілген аралықтағы F(х) функциясының
алғашқы функциясы осы
аралықтағы f(х) функциясының анықталмаған интегралы деп
аталады.
Анықтама: Берілген аралықтағы F(х) функциясының
алғашқы функциясы осы
аралықтағы f(х) функциясының анықталмаған интегралы деп
аталады.
Белгіленуі: ![]() икстен эф де икс функциясының анықталмаған
интегралы деп оқылады)
икстен эф де икс функциясының анықталмаған
интегралы деп оқылады)
Анықтамаға
сәйкес: ![]()
ІІІ. Жаңа сабақ:
1. F(b) - F(a) айырмасын y=f(x) функциясының [a;b] кесіндісіндегі анықталған интегралы деп атайды.
![]() Мұндағы a және b сандары интегралдау шектері:
a – төменгі шегі, ал b – жоғарғы
шегі.
Мұндағы a және b сандары интегралдау шектері:
a – төменгі шегі, ал b – жоғарғы
шегі.
Анықталған интегралдың негiзгi қасиеттерi.
Берiлген анықталған интегралдың бар болу шарты орындалады деп есептейiк.
10. Тұрақты санды анықталған интеграл белгiсiнiң алдына шығаруға болады:
 мұнда k=const .
мұнда k=const .
20. Бiрнеше функциялар қосындысының анықталған
интегралы қосылғыштарының анықталған интегралдарының қосындысына
тең: 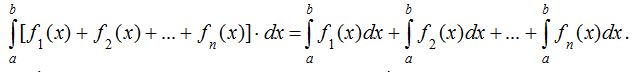 .
.
Осы екi қасиет интегралдың сызықтық қасиетi деп аталады.
30. Егер [a;b] аралығын [a;c] және [c;b] аралықтарына бөлсек, онда
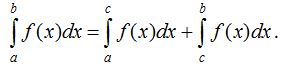
40. Егер интегралдың жоғарғы шегi мен төменгi шегiнiң орындарын ауыстырсақ, онда оның таңбасы өзгередi:
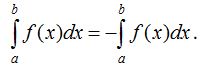 50. Жоғарғы шегi мен төменгi шегi тең болатын
интеграл 0-ге тең
50. Жоғарғы шегi мен төменгi шегi тең болатын
интеграл 0-ге тең
![]() 60. Егер [a;b] аралығындағы х айнымалысының барлық мәндерi
үшiн
60. Егер [a;b] аралығындағы х айнымалысының барлық мәндерi
үшiн ![]() болса, онда
болса, онда
![]()
70. Егер [a;b] аралығындағы х айнымалысының барлық
мәндерi үшiн ![]() болса, онда
болса, онда
![]() .
.
80. Егер [a;b] аралығында функциясының ең үлкен және ең
кiшi мәндерi сәйкес М және m сандары болса,
онда
![]()
2. Ньютон-Лейбниц формуласы.
Ньютон Исаак (1643-1727) - ағылшын астрономы, физигі, әрі математигі. ХVII ғасырда дифференциалдық және интегралдық есептеулерді математикалық практикаға енгізді.
![]() Туындыны дифференциалдау деп атаған және
интеграл белгісін енгізген ЛейбницГотфрид Вильгельм Лейбниц
(1646-1716 жж.) – XVII ғасырдағы неміс рухы туғызған терең де
жан-жақты дамыған философ. Екінші жағынан, ол - математик,
физик, саясаткер, тарихшы,
құқықтанушы.
Туындыны дифференциалдау деп атаған және
интеграл белгісін енгізген ЛейбницГотфрид Вильгельм Лейбниц
(1646-1716 жж.) – XVII ғасырдағы неміс рухы туғызған терең де
жан-жақты дамыған философ. Екінші жағынан, ол - математик,
физик, саясаткер, тарихшы,
құқықтанушы.
![]() Теорема. Егер F(X)
функциясы [a;b] аралығына f(x) функциясының алғашқы
функциясының бiрi болса, онда
Теорема. Егер F(X)
функциясы [a;b] аралығына f(x) функциясының алғашқы
функциясының бiрi болса, онда
(5)Бұл теңдiк Ньютон-Лейбниц формуласы деп аталады. Анықталған интегралдарға байланысты мысалдар келтіру.
1-есеп. ![]() .
.
Интеграл астындағы функцияның алғашқы функциясын бөлiктеп интегралдау әдiсiмен тауып және оған Ньютон-Лейбниц формуласын қолдансақ,
![]()
2-есеп. ![]() .
.
Бөліктеп интегралдау формуласы
бойынша ![]() болса, онда
болса, онда
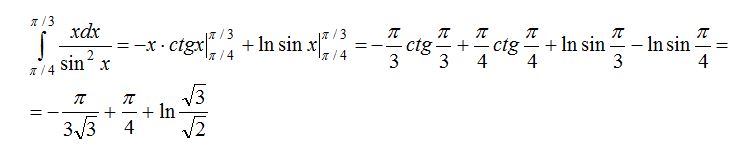
3-есеп.
![]()
4-есеп.
ІV. Жаңа
сабақты бекіту: 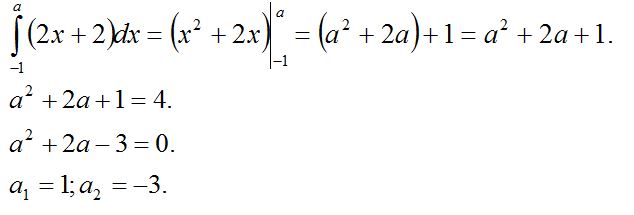
Үйге тапсырма
“Алгебра және анализ бастамалары, 11 сынып, А.Е.Әбілқасымова, 23-24 бет” 1. №42,43 (1,4)
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Тақырыбы: Анықталған интегралдың қасиеті
Тақырыбы: Анықталған интегралдың қасиеті
Сабақтың тақырыбы: «Анықталған интегралдың негізгі қасиеттері және оны есептеу»
Мақсаты
Білімділік: Студенттерге анықталған интеграл ұғымы мен қасиеттерін және интегралды есептеу үшін Ньютон-Лейбниц формуласын қолдану бойынша білік, дағдыларын қалыптастырып, білімдерін нақтылау.
Дамытушылық: интегралдарды есептеу кестелерін есте сақтау және оларды есептер шығаруда қолдана білуге дағдыландыру, логикалық ойлау қабілетін дамыту;
Тәрбиелік: Соңғы нәтижеге жету жолында табандылық пен жігерлілік көрсете білуге, өзін-өзі бағалай білуге тәрбиелеу.
Түрі: Жаңа сабақты меңгерту
Оқыту әдісі: Түсіндіру, сұрақ-жауап, жүйелеу, есеп шығарту
Әдістемелік қамтамасыз етілуі:
Көрнекіліктер: Таратпа материалдары, слайдтар, плакаттар.ОТҚ: Интерактивті тақта
Пән аралық байланыс: Физика, информатика
Сабақ құрылымы мен мазмұны
І. Ұйымдастыру кезеңі:
1. Түгелдеу, сабаққа дайындықты бақылай отырып, зейінін сабаққа аудару.
2. Өткен білімдерге сүйене отырып, оқу әрекетін дамыту
ІІ. Үй тапсырмасын сұрау: Интегралдарды есептеудің негізгі әдістері.
![]() Анықтама: Берілген аралықтағы F(х) функциясының
алғашқы функциясы осы
аралықтағы f(х) функциясының анықталмаған интегралы деп
аталады.
Анықтама: Берілген аралықтағы F(х) функциясының
алғашқы функциясы осы
аралықтағы f(х) функциясының анықталмаған интегралы деп
аталады.
Белгіленуі: ![]() икстен эф де икс функциясының анықталмаған
интегралы деп оқылады)
икстен эф де икс функциясының анықталмаған
интегралы деп оқылады)
Анықтамаға
сәйкес: ![]()
ІІІ. Жаңа сабақ:
1. F(b) - F(a) айырмасын y=f(x) функциясының [a;b] кесіндісіндегі анықталған интегралы деп атайды.
![]() Мұндағы a және b сандары интегралдау шектері:
a – төменгі шегі, ал b – жоғарғы
шегі.
Мұндағы a және b сандары интегралдау шектері:
a – төменгі шегі, ал b – жоғарғы
шегі.
Анықталған интегралдың негiзгi қасиеттерi.
Берiлген анықталған интегралдың бар болу шарты орындалады деп есептейiк.
10. Тұрақты санды анықталған интеграл белгiсiнiң алдына шығаруға болады:
 мұнда k=const .
мұнда k=const .
20. Бiрнеше функциялар қосындысының анықталған
интегралы қосылғыштарының анықталған интегралдарының қосындысына
тең: 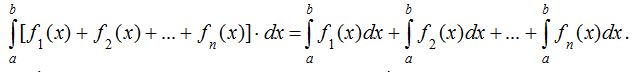 .
.
Осы екi қасиет интегралдың сызықтық қасиетi деп аталады.
30. Егер [a;b] аралығын [a;c] және [c;b] аралықтарына бөлсек, онда
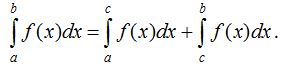
40. Егер интегралдың жоғарғы шегi мен төменгi шегiнiң орындарын ауыстырсақ, онда оның таңбасы өзгередi:
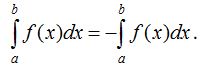 50. Жоғарғы шегi мен төменгi шегi тең болатын
интеграл 0-ге тең
50. Жоғарғы шегi мен төменгi шегi тең болатын
интеграл 0-ге тең
![]() 60. Егер [a;b] аралығындағы х айнымалысының барлық мәндерi
үшiн
60. Егер [a;b] аралығындағы х айнымалысының барлық мәндерi
үшiн ![]() болса, онда
болса, онда
![]()
70. Егер [a;b] аралығындағы х айнымалысының барлық
мәндерi үшiн ![]() болса, онда
болса, онда
![]() .
.
80. Егер [a;b] аралығында функциясының ең үлкен және ең
кiшi мәндерi сәйкес М және m сандары болса,
онда
![]()
2. Ньютон-Лейбниц формуласы.
Ньютон Исаак (1643-1727) - ағылшын астрономы, физигі, әрі математигі. ХVII ғасырда дифференциалдық және интегралдық есептеулерді математикалық практикаға енгізді.
![]() Туындыны дифференциалдау деп атаған және
интеграл белгісін енгізген ЛейбницГотфрид Вильгельм Лейбниц
(1646-1716 жж.) – XVII ғасырдағы неміс рухы туғызған терең де
жан-жақты дамыған философ. Екінші жағынан, ол - математик,
физик, саясаткер, тарихшы,
құқықтанушы.
Туындыны дифференциалдау деп атаған және
интеграл белгісін енгізген ЛейбницГотфрид Вильгельм Лейбниц
(1646-1716 жж.) – XVII ғасырдағы неміс рухы туғызған терең де
жан-жақты дамыған философ. Екінші жағынан, ол - математик,
физик, саясаткер, тарихшы,
құқықтанушы.
![]() Теорема. Егер F(X)
функциясы [a;b] аралығына f(x) функциясының алғашқы
функциясының бiрi болса, онда
Теорема. Егер F(X)
функциясы [a;b] аралығына f(x) функциясының алғашқы
функциясының бiрi болса, онда
(5)Бұл теңдiк Ньютон-Лейбниц формуласы деп аталады. Анықталған интегралдарға байланысты мысалдар келтіру.
1-есеп. ![]() .
.
Интеграл астындағы функцияның алғашқы функциясын бөлiктеп интегралдау әдiсiмен тауып және оған Ньютон-Лейбниц формуласын қолдансақ,
![]()
2-есеп. ![]() .
.
Бөліктеп интегралдау формуласы
бойынша ![]() болса, онда
болса, онда
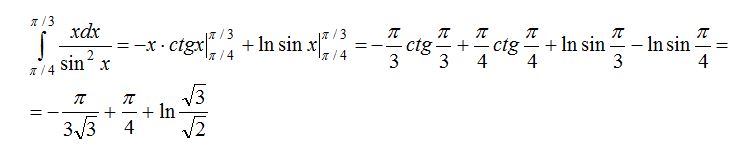
3-есеп.
![]()
4-есеп.
ІV. Жаңа
сабақты бекіту: 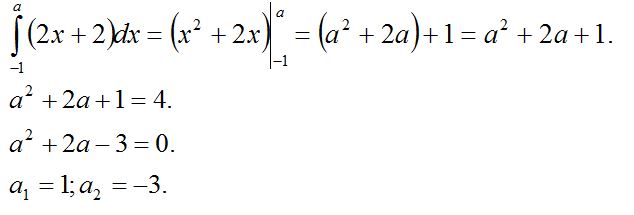
Үйге тапсырма
“Алгебра және анализ бастамалары, 11 сынып, А.Е.Әбілқасымова, 23-24 бет” 1. №42,43 (1,4)

шағым қалдыра аласыз















