Мазмұны:
Кіріспе..............................................................................................................3
-
Тейлор формуласы және қатары..............................................................4
-
Коши формуласындағы қалдық мүше................................................7
-
Лагранж формуласындағы қалдық мүше.............................................12
-
Шлемимильх-Рош түріндегі қалдық мүше..........................................15
-
Тригонометриялық функциялардың формуласының қалдық мүшелері................................................................................................17
-
Есептер..................................................................................................20
Қорытынды........................................................................................................22
Пайдаланылған әдебиеттер...............................................................................23
Кіріспе
Тейлор қатары – функцияны көрсеткішті функциялар шексіз қосындысы ретінде жазу. Тейлор қатарының дербес қосындылары болып Тейлор көпмүшелігі саналады. Rn(x)=f(x)-Sn(x) Тейлор қатарының қалдық мүшесі, мұндағы Sn(x) – Тейлор қатарының алғашқы n+1 мүшесінің қосындысы. болғанда Тейлор қатары f(x) функциясына жинақты болады, яғни формуласы шығады. Бұл формуланы 1715 жылы ағылшын математигі Б.Тейлор (1685 – 1731) тапқан, х0=0 болған кезде Маклорен қатары шығады. Осыған сүйене отырып, негізгі элементар функциялардың Тейлор қатарына жіктелуін жазуға болады.
Қазіргі ғылым мен техникада математикалық зерттеулер, модельдер, жобалар өте үлкен роль атқарады. Ол қазіргі ақпараттар жүйесінің дамуына тікелей байланысты, демек математикалық нақты сандар шешімін табуға табысты қолдану мүмкіншілігін кеңейтеді. Математика фундаменталды пән, одан дәріс беру төменгі жағдайды арастырады: а) ойдың логикалық және алгоритмдік дамуын; ә)негізгі зерттеу әдістерін меңгеру және математикалық есептердің шешімдерін таба білу; б) математикалық негізгі сандық әдістерін меңгеру және оны компьютерд орындау; в) математикалық білімді өз бетінше ұғып алуға еңбектену, қолданбалы нженерлік және экономикалық есептерге талдау жүргізу. Математиканың жалпы курсы дәстүрлі мамандар үшін оқу жоспары ойынша арнайы және жалпы техникалық пәндерді табысты оқытуға маңызды мәні бар инженерлер білімдерінің математикалық фундаментін қалайды.
1. Тейлор формуласы және қатары
![]()
![]() нүктесі төңірегінде шексіз дифференциалдана
алатын функция болсын. Формальды қатар
нүктесі төңірегінде шексіз дифференциалдана
алатын функция болсын. Формальды қатар
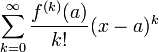
![]() функциясының
функциясының ![]() нүктесіндегі Тейлор қатары деп
аталады.
нүктесіндегі Тейлор қатары деп
аталады.
Тейлор формуласы
Теорема:
-

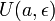
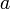 нүктесінің белгілі төңірегінде
нүктесінің белгілі төңірегінде 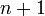 туындысы болсын
туындысы болсын -
Пусть
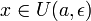
-
Пусть
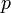 — кез келген оң
сан,
— кез келген оң
сан,
онда: ![]() үшін
үшін ![]() нүктесі
нүктесі ![]() немесе
немесе ![]() болғанда
болғанда ![]() :
:
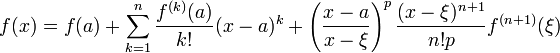 (1)
(1)
Кейбір функциялар үшін Маклорен қатарлары
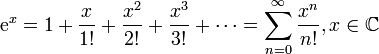
Натурал логарифм:
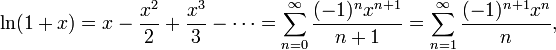 барлық
барлық ![]() үшін
үшін
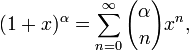 барлық
барлық ![]() үшін және барлық
үшін және барлық
![]() комплекс ан үшін,
мұндағы
комплекс ан үшін,
мұндағы
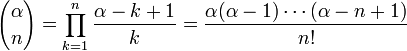
Жекеше түрі:
![]() барлық
барлық ![]() үшін
үшін
![]() барлық
барлық ![]() үшін
үшін
-
Шекті геометриялық қатар:
![]() барлық
барлық ![]() үшін
үшін
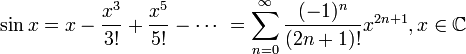
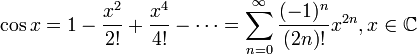
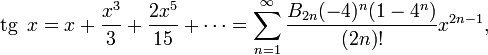 барлық
барлық
![]() үшін, мұндағы
үшін, мұндағы ![]() —
Бернулли
сандары
—
Бернулли
сандары
![]() барлық
барлық ![]()
![]() барлық
барлық ![]() үшін
үшін
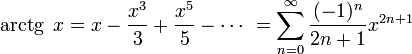 барлық
барлық ![]() үшін
үшін
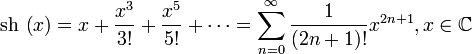
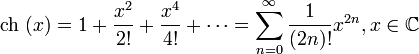
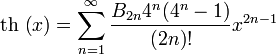 барлық
барлық ![]() үшін
үшін
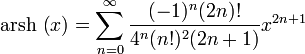 барлық
барлық ![]() үшін
үшін
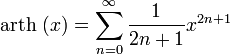 барлық
барлық ![]() үшін
үшін
Тейлор формуласы бойынша
![]()
![]()
 , (2)
, (2)
мұнда ![]() .
.
(1) теңдігін (2.) теңдікке қойсақ, онда
![]()

 . (3)
. (3)
-
теңдігінің оң жағы мен сол жағын салыстыру арқылы мына теңдеулер жүйесін аламыз:
 (4)
(4)
Егер ![]() болса, онда (4)
теңдеулер жүйесінің бір ғана шешуі бар , себебі оның матрицасының
анықтауышы - Вандермонд анықтауышы. Егер
болса, онда (4)
теңдеулер жүйесінің бір ғана шешуі бар , себебі оның матрицасының
анықтауышы - Вандермонд анықтауышы. Егер ![]() болса, онда
болса, онда
![]() коэффиценттерін әртүрлі жолдармен анықтауға
болады.
коэффиценттерін әртүрлі жолдармен анықтауға
болады.
Мысалы: Егер ![]() ,
, ![]() ,
, ![]() ,
, ![]() болса,
болса, ![]() .
.
Енді (4) жүйесін қолдансақ, онда
![]()
![]() болады да
,
болады да
,
![]()
формуласын аламыз.
Ал ![]()
деп ұйғарсақ , онда (4)
жүйеден ![]()
![]() ,
, ![]() екенін табамыз және
екенін табамыз және
![]() екенін
көреміз.
екенін
көреміз.
Жалпы бұл әдіс бойынша
берілген ![]() операторын қалаған дәлдікпен жуықтауға болады .
операторын қалаған дәлдікпен жуықтауға болады .
-
Коши формуласындағы қалдық мүше
Айталық,
![]() функциясы
функциясы ![]() облысында
үзіліссіз және Липшитц шарттарын қанағаттандырсын,
яғни
облысында
үзіліссіз және Липшитц шарттарын қанағаттандырсын,
яғни
![]() (5)
(5)
теңсіздігі орындалсын,
онда ![]() жоғарыдан
шектелген, яғни
жоғарыдан
шектелген, яғни ![]() ,
және
,
және
![]()
![]() (6)
(6)
![]() (7)
(7)
есебінің бір ғана шешуі бар.
Енді осы шешуді табу
үшін (7)- ші интегралға тік төртбұрыш әдісін қолдану арқылы (6)
теңдіктен, ![]() торында
мына теңдікті аламыз:
торында
мына теңдікті аламыз:
![]() (8)
(8)
![]()
Осыдан ![]() кезде
0(һ) нөлге ұмтылыды деп шешсек,
онда
кезде
0(һ) нөлге ұмтылыды деп шешсек,
онда ![]()
деп белгілеу арқылы
![]() , (9)
, (9)
![]()
теңдіктерін аламыз.
-
теңдігін, әдетте, Эйлер әдісі деп атайды.
Енді ![]() кезде осы әдіс
бойынша табылған
кезде осы әдіс
бойынша табылған ![]() тізбегі (6)-(7) есебінің шешуіне жинақталатынын,
яғни
тізбегі (6)-(7) есебінің шешуіне жинақталатынын,
яғни
![]()
болатынын қарастырайық.
Ол үшін ![]() функциясын
функциясын ![]() нүктесінің кіші
аймағында Тэйлор қатарына жіктейміз:
нүктесінің кіші
аймағында Тэйлор қатарына жіктейміз:
![]()
Содан кейін осы теңдікті
пайдаланып ![]() мәнін есептейміз:
мәнін есептейміз:
 (10)
(10)
Мұнда (6) теңдеуіне
сәйкес ![]() болатыны есекерілген. Енді (10) өрнегінен (9) өрнегін шегерсек,
онда
болатыны есекерілген. Енді (10) өрнегінен (9) өрнегін шегерсек,
онда
![]()
Осыдан ![]() белгілеуін еңгізіп,
белгілеуін еңгізіп,
![]() әдіс
қаталігінің абсолют мәнін бағаласақ:
әдіс
қаталігінің абсолют мәнін бағаласақ:
![]()
Соңғы теңсіздікке
![]() - Липшитц
шартын пайдаланып:
- Липшитц
шартын пайдаланып:
![]() (11)
(11)
теңсіздігін аламыз,
мұндағы ![]()
Енді (11) теңсіздігін k-ның k=0, 1, ... мәндері үшін ашып жазсақ:

Эйлер әдісі үшін
![]() болғандықтан
болғандықтан

Ал ![]() кезде
кезде ![]() болатындықтан
болатындықтан
![]()
Демек, Эйлер әдісі
![]() кезінде (6) -
(7) есебінің дәл шешуіне жинақталады және оның жинақталу реті 1-ге
тең. Егер
кезінде (6) -
(7) есебінің дәл шешуіне жинақталады және оның жинақталу реті 1-ге
тең. Егер ![]() функциясының
функциясының
![]() кесіндісінде
екінші ретті туындысы жоғарыдан шектелген деп есептеп, (7)
–ші
интегралға
орта нүктелік тік төртбұрыш формуласын қолдансақ, онда (6)-шы формуладан
кесіндісінде
екінші ретті туындысы жоғарыдан шектелген деп есептеп, (7)
–ші
интегралға
орта нүктелік тік төртбұрыш формуласын қолдансақ, онда (6)-шы формуладан
![]() (12)
(12)
формуласын аламыз. Мұндағы  Енді
Енді ![]() мәнін
мәнін
![]() деп
жуықтап алатын
болсақ, онда (12) формуласынан
деп
жуықтап алатын
болсақ, онда (12) формуласынан
![]() (13)
(13)
формуласын аламыз. Яғни бұл әдістің есептеу алгоритімі мынадай болады:
![]() ,
(14)
,
(14)
![]() , (15)
, (15)
![]()
Енді берілген Коши
есебінің бір ғана шешуі бар, ![]() функциясы
функциясы ![]() бойынша Липшитц шартын қанағаттандырады және
бойынша Липшитц шартын қанағаттандырады және ![]() 3-ші ретке дейін
дифференциалданады деп есептеп, (14)-(15) айырымдық есептің шешуі
(4)-(5) есебінің шешуіне жинақталу дәлдігі
3-ші ретке дейін
дифференциалданады деп есептеп, (14)-(15) айырымдық есептің шешуі
(4)-(5) есебінің шешуіне жинақталу дәлдігі ![]() болатынын
көрсетейік.
болатынын
көрсетейік.
Ол үшін ![]() функциясын
функциясын ![]() нүктесінде Тейлор
қатарына жіктейік:
нүктесінде Тейлор
қатарына жіктейік:
 (16)
(16)
Енді ретімен ![]() десек,
онда
десек,
онда
![]() (17)
(17)
![]() (18)
(18)
формулаларын аламыз.
Егер (18) теңдігінен (17) теңдігін шегерсек, онда
![]() (19)
(19)
теңдігін аламыз. Мұндағы
![]() .
.
Енді (19) теңдігінен (15) теңдігін шегерсек, онда
![]() теңдігін
аламыз.
теңдігін
аламыз.
![]() белгілеулерін еңгізіп
және Липшитц шартын пайдалансақ, онда соңғы
теңдіктен
белгілеулерін еңгізіп
және Липшитц шартын пайдалансақ, онда соңғы
теңдіктен
 (20)
(20)
теңсіздігін аламыз. Ал мына теңдікті
 (21)
(21)
ескерсек, онда (20) теңсіздіктен
![]()
теңсіздігін аламыз.Осыдан
 (22)
(22)
теңсіздігін шығады.
Енді k-ның k=0,1,2,... мәндері үшін
![]()
![]()
. . . . . . . . . . . . . . . . .
![]()
теңсіздігін аламыз.
Мұндағы ![]()
Тордағы ![]() түйіні
түйіні ![]() түйіндік нүкте болып
қала береді деп есептесек,
түйіндік нүкте болып
қала береді деп есептесек, ![]() деп жазуға болады
және
деп жазуға болады
және ![]() екенін ескерсек, онда
екенін ескерсек, онда

Осыдан ![]() болғандықтан
(14)-(15) айырымдық есебінің шешуі (4)-(5) есебінің шешуіне
болғандықтан
(14)-(15) айырымдық есебінің шешуі (4)-(5) есебінің шешуіне
![]() дәлдікпен
жинақталады.
дәлдікпен
жинақталады.
-
Лагранж формуласындағы қалдық мүше
Лагранждың интерполяциялау формуласы.
-
кесіндісінде жататын
 нүктелері және осы нүктелерде
нүктелері және осы нүктелерде  функциясының
мәндері-
функциясының
мәндері-  берілген. Осы функцияны интерполяциялау үшін n дәрежелі
алгебралық көпмүшені
берілген. Осы функцияны интерполяциялау үшін n дәрежелі
алгебралық көпмүшені
 (23)
(23)
қолданамыз.
Мұндағы
![]() коэффициенттерін
коэффициенттерін
![]() болатындай етіп табу керек.
болатындай етіп табу керек.
Кез-келген
үзіліссіз ![]() функциясы үшін бұл есептің шешімі біреу ғана болады.
Себебі
функциясы үшін бұл есептің шешімі біреу ғана болады.
Себебі
 (24)
(24)
теңдеулер жүйесінің аңықтауышы нольден айырықша (Вандермонд аңықтауышы).
-
көпмүшесін,
 нүктелері бойынша
тұрғызылған,
нүктелері бойынша
тұрғызылған,  функциясын интерполяциялаушы көпмүше дейміз.
функциясын интерполяциялаушы көпмүше дейміз.
(24) теңдеулер жүйесінің шешімдерін әртүрлі жолмен табуға болады. Оның көп қолданатын түрлері Лагранж бен Ньютонның интерполяциялық көпмүшеліктері.
Лагранждың интерполяциялық көпмүшелігін
 (25)
(25)
түрінде қарастырамыз. (2.2) шартын ескере отырып,
 (26)
(26)
теңдігін аламыз.
Егер
![]() (27)
(27)
болса,
онда (2.4) шарты орындалады. ![]() дәрежелі көпмүше
болғандықтан
дәрежелі көпмүше
болғандықтан ![]() коэффициентін де n дәрежелі көпмүше ретінде іздеген
дұрыс.
коэффициентін де n дәрежелі көпмүше ретінде іздеген
дұрыс.
Атап
айтқанда ![]() көпмүшесін
көпмүшесін
![]() (28)
(28)
түрінде іздейміз.
![]() шартың ескере отырып, (28)
формуладан
шартың ескере отырып, (28)
формуладан
![]()
және
 (29)
(29)
формуласын табамыз. Сонымен Лагранж көпмүшесі толық былайша жазылады.
 .
(30)
.
(30)
Егер
 десек, онда
десек, онда 
Ал
![]()
Сондықтан Лагранж көпмүшесін былайша ықшамдап жазуға болады:
 (31)
(31)
Енді интерполяциялық Лагранж көпмүшесінің жіберетін қатесін қарастырайық.
-
функциясын
 көпмүшесімен
алмастырғанда жіберетін қатеміз
көпмүшесімен
алмастырғанда жіберетін қатеміз
![]() (32)
(32)
Кейде
![]() функциясын
Лагранж көпмүшесінің қалдығы деп те атайды.
функциясын
Лагранж көпмүшесінің қалдығы деп те атайды.
Кез-келген
![]() нүктесіндегі
қалдықты табу үшін мына көмекші функцияны
қарастырамыз:
нүктесіндегі
қалдықты табу үшін мына көмекші функцияны
қарастырамыз:
![]() ,
(33)
,
(33)
мұнда
![]() -тұрақты сан.
-тұрақты сан.
![]() санын
санын
![]() болатындай,
яғни
болатындай,
яғни
![]() (34)
(34)
деп алсақ,
онда ![]() ең
болмағанда
ең
болмағанда ![]() нүктеде нольге тең болады.
нүктеде нольге тең болады.
Енді
![]() функциясының
функциясының
![]() кесіндісінде
үзіліссіз
кесіндісінде
үзіліссіз ![]() ретті туындысы бар болсын. Сонда
ретті туындысы бар болсын. Сонда ![]() , Роль теоремасы
бойынша,
, Роль теоремасы
бойынша, ![]() кесіндісінде ең болмағанда n+1 нүктеде нөлге тең, ал
кесіндісінде ең болмағанда n+1 нүктеде нөлге тең, ал ![]() -ењ , болмағанда n
нүктеде нөлге тең, т.с.
-ењ , болмағанда n
нүктеде нөлге тең, т.с. ![]() ең болмағанда бір
нүктеде нөлге тең болады. Сонымен
ең болмағанда бір
нүктеде нөлге тең болады. Сонымен ![]() табылады да
табылады да
![]() болады.
болады.
Ал
![]() болғандықтан
болғандықтан
![]() .
(35)
.
(35)
(34) және (35) формулаларды ескере отырып,
![]() (36)
(36)
формуласын аламыз.
Осыдан
![]() функциясын
жоғарыдан бағалау арқылы
функциясын
жоғарыдан бағалау арқылы
![]() .
(37)
.
(37)
теңсіздігін аламыз, мұндағы ![]() .
.
Егер
![]() дәрежесі n-нен
үлкен емес көпмүше болса, онда
дәрежесі n-нен
үлкен емес көпмүше болса, онда ![]()
Сондықтан ![]() .
.
4.Шлемимильх-Рош түріндегі қалдық мүше
![]() маңайында,
маңайында,
![]() нүктесін қоса
алғанда,
нүктесін қоса
алғанда, ![]() функциясы
берілсін.
функциясы
берілсін. ![]() нүктесінде
нүктесінде ![]() аргументіне
аргументіне ![]() өсімшесін
береміз (оң немесе теріс). Онда
өсімшесін
береміз (оң немесе теріс). Онда ![]() .
.
Егер ![]() шегі табылса, онда
оны
шегі табылса, онда
оны ![]() нүктесіндегі
нүктесіндегі
![]() функциясының туындысы деп
айтамыз, немесе
функциясының туындысы деп
айтамыз, немесе ![]() функциясы
функциясы ![]() нүктесінде дифференциалданады деп айтамыз және былай
белгілейміз:
нүктесінде дифференциалданады деп айтамыз және былай
белгілейміз:
![]() яғни,
яғни,
![]() (38)
(38)
Егер (1)-де
![]() және
және ![]() болса, онда
(1)-ді
болса, онда
(1)-ді ![]() нүктесіндегі
нүктесіндегі ![]() оң жақ
туындысы [
оң жақ
туындысы [![]() сол жақ
туындысы] деп атаймыз. Егер
сол жақ
туындысы] деп атаймыз. Егер ![]() және
және ![]() болса,
онда
болса,
онда ![]() .
.
![]() функциясын
функциясын
![]() кесіндісінде
дифференциалданады деп айтамыз, егер оның
кесіндісінде
дифференциалданады деп айтамыз, егер оның ![]() аралығындағы әрбір нүктеде
туындысы бар болса, ал
аралығындағы әрбір нүктеде
туындысы бар болса, ал ![]() және
және ![]() ұштарында
сәйкесінше
ұштарында
сәйкесінше ![]() және
және![]() табылса.
табылса.
![]() облысында
дифференциалданатын
функциялардың класын
облысында
дифференциалданатын
функциялардың класын ![]() деп
белгілейміз
деп
белгілейміз
а) Механикалық. ![]() -
-
![]() нүктесінің қозғалу заңы
болсын.
нүктесінің қозғалу заңы
болсын.
![]() нүктесінің
нүктесінің
![]() -дан
-дан ![]() -ға дейінгі аралығындағы
қозғалысын қарастыралық. Онда
-ға дейінгі аралығындағы
қозғалысын қарастыралық. Онда ![]() ал
ал ![]() - орташа жылдамдық
. Егер
- орташа жылдамдық
. Егер
![]()
шегі табылса, онда
жолдың уақыт бойынша туындысы ![]() нүктесінің
нүктесінің ![]() уақыт
аралығындағы қозғалысының жылдамдығына тең.
уақыт
аралығындағы қозғалысының жылдамдығына тең.
|
|
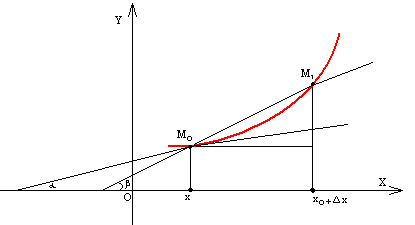
б) Геометриялық. |
![]() нүктесі қисықтың
бойымен
нүктесі қисықтың
бойымен ![]() нүктесіне
кез келген жағынан шексіз жақындағанда
нүктесіне
кез келген жағынан шексіз жақындағанда ![]() қимасының
қимасының
![]() шектелген орны табылса,
онда
шектелген орны табылса,
онда ![]()
![]() қисығына
қисығына ![]() нүктесінде жүргізілген жанама деп
аталады.
нүктесінде жүргізілген жанама деп
аталады.
Е гер қисықтың жанамасы бар болса, онда
![]() .
.
Бұдан,
![]() нүктесінде дифференциалданатын
функцияның осы нүктеде бұрыштық коэффиценті
нүктесінде дифференциалданатын
функцияның осы нүктеде бұрыштық коэффиценті
![]() болатын жанамасы бар
болады.
болатын жанамасы бар
болады.
Мысал
1. ![]() функциясының
функциясының ![]() нүктесіндегі жанамасының теңдеуін жаз.
нүктесіндегі жанамасының теңдеуін жаз.
а) ![]() .
. ![]() болғандықтан, жанаманың
теңдеуі
болғандықтан, жанаманың
теңдеуі ![]() .
. ![]() -ті
табалық:
-ті
табалық:

|
в) |
б)
|
в)
|
Оң жақ жанамасы
![]() болады, яғни
болады, яғни
![]() , ал сол жағынан
жанамасы
, ал сол жағынан
жанамасы ![]() ,
яғни
,
яғни ![]() . Бұдан,
х=
. Бұдан,
х=![]() нүктесінде берілген
нүктесінде берілген ![]() функцияның туындысы
табылмайды, бұл функция х=
функцияның туындысы
табылмайды, бұл функция х=![]() нүктесінде үзіліссіз
болғанның өзінде.
нүктесінде үзіліссіз
болғанның өзінде.
![]() болатын
нүктелер бұрыштық деп аталады.
болатын
нүктелер бұрыштық деп аталады.
5.Тригонометриялық функциялардың формуласының қалдық мүшелері
![]() ;
; ![]()
функциялары орындалады және барлық тригонометриялық формулалар орындалады:
![]() ;
;
![]()
Гиперболалық функциялар нақты аргументтің функциялары тәрізді анықталады:
![]() ;
;
![]() .
.
Бұлар тригонометриялық функциялармен былай байланысады:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
50. ![]() функциялары
сәйкес
функциялары
сәйкес ![]() ,
, ![]() ,
, ![]() ,
, ![]() функцияларына кері функциялар ретінде анықталады, және де
олардың бәрі де көп мәнді функциялар.
функцияларына кері функциялар ретінде анықталады, және де
олардың бәрі де көп мәнді функциялар.
Дәлелдеңдер:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Z
облысының
бір мәнді ![]() функциясын қарастырамыз.
функциясын қарастырамыз.
Анықтама. Егер
![]()
![]() (39)
(39)
ақырлы шегі бар болса, онда ол
шек ![]() функциясының туындысы деп
аталады және былай белгіленеді:
функциясының туындысы деп
аталады және былай белгіленеді:
![]()
Бұл шек ∆ z -тің нөлге қалай ұмтылғанына тәуелсіз.
Z
облысының ![]() нүктесінде үзіліссіз туындысы бар
нүктесінде үзіліссіз туындысы бар ![]() функциясы осы облыстың
аналитикалық функциясы деп аталады.
функциясы осы облыстың
аналитикалық функциясы деп аталады.
Шектің қасиеттері негізінде туындының негізгі қасиеттері шығады.
Қасиеттері:
-
 ,
, -
 ,
, -
 .
. -
Егер күрделі функция
 түрінде
берілсе, мұнда
түрінде
берілсе, мұнда  -
комплекс
айнымалы функция, және туындылары
-
комплекс
айнымалы функция, және туындылары  мен
мен  бар болса,
онда мына
формула орынды:
бар болса,
онда мына
формула орынды:
![]() .
.
![]() , мұндағы
n – бүтін сан. Туындысын табамыз,
ол үшін функцияның өсімшесін анықтаймыз:
, мұндағы
n – бүтін сан. Туындысын табамыз,
ол үшін функцияның өсімшесін анықтаймыз:
![]()
![]() .
.
Сонда туынды мынаған тең:
![]()
Көрсеткіштік және тригонометриялық функцияларды қарастырамыз:
![]() ;
;
![]() ;
;
![]() .
.
Бұл қатарлар
z-ң кез келген мәндерінде
жинақты, ![]() . Осының негізінде бұл
қатарларды дифференциалдауға болады.
. Осының негізінде бұл
қатарларды дифференциалдауға болады.
![]() .
.
Оң бөлігі Маклорен қатарына
дәл келеді ( ![]() -ң
жіктелуі).)
-ң
жіктелуі).)
![]()
![]() .
.
Осы тәрізді қалған қатарларды да дифференциалдаймыз:
3.
![]()
![]() ; яғни
; яғни
![]() .
.
4.
![]()
![]() ; яғни
; яғни
![]() .
.
5.
![]() .
.
6.
![]() .
.
![]() .
.
7.![]() ,
,
![]() ;
; ![]()
Қорытынды
Айталық,
![]() (1)
(1)
есебі берілсін. Бұл
есепті шешу үшін ![]() торын
алайық та осы торда (1) есебін шешу үшін мынандай айырымдық есеп
қоялық.
торын
алайық та осы торда (1) есебін шешу үшін мынандай айырымдық есеп
қоялық.

Мұндағы ![]() болуы мүмкін
.
болуы мүмкін
.
Есептің жуық шешуі мына рекурентті формула арқылы табылады.

Егер ![]() нөлге ұмтылғанда
нөлге ұмтылғанда
![]() нөлге
ұмтылса, онда (2 )-(3) есебінің шешуі (3)-(4) есебінің шешуіне
жинақталады дейміз. Егер жеткілікті аз шама
нөлге
ұмтылса, онда (2 )-(3) есебінің шешуі (3)-(4) есебінің шешуіне
жинақталады дейміз. Егер жеткілікті аз шама ![]() табылып, және
табылып, және
![]() болғанда
болғанда
![]() бағалауы
орындалса, онда айырымдық схеманың шешуі
бағалауы
орындалса, онда айырымдық схеманың шешуі ![]() жылдамдықпен (3)-(4)
есебінің шешуіне жинақталады дейді немесе айырымдық схеманың
дәлдігі
жылдамдықпен (3)-(4)
есебінің шешуіне жинақталады дейді немесе айырымдық схеманың
дәлдігі ![]() -ге
тең дейді. Мұндағы
-ге
тең дейді. Мұндағы ![]()
![]() -тан тәуелсіз сан.
-тан тәуелсіз сан.
Кейде (3)-(4) есебін
![]() функциясының
шекаралық (шеткі) нүктелердегі белгілі мәндерін теңдіктің оң жағына
шығару арқылы,
функциясының
шекаралық (шеткі) нүктелердегі белгілі мәндерін теңдіктің оң жағына
шығару арқылы,
![]() (2)
(2)
түрінде жазуға болады. Бұл жағдайда айырымдық схеманың жуықтау қателігін былайша жазады:
![]()
Ал ![]()
теңдігін
![]() ретті жуықтау
қателігі (аппроксимациясы) дейміз.
ретті жуықтау
қателігі (аппроксимациясы) дейміз.
Пайдаланылған әдебиеттер
-
Темірғалиев Н. “Математикалық анализ” - Алматы; Мектеп 1987, 288 бет.
-
Ибрашев Х. И., Еркеғұлов Ш. Т. “Математикалық анализ курсы.” – Алматы; Мектеп 2 том, 1970, 527 бет.
-
Кудрявцев А. Д. “Краткий курс математического анализа.” – Москва, Наука, 1989, 735 бет.
-
Фихтенгольц Г. М. “Основы математического анализа.” – Москва, Наука, 1968, ІІ том.
-
“Задачник по курсу математического анализа.” Под редак. Н. Я. Виленкина, Москва, 1971, ч-2.
-
Асинкин А. Г., Бутинов Е. И., Кондратьев А. С. “Краткий физико-математический справочник.” Москва, 1990, 368 стр.
-
Демидович Б. П. “Сборник задачи и упражнений по математическому анализу.” Москва, Наука, 1977.
-
“Егемен Қазақстан” 16 қазан, 2004 жыл.
-
А. Г. Аленкин, Е. И. Бутиков, А. С. Кондратьев. «Краткий физико-математический справочник» М., 1990 г.
-
Шойынбеков К. Д., Әбілқасымов А. Е., Есенова М. И., Тұрлыханова М. А. «Анализ бастамалары» оқу құралы. Алматы, 2002ж., 320 бет.
-
Данко П. Е., Попов А. Г., Кожевникова Т. Я. «Высшая математика в упражнениях и задачах» учебное пособие для студентов вузов. М., Высш.шк., 1926г.
Есептер
Лагранж интерполяциялық көпмүшесін табыңыз:
A) ![]()
B) ![]() C)
C) ![]()
D) ![]() E)
E) ![]()
4. ![]() Берiлген САТЖ үшін Гаусс
әдісінің бірінші қадамында қандай формула
алынады?
Берiлген САТЖ үшін Гаусс
әдісінің бірінші қадамында қандай формула
алынады?
№2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Тейло қатары
бойынша
Тейло қатары
бойынша
№3

![]()
![]()
![]()

Тейлор қатарына жіктеу:
№1 ![]() ч дәрежесі бойынша
жіктеңіз
ч дәрежесі бойынша
жіктеңіз
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
24
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Тақырыбы: Тейлор формуласы бойынша есептеу
Тақырыбы: Тейлор формуласы бойынша есептеу
Мазмұны:
Кіріспе..............................................................................................................3
-
Тейлор формуласы және қатары..............................................................4
-
Коши формуласындағы қалдық мүше................................................7
-
Лагранж формуласындағы қалдық мүше.............................................12
-
Шлемимильх-Рош түріндегі қалдық мүше..........................................15
-
Тригонометриялық функциялардың формуласының қалдық мүшелері................................................................................................17
-
Есептер..................................................................................................20
Қорытынды........................................................................................................22
Пайдаланылған әдебиеттер...............................................................................23
Кіріспе
Тейлор қатары – функцияны көрсеткішті функциялар шексіз қосындысы ретінде жазу. Тейлор қатарының дербес қосындылары болып Тейлор көпмүшелігі саналады. Rn(x)=f(x)-Sn(x) Тейлор қатарының қалдық мүшесі, мұндағы Sn(x) – Тейлор қатарының алғашқы n+1 мүшесінің қосындысы. болғанда Тейлор қатары f(x) функциясына жинақты болады, яғни формуласы шығады. Бұл формуланы 1715 жылы ағылшын математигі Б.Тейлор (1685 – 1731) тапқан, х0=0 болған кезде Маклорен қатары шығады. Осыған сүйене отырып, негізгі элементар функциялардың Тейлор қатарына жіктелуін жазуға болады.
Қазіргі ғылым мен техникада математикалық зерттеулер, модельдер, жобалар өте үлкен роль атқарады. Ол қазіргі ақпараттар жүйесінің дамуына тікелей байланысты, демек математикалық нақты сандар шешімін табуға табысты қолдану мүмкіншілігін кеңейтеді. Математика фундаменталды пән, одан дәріс беру төменгі жағдайды арастырады: а) ойдың логикалық және алгоритмдік дамуын; ә)негізгі зерттеу әдістерін меңгеру және математикалық есептердің шешімдерін таба білу; б) математикалық негізгі сандық әдістерін меңгеру және оны компьютерд орындау; в) математикалық білімді өз бетінше ұғып алуға еңбектену, қолданбалы нженерлік және экономикалық есептерге талдау жүргізу. Математиканың жалпы курсы дәстүрлі мамандар үшін оқу жоспары ойынша арнайы және жалпы техникалық пәндерді табысты оқытуға маңызды мәні бар инженерлер білімдерінің математикалық фундаментін қалайды.
1. Тейлор формуласы және қатары
![]()
![]() нүктесі төңірегінде шексіз дифференциалдана
алатын функция болсын. Формальды қатар
нүктесі төңірегінде шексіз дифференциалдана
алатын функция болсын. Формальды қатар
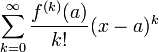
![]() функциясының
функциясының ![]() нүктесіндегі Тейлор қатары деп
аталады.
нүктесіндегі Тейлор қатары деп
аталады.
Тейлор формуласы
Теорема:
-

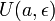
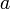 нүктесінің белгілі төңірегінде
нүктесінің белгілі төңірегінде 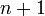 туындысы болсын
туындысы болсын -
Пусть
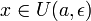
-
Пусть
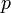 — кез келген оң
сан,
— кез келген оң
сан,
онда: ![]() үшін
үшін ![]() нүктесі
нүктесі ![]() немесе
немесе ![]() болғанда
болғанда ![]() :
:
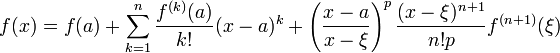 (1)
(1)
Кейбір функциялар үшін Маклорен қатарлары
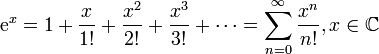
Натурал логарифм:
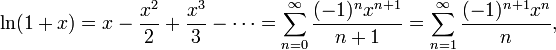 барлық
барлық ![]() үшін
үшін
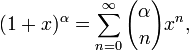 барлық
барлық ![]() үшін және барлық
үшін және барлық
![]() комплекс ан үшін,
мұндағы
комплекс ан үшін,
мұндағы
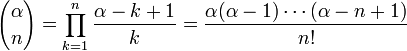
Жекеше түрі:
![]() барлық
барлық ![]() үшін
үшін
![]() барлық
барлық ![]() үшін
үшін
-
Шекті геометриялық қатар:
![]() барлық
барлық ![]() үшін
үшін
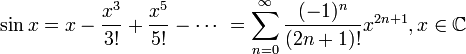
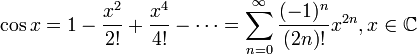
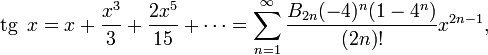 барлық
барлық
![]() үшін, мұндағы
үшін, мұндағы ![]() —
Бернулли
сандары
—
Бернулли
сандары
![]() барлық
барлық ![]()
![]() барлық
барлық ![]() үшін
үшін
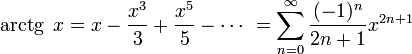 барлық
барлық ![]() үшін
үшін
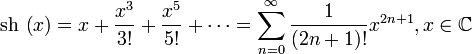
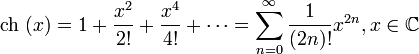
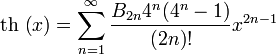 барлық
барлық ![]() үшін
үшін
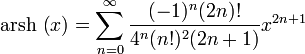 барлық
барлық ![]() үшін
үшін
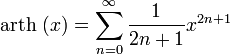 барлық
барлық ![]() үшін
үшін
Тейлор формуласы бойынша
![]()
![]()
 , (2)
, (2)
мұнда ![]() .
.
(1) теңдігін (2.) теңдікке қойсақ, онда
![]()

 . (3)
. (3)
-
теңдігінің оң жағы мен сол жағын салыстыру арқылы мына теңдеулер жүйесін аламыз:
 (4)
(4)
Егер ![]() болса, онда (4)
теңдеулер жүйесінің бір ғана шешуі бар , себебі оның матрицасының
анықтауышы - Вандермонд анықтауышы. Егер
болса, онда (4)
теңдеулер жүйесінің бір ғана шешуі бар , себебі оның матрицасының
анықтауышы - Вандермонд анықтауышы. Егер ![]() болса, онда
болса, онда
![]() коэффиценттерін әртүрлі жолдармен анықтауға
болады.
коэффиценттерін әртүрлі жолдармен анықтауға
болады.
Мысалы: Егер ![]() ,
, ![]() ,
, ![]() ,
, ![]() болса,
болса, ![]() .
.
Енді (4) жүйесін қолдансақ, онда
![]()
![]() болады да
,
болады да
,
![]()
формуласын аламыз.
Ал ![]()
деп ұйғарсақ , онда (4)
жүйеден ![]()
![]() ,
, ![]() екенін табамыз және
екенін табамыз және
![]() екенін
көреміз.
екенін
көреміз.
Жалпы бұл әдіс бойынша
берілген ![]() операторын қалаған дәлдікпен жуықтауға болады .
операторын қалаған дәлдікпен жуықтауға болады .
-
Коши формуласындағы қалдық мүше
Айталық,
![]() функциясы
функциясы ![]() облысында
үзіліссіз және Липшитц шарттарын қанағаттандырсын,
яғни
облысында
үзіліссіз және Липшитц шарттарын қанағаттандырсын,
яғни
![]() (5)
(5)
теңсіздігі орындалсын,
онда ![]() жоғарыдан
шектелген, яғни
жоғарыдан
шектелген, яғни ![]() ,
және
,
және
![]()
![]() (6)
(6)
![]() (7)
(7)
есебінің бір ғана шешуі бар.
Енді осы шешуді табу
үшін (7)- ші интегралға тік төртбұрыш әдісін қолдану арқылы (6)
теңдіктен, ![]() торында
мына теңдікті аламыз:
торында
мына теңдікті аламыз:
![]() (8)
(8)
![]()
Осыдан ![]() кезде
0(һ) нөлге ұмтылыды деп шешсек,
онда
кезде
0(һ) нөлге ұмтылыды деп шешсек,
онда ![]()
деп белгілеу арқылы
![]() , (9)
, (9)
![]()
теңдіктерін аламыз.
-
теңдігін, әдетте, Эйлер әдісі деп атайды.
Енді ![]() кезде осы әдіс
бойынша табылған
кезде осы әдіс
бойынша табылған ![]() тізбегі (6)-(7) есебінің шешуіне жинақталатынын,
яғни
тізбегі (6)-(7) есебінің шешуіне жинақталатынын,
яғни
![]()
болатынын қарастырайық.
Ол үшін ![]() функциясын
функциясын ![]() нүктесінің кіші
аймағында Тэйлор қатарына жіктейміз:
нүктесінің кіші
аймағында Тэйлор қатарына жіктейміз:
![]()
Содан кейін осы теңдікті
пайдаланып ![]() мәнін есептейміз:
мәнін есептейміз:
 (10)
(10)
Мұнда (6) теңдеуіне
сәйкес ![]() болатыны есекерілген. Енді (10) өрнегінен (9) өрнегін шегерсек,
онда
болатыны есекерілген. Енді (10) өрнегінен (9) өрнегін шегерсек,
онда
![]()
Осыдан ![]() белгілеуін еңгізіп,
белгілеуін еңгізіп,
![]() әдіс
қаталігінің абсолют мәнін бағаласақ:
әдіс
қаталігінің абсолют мәнін бағаласақ:
![]()
Соңғы теңсіздікке
![]() - Липшитц
шартын пайдаланып:
- Липшитц
шартын пайдаланып:
![]() (11)
(11)
теңсіздігін аламыз,
мұндағы ![]()
Енді (11) теңсіздігін k-ның k=0, 1, ... мәндері үшін ашып жазсақ:

Эйлер әдісі үшін
![]() болғандықтан
болғандықтан

Ал ![]() кезде
кезде ![]() болатындықтан
болатындықтан
![]()
Демек, Эйлер әдісі
![]() кезінде (6) -
(7) есебінің дәл шешуіне жинақталады және оның жинақталу реті 1-ге
тең. Егер
кезінде (6) -
(7) есебінің дәл шешуіне жинақталады және оның жинақталу реті 1-ге
тең. Егер ![]() функциясының
функциясының
![]() кесіндісінде
екінші ретті туындысы жоғарыдан шектелген деп есептеп, (7)
–ші
интегралға
орта нүктелік тік төртбұрыш формуласын қолдансақ, онда (6)-шы формуладан
кесіндісінде
екінші ретті туындысы жоғарыдан шектелген деп есептеп, (7)
–ші
интегралға
орта нүктелік тік төртбұрыш формуласын қолдансақ, онда (6)-шы формуладан
![]() (12)
(12)
формуласын аламыз. Мұндағы  Енді
Енді ![]() мәнін
мәнін
![]() деп
жуықтап алатын
болсақ, онда (12) формуласынан
деп
жуықтап алатын
болсақ, онда (12) формуласынан
![]() (13)
(13)
формуласын аламыз. Яғни бұл әдістің есептеу алгоритімі мынадай болады:
![]() ,
(14)
,
(14)
![]() , (15)
, (15)
![]()
Енді берілген Коши
есебінің бір ғана шешуі бар, ![]() функциясы
функциясы ![]() бойынша Липшитц шартын қанағаттандырады және
бойынша Липшитц шартын қанағаттандырады және ![]() 3-ші ретке дейін
дифференциалданады деп есептеп, (14)-(15) айырымдық есептің шешуі
(4)-(5) есебінің шешуіне жинақталу дәлдігі
3-ші ретке дейін
дифференциалданады деп есептеп, (14)-(15) айырымдық есептің шешуі
(4)-(5) есебінің шешуіне жинақталу дәлдігі ![]() болатынын
көрсетейік.
болатынын
көрсетейік.
Ол үшін ![]() функциясын
функциясын ![]() нүктесінде Тейлор
қатарына жіктейік:
нүктесінде Тейлор
қатарына жіктейік:
 (16)
(16)
Енді ретімен ![]() десек,
онда
десек,
онда
![]() (17)
(17)
![]() (18)
(18)
формулаларын аламыз.
Егер (18) теңдігінен (17) теңдігін шегерсек, онда
![]() (19)
(19)
теңдігін аламыз. Мұндағы
![]() .
.
Енді (19) теңдігінен (15) теңдігін шегерсек, онда
![]() теңдігін
аламыз.
теңдігін
аламыз.
![]() белгілеулерін еңгізіп
және Липшитц шартын пайдалансақ, онда соңғы
теңдіктен
белгілеулерін еңгізіп
және Липшитц шартын пайдалансақ, онда соңғы
теңдіктен
 (20)
(20)
теңсіздігін аламыз. Ал мына теңдікті
 (21)
(21)
ескерсек, онда (20) теңсіздіктен
![]()
теңсіздігін аламыз.Осыдан
 (22)
(22)
теңсіздігін шығады.
Енді k-ның k=0,1,2,... мәндері үшін
![]()
![]()
. . . . . . . . . . . . . . . . .
![]()
теңсіздігін аламыз.
Мұндағы ![]()
Тордағы ![]() түйіні
түйіні ![]() түйіндік нүкте болып
қала береді деп есептесек,
түйіндік нүкте болып
қала береді деп есептесек, ![]() деп жазуға болады
және
деп жазуға болады
және ![]() екенін ескерсек, онда
екенін ескерсек, онда

Осыдан ![]() болғандықтан
(14)-(15) айырымдық есебінің шешуі (4)-(5) есебінің шешуіне
болғандықтан
(14)-(15) айырымдық есебінің шешуі (4)-(5) есебінің шешуіне
![]() дәлдікпен
жинақталады.
дәлдікпен
жинақталады.
-
Лагранж формуласындағы қалдық мүше
Лагранждың интерполяциялау формуласы.
-
кесіндісінде жататын
 нүктелері және осы нүктелерде
нүктелері және осы нүктелерде  функциясының
мәндері-
функциясының
мәндері-  берілген. Осы функцияны интерполяциялау үшін n дәрежелі
алгебралық көпмүшені
берілген. Осы функцияны интерполяциялау үшін n дәрежелі
алгебралық көпмүшені
 (23)
(23)
қолданамыз.
Мұндағы
![]() коэффициенттерін
коэффициенттерін
![]() болатындай етіп табу керек.
болатындай етіп табу керек.
Кез-келген
үзіліссіз ![]() функциясы үшін бұл есептің шешімі біреу ғана болады.
Себебі
функциясы үшін бұл есептің шешімі біреу ғана болады.
Себебі
 (24)
(24)
теңдеулер жүйесінің аңықтауышы нольден айырықша (Вандермонд аңықтауышы).
-
көпмүшесін,
 нүктелері бойынша
тұрғызылған,
нүктелері бойынша
тұрғызылған,  функциясын интерполяциялаушы көпмүше дейміз.
функциясын интерполяциялаушы көпмүше дейміз.
(24) теңдеулер жүйесінің шешімдерін әртүрлі жолмен табуға болады. Оның көп қолданатын түрлері Лагранж бен Ньютонның интерполяциялық көпмүшеліктері.
Лагранждың интерполяциялық көпмүшелігін
 (25)
(25)
түрінде қарастырамыз. (2.2) шартын ескере отырып,
 (26)
(26)
теңдігін аламыз.
Егер
![]() (27)
(27)
болса,
онда (2.4) шарты орындалады. ![]() дәрежелі көпмүше
болғандықтан
дәрежелі көпмүше
болғандықтан ![]() коэффициентін де n дәрежелі көпмүше ретінде іздеген
дұрыс.
коэффициентін де n дәрежелі көпмүше ретінде іздеген
дұрыс.
Атап
айтқанда ![]() көпмүшесін
көпмүшесін
![]() (28)
(28)
түрінде іздейміз.
![]() шартың ескере отырып, (28)
формуладан
шартың ескере отырып, (28)
формуладан
![]()
және
 (29)
(29)
формуласын табамыз. Сонымен Лагранж көпмүшесі толық былайша жазылады.
 .
(30)
.
(30)
Егер
 десек, онда
десек, онда 
Ал
![]()
Сондықтан Лагранж көпмүшесін былайша ықшамдап жазуға болады:
 (31)
(31)
Енді интерполяциялық Лагранж көпмүшесінің жіберетін қатесін қарастырайық.
-
функциясын
 көпмүшесімен
алмастырғанда жіберетін қатеміз
көпмүшесімен
алмастырғанда жіберетін қатеміз
![]() (32)
(32)
Кейде
![]() функциясын
Лагранж көпмүшесінің қалдығы деп те атайды.
функциясын
Лагранж көпмүшесінің қалдығы деп те атайды.
Кез-келген
![]() нүктесіндегі
қалдықты табу үшін мына көмекші функцияны
қарастырамыз:
нүктесіндегі
қалдықты табу үшін мына көмекші функцияны
қарастырамыз:
![]() ,
(33)
,
(33)
мұнда
![]() -тұрақты сан.
-тұрақты сан.
![]() санын
санын
![]() болатындай,
яғни
болатындай,
яғни
![]() (34)
(34)
деп алсақ,
онда ![]() ең
болмағанда
ең
болмағанда ![]() нүктеде нольге тең болады.
нүктеде нольге тең болады.
Енді
![]() функциясының
функциясының
![]() кесіндісінде
үзіліссіз
кесіндісінде
үзіліссіз ![]() ретті туындысы бар болсын. Сонда
ретті туындысы бар болсын. Сонда ![]() , Роль теоремасы
бойынша,
, Роль теоремасы
бойынша, ![]() кесіндісінде ең болмағанда n+1 нүктеде нөлге тең, ал
кесіндісінде ең болмағанда n+1 нүктеде нөлге тең, ал ![]() -ењ , болмағанда n
нүктеде нөлге тең, т.с.
-ењ , болмағанда n
нүктеде нөлге тең, т.с. ![]() ең болмағанда бір
нүктеде нөлге тең болады. Сонымен
ең болмағанда бір
нүктеде нөлге тең болады. Сонымен ![]() табылады да
табылады да
![]() болады.
болады.
Ал
![]() болғандықтан
болғандықтан
![]() .
(35)
.
(35)
(34) және (35) формулаларды ескере отырып,
![]() (36)
(36)
формуласын аламыз.
Осыдан
![]() функциясын
жоғарыдан бағалау арқылы
функциясын
жоғарыдан бағалау арқылы
![]() .
(37)
.
(37)
теңсіздігін аламыз, мұндағы ![]() .
.
Егер
![]() дәрежесі n-нен
үлкен емес көпмүше болса, онда
дәрежесі n-нен
үлкен емес көпмүше болса, онда ![]()
Сондықтан ![]() .
.
4.Шлемимильх-Рош түріндегі қалдық мүше
![]() маңайында,
маңайында,
![]() нүктесін қоса
алғанда,
нүктесін қоса
алғанда, ![]() функциясы
берілсін.
функциясы
берілсін. ![]() нүктесінде
нүктесінде ![]() аргументіне
аргументіне ![]() өсімшесін
береміз (оң немесе теріс). Онда
өсімшесін
береміз (оң немесе теріс). Онда ![]() .
.
Егер ![]() шегі табылса, онда
оны
шегі табылса, онда
оны ![]() нүктесіндегі
нүктесіндегі
![]() функциясының туындысы деп
айтамыз, немесе
функциясының туындысы деп
айтамыз, немесе ![]() функциясы
функциясы ![]() нүктесінде дифференциалданады деп айтамыз және былай
белгілейміз:
нүктесінде дифференциалданады деп айтамыз және былай
белгілейміз:
![]() яғни,
яғни,
![]() (38)
(38)
Егер (1)-де
![]() және
және ![]() болса, онда
(1)-ді
болса, онда
(1)-ді ![]() нүктесіндегі
нүктесіндегі ![]() оң жақ
туындысы [
оң жақ
туындысы [![]() сол жақ
туындысы] деп атаймыз. Егер
сол жақ
туындысы] деп атаймыз. Егер ![]() және
және ![]() болса,
онда
болса,
онда ![]() .
.
![]() функциясын
функциясын
![]() кесіндісінде
дифференциалданады деп айтамыз, егер оның
кесіндісінде
дифференциалданады деп айтамыз, егер оның ![]() аралығындағы әрбір нүктеде
туындысы бар болса, ал
аралығындағы әрбір нүктеде
туындысы бар болса, ал ![]() және
және ![]() ұштарында
сәйкесінше
ұштарында
сәйкесінше ![]() және
және![]() табылса.
табылса.
![]() облысында
дифференциалданатын
функциялардың класын
облысында
дифференциалданатын
функциялардың класын ![]() деп
белгілейміз
деп
белгілейміз
а) Механикалық. ![]() -
-
![]() нүктесінің қозғалу заңы
болсын.
нүктесінің қозғалу заңы
болсын.
![]() нүктесінің
нүктесінің
![]() -дан
-дан ![]() -ға дейінгі аралығындағы
қозғалысын қарастыралық. Онда
-ға дейінгі аралығындағы
қозғалысын қарастыралық. Онда ![]() ал
ал ![]() - орташа жылдамдық
. Егер
- орташа жылдамдық
. Егер
![]()
шегі табылса, онда
жолдың уақыт бойынша туындысы ![]() нүктесінің
нүктесінің ![]() уақыт
аралығындағы қозғалысының жылдамдығына тең.
уақыт
аралығындағы қозғалысының жылдамдығына тең.
|
|
б) Геометриялық. |
![]() нүктесі қисықтың
бойымен
нүктесі қисықтың
бойымен ![]() нүктесіне
кез келген жағынан шексіз жақындағанда
нүктесіне
кез келген жағынан шексіз жақындағанда ![]() қимасының
қимасының
![]() шектелген орны табылса,
онда
шектелген орны табылса,
онда ![]()
![]() қисығына
қисығына ![]() нүктесінде жүргізілген жанама деп
аталады.
нүктесінде жүргізілген жанама деп
аталады.
Е гер қисықтың жанамасы бар болса, онда
![]() .
.
Бұдан,
![]() нүктесінде дифференциалданатын
функцияның осы нүктеде бұрыштық коэффиценті
нүктесінде дифференциалданатын
функцияның осы нүктеде бұрыштық коэффиценті
![]() болатын жанамасы бар
болады.
болатын жанамасы бар
болады.
Мысал
1. ![]() функциясының
функциясының ![]() нүктесіндегі жанамасының теңдеуін жаз.
нүктесіндегі жанамасының теңдеуін жаз.
а) ![]() .
. ![]() болғандықтан, жанаманың
теңдеуі
болғандықтан, жанаманың
теңдеуі ![]() .
. ![]() -ті
табалық:
-ті
табалық:

|
в) |
б)
|
в)
|
Оң жақ жанамасы
![]() болады, яғни
болады, яғни
![]() , ал сол жағынан
жанамасы
, ал сол жағынан
жанамасы ![]() ,
яғни
,
яғни ![]() . Бұдан,
х=
. Бұдан,
х=![]() нүктесінде берілген
нүктесінде берілген ![]() функцияның туындысы
табылмайды, бұл функция х=
функцияның туындысы
табылмайды, бұл функция х=![]() нүктесінде үзіліссіз
болғанның өзінде.
нүктесінде үзіліссіз
болғанның өзінде.
![]() болатын
нүктелер бұрыштық деп аталады.
болатын
нүктелер бұрыштық деп аталады.
5.Тригонометриялық функциялардың формуласының қалдық мүшелері
![]() ;
; ![]()
функциялары орындалады және барлық тригонометриялық формулалар орындалады:
![]() ;
;
![]()
Гиперболалық функциялар нақты аргументтің функциялары тәрізді анықталады:
![]() ;
;
![]() .
.
Бұлар тригонометриялық функциялармен былай байланысады:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
50. ![]() функциялары
сәйкес
функциялары
сәйкес ![]() ,
, ![]() ,
, ![]() ,
, ![]() функцияларына кері функциялар ретінде анықталады, және де
олардың бәрі де көп мәнді функциялар.
функцияларына кері функциялар ретінде анықталады, және де
олардың бәрі де көп мәнді функциялар.
Дәлелдеңдер:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Z
облысының
бір мәнді ![]() функциясын қарастырамыз.
функциясын қарастырамыз.
Анықтама. Егер
![]()
![]() (39)
(39)
ақырлы шегі бар болса, онда ол
шек ![]() функциясының туындысы деп
аталады және былай белгіленеді:
функциясының туындысы деп
аталады және былай белгіленеді:
![]()
Бұл шек ∆ z -тің нөлге қалай ұмтылғанына тәуелсіз.
Z
облысының ![]() нүктесінде үзіліссіз туындысы бар
нүктесінде үзіліссіз туындысы бар ![]() функциясы осы облыстың
аналитикалық функциясы деп аталады.
функциясы осы облыстың
аналитикалық функциясы деп аталады.
Шектің қасиеттері негізінде туындының негізгі қасиеттері шығады.
Қасиеттері:
-
 ,
, -
 ,
, -
 .
. -
Егер күрделі функция
 түрінде
берілсе, мұнда
түрінде
берілсе, мұнда  -
комплекс
айнымалы функция, және туындылары
-
комплекс
айнымалы функция, және туындылары  мен
мен  бар болса,
онда мына
формула орынды:
бар болса,
онда мына
формула орынды:
![]() .
.
![]() , мұндағы
n – бүтін сан. Туындысын табамыз,
ол үшін функцияның өсімшесін анықтаймыз:
, мұндағы
n – бүтін сан. Туындысын табамыз,
ол үшін функцияның өсімшесін анықтаймыз:
![]()
![]() .
.
Сонда туынды мынаған тең:
![]()
Көрсеткіштік және тригонометриялық функцияларды қарастырамыз:
![]() ;
;
![]() ;
;
![]() .
.
Бұл қатарлар
z-ң кез келген мәндерінде
жинақты, ![]() . Осының негізінде бұл
қатарларды дифференциалдауға болады.
. Осының негізінде бұл
қатарларды дифференциалдауға болады.
![]() .
.
Оң бөлігі Маклорен қатарына
дәл келеді ( ![]() -ң
жіктелуі).)
-ң
жіктелуі).)
![]()
![]() .
.
Осы тәрізді қалған қатарларды да дифференциалдаймыз:
3.
![]()
![]() ; яғни
; яғни
![]() .
.
4.
![]()
![]() ; яғни
; яғни
![]() .
.
5.
![]() .
.
6.
![]() .
.
![]() .
.
7.![]() ,
,
![]() ;
; ![]()
Қорытынды
Айталық,
![]() (1)
(1)
есебі берілсін. Бұл
есепті шешу үшін ![]() торын
алайық та осы торда (1) есебін шешу үшін мынандай айырымдық есеп
қоялық.
торын
алайық та осы торда (1) есебін шешу үшін мынандай айырымдық есеп
қоялық.

Мұндағы ![]() болуы мүмкін
.
болуы мүмкін
.
Есептің жуық шешуі мына рекурентті формула арқылы табылады.

Егер ![]() нөлге ұмтылғанда
нөлге ұмтылғанда
![]() нөлге
ұмтылса, онда (2 )-(3) есебінің шешуі (3)-(4) есебінің шешуіне
жинақталады дейміз. Егер жеткілікті аз шама
нөлге
ұмтылса, онда (2 )-(3) есебінің шешуі (3)-(4) есебінің шешуіне
жинақталады дейміз. Егер жеткілікті аз шама ![]() табылып, және
табылып, және
![]() болғанда
болғанда
![]() бағалауы
орындалса, онда айырымдық схеманың шешуі
бағалауы
орындалса, онда айырымдық схеманың шешуі ![]() жылдамдықпен (3)-(4)
есебінің шешуіне жинақталады дейді немесе айырымдық схеманың
дәлдігі
жылдамдықпен (3)-(4)
есебінің шешуіне жинақталады дейді немесе айырымдық схеманың
дәлдігі ![]() -ге
тең дейді. Мұндағы
-ге
тең дейді. Мұндағы ![]()
![]() -тан тәуелсіз сан.
-тан тәуелсіз сан.
Кейде (3)-(4) есебін
![]() функциясының
шекаралық (шеткі) нүктелердегі белгілі мәндерін теңдіктің оң жағына
шығару арқылы,
функциясының
шекаралық (шеткі) нүктелердегі белгілі мәндерін теңдіктің оң жағына
шығару арқылы,
![]() (2)
(2)
түрінде жазуға болады. Бұл жағдайда айырымдық схеманың жуықтау қателігін былайша жазады:
![]()
Ал ![]()
теңдігін
![]() ретті жуықтау
қателігі (аппроксимациясы) дейміз.
ретті жуықтау
қателігі (аппроксимациясы) дейміз.
Пайдаланылған әдебиеттер
-
Темірғалиев Н. “Математикалық анализ” - Алматы; Мектеп 1987, 288 бет.
-
Ибрашев Х. И., Еркеғұлов Ш. Т. “Математикалық анализ курсы.” – Алматы; Мектеп 2 том, 1970, 527 бет.
-
Кудрявцев А. Д. “Краткий курс математического анализа.” – Москва, Наука, 1989, 735 бет.
-
Фихтенгольц Г. М. “Основы математического анализа.” – Москва, Наука, 1968, ІІ том.
-
“Задачник по курсу математического анализа.” Под редак. Н. Я. Виленкина, Москва, 1971, ч-2.
-
Асинкин А. Г., Бутинов Е. И., Кондратьев А. С. “Краткий физико-математический справочник.” Москва, 1990, 368 стр.
-
Демидович Б. П. “Сборник задачи и упражнений по математическому анализу.” Москва, Наука, 1977.
-
“Егемен Қазақстан” 16 қазан, 2004 жыл.
-
А. Г. Аленкин, Е. И. Бутиков, А. С. Кондратьев. «Краткий физико-математический справочник» М., 1990 г.
-
Шойынбеков К. Д., Әбілқасымов А. Е., Есенова М. И., Тұрлыханова М. А. «Анализ бастамалары» оқу құралы. Алматы, 2002ж., 320 бет.
-
Данко П. Е., Попов А. Г., Кожевникова Т. Я. «Высшая математика в упражнениях и задачах» учебное пособие для студентов вузов. М., Высш.шк., 1926г.
Есептер
Лагранж интерполяциялық көпмүшесін табыңыз:
A) ![]()
B) ![]() C)
C) ![]()
D) ![]() E)
E) ![]()
4. ![]() Берiлген САТЖ үшін Гаусс
әдісінің бірінші қадамында қандай формула
алынады?
Берiлген САТЖ үшін Гаусс
әдісінің бірінші қадамында қандай формула
алынады?
№2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Тейло қатары
бойынша
Тейло қатары
бойынша
№3

![]()
![]()
![]()

Тейлор қатарына жіктеу:
№1 ![]() ч дәрежесі бойынша
жіктеңіз
ч дәрежесі бойынша
жіктеңіз
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
24

шағым қалдыра аласыз