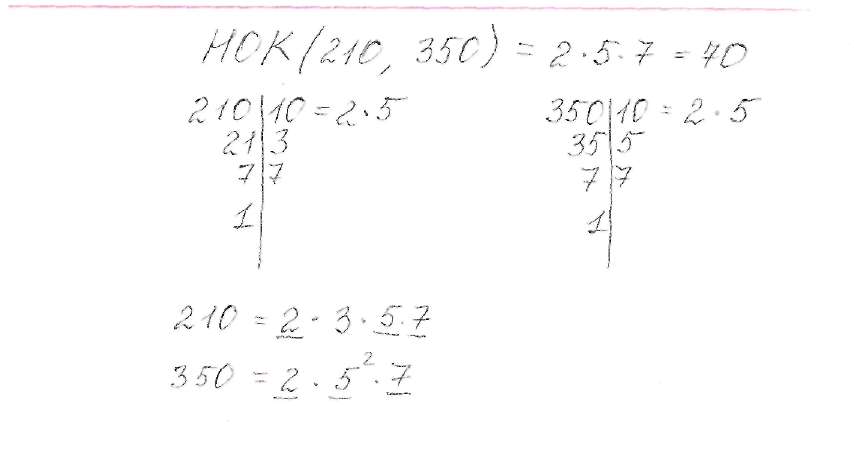Тақырыптық сабақ жоспары 5 сынып

Раздел

Повторение курса математики 5 класса

ФИО педагога

Ахметжанова В.В

Дата

Класс: 5

Количество присутствующих:

Количество отсутствующих:

Тема урока

Повторение. Делимость натуральных чисел

Цели обучения в соответствии с учебной программой

5.5.1.2 использовать НОД и НОК при решении текстовых задач;

Цели урока

Учащийся:

использует НОД и НОК при решении текстовых задач;

Ход урока

Этап урока /Время

Действия педагога

Действия ученика

Оценивание

Ресурсы

Приветствие, создание коллаборатив

ной среды/ 2 мин

Организует актуализацию требований к ученику с позиции учебной деятельности.

Создает условия для формирования внутренней потребности учеников во включение в учебную деятельность.

Приветствует учеников. Прием «Поделись улыбкой».

Знакомит с темой и целью урока.

Принимают участие в постановке темы (цели) урока. Осмысливают поставленную цель.

Актуализация знаний/

8мин

Работа с классом.

1.Устный счет

Назовите пары взаимно простых чисел: 8 и 10; 44 и 38; 40 и 99; 14 и 7; 34 и 17; 100 и 13; 44 и 20; 41 и 82; 10 и 21; 15 и 16; 4 и 63; 8 и 12

Почему они являются взаимно простыми?

Молодцы!

2.Помогите найти ошибку.

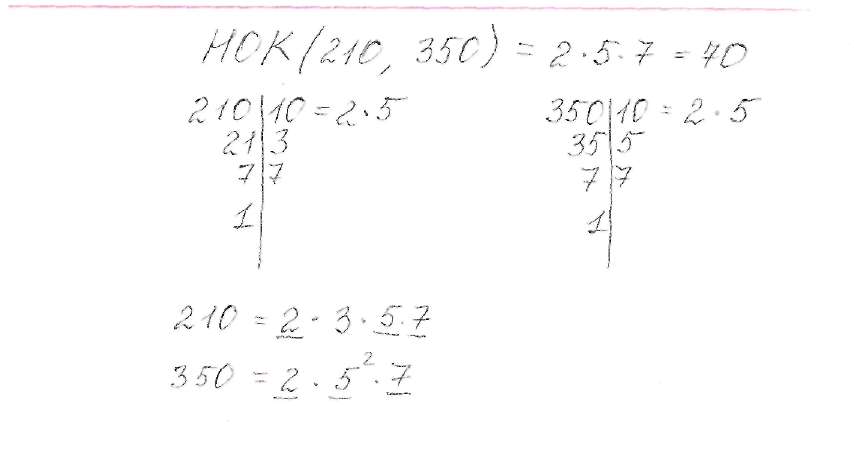
называет

взаимно простые:

40 и 99; 100 и 13; 10 и 21; 15 и 16; 4 и 63.

Потому, что их наибольший общий делитель равен 1.

Проверяют разложение на множители выполнено верно. Определяют неправильно выбраны множители для нахождения НОК. Надо было взять все множители в наибольшей степени.

НОК(210; 350) = 2∙3∙5²∙7=1050

За каждый правильный ответ 1 балл

презентация

Решение задач

17 мин

Формативное оценивание

10мин

Задача№1.

Вчера в магазин привезли 2145 белых роз, 238 красных и 173 желтых. Необходимо составить букеты, поровну распределив розы так, чтобы не осталось ни одной лишней. Но пока ничего не вышло. Удастся ли это сделать?

Задача№2.

Длина шага Бори 50 см, а его отца – 70 см. Боря утверждает, что первый раз, сделав целое количество шагов, они с папой окажутся на одинаковом расстоянии от начала пути через 3 метра, а папа не соглашается. Кто прав в этом споре?

Задача №3.

Каково наибольшее количество учеников, между которыми можно распределить 112 тетрадей в клетку и 140 тетрадей в линейку?

Организует выполнение учащимися самостоятельной работы на знания и умения, самопроверку, выявление места и причины затруднений, работу над ошибками.

Земельный участок имеет форму прямоугольника, длина которого 36 м, а ширина 30 м. Участок нужно разделить на квадратные участки. Какие наибольшие квадратные участки можно получить и сколько таких участков?

Дескриптор:

-записывает краткую запись условия задачи;

-использует свойство НОК/НОД;

-находит площадь прямоугольного участка;

- находит площадь квадрата;

-находит решение задачи;

- записывает ответ

Составляет текст задачи, по краткой записи и записывает решение задач в тетрадь

НОД(2145; 238) = 1

Нет, т.к. числа 2145 и 238 взаимно простые, а число 173 само простое.

НОК(50;70)= 350 см. а не 3 метра

Ответ: Прав папа.

Определяет в задаче необходимость найти наибольший общий делитель чисел 112 и 140. Раскладывает на множители эти числа.

112 = 2⁴∙7;

140 = 2²∙5∙7

НОД (112,140)= 2²∙7=28 – наибольшее количество учеников.

Составляет текст краткой записи задачи и решение

находит наибольший общий делитель:

НОД(36; 30) = 6 м – размеры квадрата.

Находит площадь прямоугольного участка.

36 · 30 = 1080 (м²) – площадь прямоугольника.

Теперь, находит площадь квадрата.

6² = 36 м² – площадь квадрата.

Находит число квадратов в прямоугольном участке.

1080 : 36 = 30 – число квадратов

Ответ: 30 квадратов со стороной 6 м.

Оценивание задач учителем

ФО по дескриптору

презентация

Рефлексия

5 мин

Ребята, мы с вами решили задачи, в которых нет ни слова про делители и кратные, но именно эти понятия помогли вам их решить.

Ответить на вопросы:

Что узнал?

Чему научился?

Что осталось непонятным?

Над чем надо поработать?

Раздел

Повторение курса математики 5 класса

ФИО педагога

Дата

Класс: 5

Количество присутствующих:

Количество отсутствующих:

Тема урока

Повторение. Делимость натуральных чисел

Цели обучения в соответствии с учебной программой

5.5.1.2 использовать НОД и НОК при решении текстовых задач;

Цели урока

Учащийся:

использует НОД и НОК при решении текстовых задач;

Порядок действий

Ресурсы

(заполняется учителем)

Выполнение

Целеполагание.

Ознакомление учащихся с темой урока, ЦО.

Определить цели урока, определить ожидания к концу урока.

Открой тетрадь, запиши число,

тему урока

Изучи

Просмотри видео-урок

- https://youtu.be/ZgULPklWQUk

- https://youtu.be/8i9tR-uXlmU

Просмотри видео в чате

Повтори

Выполни

1.Устный счет

Назовите пары взаимно простых чисел: 8 и 10; 44 и 38; 40 и 99; 14 и 7; 34 и 17; 100 и 13; 44 и 20; 41 и 82; 10 и 21; 15 и 16; 4 и 63; 8 и 12

Почему они являются взаимно простыми?

2.Помогите найти ошибку.

Задача№1.

Вчера в магазин привезли 2145 белых роз, 238 красных и 173 желтых. Необходимо составить букеты, поровну распределив розы так, чтобы не осталось ни одной лишней. Но пока ничего не вышло. Удастся ли это сделать?

Решение :

НОД(2145; 238) = 1

Нет, т.к. числа 2145 и 238 взаимно простые, а число 173 само простое.

Ответ :

Задача№2.

Длина шага Бори 50 см, а его отца – 70 см. Боря утверждает, что первый раз, сделав целое количество шагов, они с папой окажутся на одинаковом расстоянии от начала пути через 3 метра, а папа не соглашается. Кто прав в этом споре?

Решение:

НОК(50;70)= 350 см. а не 3 метра

Ответ: Прав папа.

Задача №3.

578тг - Сатып алу

Материал ұнаса әріптестеріңізбен бөлісіңіз

Ватсапта бөлісу Телеграммда бөлісу Фейсбукта бөлісу Сілтемені көшіру

Материал жариялап тегін сертификат алыңыз!

Бұл сертификат «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жарияланғанын растайды. Журнал Қазақстан Республикасы Ақпарат және Қоғамдық даму министрлігінің №KZ09VPY00029937 куәлігін алған. Сондықтан аттестацияға жарамды

Материал жариялау Сертификатты жүктеу

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Тізімді көру

Ұқсас материалдар

Дайын ҚМЖ. Барлық пәндерден 2022-2023 оқу жылына, жаңа бұйрыққа сай жасалған

Сертификатталған тренер жасаған

01.01.2023

17 863

13 694

ҚР Білім және Ғылым министірлігінің стандарты бойынша жасалған. 2022-2023 оқу жылына арналған

Барлық пәндер

Барлық материалдар

Барлық сыныптар

Математика пәні бойынша барлық материалдарды көру

Іс-шаралар кестесі

Педагогтардың біліктілігін арттыру курстары