Фамилия,Имя._____________________ Класс______ Дата_______________

1 четверть

Тема: Основные понятия геометрии. Аксиомы. Теоремы.

Цели обучения:

7.1.1.1 знать основные фигуры планиметрии: точка, прямая;

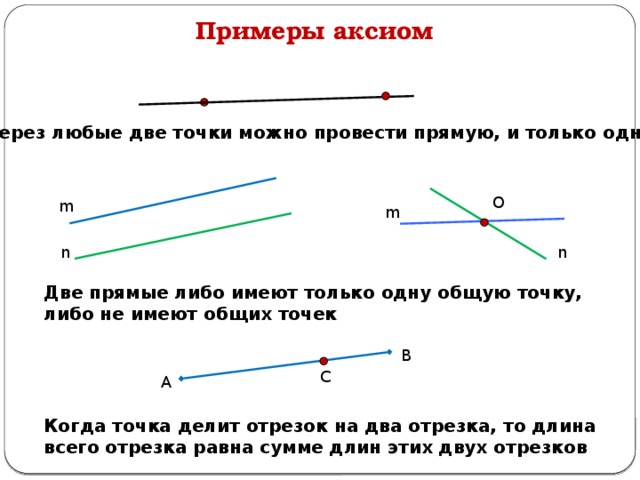
7.1.2.2 знать и применять аксиомы принадлежности точек и прямых

7.1.1.5 знать определения отрезка, луча, угла, полуплоскости;

7.1.1.6 знать и применять аксиомы измерения отрезков и углов;

Аксиома:

• Аксиома — это утверждение, которое принимается за истину без доказательства. В основе геометрии лежат аксиомы, которые служат фундаментом для выведения теорем и решений геометрических задач.

• Пример: В классической геометрии аксиома Евклида о параллельных прямых звучит так: "Через любую точку вне данной прямой можно провести ровно одну прямую, параллельную данной."

Аксиомы и теоремы

Математические утверждения о геометрических фигурах

Определения геометрических фигур

Свойства

геометрических фигур

Математические утверждения о свойствах геометрических фигурах, требующие объяснения (доказательства)

Математические утверждения о свойствах геометрических фигурах как исходные, само собой разумеющие

Теорема

Аксиома

Теорема:

• Теорема — это утверждение, обоснованное аксиомами и ранее доказанными теоремами. Теоремы требуют доказательства и часто имеют практическое применение в задачах.

• Пример: Теорема Пифагора, которая утверждает, что в прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы: a2+b2=c2a2+b2=c2.

• Объяснение.

Аксиомы — это основные "кирпичики" математических истин, на которых строятся доказательства теорем.

Убедиться, что они понимают, что теоремы — это утверждения, которые необходимо доказать, опираясь на аксиомы.

Демонстрация:

• Посмотрите простую визуальную модель

Или с помощью программного обеспечения, такого как GeoGebra, для иллюстрации теоремы Пифагора.

Перейдите по ссылке: https://www.geogebra.org/classic

Обсуждение:

• Почему аксиомы принимаются без доказательства и как теоремы формируют основу для дальнейших математических открытий?

Быстрый темп развития науки и техники требует от учителя естественно- математического направления развиваться еще быстрее, то есть идти на шаг вперед. Образование не стоит на месте. Основной задачей организаций обучения состоит в том, чтобы современный педагог смог не только организовать правильно процесс обучения, но и смог организовать обучение на том уровне, который даст высокую степень обученности обучаемого. Говоря о высокой степени обученности, я имею ввиду приемы и методы, применяемые педагогом на уроке. Работая в школе, наблюдала спад заинтересованности учеников к предметам естественно- математического цикла. Проведя анализ, пришла к выводу, что ученик воспринимает ту информацию, над которой он работал самостоятельно. Основываясь на выводах, решила приступить к созданию рабочих листов с целью привлечения ученика к самостоятельному познанию предмета. Результат не заставил себя ждать. Качество преподавания значительно выросло, даже ученики с низкой мотивацией стали показывать впечатлительный результат. Теперь основой в моем преподавании – рабочие индивидуальные рабочие листы. Данная разработка предусматривает различные педагогические технологии, одной из которых является технология личностно- ориентированного обучения, применение искусственного интеллекта.