
Жансен Кереев атындағы орта мектебінің математика пәні мұғалімі Жанбауова Маруан Сакеновнаның дайындаған баяндамасы.
Тақырыбы: «Теңсіздіктерді графиктік тәсілмен шешу әдісі»
1.мысал теңсіздікті графиктік тәсілмен шешейік: х532х
Шешуі:
у=х5 және у=32х функциясының графигін салайық: (сурет. 1).
у=х5 функциясының графигі парабола, мына нүктелер арқылы өтеді: (-1;-1); (0;0) ;(1;1)
у=32х функциясының графигін cалу үшін таблицаны толтырайық
|
|
0 |
|
|
|
3 |
0 |

Графиктертер (1;1) нүктесінде қиылысады. басқа қиылысу нүктесі болмайды, себебі у=х5 функциясы монотонды өспелі, ал у=32х функциясы монотонды кемімелі ендеше қиылысу нүктесі жалғыз нүкте.
Жауабы: х=1;
Ал х532х болса, онда у=х5 функциясының графигі у=32х функциясының графигінің үстінде болуы шарт ал бұл х1 болғанда ғана орындалады.
Ал егер де х532х болса, онда онда у=х5 функциясының графигі у=32х функциясының графигінің астында болуы шарт ал бұл х1 болғанда ғана орындалады.
Жауабы: х 1 немесе х1
2 мысал . х-22х1 теңсіздігін шешіңдер:
Шешуі : және у=2х1 функциясының
графигін
салайық.
және у=2х1 функциясының
графигін
салайық.
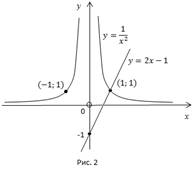
 теңдеуінің түбірлерін
табайық:
теңдеуінің түбірлерін
табайық:
Егер х болса, шешімі жоқ.
Егер х болса, онда тек бір ғана х=1 шешімі болады.
 теңсіздігі орындалу үшін
гипербола
теңсіздігі орындалу үшін
гипербола  түзудің үстінгі бөлігінде
түзудің үстінгі бөлігінде
 болуы керек. Ал бұл шарт тек
0х1 және х0орындалады.
болуы керек. Ал бұл шарт тек
0х1 және х0орындалады.
Жауабы: х(-;0)(0;1)
3 мысал . теңсіздікті графиктік тәсілмен шешіңдер:
а) х3 ә) х3
ә) х3
Шешуі: Анықталу облысы х0
 және
және  функцияларының
графиктерін салайық:
х0
функцияларының
графиктерін салайық:
х0

а)  функциясының графигі
функциясының графигі  функциясының графигінің үстінгі бөлігінде, мұндағы
х0;1
функциясының графигінің үстінгі бөлігінде, мұндағы
х0;1
ә)  функциясының графигі
функциясының графигі  функциясының графигінің астыңғы бөлігінде, мұндағы
х1. Шарты бойынша теңсіздік
белгісі қатаң болмағандықтан
х=0
функциясының графигінің астыңғы бөлігінде, мұндағы
х1. Шарты бойынша теңсіздік
белгісі қатаң болмағандықтан
х=0
Жауабы: а) х0;1 ә) х1;+x=0
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Теңсіздіктерді графиктік тәсілдермен шығару.
Теңсіздіктерді графиктік тәсілдермен шығару.
Жансен Кереев атындағы орта мектебінің математика пәні мұғалімі Жанбауова Маруан Сакеновнаның дайындаған баяндамасы.
Тақырыбы: «Теңсіздіктерді графиктік тәсілмен шешу әдісі»
1.мысал теңсіздікті графиктік тәсілмен шешейік: х532х
Шешуі:
у=х5 және у=32х функциясының графигін салайық: (сурет. 1).
у=х5 функциясының графигі парабола, мына нүктелер арқылы өтеді: (-1;-1); (0;0) ;(1;1)
у=32х функциясының графигін cалу үшін таблицаны толтырайық
|
|
0 |
|
|
|
3 |
0 |

Графиктертер (1;1) нүктесінде қиылысады. басқа қиылысу нүктесі болмайды, себебі у=х5 функциясы монотонды өспелі, ал у=32х функциясы монотонды кемімелі ендеше қиылысу нүктесі жалғыз нүкте.
Жауабы: х=1;
Ал х532х болса, онда у=х5 функциясының графигі у=32х функциясының графигінің үстінде болуы шарт ал бұл х1 болғанда ғана орындалады.
Ал егер де х532х болса, онда онда у=х5 функциясының графигі у=32х функциясының графигінің астында болуы шарт ал бұл х1 болғанда ғана орындалады.
Жауабы: х 1 немесе х1
2 мысал . х-22х1 теңсіздігін шешіңдер:
Шешуі : және у=2х1 функциясының
графигін
салайық.
және у=2х1 функциясының
графигін
салайық.

 теңдеуінің түбірлерін
табайық:
теңдеуінің түбірлерін
табайық:
Егер х болса, шешімі жоқ.
Егер х болса, онда тек бір ғана х=1 шешімі болады.
 теңсіздігі орындалу үшін
гипербола
теңсіздігі орындалу үшін
гипербола  түзудің үстінгі бөлігінде
түзудің үстінгі бөлігінде
 болуы керек. Ал бұл шарт тек
0х1 және х0орындалады.
болуы керек. Ал бұл шарт тек
0х1 және х0орындалады.
Жауабы: х(-;0)(0;1)
3 мысал . теңсіздікті графиктік тәсілмен шешіңдер:
а) х3 ә) х3
ә) х3
Шешуі: Анықталу облысы х0
 және
және  функцияларының
графиктерін салайық:
х0
функцияларының
графиктерін салайық:
х0

а)  функциясының графигі
функциясының графигі  функциясының графигінің үстінгі бөлігінде, мұндағы
х0;1
функциясының графигінің үстінгі бөлігінде, мұндағы
х0;1
ә)  функциясының графигі
функциясының графигі  функциясының графигінің астыңғы бөлігінде, мұндағы
х1. Шарты бойынша теңсіздік
белгісі қатаң болмағандықтан
х=0
функциясының графигінің астыңғы бөлігінде, мұндағы
х1. Шарты бойынша теңсіздік
белгісі қатаң болмағандықтан
х=0
Жауабы: а) х0;1 ә) х1;+x=0

шағым қалдыра аласыз
















