Тіктөртбұрыштың ауданы

Пәні: алгебра

№ 198ЖББМ директорының ОІЖ орынбасары:

Күні:

Сынып: 9

Сабақ реті:1

Тақырыбы: Тіктөртбұрыштың ауданы

Мақсат:

Жаңа білім

Тіктөртбұрыштың ауданының анықтамасын біледі. Оны қалай дұрыс дәлелдеуді біледі. Тіктөртбұрыштың қабырғаларын салыстырады.

Жаңа түсінік

Тіктөртбұрыштың ауданын табу теоремасын парафразалайды. Тіктөртбұрыштың ауданын қалай табу керек екенін түсінеді

Қолданым әрекеті

Тіктөртбұрыштың ауданын табуда берілген теореманы қолданады.

Талдау әрекеті

Тіктөртбұрыштың ауданын табу теоремасының үшінші жағдайдағы дәлелін талдайды.

Шығармашылық әрекет

Сабақта өткен материалды қайта қарайды. Оның ішінде: Тіктөртбұрыштың ауданын табу теоремасының үш жағдайын қарайды.

Бағамдау әрекеті

Тіктөртбұрыштың, квадраттың аудандарын есептейді. Тіктөртбұрыштың қабырғаларын салыстырады.

Сабақ құрылымы:

І. Ақпарат алмасу (10 мин.).

ІІ. Алғашқы бекіту (4 мин.).

ІІІ. Құзырлылық қалыптастыру (15 мин.).

ІV. Шығармашылық қалыптастыру (8 мин.).

V.Бағамдау - бағалау (3 мин.).

Сабақ типі: фронтальді, топтық

Оқыту әдісі: репродуктивті, ішінара ізденушілік

Мұғалім іс-әрекетінің тәсілі: Оқушыға жол сілтеу

Негізгі ұғымдар мен терминдер: Aудан, тіктөртбұрыш, квадрат.

Оқушыда дағды қалыптастыру:

Тақырып бойынша әртүрлі ерекше сұрақтарды шешу, белгілеген мақсатқа қол жеткізу, өзін-өзі дамыту, топпен жұмыс істеу және топ жұмысының нәтижесін көру, өз ойын сынып алдында қорғай білу, өзгелердің жауабын көңіл бөліп оларды талдау.

Ақпарат көздері: Қайдасов, Ж., Хабарова, Г., Абдиева, А. Геометрия 8 сынып оқулығы. Алматы «Мектеп» 2012.

Оқушы жетістігін бағалау: Оқушыға сабақ блоктарының деңгейлік тапсырмаларын уақытылы орындауы, топтық жұмысқа қатысуы мен үй жұмысын орындауына байланысты баға қойылады.

Үй тапсырмасы:

1. Ені 3.366665см, ал ұзындығы 4см. Тіктөртбұрыштың ауданын табу қай жағдайға жатады.

2. Ені 3.366665см, ал ұзындығы 4см. n нешеге тең?

3. Ені 3.366665см, ал ұзындығы 4см. Ауданын табыңыз

БОНУС. Ені 3см, ал ұзындығы 4см. n нешеге тең?

САБАҚ БЛОКТАРЫ ○

і. аҚПАРАТ алмасу

1 – слайд (титул)

2 – слайд Сабақтың мақсаты

3 – слайд Тақырып жоспары

4 – слайд Тіктөртбұрыштың ауданы туралы теорема

2 3 – теорема. Тіктөртбұрыштың ауданы оның іргелес жатқан екі қабырғасының көбейтіндісіне тең.

S = ab

5 – слайд Тіктөртбұрыштың ауданы туралы теорема

Теореманың дәлелі:

Төртбұрыштың а және b қабырғаларының ұзындықтарына байланысты теореманың дәлелін үш жағдайға бөлеміз:

1) a мен b – натурал сандар

2) a мен b – ондық бөлшектер

3) а мен b – шексіз ондық бөлшек

6 – слайд Тіктөртбұрыштың ауданы туралы теорема

Теореманың дәлелі:

1. a мен b – натурал сандар.

Ұзындығы а болған қабырғасын а бөлікке, ал ұзындығы b болған қабырғасын b бөлікке бөлеміз.

Сонда, бізде бірлік квадраттар шығады. Ал, ол квадраттардың жалпы саны ab. Бірлік квадраттың ауданы 1 болғандықтан, төртбұрыштың ауданы 1*ab = ab болады.

7 – слайд Тіктөртбұрыштың ауданы туралы теорема

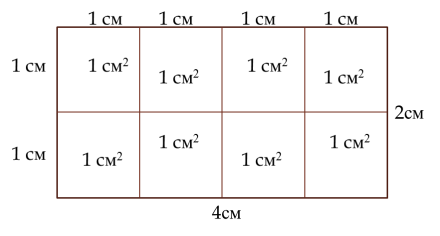М ысалы: Бізге a = 4см, b = 2см тіктөртбұрыш берілсін. а қабырғасын тең 4 бөлікке бөлеміз. b қабырғасын тең 2 бөлікке бөлеміз. Сонда, 8 бірлік квадраттар шығады. Яғни, берілген төртбұрыштың ауданы – 8cм²

8 – слайд Тіктөртбұрыштың ауданы туралы теорема

Теореманың дәлелі:

2) a мен b – ондық бөлшектер.

Сол ондық бөлшектің ұзындығына байланысты a және b қабырғаларын бірлік кесінділерге бөлеміз. Мысалы, ұзындығын 10ⁿ деп алайық, яғни бұл бірлік кесіндіміздің ұзындығы.

Ал, енді a және b қабырғаларын бірлік кесінділерге бөлгендіктен, онда 10ⁿ a және 10ⁿ b бөлшектер шығады.

Осыдан, бізде 10²ⁿ ab бірлік квадраттар шығады. Ал, әрбір бірлік квадраттың ауданы 1/10ⁿ х1/10ⁿ =1/10²ⁿ

Яғни, берілген тіктөртбұрыштың ауданы:

10²ⁿ ab х1/10²ⁿ = ab

9 – слайд Тіктөртбұрыштың ауданы туралы теорема

Теореманың дәлелі:

3) а мен b – шексіз ондық бөлшек

а және b сандарын астынан және үстінен шектейтін ондық бөлшектер алайық (шексіз емес): a₁<a<a₂ , b₁<b<b₂

a₁,a₂ , b₁,b₂ тікбұрышты үшбұрыштың қабырғалары деп алатын болсақ, біз білеміз олардың аудандары: S₁ = a₁*b₁ , S₂ = a₂*b₂

Және, қабырғалары a₁,a₂ болатын тіктөртбұрышты берілген үшбұрыштың ішіне орналастыруға болады,

Aл, берілген тіктөртбұрышты қабырғалы b₁,b₂ тіктөртбұрыштың ішіне сыйзығызуға болады.

Демек берілген тіктөртбұрыштың ауданы a₁*b₁ және a₂*b₂ сандарының аралығында болады және әрдайым a₁b₁ < ab < a₂b₂

Ал, a₁b₁ және a₂b₂ алдын ала көрсетілген кез-келген дәлдікпен алынған n мейлінше үлкен болғандағы ab-ның жуық мәндері болғандықтан,

S = ab

10 – слайд Тіктөртбұрыштың ауданы туралы теорема

М ЫСАЛ: Егер a = 5 см, b = 4 см болса, S = ?

S = ab

S = 5*4 = 20

S = 20 см²

1 1 – слайд Квадраттың ауданы

Тіктөртбұрыштың ауданы оның іргелес жатқан екі қабырғасының көбейтіндісіне тең. Ал, Квадраттың қабырғалары тең. Яғни, Квадраттың ауданы бір қабырғасының квадратына тең.

1 2 – слайд Квадраттың ауданы

МЫСАЛ: Квадраттың қабырғасы 5 см болса, S = ?

S = a²

S = 5² = 25

S = 25 см²

іі. алғашқы бекіту

Тіктөртбұрыштың ауданы туралы теорема

Теореманың дәлелі. Бүтін, бөлшек, шексіз бөлшек қабырғалары үшін

Квадраттың ауданы

ііі. құзырлылық қалыптастыру

іV. шығармашылық әрекет