3-тоқсанға арналған жиынтық бағалау

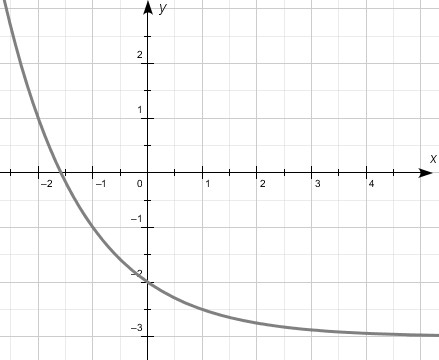
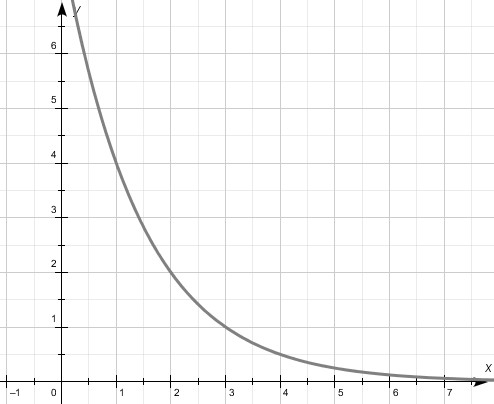
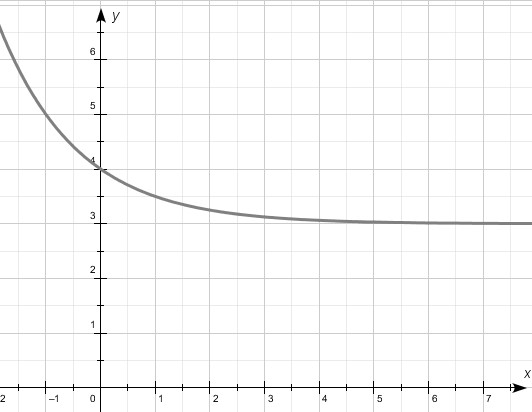
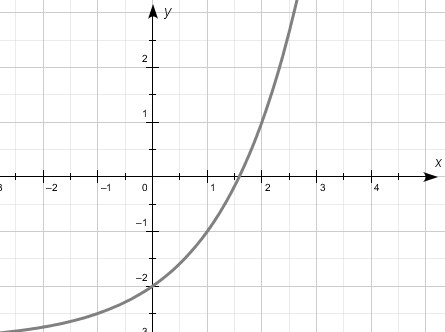
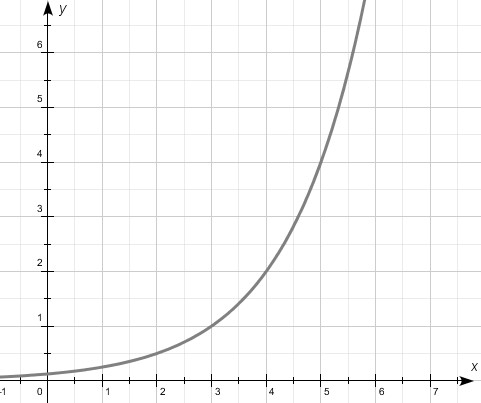
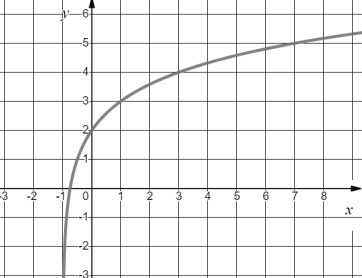
1. функциясы берілген.

1. Графиктердің қайсысы берілген функцияға сәйкес келетінін анықтаңыз.

[1]

2. Берілген функцияның өсу/кему аралықтарын жазыңыз. [1]

2. Логарифм анықтамасын қолданып, берілген теңдіктерді логарифм арқылы жазыңыз:

а) 2⁵ =32 b) 10³ =1000 c) 10⁻² ₌ 0,01. [2]

2. Есептеңіз: log₃15−log₃ 7 log₇ 5. [3]

3. y=log₂(x+1)+2 функциясының графигін салыңыз.

[2]

2. y = 4^x+1 +2x³ −7 функциясы берілген.

Берілген функцияның туындысын табыңыз. [1]

1. Берілген функцияның интегралын табыңыз. [1]

2. Егер ? = ln (? + 3) + ???₂( ? + 2) болса, мәнін есептеңіз. [2]

3. 4^x −3 2^х −4 = 0 теңдеуін шешіңіз. [2]

4. 7^x−3 −5^х−3 0 теңсіздігінің ең үлкен бүтін шешімін табыңыз. [3]

5. f (x) ₌ log₃(x₋1) және g(x) = log₃(x² −x−16) функциялары берілген.

   1. Функция графиктерінің қиылысу нүктесінің координаталарын табыңыз. [3]

   2. g(x) = log₃(x² −x−16) функциясының графигі f (x) ₌ log₃(x₋1) графигінен жоғары орналасқан аралықты анықтаңыз. [4]

Балл қою кестесі

№	Жауап	Балл	Қосымша ақпарат
1a	A	1
1b	х (− ;+ ) кемиді	1
2	???2 3 2 = 5; lg1000 = 3; lg0,01= −2	2	Кез келген бір дұрыс жазылған теңдік үшін 1 балл беріледі
3	log 5 log 5 l og3 7 log7 5 = 7 ; 7 = log3 5 log7 3 log7 3	1	Логарифмнің қасиетін қолданғаны үшін
	???3 1 5 − ???3 5 = ???3	1	Логарифмнің қасиетін қолданғаны үшін
	???3 3 = 1	1
4		2	Графиктің дұрыс формасы үшін 1 балл
5a	= 4x+1 ln4+6x2	1
5b	F C	1
6	?′ ?	1
	?′	1
7	х ?	1
	2х = 4 x = 2	1
8	х	1	Альтернативті қабылданады	шешім
	, x3	1
	Ең үлкен бүтін шешім х = 3	1
9a	log3(x−1) = log3(x2 −x−16)	1
	x2 −2x−15= 0 { ? − 1 > 0 ⇒ ?	1
		1
9b	log3(x2 −x−16>og3(x−1) немесе ???̶ ̶	1
	? { ?	1
	? , { , ?	1	Көрінеді тұспалданады	немесе
	x (5;+ ) аралығында g(x) = log3(x2 −x−16) функциясының графигі f (x) = log3(x−1) графигінен жоғары орналасқан	1	Жүктеу ЖИ арқылы жасау ЖИ арқылы жасау Бөлісу 1 - айлық Материал тарифі -96% жеңілдік 00 05 00 ҚМЖ Ашық сабақ Тәрбие сағаты Презентация БЖБ, ТЖБ тесттер Көрнекіліктер Балабақшаға арнарлған құжаттар Мақала, Эссе Дидактикалық ойындар және тағы басқа 400 000 материал Барлық 400 000 материалдарды шексіз жүктеу мүмкіндігіне ие боласыз 1 990 ₸ 49 000₸ 1 айға қосылу Таңдау Материалға шағымдану Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз Жариялаған: математика пәні мұғалімі 14 Наурыз 2024 774 Шағым жылдам қаралу үшін барынша толық ақпарат жіберіңіз Шағымды қалдыру ТЖБ-3 алгебра 11-сынып, 3-тоқсан ҚГБ Тақырып бойынша 11 материал табылды ТЖБ-3 алгебра 11-сынып, 3-тоқсан ҚГБ Материал туралы қысқаша түсінік ТЖБ-3 алгебра 11-сынып, 3-тоқсан ҚГБ Материалды жүктеу Материалдың қысқаша нұсқасы 3-тоқсанға арналған жиынтық бағалау 1. функциясы берілген. Графиктердің қайсысы берілген функцияға сәйкес келетінін анықтаңыз. А В С D E [1] Берілген функцияның өсу/кему аралықтарын жазыңыз. [1] Логарифм анықтамасын қолданып, берілген теңдіктерді логарифм арқылы жазыңыз: а) 25 =32 b) 103 =1000 c) 10−2 = 0,01. [2] Есептеңіз: log315−log3 7 log7 5. [3] y=log2(x+1)+2 функциясының графигін салыңыз. [2] y = 4x+1 +2x3 −7 функциясы берілген. Берілген функцияның туындысын табыңыз. [1] Берілген функцияның интегралын табыңыз. [1] Егер ? = ln (? + 3) + ???2( ? + 2) болса, мәнін есептеңіз. [2] 4x −3 2х −4 = 0 теңдеуін шешіңіз. [2] 7x−3 −5х−3 0 теңсіздігінің ең үлкен бүтін шешімін табыңыз. [3] f (x) = log3(x−1) және g(x) = log3(x2 −x−16) функциялары берілген. Функция графиктерінің қиылысу нүктесінің координаталарын табыңыз. [3] g(x) = log3(x2 −x−16) функциясының графигі f (x) = log3(x−1) графигінен жоғары орналасқан аралықты анықтаңыз. [4] Балл қою кестесі № Жауап Балл Қосымша ақпарат 1a A 1 1b х (− ;+ ) кемиді 1 2 ???2 3 2 = 5; lg1000 = 3; lg0,01= −2 2 Кез келген бір дұрыс жазылған теңдік үшін 1 балл беріледі 3 log 5 log 5 l og3 7 log7 5 = 7 ; 7 = log3 5 log7 3 log7 3 1 Логарифмнің қасиетін қолданғаны үшін ???3 1 5 − ???3 5 = ???3 1 Логарифмнің қасиетін қолданғаны үшін ???3 3 = 1 1 4 2 Графиктің дұрыс формасы үшін 1 балл 5a = 4x+1 ln4+6x2 1 5b F C 1 6 ?′ ? 1 ?′ 1 7 х ? 1 2х = 4 x = 2 1 8 х 1 Альтернативті қабылданады шешім , x3 1 Ең үлкен бүтін шешім х = 3 1 9a log3(x−1) = log3(x2 −x−16) 1 x2 −2x−15= 0 { ? − 1 > 0 ⇒ ? 1 1 9b log3(x2 −x−16>og3(x−1) немесе ???̶ ̶ 1 ? { ? 1 ? , { , ? 1 Көрінеді тұспалданады немесе x (5;+ ) аралығында g(x) = log3(x2 −x−16) функциясының графигі f (x) = log3(x−1) графигінен жоғары орналасқан 1 Материалды жүктеу Жүктеу Сақтау Бөлісу ЖИ арқылы жасау Файл форматы: docx Алгебра Басқа 11 сынып 14.03.2024 774 Жүктеу Сақтау ЖИ арқылы жасау Жариялаған: математика пәні мұғалімі Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз, шағым қалдыра аласыз Қазақстандағы ең үлкен материалдар базасынан іздеу Сіз үшін 400 000 ұстаздардың еңбегі мен тәжірибесін біріктіріп, ең үлкен материалдар базасын жасадық. Төменде керек материалды іздеп, жүктеп алып сабағыңызға қолдана аласыз Іздеу Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз! Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі. Толығырақ Оқу-ағарту министірлігінің ресми жауабы Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз! Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз! Жариялау Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз! Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз! Жариялау Министірлікпен келісілген курстар тізімі Химия пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Тарих пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Биология пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Ағылшын тілі пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ География пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Информатика пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Мектепке дейінгі білім беру бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ «Қазақ тілі» жəне «Қазақ əдебиеті» бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Дене шынықтыру пәні бойынша педагогтің пәндік және кәсіби құзыреттілігін дамыту 80/108 сағат Толығырақ Білім алушылардың білім сапасын арттыру мақсатында сабақта цифрлық технологияларды қолдану 80/108 сағат Толығырақ Инклюзивті білім беру жүйесінде ерекше білім беру қажеттілігі бар білім алушыға психологиялық-педагогикалық қолдау көрсету бойынша педагогтердің кәсіби және пәндік құзыреттіліктерін дамыту 80/108 сағат Толығырақ