
Тақырыбы: Төртбұрыштардың ауданын табу.
Төртбұрыш – төрт қабырғасы және төрт бұрышы бар жалпақ геометриялық фигура. Геометрияда төртбұрыштардың ауданын табу оқу тапсырмаларында да, нақты өмірде де жиі кездесетін маңызды міндеттердің бірі болып табылады, мысалы, бөлмелердің, жер учаскелерінің немесе құрылыс жобаларының ауданын есептеу кезінде. Төртбұрыштың пішініне байланысты оның ауданын әртүрлі тәсілдермен есептеуге болады. Бұл мақалада төртбұрыштардың негізгі түрлерін және олардың ауданын қалай есептеу керектігін қарастырамыз.
Төртбұрыштардың негізгі түрлері:
Төртбұрыштар пішіні мен бұрыштарына қарай бірнеше түрге бөлінеді. Ең көп тарағандарына тіктөртбұрыш, шаршы, параллелограмм, ромб және трапеция жатады. Олардың әрқайсысының өзіндік сипаттамалары мен ауданды табу формулалары бар.
1. Тіктөртбұрыш
Анықтама 1: Тіктөртбұрыш деп барлық бұрыштары тік (90 градус) және қарама-қарсы қабырғалары параллель және ұзындығы бірдей төртбұрышты айтады. Бұл төртбұрыштардың негізгі түрлерінің бірі.
Сипаты:
- Тік төртбұрыштың қарама-қарсы қабырғалары тең.
- Барлық бұрыштар тең және 90 градусқа тең.
- Тік төртбұрыштың диагональдары тең, бір-бірін қиып, екіге бөледі.
Қолданылуы: Тіктөртбұрыштар құрылыста (мысалы, қабырғалардың немесе бөлмелердің ауданын есептеу кезінде), сондай-ақ дизайн және сәулет сияқты салаларда жиі кездеседі.
2. Квадрат (тіктөртбұрыштың ерекше жағдайы)
Анықтама 2: Шаршы - барлық қабырғалары тең тіктөртбұрыштың ерекше жағдайы. Барлық бұрыштар да 90 градус.
Сипаты:
- Шаршының төрт қабырғасы тең.
- Барлық бұрыштар тік бұрыштар, 90 градус.
- Шаршының диагональдары тең, тік бұрыш жасап қиылысады және бір-бірін екіге бөледі.
Қолданылуы: Шаршы симметрияға қатысты әртүрлі есептерде жиі кездеседі, мысалы, плиткаларды, паркетті жобалауда, сондай-ақ қалыпты пішіні бар объектілердің ауданын есептеуде.
3. Параллелограмм
Анықтама 3: Параллелограмм деп қарама-қарсы қабырғалары жұппен параллель болатын төртбұрышты айтады. Бұл тіктөртбұрышты жалпылау, бірақ қабырғалар арасындағы бұрыштар 90 градустан басқа болуы мүмкін.
Сипаты:
- Параллелограмның қарама-қарсы қабырғаларының ұзындығы мен параллельдігі бірдей.
- Қарама-қарсы бұрыштар тең.
- Бір қабырғаға іргелес бұрыштардың қосындысы 180 градус.
- Параллелограммның диагональдары бір-бірін қиып, екіге бөледі, бірақ міндетті түрде тең емес.
Параллелограммдардың ерекше түрлері:
- Ромб: барлық қабырғалары тең, бірақ бұрыштары міндетті түрде 90 градус болмайтын параллелограмның ерекше жағдайы.
- Тіктөртбұрыш: барлық бұрыштары 90 градусқа тең болатын параллелограмның ерекше жағдайы.
Қолданылуы: Параллелограммдар құрылыста және сәулетте көлбеу шатырларды, жақтауларды және басқа құрылымдарды жасау кезінде жиі кездеседі.
4. Ромбты төртбұрыш (диагональ)
Анықтама 4: Қабырғаларымен тік бұрыш жасайтын диагональдары бар тіктөртбұрыш. Бұл симметрия мәселелерінде немесе күрделі геометриялық есептерді шешуде пайда болатын тіктөртбұрыштың сирек қарастырылатын түрі.
Сипаты:
- Диагональдар 90 градус бұрышпен қиылысады.
- Қабырғалары тең, бірақ олардың арасындағы бұрыштар әрқашан дұрыс бола бермейді.
Қолданылуы: Тіктөртбұрыштың бұл түрін арнайы есептер мен теориялық геометриядан табуға болады.
5. Трапеция
Анықтама 5: Трапеция деп тек екі қарама-қарсы қабырғасы параллель болатын төртбұрышты айтады. Бұл параллель қабырғалар табандар, ал қалған екеуі қабырғалар деп аталады.
Сипаты:
- Трапецияның екі қабырғасы ғана параллель (негіздері).
- Тараптар тең немесе тең емес болуы мүмкін.
- Трапециялар болуы мүмкін:
- Тең қырлы – жақтары тең болса;
- Тікбұрышты – егер негіз мен қабырға арасындағы бұрыштардың бірі 90 градус болса.
Қолданылуы: Трапециялар геометрия есептерінде және нақты өмірде жер учаскелерін есептеу кезінде, сондай-ақ сәулет пен құрылыста жиі кездеседі.
Төртбұрыштардың ауданын табу формулалары.
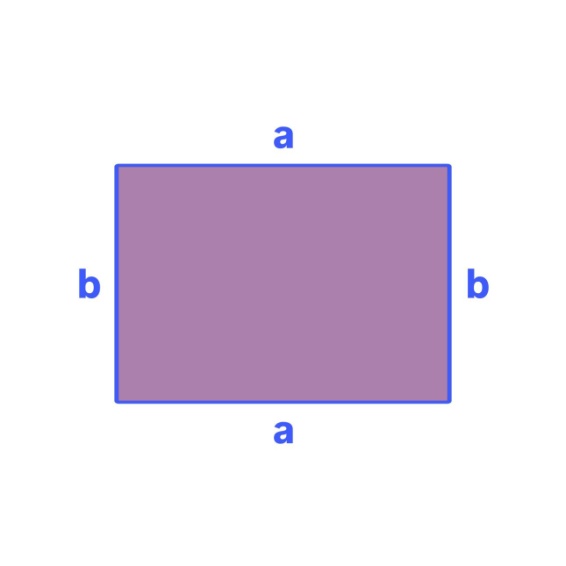
1. Тіктөртбұрыштың ауданын табу форуласы:

Мұндағы –
ұзындығы,
–
ұзындығы,  -
ені.
-
ені.
Мысал 1.
Берілгені:Ұзындығы 8см, ені 5 см болатын тіктөртбұрыштың ауданын табыңыз.
Шешуі:

Жауабы:
 .
.
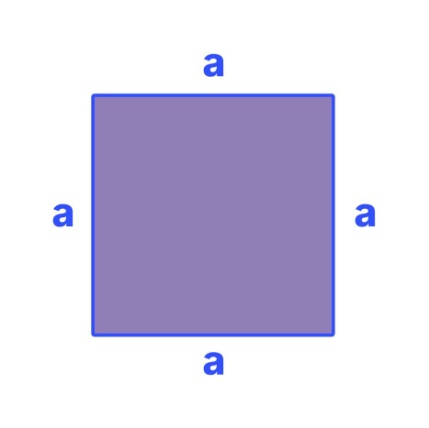
2. Квадраттың ауданын табу формуласы:

Мұндағы
 - квадраттың
қабырғасының ұзындығы.
- квадраттың
қабырғасының ұзындығы.
Мысал 2.
Берілгені: Қабырғасы 6см болатын квалраттың ауданын табыңыз.
Шешуі:

Жауабы: .
.
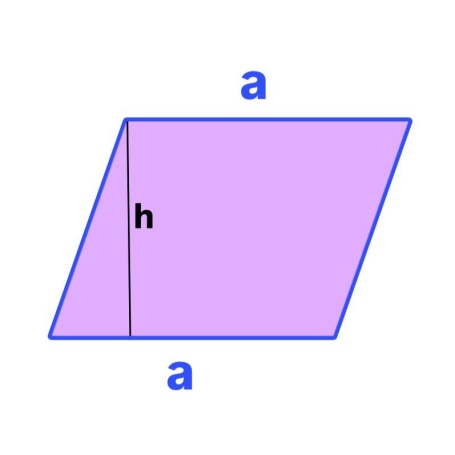
3. Параллелограммның ауданын табу формуласы:

Мұндағы
 – табанының
ұзындығы,
– табанының
ұзындығы,  – табанына түсірілген
биіктіктің ұзындығы.
– табанына түсірілген
биіктіктің ұзындығы.
Мысал 3.
Берілгені: Табанының ұзындығы 7см, ал биіктігі 4см болатын параллелограммның ауданын табыңыз.
Шешуі:

Жауабы:
 .
.
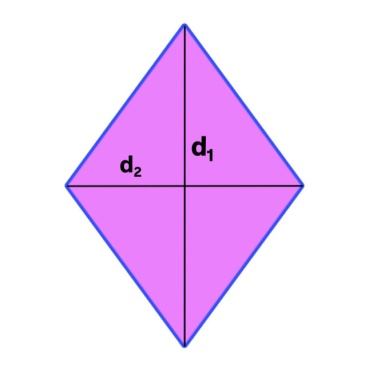
4. Ромбтың ауданын табу формуласы:

Мұндағы
 және
және  – ромбтың
диагональдарының ұзындығы.
– ромбтың
диагональдарының ұзындығы.
Мысал 4.
Берілгені: Диагоналдарының ұзындығы 10см және 8см болатын ромбтың ауданын табыңыз.
Шешуі:

Жауабы:
 .
.
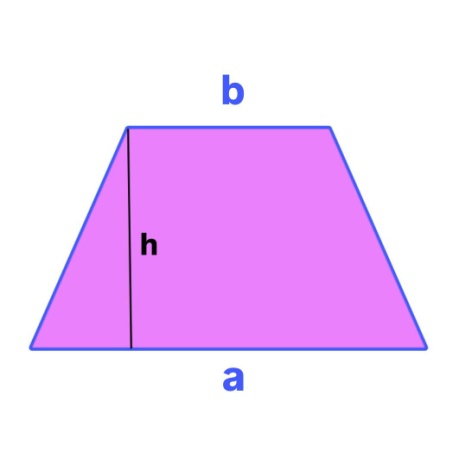
5. Тарпецияның ауданын табу формуласы:

Мұндағы
 және
және  – табандарының
ұзындықтары,
– табандарының
ұзындықтары,  – табандарының арасына
түсірілген биіктіктің ұзындығы.
– табандарының арасына
түсірілген биіктіктің ұзындығы.
Мысал 5.
Берілгені: Табандарының ұзындығы 9см және 5см болатын және табандарының арасындағы биіктіктің ұзындығы 6см болатын трапецияның ауданын табыңыз.
Шешуі:

Жауабы: .
.
Қорытынды
Бұл мақалада төртбұрыштардың негізгі түрлері және олардың ауданын табу формулалары талқыланды. Бұл формулаларды дұрыс пайдалану бөлмелердің ауданын есептеуден бастап күрделі құрылыс есептеулеріне дейін геометрияға қатысты көптеген практикалық мәселелерді шешуге көмектеседі. Геометрияның негіздерін түсіну математикалық білімді өмірде дәлірек және тиімді пайдалануға мүмкіндік береді.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Төртбұрыштардың ауданын табу
Төртбұрыштардың ауданын табу
Тақырыбы: Төртбұрыштардың ауданын табу.
Төртбұрыш – төрт қабырғасы және төрт бұрышы бар жалпақ геометриялық фигура. Геометрияда төртбұрыштардың ауданын табу оқу тапсырмаларында да, нақты өмірде де жиі кездесетін маңызды міндеттердің бірі болып табылады, мысалы, бөлмелердің, жер учаскелерінің немесе құрылыс жобаларының ауданын есептеу кезінде. Төртбұрыштың пішініне байланысты оның ауданын әртүрлі тәсілдермен есептеуге болады. Бұл мақалада төртбұрыштардың негізгі түрлерін және олардың ауданын қалай есептеу керектігін қарастырамыз.
Төртбұрыштардың негізгі түрлері:
Төртбұрыштар пішіні мен бұрыштарына қарай бірнеше түрге бөлінеді. Ең көп тарағандарына тіктөртбұрыш, шаршы, параллелограмм, ромб және трапеция жатады. Олардың әрқайсысының өзіндік сипаттамалары мен ауданды табу формулалары бар.
1. Тіктөртбұрыш
Анықтама 1: Тіктөртбұрыш деп барлық бұрыштары тік (90 градус) және қарама-қарсы қабырғалары параллель және ұзындығы бірдей төртбұрышты айтады. Бұл төртбұрыштардың негізгі түрлерінің бірі.
Сипаты:
- Тік төртбұрыштың қарама-қарсы қабырғалары тең.
- Барлық бұрыштар тең және 90 градусқа тең.
- Тік төртбұрыштың диагональдары тең, бір-бірін қиып, екіге бөледі.
Қолданылуы: Тіктөртбұрыштар құрылыста (мысалы, қабырғалардың немесе бөлмелердің ауданын есептеу кезінде), сондай-ақ дизайн және сәулет сияқты салаларда жиі кездеседі.
2. Квадрат (тіктөртбұрыштың ерекше жағдайы)
Анықтама 2: Шаршы - барлық қабырғалары тең тіктөртбұрыштың ерекше жағдайы. Барлық бұрыштар да 90 градус.
Сипаты:
- Шаршының төрт қабырғасы тең.
- Барлық бұрыштар тік бұрыштар, 90 градус.
- Шаршының диагональдары тең, тік бұрыш жасап қиылысады және бір-бірін екіге бөледі.
Қолданылуы: Шаршы симметрияға қатысты әртүрлі есептерде жиі кездеседі, мысалы, плиткаларды, паркетті жобалауда, сондай-ақ қалыпты пішіні бар объектілердің ауданын есептеуде.
3. Параллелограмм
Анықтама 3: Параллелограмм деп қарама-қарсы қабырғалары жұппен параллель болатын төртбұрышты айтады. Бұл тіктөртбұрышты жалпылау, бірақ қабырғалар арасындағы бұрыштар 90 градустан басқа болуы мүмкін.
Сипаты:
- Параллелограмның қарама-қарсы қабырғаларының ұзындығы мен параллельдігі бірдей.
- Қарама-қарсы бұрыштар тең.
- Бір қабырғаға іргелес бұрыштардың қосындысы 180 градус.
- Параллелограммның диагональдары бір-бірін қиып, екіге бөледі, бірақ міндетті түрде тең емес.
Параллелограммдардың ерекше түрлері:
- Ромб: барлық қабырғалары тең, бірақ бұрыштары міндетті түрде 90 градус болмайтын параллелограмның ерекше жағдайы.
- Тіктөртбұрыш: барлық бұрыштары 90 градусқа тең болатын параллелограмның ерекше жағдайы.
Қолданылуы: Параллелограммдар құрылыста және сәулетте көлбеу шатырларды, жақтауларды және басқа құрылымдарды жасау кезінде жиі кездеседі.
4. Ромбты төртбұрыш (диагональ)
Анықтама 4: Қабырғаларымен тік бұрыш жасайтын диагональдары бар тіктөртбұрыш. Бұл симметрия мәселелерінде немесе күрделі геометриялық есептерді шешуде пайда болатын тіктөртбұрыштың сирек қарастырылатын түрі.
Сипаты:
- Диагональдар 90 градус бұрышпен қиылысады.
- Қабырғалары тең, бірақ олардың арасындағы бұрыштар әрқашан дұрыс бола бермейді.
Қолданылуы: Тіктөртбұрыштың бұл түрін арнайы есептер мен теориялық геометриядан табуға болады.
5. Трапеция
Анықтама 5: Трапеция деп тек екі қарама-қарсы қабырғасы параллель болатын төртбұрышты айтады. Бұл параллель қабырғалар табандар, ал қалған екеуі қабырғалар деп аталады.
Сипаты:
- Трапецияның екі қабырғасы ғана параллель (негіздері).
- Тараптар тең немесе тең емес болуы мүмкін.
- Трапециялар болуы мүмкін:
- Тең қырлы – жақтары тең болса;
- Тікбұрышты – егер негіз мен қабырға арасындағы бұрыштардың бірі 90 градус болса.
Қолданылуы: Трапециялар геометрия есептерінде және нақты өмірде жер учаскелерін есептеу кезінде, сондай-ақ сәулет пен құрылыста жиі кездеседі.
Төртбұрыштардың ауданын табу формулалары.
1. Тіктөртбұрыштың ауданын табу форуласы:

Мұндағы –
ұзындығы,
–
ұзындығы,  -
ені.
-
ені.

Мысал 1.
Берілгені:Ұзындығы 8см, ені 5 см болатын тіктөртбұрыштың ауданын табыңыз.
Шешуі:

Жауабы:
 .
.
2. Квадраттың ауданын табу формуласы:

Мұндағы
 - квадраттың
қабырғасының ұзындығы.
- квадраттың
қабырғасының ұзындығы.

Мысал 2.
Берілгені: Қабырғасы 6см болатын квалраттың ауданын табыңыз.
Шешуі:

Жауабы: .
.
3. Параллелограммның ауданын табу формуласы:

Мұндағы
 – табанының
ұзындығы,
– табанының
ұзындығы,  – табанына түсірілген
биіктіктің ұзындығы.
– табанына түсірілген
биіктіктің ұзындығы.

Мысал 3.
Берілгені: Табанының ұзындығы 7см, ал биіктігі 4см болатын параллелограммның ауданын табыңыз.
Шешуі:

Жауабы:
 .
.
4. Ромбтың ауданын табу формуласы:

Мұндағы
 және
және  – ромбтың
диагональдарының ұзындығы.
– ромбтың
диагональдарының ұзындығы.

Мысал 4.
Берілгені: Диагоналдарының ұзындығы 10см және 8см болатын ромбтың ауданын табыңыз.
Шешуі:

Жауабы:
 .
.
5. Тарпецияның ауданын табу формуласы:

Мұндағы
 және
және  – табандарының
ұзындықтары,
– табандарының
ұзындықтары,  – табандарының арасына
түсірілген биіктіктің ұзындығы.
– табандарының арасына
түсірілген биіктіктің ұзындығы.

Мысал 5.
Берілгені: Табандарының ұзындығы 9см және 5см болатын және табандарының арасындағы биіктіктің ұзындығы 6см болатын трапецияның ауданын табыңыз.
Шешуі:

Жауабы: .
.
Қорытынды
Бұл мақалада төртбұрыштардың негізгі түрлері және олардың ауданын табу формулалары талқыланды. Бұл формулаларды дұрыс пайдалану бөлмелердің ауданын есептеуден бастап күрделі құрылыс есептеулеріне дейін геометрияға қатысты көптеген практикалық мәселелерді шешуге көмектеседі. Геометрияның негіздерін түсіну математикалық білімді өмірде дәлірек және тиімді пайдалануға мүмкіндік береді.

шағым қалдыра аласыз















