
Тригонометрия тарихы математика сабақтарында
Карыбаева Сауле Шешкеновна – Қарақол орта мектеп-балабақшасының
математика пәнінің мұғаліміі
Тригонометрия ұғымдарымен мектеп оқушылары алғаш рет планиметрия курсында танысады. Кез келген жаңа ұғымға оқушы тарапынан: «Бұл жаңалықты ең алғаш кім және не үшін ашты. Бізге ол қаншалықты қажет?» деген сұрақ қойылуы заңды. Мұғалімді де жаңа тақырыпты оқыту қажеттілігі, дәлірек айтсақ, оқушының оқу қызметінің қажеттілігі, жаңа ұғымының қандай тәжірибелік негізде пайда болғандығы, тарихи даму кезеңдері, қазіргі кезде ғылым мен тәжірибеде алатын орны толғандырады. Оқушының өзін қызықтыратын объектіге талғап қарауынан сол объектінін (жаңа ұғымның) сырын ашуға деген тілек, талпыныс, қызығу, қажетсіну себептері туындайды «Таңырқау –жаңалық ашудың анасы» -деп физик Луи де Бройль тегін айтпаған Оқушыны бәрінен гөрі көп таңырқатып, оны проблемалық ситуацияға душар ететін нәрсе –ақпараттың жаңалығы, әдеттен тысқарылығы, кенеттілігі, оғаштығы, бұрынғы түсініктерге сәйкессіздігі, әсемдігі болып саналады. Тұтас алғанда бұлар танымдық қызығудың сезімдік –ойлау процестерін ширата түсетін аса күшті түрткілер болып табылады.
Б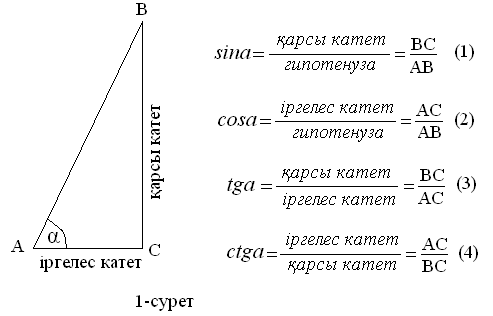 ұл
мақалада біз мұғалім сабақты қызықты өткізу үшін тригономтерияның
алғашқы ұғымдарынан бастап, қандай тарихи материалдарды
пайдалануына болатынына тоқталмақпыз.
ұл
мақалада біз мұғалім сабақты қызықты өткізу үшін тригономтерияның
алғашқы ұғымдарынан бастап, қандай тарихи материалдарды
пайдалануына болатынына тоқталмақпыз.
Сонымен, ең алғаш тригонометрия-лық қатыстар геометрия курсында енгізіледі. Тік бұрышты үшбұрыш қарастырылады (1–сурет)
Оқушылар бұл анықтамаларды оңай есте сақтауы үшін (1-4) тірек сигналдарын пайдалану тиімді. Келтірілген анықтамалар мен белгілеулер оқушы көңіліне қонымсыз бұрынғы түсініктерге сәйкессіз, оғаш, күрделі көрінуі мүмкін. Сондықтан оқу материалын түсіну үшін жаңа ұғымның тереңіне үңіліп, тарихына назар аударамыз.
Ежелгі мысырлықтар (б.э.д.ІІ ғ., мүмкін одан да бұрын) құрылыс салып, үй тұрғызу, жер өлшеу үшін қарапайым құрал –жіпті қолданған. Олар құрылыста жіп керетін арнайы мамандарды гарпедонаптар деп атаған. Жіп –кірпіштер мен тастарды қалағанда түзу сызық сызу үшін қажет болған. Сызық–линия (орысша). Этимологиясына үңілсек, линия латынның linea –«жіп» сөзінен алынған, бұл сөз XVIII ғасырдың басында неміс тілінен енген сөз.
Сондай-ақ жіп құрылыста тік бұрыш алу үшін қажет болған, өйткені тік бұрышқа шаблон (үлгі) болатындай табиғи заттар болмаған.
Е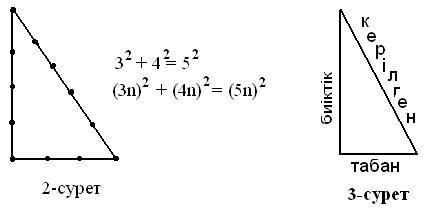 желгі
мысырлықтар жіпті түйін салып тең 12-ге бөліп, ұштарын біріктірген.
Содан кейін қабырғалары 3,4,5 бөлікке тең үшбұрыш шығатындай етіп,
жіпті керген кезде үлкен қабырғаға қарсы жатқан бұрыш тік болған.
Содан бері қабырғалары 3, 4, 5 бірлікке тең
үшбұрышты–египеттік үшбұрыш деп атайды.
(2–сурет).
желгі
мысырлықтар жіпті түйін салып тең 12-ге бөліп, ұштарын біріктірген.
Содан кейін қабырғалары 3,4,5 бөлікке тең үшбұрыш шығатындай етіп,
жіпті керген кезде үлкен қабырғаға қарсы жатқан бұрыш тік болған.
Содан бері қабырғалары 3, 4, 5 бірлікке тең
үшбұрышты–египеттік үшбұрыш деп атайды.
(2–сурет).
Сондай-ақ тік бұрышты үшбұрыштар Ахмес папирусында кездеседі, ал вавилондық геометрияда тіпті маңызды орын алады. «Гипотенуза» гректің «ипотейнуза» - «керілген», «катет» гректің «катетос» - «перпендикуляр», «тіп-тік» сөзінен алынған. Орта ғасырларда катет–тік бұрышты үшбұрыштың биіктігі, екінші катет–табаны (3сурет) атала бастайды.
Тік бұрышты үшбұрыштың қабырғаларының қатынасын қарастыру ұқсастықтан туындаған. Ежелгі мысырлықтар пирамида құрылысын салу барысында, пирамида жағын қандай бұрышпен тегістеу керектігін білген.
4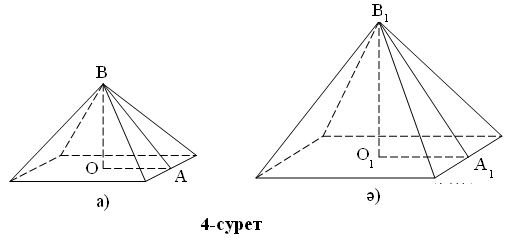 (а) суретте
пирамиданың кішкене макеті, 4(ә) –суретте пирамиданың өзі
көрсетілген делік. Сонда АОВ үшбұрышының қабырғаларының қатынасы
сәйкесінше синус, косинус, тангенс, котангенсті бейнелесе, онда
оған ұқсас пирамиданың өзінде де сол қатынастар сақталады. Мысалы
пирамида биіктігінің апофемаға қатынасы
ОВ:АВ=О1В1:А1В1. Осыдан кейін ұқсас үшбұрыштардың сәйкес бұрыштары тең,
олай болса тең бұрыштардың тригонометриялық функциялары тең деген
қорытындыға келеміз.
(а) суретте
пирамиданың кішкене макеті, 4(ә) –суретте пирамиданың өзі
көрсетілген делік. Сонда АОВ үшбұрышының қабырғаларының қатынасы
сәйкесінше синус, косинус, тангенс, котангенсті бейнелесе, онда
оған ұқсас пирамиданың өзінде де сол қатынастар сақталады. Мысалы
пирамида биіктігінің апофемаға қатынасы
ОВ:АВ=О1В1:А1В1. Осыдан кейін ұқсас үшбұрыштардың сәйкес бұрыштары тең,
олай болса тең бұрыштардың тригонометриялық функциялары тең деген
қорытындыға келеміз.
Аңыз бойынша Фалес (б.э.д. VI ғ. ежелгі грек оқымыстысы) бір пирамиданың көлеңкесі бойынша оның биіктігін дәл тауып, мысыр патшасы Амазисті таң қалдырған көрінеді. Фалестің болжамы ұқсастыққа негізделгені айқын. Күннің бір уағында дененің көлеңкесі дене биіктігіне тең болады. Фалес өз көлеңкесі өзінің бойының ұзындығына тең болатын кезді күтіп, дәл сол уақытта пирамида көлеңкесінің ұзындығын өлшеп, биіктігін анықтаған.
Ерте кездерден бастап, үшбұрыштардың ұқсастық қасиетіне сүйеніп, кез келген нүктеден адам жете алмайтын нүктеге дейінгі қашықтықтарды есептейтін мысалдарды кездестіруге болады.
«Тригонометрия» сөзі гректің «тригоном» -«үшбұрыш», «метрейн» -«өлшеуіш» сөздерінен алынған. Бұл сөз алғаш рет (1505) неміс геологы және математигі Питискустың еңбегінде кездеседі. Басқа сөзбен айтқанда тригонометрия – үщбұрыштарды өлшеу жөніндегі ғылым.
Ерте кезде тригонометрия астрономияның бір бөлімі ретінде қарастырылды. Теңізде жүзу, жұлдыздар бойынша кеменің дұрыс бағытын анықтау, күннің, айдың тұтылуын анықтау, бетпақ далада керуеннің қозғалыс жолын айқындау, дәл күнтізбе енгізу, жер өңдеу, т.б. мәселелер астрономияның онымен қоса тригонометрияның дамуына жол ашты. Сфералық және жазықтықтағы тригонометрия қатар дамыды.
Тригонометриялық
есептеулердің бастамасы ретінде алғашқы тригонометриялық кестелерді
(хордалар кестесі) б.э.д. ІІ ғасырда ежелгі грек астрономы Гиппарх
жасады. Кейіннен тригонометрия туралы толық мағлұматтар грек
астрономы Птолемейдің (б.э. ІІ ғ) 13 кітаптан т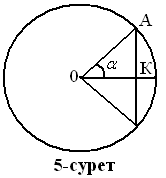 ұратын
«Альмагест» еңбегінде қамтылды. Түзу сызықты және сфералық
тригонометрия мағлұматтары «Альмагестің» І кітабында баяндалды.
Қазіргі айтылатын α бұрышының синусы, ол кітапта шамасы 2α –ға тең
центрлік бұрышқа тірелетін жарты хорда ретінде зерттеледі (5
–сурет). Вавилондық күнтізбеде бір жылда 360 күн болған. Соған
негіздеп Птолемей шеңберді 360º градусқа, диаметрді 120 бөлікке
бөлді. 1 градусты 60´ минутқа, 1 минутты 60´´секундқа, 1 секундты
60´´´ терцинаға, т.с.с. бөлді (ол кезде 60-тың санау жүйесі
қалыптасқан). Гипотенузасы диаметрге тең тік бұрышты үшбұрыш үшін
Пифагор теоремасын былай жазды (5-сурет):
ұратын
«Альмагест» еңбегінде қамтылды. Түзу сызықты және сфералық
тригонометрия мағлұматтары «Альмагестің» І кітабында баяндалды.
Қазіргі айтылатын α бұрышының синусы, ол кітапта шамасы 2α –ға тең
центрлік бұрышқа тірелетін жарты хорда ретінде зерттеледі (5
–сурет). Вавилондық күнтізбеде бір жылда 360 күн болған. Соған
негіздеп Птолемей шеңберді 360º градусқа, диаметрді 120 бөлікке
бөлді. 1 градусты 60´ минутқа, 1 минутты 60´´секундқа, 1 секундты
60´´´ терцинаға, т.с.с. бөлді (ол кезде 60-тың санау жүйесі
қалыптасқан). Гипотенузасы диаметрге тең тік бұрышты үшбұрыш үшін
Пифагор теоремасын былай жазды (5-сурет):
(хорда а)2 + (хорда (1800 - а)2 = (диаметр) 2
Бұл бүгіндегі sin2 α+cos2α=1 формуласына сәйкес келеді. Хорда грек сөзі – «садақ кермесі» дегенді білдіреді. Птолемей 5 ондық таңбаға дейінгі дәлдікпен синустар (хордалар) кестесін жасады. Ол кез үшін хордалар кестесі көптеген практикалық, астрономиялық есептерді шешуде зор маңызға ие болды. Келесі кезеңде тригонометрияның қарыштап дамуына үнді оқымыстылары зор үлес қосты. IV-V ғасырларда арнайы терминдер үндінің ұлы ғалымы Ариабхаттың (476-550 ж.ж. шамасында) астрономиялық еңбектерінде көріне бастады.. Үндінің алғашқы Жер серігі де осы есіммен аталады. Ол АК (5-сурет) кесіндісін ардхаджива (ардха-жарты, джива-садақ кермесі) деп атайды. Кейін келе қысқаша джива атауы қалды.
VІІІ ғасырдан бастап араб математиктері джива сөзін джиба, кейіннен «джайб» -«дөңестік» сөзімен алмастырады. ХІІ ғасырда Европада латын тілі ғылым тілі ретінде бел алып тұрғанда европа ғалымдары араб тіліндегі математикалық мәтіндерді аударғанда «джайб» сөзін латынның «sinus»-«иілу», «қисықтық» сөзімен алмастырады және бұл сөз бүгінге дейін сақталып қалды. Косинус сөзі кейін пайда болды. Ол латынның «сomplementy sinus» - «толықтауыш синус» деген сөз тіркесінің қысқартылған түрі, яғни cosα=sin(900 – α).
ІХ-Х ғасырларда Орта Азия мен Таяу Шығыс математикалық зерттеулердің орталығына айналды. Араб математиктерінің еңбектерінің нәтижесінде тригонометрия жеке ғылым ретінде астрономиядан бөлініп шығады.
Х ғасырда араб математигі Абу-л-Вафа (Мұхаммед-әл-Бузджани) тангенс, котангенс, секанс, косеканс атауын енгізеді және тангенстер мен котангенстер кестесін жасайды. Сондай-ақ Мұхаммед ибн Муса әл-Хорезми (ІХ ғ.) синустар мен котангенстер кестесін жасайды.
Әбу Райхан Бируни (Х-ХІ ғ.ғ.) бірлік шеңберді енгізу арқылы есептеу жұмыстарын әлдеқайда жеңілдетеді. ХІІ ғасырды ғалым-энциклопедист, мемлекет қайраткері Насир-ад-Дин ат-Туси «Жазық төртбұрыштар» трактатында жазық және сфералық тригонометрияны математиканың жеке бөлімі ретінде астрономиядан бөлек қарастырады. Ислам елдерімен салыстырғанда Европада тригонометрия тек ХІ ғасырда жеке ғылым ретінде қалыптасып, дами бастады. Бұл кезеңнің көрнекті өкілі неміс астрономы, әрі математигі профессор Регимонтан.
Ол синустар кестесін аралығы 1 секундтан 7 ондық таңбаға дейінгі дәлдікпен жасайды және «Үшбұрыштың барлық түрлері туралы 5 кітап» атты тригонометриялық еңбегін жарыққа шығарады.
«Тангенс» латын сөзі «tangens» - «жанама» (жанама кесіндісі) дегенді білдіреді.. Бұл атауды 1583 жылы дат математигі Томас Финк енгізді. Ал, «котангенс» - «complementy tangens» - «толықтауыш тангенс» ұғымын білдіреді. Бұл атауды ең алғаш 1620 жылы ағылшын ғалымы Эдмунт Гутер енгізді.
ХVІ ғасырда француз математигі Франсуа Виет (1540-1603) тригонометрияны куб теңдеулерді шешуге қолданып, оны алгебрамен байланстырды. Сондай-ақ, ол әріпті белгілеудің негізін салды. Швейцар математигі Иоганн Бернулли (1667-1747) тригонометриялық функциялардың sinх, cosх (1739ж.) белгілеулерін пайдаланды.
ХVІІ- ХІХ ғасырларда тригонометрия математикалық анализдің бір тарауы ретінде қарастырыла бастады. Бұл орайда швейцар математигі, ұзақ жылдар Петербург ғылым академиясында қызмет еткен Леонардо Эйлердің (1707-1783) орасан зор еңбегін атап өту керек. Эйлер тригонометрияның мазмұнын жетілдіріп, бір жүйеге келтіріп, жан-жақты баяндады.
Ол бүгінде қолданылып жүрген тригонометриялық функциялардың анықтамаларын енгізді. Кез келген бұрыштың тригонометриялық функцияларын қарастырып, әрбір ширектегі функция таңбаларын анықтап, келтіру формулаларын қорытты. Аргументі бұрыш пен доға, сондай-ақ, кез келген сан болғандағы тригонометриялық функцияның қасиеттерін баяндап, формулаларын қорытты, тригонометриялық теңдеулер мен теңзіздіктерді шешуді қарастырып, sinх, cosх, tgх, сtgх, т.б. белгілеулерді пайдаланды. Эйлерден кейін тригонометрия дайын формулаларды пайдаланып есептеу түріне келіп, жұмыс ықшамдалды. Бұл теорияны ХІХ ғасырда Н.И.Лобачевский, т.б. ғалымдар жалғастырып дамытты.
Бізге белгілі тригонометриялық формулалардың көпшілігінің геометриялық формасын ежелгі грек, үнді, араб математиктері тапқан. Кейіннен Европа, Азия математиктері де дәл осы жаңалықтарды ашып, толықтырып, жүйелеген.
Мысалы: sin2α+cos2α=1, sin(α±β)=sinα*cosβ±cosα*sinβ, sin2α/2=(1–cosα)/2 формулаларын Птоломей, sinα=2sinα/2*cosα/2 формуласын Абу-л-Вафа, tg(α±β), sес(α±β) формулаларын 1706 жылы Петербург математигі Я.Герман қорытты, tg2α=2tg α/(1–tg2α) формуласын ХVІІ ғасырда ағылшын Джон Пелль, француз Г.Роберваль, т.б. математиктер әр түрлі әдістермен дәлелдеді. Ал, сtg2α=1/2(сtg α–tgα) формуласы ең алғаш Л.Эйлердің «Анализге кіріспе» еңбегінде жарық көрді. ХVІІ ғасырда дат ғалымы Тихо Браге cosα*cosβ=1/2[cos(α+β)+cos(α-β)] формуласын пайдаланған. sinα-sinβ ережесін ХVІІ ғасырда ағылшын ғалымы Джон Непер еңбектерінен кездестіруге болады.
Бүгінде тригонометрия математиканың жеке тармағы емес. Атап айтқанда, тригонометриялық функциялардың қасиеттерін математикалық анализ, ал үшбұрыштарды шешуді геометрия қарастырады.
Пайдаланылған әдебиеттер:
-
Глейзер .И. История математики в школе: VІІ-VІІІ кл. – М. Просвещение, 1982
-
Глейзер .И. История математики в школе: ІХ-Х кл. – М. Просвещение, 1983
-
Рыбников К.А. История математики: Учебник – М. Изд-во МГУ, 1994
-
Журнал «Математика в школе», №3, 2005 г.,
Шығыс Қазақстан облысы
Үржар ауданы
Тел: 87756214578
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Тригонометрия тарихы
Тригонометрия тарихы
Тригонометрия тарихы математика сабақтарында
Карыбаева Сауле Шешкеновна – Қарақол орта мектеп-балабақшасының
математика пәнінің мұғаліміі
Тригонометрия ұғымдарымен мектеп оқушылары алғаш рет планиметрия курсында танысады. Кез келген жаңа ұғымға оқушы тарапынан: «Бұл жаңалықты ең алғаш кім және не үшін ашты. Бізге ол қаншалықты қажет?» деген сұрақ қойылуы заңды. Мұғалімді де жаңа тақырыпты оқыту қажеттілігі, дәлірек айтсақ, оқушының оқу қызметінің қажеттілігі, жаңа ұғымының қандай тәжірибелік негізде пайда болғандығы, тарихи даму кезеңдері, қазіргі кезде ғылым мен тәжірибеде алатын орны толғандырады. Оқушының өзін қызықтыратын объектіге талғап қарауынан сол объектінін (жаңа ұғымның) сырын ашуға деген тілек, талпыныс, қызығу, қажетсіну себептері туындайды «Таңырқау –жаңалық ашудың анасы» -деп физик Луи де Бройль тегін айтпаған Оқушыны бәрінен гөрі көп таңырқатып, оны проблемалық ситуацияға душар ететін нәрсе –ақпараттың жаңалығы, әдеттен тысқарылығы, кенеттілігі, оғаштығы, бұрынғы түсініктерге сәйкессіздігі, әсемдігі болып саналады. Тұтас алғанда бұлар танымдық қызығудың сезімдік –ойлау процестерін ширата түсетін аса күшті түрткілер болып табылады.
Б ұл
мақалада біз мұғалім сабақты қызықты өткізу үшін тригономтерияның
алғашқы ұғымдарынан бастап, қандай тарихи материалдарды
пайдалануына болатынына тоқталмақпыз.
ұл
мақалада біз мұғалім сабақты қызықты өткізу үшін тригономтерияның
алғашқы ұғымдарынан бастап, қандай тарихи материалдарды
пайдалануына болатынына тоқталмақпыз.
Сонымен, ең алғаш тригонометрия-лық қатыстар геометрия курсында енгізіледі. Тік бұрышты үшбұрыш қарастырылады (1–сурет)
Оқушылар бұл анықтамаларды оңай есте сақтауы үшін (1-4) тірек сигналдарын пайдалану тиімді. Келтірілген анықтамалар мен белгілеулер оқушы көңіліне қонымсыз бұрынғы түсініктерге сәйкессіз, оғаш, күрделі көрінуі мүмкін. Сондықтан оқу материалын түсіну үшін жаңа ұғымның тереңіне үңіліп, тарихына назар аударамыз.
Ежелгі мысырлықтар (б.э.д.ІІ ғ., мүмкін одан да бұрын) құрылыс салып, үй тұрғызу, жер өлшеу үшін қарапайым құрал –жіпті қолданған. Олар құрылыста жіп керетін арнайы мамандарды гарпедонаптар деп атаған. Жіп –кірпіштер мен тастарды қалағанда түзу сызық сызу үшін қажет болған. Сызық–линия (орысша). Этимологиясына үңілсек, линия латынның linea –«жіп» сөзінен алынған, бұл сөз XVIII ғасырдың басында неміс тілінен енген сөз.
Сондай-ақ жіп құрылыста тік бұрыш алу үшін қажет болған, өйткені тік бұрышқа шаблон (үлгі) болатындай табиғи заттар болмаған.
Е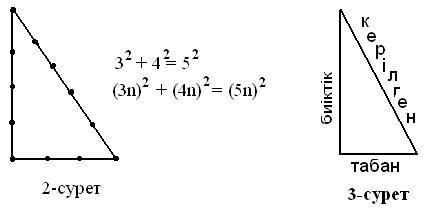 желгі
мысырлықтар жіпті түйін салып тең 12-ге бөліп, ұштарын біріктірген.
Содан кейін қабырғалары 3,4,5 бөлікке тең үшбұрыш шығатындай етіп,
жіпті керген кезде үлкен қабырғаға қарсы жатқан бұрыш тік болған.
Содан бері қабырғалары 3, 4, 5 бірлікке тең
үшбұрышты–египеттік үшбұрыш деп атайды.
(2–сурет).
желгі
мысырлықтар жіпті түйін салып тең 12-ге бөліп, ұштарын біріктірген.
Содан кейін қабырғалары 3,4,5 бөлікке тең үшбұрыш шығатындай етіп,
жіпті керген кезде үлкен қабырғаға қарсы жатқан бұрыш тік болған.
Содан бері қабырғалары 3, 4, 5 бірлікке тең
үшбұрышты–египеттік үшбұрыш деп атайды.
(2–сурет).
Сондай-ақ тік бұрышты үшбұрыштар Ахмес папирусында кездеседі, ал вавилондық геометрияда тіпті маңызды орын алады. «Гипотенуза» гректің «ипотейнуза» - «керілген», «катет» гректің «катетос» - «перпендикуляр», «тіп-тік» сөзінен алынған. Орта ғасырларда катет–тік бұрышты үшбұрыштың биіктігі, екінші катет–табаны (3сурет) атала бастайды.
Тік бұрышты үшбұрыштың қабырғаларының қатынасын қарастыру ұқсастықтан туындаған. Ежелгі мысырлықтар пирамида құрылысын салу барысында, пирамида жағын қандай бұрышпен тегістеу керектігін білген.
4 (а) суретте
пирамиданың кішкене макеті, 4(ә) –суретте пирамиданың өзі
көрсетілген делік. Сонда АОВ үшбұрышының қабырғаларының қатынасы
сәйкесінше синус, косинус, тангенс, котангенсті бейнелесе, онда
оған ұқсас пирамиданың өзінде де сол қатынастар сақталады. Мысалы
пирамида биіктігінің апофемаға қатынасы
ОВ:АВ=О1В1:А1В1. Осыдан кейін ұқсас үшбұрыштардың сәйкес бұрыштары тең,
олай болса тең бұрыштардың тригонометриялық функциялары тең деген
қорытындыға келеміз.
(а) суретте
пирамиданың кішкене макеті, 4(ә) –суретте пирамиданың өзі
көрсетілген делік. Сонда АОВ үшбұрышының қабырғаларының қатынасы
сәйкесінше синус, косинус, тангенс, котангенсті бейнелесе, онда
оған ұқсас пирамиданың өзінде де сол қатынастар сақталады. Мысалы
пирамида биіктігінің апофемаға қатынасы
ОВ:АВ=О1В1:А1В1. Осыдан кейін ұқсас үшбұрыштардың сәйкес бұрыштары тең,
олай болса тең бұрыштардың тригонометриялық функциялары тең деген
қорытындыға келеміз.
Аңыз бойынша Фалес (б.э.д. VI ғ. ежелгі грек оқымыстысы) бір пирамиданың көлеңкесі бойынша оның биіктігін дәл тауып, мысыр патшасы Амазисті таң қалдырған көрінеді. Фалестің болжамы ұқсастыққа негізделгені айқын. Күннің бір уағында дененің көлеңкесі дене биіктігіне тең болады. Фалес өз көлеңкесі өзінің бойының ұзындығына тең болатын кезді күтіп, дәл сол уақытта пирамида көлеңкесінің ұзындығын өлшеп, биіктігін анықтаған.
Ерте кездерден бастап, үшбұрыштардың ұқсастық қасиетіне сүйеніп, кез келген нүктеден адам жете алмайтын нүктеге дейінгі қашықтықтарды есептейтін мысалдарды кездестіруге болады.
«Тригонометрия» сөзі гректің «тригоном» -«үшбұрыш», «метрейн» -«өлшеуіш» сөздерінен алынған. Бұл сөз алғаш рет (1505) неміс геологы және математигі Питискустың еңбегінде кездеседі. Басқа сөзбен айтқанда тригонометрия – үщбұрыштарды өлшеу жөніндегі ғылым.
Ерте кезде тригонометрия астрономияның бір бөлімі ретінде қарастырылды. Теңізде жүзу, жұлдыздар бойынша кеменің дұрыс бағытын анықтау, күннің, айдың тұтылуын анықтау, бетпақ далада керуеннің қозғалыс жолын айқындау, дәл күнтізбе енгізу, жер өңдеу, т.б. мәселелер астрономияның онымен қоса тригонометрияның дамуына жол ашты. Сфералық және жазықтықтағы тригонометрия қатар дамыды.
Тригонометриялық
есептеулердің бастамасы ретінде алғашқы тригонометриялық кестелерді
(хордалар кестесі) б.э.д. ІІ ғасырда ежелгі грек астрономы Гиппарх
жасады. Кейіннен тригонометрия туралы толық мағлұматтар грек
астрономы Птолемейдің (б.э. ІІ ғ) 13 кітаптан т ұратын
«Альмагест» еңбегінде қамтылды. Түзу сызықты және сфералық
тригонометрия мағлұматтары «Альмагестің» І кітабында баяндалды.
Қазіргі айтылатын α бұрышының синусы, ол кітапта шамасы 2α –ға тең
центрлік бұрышқа тірелетін жарты хорда ретінде зерттеледі (5
–сурет). Вавилондық күнтізбеде бір жылда 360 күн болған. Соған
негіздеп Птолемей шеңберді 360º градусқа, диаметрді 120 бөлікке
бөлді. 1 градусты 60´ минутқа, 1 минутты 60´´секундқа, 1 секундты
60´´´ терцинаға, т.с.с. бөлді (ол кезде 60-тың санау жүйесі
қалыптасқан). Гипотенузасы диаметрге тең тік бұрышты үшбұрыш үшін
Пифагор теоремасын былай жазды (5-сурет):
ұратын
«Альмагест» еңбегінде қамтылды. Түзу сызықты және сфералық
тригонометрия мағлұматтары «Альмагестің» І кітабында баяндалды.
Қазіргі айтылатын α бұрышының синусы, ол кітапта шамасы 2α –ға тең
центрлік бұрышқа тірелетін жарты хорда ретінде зерттеледі (5
–сурет). Вавилондық күнтізбеде бір жылда 360 күн болған. Соған
негіздеп Птолемей шеңберді 360º градусқа, диаметрді 120 бөлікке
бөлді. 1 градусты 60´ минутқа, 1 минутты 60´´секундқа, 1 секундты
60´´´ терцинаға, т.с.с. бөлді (ол кезде 60-тың санау жүйесі
қалыптасқан). Гипотенузасы диаметрге тең тік бұрышты үшбұрыш үшін
Пифагор теоремасын былай жазды (5-сурет):
(хорда а)2 + (хорда (1800 - а)2 = (диаметр) 2
Бұл бүгіндегі sin2 α+cos2α=1 формуласына сәйкес келеді. Хорда грек сөзі – «садақ кермесі» дегенді білдіреді. Птолемей 5 ондық таңбаға дейінгі дәлдікпен синустар (хордалар) кестесін жасады. Ол кез үшін хордалар кестесі көптеген практикалық, астрономиялық есептерді шешуде зор маңызға ие болды. Келесі кезеңде тригонометрияның қарыштап дамуына үнді оқымыстылары зор үлес қосты. IV-V ғасырларда арнайы терминдер үндінің ұлы ғалымы Ариабхаттың (476-550 ж.ж. шамасында) астрономиялық еңбектерінде көріне бастады.. Үндінің алғашқы Жер серігі де осы есіммен аталады. Ол АК (5-сурет) кесіндісін ардхаджива (ардха-жарты, джива-садақ кермесі) деп атайды. Кейін келе қысқаша джива атауы қалды.
VІІІ ғасырдан бастап араб математиктері джива сөзін джиба, кейіннен «джайб» -«дөңестік» сөзімен алмастырады. ХІІ ғасырда Европада латын тілі ғылым тілі ретінде бел алып тұрғанда европа ғалымдары араб тіліндегі математикалық мәтіндерді аударғанда «джайб» сөзін латынның «sinus»-«иілу», «қисықтық» сөзімен алмастырады және бұл сөз бүгінге дейін сақталып қалды. Косинус сөзі кейін пайда болды. Ол латынның «сomplementy sinus» - «толықтауыш синус» деген сөз тіркесінің қысқартылған түрі, яғни cosα=sin(900 – α).
ІХ-Х ғасырларда Орта Азия мен Таяу Шығыс математикалық зерттеулердің орталығына айналды. Араб математиктерінің еңбектерінің нәтижесінде тригонометрия жеке ғылым ретінде астрономиядан бөлініп шығады.
Х ғасырда араб математигі Абу-л-Вафа (Мұхаммед-әл-Бузджани) тангенс, котангенс, секанс, косеканс атауын енгізеді және тангенстер мен котангенстер кестесін жасайды. Сондай-ақ Мұхаммед ибн Муса әл-Хорезми (ІХ ғ.) синустар мен котангенстер кестесін жасайды.
Әбу Райхан Бируни (Х-ХІ ғ.ғ.) бірлік шеңберді енгізу арқылы есептеу жұмыстарын әлдеқайда жеңілдетеді. ХІІ ғасырды ғалым-энциклопедист, мемлекет қайраткері Насир-ад-Дин ат-Туси «Жазық төртбұрыштар» трактатында жазық және сфералық тригонометрияны математиканың жеке бөлімі ретінде астрономиядан бөлек қарастырады. Ислам елдерімен салыстырғанда Европада тригонометрия тек ХІ ғасырда жеке ғылым ретінде қалыптасып, дами бастады. Бұл кезеңнің көрнекті өкілі неміс астрономы, әрі математигі профессор Регимонтан.
Ол синустар кестесін аралығы 1 секундтан 7 ондық таңбаға дейінгі дәлдікпен жасайды және «Үшбұрыштың барлық түрлері туралы 5 кітап» атты тригонометриялық еңбегін жарыққа шығарады.
«Тангенс» латын сөзі «tangens» - «жанама» (жанама кесіндісі) дегенді білдіреді.. Бұл атауды 1583 жылы дат математигі Томас Финк енгізді. Ал, «котангенс» - «complementy tangens» - «толықтауыш тангенс» ұғымын білдіреді. Бұл атауды ең алғаш 1620 жылы ағылшын ғалымы Эдмунт Гутер енгізді.
ХVІ ғасырда француз математигі Франсуа Виет (1540-1603) тригонометрияны куб теңдеулерді шешуге қолданып, оны алгебрамен байланстырды. Сондай-ақ, ол әріпті белгілеудің негізін салды. Швейцар математигі Иоганн Бернулли (1667-1747) тригонометриялық функциялардың sinх, cosх (1739ж.) белгілеулерін пайдаланды.
ХVІІ- ХІХ ғасырларда тригонометрия математикалық анализдің бір тарауы ретінде қарастырыла бастады. Бұл орайда швейцар математигі, ұзақ жылдар Петербург ғылым академиясында қызмет еткен Леонардо Эйлердің (1707-1783) орасан зор еңбегін атап өту керек. Эйлер тригонометрияның мазмұнын жетілдіріп, бір жүйеге келтіріп, жан-жақты баяндады.
Ол бүгінде қолданылып жүрген тригонометриялық функциялардың анықтамаларын енгізді. Кез келген бұрыштың тригонометриялық функцияларын қарастырып, әрбір ширектегі функция таңбаларын анықтап, келтіру формулаларын қорытты. Аргументі бұрыш пен доға, сондай-ақ, кез келген сан болғандағы тригонометриялық функцияның қасиеттерін баяндап, формулаларын қорытты, тригонометриялық теңдеулер мен теңзіздіктерді шешуді қарастырып, sinх, cosх, tgх, сtgх, т.б. белгілеулерді пайдаланды. Эйлерден кейін тригонометрия дайын формулаларды пайдаланып есептеу түріне келіп, жұмыс ықшамдалды. Бұл теорияны ХІХ ғасырда Н.И.Лобачевский, т.б. ғалымдар жалғастырып дамытты.
Бізге белгілі тригонометриялық формулалардың көпшілігінің геометриялық формасын ежелгі грек, үнді, араб математиктері тапқан. Кейіннен Европа, Азия математиктері де дәл осы жаңалықтарды ашып, толықтырып, жүйелеген.
Мысалы: sin2α+cos2α=1, sin(α±β)=sinα*cosβ±cosα*sinβ, sin2α/2=(1–cosα)/2 формулаларын Птоломей, sinα=2sinα/2*cosα/2 формуласын Абу-л-Вафа, tg(α±β), sес(α±β) формулаларын 1706 жылы Петербург математигі Я.Герман қорытты, tg2α=2tg α/(1–tg2α) формуласын ХVІІ ғасырда ағылшын Джон Пелль, француз Г.Роберваль, т.б. математиктер әр түрлі әдістермен дәлелдеді. Ал, сtg2α=1/2(сtg α–tgα) формуласы ең алғаш Л.Эйлердің «Анализге кіріспе» еңбегінде жарық көрді. ХVІІ ғасырда дат ғалымы Тихо Браге cosα*cosβ=1/2[cos(α+β)+cos(α-β)] формуласын пайдаланған. sinα-sinβ ережесін ХVІІ ғасырда ағылшын ғалымы Джон Непер еңбектерінен кездестіруге болады.
Бүгінде тригонометрия математиканың жеке тармағы емес. Атап айтқанда, тригонометриялық функциялардың қасиеттерін математикалық анализ, ал үшбұрыштарды шешуді геометрия қарастырады.
Пайдаланылған әдебиеттер:
-
Глейзер .И. История математики в школе: VІІ-VІІІ кл. – М. Просвещение, 1982
-
Глейзер .И. История математики в школе: ІХ-Х кл. – М. Просвещение, 1983
-
Рыбников К.А. История математики: Учебник – М. Изд-во МГУ, 1994
-
Журнал «Математика в школе», №3, 2005 г.,
Шығыс Қазақстан облысы
Үржар ауданы
Тел: 87756214578

шағым қалдыра аласыз















