
«Бекітілді»
|
Күні: Мұғалімнің аты-жөні:. Сынып: 10 |
|
|
Сабақ тақырыбы |
Тригонометриялық теңсіздіктерді шешу |
|
Осы сабақта қол жеткізілетін оқу мақсаттары |
Қарапайым тригонометриялық теңсіздіктердің барлық түрлерімен, олардың шешімінің бар және жоқ болу шарттарымен таныстыру. Тригонометриялық теңсіздіктерді шешу алгоритмін беру, оны есеп шығаруда қолдану білік, дағдыларын қалыптастыру, |
|
Сабақ мақсаттары: |
Барлық оқушылар: тригонометриялық теңсіздік ұғымын меңгереді және оның шешу жолдарын үйренеді |
|
|
Оқушылардың басым бөлігі: Тригонометриялық теңсіздіктерді шешу алгоритмін біледі. |
|
|
Кейбір оқушылар: Тригонометриялық теңсіздіктерді шешу алгоритмін қолданып, есеп шығарады |
|
Тілдік мақсат: |
Негізгі сөздер мен тіркесте Тригонометриялық теңсіздік |
|
|
ой –түрткі сұрақтар мен жауаптар |
|
Алдыңғы оқу |
Тригонометриялық теңдеулерді шешу |
Сабақ барысы
|
Сабақтың жоспарланған кезеңдері |
Сабақтағы жоспарланған іс-әрекет |
|
|
Сабақтың басы |
Ұйымдастыру Өткенді еске түсіру: 1. Тригонометриялық теңдеу дегеніміз не? 2. Қарапайым тригонометриялық теңдеу дегеніміз не? 3. Тригонометриялық теңдеуді шешу дегеніміз не? Жаңа сабақ: Анықтама: Тригонометриялық өрнектерден құралған теңсіздіктерді тригонометриялық теңсіздіктер деп атайды. Тригонометриялық теңсіздіктерді түрлендіру арқылы төмендегідей қарапайым тригонометриялық теңсіздіктерге келтіріп шешеді: Cos x ≥а; Sin
x Анықтама бойынша бірлік шеңбердің бойындағы нүктенің абсциссасын cosx, ординатасын sinх деп аламыз, яғни В(cosx; sinх) Тригонометриялық теңсіздіктерді шешу үшін қолданылатын алгоритмдер:
1-мысал: sin x
≤
Теңсіздіктің жалпы шешімін жазамыз:
2-мысал.
Е
Демек,
|
|
|
Сабақтың ортасы |
Тригонометриялық теңсіздіктердің шешімдерінің формулалары: sinxπ-arcsina+2πk < x < arcsina+2πk sinx>a ↔ arcsina+2πk < x < π-arcsina+2πk cosx cosx>a ↔ -arccosa+2πk < x < arccosa+2πk tgx>a ↔ arctga+πk < x < π/2+πk tgx ctgx>a ↔ πk < x < arcctga+πk ctgx π+ πk №1
|
|
|
Сабақтың соңы |
Үйге тапсырма: қайталау |
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
"Тригонометриялқ теңсіздіктерді шешу" 10 класс
"Тригонометриялқ теңсіздіктерді шешу" 10 класс
«Бекітілді»
|
Күні: Мұғалімнің аты-жөні:. Сынып: 10 |
|
|
Сабақ тақырыбы |
Тригонометриялық теңсіздіктерді шешу |
|
Осы сабақта қол жеткізілетін оқу мақсаттары |
Қарапайым тригонометриялық теңсіздіктердің барлық түрлерімен, олардың шешімінің бар және жоқ болу шарттарымен таныстыру. Тригонометриялық теңсіздіктерді шешу алгоритмін беру, оны есеп шығаруда қолдану білік, дағдыларын қалыптастыру, |
|
Сабақ мақсаттары: |
Барлық оқушылар: тригонометриялық теңсіздік ұғымын меңгереді және оның шешу жолдарын үйренеді |
|
|
Оқушылардың басым бөлігі: Тригонометриялық теңсіздіктерді шешу алгоритмін біледі. |
|
|
Кейбір оқушылар: Тригонометриялық теңсіздіктерді шешу алгоритмін қолданып, есеп шығарады |
|
Тілдік мақсат: |
Негізгі сөздер мен тіркесте Тригонометриялық теңсіздік |
|
|
ой –түрткі сұрақтар мен жауаптар |
|
Алдыңғы оқу |
Тригонометриялық теңдеулерді шешу |
Сабақ барысы
|
Сабақтың жоспарланған кезеңдері |
Сабақтағы жоспарланған іс-әрекет |
|
|
Сабақтың басы |
Ұйымдастыру Өткенді еске түсіру: 1. Тригонометриялық теңдеу дегеніміз не? 2. Қарапайым тригонометриялық теңдеу дегеніміз не? 3. Тригонометриялық теңдеуді шешу дегеніміз не? Жаңа сабақ: Анықтама: Тригонометриялық өрнектерден құралған теңсіздіктерді тригонометриялық теңсіздіктер деп атайды. Тригонометриялық теңсіздіктерді түрлендіру арқылы төмендегідей қарапайым тригонометриялық теңсіздіктерге келтіріп шешеді: Cos x ≥а; Sin
x Анықтама бойынша бірлік шеңбердің бойындағы нүктенің абсциссасын cosx, ординатасын sinх деп аламыз, яғни В(cosx; sinх) Тригонометриялық теңсіздіктерді шешу үшін қолданылатын алгоритмдер:
1-мысал: sin x
≤
Теңсіздіктің жалпы шешімін жазамыз:
2-мысал.
Е
Демек,
|
|
|
Сабақтың ортасы |
Тригонометриялық теңсіздіктердің шешімдерінің формулалары: sinxπ-arcsina+2πk < x < arcsina+2πk sinx>a ↔ arcsina+2πk < x < π-arcsina+2πk cosx cosx>a ↔ -arccosa+2πk < x < arccosa+2πk tgx>a ↔ arctga+πk < x < π/2+πk tgx ctgx>a ↔ πk < x < arcctga+πk ctgx π+ πk №1
|
|
|
Сабақтың соңы |
Үйге тапсырма: қайталау |
|

шағым қалдыра аласыз


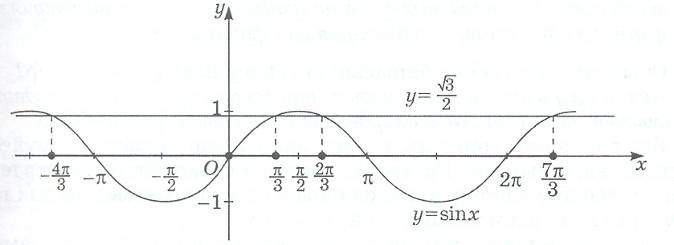 нді берілген теңсіздікті қанағаттандыратын
абсисса осінің бас аралығындағы шеткі нүктелерінің
абсциссаларын
нді берілген теңсіздікті қанағаттандыратын
абсисса осінің бас аралығындағы шеткі нүктелерінің
абсциссаларын












