
Алгебра 9
Бекей Р Е № 65 мектеп-гимназиясының математика мұғалімі
Сабақтың тақырыбы:
ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАР ЖӘНЕ ОЛАРДЫҢ
ҚАСИЕТТЕРІ
Бүгінгі сабақта: бірлік шеңбер көмегімен тригонометриялық функциялардың таңбатұрақтылық аралықтарын және бірсарындылығын табуды үйренесіздер.
Радиусы 1-ге тең центрі координаталар басында жататын шеңберді бірлік шеңбер деп атайды.
Анықтама бойынша бірлік
тригонометриялық дөңгелекте sinα=y,cosα=x,
tgα= , ctgα=
, ctgα= теңдіктері орындалады
теңдіктері орындалады
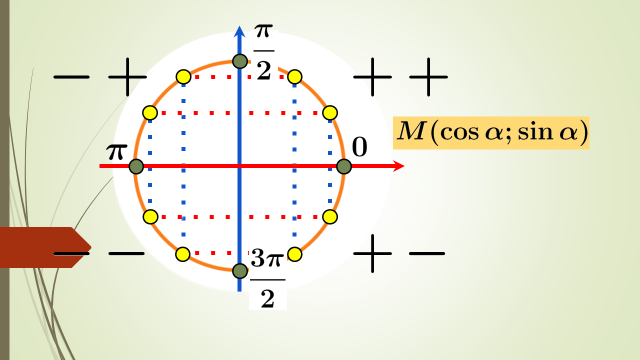
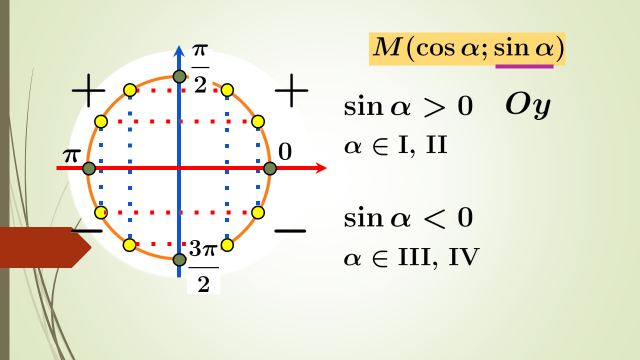
Егер М(х;у)  І ,бірінші ширекте жатса,онда
х
І ,бірінші ширекте жатса,онда
х  0,у
0,у
 ,сондықтан sin α
,сондықтан sin α  ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері орындалады
теңсіздіктері орындалады
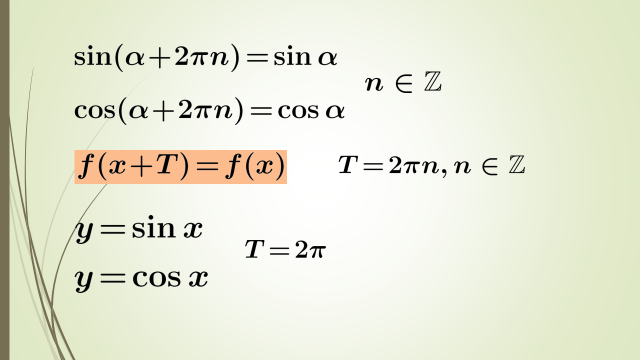
Егер М(х;у)  ІІ ,Екінші ширекте жатса,онда
х
ІІ ,Екінші ширекте жатса,онда
х  0,у
0,у
 ,сондықтан sin α
,сондықтан sin α  ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері орындалады
теңсіздіктері орындалады
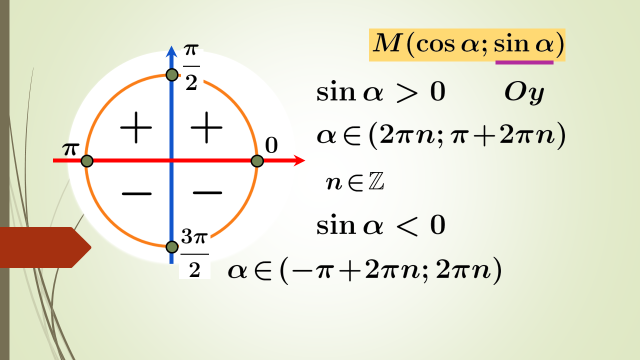
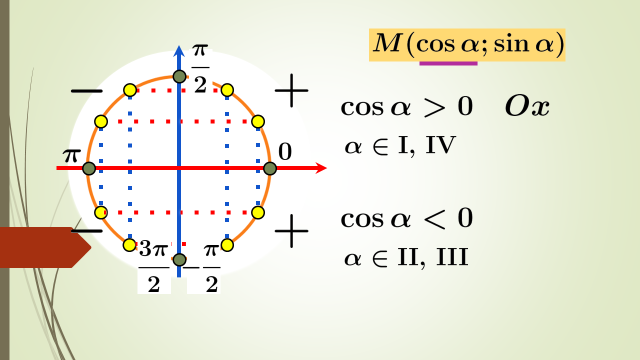
Егер М(х;у)  ІІІ ,Үшінші ширекте жатса,онда
х
ІІІ ,Үшінші ширекте жатса,онда
х  0,у
0,у
 ,сондықтан sin α
,сондықтан sin α  ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері орындалады.
Егер М(х;у)
теңсіздіктері орындалады.
Егер М(х;у)  ІV
,төртінші ширекте жатса,онда х
ІV
,төртінші ширекте жатса,онда х 0,
0,
у  ,сондықтан sin α
,сондықтан sin α
 ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері
орындалады.
теңсіздіктері
орындалады.
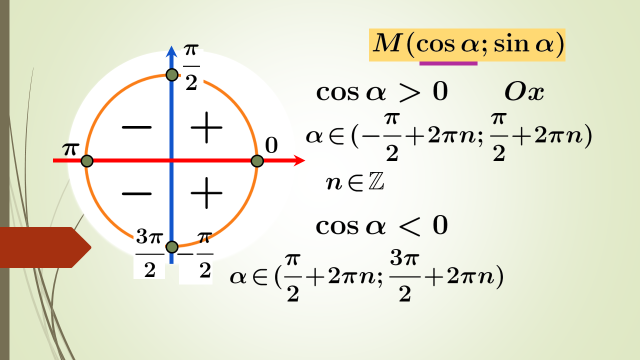
Функция тақ немесе жұп болуы үшін оның анықталу облысы координаталар бас нүктесіне қатысты симметриялы болуы керек.
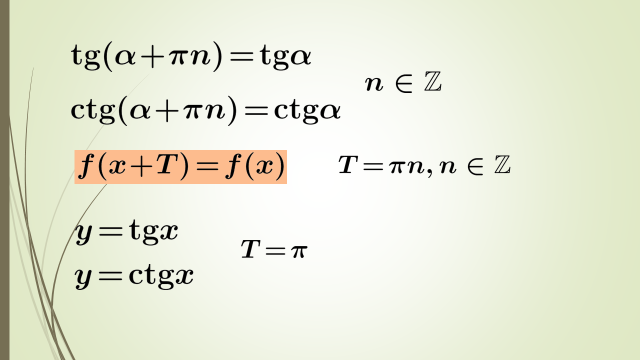
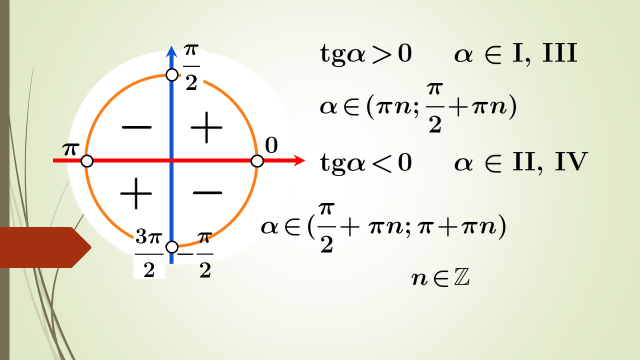
Егер Т саны у=f(х) функциясының периоды болса,онда бұл функция үшін +-2Т,+-3Т,+-4Т,…. Сандары да период болады.Сонымен , әрбір периодты функцияның шексіз көп периодтары болады.
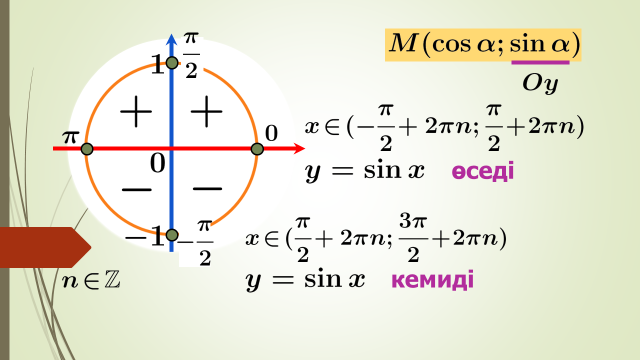
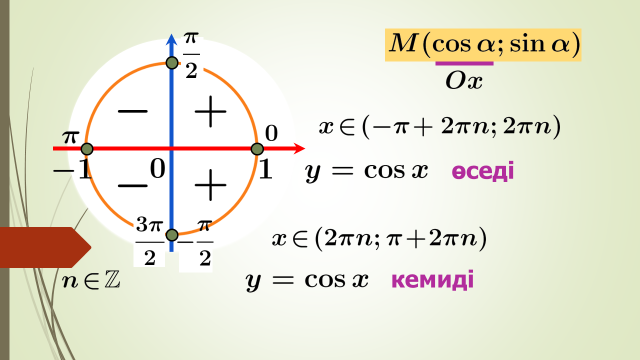

Бұл есептерді шешу үщін тригонометриялық фукнциялардың периодтылығын ескеру керек

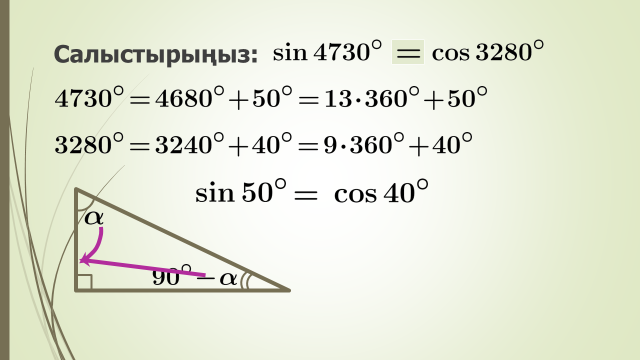
Сонымен,бүгінгі сабақта тригонометриялық функциялардың қасиеттерімен таныстық.Тригонометриялық функциялардың қасиеттеріне есептер шығардық.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Тригонометриялық функциялар және олардың қасиеттері. 9-сынып ҚМЖ
Тригонометриялық функциялар және олардың қасиеттері. 9-сынып ҚМЖ
Алгебра 9
Бекей Р Е № 65 мектеп-гимназиясының математика мұғалімі
Сабақтың тақырыбы:
ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАР ЖӘНЕ ОЛАРДЫҢ
ҚАСИЕТТЕРІ
Бүгінгі сабақта: бірлік шеңбер көмегімен тригонометриялық функциялардың таңбатұрақтылық аралықтарын және бірсарындылығын табуды үйренесіздер.
Радиусы 1-ге тең центрі координаталар басында жататын шеңберді бірлік шеңбер деп атайды.
Анықтама бойынша бірлік
тригонометриялық дөңгелекте sinα=y,cosα=x,
tgα= , ctgα=
, ctgα= теңдіктері орындалады
теңдіктері орындалады


Егер М(х;у)  І ,бірінші ширекте жатса,онда
х
І ,бірінші ширекте жатса,онда
х  0,у
0,у
 ,сондықтан sin α
,сондықтан sin α  ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері орындалады
теңсіздіктері орындалады
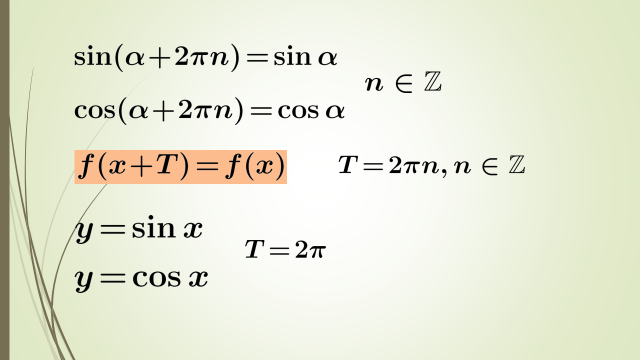
Егер М(х;у)  ІІ ,Екінші ширекте жатса,онда
х
ІІ ,Екінші ширекте жатса,онда
х  0,у
0,у
 ,сондықтан sin α
,сондықтан sin α  ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері орындалады
теңсіздіктері орындалады


Егер М(х;у)  ІІІ ,Үшінші ширекте жатса,онда
х
ІІІ ,Үшінші ширекте жатса,онда
х  0,у
0,у
 ,сондықтан sin α
,сондықтан sin α  ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері орындалады.
Егер М(х;у)
теңсіздіктері орындалады.
Егер М(х;у)  ІV
,төртінші ширекте жатса,онда х
ІV
,төртінші ширекте жатса,онда х 0,
0,
у  ,сондықтан sin α
,сондықтан sin α
 ,
, ,
,
tgα , ctgα
, ctgα теңсіздіктері
орындалады.
теңсіздіктері
орындалады.

Функция тақ немесе жұп болуы үшін оның анықталу облысы координаталар бас нүктесіне қатысты симметриялы болуы керек.
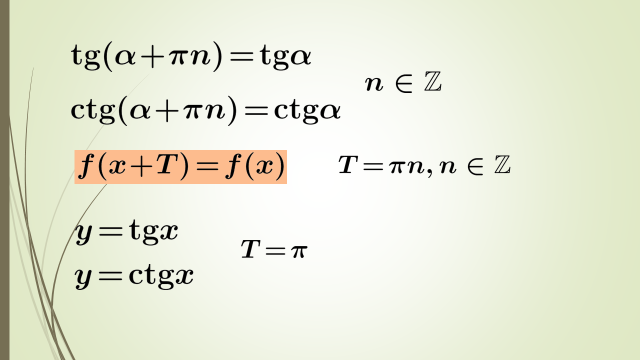
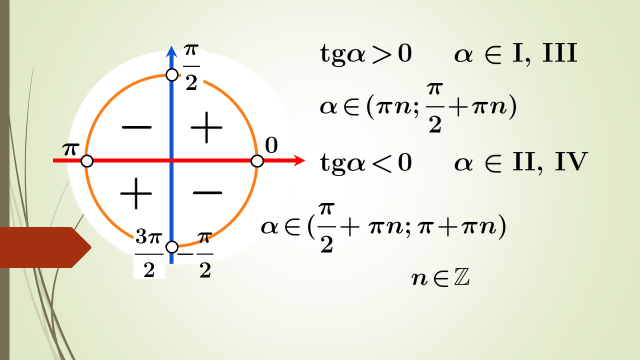
Егер Т саны у=f(х) функциясының периоды болса,онда бұл функция үшін +-2Т,+-3Т,+-4Т,…. Сандары да период болады.Сонымен , әрбір периодты функцияның шексіз көп периодтары болады.



Бұл есептерді шешу үщін тригонометриялық фукнциялардың периодтылығын ескеру керек


Сонымен,бүгінгі сабақта тригонометриялық функциялардың қасиеттерімен таныстық.Тригонометриялық функциялардың қасиеттеріне есептер шығардық.

шағым қалдыра аласыз















