
Ашық сабақ: Туынды. Натурал көрсеткішті дәрежелік функцияның туындысы. «Түркістан» көпсалалы жоғары медицина колледжі
Математика пәнінің оқытушысы
Жағыпарова Данагүл Дәулетқызы
Сабақтың типі: теориялық сабақ
Оқыту әдістері: топта жұмыс істеуге негізделген оқыту-(TBL), өзекті материалдарға шолу, тақырыптың мазмұнын ашу
Формативті бағалау: OA/MCQ
|
Сілтеме |
Блум таксономиясы, оқулық. |
|
Жалпы мақсаттар |
а) оқулық: Студенттерге функцияның туындысын табу ережелерін таныстыру, ережелерді қолдану тәртібін меңгерту, дәрежелік функцияның туындысын табу формуласын таныстыру, функцияның туындысын табу есептерін шешуді үйрету. ә) дамытушылық: Студенттердің ойлау қабілеттерін дамыту, ой өрістерін кеңейту; б) тәрбиелік: Студенттерді таза жазуға, ұқыптылыққа, көп еңбектенуге тәрбиелеу. |
|
Оқыту нәтижелері |
– Функцияның туындысын табу ережелерін жазып бере алады; – Дәрежелік функцияның формуласын қолдана біледі; – Функцияның туындыларын таба алады; –Есептер шығару кезінде осы жоғарыда айтылған білімдерді сабақтастырады. |
|
Негізгі идеялар |
– Функцияның туындысын табу ережелерін қолдана отырып қарапайым дәрежелік функциялардың туындыларын анықтау; –Уәжді ынталандыру, бірлесе отырып орындалатын жұмыстар негізінде материалды меңгеру, бір-біріне көмек беру; – Өзіндік ойын айта білуге дағдыландыру. |
Көрнекіліктер: интербелсенді тақта, жетон, кестелер.
Сабақтың әдісі: ой қозғау әдісі
Сабақтың түрі: Аралас сабақ. Жаңа сабақты меңгерту.
Пән аралық байланыс: Физика, орыс тілі, халықтық педагогика, тарих.
Сабақтың жоспары:
Сабақ уақытын бөлу картасы
|
№ |
Сабақ бөлімінің аты |
Теориялық сабақ 2 сағ |
|
1 |
Ұйымдастыру кезеңі |
3-5 мин |
|
2 |
Үй тапсырмасын сұрау |
20-25 мин |
|
3 |
Жаңа тақырыпты түсіндіру |
25-30 мин |
|
4 |
Жаңа тақырыпты бекіту |
10-15 мин |
|
5 |
Сабақты қорыту және бағалау |
7-10 мин |
|
6 |
Үйге тапсырма беру |
5-7 мин |
|
|
Барлығы: |
90 мин |
Сабақтың барысы: Ұйымдастыру кезеңі.
Студенттердің сабаққа қатысуы мен дайындығын қадағалау. Студенттердің зейінін сабаққа шоғырландыру. (2 мин)
Функцияның түрлеріне қарай топтағы студенттерді 3- ке бөлемін.
Кейін алдыңғы білімдерін тексеру мақсатында
Ойлан, Топтас, Пікірлес әдісін пайдаланамын. Сұрақтар оқимын сол сұрақтарға жауаптарды студенттер топтарымен бірлесіп ақылдаса отырып жауаптарын оқиды. (10 мин)
Сұрақтар:
1-топқа: Жылдамдықтың уақыт бойынша туындысы неге тең?
2-топқа: Координатаның уақыт бойынша туындысы неге тең?
3-топқа: Орташа жылдамдық дегеніміз не?
1-топ «Бәйтерек» тобы
2-топ «Пирамида» тобы
3-топ «Хан шатыр» тобы
Жаңа сабақты түсіндіру. Сабақтың тақырыбы: Туынды. Натурал көрсеткішті дәрежелік функцияның туындысы.
|
Тілдік мақсат |
|
|
|
|
||
|
|
||
|
|
|
|
Сабақтың тақырыбы мен мақсаттарын таныстыру және талқылау. Студенттермен диалогтық оқытуды іске асыра отырып, сұрақтар қою арқылы жаңа сабақтың мазмұнын ашамын.
Теория бойынша сұрақтар қойылады.
-
Механиканың негізгі мақсаты не?
-
Туынды дегеніміз не?
-
Туындының геометриялық мағынасы неде?
-
Үдеу дегеніміз не?
-
Лездік жылдамдық дегеніміз не?
-
Туындының механикалық мағынасын қалай түсінесің?
-
Белгілі бір уақыттағы үдеу мен жылдамдықтың формуласы?
у = f(x) функциясының х0 нүктесіндегі туындысы f(x0) осы функция графигінің (х0; f(x0)) нүктесі арқылы өтетін жанаманың бұрыштық коэффициетіне немесе бұрыштың тангенсіне тең.
f(x0)=tga=k
у = f(x) функциясының х нүктесіндегі f¢(x) туындысы оның х нүктесіндегі өзгеру жылдамдығын анықтайды.
Мысалы: S(t) = 6t2 – 5t + 4 заңы бойынша түзу сызықты қозғалған дененің t = 1с кезіндегі қозғалыс жылдамдығын тап.
Жауабы: 7м/с
Жылдамдықтан алынған туынды үдеуге тең.
Мысалы: S(t) = 3t3 – 9t2 + 6t – 14 заңы бойынша түзу сызықты қозғалған дененің t = 2с кезіндегі дененің үдеуін тап.
Жауабы: 18м/с2
Мысалы: f(x) = 5x3+4x2+21x–19 функциясының графигіне абсциссасы х0 = 1 нүктесінде жүргізілген жанаманың теңдеуін жаз.
f(1) = 5×13 + 4 ×12 + 21 ×1 – 19 = 5 + 4 + 21 – 19 = 11
f¢(x) = 15x2 + 8x + 21
f¢(1) = 15×12 + 8×1 + 21 = 15 + 8 + 21 = 44
y = 11 + 44(x – 1) = 11 + 44x – 44 = 44x – 33
у = f(x) функциясының х0 нүктесіндегі туындысы f¢(x0) осы функция графигінің (х0; f(x0)) нүктесі арқылы өтетін жанаманың бұрыштық коэффициетіне немесе бұрыштың тангенсіне тең.
Мысалы: f(x) = 4x2 – 5x + 6 функциясы графигінің берілген М(1;2) нүктесінен өтетін жанамасының абсцисса осіне көлбеулік бұрышының тангенсін тап.
f¢(x) = 8x -- 5
f¢(1) = 8 × 1 – 5 = 8 – 5 = 3
f(x) = 7x2 + 29x + 6 функциясы графигінің берілген М(-2;5) нүктесінен өтетін жанамасының абсцисса осіне көлбеулік бұрышын тап.
f¢(x) = 14x + 29
f¢(-2) = 14 × (-2) + 35 = -28 + 29 = 1
-
Семантикалық карта
|
№ |
|
cosx |
nxn-1 |
|
cos 2x |
|
u'v+uv' |
|
-sin x |
|
1 |
( |
|
|
|
|
|
|
|
|
|
2 |
( |
|
|
|
|
|
|
|
|
|
3 |
sin'x |
|
|
|
|
|
|
|
|
|
4 |
cos'x |
|
|
|
|
|
|
|
|
|
5 |
( |
|
|
|
|
|
|
|
|
|
6 |
tg'x |
|
|
|
|
|
|
|
|
|
7 |
(xn)' |
|
|
|
|
|
|
|
|
|
8 |
( |
|
|
|
|
|
|
|
|
-
Тест. Есеп пен тест жауабының сәйкестігін анықта:
|
І нұсқа |
|||||||||
|
1 |
х6 |
5 |
х2 |
9 |
2x |
13 |
|
17 |
2x10 |
|
2 |
3х-5 |
6 |
|
10 |
ax+b |
14 |
6x5 |
18 |
20x9 |
|
3 |
0 |
7 |
а |
11 |
-4sin x |
15 |
|
19 |
30x4 |
|
4 |
|
8 |
4 cos x |
12 |
4sin x |
16 |
2 |
20 |
-15x-6 |
|
ІІ нұсқа |
|||||||||
|
1 |
х8 |
5 |
0 |
9 |
56x6 |
13 |
|
17 |
-3x-7 |
|
2 |
8х7 |
6 |
5 cos x |
10 |
x-5 |
14 |
|
18 |
5sin x |
|
3 |
|
7 |
42x5 |
11 |
-5x-6 |
15 |
|
19 |
-5 cos x |
|
4 |
20 |
8 |
-5sin x |
12 |
21x-8 |
16 |
|
20 |
|
-
Есептер шығару. Әр топ 10 минут уақыт аралығында есептер шығарады және бір-бірін критерий арқылы бағалайды.
|
1 |
у=3х |
3 |
у=
х2+3 |
5 |
у=4-х4 |
|
2 |
у=4х2 |
4 |
у=3х2+2х+5 |
6 |
у= |

Мысал 2:
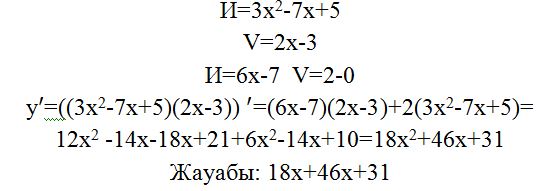

Сабақты бекіту: «Алтын қақпа» ойыны арқылы студенттерге сұрақтар қоя отырып, сабақты бекітемін.
Кері байланыс: Студенттер топ бойынша шешім қабылдап, сұрақтарға жауап береді, есептерді шығарады. Жаңа сабақ бойынша түсінік қалыптастырады.
-
«Тас қақпа» 5 сұрақтан тұрады

-
«Күміс қақпа» Қазақстан Республикасы бойынша ең мықты математиктер.
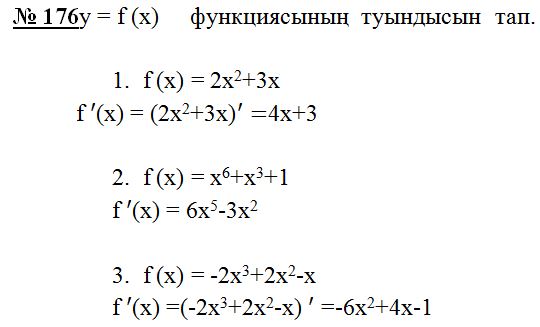
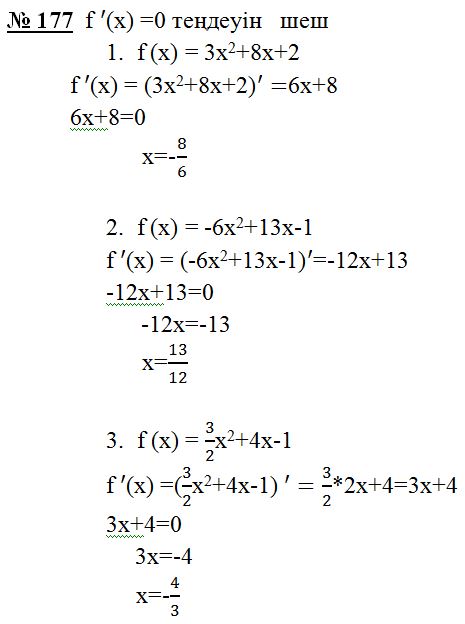
-
«Алтын қақпа» Дүние жүзі бойынша ең мықты математиктер


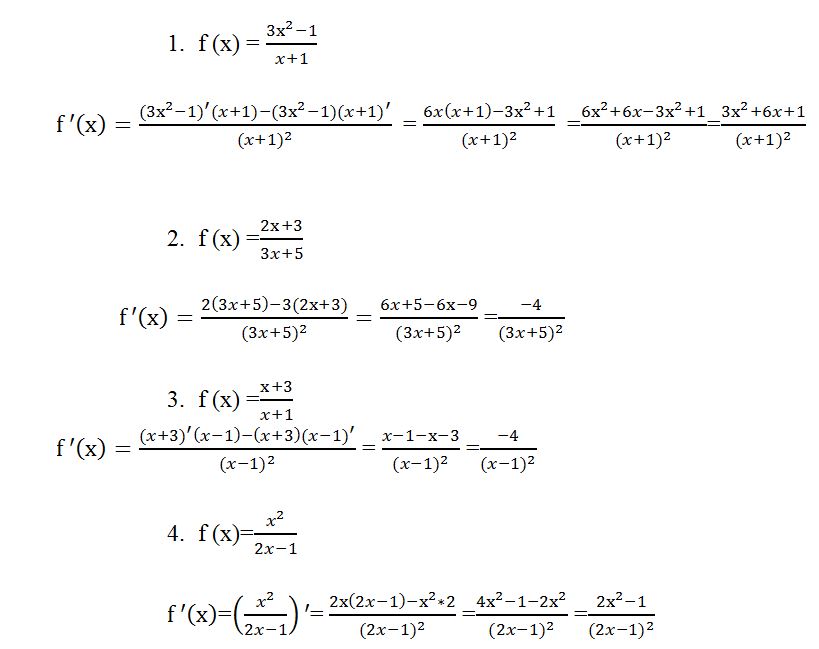
«Insert» әдісі. Оқушылар стикерлерге төмендегі сұрақтарға жауап береді.(5 мин)
Мен жақсы түсіндім..........
Менің сұрағым бар...........
Мен түсінген жоқпын, өйткені............
Жаңа ғасырдағы математикаға жаңаша көзқарас.
Студенттерді бағалау
Үйге тапсырма беру
-
Дәрежелік функцияның туындысы.
-
Туынды анықтамасы.
-
Диференциалдау деген не?
-
1 ереже
-
2 ереже
-
3 ереже
Студенттер бүгінгі сабақ бойынша өз ойларын «Блоб» ағашына жазып қалдырады.

Пайдаланылатын әдебиеттер: 1. Әбілқасымова, К.Д. Шойынбеков «Алгебра және анализ бастамалары». Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10-сыныбына арналған оқулық. Алматы, Мектеп, 2006
2. Қосымша әдебиет:
1. Алгебра және анализ бастамалары, под ред. Яковлева.ч. I, II, 1987
Интернет желісі
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Туынды. Натурал көрсеткішті дәрежелік функцияның туындысы
Туынды. Натурал көрсеткішті дәрежелік функцияның туындысы
Ашық сабақ: Туынды. Натурал көрсеткішті дәрежелік функцияның туындысы. «Түркістан» көпсалалы жоғары медицина колледжі
Математика пәнінің оқытушысы
Жағыпарова Данагүл Дәулетқызы
Сабақтың типі: теориялық сабақ
Оқыту әдістері: топта жұмыс істеуге негізделген оқыту-(TBL), өзекті материалдарға шолу, тақырыптың мазмұнын ашу
Формативті бағалау: OA/MCQ
|
Сілтеме |
Блум таксономиясы, оқулық. |
|
Жалпы мақсаттар |
а) оқулық: Студенттерге функцияның туындысын табу ережелерін таныстыру, ережелерді қолдану тәртібін меңгерту, дәрежелік функцияның туындысын табу формуласын таныстыру, функцияның туындысын табу есептерін шешуді үйрету. ә) дамытушылық: Студенттердің ойлау қабілеттерін дамыту, ой өрістерін кеңейту; б) тәрбиелік: Студенттерді таза жазуға, ұқыптылыққа, көп еңбектенуге тәрбиелеу. |
|
Оқыту нәтижелері |
– Функцияның туындысын табу ережелерін жазып бере алады; – Дәрежелік функцияның формуласын қолдана біледі; – Функцияның туындыларын таба алады; –Есептер шығару кезінде осы жоғарыда айтылған білімдерді сабақтастырады. |
|
Негізгі идеялар |
– Функцияның туындысын табу ережелерін қолдана отырып қарапайым дәрежелік функциялардың туындыларын анықтау; –Уәжді ынталандыру, бірлесе отырып орындалатын жұмыстар негізінде материалды меңгеру, бір-біріне көмек беру; – Өзіндік ойын айта білуге дағдыландыру. |
Көрнекіліктер: интербелсенді тақта, жетон, кестелер.
Сабақтың әдісі: ой қозғау әдісі
Сабақтың түрі: Аралас сабақ. Жаңа сабақты меңгерту.
Пән аралық байланыс: Физика, орыс тілі, халықтық педагогика, тарих.
Сабақтың жоспары:
Сабақ уақытын бөлу картасы
|
№ |
Сабақ бөлімінің аты |
Теориялық сабақ 2 сағ |
|
1 |
Ұйымдастыру кезеңі |
3-5 мин |
|
2 |
Үй тапсырмасын сұрау |
20-25 мин |
|
3 |
Жаңа тақырыпты түсіндіру |
25-30 мин |
|
4 |
Жаңа тақырыпты бекіту |
10-15 мин |
|
5 |
Сабақты қорыту және бағалау |
7-10 мин |
|
6 |
Үйге тапсырма беру |
5-7 мин |
|
|
Барлығы: |
90 мин |
Сабақтың барысы: Ұйымдастыру кезеңі.
Студенттердің сабаққа қатысуы мен дайындығын қадағалау. Студенттердің зейінін сабаққа шоғырландыру. (2 мин)
Функцияның түрлеріне қарай топтағы студенттерді 3- ке бөлемін.
Кейін алдыңғы білімдерін тексеру мақсатында
Ойлан, Топтас, Пікірлес әдісін пайдаланамын. Сұрақтар оқимын сол сұрақтарға жауаптарды студенттер топтарымен бірлесіп ақылдаса отырып жауаптарын оқиды. (10 мин)
Сұрақтар:
1-топқа: Жылдамдықтың уақыт бойынша туындысы неге тең?
2-топқа: Координатаның уақыт бойынша туындысы неге тең?
3-топқа: Орташа жылдамдық дегеніміз не?
1-топ «Бәйтерек» тобы
2-топ «Пирамида» тобы
3-топ «Хан шатыр» тобы
Жаңа сабақты түсіндіру. Сабақтың тақырыбы: Туынды. Натурал көрсеткішті дәрежелік функцияның туындысы.
|
Тілдік мақсат |
|
|
|
|
||
|
|
||
|
|
|
|
Сабақтың тақырыбы мен мақсаттарын таныстыру және талқылау. Студенттермен диалогтық оқытуды іске асыра отырып, сұрақтар қою арқылы жаңа сабақтың мазмұнын ашамын.
Теория бойынша сұрақтар қойылады.
-
Механиканың негізгі мақсаты не?
-
Туынды дегеніміз не?
-
Туындының геометриялық мағынасы неде?
-
Үдеу дегеніміз не?
-
Лездік жылдамдық дегеніміз не?
-
Туындының механикалық мағынасын қалай түсінесің?
-
Белгілі бір уақыттағы үдеу мен жылдамдықтың формуласы?
у = f(x) функциясының х0 нүктесіндегі туындысы f(x0) осы функция графигінің (х0; f(x0)) нүктесі арқылы өтетін жанаманың бұрыштық коэффициетіне немесе бұрыштың тангенсіне тең.
f(x0)=tga=k
у = f(x) функциясының х нүктесіндегі f¢(x) туындысы оның х нүктесіндегі өзгеру жылдамдығын анықтайды.
Мысалы: S(t) = 6t2 – 5t + 4 заңы бойынша түзу сызықты қозғалған дененің t = 1с кезіндегі қозғалыс жылдамдығын тап.
Жауабы: 7м/с
Жылдамдықтан алынған туынды үдеуге тең.
Мысалы: S(t) = 3t3 – 9t2 + 6t – 14 заңы бойынша түзу сызықты қозғалған дененің t = 2с кезіндегі дененің үдеуін тап.
Жауабы: 18м/с2
Мысалы: f(x) = 5x3+4x2+21x–19 функциясының графигіне абсциссасы х0 = 1 нүктесінде жүргізілген жанаманың теңдеуін жаз.
f(1) = 5×13 + 4 ×12 + 21 ×1 – 19 = 5 + 4 + 21 – 19 = 11
f¢(x) = 15x2 + 8x + 21
f¢(1) = 15×12 + 8×1 + 21 = 15 + 8 + 21 = 44
y = 11 + 44(x – 1) = 11 + 44x – 44 = 44x – 33
у = f(x) функциясының х0 нүктесіндегі туындысы f¢(x0) осы функция графигінің (х0; f(x0)) нүктесі арқылы өтетін жанаманың бұрыштық коэффициетіне немесе бұрыштың тангенсіне тең.
Мысалы: f(x) = 4x2 – 5x + 6 функциясы графигінің берілген М(1;2) нүктесінен өтетін жанамасының абсцисса осіне көлбеулік бұрышының тангенсін тап.
f¢(x) = 8x -- 5
f¢(1) = 8 × 1 – 5 = 8 – 5 = 3
f(x) = 7x2 + 29x + 6 функциясы графигінің берілген М(-2;5) нүктесінен өтетін жанамасының абсцисса осіне көлбеулік бұрышын тап.
f¢(x) = 14x + 29
f¢(-2) = 14 × (-2) + 35 = -28 + 29 = 1
-
Семантикалық карта
|
№ |
|
cosx |
nxn-1 |
|
cos 2x |
|
u'v+uv' |
|
-sin x |
|
1 |
( |
|
|
|
|
|
|
|
|
|
2 |
( |
|
|
|
|
|
|
|
|
|
3 |
sin'x |
|
|
|
|
|
|
|
|
|
4 |
cos'x |
|
|
|
|
|
|
|
|
|
5 |
( |
|
|
|
|
|
|
|
|
|
6 |
tg'x |
|
|
|
|
|
|
|
|
|
7 |
(xn)' |
|
|
|
|
|
|
|
|
|
8 |
( |
|
|
|
|
|
|
|
|
-
Тест. Есеп пен тест жауабының сәйкестігін анықта:
|
І нұсқа |
|||||||||
|
1 |
х6 |
5 |
х2 |
9 |
2x |
13 |
|
17 |
2x10 |
|
2 |
3х-5 |
6 |
|
10 |
ax+b |
14 |
6x5 |
18 |
20x9 |
|
3 |
0 |
7 |
а |
11 |
-4sin x |
15 |
|
19 |
30x4 |
|
4 |
|
8 |
4 cos x |
12 |
4sin x |
16 |
2 |
20 |
-15x-6 |
|
ІІ нұсқа |
|||||||||
|
1 |
х8 |
5 |
0 |
9 |
56x6 |
13 |
|
17 |
-3x-7 |
|
2 |
8х7 |
6 |
5 cos x |
10 |
x-5 |
14 |
|
18 |
5sin x |
|
3 |
|
7 |
42x5 |
11 |
-5x-6 |
15 |
|
19 |
-5 cos x |
|
4 |
20 |
8 |
-5sin x |
12 |
21x-8 |
16 |
|
20 |
|
-
Есептер шығару. Әр топ 10 минут уақыт аралығында есептер шығарады және бір-бірін критерий арқылы бағалайды.
|
1 |
у=3х |
3 |
у=
х2+3 |
5 |
у=4-х4 |
|
2 |
у=4х2 |
4 |
у=3х2+2х+5 |
6 |
у= |

Мысал 2:
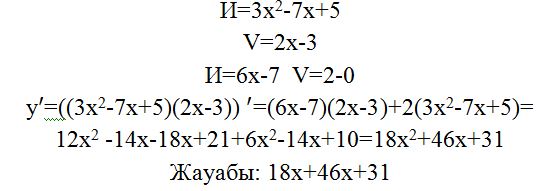

Сабақты бекіту: «Алтын қақпа» ойыны арқылы студенттерге сұрақтар қоя отырып, сабақты бекітемін.
Кері байланыс: Студенттер топ бойынша шешім қабылдап, сұрақтарға жауап береді, есептерді шығарады. Жаңа сабақ бойынша түсінік қалыптастырады.
-
«Тас қақпа» 5 сұрақтан тұрады

-
«Күміс қақпа» Қазақстан Республикасы бойынша ең мықты математиктер.
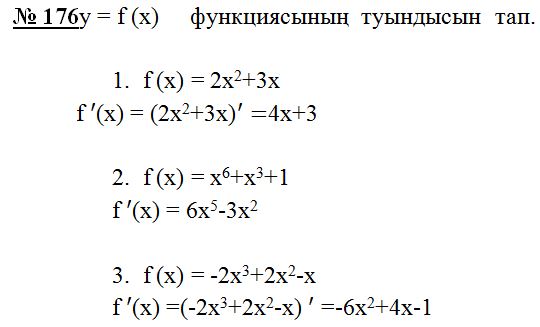
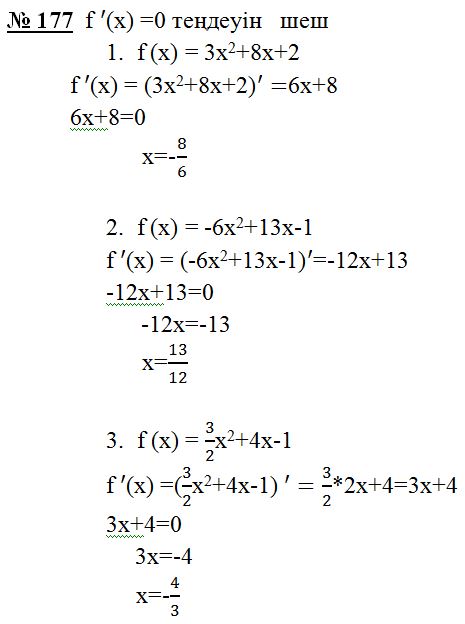
-
«Алтын қақпа» Дүние жүзі бойынша ең мықты математиктер


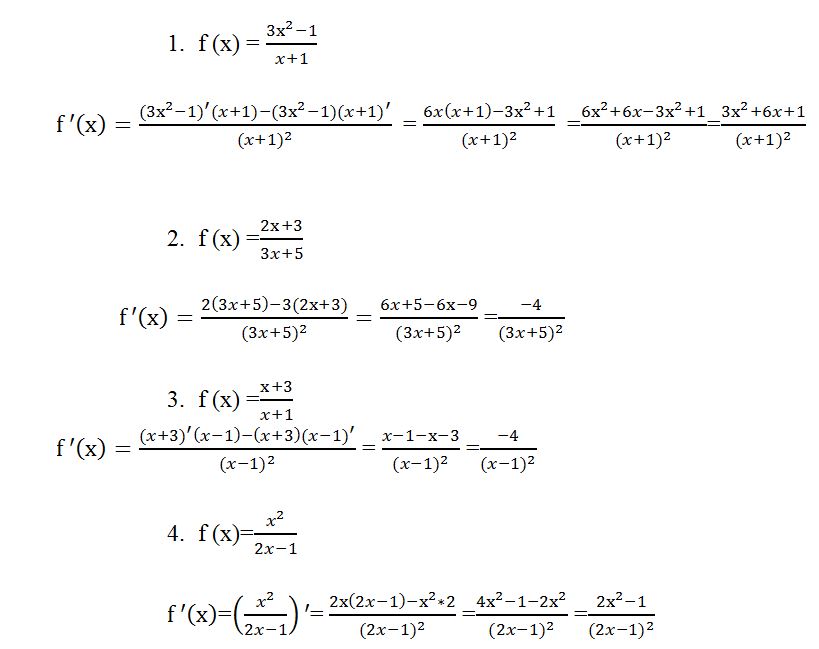
«Insert» әдісі. Оқушылар стикерлерге төмендегі сұрақтарға жауап береді.(5 мин)
Мен жақсы түсіндім..........
Менің сұрағым бар...........
Мен түсінген жоқпын, өйткені............
Жаңа ғасырдағы математикаға жаңаша көзқарас.
Студенттерді бағалау
Үйге тапсырма беру
-
Дәрежелік функцияның туындысы.
-
Туынды анықтамасы.
-
Диференциалдау деген не?
-
1 ереже
-
2 ереже
-
3 ереже
Студенттер бүгінгі сабақ бойынша өз ойларын «Блоб» ағашына жазып қалдырады.

Пайдаланылатын әдебиеттер: 1. Әбілқасымова, К.Д. Шойынбеков «Алгебра және анализ бастамалары». Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10-сыныбына арналған оқулық. Алматы, Мектеп, 2006
2. Қосымша әдебиет:
1. Алгебра және анализ бастамалары, под ред. Яковлева.ч. I, II, 1987
Интернет желісі

шағым қалдыра аласыз















