Туындыны оқытудағы
пәнаралық байланыстар
Математика сабақтарында
пәнаралық есептердің қажеттілігі – бұл пәннің көп ұғымдары нақты
физикалық – техникалық, экономикалық мазмұнды есептерді шешу арқылы
енгізіу қажеттігінен туындайды. Мысалы: вектор, туынды, интеграл
ұғымдары, тәуелділіктің графиктік кескіні, теңдеулер және олардың
жүйелері, теңсіздіктер және олардың жүйелері және тағы басқа
есептерді құрастыру дағдыларын қалыптастыру мақсатынан да
туындайды.
Математиканы оқытуда техника
мен оған жақын ғылымдарда оны қолдану, халықшаруашылығы мен
тұрмыста қолдануға бағыттау, немесе оқытуға политехникалық бағыт
беру, яғни физика, химия, география, сызу, технология сабақтары
курсымен байланыс орнату, мысалдар шығарту, оқушылардың өз бетінше
есептей білу дағдыларын қалыптастыру.
Математикалық анализдің
элементтерін оқып – біле отырып, оқушылар оның қолданбалы
мүмкіндігін бағалап және меңгеріп, математикалық анализдің
элементтерін кәсіптік есептерді шешуге қолдану дағдысын
ашады.
Туындының экономикалық
мағынасы
Өндірілген өнім мөлшерінен
уақыт бойынша
туындының еңбек өнімділігін беретінін көрдік. Енді
туындының экономикалық мағынасын көрсететін тағы
бір ұғымды береміз.
Өндіріс шығындарын өндірілетін өнімнің
мөлшері х-ке тәуелі функция ретінде карастырамыз. Өнімнің
өсімі ∆х болса, оңі өндіріс шығынының
өсімшесі ∆у, ал өнім бірлігіне
жұмсалатын өндіріс шығынының орта
өсімшесі ∆у/∆х болады. Сонда
туынды у'=lim∆х
→0∆у/∆х өндірстің шекті шығынын береді
және қосымша өнімнің бірлігіне жұмсалатын қосымша шығынды жуықтап
сипаттайды. Шекті шығындар өндіріс күші (шығарылатын өнім
көлемі) х-ке тәуелді және тұрақты емес тек айнымалы өндіріс
шығындарымен (шикізат, жанармай және т.б.)
анықталады. Осы сияқты шекті табыс, шекті өнім, шекті пайдалылық, шекті өнімділік және
басқа шекті шамаларды қарастыруға
болады.
Шекті шамалар экономикалық ұғымдардың өзгеру
барысын сипаттайды. Туынды кайсыбір экономикалық объектінің
басқа бір объектіге
қарағанда өзгеру жылдамдығын
анықтайды.
Кейбір жағдайларда
экономикалық көрсеткіштердің үзіліссіз еместігіне
қарамастан шекті шамаларды ұтымды пайдалануға болады.
Мысал ретінде монополистік және
бәсекелік рынок жағдайындағы орта және шекті
табыстардың байланысын қараймыз. Өнімді сатқаннан шыққан жиынтық табысты өнім
бірлігінің бағасымен өнім санының
көбейтіндісі ретінде анықтауға болады:
Монополистік
нарық Еркін бәсекелік нарық
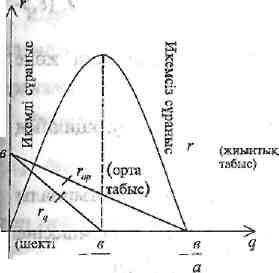

r = pq, r — жиынтық табыс, р-өнім бірлігінің бағасы,
q – өнім саны. Монополия жағдайында бір
немесе бірнеше фирма белгілі саладағы өнім ұсынысын, демек өнім
бағасын толығымен қадағалайды. Әрине, бағаның өсуіне байланысты
өнімге деген сұраныс азайады. Сұраныстың азаюы р = аq + в, (а <
0, в > 0) кемімелі функциясы
арқылы берілсін делік.
Мұндағы р
=
р(q)~өнім саны
q-ға тәуелді сұраныс мөлшері.
Соңда сатылған өнімнен түсетін жиынтық табыс
r = (аq +
в)q=аq2 +
вq, өнім бірлігінен түсетін орта
табыс rор = r/q = аq+
в,
ал шекті табыс, яғни қосымша
өнім бірлігінен түсетін қосымша табыс
r,q = 2аq+
в болады.
Сонымен монополистік нарық жағдайында сатылған өнім саны өскен сайын шекті табыс кемиді. Ол орта табыстың
аз жылдамдықпен азаюуына соқгырады.
Нарыққа өнім шығаратындар өте көп және жеке фирма бағаның
деңгейін қадағалай алмайтын бәсекелік жағдайында сатылатын өнім
саны тұрақты, мысалы, р = в болады. Сонда жиынтық табыс r = вq, орта табыс rор = r/q = в, ал шекті табыс, яғни қосымша өнім бірлігінен
түсетін қосымша табыс r,q = 2аq+
в болады.
Сонымен еркін бәсекелестік нарық жағдайында орта және шекті
табыстар өзара тең болады.
Туындының экономикада
қолданылуы
Туындының экономикада қолданылуының кейбір
мысалдарын қарастырамыз. Өндіру және
тұтыну, сұраныс және ұсыныс
теорияларының негізгі
заңдары
осы бөлімде
келтірілген тұжырымдарға
негізделеді.
Алдымен Ферма теоремасының экономикалық
қолдануына тоқталайық.
Ферма теоремасы. Егер X аралығында дифференци
алданатын
■
у=ƒ(х) функциясы осы аралықтың ішінде жатқан бір
х0 нүктесінде өзінің
ең үлкен немесе ең кіші мәнін қабылдаса, онда оның туындысы
х0 нүктесінде н
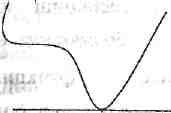
өлге тең болады: ƒ''(хо) =
0.
Өндіру теориясының негізгі
заңдарының бірі былай айтылады: Өндірушіге тиімді тауар көлемі шектік шығын
мен шектік
табыстың
теңдігімен
анықталады.
Өнім көлемі х-ке тәуелді табыс
функциясы — 0(х), пайда
функциясы – С(х), ал шығын функциясы –S(х) болсын. Сонда С(х) = D(х) - S(х). Әрине, пайда С(х) максималды мән алатын
өнім көлемі х = х0 өндірістің тиімді деңгейі болады.
Сондықтан Ферма теоремасы бойынша бұл нүктеде
С'(х0) = 0, С'(х)=D(х)-S(х) болғандықтан D'(х0)=S'(х0). Сонымен жоғарыда айтылған
экономикалық
зандылыққа
келдік.
Өңдіріс
теориясының
басқа бір маңызды
ұғымы
— орта
шығындары ең аз (минимальді) болатын тиімді өндіріс
деңгейі. Сәйкес экономикалық заң былай
айтылады: орта және шектік шығындардың теңдігімен ең тиімді өндіріс деңгейі
анықталады.
Бұл
шартта Ферма
теоремасының салдары
ретінде айтылады.
Егер S(х) – х өнім көлеміне тәуелді шығын
мөлшері болса, онда S(х)/х, яғни тауарды шығарудағы шығын
көлемінің
тауар
санына қатынасы
орта
шығынды береді. Бұл
шаманың минимумы оның
күдікті
нүктесінде болады. Сондықтан
(S(х)/х)'= S' (х) ·х -
S(х)/х2=0 → S' (х) ·х - S(х) =0 →S' (х) =
S(х)/х
яғни минимум (тиімді өндіріс
деңгейі) орта жөне шектік шығында өзара тең
болатын х
- тің мөнінде
қабылданады.
Функция графигінің
дөңестік ұғымының
да экономикалық
мағынасы
бар. Ең
көп таралған экономикалық
зандылықтарды бірі
–
кемімелі табыс заңы былай
айтылады: Өндіріс өскен
сайын
әрбір жаңа ресурстан (еңбек
ресурсын, технологиялық,
ресурс
алынған қосымша өнім бір уақыттан
кейін кеми бастайды. Басқа
сөзбен
айтқанда, егер
Δх –
ресурс өсімшесі,
ал Δу
— шығатын
өнім
өсімшесі болса,
онда Δу/Δх шамасы х өскен сайын
кемиді.
Сонымен, кемімелі табыс
заңы былай айтылады: қолданылған ресурсқа тәуелді өнім көлемін
беретін у = ƒ(х) функциясы
графигінің
дөңестігі жоғары
бағытталған.
Экономикалық теорияның
басқа
бір іргелі
ұғымы –
ол
пайдалылық функциясы U =
U(х). Мұнда
х
– тауар, ал
U
– пайдалылық. Бұл шама жеке
тұтынушы үшін өте субъективті, ал
жалпы
қоғам үшін жеткілікті объективті
болады. Кемімелі пайдалылық заңын былай
айтады: Тауар
көлемі өскен сайын
бір уақытшан
кейін әрбір жаңа тауардан алынатын
қосымша
пайдалылық
кеми бастайды.
Кемімелі пайдалылық заңы
сұраныс
және ұсыныс
теориясының математикалық зерттеулерінің
негізі болады.
Туынды
y=f(x) функциясы x нүктенің белгілі бір
маңайында аңықталсын.
Анықтама.
шегі бар болса онда бұл
шек y=f(x) функциясының x нүктедегі туындысы деп аталады
және  не
не  (x) деп
белгіленеді.
(x) деп
белгіленеді.
Яғни 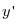 (x)=
(x)=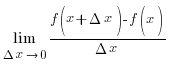
Мысал.
y=x2 функциясының x = 1 нүктедегі туындысын
есептейік:
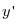 (x)
=
(x)
=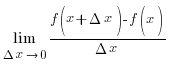
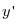 (x)
=
(x)
=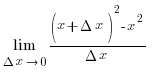
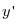 (x)
=
(x)
=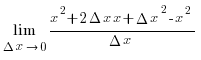
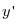 (x)
=
(x)
=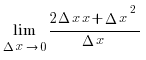
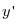 (x)
=
(x)
=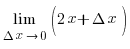
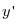 (x) =
2x
(x) =
2x
Сонымен ( x2 )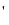 = 2x
= 2x
x=1, 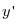 (1) = 2·1 = 2
(1) = 2·1 = 2
Туындылар кестесі
Кейбір элементарлы
функциялардың туындылар кестесі:
1. sin´x =
cosx
2. cos´x =
-sinx
3. tg
´x = 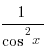
4. ctg
´x = 
5. (ax)´ =ln
a · ax ,
мұндағы a>0, a =
e болса онда (ex)´ =
ex
6. (xn)´ = n ·
xn-1 ,
мұндағы n тұрақты сан
7. (lnx)´
= 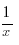
8. (arcsinx)´
= 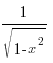
8. (arccosx)´
= 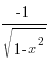
9. (logax)´
= 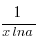
10. (arctgx)´
= 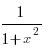
11. (arcctgx)´
= 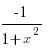
Жаттығулар.
Туындылар кестесін және туындының қасиеттерің пайдалана отырып мына туындыларды есептеңіз:
a)
y=x2+x+1, y′ -?
b) y=x cosx, y′
-?
c) y=x sinx, y′ -?
d) y=sin(2x), y′ -?
Енді бұл формулалардың біреуін дәлелдейік,
мәселен бірінші туындыны дәлелдейік.
Дәлелдеуі:
1. sin´x =
cosx
sin´x
= 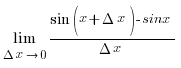
мына формуланы пайдаланайық sin α –
sin β = 2
sin(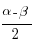 ) cos(
) cos(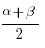 ):
):
sin
(x+ Δ x) – sin x = 2
sin(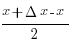 ) cos(
) cos(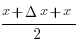 )
)
sin
(x+ Δ x) – sin x = 2
sin(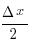 ) cos(
) cos(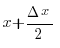 )
)
Бұл өрнекті жоғарыдағы формулаға қоямыз:
sin´x = 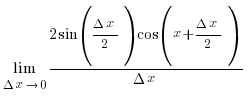
sin´x = 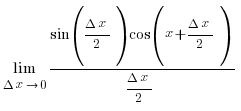
бірінші тамаша шек  бойынша
бойынша
соңдықтан:
sin´x = cosx
Осы
әдіспен cos´x =
-sinx формуласын дәлелдеңіз
Жаттығу.
3
және 4 формулаларды (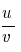 )´=
)´= 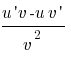 ережесінің көмегімен
дәлелдеңіз.
ережесінің көмегімен
дәлелдеңіз.
Есеп.
Екінші тамаша шектін көмегімен мына формуланы
дәлелдеңіз (ex)´ = ex.
Туындылар кестесі туындыны есептеуде көп
қолданылады соңдықтан бұл кестені есте сақтау
жөн.









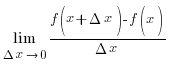
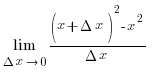
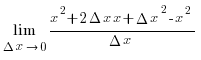
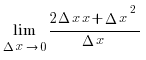
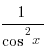
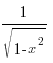
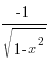
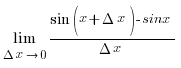
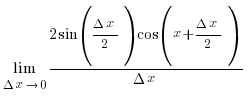
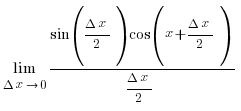
 бойынша
бойынша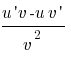 ережесінің көмегімен
дәлелдеңіз.
ережесінің көмегімен
дәлелдеңіз.











