
Семей қаласы ,"Көлік колледжі" КМКҚ
математика пәнінің оқытушысы
Жумадилова Жадыра Шарипхановна
+7 775 998 46 70
Туынды. Туындының қолданылуы
1 – бөлім
Туынды табу кестесі
|
f (x) |
f ' (x) |
|
y= C |
y' = 0 |
|
y=x |
y' =1 |
|
y= |
y'
=n |
|
y= |
y'
=− |
|
y= |
y'
=− |
|
y= |
y'
= |
|
y = |
y'
= |
|
y= |
y'
= |
|
y= |
y'
= |
|
y= |
y'
= |
|
y= |
y'
= |
|
y=sin x |
y' = cos x |
|
y=cos x |
y' = − sin x |
|
y=tg x |
y'
= |
|
y=ctg x |
y'
=
−
|
|
y=arcsin x |
y'
= |
|
y=arcos x |
y'
=− |
|
y=arctg x |
y'
= |
|
y= arcctg x |
y'
=− |
2-бөлім. Теориялық бөлім
Функцияның шегі.
x саны x0 санына ұмтыла берсін, бірақ оған тең болмасын. Бұны x→x0 деп белгілейміз.
Мысалы мына сандар тізбегінің n-ші мүшесі, n өскен сайын нөлге ұмтылады (бірақ нөлге тең болмайды):
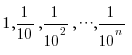 ,…
,…
Анықтама.
A саны y=f(x) функциясының x→x0 ұмтылғандағы шегі деп аталады, егер x0 санына ұмтылған кез келген x1, x2, x3,… сандар тізбегі үшін сәйкесінше f(x1), f(x2), f(x3),… сандар тізбегі A санына ұмтылса.
Бұны 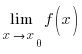 = A деп
белгілейді.
= A деп
белгілейді.
Мысал.
y = x2 болса онда ![]() . Өйткені нөлге ұмтылған кез
келген x1, x2, x3,… сандар тізбегі
үшін x12, x22, x32,… сандар тізбегі де нөлге ұмтылады
ғой.
. Өйткені нөлге ұмтылған кез
келген x1, x2, x3,… сандар тізбегі
үшін x12, x22, x32,… сандар тізбегі де нөлге ұмтылады
ғой.
Мына тамаша шектерді есте сақтау жөн:
1). 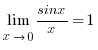 (бірінші тамаша
шек).
(бірінші тамаша
шек).
2). ![]() (1+
(1+![]() ) x = e,
мұндағы e
) x = e,
мұндағы e![]() 2,718…
(екінші тамаша шек).
2,718…
(екінші тамаша шек).
Үзіліссіз функция.
Аңықтама y=f(x) функциясы:
a). x0 нүктенің белгілі бір маңайында аңықталса.
b). ![]() (x)=
(x)=![]() (x0)
(x0)
Онда y=f(x) функциясы x0 нүктеде үзіліссіз деп аталады.
Мысал.
y =
x2 функциясы x=0 нүктеде
үзіліссіз, өйткені бұл функция біріншіден осы нүктенің аймағында
аңықталған, екіншіден ![]() , y(0) = 0,
яғни
, y(0) = 0,
яғни ![]() (x) = y
(0)
(x) = y
(0)
Аңықтама.
y=f(x) функциясы B сандар жиынының кез келген нүктесінде үзіліссіз болса, онда бұл y=f(x) функциясы B сандар жиынында үзіліссіз деп аталады.
Мысал.
y = x2 функциясы нақты сандар жиынында үзіліссіз. Жаттығу.
![]() функциясы [0;
1] сегментінде үзіліссіз бе?
функциясы [0;
1] сегментінде үзіліссіз бе?
Шектелген функциялар.
Егер бiр М саны табылып, Х жиынындағы барлық х саны үшiн мына теңсiздiк f(x)£M орындалса, онда f(x) функциясын X жиынында жоғарғы жағынан шектелген функция деп атайды.
Егер бiр М саны табылып, Х жиынының барлық х саны үшiн мына теңсiздiк f(x)³M орындалса,онда f(x) функциясын X жиынында төменгi жағынан шектелген функция деп атайды.
Егер бiр оң C саны табылып, Х жиынының барлық х саны үшiн мына теңсiздiк ôf(x)ô£C орындалса, онда f(x) функциясын X жиынында шектелген функция деп атайды.
Шектелген функциялардың қасиеттерi.
-
Егер f(x) және g(x) функцияларының екеуi де бiрдей X жиынында анықталған, шектелген функциялар болса, онда f(x)+g(x), f(x)-g(x), f(x)g(x), ôf(x)ô функциялары да Х жиынында анықталған, шектелген функциялар болады.
-
Егер f(x) және g(x) функциялары X жиынында анықталған, ал f(x) функциясы Х жиынында шектелген және g(x) функциясы үшiн ôg(x)ô>M>0 теңсiздiгi орындалса, онда
 функциясы X
жиынында шектелген функция болады
функциясы X
жиынында шектелген функция болады -
Егер f(x) функциясы X жиынында анықталған және шектелген функциялар болса, онда
 af(x), cos f(x), sin f(x), arcsin f(x), arccos
f(x), arctg f(x),
af(x), cos f(x), sin f(x), arcsin f(x), arccos
f(x), arctg f(x),
arcctg f(x) функциялары да Х жиынында анықталған, шектелген функциялар болады.
Туындының анықтамасы
Функцияны қарапайым қозғалыстар, құбылыстар мен процестерді және олардың өзгерісін математикалық модель тұрғысынан зерттеу мақсатында қолданады.
Аргумент және функцияның өсімшелері ұғымдарын анықтап алайық.
у=f(х) функциясы берілсін. Аргументтің х және х1мәндері функцияның анықталу облысынан алынған.
Анықтама: х1 –х айырымын аргументтің х нүктесіндегі өсімшесі д.а.
Өсімшені Δх таңбасымен белгілеп, “дельта икс” деп оқиды, яғни Δх= х1-х
Аргумент х-ке Δх өсімшесін бергенде у = f(х) функциясы да өсімше қабылдайды. Бұл функцияның өсімшесі Δу деп белгіленіп, Δу = (у + Δу) – у немесе Δу = f(х + Δх) – f(х) теңдігімен анықталады.
Анықтама.  қатынасының аргумент
өсімшесі Δх-тің нөлге ұмтылғандағы шегі бар болса, онда ол шекті у
= f(х) функциясының х нүктесіндегі туындысы деп
атайды.
қатынасының аргумент
өсімшесі Δх-тің нөлге ұмтылғандағы шегі бар болса, онда ол шекті у
= f(х) функциясының х нүктесіндегі туындысы деп
атайды.
у = f(х) функциясының х нүктесіндегі туындысының белгіленуі:
у' =f'(х), f'(х)-тің оқылуы: х-тен эф штрих
Функцияның туындысын табу амалын функцияны дифференциалдау деп атайды.
Анықтама бойынша туындыны табу алгоритмі:
1) аргументке Δх өсімшесін беру;
2) Δх өсімшеге сәйкес функция өсімшесін, яғни Δу = f(х + Δх) – f(х) анықтау;
3) функцияның өсімшесінің аргумент өсімшесіне қатынасын табу, яғни

4) соңғы теңдіктен аргумент өсімшесі нөлге ұмтылғандағы шекті анықтау:
lim Δу = lim f(х + Δх) – f(х) =f'(х)
Δх→0 Δх Δх→0 Δх
Туындының геометриялық мағынасы.
Ф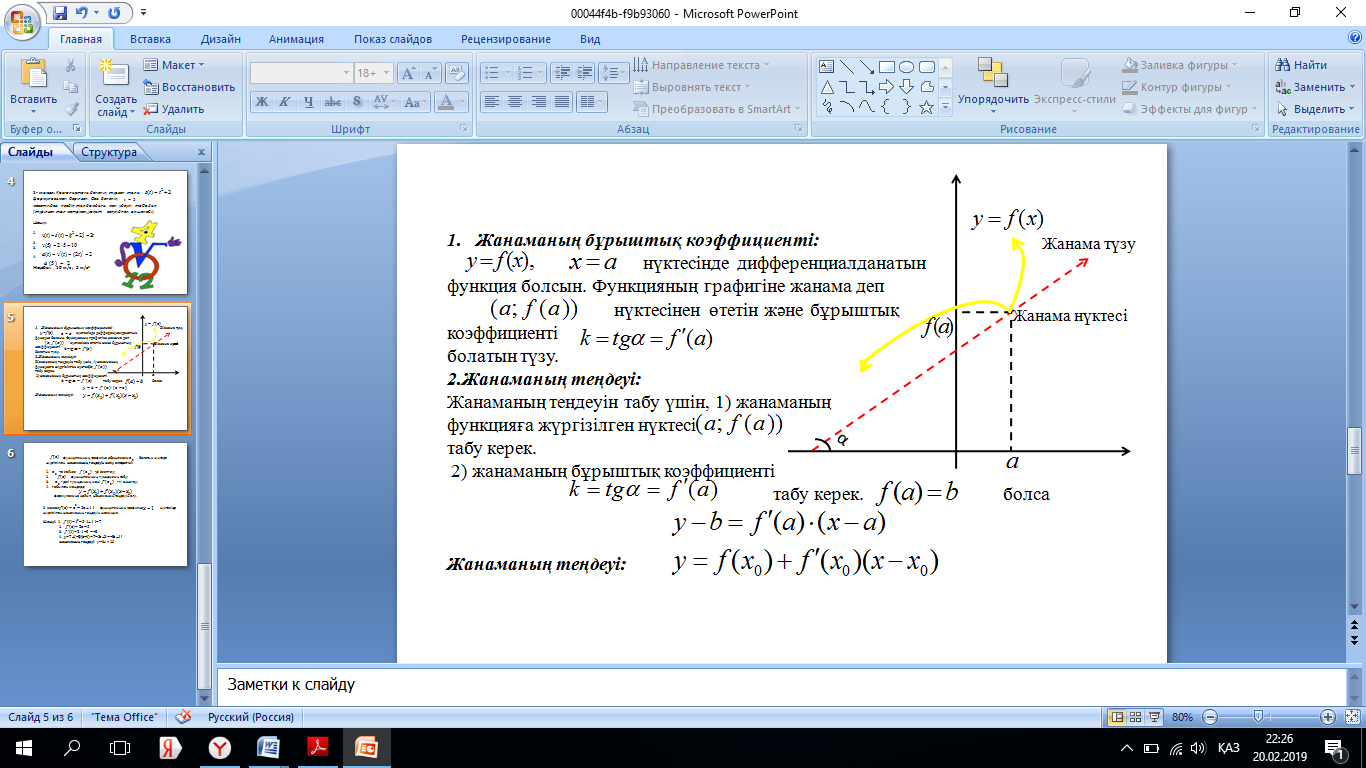 ункцияның
дифференциалдануы.
ункцияның
дифференциалдануы.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Туындыны қолдану
Туындыны қолдану
Семей қаласы ,"Көлік колледжі" КМКҚ
математика пәнінің оқытушысы
Жумадилова Жадыра Шарипхановна
+7 775 998 46 70
Туынды. Туындының қолданылуы
1 – бөлім
Туынды табу кестесі
|
f (x) |
f ' (x) |
|
y= C |
y' = 0 |
|
y=x |
y' =1 |
|
y= |
y'
=n |
|
y= |
y'
=− |
|
y= |
y'
=− |
|
y= |
y'
= |
|
y = |
y'
= |
|
y= |
y'
= |
|
y= |
y'
= |
|
y= |
y'
= |
|
y= |
y'
= |
|
y=sin x |
y' = cos x |
|
y=cos x |
y' = − sin x |
|
y=tg x |
y'
= |
|
y=ctg x |
y'
=
−
|
|
y=arcsin x |
y'
= |
|
y=arcos x |
y'
=− |
|
y=arctg x |
y'
= |
|
y= arcctg x |
y'
=− |
2-бөлім. Теориялық бөлім
Функцияның шегі.
x саны x0 санына ұмтыла берсін, бірақ оған тең болмасын. Бұны x→x0 деп белгілейміз.
Мысалы мына сандар тізбегінің n-ші мүшесі, n өскен сайын нөлге ұмтылады (бірақ нөлге тең болмайды):
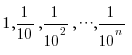 ,…
,…
Анықтама.
A саны y=f(x) функциясының x→x0 ұмтылғандағы шегі деп аталады, егер x0 санына ұмтылған кез келген x1, x2, x3,… сандар тізбегі үшін сәйкесінше f(x1), f(x2), f(x3),… сандар тізбегі A санына ұмтылса.
Бұны 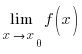 = A деп
белгілейді.
= A деп
белгілейді.
Мысал.
y = x2 болса онда ![]() . Өйткені нөлге ұмтылған кез
келген x1, x2, x3,… сандар тізбегі
үшін x12, x22, x32,… сандар тізбегі де нөлге ұмтылады
ғой.
. Өйткені нөлге ұмтылған кез
келген x1, x2, x3,… сандар тізбегі
үшін x12, x22, x32,… сандар тізбегі де нөлге ұмтылады
ғой.
Мына тамаша шектерді есте сақтау жөн:
1). 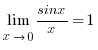 (бірінші тамаша
шек).
(бірінші тамаша
шек).
2). ![]() (1+
(1+![]() ) x = e,
мұндағы e
) x = e,
мұндағы e![]() 2,718…
(екінші тамаша шек).
2,718…
(екінші тамаша шек).
Үзіліссіз функция.
Аңықтама y=f(x) функциясы:
a). x0 нүктенің белгілі бір маңайында аңықталса.
b). ![]() (x)=
(x)=![]() (x0)
(x0)
Онда y=f(x) функциясы x0 нүктеде үзіліссіз деп аталады.
Мысал.
y =
x2 функциясы x=0 нүктеде
үзіліссіз, өйткені бұл функция біріншіден осы нүктенің аймағында
аңықталған, екіншіден ![]() , y(0) = 0,
яғни
, y(0) = 0,
яғни ![]() (x) = y
(0)
(x) = y
(0)
Аңықтама.
y=f(x) функциясы B сандар жиынының кез келген нүктесінде үзіліссіз болса, онда бұл y=f(x) функциясы B сандар жиынында үзіліссіз деп аталады.
Мысал.
y = x2 функциясы нақты сандар жиынында үзіліссіз. Жаттығу.
![]() функциясы [0;
1] сегментінде үзіліссіз бе?
функциясы [0;
1] сегментінде үзіліссіз бе?
Шектелген функциялар.
Егер бiр М саны табылып, Х жиынындағы барлық х саны үшiн мына теңсiздiк f(x)£M орындалса, онда f(x) функциясын X жиынында жоғарғы жағынан шектелген функция деп атайды.
Егер бiр М саны табылып, Х жиынының барлық х саны үшiн мына теңсiздiк f(x)³M орындалса,онда f(x) функциясын X жиынында төменгi жағынан шектелген функция деп атайды.
Егер бiр оң C саны табылып, Х жиынының барлық х саны үшiн мына теңсiздiк ôf(x)ô£C орындалса, онда f(x) функциясын X жиынында шектелген функция деп атайды.
Шектелген функциялардың қасиеттерi.
-
Егер f(x) және g(x) функцияларының екеуi де бiрдей X жиынында анықталған, шектелген функциялар болса, онда f(x)+g(x), f(x)-g(x), f(x)g(x), ôf(x)ô функциялары да Х жиынында анықталған, шектелген функциялар болады.
-
Егер f(x) және g(x) функциялары X жиынында анықталған, ал f(x) функциясы Х жиынында шектелген және g(x) функциясы үшiн ôg(x)ô>M>0 теңсiздiгi орындалса, онда
 функциясы X
жиынында шектелген функция болады
функциясы X
жиынында шектелген функция болады -
Егер f(x) функциясы X жиынында анықталған және шектелген функциялар болса, онда
 af(x), cos f(x), sin f(x), arcsin f(x), arccos
f(x), arctg f(x),
af(x), cos f(x), sin f(x), arcsin f(x), arccos
f(x), arctg f(x),
arcctg f(x) функциялары да Х жиынында анықталған, шектелген функциялар болады.
Туындының анықтамасы
Функцияны қарапайым қозғалыстар, құбылыстар мен процестерді және олардың өзгерісін математикалық модель тұрғысынан зерттеу мақсатында қолданады.
Аргумент және функцияның өсімшелері ұғымдарын анықтап алайық.
у=f(х) функциясы берілсін. Аргументтің х және х1мәндері функцияның анықталу облысынан алынған.
Анықтама: х1 –х айырымын аргументтің х нүктесіндегі өсімшесі д.а.
Өсімшені Δх таңбасымен белгілеп, “дельта икс” деп оқиды, яғни Δх= х1-х
Аргумент х-ке Δх өсімшесін бергенде у = f(х) функциясы да өсімше қабылдайды. Бұл функцияның өсімшесі Δу деп белгіленіп, Δу = (у + Δу) – у немесе Δу = f(х + Δх) – f(х) теңдігімен анықталады.
Анықтама.  қатынасының аргумент
өсімшесі Δх-тің нөлге ұмтылғандағы шегі бар болса, онда ол шекті у
= f(х) функциясының х нүктесіндегі туындысы деп
атайды.
қатынасының аргумент
өсімшесі Δх-тің нөлге ұмтылғандағы шегі бар болса, онда ол шекті у
= f(х) функциясының х нүктесіндегі туындысы деп
атайды.
у = f(х) функциясының х нүктесіндегі туындысының белгіленуі:
у' =f'(х), f'(х)-тің оқылуы: х-тен эф штрих
Функцияның туындысын табу амалын функцияны дифференциалдау деп атайды.
Анықтама бойынша туындыны табу алгоритмі:
1) аргументке Δх өсімшесін беру;
2) Δх өсімшеге сәйкес функция өсімшесін, яғни Δу = f(х + Δх) – f(х) анықтау;
3) функцияның өсімшесінің аргумент өсімшесіне қатынасын табу, яғни

4) соңғы теңдіктен аргумент өсімшесі нөлге ұмтылғандағы шекті анықтау:
lim Δу = lim f(х + Δх) – f(х) =f'(х)
Δх→0 Δх Δх→0 Δх
Туындының геометриялық мағынасы.
Ф ункцияның
дифференциалдануы.
ункцияның
дифференциалдануы.


шағым қалдыра аласыз



































