Туындының физикалық және геометриялық мағынасы.

Сабақ тақырыбы: Туындының физикалық және геометриялық мағынасы. Функция дифференциалы ұғымы

Сабақ мақсаты: Туындының физикалық және геометриялық мағынасын және функцияның х нүктесіндегі дифференциалдың және жуық есептеудің формуласын білу, есеп  шығаруда қолдануды үйрену.

Осы сабақта қол жеткізетін оқу нәтижесі:

Барлық оқушылар:Физикалық және геометриялық есептерге туындының формуласын пайдаланып жылдамдықты таба білу.

Оқушылардың басым бөлігі: Формуланы қорытып шығара білу

Кейбір оқушылар: а-деңгейіндегі есептерді шығара білу.

Бағалау критерилері: Туындының физикалық және геометриялық мағынасын біледі;

функцияның х нүктесіндегі дифференциалдың формуласын біледі;

Физикалық және геометриялық есептерге туындының формуласын пайдалануды біледі.

Алдымен туындының физикалық мағынасын қарастырайық. Түзу сызық бойымен қозғалған физикалық дененің t уақыт ішінде жүріп өткен жолы s(t) функциясымен берілсін. Қозғалыстағы дененің уақыт өткенен кейінгі жолы функциясымен анықталады. Сонда уақыт t-дан дейін өзгергенде, жолдың шамасы айырымымен анықталады. Енді осы айырымды уақытқа бөлеміз, онда қозңалыстағы дененің орташа жылдамдығы шығады: Соңғы өрнектен нөлге ұмтылғанда шекке көшcек

теңдігін аламыз.

Мұндағы s(t) – қозғалыстағы дененің t уақыт ішіндегі жүрген жолы,

– қозғалыстағы дененің t уақыт мезетіндегі лездік жылдамдығы.

Жалпы, y=f(x)функциясының х нүктесіндегі f (x) туындысы оның х нүктесіндегі өзгеру жылдамдығын береді. Бұл туындыынң физикалық мағынасы.

Туынды ұғымы физикадан кеңінен қолданылады.

Мысал. 1. Ньютонның екінші заңы бойынша күш пен импульс F=p қатынасымен байланысқан; өткізгіштің көлденең қимасы арқылы өткен заряд мөлшері ток үншін анықтайды, яғни ;Ox осі бойымен ғана өзгергеретін электростатикалық өрісте кернеу мен потенциал қатынасымен байланысқан.

№42.2. 1) Нүкте түзу бойымен заңымен қозғалады, мұндағы s шамасы метрмен, t секундпен өлшенеді. деп алып, болғандағы лездік жылдамдықты және , уақыт аралығындағы орташа жылдамдықтың өзгерісін табыңдар.

Шешуі. – қозғалыстағы дененің t уақыт мезетіндегі лездік жылдамдығы екенін ескерсек. Онда

Енді туындының геометриялық мағынасын қарастырайық. y=f(x)функциясының графигі берілсін.

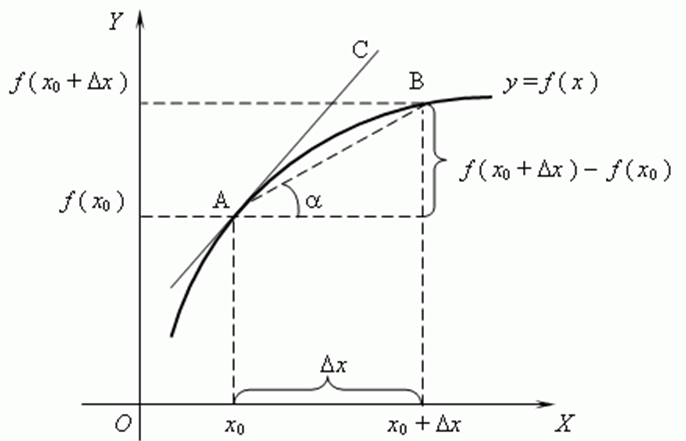
Суреттен y=f(x)функциясының графигінің кез келген кз келген А және В екі нүктесі үшін

tg теңдігі орындалатынын көреміз, мұндағы бұрышы –АВ қиюшысының Ох осіне көлбеулік бұрыш. Анүктесінің орнын айқындап, В нүктесіне қарай жылжытсақ, онда шексіз кеми отырып, 0 санына жақындайды. Демек, қатынасының шегі абсциссасы болатын нүктеде жүргізілген жанаманың бұрыштық коффициентіне тең:

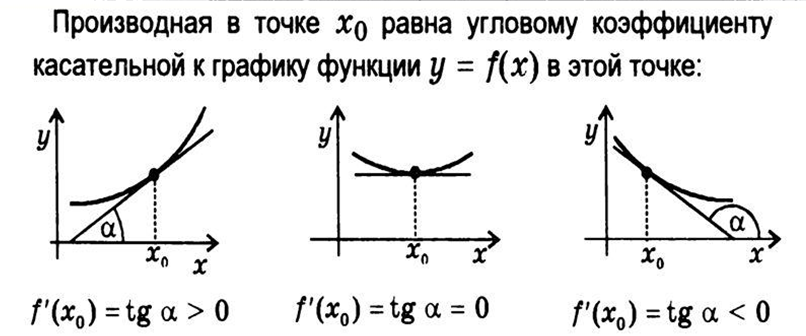
Осыдан шығатын қорытынды: нүктедегі функцияның туындысы функция графигіне осы нүктеде жүргізілген жанаманың бұрыштық коэффициентіне тең. Бұл туындының геометрикалық мағынасы.Бұрыш шамаларының түрлеріне қарап төмендегі суретте көрсетілгендей болады:

Анықтама. өсімшесінің негізігі сызықтық бөлігі функцияның х нүктесіндегі дифференцмалы деп аталады.

– дифференциалды табу формуласы.

функциясының дифференциалын табу формуласы.

Мысал.2. функциясының дифференциалын табайық.

Шешуі. Ол үшін формуласын қолданамыз:

– кез келген дефференциалданатын функцияның жуық өсімшесін табу формуласы. Өсімшеге қарағанда дифференциал оңай табылатындықтан формуласы практикада кеңінен қолданылады.

Мысал. x=2 және болғандағы функциясының жуық мәнін есептейік.

Шешуі: Дифференциалды табу формуласын қолданамыз:

-функцияның жуық мәнін есептеу формуласы.

Үй тапсырмасы.

№42.2. 2) Нүкте түзу бойымен заңымен қозғалады, мұндағы s шамасы метрмен, t секундпен өлшенеді. Қандай уақыт мезетінде жылдамдық нөлге тең болады?

№42.4. f(x) функциясының туындысын қолданып, табыңдар:

-1; ;

№42.6. формуласын қолданып фуекциясы үшін өрнектің жуық мәнін табыңдар: