|
Бөлім: |
Үшбұрыштар |
|
|
Педагогтің аты-жөні |
|
|
|
Күні: |
14.10.2021 |
|
|
Сынып: 7 |
Қатысушылар саны: Қатыспағандар саны: |
|
|
Сабақтың тақырыбы |
Үшбұрыштың биссектрисы, медианасы, биіктігі және орта сызығы |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
7.1.1.14 теңқабырғалы, теңбүйірлі, тікбұрышты үшбұрыштардың элементтерін білу; |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Басы 5 мин |
Ұйымдастыру бөлімі:Оқушылармен амандасу,түгендеу. |
|
|
|
|
Ортасы 35 мин |
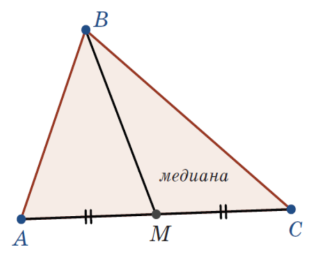
Үшбұрыштың медианасы
Үшбұрыштың төбесін қарсы жатқан қабырғасының ортасымен қосатын түзудің кесіндісін үшбұрыштың медианасы деп атайды. Δ ABC: AM = MC, BM кесіндісі — АВС үшбұрышының медианасы Үшбұрыш биссектрисасы
Үшбұрыштың төбесінен қарсы жатқан қабырғасымен қиылысу нүктесіне дейінгі биссектрисаның кесіндісін үшбұрыштың биссектрисасы деп атайды. Δ ABC: ∠BAD = ∠DAC AD кесіндісі — АВС үшбұрышының биссектрисасы Үшбұрыш биіктігі
Үшбұрыштың төбесінен қарсы жатқан қарбырғаға түсірілген перпендикулярдың кесіндісін үшбұрыштың биіктігі деп аталады. Δ ABC: AH ⊥ BC AH кесіндісі — АВС үшбұрышының биіктігі |
Мысалдарды мұғаліммен бірге талдайды 1. Табаны ВС болатын тең бүйірлі ABC үшбұрышының периметрі 40 см-ге, ал тең қабырғалы BCD үшбұрышының периметрі 45 см-ге тең. АВ және ВС қабырғаларының ұзындықтарын тап. 2. Табаны ВС болатын тең бүйірлі ABC үшбұрышының AM медианасы жүргізілген. АМ медианасының ұзындығын тап, егер ABC үшбұрышының периметрі 32 см-ге, ал АВМ үшбұрышының периметрі 24 см-ге тең болса. 3. Периметрі 20 см-ге тең АВС үшбұрышының АM медианасы оны екі үшбұрышқа бөледі. АВМ үшбұрышының периметрі 13, ал АМС үшбұрышының периметрі 12 см-ге тең. АМ медианасының ұзындығы неге тең? 4. Егер үшбұрыштың медианасы оның биіктігімен сәйкес болса, онда үшбұрыштың тең бүйірлі болатынын дәлелде. |
|
Оқулық
Қосымша тапсырма: сызғыш |
|
Соңы 5 мин |
Сабақты бекіту “Бізді қоршаған әлемдегі үшбұрыштар” жайлы жинаған қызықты мәліметтеріңмен сыныптастарыңмен бөлісіңдер Рефлексия |
Рефлексия. Оқушыларға стикерлер таратылады. - Сабақ маған түсініксіз - Тақырыпты түсіндім,бірақ есептеген кезде қиналамын Маған сабақ ұнады.Тақырыпты меңгерді |
|
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Үшбұрыштың биссектрисы, медианасы, биіктігі және орта сызығы
Үшбұрыштың биссектрисы, медианасы, биіктігі және орта сызығы
|
Бөлім: |
Үшбұрыштар |
|
|
Педагогтің аты-жөні |
|
|
|
Күні: |
14.10.2021 |
|
|
Сынып: 7 |
Қатысушылар саны: Қатыспағандар саны: |
|
|
Сабақтың тақырыбы |
Үшбұрыштың биссектрисы, медианасы, биіктігі және орта сызығы |
|
|
Оқу бағдарламасына сәйкес оқыту мақсаттары |
7.1.1.14 теңқабырғалы, теңбүйірлі, тікбұрышты үшбұрыштардың элементтерін білу; |
|
|
Сабақтың мақсаты |
|
|
Сабақтың барысы
|
Сабақтың кезеңі/ уақыт |
Педагогтің әрекеті |
Оқушының әрекеті |
Бағалау |
Ресурстар |
|
Басы 5 мин |
Ұйымдастыру бөлімі:Оқушылармен амандасу,түгендеу. |
|
|
|
|
Ортасы 35 мин |
Үшбұрыштың медианасы
Үшбұрыштың төбесін қарсы жатқан қабырғасының ортасымен қосатын түзудің кесіндісін үшбұрыштың медианасы деп атайды. Δ ABC: AM = MC, BM кесіндісі — АВС үшбұрышының медианасы Үшбұрыш биссектрисасы
Үшбұрыштың төбесінен қарсы жатқан қабырғасымен қиылысу нүктесіне дейінгі биссектрисаның кесіндісін үшбұрыштың биссектрисасы деп атайды. Δ ABC: ∠BAD = ∠DAC AD кесіндісі — АВС үшбұрышының биссектрисасы Үшбұрыш биіктігі
Үшбұрыштың төбесінен қарсы жатқан қарбырғаға түсірілген перпендикулярдың кесіндісін үшбұрыштың биіктігі деп аталады. Δ ABC: AH ⊥ BC AH кесіндісі — АВС үшбұрышының биіктігі |
Мысалдарды мұғаліммен бірге талдайды 1. Табаны ВС болатын тең бүйірлі ABC үшбұрышының периметрі 40 см-ге, ал тең қабырғалы BCD үшбұрышының периметрі 45 см-ге тең. АВ және ВС қабырғаларының ұзындықтарын тап. 2. Табаны ВС болатын тең бүйірлі ABC үшбұрышының AM медианасы жүргізілген. АМ медианасының ұзындығын тап, егер ABC үшбұрышының периметрі 32 см-ге, ал АВМ үшбұрышының периметрі 24 см-ге тең болса. 3. Периметрі 20 см-ге тең АВС үшбұрышының АM медианасы оны екі үшбұрышқа бөледі. АВМ үшбұрышының периметрі 13, ал АМС үшбұрышының периметрі 12 см-ге тең. АМ медианасының ұзындығы неге тең? 4. Егер үшбұрыштың медианасы оның биіктігімен сәйкес болса, онда үшбұрыштың тең бүйірлі болатынын дәлелде. |
|
Оқулық
Қосымша тапсырма: сызғыш |
|
Соңы 5 мин |
Сабақты бекіту “Бізді қоршаған әлемдегі үшбұрыштар” жайлы жинаған қызықты мәліметтеріңмен сыныптастарыңмен бөлісіңдер Рефлексия |
Рефлексия. Оқушыларға стикерлер таратылады. - Сабақ маған түсініксіз - Тақырыпты түсіндім,бірақ есептеген кезде қиналамын Маған сабақ ұнады.Тақырыпты меңгерді |
|
|

шағым қалдыра аласыз