
Кіріспе
Геометрия-математиканың әртүрлі фигуралар мен олардың қасиеттерін қарастыратын саласы. Геометрия үшбұрыштан басталады. Екі жарым мыңжылдықта Үшбұрыш геометрияның символы болды; бірақ ол тек символ ғана емес, Үшбұрыш - геометрия атомы.
Мен өз жұмысымда үшбұрыштың биссектрисалары, медианалары мен биіктіктерінің қиылысу нүктелерінің қасиеттерін қарастырамын, олардың керемет қасиеттері мен Үшбұрыш сызықтары туралы айтатын боламын.
Геометрия курсында оқылатын осындай нүктелердің қатарына мыналар жатады:
а) биссектрисалардың қиылысу нүктесі (жазылған шеңбердің ортасы);
б) ортаңғы перпендикулярлардың қиылысу нүктесі (сипатталған шеңбердің центрі);
в) биіктіктердің қиылысу нүктесі (ортоцентр);
г) медианалардың қиылысу нүктесі (центроид).
Өзектілігі: үшбұрыш және оның керемет нүктелерінің қасиеттері туралы біліміді кеңейту
Мақсаты: үшбұрышты оның керемет нүктелеріне зерттеу, олардың жіктелуі мен қасиеттерін зерттеу.
Тапсырмалар:
1. Қажетті әдебиеттерді қарастыру
2. Үшбұрыштың керемет нүктелерінің жіктелуін зерттеу
3. Үшбұрыштың керемет нүктелерін құра білу.
Жобаның гипотезасы: кез-келген үшбұрышта керемет нүктелерді таба білу геометриялық есептерді шешуге мүмкіндік береді.
Үшбұрыштың керемет нүктелері туралы тарихи мәліметтер
Төртінші "бастау" кітабында Евклид "берілген үшбұрышқа шеңбер жазу"мәселесін шешеді. Шешімнен үшбұрыштың ішкі бұрыштарының үш биссектрисасы бір нүктеде – жазылған шеңбердің ортасында қиылысады. Евклидтің басқа мәселесін шешуден олардың ортасында үшбұрыштың қабырғаларына қалпына келтірілген перпендикулярлар да бір нүктеде-сипатталған шеңбердің ортасында қиылысады. "Бастауларда "үшбұрыштың үш биіктігі ортоцентр деп аталатын бір нүктеде қиылысатыны туралы айтылмайды (грекше" ортос "сөзі" түзу","дұрыс" дегенді білдіреді). Бұл ұсыныс Архимед, Папп, Проклға белгілі болды.
Үшбұрыштың төртінші ерекше нүктесі-медианалардың қиылысу нүктесі. Архимед оның үшбұрыштың ауырлық орталығы (барицентрі) екенін дәлелдеді. Жоғарыда аталған төрт нүктеге ерекше назар аударылды және XVIII ғасырдан бастап олар үшбұрыштың "керемет" немесе "ерекше" нүктелері деп аталды.
Осы және басқа нүктелермен байланысты үшбұрыштың қасиеттерін зерттеу бастауыш математиканың жаңа саласын – "Үшбұрыш геометриясын" немесе "үшбұрыштың жаңа геометриясын" құрудың бастамасы болды, оның негізін қалаушылардың бірі Леонард Эйлер болды. 1765 жылы Эйлер кез-келген үшбұрышта ортоцентр, бариентр және сипатталған шеңбердің центрі кейінірек "Эйлер сызығы"деп аталатын бір түзуде жатқанын дәлелдеді.
1.1 Үшбұрыш
Ү
А
шбұрыш-бір түзуде жатпайтын үш нүктеден және осы нүктелерді жұптастыратын үш сегменттен тұратын геометриялық фигура. Нүктелер-үшбұрыштың шыңдары, сегменттер — үшбұрыштың қабырғалары.

В
А,В,С – нүктелеріАВ, АС, ВС – қабырғалары
С
В
Әр үшбұрышпен байланысты төрт нүкте бар:
1) медианалардың қиылысу нүктесі;
2) биссектрисалардың қиылысу нүктесі;
3) биіктіктердің қиылысу нүктесі.
4) ортаңғы перпендикулярлардың қиылысу нүктесі;
1.2. Үшбұрыштың медианалары
Үшбұрыштың мединасы-үшбұрыштың төбесін қарама-қарсы жақтың ортасымен байланыстыратын кесінді (1-сурет). Медиананың үшбұрыштың қабырғасымен қиылысу нүктесі медиананың негізі деп аталады.
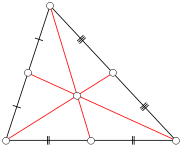
1-сурет. Үшбұрыштың медианасы
Біз үшбұрыштың бүйірлерінің ортасын саламыз және шыңдардың әрқайсысын қарама-қарсы жақтың ортасымен байланыстыратын сегменттер саламыз. Мұндай сегменттер медиана деп аталады.
Тағы да, біз бұл сегменттердің бір нүктеде қиылысатынын байқаймыз. Егер медианалардың алынған сегменттерінің ұзындығын өлшейтін болсақ, онда тағы бір қасиетті тексеруге болады: медианалардың қиылысу нүктесі барлық медианаларды 2:1-ге қатысты бөледі, шыңдардан есептейді. Сонымен қатар, медианалардың қиылысу нүктесінде иненің ұшына сүйенетін Үшбұрыш тепе-теңдікте! Мұндай қасиетке ие нүкте ауырлық центрі (барицентр) деп аталады. Тең массаның центрі кейде центроид деп аталады. Сондықтан үшбұрыштың медианаларының қасиеттерін келесідей тұжырымдауға болады:үшбұрыштың медианалары ауырлық центрінде қиылысады және қиылысу нүктесі шыңнан санағанда 2:1 қатынасында бөлінеді.
1.3. Үшбұрыштың биссектрисалары
Үшбұрыштың биссектрисасы бұрыштың жоғарғы жағынан оның қарама-қарсы жағымен қиылысына дейін тартылған бұрыштың биссектрисасының сегменті деп аталады. Үшбұрыштың үш шыңына сәйкес келетін үш биссектрисасы бар (2-сурет).

2-сурет. Үшбұрыштың бисектрисасы
ABC ерікті үшбұрышында біз оның бұрыштарының биссектрисаларын сызамыз. Тағы да, дәл құрылыста барлық үш биссектриса бір нүктеде қиылысады D. D нүктесі де ерекше: ол үшбұрыштың барлық үш қабырғасынан бірдей қашықтықта орналасқан. DA 1, DB 1 және DC1 перпендикулярларын үшбұрыштың бүйірлеріне түсіру арқылы бұған көз жеткізуге болады. Олардың барлығы бір-біріне тең: DA1=DB1=DC1.
Егер шеңберді D нүктесінде центрмен және da 1 радиусымен сызсаңыз, онда ол үшбұрыштың барлық үш жағына тиеді (яғни олардың әрқайсысында тек бір ортақ нүкте болады). Мұндай шеңбер үшбұрышқа жазылған деп аталады. Сонымен, үшбұрыштың бұрыштарының биссектрисалары жазылған шеңбердің ортасында қиылысады.
1.4. Үшбұрыштағы биіктіктер
Үшбұрыштың биіктігі-үшбұрыштың төбесінен қарама-қарсы жаққа немесе қарама-қарсы жаққа сәйкес келетін түзуге түсірілген перпендикуляр. Үшбұрыштың түріне байланысты Биіктік үшбұрыштың ішінде болуы мүмкін (үшбұрышты үшбұрыш үшін), оның қабырғасына сәйкес келуі мүмкін (тікбұрышты үшбұрыштың аяғы) немесе үшбұрыштың сыртында доғал үшбұрышта жүруі мүмкін (3-сурет).
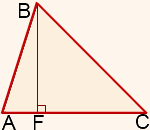

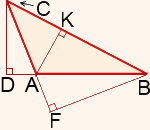
3-сурет. Үшбұрыштың биіктіктері
• Егер үшбұрышта үш биіктік салынса, онда олардың барлығы бір нүктеде қиылысады H. бұл нүкте ортоцентр деп аталады. (Сурет 4).
Құрылыстардың көмегімен үшбұрыштың түріне байланысты ортоцентр әртүрлі орналасқанын тексеруге болады:
* үшбұрышты үшбұрыштың ішінде-ішінде;
* тікбұрышты – гипотенузада;
* доғал бұрышта-сыртта.
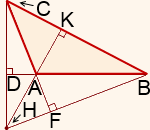
4-сурет.Үшбұрыштың орта центрі
Осылайша біз үшбұрыштың тағы бір керемет нүктесімен таныстық және мынаны айта аламыз: үшбұрыштың биіктігі ортоцентрде қиылысады.
1.5. Үшбұрыштың қабырғаларына ортаңғы перпендикулярлар
Сегментке ортаңғы перпендикуляр — берілген сегментке перпендикуляр және оның ортасынан өтетін түзу.
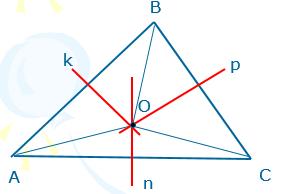
Біз ABC ерікті үшбұрышын саламыз және оның қабырғаларына перпендикуляр сызамыз. Егер құрылыс дәл орындалса,онда барлық перпендикулярлар бір нүктеде қиылысады-O нүктесі. Басқаша айтқанда, егер үшбұрыштың бір шыңынан өтетін О нүктесінде центрі бар шеңбер сызылса, онда ол оның қалған екі шыңынан да өтеді.
Үшбұрыштың барлық төбелерінен өтетін шеңбер оның жанында сипатталған деп аталады. Сондықтан үшбұрыштың белгіленген қасиетін келесідей тұжырымдауға болады: үшбұрыштың қабырғаларына ортаңғы перпендикулярлар сипатталған шеңбердің ортасында қиылысады (5-сурет).
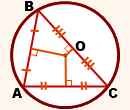
5-сурет. Шеңберге жазылған үшбұрыш
2 тарау. Үшбұрыштың керемет нүктелерін зерттеу.
Үшбұрыштардағы биіктікті зерттеу
Үшбұрыштың барлық үш биіктігі бір нүктеде қиылысады. Бұл нүкте үшбұрыштың ортоцентрі деп аталады.
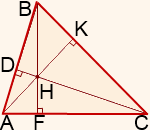
Үшбұрышты үшбұрыштың биіктігі үшбұрыштың ішінде орналасқан.
Тиісінше, биіктіктердің қиылысу нүктесі де үшбұрыштың ішінде орналасқан.
Тік бұрышты үшбұрышта екі биіктік қабырғаларға сәйкес келеді. (Бұл өткір бұрыштардың шыңдарынан аяққа қарай сызылған биіктіктер).
Гипотенузаға жүргізілген биіктік үшбұрыштың ішінде жатыр .

АС-айнымалы ток-шыңнан AB жағына қарай тартылған биіктік.
AB-в шыңынан айнымалы ток жағына қарай тартылған биіктік.
AK-тік бұрыштың жоғарғы жағынан ӘК гипотенузасына тартылған биіктік.
Тік бұрышты үшбұрыштың биіктігі тік бұрыштың жоғарғы жағында қиылысады (а-ортоцентр).
Үшбұрыштың доғал бұрышында үшбұрыштың ішінде бір ғана биіктік бар — бұл доғал бұрыштың жоғарғы жағынан сызылған биіктік.
Қалған екі биіктік үшбұрыштың сыртында жатыр және үшбұрыштың бүйірлерінің жалғасына қарай төмендейді.

AK-BC жағына тартылған биіктік.
BF-АС жағының жалғасына жүргізілген биіктік.
CD-бұл AB жағының жалғасына жүргізілген биіктік.
Доғал үшбұрыштың биіктіктерінің қиылысу нүктесі де үшбұрыштың сыртында орналасқан:

АВС үшбұрышының ортацентрі–Н
Үшбұрыштағы биссектрисаларды зерттеу
Үшбұрыштың биссектрисасы үшбұрыштың ішінде орналасқан үшбұрыштың (сәуленің) бұрышының биссектрисасының бөлігі болып табылады.
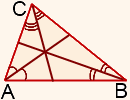 Үшбұрыштың барлық үш
биссектрисасы бір нүктеде қиылысады.
Үшбұрыштың барлық үш
биссектрисасы бір нүктеде қиылысады.
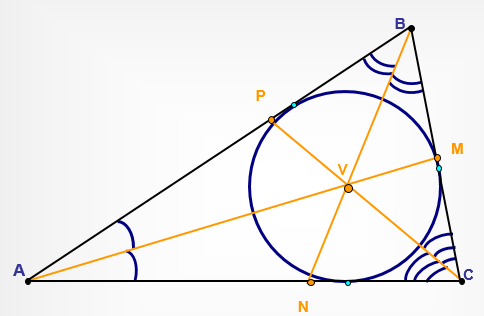
Үшбұрышты, доғал және тікбұрышты үшбұрыштардағы биссектрисалардың қиылысу нүктесі үшбұрышқа жазылған шеңбердің ортасы болып табылады және ішінде орналасқан.
Үшбұрыштағы медианаларды зерттеу
Үшбұрыштың үш төбесі мен үш қабырғасы болғандықтан, қарама-қарсы жақтың төбесі мен ортасын байланыстыратын сегменттер де үшеу.
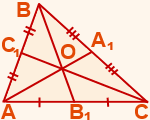
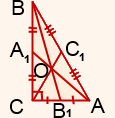
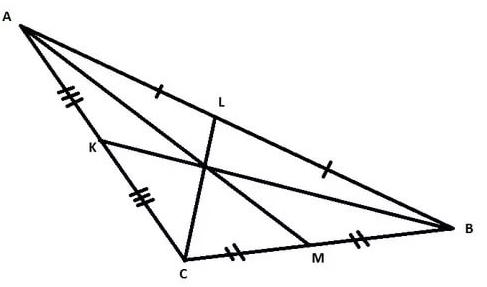
Осы үшбұрыштарды зерттегеннен кейін Мен кез-келген үшбұрышта медианалар бір нүктеде қиылысатынын түсіндім. Бұл нүкте үшбұрыштың ауырлық центрі деп аталады.
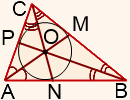
Үшбұрыштың бүйіріне ортаңғы перпендикулярларды зерттеу
Үшбұрыштың ортаңғы перпендикуляры-үшбұрыштың қабырғасының ортасына қарай сызылған перпендикуляр.
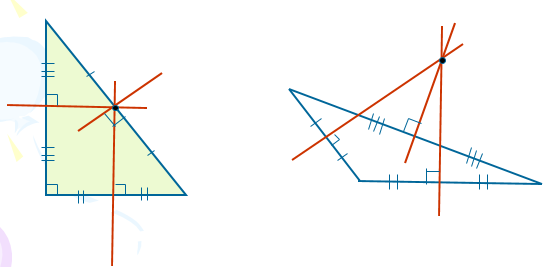
Үшбұрыштың үш ортаңғы перпендикуляры бір нүктеде қиылысады, сипатталған шеңбердің центрі болып табылады.
Үшбұрышты үшбұрыштағы ортаңғы перпендикулярлардың қиылысу нүктесі үшбұрыштың ішінде орналасқан; доғал бұрышта-үшбұрыштың сыртында; тік бұрышты – гипотенузаның ортасында.
Қорытынды
Атқарылған жұмыс барысында біз келесі тұжырымдарға келеміз:
1. Мақсатқа қол жеткізілді: біз үшбұрышты зерттеп, оның керемет нүктелерін таптық.
2. Қойылған міндеттер шешілді:
1). Қажетті әдебиеттерді зерттедік;
2). Үшбұрыштың керемет нүктелерінің жіктелуін зерттеді;
3). Үшбұрыштың керемет нүктелерін салуды үйренді;
4). Буклетті безендіру үшін зерттелген материалды қорытындылады.
Үшбұрыштың керемет нүктелерін таба білу құрылыс мәселелерін шешуге көмектеседі деген Гипотеза расталды.
Жұмыста үшбұрыштың керемет нүктелерін салу әдістері дәйекті түрде көрсетілген, геометриялық құрылымдар туралы тарихи мәліметтер келтірілген.
Бұл жұмыстың мәліметтері 7-сыныптағы геометрия сабақтарында пайдалы болуы мүмкін. Кітапша берілген тақырып бойынша геометрия бойынша анықтамалық бола алады.
Пайдаланылған әдебиеттер тізімі
-
Учебник. Л.С. Атанасян «Геометрия 7-9 классы Мнемозина,2015.
-
Википедияhttps://ru.wikipedia.org/wiki/Геометрия#/media/File:Euclid%27s_postulates.png
-
Портал Алые Паруса https://ru.wikipedia.org/wiki/Геометрия
-
Ведущий образовательный портал России http://cendomzn.ucoz.ru/index/0-15157
10
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Үшбұрыштың тамаша нүктелері
Үшбұрыштың тамаша нүктелері
Кіріспе
Геометрия-математиканың әртүрлі фигуралар мен олардың қасиеттерін қарастыратын саласы. Геометрия үшбұрыштан басталады. Екі жарым мыңжылдықта Үшбұрыш геометрияның символы болды; бірақ ол тек символ ғана емес, Үшбұрыш - геометрия атомы.
Мен өз жұмысымда үшбұрыштың биссектрисалары, медианалары мен биіктіктерінің қиылысу нүктелерінің қасиеттерін қарастырамын, олардың керемет қасиеттері мен Үшбұрыш сызықтары туралы айтатын боламын.
Геометрия курсында оқылатын осындай нүктелердің қатарына мыналар жатады:
а) биссектрисалардың қиылысу нүктесі (жазылған шеңбердің ортасы);
б) ортаңғы перпендикулярлардың қиылысу нүктесі (сипатталған шеңбердің центрі);
в) биіктіктердің қиылысу нүктесі (ортоцентр);
г) медианалардың қиылысу нүктесі (центроид).
Өзектілігі: үшбұрыш және оның керемет нүктелерінің қасиеттері туралы біліміді кеңейту
Мақсаты: үшбұрышты оның керемет нүктелеріне зерттеу, олардың жіктелуі мен қасиеттерін зерттеу.
Тапсырмалар:
1. Қажетті әдебиеттерді қарастыру
2. Үшбұрыштың керемет нүктелерінің жіктелуін зерттеу
3. Үшбұрыштың керемет нүктелерін құра білу.
Жобаның гипотезасы: кез-келген үшбұрышта керемет нүктелерді таба білу геометриялық есептерді шешуге мүмкіндік береді.
Үшбұрыштың керемет нүктелері туралы тарихи мәліметтер
Төртінші "бастау" кітабында Евклид "берілген үшбұрышқа шеңбер жазу"мәселесін шешеді. Шешімнен үшбұрыштың ішкі бұрыштарының үш биссектрисасы бір нүктеде – жазылған шеңбердің ортасында қиылысады. Евклидтің басқа мәселесін шешуден олардың ортасында үшбұрыштың қабырғаларына қалпына келтірілген перпендикулярлар да бір нүктеде-сипатталған шеңбердің ортасында қиылысады. "Бастауларда "үшбұрыштың үш биіктігі ортоцентр деп аталатын бір нүктеде қиылысатыны туралы айтылмайды (грекше" ортос "сөзі" түзу","дұрыс" дегенді білдіреді). Бұл ұсыныс Архимед, Папп, Проклға белгілі болды.
Үшбұрыштың төртінші ерекше нүктесі-медианалардың қиылысу нүктесі. Архимед оның үшбұрыштың ауырлық орталығы (барицентрі) екенін дәлелдеді. Жоғарыда аталған төрт нүктеге ерекше назар аударылды және XVIII ғасырдан бастап олар үшбұрыштың "керемет" немесе "ерекше" нүктелері деп аталды.
Осы және басқа нүктелермен байланысты үшбұрыштың қасиеттерін зерттеу бастауыш математиканың жаңа саласын – "Үшбұрыш геометриясын" немесе "үшбұрыштың жаңа геометриясын" құрудың бастамасы болды, оның негізін қалаушылардың бірі Леонард Эйлер болды. 1765 жылы Эйлер кез-келген үшбұрышта ортоцентр, бариентр және сипатталған шеңбердің центрі кейінірек "Эйлер сызығы"деп аталатын бір түзуде жатқанын дәлелдеді.
1.1 Үшбұрыш
Ү
А
шбұрыш-бір түзуде жатпайтын үш нүктеден және осы нүктелерді жұптастыратын үш сегменттен тұратын геометриялық фигура. Нүктелер-үшбұрыштың шыңдары, сегменттер — үшбұрыштың қабырғалары.

В
А,В,С – нүктелеріАВ, АС, ВС – қабырғалары
С
В
Әр үшбұрышпен байланысты төрт нүкте бар:
1) медианалардың қиылысу нүктесі;
2) биссектрисалардың қиылысу нүктесі;
3) биіктіктердің қиылысу нүктесі.
4) ортаңғы перпендикулярлардың қиылысу нүктесі;
1.2. Үшбұрыштың медианалары
Үшбұрыштың мединасы-үшбұрыштың төбесін қарама-қарсы жақтың ортасымен байланыстыратын кесінді (1-сурет). Медиананың үшбұрыштың қабырғасымен қиылысу нүктесі медиананың негізі деп аталады.

1-сурет. Үшбұрыштың медианасы
Біз үшбұрыштың бүйірлерінің ортасын саламыз және шыңдардың әрқайсысын қарама-қарсы жақтың ортасымен байланыстыратын сегменттер саламыз. Мұндай сегменттер медиана деп аталады.
Тағы да, біз бұл сегменттердің бір нүктеде қиылысатынын байқаймыз. Егер медианалардың алынған сегменттерінің ұзындығын өлшейтін болсақ, онда тағы бір қасиетті тексеруге болады: медианалардың қиылысу нүктесі барлық медианаларды 2:1-ге қатысты бөледі, шыңдардан есептейді. Сонымен қатар, медианалардың қиылысу нүктесінде иненің ұшына сүйенетін Үшбұрыш тепе-теңдікте! Мұндай қасиетке ие нүкте ауырлық центрі (барицентр) деп аталады. Тең массаның центрі кейде центроид деп аталады. Сондықтан үшбұрыштың медианаларының қасиеттерін келесідей тұжырымдауға болады:үшбұрыштың медианалары ауырлық центрінде қиылысады және қиылысу нүктесі шыңнан санағанда 2:1 қатынасында бөлінеді.
1.3. Үшбұрыштың биссектрисалары
Үшбұрыштың биссектрисасы бұрыштың жоғарғы жағынан оның қарама-қарсы жағымен қиылысына дейін тартылған бұрыштың биссектрисасының сегменті деп аталады. Үшбұрыштың үш шыңына сәйкес келетін үш биссектрисасы бар (2-сурет).

2-сурет. Үшбұрыштың бисектрисасы
ABC ерікті үшбұрышында біз оның бұрыштарының биссектрисаларын сызамыз. Тағы да, дәл құрылыста барлық үш биссектриса бір нүктеде қиылысады D. D нүктесі де ерекше: ол үшбұрыштың барлық үш қабырғасынан бірдей қашықтықта орналасқан. DA 1, DB 1 және DC1 перпендикулярларын үшбұрыштың бүйірлеріне түсіру арқылы бұған көз жеткізуге болады. Олардың барлығы бір-біріне тең: DA1=DB1=DC1.
Егер шеңберді D нүктесінде центрмен және da 1 радиусымен сызсаңыз, онда ол үшбұрыштың барлық үш жағына тиеді (яғни олардың әрқайсысында тек бір ортақ нүкте болады). Мұндай шеңбер үшбұрышқа жазылған деп аталады. Сонымен, үшбұрыштың бұрыштарының биссектрисалары жазылған шеңбердің ортасында қиылысады.
1.4. Үшбұрыштағы биіктіктер
Үшбұрыштың биіктігі-үшбұрыштың төбесінен қарама-қарсы жаққа немесе қарама-қарсы жаққа сәйкес келетін түзуге түсірілген перпендикуляр. Үшбұрыштың түріне байланысты Биіктік үшбұрыштың ішінде болуы мүмкін (үшбұрышты үшбұрыш үшін), оның қабырғасына сәйкес келуі мүмкін (тікбұрышты үшбұрыштың аяғы) немесе үшбұрыштың сыртында доғал үшбұрышта жүруі мүмкін (3-сурет).



3-сурет. Үшбұрыштың биіктіктері
• Егер үшбұрышта үш биіктік салынса, онда олардың барлығы бір нүктеде қиылысады H. бұл нүкте ортоцентр деп аталады. (Сурет 4).
Құрылыстардың көмегімен үшбұрыштың түріне байланысты ортоцентр әртүрлі орналасқанын тексеруге болады:
* үшбұрышты үшбұрыштың ішінде-ішінде;
* тікбұрышты – гипотенузада;
* доғал бұрышта-сыртта.

4-сурет.Үшбұрыштың орта центрі
Осылайша біз үшбұрыштың тағы бір керемет нүктесімен таныстық және мынаны айта аламыз: үшбұрыштың биіктігі ортоцентрде қиылысады.
1.5. Үшбұрыштың қабырғаларына ортаңғы перпендикулярлар
Сегментке ортаңғы перпендикуляр — берілген сегментке перпендикуляр және оның ортасынан өтетін түзу.
Біз ABC ерікті үшбұрышын саламыз және оның қабырғаларына перпендикуляр сызамыз. Егер құрылыс дәл орындалса,онда барлық перпендикулярлар бір нүктеде қиылысады-O нүктесі. Басқаша айтқанда, егер үшбұрыштың бір шыңынан өтетін О нүктесінде центрі бар шеңбер сызылса, онда ол оның қалған екі шыңынан да өтеді.
Үшбұрыштың барлық төбелерінен өтетін шеңбер оның жанында сипатталған деп аталады. Сондықтан үшбұрыштың белгіленген қасиетін келесідей тұжырымдауға болады: үшбұрыштың қабырғаларына ортаңғы перпендикулярлар сипатталған шеңбердің ортасында қиылысады (5-сурет).

5-сурет. Шеңберге жазылған үшбұрыш
2 тарау. Үшбұрыштың керемет нүктелерін зерттеу.
Үшбұрыштардағы биіктікті зерттеу
Үшбұрыштың барлық үш биіктігі бір нүктеде қиылысады. Бұл нүкте үшбұрыштың ортоцентрі деп аталады.

Үшбұрышты үшбұрыштың биіктігі үшбұрыштың ішінде орналасқан.
Тиісінше, биіктіктердің қиылысу нүктесі де үшбұрыштың ішінде орналасқан.
Тік бұрышты үшбұрышта екі биіктік қабырғаларға сәйкес келеді. (Бұл өткір бұрыштардың шыңдарынан аяққа қарай сызылған биіктіктер).
Гипотенузаға жүргізілген биіктік үшбұрыштың ішінде жатыр .

АС-айнымалы ток-шыңнан AB жағына қарай тартылған биіктік.
AB-в шыңынан айнымалы ток жағына қарай тартылған биіктік.
AK-тік бұрыштың жоғарғы жағынан ӘК гипотенузасына тартылған биіктік.
Тік бұрышты үшбұрыштың биіктігі тік бұрыштың жоғарғы жағында қиылысады (а-ортоцентр).
Үшбұрыштың доғал бұрышында үшбұрыштың ішінде бір ғана биіктік бар — бұл доғал бұрыштың жоғарғы жағынан сызылған биіктік.
Қалған екі биіктік үшбұрыштың сыртында жатыр және үшбұрыштың бүйірлерінің жалғасына қарай төмендейді.

AK-BC жағына тартылған биіктік.
BF-АС жағының жалғасына жүргізілген биіктік.
CD-бұл AB жағының жалғасына жүргізілген биіктік.
Доғал үшбұрыштың биіктіктерінің қиылысу нүктесі де үшбұрыштың сыртында орналасқан:

АВС үшбұрышының ортацентрі–Н
Үшбұрыштағы биссектрисаларды зерттеу
Үшбұрыштың биссектрисасы үшбұрыштың ішінде орналасқан үшбұрыштың (сәуленің) бұрышының биссектрисасының бөлігі болып табылады.
 Үшбұрыштың барлық үш
биссектрисасы бір нүктеде қиылысады.
Үшбұрыштың барлық үш
биссектрисасы бір нүктеде қиылысады.


Үшбұрышты, доғал және тікбұрышты үшбұрыштардағы биссектрисалардың қиылысу нүктесі үшбұрышқа жазылған шеңбердің ортасы болып табылады және ішінде орналасқан.
Үшбұрыштағы медианаларды зерттеу
Үшбұрыштың үш төбесі мен үш қабырғасы болғандықтан, қарама-қарсы жақтың төбесі мен ортасын байланыстыратын сегменттер де үшеу.



Осы үшбұрыштарды зерттегеннен кейін Мен кез-келген үшбұрышта медианалар бір нүктеде қиылысатынын түсіндім. Бұл нүкте үшбұрыштың ауырлық центрі деп аталады.
Үшбұрыштың бүйіріне ортаңғы перпендикулярларды зерттеу
Үшбұрыштың ортаңғы перпендикуляры-үшбұрыштың қабырғасының ортасына қарай сызылған перпендикуляр.

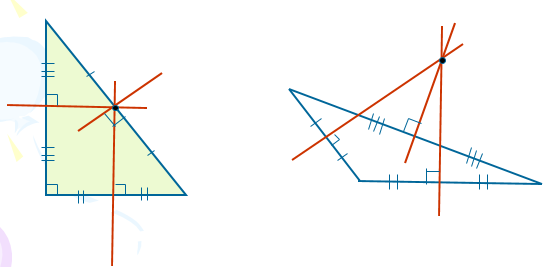
Үшбұрыштың үш ортаңғы перпендикуляры бір нүктеде қиылысады, сипатталған шеңбердің центрі болып табылады.
Үшбұрышты үшбұрыштағы ортаңғы перпендикулярлардың қиылысу нүктесі үшбұрыштың ішінде орналасқан; доғал бұрышта-үшбұрыштың сыртында; тік бұрышты – гипотенузаның ортасында.
Қорытынды
Атқарылған жұмыс барысында біз келесі тұжырымдарға келеміз:
1. Мақсатқа қол жеткізілді: біз үшбұрышты зерттеп, оның керемет нүктелерін таптық.
2. Қойылған міндеттер шешілді:
1). Қажетті әдебиеттерді зерттедік;
2). Үшбұрыштың керемет нүктелерінің жіктелуін зерттеді;
3). Үшбұрыштың керемет нүктелерін салуды үйренді;
4). Буклетті безендіру үшін зерттелген материалды қорытындылады.
Үшбұрыштың керемет нүктелерін таба білу құрылыс мәселелерін шешуге көмектеседі деген Гипотеза расталды.
Жұмыста үшбұрыштың керемет нүктелерін салу әдістері дәйекті түрде көрсетілген, геометриялық құрылымдар туралы тарихи мәліметтер келтірілген.
Бұл жұмыстың мәліметтері 7-сыныптағы геометрия сабақтарында пайдалы болуы мүмкін. Кітапша берілген тақырып бойынша геометрия бойынша анықтамалық бола алады.
Пайдаланылған әдебиеттер тізімі
-
Учебник. Л.С. Атанасян «Геометрия 7-9 классы Мнемозина,2015.
-
Википедияhttps://ru.wikipedia.org/wiki/Геометрия#/media/File:Euclid%27s_postulates.png
-
Портал Алые Паруса https://ru.wikipedia.org/wiki/Геометрия
-
Ведущий образовательный портал России http://cendomzn.ucoz.ru/index/0-15157
10

шағым қалдыра аласыз















