
Головоломный лабиринты
Рис. 5
Внеклассная работа по математике
Тема: Лабиринты. Пути решения.
Ф.И., класс:
Булыга Ангелина, 10 «Б» класс
Джаксылыкова Милана, 10 «Б» класс
Учитель математики: Коровина Светлана Анатольевна
Содержание:
-
Введение………………………………………………..2
-
Что такое лабиринт? …………………………………..2
-
Виды лабиринтов………………………………………3
4. Способы выхода из лабиринтов………………………...7
4.1 Теорема Тремо………………………………………7
4.2 Правило правой и левой руки……………………..9
5. Задачи про лабиринты…………………………………...11
6. Заключение……………………………………………….18
7. Вывод……………………………………………………..18
8. Список используемой литературы……………………...19
Цель:
Изучить историю возникновения лабиринтов и методы решения задач о лабиринтах.
Задачи:
-
Провести отбор материала, связанного с лабиринтами.
-
Выявление различных методов нахождения выходов из лабиринтов и применение их к решению задач.
-
Нахождение связи лабиринтов с нашей жизнью.
-
Создать брошюру с задачами о лабиринтах.
Гипотеза.
-
Безвыходных лабиринтов нет.
-
Метод правой (левой) руки является наиболее простым и верным, но применим только к односвязным лабиринтам и в том случае, когда не требуется отыскать кратчайший путь.
-
Метод зачеркивания тупиковых ходов является универсальным для решения любого типа лабиринтов.
-
Зная правило построения лабиринта, можно составлять алгоритм его прохождения.
1.Введение.
Идя по жизни, мы понятия не имеем, где окажемся завтра. Мы стремимся к цели, но не знаем, как ее достичь. Плутаем, рискуя оказаться в тупике. Ломаем голову: какую дорогу выбрать? Символ нашей жизни - лабиринт. История лабиринтов длинна, сложна и запутанна. Как и жизнь человека.
Сократ.
Наверняка, многие из нас встречали в каких - либо журналах или газетах такое занимательное развлечение, как лабиринты. Но не все знают - что такое «лабиринты» и откуда они появились. Хотя с лабиринтами встречаемся довольно часто: в рисунках ребенка, чертежах конструкторов, схемах работы городского транспорта можно заметить тот или иной вариант лабиринта. Так что же это такое «лабиринт»?
2.Что такое лабиринт?
Слово «Лабиринт» произошло от греческого и означает ходы в подземельях.
Другой источник утверждает: «Лабиринт - храм Зевса Лабрандского на Крите, т.е. Labrynthios, поскольку основным символом и атрибутом этого Зевса является топор (по греч. - labrys). Среди рисунков во многих помещениях дворца часто встречаются изображения двустороннего топорика. Это символический знак, связанный с религиозным культом критских жителей. Такие же топорики были найдены среди сталактитов и сталагмитов в одной из пещер, где, по преданию, родился Зевс. Двойная секира с острием по-гречески называется "лабрис". Ученые предполагают, что именно отсюда происходит слово "лабиринт", которым первоначально называли "дом двойного топора" - дворец царя Миноса.»
Действительно, существует очень много природных подземных пещер с таким огромным количеством перекрещивающихся коридоров, закоулков и тупиков, что нетрудно в них заблудиться и потеряться.
Примеры такого же рода, но уже искусственных лабиринтов, могут представить шахты иных рудников, или так называемые «катакомбы».
В конце концов, словом «лабиринт» чаще всего обозначали именно искусственное сооружение, составленное из большого числа аллей или галерей, бесчисленные разветвления, перекрестки и тупики, которые заставляли попавшего туда бесконечно блуждать в тщетных поисках выхода. Об устройстве таких лабиринтов слагались целые легенды.
Известнее всего легенда о лабиринте, построенном мастером Дедалом на острове Крит для мифического же царя Миноса. В этом лабиринте обитало грозное чудовище с головой быка и туловищем человека: Минотавр.
3.Виды лабиринтов.
Существуют несколько видов лабиринтов вот самые популярные из них.
Церковные лабиринты
Европы.
Ранние христианские церкви с энтузиазмом переняли традицию
лабиринта. В первую очередь это был символ самой церкви, например
выбитый на каменных стенах собора в Лукке (Италия) или вышитый на
облачении усопших епископов, которые были изображены лежащими в
лоне церкви.

Головоломный лабиринт.
Головоломные лабиринты используются для развития логического мышления.

Лабиринты в других областях человеческой
деятельности.
Заметим, что далеко не все лабиринтные структуры поддаются
непосредственному наблюдению. Есть любопытная теория, что
структурой именно такого рода является, например, модель развития
индоевропейских языков, а также любой языковый (лингвистический)
лабиринт.

Дерновые лабиринты.
В XIII-XIX веках лабиринтами называли особого рода садовые украшения, состоящие из более или менее высоких живых изгородей или из трельяжей, обсаженные растениями. Они были расположены так, что между ними образуются дорожки, ведущие к одному центру, но изгибающиеся в разные стороны и сообщающиеся между собой столь замысловато, что гуляющему не легко добраться до этого центра, также как и найти обратный путь.
![]()
«Живой» лабиринт
Ленинградские катакомбы.
Оказалось, что катакомбы, известные нам по многим детским фильмам, - есть разновидность лабиринтов.
Катакомбы Ленинградской области можно разделить на 4 типа:
1. Бывшие разработки кварцевого песка (Саблино, Старая Ладога, Борщево).
2. Бывшие разработки известняки и камня. (Телези, Аропаккузи, Кипень, Береговая).
3. Подземные ходы специального назначения. (Румболовская гора и гора Парнас).
4. Карстовые и псевдокарстовые полости. (Жихарево и частично Рождествено).
Катакомба Береговая.
Катакомба Береговая (Янтарная, Помойка) расположена на левом берегу реки Тосна, немного выше по течению возле автомобильного моста. Имеет три входа, которые легко найти при движении по дороге с автобусной остановки в сторону моста. Главный вход (Воронка) выходит прямо в обрыв берега реки. Спуск к нему начинается от земляного бугра (в народе - «Пьяной горки»), расположенной почти у самого моста. Подойдя около нее к обрыву, можно увидеть поросшую мелколесьем воронку в склоне. Правее нее есть металлическая лестница, по которой подходят ко входу. Спуститься можно еще по тропе левее воронки. На входе в пещеру стоит металлическая дверь. Ниже воронки из пещеры вытекает ручей. Второй вход в пещеру (Решетка) расположен несколько выше по течению (правее, если смотреть от дороги), примерно в 100м. Ориентиром служит бетонный столб ЛЭП в центральной части площадки для разворота автомобилей. Несколько левее его вниз по склону спускается желоб, по которому нужно спуститься на небольшую террасу. Здесь расположен металлический люк, через который по металлической лестнице можно спуститься в пещеру. Третий вход (Трупы) расположен на левой стороне автодороги. Около начала спуска к мосту следует свернуть на поле влево и выйти на поле, где искать овраг. В овраге течет ручей, по которому и следует войти через провал в пещеру. Из входов третий наименее комфортен.
Катакомба Береговая на настоящий момент, в связи с падением уровня озера и исследованием заозерной части, является самой протяженной в Саблино. Общая длина ее ходов превышает 7000м (привходовой части - 3500м). Высота потолков в привходовой части 160-180см, с залами выше 500см, в заозерной части колеблется в пределах от 50 до 350см.
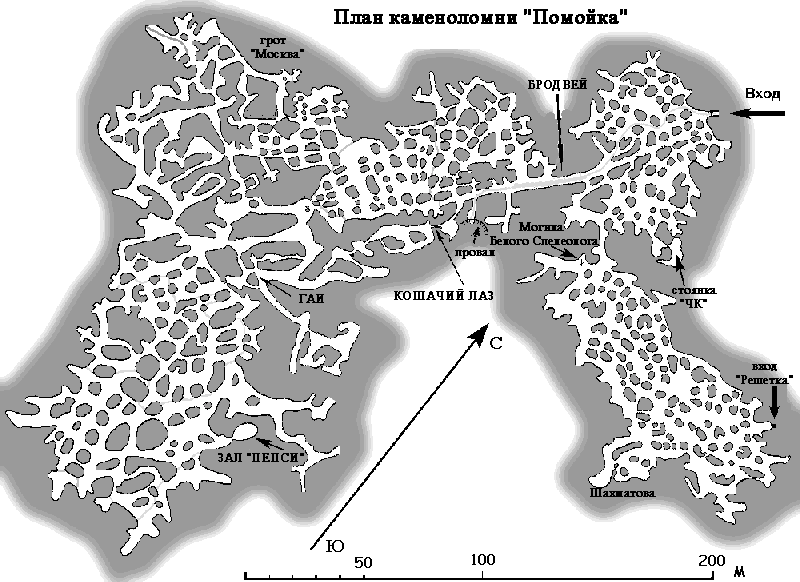
Лабиринт как геометрическая сеть.
Аллеи, дорожки, коридоры, галереи, шахты и т. п.. Лабиринты тянутся, изгибаясь во все стороны, перекрещиваются, расходятся по всевозможным направлениям, ответвляются, образуют тупики и т. п.. Но мы для большей ясности рассмотрения вопроса, все перекрестки обозначим просто точками, а все эти аллеи, коридоры и т. д. будем принимать просто за линии, прямые или кривые, плоские или нет – все равно, но эти линии соединяют наши точки.
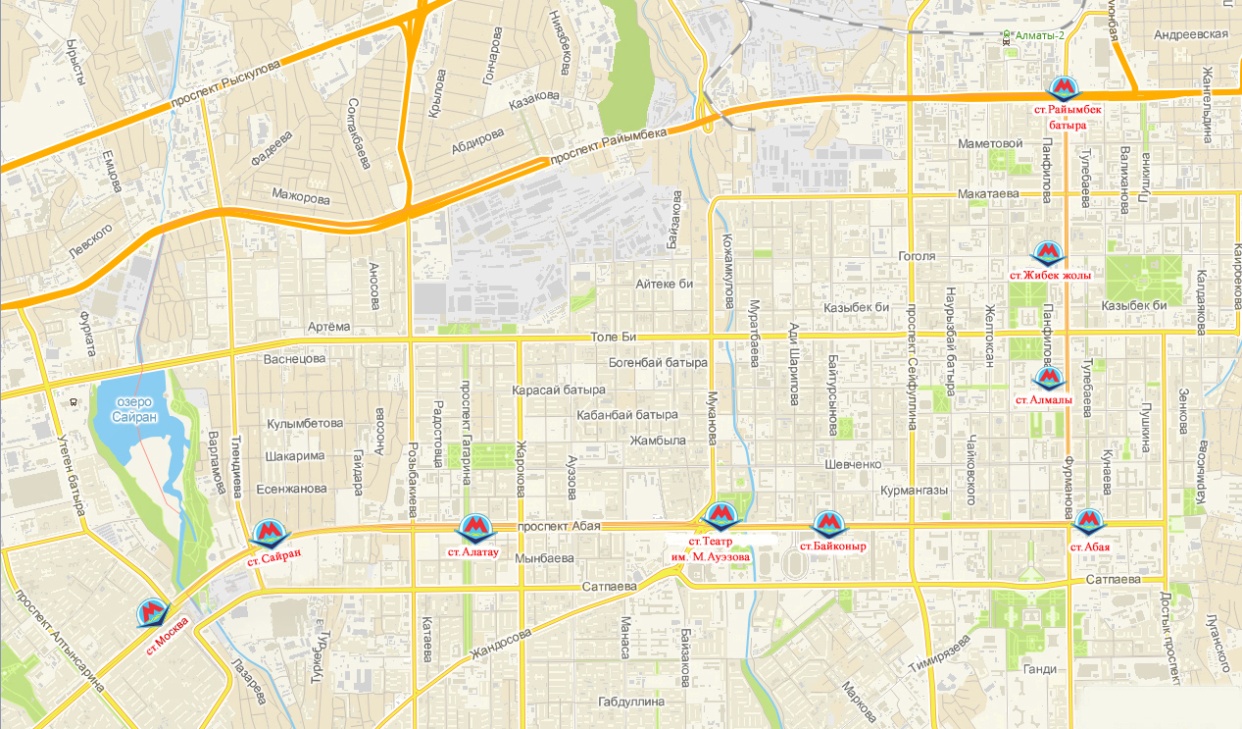
Схема метрополитена г.Алматы.
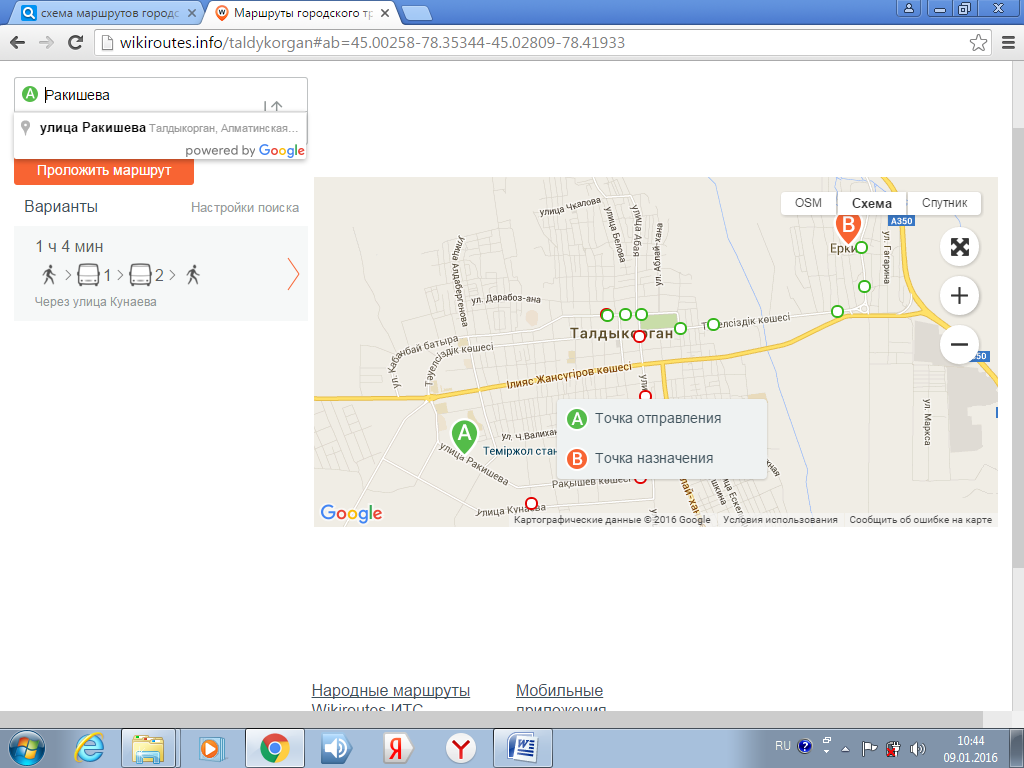
Схема движения городского транспорта г. Талдыкорган.
4.Способы выхода из лабиринта.
4.1Теорема Тремо.
Универсальный алгоритм прохождения любых лабиринтов был описан только через столетие в книге французского математика Э. Люка "Recreations matematiques", изданной в 1882 году. Интересно, что Люка при описании алгоритма указал на первенство другого французского математика М. Тремо. Таким образом, алгоритм стал известен как алгоритм Люка-Тремо.
Тремо предлагает следующие правила: выйдя из любой точки лабиринта, надо сделать отметку на его стене (крест) и двигаться в произвольном направлении до тупика или перекрестка; в первом случае вернуться назад, поставить второй крест, свидетельствующий, что путь пройден дважды - туда и назад, и идти в направлении, не пройденном ни разу, или пройденном один раз; во втором - идти по произвольному направлению, отмечая каждый перекресток на входе и на выходе одним крестом; если на перекресте один крест уже имеется, то следует идти новым путем, если нет - то пройденным путем, отметив его вторым крестом.
Зная алгоритм Тремо, можно скорректировать поведение легендарного Тесея. Вдохновленный подарком любимой Ариадны, он уверенно идет по лабиринту. Вдруг перед ним возникает ход, по которому уже протянута нить... Что делать? Ни в коем случае не пересекать ее, а вернуться по уже известному пути, сдваивая нить, пока не найдется еще один непройденный ход.
Применив вариант алгоритма Тремо, отец теории информации Клод Шеннон (Claude Elwood Shannon) построил одного из первых самообучающихся роботов. Шеннон дал ему звучное имя "Тесей", но в истории "Тесей" стал больше известен как "мышь" Шеннона. "Мышь" сначала обследовала весь лабиринт, а затем (во второй раз) проходила весь путь значительно быстрее, избегая участков, пройденных дважды.
Тремо предлагает примерно такой вариант решения задач о лабиринтах. Всякий раз, идя по любому коридору в первый раз, ставим при входе в коридор и при выходе из коридора на стене по черточке, если идем по коридору вторично, то перечеркиваем черточки. Если мы имеем дело с действительным лабиринтом, или галереями подземных шахт, с разветвлениями пещер и т. д., то блуждающему в этих шахтах вместо черточек на бумаге придется делать уже иной знак, чтобы ориентироваться, и класть, например, камень при входе и выходе из каждого перекрестка – в галерее, которую он покидает, и в той, в которую он входит.
1. Если подошли к перекрестку, на котором ни разу небыли, то дальше идем по любому коридору (рис. 1), если же попали в тупик – идем обратно (рис. 2).
2. Если подошли к перекрестку, где уже побывали, и подошли к нему по такой дороге, по которой мы идем в первый раз, то немедленно отправляемся обратно (рис. 3).
3. Если подошли к перекрестку таким путем, по которому уже дважды шли, то далее, если есть коридоры, по которым ещё ни разу не ходили, идем по любому из них (рис. 4).
Если же таких коридоров нет, то идем по любому пройденному один раз (рис. 5).
![]()
перекресток


перекресток
Рис. 1
Рис. 2
тупик


Рис. 4
перекресток
Рис. 3
перекресток

4.2 Правила правой и левой руки.
Одним из самых простых правил для прохождения лабиринта является правило "одной руки": двигаясь по лабиринту, надо все время касаться правой или левой рукой его стены. Этот алгоритм, вероятно, был известен еще древним грекам. Придется пройти долгий путь, заходя во все тупики, но в итоге цель будет достигнута. Хотя у этого правила и есть один недостаток, но о нем мы поговорим позже.
Попробуем описать робота, действующего в соответствии с правилом "правой руки".
В начале своей работы робот должен найти стену, по которой он будет следовать. Для этого он может просто двигаться вперед, пока не упрется в преграду.
После того как робот наткнулся на препятствие, он начинает передвигаться в соответствии с правилом "правой руки".
Двигаясь вдоль стены, робот следит, есть ли проход справа. Если проход есть, робот должен идти по нему, чтобы не оторваться от стены справа.
Если прохода нет - впереди стена - робот поворачивает налево. Если прохода снова нет, он еще раз поворачивает налево, таким образом разворачиваясь на 180 градусов, и идет в обратном направлении.
Блок-схема алгоритма для робота, работающего по правилу "правой руки", представлена на рисунке.
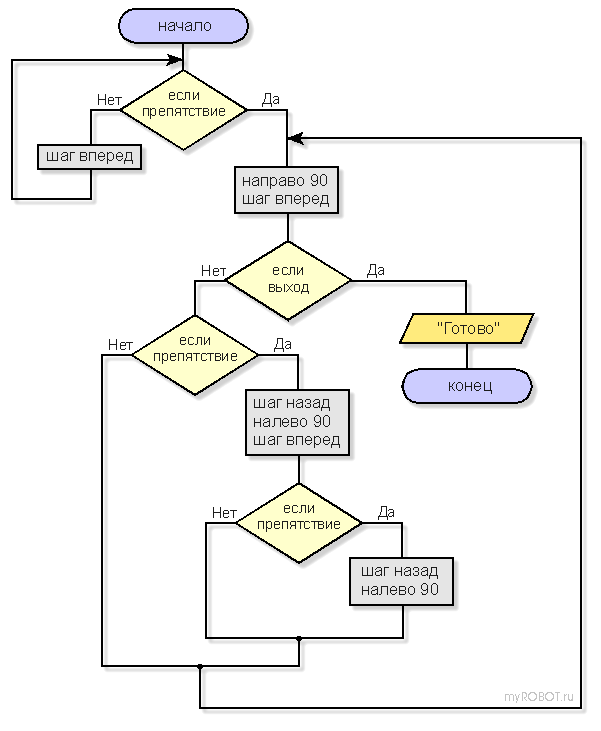
Е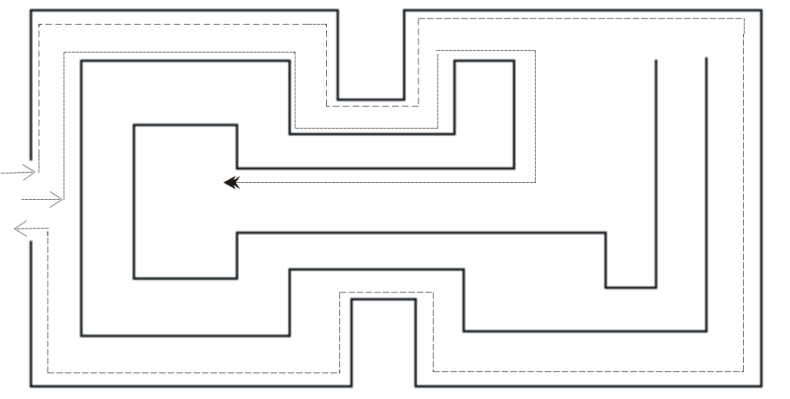 сли известно, что у лабиринта нет отдельно
стоящих стенок, то есть нет замкнутых маршрутов, по которым можно
возвращаться в исходную точку, то такой лабиринт называют
односвязным и его всегда можно обойти полностью, применив правило
"одной руки".
сли известно, что у лабиринта нет отдельно
стоящих стенок, то есть нет замкнутых маршрутов, по которым можно
возвращаться в исходную точку, то такой лабиринт называют
односвязным и его всегда можно обойти полностью, применив правило
"одной руки".
Если же лабиринт содержит отдельно стоящие стенки, то, применяя правило "одной руки", не всегда можно пройти все коридоры и тупики. Лабиринты с отдельно стоящими стенками и с замкнутыми маршрутами называются многосвязными. При этом многосвязные лабиринты можно разделить на две группы: без "петли" вокруг цели (замкнутый маршрут не проходит вокруг цели) и с замкнутой "петлей" вокруг цели (цель можно обойти по замкнутому маршруту).
В многосвязных лабиринтах второй группы правило "одной руки" не работает и, применяя его, достичь цели невозможно. Но и эти лабиринты можно пройти, полагаясь на точный алгоритм.
Решение задачи о таких лабиринтах принадлежит
сравнительно позднему времени, и начало ему положено Леонардом
Эйлером. Эйлер не без оснований полагал, что выход из любого
лабиринта может быть найден, и притом сравнительно простым
пут![]()
![]()
![]()
Рис. 3
перекресток
Рис. 1
ем.
5.Примеры задач на лабиринты.
Рассмотрим два простейших правила решения задач с лабиринтами, все стены которого имеют вид одной, нигде не пересекающей себя замкнутой линии (вход закрыт воротами). Отметим две точки на плане лабиринта.
-
Если обе точки находятся либо внутри, либо снаружи лабиринта, то любая соединяющая их линия пересечет границу лабиринта четное число раз.
-
Е
 сли одна точка находится снаружи лабиринта, а другие
внутри, то любая соединяющая их линия пересечет границу лабиринта
такого вида нечетное число раз.
сли одна точка находится снаружи лабиринта, а другие
внутри, то любая соединяющая их линия пересечет границу лабиринта
такого вида нечетное число раз.
Н апример, отметим точку
А внутри лабиринта и точку
B
снаружи лабиринта. Соединим эти точки линией. Она
пересекает границу лабиринта пять раз, то есть нечетное количество
раз.
апример, отметим точку
А внутри лабиринта и точку
B
снаружи лабиринта. Соединим эти точки линией. Она
пересекает границу лабиринта пять раз, то есть нечетное количество
раз.
Задача №1.
На цирковой арене.
Н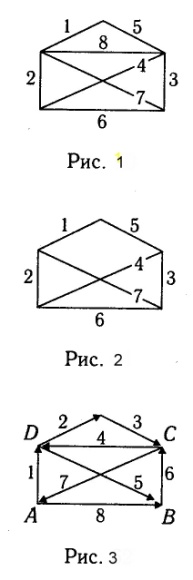 а цирковой арене выступал канатоходец. На высоте
трех метров от земли на пяти столбах был натянуты канаты, по
которым он должен был проходить. Канаты были натянуты так, как это
показано на рисунке 1.
а цирковой арене выступал канатоходец. На высоте
трех метров от земли на пяти столбах был натянуты канаты, по
которым он должен был проходить. Канаты были натянуты так, как это
показано на рисунке 1.
Канатоходец должен был пройти по восьми канатам таким образом, чтобы по каждому из них пройти всего один раз. И это ему всегда удавалось, хотя он и не возвращался в то же место, откуда выходил. Но во время одного из выступлений оборвался канат №8, и осталось всего семь канатов (рис.2).
Может ли теперь канатоходец пройти все канаты, проходя по каждому из них всего раз? Покажите, как ходил канатоходец, когда все канаты были целы, и ответьте на поставленный вопрос.
Решение:
Когда все канаты были целы, канатоходец, выходя из точки А, заканчивал свой путь в точке В (рис.3). После того, как оборвался канат №8, канатоходец не сможет обойти все канаты по одному разу.
Задача №2.
Тропинки в садах.
В саду Александра Ивановича тропинки проложены, как это показано на рис. 4, а у Бориса Борисовича - как показано на рис. 5. Кто из них может обойти все тропинки, проходя по каждой всего один раз?
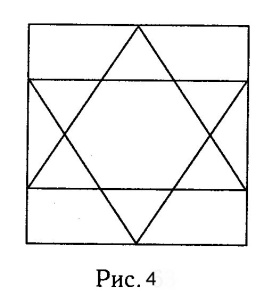
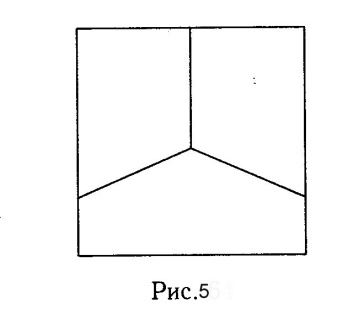
Ответ: Александр Иванович.
Задача №3.
Среди георгин.
С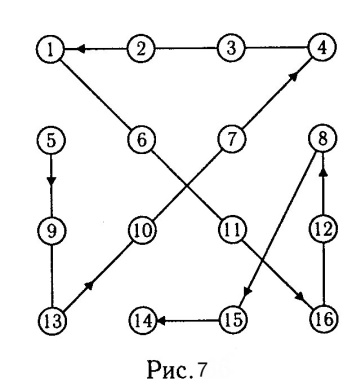 адовник имел квадратную клумбу 4*4 метра, на
которой он вырастил 16 кустов георгин. Расстояние между кустами
было 1 метр. Пока кусты еще не расцвели, цветовод обходил все
кусты, идя по кратчайшему пути, но когда чудесные цветы
распустились, садовник обходил их по самому длинному пути. К
каждому цветку он подходил всего один раз. Как выглядел самый
короткий путь от куста к кусту, а как самый
длинный?
адовник имел квадратную клумбу 4*4 метра, на
которой он вырастил 16 кустов георгин. Расстояние между кустами
было 1 метр. Пока кусты еще не расцвели, цветовод обходил все
кусты, идя по кратчайшему пути, но когда чудесные цветы
распустились, садовник обходил их по самому длинному пути. К
каждому цветку он подходил всего один раз. Как выглядел самый
короткий путь от куста к кусту, а как самый
длинный?
Р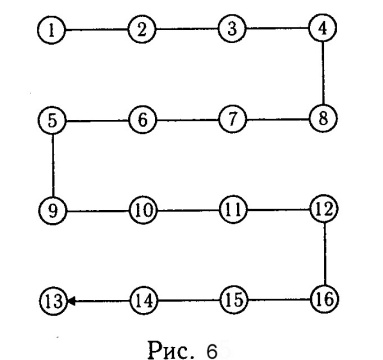 ешение:
ешение:
-
Самый кратчайший путь:
1;2;3;4;8;7;6;5;9;10;11;12;16;15;14;13 (рис.6)
-
Самый длинный путь:
5;9;13;10;7;4;3;2;1;6;11;16;12;8;15;14 (рис.7)
Задача №4.
Задача садовника.
С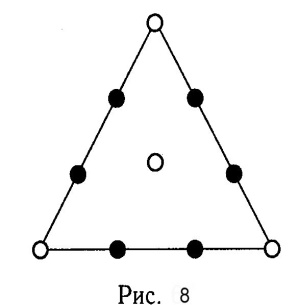 адовнику поручили высадить 10 деревьев на
площадке в форме равностороннего треугольника. Садовник имел два
сорта деревьев: 10 акаций и 10 лип. Чтобы придать некоторое
разнообразие саду, он решил несколько акаций и несколько лип,
причем так, чтобы на каждой стороне каждого из четырех
равносторонних треугольников, которые при этом образовались, росло
не больше двух деревьев того же сорта. Как он это
сделал?
адовнику поручили высадить 10 деревьев на
площадке в форме равностороннего треугольника. Садовник имел два
сорта деревьев: 10 акаций и 10 лип. Чтобы придать некоторое
разнообразие саду, он решил несколько акаций и несколько лип,
причем так, чтобы на каждой стороне каждого из четырех
равносторонних треугольников, которые при этом образовались, росло
не больше двух деревьев того же сорта. Как он это
сделал?
Решение:
С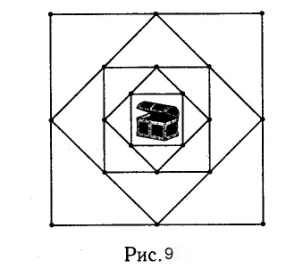 адовник посадил 4 акации и 6 лип
(рис.8).
адовник посадил 4 акации и 6 лип
(рис.8).
Задача №5.
Клад.
Н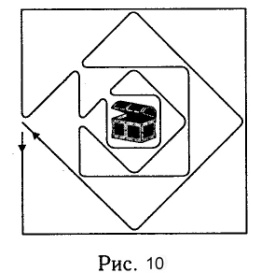 а рис.9 представлена схема лабиринта. Стороны
пяти квадратов, вписаны один в другой,- это коридоры, ведущие к
наименьшему внутреннему квадрату, где закрыт клад. Клад обладает
таким свойством, что получить его может только тот, кто придет за
ним и выйдет из лабиринта, пройдя все коридоры по одному разу. Ни
один коридор, даже частично, нельзя пройти дважды. Попытайте
счастья.
а рис.9 представлена схема лабиринта. Стороны
пяти квадратов, вписаны один в другой,- это коридоры, ведущие к
наименьшему внутреннему квадрату, где закрыт клад. Клад обладает
таким свойством, что получить его может только тот, кто придет за
ним и выйдет из лабиринта, пройдя все коридоры по одному разу. Ни
один коридор, даже частично, нельзя пройти дважды. Попытайте
счастья.
Решение:
Путь к кладу и обратно показан на рисунке 10.
Задача № 6.. (из тестов по математической грамотности)
Беседуют
трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову:
«Любопытно, что один из нас белокурый, другой брюнет, третий рыжий,
но ни у кого цвет волос не соответствует фамилии». Какой цвет волос
имеет каждый из друзей?
Приведем
подробное решение. Построим граф отношения, заданного в условии
задачи. Для этого, прежде всего, выделим множество
фамилий М и
множество цветов
волос К, элементы
которых будем обозначать точками. Точки
множества М назовем
буквами Б, Ч, Р (Белокуров, Чернов и Рыжов); точки второго
множества – б, бр, р (белокурый, брюнет, рыжий). Если точке из
одного множества соответствует точка из другого, мы их соединим
сплошной линией, а если не соответствует – штриховой. Условие
задачи указывает лишь на несоответствия, поэтому вначале должен
возникнуть граф, изображенный на рисунке Рисунок
1.
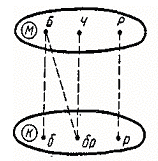
Рисунок
1
Из условия
задачи следует, что для каждой точки из
множества М существует одна и только одна тонка из
множеств К, которая
соответствует первой и, наоборот, каждой точке из
множества К соответствует одна и только одна точка из
множества М. Задача
сводится к тому, чтобы найти это единственно возможное соответствие
между элементами
множеств М и К, т. е. к
нахождению трех сплошных линий, соединяющих соответствующие точки
множеств.
Принцип решения
задачи прост. Если какая-то точка оказывается соединенной с двумя
точками другого множества штриховыми линиями, то с его третьей
точкой ее необходимо соединить сплошной линией. Поэтому граф на
рисунке Рисунок 1 дополняется сплошными линиями, соединяющими точки
Б и р, Р и бр (рис. Рисунок
2).
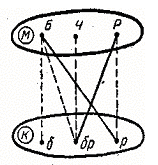
Рисунок
2
Далее остается
соединить сплошной линией точку Ч и точку б, так как точка Ч
соединена с точкой бр штриховой линией, а точка р уже «занята»
(рис. 7).

Рисунок 7
Таким образом,
на графе этого рисунка автоматически прочитываем ответ: Белокуров —
рыжий, Чернов — белокурый, Рыжов –
брюнет.
Задача № 7. (из тестов по математической грамотности)
В футбольном турнире участвуют 5 команд. Данные представлены в турнирной таблице:

Примечание: * - в ячейках указаны счета матчей, например: команда «Челси» выиграла у команды «Барселона» со счетом 2:1. У какой команды самая малая (худшая) разница забитых и пропущенных голов?
А) «Челси» В) «Аякс» С) «Милан» D) «Бавария» Е) «Барселона»
Решение: Необходимо путем подсчета высчитать количество побед и поражений у каждой команды:
«Челси» - побед 5, поражений – 5
«Барселона» - побед 7, поражений – 6
«Аякс» - побед 6, поражений – 8
«Бавария» - побед 9, поражений – 7
«Милан» - побед 4, поражений – 5
Теперь вычисляем разницу между победами и поражениями, получается , что самая маленькая разница у команды «Челси» равна 0.
Ответ: А
Задача № 8. (из тестов по математической грамотности)
Цифры внутри рисунка получены по определенному закону арифметических действий. Какая цифра должна быть вместо вопросительного знака?

А) 39 В) 153 С) 48 D) 93 Е) 33
Решение :
Необходимо путем подбора, проб и исключений подобрать нужную закономерность, по которой составлены прямоугольники. Получаем, у первого рисунка 11*13-4*2=135, проверяем справедливость для второго рисунка 9*11-5*3=84. Справедливость закона подтверждается, т.о. применяем подобранный метод для третьего рисунка 7*9-6*4=39.
Ответ: А
Задача № 9. (из тестов по математической грамотности)
На каждой грани бумажного кубика написана цифра 1; 2 или 3, причем цифры на противоположных гранях – одинаковые. Какая из фигурок может получиться, если этот кубик разрезать по некоторым ребрам и развернуть?
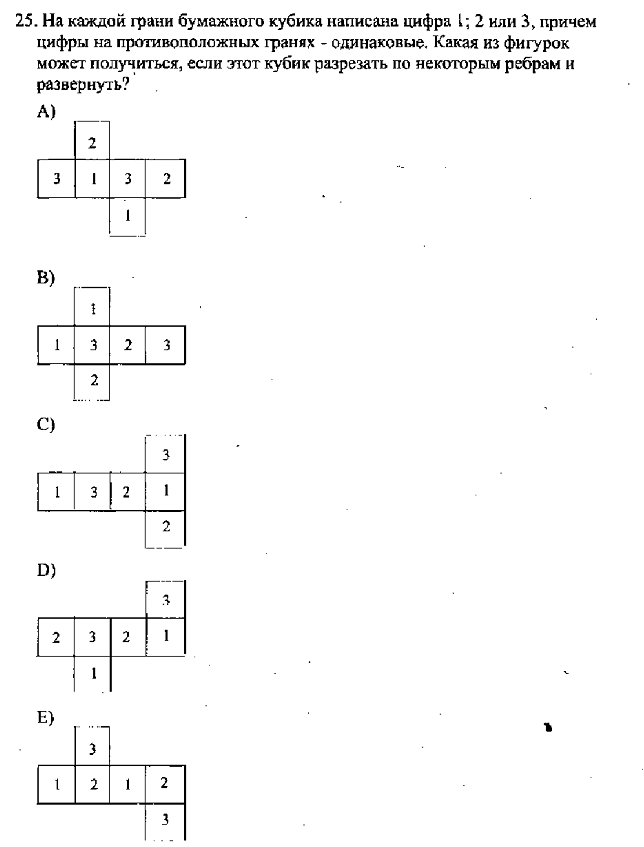
Решение:
Путем перебора возможных вариантов, проверяем расположение цифр на каждом кубике в собранном виде. Получаем, что в первом, втором, третьем и четвертом вариантах некоторые цифры располагаются рядом друг с другом, что противоречит условию задачи. Поэтому правильным является последний вариант.
Ответ: Е
Задача № 10. (из тестов по математической грамотности)
Каждой букве соответствует одна из цифр от 0 до 9. Какая цифра соответствует букве С, если

А) 7 В) 5 С) 2 D) 3 Е) 4
Методом подбора определяем, что букве С соответствует число 3, таким образом букве А соответствует число 7.
Ответ: Д
Задача№11. (из тестов по математической грамотности)
Какое число можно подставить вместо вопросительного знака?
Решение: Определим закономерность: 66=42+30
- 
91 = 56+42-
? = 20+12 - 
? = 20+12 – 4 => ? = 28
Ответ: 28
Задача № 12. (из тестов по математической грамотности)
Задача № 13. (из тестов по математической грамотности)
В семье трое детей – два мальчика и одна девочка. Их имена начинаются с букв А. В и Г. Среди имен, начинающихся с букв А и В, есть имя одного мальчика. Среди имен, начинающихся с букв В и Г, также есть имя одного мальчика. С какой буквы начинается имя девочки?
А) с буквы А
В)с любой буквы
С) с букв В или Г
D) с буквы В
E)с буквы Г
Ответ: D) с буквы В
Задача № 14. (из тестов по математической грамотности)
Один из пяти братьев – Андрей, Витя, Дима, Толя или Юра разбил окно. Андрей сказал: “Это сделал или Витя, или Толя”. Витя сказал: “Это сделал не я и не Юра”. Дима сказал: “Нет, один из них сказал правду, а другой – неправду”. Юра сказал: “Нет, Дима, ты не прав”. Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду. Кто же из братьев разбил окно?
А) Толя
В) Витя
С) Дима
D) Андрей
E) Юра
Ответ: А) Толя
Задача № 15. (из тестов по математической грамотности)
По какому правилу сформирована нижеуказанная
числовая последовательность. Написать следующую строку
1
11
21
1211
111221
312211
13112221
А) 112231121
В) 1113213112
С) 1123123111
D) 1113213211
E) 2221321122
Ответ: D) 1113213211
6.Заключение.
Лабиринты – это странные явления природы или затейливые постройки человека, заставляют задумываться над поиском выхода из них.
Теория графов и ее применение к решению задач о лабиринтах довольно увлекательный материал, позволяющий на практике найти поиск выхода из тупика. В нашей работе рассмотрен исторический материал и математический. Эта та ситуация, которая позволяет продемонстрировать тесную связь математики не только с точными, но и гуманитарными дисциплинами. Конечно, очень жаль, что пока мы пытались найти поиск выхода из тупика только на бумаге с помощью карандаша, но хочется верить, что когда–нибудь у нас появится настоящая возможность проверить теорию выхода из тупика лабиринта на практике.
7.Вывод
В каждом задании, представленном в форме лабиринта, тесно переплетаются ЛОГИКА, ТВОРЧЕСТВО и ИНТЕЛЛЕКТ. Многие считают решение занимательных задач, таких, как лабиринты, средством для приятного времяпрепровождения, отдыха, но если вдуматься, то становится ясной их гораздо более важная роль. Несомненно, что именно решение занимательных задач является одним из самых мощных инструментов развития человеческого интеллекта. Не зря люди передавали эти задачи устно и письменно из поколения в поколение. В результате проведенной исследовательской работы мы узнали универсальный способ прохождения любого лабиринта, и теперь мы точно знаем, что найдем выход из любой пещеры, из любого дернового или ледового лабиринта, которые часто строят для забавы. В ходе выполнения работы мы узнали много нового. А некоторые новые понятия нас очень заинтересовали. Мы считаем, что путь жизни каждого лежит через свой лабиринт и каждый найдёт в нём свой выход.
Использованная литература.
-
Наглядная геометрия. И. Ф.Шарыгин, Л. Н. Ерганжиева изд. Культурно – производительный центр «Марта» (Москва 1992 год)
-
В царстве смекалки. Е. И. Игнатьев, изд. «Наука» (Москва 1979 год)
-
Увлекательная математика. И. Леман, изд. «Знание», (Москва, 1985 год)
-
Математика, занятия школьного кружка. О. Шейнина, изд. «НЦ ЭНАС», (Москва, 2003 год)
-
http://www.komok.ru/
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Внеклассная работа по математике "Лабиринты. Пути решения."
Внеклассная работа по математике "Лабиринты. Пути решения."
Головоломный лабиринты
Рис. 5
Внеклассная работа по математике
Тема: Лабиринты. Пути решения.
Ф.И., класс:
Булыга Ангелина, 10 «Б» класс
Джаксылыкова Милана, 10 «Б» класс
Учитель математики: Коровина Светлана Анатольевна
Содержание:
-
Введение………………………………………………..2
-
Что такое лабиринт? …………………………………..2
-
Виды лабиринтов………………………………………3
4. Способы выхода из лабиринтов………………………...7
4.1 Теорема Тремо………………………………………7
4.2 Правило правой и левой руки……………………..9
5. Задачи про лабиринты…………………………………...11
6. Заключение……………………………………………….18
7. Вывод……………………………………………………..18
8. Список используемой литературы……………………...19
Цель:
Изучить историю возникновения лабиринтов и методы решения задач о лабиринтах.
Задачи:
-
Провести отбор материала, связанного с лабиринтами.
-
Выявление различных методов нахождения выходов из лабиринтов и применение их к решению задач.
-
Нахождение связи лабиринтов с нашей жизнью.
-
Создать брошюру с задачами о лабиринтах.
Гипотеза.
-
Безвыходных лабиринтов нет.
-
Метод правой (левой) руки является наиболее простым и верным, но применим только к односвязным лабиринтам и в том случае, когда не требуется отыскать кратчайший путь.
-
Метод зачеркивания тупиковых ходов является универсальным для решения любого типа лабиринтов.
-
Зная правило построения лабиринта, можно составлять алгоритм его прохождения.
1.Введение.
Идя по жизни, мы понятия не имеем, где окажемся завтра. Мы стремимся к цели, но не знаем, как ее достичь. Плутаем, рискуя оказаться в тупике. Ломаем голову: какую дорогу выбрать? Символ нашей жизни - лабиринт. История лабиринтов длинна, сложна и запутанна. Как и жизнь человека.
Сократ.
Наверняка, многие из нас встречали в каких - либо журналах или газетах такое занимательное развлечение, как лабиринты. Но не все знают - что такое «лабиринты» и откуда они появились. Хотя с лабиринтами встречаемся довольно часто: в рисунках ребенка, чертежах конструкторов, схемах работы городского транспорта можно заметить тот или иной вариант лабиринта. Так что же это такое «лабиринт»?
2.Что такое лабиринт?
Слово «Лабиринт» произошло от греческого и означает ходы в подземельях.
Другой источник утверждает: «Лабиринт - храм Зевса Лабрандского на Крите, т.е. Labrynthios, поскольку основным символом и атрибутом этого Зевса является топор (по греч. - labrys). Среди рисунков во многих помещениях дворца часто встречаются изображения двустороннего топорика. Это символический знак, связанный с религиозным культом критских жителей. Такие же топорики были найдены среди сталактитов и сталагмитов в одной из пещер, где, по преданию, родился Зевс. Двойная секира с острием по-гречески называется "лабрис". Ученые предполагают, что именно отсюда происходит слово "лабиринт", которым первоначально называли "дом двойного топора" - дворец царя Миноса.»
Действительно, существует очень много природных подземных пещер с таким огромным количеством перекрещивающихся коридоров, закоулков и тупиков, что нетрудно в них заблудиться и потеряться.
Примеры такого же рода, но уже искусственных лабиринтов, могут представить шахты иных рудников, или так называемые «катакомбы».
В конце концов, словом «лабиринт» чаще всего обозначали именно искусственное сооружение, составленное из большого числа аллей или галерей, бесчисленные разветвления, перекрестки и тупики, которые заставляли попавшего туда бесконечно блуждать в тщетных поисках выхода. Об устройстве таких лабиринтов слагались целые легенды.
Известнее всего легенда о лабиринте, построенном мастером Дедалом на острове Крит для мифического же царя Миноса. В этом лабиринте обитало грозное чудовище с головой быка и туловищем человека: Минотавр.
3.Виды лабиринтов.
Существуют несколько видов лабиринтов вот самые популярные из них.
Церковные лабиринты
Европы.
Ранние христианские церкви с энтузиазмом переняли традицию
лабиринта. В первую очередь это был символ самой церкви, например
выбитый на каменных стенах собора в Лукке (Италия) или вышитый на
облачении усопших епископов, которые были изображены лежащими в
лоне церкви.

Головоломный лабиринт.
Головоломные лабиринты используются для развития логического мышления.

Лабиринты в других областях человеческой
деятельности.
Заметим, что далеко не все лабиринтные структуры поддаются
непосредственному наблюдению. Есть любопытная теория, что
структурой именно такого рода является, например, модель развития
индоевропейских языков, а также любой языковый (лингвистический)
лабиринт.

Дерновые лабиринты.
В XIII-XIX веках лабиринтами называли особого рода садовые украшения, состоящие из более или менее высоких живых изгородей или из трельяжей, обсаженные растениями. Они были расположены так, что между ними образуются дорожки, ведущие к одному центру, но изгибающиеся в разные стороны и сообщающиеся между собой столь замысловато, что гуляющему не легко добраться до этого центра, также как и найти обратный путь.
![]()
«Живой» лабиринт
Ленинградские катакомбы.
Оказалось, что катакомбы, известные нам по многим детским фильмам, - есть разновидность лабиринтов.
Катакомбы Ленинградской области можно разделить на 4 типа:
1. Бывшие разработки кварцевого песка (Саблино, Старая Ладога, Борщево).
2. Бывшие разработки известняки и камня. (Телези, Аропаккузи, Кипень, Береговая).
3. Подземные ходы специального назначения. (Румболовская гора и гора Парнас).
4. Карстовые и псевдокарстовые полости. (Жихарево и частично Рождествено).
Катакомба Береговая.
Катакомба Береговая (Янтарная, Помойка) расположена на левом берегу реки Тосна, немного выше по течению возле автомобильного моста. Имеет три входа, которые легко найти при движении по дороге с автобусной остановки в сторону моста. Главный вход (Воронка) выходит прямо в обрыв берега реки. Спуск к нему начинается от земляного бугра (в народе - «Пьяной горки»), расположенной почти у самого моста. Подойдя около нее к обрыву, можно увидеть поросшую мелколесьем воронку в склоне. Правее нее есть металлическая лестница, по которой подходят ко входу. Спуститься можно еще по тропе левее воронки. На входе в пещеру стоит металлическая дверь. Ниже воронки из пещеры вытекает ручей. Второй вход в пещеру (Решетка) расположен несколько выше по течению (правее, если смотреть от дороги), примерно в 100м. Ориентиром служит бетонный столб ЛЭП в центральной части площадки для разворота автомобилей. Несколько левее его вниз по склону спускается желоб, по которому нужно спуститься на небольшую террасу. Здесь расположен металлический люк, через который по металлической лестнице можно спуститься в пещеру. Третий вход (Трупы) расположен на левой стороне автодороги. Около начала спуска к мосту следует свернуть на поле влево и выйти на поле, где искать овраг. В овраге течет ручей, по которому и следует войти через провал в пещеру. Из входов третий наименее комфортен.
Катакомба Береговая на настоящий момент, в связи с падением уровня озера и исследованием заозерной части, является самой протяженной в Саблино. Общая длина ее ходов превышает 7000м (привходовой части - 3500м). Высота потолков в привходовой части 160-180см, с залами выше 500см, в заозерной части колеблется в пределах от 50 до 350см.

Лабиринт как геометрическая сеть.
Аллеи, дорожки, коридоры, галереи, шахты и т. п.. Лабиринты тянутся, изгибаясь во все стороны, перекрещиваются, расходятся по всевозможным направлениям, ответвляются, образуют тупики и т. п.. Но мы для большей ясности рассмотрения вопроса, все перекрестки обозначим просто точками, а все эти аллеи, коридоры и т. д. будем принимать просто за линии, прямые или кривые, плоские или нет – все равно, но эти линии соединяют наши точки.

Схема метрополитена г.Алматы.

Схема движения городского транспорта г. Талдыкорган.
4.Способы выхода из лабиринта.
4.1Теорема Тремо.
Универсальный алгоритм прохождения любых лабиринтов был описан только через столетие в книге французского математика Э. Люка "Recreations matematiques", изданной в 1882 году. Интересно, что Люка при описании алгоритма указал на первенство другого французского математика М. Тремо. Таким образом, алгоритм стал известен как алгоритм Люка-Тремо.
Тремо предлагает следующие правила: выйдя из любой точки лабиринта, надо сделать отметку на его стене (крест) и двигаться в произвольном направлении до тупика или перекрестка; в первом случае вернуться назад, поставить второй крест, свидетельствующий, что путь пройден дважды - туда и назад, и идти в направлении, не пройденном ни разу, или пройденном один раз; во втором - идти по произвольному направлению, отмечая каждый перекресток на входе и на выходе одним крестом; если на перекресте один крест уже имеется, то следует идти новым путем, если нет - то пройденным путем, отметив его вторым крестом.
Зная алгоритм Тремо, можно скорректировать поведение легендарного Тесея. Вдохновленный подарком любимой Ариадны, он уверенно идет по лабиринту. Вдруг перед ним возникает ход, по которому уже протянута нить... Что делать? Ни в коем случае не пересекать ее, а вернуться по уже известному пути, сдваивая нить, пока не найдется еще один непройденный ход.
Применив вариант алгоритма Тремо, отец теории информации Клод Шеннон (Claude Elwood Shannon) построил одного из первых самообучающихся роботов. Шеннон дал ему звучное имя "Тесей", но в истории "Тесей" стал больше известен как "мышь" Шеннона. "Мышь" сначала обследовала весь лабиринт, а затем (во второй раз) проходила весь путь значительно быстрее, избегая участков, пройденных дважды.
Тремо предлагает примерно такой вариант решения задач о лабиринтах. Всякий раз, идя по любому коридору в первый раз, ставим при входе в коридор и при выходе из коридора на стене по черточке, если идем по коридору вторично, то перечеркиваем черточки. Если мы имеем дело с действительным лабиринтом, или галереями подземных шахт, с разветвлениями пещер и т. д., то блуждающему в этих шахтах вместо черточек на бумаге придется делать уже иной знак, чтобы ориентироваться, и класть, например, камень при входе и выходе из каждого перекрестка – в галерее, которую он покидает, и в той, в которую он входит.
1. Если подошли к перекрестку, на котором ни разу небыли, то дальше идем по любому коридору (рис. 1), если же попали в тупик – идем обратно (рис. 2).
2. Если подошли к перекрестку, где уже побывали, и подошли к нему по такой дороге, по которой мы идем в первый раз, то немедленно отправляемся обратно (рис. 3).
3. Если подошли к перекрестку таким путем, по которому уже дважды шли, то далее, если есть коридоры, по которым ещё ни разу не ходили, идем по любому из них (рис. 4).
Если же таких коридоров нет, то идем по любому пройденному один раз (рис. 5).
![]()
перекресток


перекресток
Рис. 1
Рис. 2
тупик


Рис. 4
перекресток
Рис. 3
перекресток

4.2 Правила правой и левой руки.
Одним из самых простых правил для прохождения лабиринта является правило "одной руки": двигаясь по лабиринту, надо все время касаться правой или левой рукой его стены. Этот алгоритм, вероятно, был известен еще древним грекам. Придется пройти долгий путь, заходя во все тупики, но в итоге цель будет достигнута. Хотя у этого правила и есть один недостаток, но о нем мы поговорим позже.
Попробуем описать робота, действующего в соответствии с правилом "правой руки".
В начале своей работы робот должен найти стену, по которой он будет следовать. Для этого он может просто двигаться вперед, пока не упрется в преграду.
После того как робот наткнулся на препятствие, он начинает передвигаться в соответствии с правилом "правой руки".
Двигаясь вдоль стены, робот следит, есть ли проход справа. Если проход есть, робот должен идти по нему, чтобы не оторваться от стены справа.
Если прохода нет - впереди стена - робот поворачивает налево. Если прохода снова нет, он еще раз поворачивает налево, таким образом разворачиваясь на 180 градусов, и идет в обратном направлении.
Блок-схема алгоритма для робота, работающего по правилу "правой руки", представлена на рисунке.

Е сли известно, что у лабиринта нет отдельно
стоящих стенок, то есть нет замкнутых маршрутов, по которым можно
возвращаться в исходную точку, то такой лабиринт называют
односвязным и его всегда можно обойти полностью, применив правило
"одной руки".
сли известно, что у лабиринта нет отдельно
стоящих стенок, то есть нет замкнутых маршрутов, по которым можно
возвращаться в исходную точку, то такой лабиринт называют
односвязным и его всегда можно обойти полностью, применив правило
"одной руки".
Если же лабиринт содержит отдельно стоящие стенки, то, применяя правило "одной руки", не всегда можно пройти все коридоры и тупики. Лабиринты с отдельно стоящими стенками и с замкнутыми маршрутами называются многосвязными. При этом многосвязные лабиринты можно разделить на две группы: без "петли" вокруг цели (замкнутый маршрут не проходит вокруг цели) и с замкнутой "петлей" вокруг цели (цель можно обойти по замкнутому маршруту).
В многосвязных лабиринтах второй группы правило "одной руки" не работает и, применяя его, достичь цели невозможно. Но и эти лабиринты можно пройти, полагаясь на точный алгоритм.
Решение задачи о таких лабиринтах принадлежит
сравнительно позднему времени, и начало ему положено Леонардом
Эйлером. Эйлер не без оснований полагал, что выход из любого
лабиринта может быть найден, и притом сравнительно простым
пут![]()
![]()
![]()
Рис. 3
перекресток
Рис. 1
ем.
5.Примеры задач на лабиринты.
Рассмотрим два простейших правила решения задач с лабиринтами, все стены которого имеют вид одной, нигде не пересекающей себя замкнутой линии (вход закрыт воротами). Отметим две точки на плане лабиринта.
-
Если обе точки находятся либо внутри, либо снаружи лабиринта, то любая соединяющая их линия пересечет границу лабиринта четное число раз.
-
Е
 сли одна точка находится снаружи лабиринта, а другие
внутри, то любая соединяющая их линия пересечет границу лабиринта
такого вида нечетное число раз.
сли одна точка находится снаружи лабиринта, а другие
внутри, то любая соединяющая их линия пересечет границу лабиринта
такого вида нечетное число раз.
Н апример, отметим точку
А внутри лабиринта и точку
B
снаружи лабиринта. Соединим эти точки линией. Она
пересекает границу лабиринта пять раз, то есть нечетное количество
раз.
апример, отметим точку
А внутри лабиринта и точку
B
снаружи лабиринта. Соединим эти точки линией. Она
пересекает границу лабиринта пять раз, то есть нечетное количество
раз.
Задача №1.
На цирковой арене.
Н а цирковой арене выступал канатоходец. На высоте
трех метров от земли на пяти столбах был натянуты канаты, по
которым он должен был проходить. Канаты были натянуты так, как это
показано на рисунке 1.
а цирковой арене выступал канатоходец. На высоте
трех метров от земли на пяти столбах был натянуты канаты, по
которым он должен был проходить. Канаты были натянуты так, как это
показано на рисунке 1.
Канатоходец должен был пройти по восьми канатам таким образом, чтобы по каждому из них пройти всего один раз. И это ему всегда удавалось, хотя он и не возвращался в то же место, откуда выходил. Но во время одного из выступлений оборвался канат №8, и осталось всего семь канатов (рис.2).
Может ли теперь канатоходец пройти все канаты, проходя по каждому из них всего раз? Покажите, как ходил канатоходец, когда все канаты были целы, и ответьте на поставленный вопрос.
Решение:
Когда все канаты были целы, канатоходец, выходя из точки А, заканчивал свой путь в точке В (рис.3). После того, как оборвался канат №8, канатоходец не сможет обойти все канаты по одному разу.
Задача №2.
Тропинки в садах.
В саду Александра Ивановича тропинки проложены, как это показано на рис. 4, а у Бориса Борисовича - как показано на рис. 5. Кто из них может обойти все тропинки, проходя по каждой всего один раз?


Ответ: Александр Иванович.
Задача №3.
Среди георгин.
С адовник имел квадратную клумбу 4*4 метра, на
которой он вырастил 16 кустов георгин. Расстояние между кустами
было 1 метр. Пока кусты еще не расцвели, цветовод обходил все
кусты, идя по кратчайшему пути, но когда чудесные цветы
распустились, садовник обходил их по самому длинному пути. К
каждому цветку он подходил всего один раз. Как выглядел самый
короткий путь от куста к кусту, а как самый
длинный?
адовник имел квадратную клумбу 4*4 метра, на
которой он вырастил 16 кустов георгин. Расстояние между кустами
было 1 метр. Пока кусты еще не расцвели, цветовод обходил все
кусты, идя по кратчайшему пути, но когда чудесные цветы
распустились, садовник обходил их по самому длинному пути. К
каждому цветку он подходил всего один раз. Как выглядел самый
короткий путь от куста к кусту, а как самый
длинный?
Р ешение:
ешение:
-
Самый кратчайший путь:
1;2;3;4;8;7;6;5;9;10;11;12;16;15;14;13 (рис.6)
-
Самый длинный путь:
5;9;13;10;7;4;3;2;1;6;11;16;12;8;15;14 (рис.7)
Задача №4.
Задача садовника.
С адовнику поручили высадить 10 деревьев на
площадке в форме равностороннего треугольника. Садовник имел два
сорта деревьев: 10 акаций и 10 лип. Чтобы придать некоторое
разнообразие саду, он решил несколько акаций и несколько лип,
причем так, чтобы на каждой стороне каждого из четырех
равносторонних треугольников, которые при этом образовались, росло
не больше двух деревьев того же сорта. Как он это
сделал?
адовнику поручили высадить 10 деревьев на
площадке в форме равностороннего треугольника. Садовник имел два
сорта деревьев: 10 акаций и 10 лип. Чтобы придать некоторое
разнообразие саду, он решил несколько акаций и несколько лип,
причем так, чтобы на каждой стороне каждого из четырех
равносторонних треугольников, которые при этом образовались, росло
не больше двух деревьев того же сорта. Как он это
сделал?
Решение:
С адовник посадил 4 акации и 6 лип
(рис.8).
адовник посадил 4 акации и 6 лип
(рис.8).
Задача №5.
Клад.
Н а рис.9 представлена схема лабиринта. Стороны
пяти квадратов, вписаны один в другой,- это коридоры, ведущие к
наименьшему внутреннему квадрату, где закрыт клад. Клад обладает
таким свойством, что получить его может только тот, кто придет за
ним и выйдет из лабиринта, пройдя все коридоры по одному разу. Ни
один коридор, даже частично, нельзя пройти дважды. Попытайте
счастья.
а рис.9 представлена схема лабиринта. Стороны
пяти квадратов, вписаны один в другой,- это коридоры, ведущие к
наименьшему внутреннему квадрату, где закрыт клад. Клад обладает
таким свойством, что получить его может только тот, кто придет за
ним и выйдет из лабиринта, пройдя все коридоры по одному разу. Ни
один коридор, даже частично, нельзя пройти дважды. Попытайте
счастья.
Решение:
Путь к кладу и обратно показан на рисунке 10.
Задача № 6.. (из тестов по математической грамотности)
Беседуют
трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову:
«Любопытно, что один из нас белокурый, другой брюнет, третий рыжий,
но ни у кого цвет волос не соответствует фамилии». Какой цвет волос
имеет каждый из друзей?
Приведем
подробное решение. Построим граф отношения, заданного в условии
задачи. Для этого, прежде всего, выделим множество
фамилий М и
множество цветов
волос К, элементы
которых будем обозначать точками. Точки
множества М назовем
буквами Б, Ч, Р (Белокуров, Чернов и Рыжов); точки второго
множества – б, бр, р (белокурый, брюнет, рыжий). Если точке из
одного множества соответствует точка из другого, мы их соединим
сплошной линией, а если не соответствует – штриховой. Условие
задачи указывает лишь на несоответствия, поэтому вначале должен
возникнуть граф, изображенный на рисунке Рисунок
1.

Рисунок
1
Из условия
задачи следует, что для каждой точки из
множества М существует одна и только одна тонка из
множеств К, которая
соответствует первой и, наоборот, каждой точке из
множества К соответствует одна и только одна точка из
множества М. Задача
сводится к тому, чтобы найти это единственно возможное соответствие
между элементами
множеств М и К, т. е. к
нахождению трех сплошных линий, соединяющих соответствующие точки
множеств.
Принцип решения
задачи прост. Если какая-то точка оказывается соединенной с двумя
точками другого множества штриховыми линиями, то с его третьей
точкой ее необходимо соединить сплошной линией. Поэтому граф на
рисунке Рисунок 1 дополняется сплошными линиями, соединяющими точки
Б и р, Р и бр (рис. Рисунок
2).

Рисунок
2
Далее остается
соединить сплошной линией точку Ч и точку б, так как точка Ч
соединена с точкой бр штриховой линией, а точка р уже «занята»
(рис. 7).

Рисунок 7
Таким образом,
на графе этого рисунка автоматически прочитываем ответ: Белокуров —
рыжий, Чернов — белокурый, Рыжов –
брюнет.
Задача № 7. (из тестов по математической грамотности)
В футбольном турнире участвуют 5 команд. Данные представлены в турнирной таблице:

Примечание: * - в ячейках указаны счета матчей, например: команда «Челси» выиграла у команды «Барселона» со счетом 2:1. У какой команды самая малая (худшая) разница забитых и пропущенных голов?
А) «Челси» В) «Аякс» С) «Милан» D) «Бавария» Е) «Барселона»
Решение: Необходимо путем подсчета высчитать количество побед и поражений у каждой команды:
«Челси» - побед 5, поражений – 5
«Барселона» - побед 7, поражений – 6
«Аякс» - побед 6, поражений – 8
«Бавария» - побед 9, поражений – 7
«Милан» - побед 4, поражений – 5
Теперь вычисляем разницу между победами и поражениями, получается , что самая маленькая разница у команды «Челси» равна 0.
Ответ: А
Задача № 8. (из тестов по математической грамотности)
Цифры внутри рисунка получены по определенному закону арифметических действий. Какая цифра должна быть вместо вопросительного знака?

А) 39 В) 153 С) 48 D) 93 Е) 33
Решение :
Необходимо путем подбора, проб и исключений подобрать нужную закономерность, по которой составлены прямоугольники. Получаем, у первого рисунка 11*13-4*2=135, проверяем справедливость для второго рисунка 9*11-5*3=84. Справедливость закона подтверждается, т.о. применяем подобранный метод для третьего рисунка 7*9-6*4=39.
Ответ: А
Задача № 9. (из тестов по математической грамотности)
На каждой грани бумажного кубика написана цифра 1; 2 или 3, причем цифры на противоположных гранях – одинаковые. Какая из фигурок может получиться, если этот кубик разрезать по некоторым ребрам и развернуть?

Решение:
Путем перебора возможных вариантов, проверяем расположение цифр на каждом кубике в собранном виде. Получаем, что в первом, втором, третьем и четвертом вариантах некоторые цифры располагаются рядом друг с другом, что противоречит условию задачи. Поэтому правильным является последний вариант.
Ответ: Е
Задача № 10. (из тестов по математической грамотности)
Каждой букве соответствует одна из цифр от 0 до 9. Какая цифра соответствует букве С, если

А) 7 В) 5 С) 2 D) 3 Е) 4
Методом подбора определяем, что букве С соответствует число 3, таким образом букве А соответствует число 7.
Ответ: Д
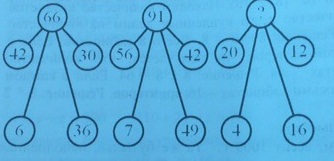
Задача№11. (из тестов по математической грамотности)
Какое число можно подставить вместо вопросительного знака?

Решение: Определим закономерность: 66=42+30
- 
91 = 56+42-
? = 20+12 - 
? = 20+12 – 4 => ? = 28
Ответ: 28
Задача № 12. (из тестов по математической грамотности)
Задача № 13. (из тестов по математической грамотности)
В семье трое детей – два мальчика и одна девочка. Их имена начинаются с букв А. В и Г. Среди имен, начинающихся с букв А и В, есть имя одного мальчика. Среди имен, начинающихся с букв В и Г, также есть имя одного мальчика. С какой буквы начинается имя девочки?
А) с буквы А
В)с любой буквы
С) с букв В или Г
D) с буквы В
E)с буквы Г
Ответ: D) с буквы В
Задача № 14. (из тестов по математической грамотности)
Один из пяти братьев – Андрей, Витя, Дима, Толя или Юра разбил окно. Андрей сказал: “Это сделал или Витя, или Толя”. Витя сказал: “Это сделал не я и не Юра”. Дима сказал: “Нет, один из них сказал правду, а другой – неправду”. Юра сказал: “Нет, Дима, ты не прав”. Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду. Кто же из братьев разбил окно?
А) Толя
В) Витя
С) Дима
D) Андрей
E) Юра
Ответ: А) Толя
Задача № 15. (из тестов по математической грамотности)
По какому правилу сформирована нижеуказанная
числовая последовательность. Написать следующую строку
1
11
21
1211
111221
312211
13112221
А) 112231121
В) 1113213112
С) 1123123111
D) 1113213211
E) 2221321122
Ответ: D) 1113213211
6.Заключение.
Лабиринты – это странные явления природы или затейливые постройки человека, заставляют задумываться над поиском выхода из них.
Теория графов и ее применение к решению задач о лабиринтах довольно увлекательный материал, позволяющий на практике найти поиск выхода из тупика. В нашей работе рассмотрен исторический материал и математический. Эта та ситуация, которая позволяет продемонстрировать тесную связь математики не только с точными, но и гуманитарными дисциплинами. Конечно, очень жаль, что пока мы пытались найти поиск выхода из тупика только на бумаге с помощью карандаша, но хочется верить, что когда–нибудь у нас появится настоящая возможность проверить теорию выхода из тупика лабиринта на практике.
7.Вывод
В каждом задании, представленном в форме лабиринта, тесно переплетаются ЛОГИКА, ТВОРЧЕСТВО и ИНТЕЛЛЕКТ. Многие считают решение занимательных задач, таких, как лабиринты, средством для приятного времяпрепровождения, отдыха, но если вдуматься, то становится ясной их гораздо более важная роль. Несомненно, что именно решение занимательных задач является одним из самых мощных инструментов развития человеческого интеллекта. Не зря люди передавали эти задачи устно и письменно из поколения в поколение. В результате проведенной исследовательской работы мы узнали универсальный способ прохождения любого лабиринта, и теперь мы точно знаем, что найдем выход из любой пещеры, из любого дернового или ледового лабиринта, которые часто строят для забавы. В ходе выполнения работы мы узнали много нового. А некоторые новые понятия нас очень заинтересовали. Мы считаем, что путь жизни каждого лежит через свой лабиринт и каждый найдёт в нём свой выход.
Использованная литература.
-
Наглядная геометрия. И. Ф.Шарыгин, Л. Н. Ерганжиева изд. Культурно – производительный центр «Марта» (Москва 1992 год)
-
В царстве смекалки. Е. И. Игнатьев, изд. «Наука» (Москва 1979 год)
-
Увлекательная математика. И. Леман, изд. «Знание», (Москва, 1985 год)
-
Математика, занятия школьного кружка. О. Шейнина, изд. «НЦ ЭНАС», (Москва, 2003 год)
-
http://www.komok.ru/

шағым қалдыра аласыз


















