
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ
КАЗАХСТАН
АО «Национальный центр повышения квалификации «Өрлеу»
«Институт повышения квалификации педагогических работников по СКО»
филиал
Курсы повышения квалификации учителей физики
«Развитие профессиональных компетенций учителя физики»
05.11-16.11.2018 г.
Самостоятельная работа
на тему «Явления переноса. Молекулярные потоки и динамическое равновесие»
Выполнил: учитель физики «КГУ Беловская средняя школа»
Кызылжарский район
Кузьмин В.В,
Проверила: Мунжасарова Г.Ж..
г. Петропавловск
2018
Оглавление
Средняя длина свободного пробега 4
Обобщённое уравнение переноса 7
Список используемой литературы: 13
Введение.
Газ, находящийся в равновесном состоянии, при постоянных внешних условиях характеризуется неизменностью во времени и во всех точках занимаемого объёма таких величин как давление, температура, относительное число молекул разного сорта и т.д. Но, несмотря на важную роль равновесных состояний, они всё же являются особым случаем и во многих задачах, представляющих огромный физический интерес, мы имеем дело с системами, не находящимися в равновесии.
Отклонение системы от равновесного состояния приводит к возникновению термодинамических потоков, связанных с переносом вещества, энергии, импульса и т.д. из одной части занимаемого объёма в другую. Подобные процессы получили название явлений переноса. При наличии в среде различной концентрации примеси возникают диффузионные потоки, т.е. перенос массы (явление диффузии); в случае разной температуры - тепловые потоки, т.е. перенос энергии (явление теплопроводности); при различной скорости течения потоков - перенос импульса (явление вязкости); при наложении электрического поля на систему свободных зарядов – потоки зарядов (ток), т.е. перенос зарядов (явление электропроводности).
При изучении систем, не находящихся в равновесии, мы сталкиваемся с достаточно сложной проблемой, связанной с необходимостью исследовать специфический характер взаимодействий, приводящий в конце концов систему в равновесное состояние. Однако, ситуация сильно упрощается в случае разреженных газов, о которых и пойдёт речь далее. Несмотря на приближённый характер последующих вычислений, они всё же дают возможность исходя из достаточно простых соображений, получить ясное представление о физической сути рассматриваемых явлений. Кроме того, с их помощью удаётся получить сравнительно хорошие численные оценки и правильно предсказать зависимость от всех существенных параметров.
С точки зрения молекулярно-кинетической теории основной причиной явлений переноса в газе является тепловое хаотическое движение молекул. Находясь в постоянном хаотическом движении, молекулы, соударяясь между собой, в конце концов, приводят газ в состояние равновесия. Происходит выравнивание температуры в различных частях газа, выравнивание концентраций веществ в смеси, выравнивание скоростей движущихся друг относительно друга слоёв газа и т.д. Рассмотрение процесса сильно упрощается, если считать газ настолько разреженным, что становится справедливым следующее приближение: время между соударениями молекул много меньше времени, затрачиваемого на соударение; вероятность одновременного столкновения трёх молекул пренебрежимо мала и имеют место только столкновения двух частиц; среднее расстояние между молекулами велико по сравнению со средней длиной волны де Бройля молекулы, что позволяет избежать квантовомеханических подходов.
Средняя длина свободного пробега
Начнём с рассмотрения столкновений между
молекулами разреженного газа. Среднее расстояние
 , проходимое молекулой между двумя
последовательными столкновениями называется
средней длиной свободного
пробега.
Рассмотрим молекулу В радиуса r,
сближающуюся с другой молекулой В'
радиуса r' с
относительной скоростью
, проходимое молекулой между двумя
последовательными столкновениями называется
средней длиной свободного
пробега.
Рассмотрим молекулу В радиуса r,
сближающуюся с другой молекулой В'
радиуса r' с
относительной скоростью  (рис.1). Пусть расстояние между центрами
обеих молекул при их максимальном сближении равно
b.
Тогда молекулы испытают столкновение если b>r+r’.
Представим, что молекула В несёт на себе диск
радиусом r + r',
центр которого совпадает с центром молекулы, а плоскость диска
перпендикулярна к вектору относительной скорости
(рис.1). Пусть расстояние между центрами
обеих молекул при их максимальном сближении равно
b.
Тогда молекулы испытают столкновение если b>r+r’.
Представим, что молекула В несёт на себе диск
радиусом r + r',
центр которого совпадает с центром молекулы, а плоскость диска
перпендикулярна к вектору относительной скорости
 . Тогда столкновение произойдёт только
в том случае, если центр молекулы В' окажется
. Тогда столкновение произойдёт только
в том случае, если центр молекулы В' окажется
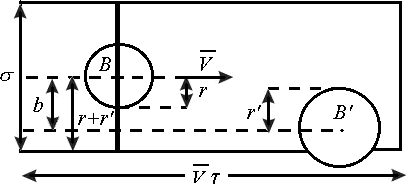
Рис.1.
внутри объёма, занятого воображаемым диском с поверхностью σ , называемой полным поперечным сечением
 (1)
(1)
или если молекулы одинаковые
 .
.
Воображаемый диск с поверхностью σ за время τ
вырезает в пространстве объём σ τ.
Если время τ будет равно среднему времени свободного пробега
молекулы, т.е. среднему времени между двумя последовательными
столкновениями молекул τ , то вырезанный объём будет содержать в
среднем одну молекулу, т.е. σ
τ.
Если время τ будет равно среднему времени свободного пробега
молекулы, т.е. среднему времени между двумя последовательными
столкновениями молекул τ , то вырезанный объём будет содержать в
среднем одну молекулу, т.е. σ τn=1,
где n -
число молекул в единице объёма газа. Тогда
τn=1,
где n -
число молекул в единице объёма газа. Тогда  =1/σ
=1/σ n и,
принимая во внимание, что
n и,
принимая во внимание, что  , где
, где  - средняя скорость движения молекул
и
- средняя скорость движения молекул
и  ≈
≈  (что можно получить в результате
усреднения), получим
(что можно получить в результате
усреднения), получим
 (2)
(2)
Диффузия
Рассмотрим вещество, состоящее из одинаковых молекул, но предположим, что часть их каким-то образом помечена. Пусть n1 число помеченных молекул в единице объёма. В состоянии равновесия меченые молекулы равномерно распределены по всему объёму и, соответственно, n1 не зависит от координат. Допустим, однако, что распределение не является однородным и n1 зависит от координат, пусть для простоты рассуждений n1 зависит только от одной координаты x, т.е. n1 = n1(x) . При этом предполагается, что полное число молекул в единице объёма остаётся постоянным, так что результирующее перемещение молекул вещества отсутствует. Такое состояние не является равновесным. Меченые молекулы вследствие теплового движения будут перемещаться в сосуде в сторону меньшей концентрации этих молекул, чтобы достичь равновесного состояния, когда они будут равномерно распределены по всему объёму. Этот процесс носит название самодиффузии. На место переместившихся меченых молекул приходят другие молекулы, так что давление газа остаётся неизменным, но происходит перенос массы газы.
Будем считать, что все молекулы движутся с
одинаковой скоростью, равной их средней скорости
 . Одна треть из всех находящихся в
единице объёма n молекул имеют составляющие скорости, направленные
вдоль оси x, у половины этих молекул скорости направлены вдоль + x
, а у другой половины вдоль – x (см. рис.2). Тогда количество
молекул, пролетающих за единицу времени через единичную площадку в
направлении снизу вверх равно
. Одна треть из всех находящихся в
единице объёма n молекул имеют составляющие скорости, направленные
вдоль оси x, у половины этих молекул скорости направлены вдоль + x
, а у другой половины вдоль – x (см. рис.2). Тогда количество
молекул, пролетающих за единицу времени через единичную площадку в
направлении снизу вверх равно
|
|
|
(3) |
и столько же молекул движутся сверху вниз.
Молекулы, пересекающие плоскость снизу, испытали последнее
столкновение в среднем на расстоянии  от плоскости. Так как
n1 = n1(x)
, то среднее число молекул,
пересекающих за единицу времени через
единичную площадку плоскости в направлении снизу
вверх N+(x) и
сверху вниз N−(x) ,
равны, соответственно
от плоскости. Так как
n1 = n1(x)
, то среднее число молекул,
пересекающих за единицу времени через
единичную площадку плоскости в направлении снизу
вверх N+(x) и
сверху вниз N−(x) ,
равны, соответственно
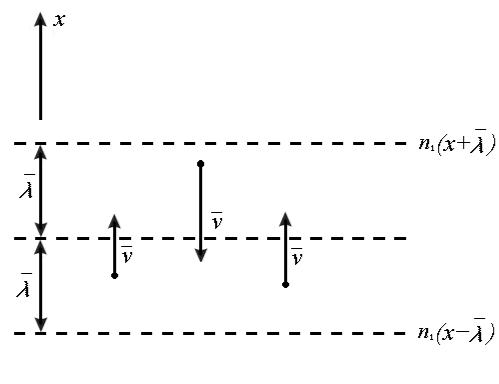
Рис.2.

Принимая во внимание, что  получим результирующую плотность потока
молекул N(x)
через единичную поверхность в направлении
+x
получим результирующую плотность потока
молекул N(x)
через единичную поверхность в направлении
+x
|
|
|
(4) |
где  – коэффициент
самодиффузии.
– коэффициент
самодиффузии.
Умножая на массу молекулы m обе части равенства (4), получим выражение для плотности потока массы, т.е. массы, переносимой через единичную площадку в единицу времени M
|
|
|
(5) |
которое называется законом Фика,
где  - плотность
меченых молекул.
- плотность
меченых молекул.
Знак минус в (4) и (5) отражает то обстоятельство, что поток массы (поток молекул) направлен в сторону убывания концентрации.
Принимая во внимание, что
|
|
|
(6) |
|
|
|
|
и соотношение (2), в предположении, что молекулы являются твёрдыми шариками, площадь поперечного сечения σ (1) которых не зависит от температуры, можно показать, что значение коэффициента самодиффузии D растет с повышением температуры D~T3/2.
Из соотношений (2) и (6) следует, что коэффициент
самодиффузии D уменьшается c
увеличением концентрации n и
давления p,
т.е. D~1/n~1/p. Это связано с
уменьшением длины свободного пробега  при увеличении концентрации молекул, что приводит
к более частым соударениям диффундирующих частиц с молекулами газа
т.е. переносится на меньшее
расстояние.
при увеличении концентрации молекул, что приводит
к более частым соударениям диффундирующих частиц с молекулами газа
т.е. переносится на меньшее
расстояние.
Обобщённое уравнение переноса
Поскольку все явления переноса имеют в основе общие физические закономерности, то после рассмотрения явления диффузии очень просто получить так называемое обобщённое уравнение переноса, удобное для анализа конкретных процессов переноса.
Пусть некоторая физическая величина a характеризует определённое молекулярное свойство, это может быть масса, энергия, импульс. При этом будем считать, что переносимую величину можно отнести к одной молекуле. (Если речь идет, например, о переносе энергии, то отнесенной к одной молекуле величиной будет полная энергия молекулы.) Будем считать, что величина a(x) изменяется в зависимости от координаты x.
Для количественного описания потока вводят величину A, называемую плотностью потока и численно равную количеству физической величины a(x), переносимой за единицу времени через единичную поверхность. Если рассматриваемая система находится в состоянии, близком к равновесию, то плотность потока A пропорциональна соответствующей физической величины a(x) в той же точке.
В уравнении, описывающем процесс диффузии (5), величина A представляет собой плотность потока массы M, а в качестве переносимой величины a выступает масса молекулы. Тогда, если величина a зависит только от одной пространственной переменной x (случай одномерной среды), выражение для плотности потока будет иметь следующий вид
|
|
|
(7) |
Знак минус в выражении (7) указывает на то, что поток направлен в сторону уменьшения величины a. Параметры a и A в уравнении (7), отвечающие основным явлениям переноса (диффузии, вязкости, теплопроводности и электропроводности) и соответствующие коэффициенты переноса представлены в таблице 1, причём A представляет собой макропараметр, в то время как a является молекулярной характеристикой.
Таблица 1.
|
Явление |
Диффузия |
Вячкость |
Теплопроводность |
Электропроводность |
|
a |
m |
mu |
3/2kT |
q |
|
A |
M |
F |
Q |
j |
|
Коэффициент переноса |
|
|
|
|
Теплопроводность
Если в некоторой среде создать вдоль оси x градиент температуры, то возникает поток тепла. Допустим, что распределение температур в газе не является однородным, т.е. температура зависит от координаты T=T(x) (рис.4).
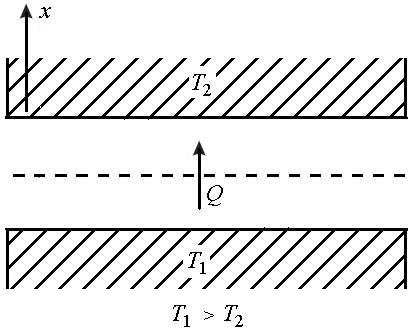
Рис.3.
Газ в этомслучае находится в неравновесном состоянии, и стремление к достижению равновесия проявится в возникновении потока тепла Q, направленного от участков газа, обладающих высокой температурой, к участкам с низкой температурой.
Рассмотрим в газе некоторую
плоскость x=Const,
где T=T(x). Количество тепла, перенесённое за единицу времени
через единицу поверхности плоскости в направлении
+x,
называется плотностью потока тепла Q.
Механизм переноса тепла заключается в том, что молекулы газа
пересекают плоскость сверху и снизу. Если в верхней области газа
температура больше, чем в нижней (∂T/∂x>0), то средняя кинетическая
энергия  молекул в верхней области больше, чем
энергия молекул в нижней. Энергия молекул, приходящих снизу меньше,
чем у молекул, пересекающих плоскость сверху. В результате
происходит перенос энергии из области над плоскостью в область под
ней. При столкновениях молекулы с большей энергией передают часть
энергии молекулам с меньшей энергией. Вследствие столкновений
молекул друг с другом в результате хаотического движения происходит
выравнивание энергии в разных областях пространства, а,
следовательно, и выравнивание температур. Перенос энергии и
обуславливает процесс теплопроводности в
газах.
молекул в верхней области больше, чем
энергия молекул в нижней. Энергия молекул, приходящих снизу меньше,
чем у молекул, пересекающих плоскость сверху. В результате
происходит перенос энергии из области над плоскостью в область под
ней. При столкновениях молекулы с большей энергией передают часть
энергии молекулам с меньшей энергией. Вследствие столкновений
молекул друг с другом в результате хаотического движения происходит
выравнивание энергии в разных областях пространства, а,
следовательно, и выравнивание температур. Перенос энергии и
обуславливает процесс теплопроводности в
газах.
Тогда при замене в (7) A на поток тепла Q, а в качестве a рассматривая энергию теплового движения молекулы 3/2kT, получим следующее соотношение
|
|
|
(8) |
где æ- коэффициент теплопроводности и
|
|
|
(9) |
 - удельная теплоёмкость при постоянном
объёме, ρ - плотность газа. Знак минус показывает, что тепло течет
в направлении убывания температуры. Выражение (8) представляет
собой закон теплопроводности Фурье.
- удельная теплоёмкость при постоянном
объёме, ρ - плотность газа. Знак минус показывает, что тепло течет
в направлении убывания температуры. Выражение (8) представляет
собой закон теплопроводности Фурье.
Проанализируем зависимость коэффициента
теплопроводности æ от
температуры. В предположении, что молекулы представляют собой
твёрдые шары, æ зависит от температуры так же, как
 (6), т.е. æ~
(6), т.е. æ~ . Однако, в общем случае оказывается,
что σ,
а, следовательно, и
. Однако, в общем случае оказывается,
что σ,
а, следовательно, и  зависят от относительной скорости
молекул
зависят от относительной скорости
молекул  , в то время как υ~
, в то время как υ~ . В результате, зависимость
æ от
температуры оказывается более сильной, приблизительно
æ~T0,7.
Это связано с тем, что кроме больших и короткодействующих сил
отталкивания, между молекулами действуют проявляющиеся на
относительно больших расстояниях слабые силы притяжения. Эти силы
увеличивают вероятность рассеяния молекулы, но с увеличением
температуры эффективность их действия уменьшается, т.к. средняя
скорость молекул возрастает, и те же силы вызывают меньшее
отклонение. Поэтому поперечное сечение несколько уменьшается с
увеличением T,
а, следовательно, и æ возрастает несколько быстрее чем
. В результате, зависимость
æ от
температуры оказывается более сильной, приблизительно
æ~T0,7.
Это связано с тем, что кроме больших и короткодействующих сил
отталкивания, между молекулами действуют проявляющиеся на
относительно больших расстояниях слабые силы притяжения. Эти силы
увеличивают вероятность рассеяния молекулы, но с увеличением
температуры эффективность их действия уменьшается, т.к. средняя
скорость молекул возрастает, и те же силы вызывают меньшее
отклонение. Поэтому поперечное сечение несколько уменьшается с
увеличением T,
а, следовательно, и æ возрастает несколько быстрее чем
 .
.
В отличие от коэффициента диффузии
D,
значение коэффициента теплопроводности æ,
как следует из (9), не зависит от концентрации молекул газа и
давления. Эта особенность связана с тем, что с увеличение давления
в переносе тепла и импульса участвует большее количество молекул
(ρ~p),
но при этом, вследствие меньшей длины свободного пробега
( ~1/p),
энергия и импульс передаются на меньшие
расстояния.
~1/p),
энергия и импульс передаются на меньшие
расстояния.
Вакуумные явления
Все явления переноса тесно связаны со
столкновениями между молекулами. Представляет интерес изучение
свойств газа в условиях, когда между молекулами нет столкновений.
Т.к. длина свободного пробега  обратно пропорциональна давлению, то при
уменьшении давления длина свободного пробега становится
сопоставимой с характерными размерами сосуда
L
обратно пропорциональна давлению, то при
уменьшении давления длина свободного пробега становится
сопоставимой с характерными размерами сосуда
L
|
|
|
(10) |
Такое состояние называется вакуумом. Понятие
вакуума является понятием относительным: чем меньше размеры сосуда,
тем при больших давлениях создаётся вакуум. Начиная с некоторого
давления (например, при давлении порядка
10-6 мм.
рт. ст.  достигает нескольких десятков метров),
длина свободного пробега становится больше размеров сосуда и
молекулы будут преимущественно сталкиваться со стенками сосуда, а
не с другими молекулами. Это приводит к существенному изменению
физического механизма всех явлений переноса. В условиях вакуума
теряет смысл говорить о давлении одной части газа на другую, а это
значит, что трение перестаёт быть внутренним. Имеет смысл говорить
только о силе трения, испытываемого движущимся телом. Теряет также
смысл понятие теплопроводности, как процесса передачи энергии от
одного слоя газа другому, следует говорить о теплопередаче между
стенками сосуда. Эффективное значение средней длины свободного
пробега становится приблизительно равным L (
достигает нескольких десятков метров),
длина свободного пробега становится больше размеров сосуда и
молекулы будут преимущественно сталкиваться со стенками сосуда, а
не с другими молекулами. Это приводит к существенному изменению
физического механизма всех явлений переноса. В условиях вакуума
теряет смысл говорить о давлении одной части газа на другую, а это
значит, что трение перестаёт быть внутренним. Имеет смысл говорить
только о силе трения, испытываемого движущимся телом. Теряет также
смысл понятие теплопроводности, как процесса передачи энергии от
одного слоя газа другому, следует говорить о теплопередаче между
стенками сосуда. Эффективное значение средней длины свободного
пробега становится приблизительно равным L ( = Const = L). Т.е. величина
= Const = L). Т.е. величина
 больше не зависит от концентрации
молекул газа в сосуде . Коэффициенты æ и η в
этом случае оказываются пропорциональными плотности
ρ, а
следовательно, и давлению p,
т.е. æ, η~
больше не зависит от концентрации
молекул газа в сосуде . Коэффициенты æ и η в
этом случае оказываются пропорциональными плотности
ρ, а
следовательно, и давлению p,
т.е. æ, η~ p~ρ.
Схематически зависимость коэффициентов æ и η от
давления газа показана на рис.4.
p~ρ.
Схематически зависимость коэффициентов æ и η от
давления газа показана на рис.4.

рис.4.
Примеры задач.
В данной самостоятельной работе мы приводим некоторый теоретически материал относящийся к явлениям переноса, молекулярным потокам и динамическому равновесию, а также разбираем две задачи по данной теме.
Первая задача.
Кубический сосуд объёмом V = 1 л заполнен воздухом. Одна из стенок поддерживается при температуре T1, противоположная ей — при температуре T2, остальные стенки теплоизолированы. Найдите отношение средних частот соударений молекул со стенками и рассмотрите два случая: а) давление в сосуде равно атмосферному p0 = 1 атм; б) сосуд откачан до давления p = 10
Решение:
Будем считать, что температуры T1 и T2 не очень сильно отличаются от 273 К. Тогда в случае а) средняя длина свободного пробега молекул во много раз меньше размеров сосуда. Поэтому частота f ударов молекул о стенку пропорциональна концентрации n и скорости v движения молекул в тонком слое, прилегающем к рассматриваемой стенке:

Так как давление, оказываемое газом на стенки сосуда, должно быть
одинаковым, то n1T1 = n2T2, откуда

Для того, чтобы рассмотреть случай б), оценим среднюю длину свободного пробега молекул L при давлении p = 10-9 атм. Так как

где L0 = 10-5 см. Отсюда получаем L ˜ 104 см. Это намного больше, чем расстояние между стенками кубического сосуда объёмом 1 литр, которое равно 10 см. Поэтому количество молекул, ударяющихся при давлении p в каждую из стенок за некоторый промежуток времени, будет одним и тем же, и f1/f2 = 1.
Вторая задача.
После тёплых дней резко ударил мороз, и поверхность озера покрылась льдом. Через сутки после похолодания толщина льда составила d1=3см. Строителям требуется переправить груз на противоположный берег озера, но для безопасности требуется лёд толщиной не менее d2=10см. Через сколько дней после установления морозов можно осуществить перевозку груза, если погода не изменится, а меры по искусственному ускорению процесса наращивания льда не предпринимаются?
Решение:
Лёд на поверхности озера образуется из-за оттока тепла от воды через толщу льда. Процесс этот достаточно медленный, поэтому будем считать, что внутри льда в любой момент времени существует стационарное — линейное — распределение температуры по толщине. Кроме того, будем пренебрегать малым количеством тепла, выделяющимся за счёт постепенного охлаждения нарастающего слоя льда, по сравнению с теплотой кристаллизации воды. Пусть в некоторый момент времени t слой льда имеет толщину x. Тогда количество теплоты ΔQ, проходящее за малый промежуток времени Δt через ледяной цилиндр с площадью основания S, равно
 ,
,
где ΔT — постоянная разность температур между водой и воздухом, η — коэффициент пропорциональности, называемый коэффициентом теплопроводности. Эта теплота отнимается от небольшого слоя воды, непосредственно примыкающего ко льду и превращающегося при замерзании в слой льда толщиной Δx:
 ,
,
где p — плотность льда, λ — удельная теплота замерзания воды. Приравнивая записанные выражения, получим, что
 ,
,
откуда  ,
,
то есть толщина слоя льда увеличивается пропорционально корню квадратному из времени, прошедшего с момента, когда мороз «ударил».
Следовательно, если за время τ1=1сутки на озере нарос слой льда толщиной d1=3смd1=3см, то слой толщиной d2=10см нарастёт за время
 ..
..
Список используемой литературы:
-
Задачи Московских городских олимпиад по физике, 1986-2005- 623 с.
-
Исследование теплопроводностии диффузии газов, Учебно-методическое пособие. Саратов: Издательский центр «Рата», 2008. – 36 с.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Явления переноса. Молекулярные потоки и динамическое равновесие.
Явления переноса. Молекулярные потоки и динамическое равновесие.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ
КАЗАХСТАН
АО «Национальный центр повышения квалификации «Өрлеу»
«Институт повышения квалификации педагогических работников по СКО»
филиал
Курсы повышения квалификации учителей физики
«Развитие профессиональных компетенций учителя физики»
05.11-16.11.2018 г.
Самостоятельная работа
на тему «Явления переноса. Молекулярные потоки и динамическое равновесие»
Выполнил: учитель физики «КГУ Беловская средняя школа»
Кызылжарский район
Кузьмин В.В,
Проверила: Мунжасарова Г.Ж..
г. Петропавловск
2018
Оглавление
Средняя длина свободного пробега 4
Обобщённое уравнение переноса 7
Список используемой литературы: 13
Введение.
Газ, находящийся в равновесном состоянии, при постоянных внешних условиях характеризуется неизменностью во времени и во всех точках занимаемого объёма таких величин как давление, температура, относительное число молекул разного сорта и т.д. Но, несмотря на важную роль равновесных состояний, они всё же являются особым случаем и во многих задачах, представляющих огромный физический интерес, мы имеем дело с системами, не находящимися в равновесии.
Отклонение системы от равновесного состояния приводит к возникновению термодинамических потоков, связанных с переносом вещества, энергии, импульса и т.д. из одной части занимаемого объёма в другую. Подобные процессы получили название явлений переноса. При наличии в среде различной концентрации примеси возникают диффузионные потоки, т.е. перенос массы (явление диффузии); в случае разной температуры - тепловые потоки, т.е. перенос энергии (явление теплопроводности); при различной скорости течения потоков - перенос импульса (явление вязкости); при наложении электрического поля на систему свободных зарядов – потоки зарядов (ток), т.е. перенос зарядов (явление электропроводности).
При изучении систем, не находящихся в равновесии, мы сталкиваемся с достаточно сложной проблемой, связанной с необходимостью исследовать специфический характер взаимодействий, приводящий в конце концов систему в равновесное состояние. Однако, ситуация сильно упрощается в случае разреженных газов, о которых и пойдёт речь далее. Несмотря на приближённый характер последующих вычислений, они всё же дают возможность исходя из достаточно простых соображений, получить ясное представление о физической сути рассматриваемых явлений. Кроме того, с их помощью удаётся получить сравнительно хорошие численные оценки и правильно предсказать зависимость от всех существенных параметров.
С точки зрения молекулярно-кинетической теории основной причиной явлений переноса в газе является тепловое хаотическое движение молекул. Находясь в постоянном хаотическом движении, молекулы, соударяясь между собой, в конце концов, приводят газ в состояние равновесия. Происходит выравнивание температуры в различных частях газа, выравнивание концентраций веществ в смеси, выравнивание скоростей движущихся друг относительно друга слоёв газа и т.д. Рассмотрение процесса сильно упрощается, если считать газ настолько разреженным, что становится справедливым следующее приближение: время между соударениями молекул много меньше времени, затрачиваемого на соударение; вероятность одновременного столкновения трёх молекул пренебрежимо мала и имеют место только столкновения двух частиц; среднее расстояние между молекулами велико по сравнению со средней длиной волны де Бройля молекулы, что позволяет избежать квантовомеханических подходов.
Средняя длина свободного пробега
Начнём с рассмотрения столкновений между
молекулами разреженного газа. Среднее расстояние
 , проходимое молекулой между двумя
последовательными столкновениями называется
средней длиной свободного
пробега.
Рассмотрим молекулу В радиуса r,
сближающуюся с другой молекулой В'
радиуса r' с
относительной скоростью
, проходимое молекулой между двумя
последовательными столкновениями называется
средней длиной свободного
пробега.
Рассмотрим молекулу В радиуса r,
сближающуюся с другой молекулой В'
радиуса r' с
относительной скоростью  (рис.1). Пусть расстояние между центрами
обеих молекул при их максимальном сближении равно
b.
Тогда молекулы испытают столкновение если b>r+r’.
Представим, что молекула В несёт на себе диск
радиусом r + r',
центр которого совпадает с центром молекулы, а плоскость диска
перпендикулярна к вектору относительной скорости
(рис.1). Пусть расстояние между центрами
обеих молекул при их максимальном сближении равно
b.
Тогда молекулы испытают столкновение если b>r+r’.
Представим, что молекула В несёт на себе диск
радиусом r + r',
центр которого совпадает с центром молекулы, а плоскость диска
перпендикулярна к вектору относительной скорости
 . Тогда столкновение произойдёт только
в том случае, если центр молекулы В' окажется
. Тогда столкновение произойдёт только
в том случае, если центр молекулы В' окажется

Рис.1.
внутри объёма, занятого воображаемым диском с поверхностью σ , называемой полным поперечным сечением
 (1)
(1)
или если молекулы одинаковые
 .
.
Воображаемый диск с поверхностью σ за время τ
вырезает в пространстве объём σ τ.
Если время τ будет равно среднему времени свободного пробега
молекулы, т.е. среднему времени между двумя последовательными
столкновениями молекул τ , то вырезанный объём будет содержать в
среднем одну молекулу, т.е. σ
τ.
Если время τ будет равно среднему времени свободного пробега
молекулы, т.е. среднему времени между двумя последовательными
столкновениями молекул τ , то вырезанный объём будет содержать в
среднем одну молекулу, т.е. σ τn=1,
где n -
число молекул в единице объёма газа. Тогда
τn=1,
где n -
число молекул в единице объёма газа. Тогда  =1/σ
=1/σ n и,
принимая во внимание, что
n и,
принимая во внимание, что  , где
, где  - средняя скорость движения молекул
и
- средняя скорость движения молекул
и  ≈
≈  (что можно получить в результате
усреднения), получим
(что можно получить в результате
усреднения), получим
 (2)
(2)
Диффузия
Рассмотрим вещество, состоящее из одинаковых молекул, но предположим, что часть их каким-то образом помечена. Пусть n1 число помеченных молекул в единице объёма. В состоянии равновесия меченые молекулы равномерно распределены по всему объёму и, соответственно, n1 не зависит от координат. Допустим, однако, что распределение не является однородным и n1 зависит от координат, пусть для простоты рассуждений n1 зависит только от одной координаты x, т.е. n1 = n1(x) . При этом предполагается, что полное число молекул в единице объёма остаётся постоянным, так что результирующее перемещение молекул вещества отсутствует. Такое состояние не является равновесным. Меченые молекулы вследствие теплового движения будут перемещаться в сосуде в сторону меньшей концентрации этих молекул, чтобы достичь равновесного состояния, когда они будут равномерно распределены по всему объёму. Этот процесс носит название самодиффузии. На место переместившихся меченых молекул приходят другие молекулы, так что давление газа остаётся неизменным, но происходит перенос массы газы.
Будем считать, что все молекулы движутся с
одинаковой скоростью, равной их средней скорости
 . Одна треть из всех находящихся в
единице объёма n молекул имеют составляющие скорости, направленные
вдоль оси x, у половины этих молекул скорости направлены вдоль + x
, а у другой половины вдоль – x (см. рис.2). Тогда количество
молекул, пролетающих за единицу времени через единичную площадку в
направлении снизу вверх равно
. Одна треть из всех находящихся в
единице объёма n молекул имеют составляющие скорости, направленные
вдоль оси x, у половины этих молекул скорости направлены вдоль + x
, а у другой половины вдоль – x (см. рис.2). Тогда количество
молекул, пролетающих за единицу времени через единичную площадку в
направлении снизу вверх равно
|
|
|
(3) |
и столько же молекул движутся сверху вниз.
Молекулы, пересекающие плоскость снизу, испытали последнее
столкновение в среднем на расстоянии  от плоскости. Так как
n1 = n1(x)
, то среднее число молекул,
пересекающих за единицу времени через
единичную площадку плоскости в направлении снизу
вверх N+(x) и
сверху вниз N−(x) ,
равны, соответственно
от плоскости. Так как
n1 = n1(x)
, то среднее число молекул,
пересекающих за единицу времени через
единичную площадку плоскости в направлении снизу
вверх N+(x) и
сверху вниз N−(x) ,
равны, соответственно

Рис.2.

Принимая во внимание, что  получим результирующую плотность потока
молекул N(x)
через единичную поверхность в направлении
+x
получим результирующую плотность потока
молекул N(x)
через единичную поверхность в направлении
+x
|
|
|
(4) |
где  – коэффициент
самодиффузии.
– коэффициент
самодиффузии.
Умножая на массу молекулы m обе части равенства (4), получим выражение для плотности потока массы, т.е. массы, переносимой через единичную площадку в единицу времени M
|
|
|
(5) |
которое называется законом Фика,
где  - плотность
меченых молекул.
- плотность
меченых молекул.
Знак минус в (4) и (5) отражает то обстоятельство, что поток массы (поток молекул) направлен в сторону убывания концентрации.
Принимая во внимание, что
|
|
|
(6) |
|
|
|
|
и соотношение (2), в предположении, что молекулы являются твёрдыми шариками, площадь поперечного сечения σ (1) которых не зависит от температуры, можно показать, что значение коэффициента самодиффузии D растет с повышением температуры D~T3/2.
Из соотношений (2) и (6) следует, что коэффициент
самодиффузии D уменьшается c
увеличением концентрации n и
давления p,
т.е. D~1/n~1/p. Это связано с
уменьшением длины свободного пробега  при увеличении концентрации молекул, что приводит
к более частым соударениям диффундирующих частиц с молекулами газа
т.е. переносится на меньшее
расстояние.
при увеличении концентрации молекул, что приводит
к более частым соударениям диффундирующих частиц с молекулами газа
т.е. переносится на меньшее
расстояние.
Обобщённое уравнение переноса
Поскольку все явления переноса имеют в основе общие физические закономерности, то после рассмотрения явления диффузии очень просто получить так называемое обобщённое уравнение переноса, удобное для анализа конкретных процессов переноса.
Пусть некоторая физическая величина a характеризует определённое молекулярное свойство, это может быть масса, энергия, импульс. При этом будем считать, что переносимую величину можно отнести к одной молекуле. (Если речь идет, например, о переносе энергии, то отнесенной к одной молекуле величиной будет полная энергия молекулы.) Будем считать, что величина a(x) изменяется в зависимости от координаты x.
Для количественного описания потока вводят величину A, называемую плотностью потока и численно равную количеству физической величины a(x), переносимой за единицу времени через единичную поверхность. Если рассматриваемая система находится в состоянии, близком к равновесию, то плотность потока A пропорциональна соответствующей физической величины a(x) в той же точке.
В уравнении, описывающем процесс диффузии (5), величина A представляет собой плотность потока массы M, а в качестве переносимой величины a выступает масса молекулы. Тогда, если величина a зависит только от одной пространственной переменной x (случай одномерной среды), выражение для плотности потока будет иметь следующий вид
|
|
|
(7) |
Знак минус в выражении (7) указывает на то, что поток направлен в сторону уменьшения величины a. Параметры a и A в уравнении (7), отвечающие основным явлениям переноса (диффузии, вязкости, теплопроводности и электропроводности) и соответствующие коэффициенты переноса представлены в таблице 1, причём A представляет собой макропараметр, в то время как a является молекулярной характеристикой.
Таблица 1.
|
Явление |
Диффузия |
Вячкость |
Теплопроводность |
Электропроводность |
|
a |
m |
mu |
3/2kT |
q |
|
A |
M |
F |
Q |
j |
|
Коэффициент переноса |
|
|
|
|
Теплопроводность
Если в некоторой среде создать вдоль оси x градиент температуры, то возникает поток тепла. Допустим, что распределение температур в газе не является однородным, т.е. температура зависит от координаты T=T(x) (рис.4).

Рис.3.
Газ в этомслучае находится в неравновесном состоянии, и стремление к достижению равновесия проявится в возникновении потока тепла Q, направленного от участков газа, обладающих высокой температурой, к участкам с низкой температурой.
Рассмотрим в газе некоторую
плоскость x=Const,
где T=T(x). Количество тепла, перенесённое за единицу времени
через единицу поверхности плоскости в направлении
+x,
называется плотностью потока тепла Q.
Механизм переноса тепла заключается в том, что молекулы газа
пересекают плоскость сверху и снизу. Если в верхней области газа
температура больше, чем в нижней (∂T/∂x>0), то средняя кинетическая
энергия  молекул в верхней области больше, чем
энергия молекул в нижней. Энергия молекул, приходящих снизу меньше,
чем у молекул, пересекающих плоскость сверху. В результате
происходит перенос энергии из области над плоскостью в область под
ней. При столкновениях молекулы с большей энергией передают часть
энергии молекулам с меньшей энергией. Вследствие столкновений
молекул друг с другом в результате хаотического движения происходит
выравнивание энергии в разных областях пространства, а,
следовательно, и выравнивание температур. Перенос энергии и
обуславливает процесс теплопроводности в
газах.
молекул в верхней области больше, чем
энергия молекул в нижней. Энергия молекул, приходящих снизу меньше,
чем у молекул, пересекающих плоскость сверху. В результате
происходит перенос энергии из области над плоскостью в область под
ней. При столкновениях молекулы с большей энергией передают часть
энергии молекулам с меньшей энергией. Вследствие столкновений
молекул друг с другом в результате хаотического движения происходит
выравнивание энергии в разных областях пространства, а,
следовательно, и выравнивание температур. Перенос энергии и
обуславливает процесс теплопроводности в
газах.
Тогда при замене в (7) A на поток тепла Q, а в качестве a рассматривая энергию теплового движения молекулы 3/2kT, получим следующее соотношение
|
|
|
(8) |
где æ- коэффициент теплопроводности и
|
|
|
(9) |
 - удельная теплоёмкость при постоянном
объёме, ρ - плотность газа. Знак минус показывает, что тепло течет
в направлении убывания температуры. Выражение (8) представляет
собой закон теплопроводности Фурье.
- удельная теплоёмкость при постоянном
объёме, ρ - плотность газа. Знак минус показывает, что тепло течет
в направлении убывания температуры. Выражение (8) представляет
собой закон теплопроводности Фурье.
Проанализируем зависимость коэффициента
теплопроводности æ от
температуры. В предположении, что молекулы представляют собой
твёрдые шары, æ зависит от температуры так же, как
 (6), т.е. æ~
(6), т.е. æ~ . Однако, в общем случае оказывается,
что σ,
а, следовательно, и
. Однако, в общем случае оказывается,
что σ,
а, следовательно, и  зависят от относительной скорости
молекул
зависят от относительной скорости
молекул  , в то время как υ~
, в то время как υ~ . В результате, зависимость
æ от
температуры оказывается более сильной, приблизительно
æ~T0,7.
Это связано с тем, что кроме больших и короткодействующих сил
отталкивания, между молекулами действуют проявляющиеся на
относительно больших расстояниях слабые силы притяжения. Эти силы
увеличивают вероятность рассеяния молекулы, но с увеличением
температуры эффективность их действия уменьшается, т.к. средняя
скорость молекул возрастает, и те же силы вызывают меньшее
отклонение. Поэтому поперечное сечение несколько уменьшается с
увеличением T,
а, следовательно, и æ возрастает несколько быстрее чем
. В результате, зависимость
æ от
температуры оказывается более сильной, приблизительно
æ~T0,7.
Это связано с тем, что кроме больших и короткодействующих сил
отталкивания, между молекулами действуют проявляющиеся на
относительно больших расстояниях слабые силы притяжения. Эти силы
увеличивают вероятность рассеяния молекулы, но с увеличением
температуры эффективность их действия уменьшается, т.к. средняя
скорость молекул возрастает, и те же силы вызывают меньшее
отклонение. Поэтому поперечное сечение несколько уменьшается с
увеличением T,
а, следовательно, и æ возрастает несколько быстрее чем
 .
.
В отличие от коэффициента диффузии
D,
значение коэффициента теплопроводности æ,
как следует из (9), не зависит от концентрации молекул газа и
давления. Эта особенность связана с тем, что с увеличение давления
в переносе тепла и импульса участвует большее количество молекул
(ρ~p),
но при этом, вследствие меньшей длины свободного пробега
( ~1/p),
энергия и импульс передаются на меньшие
расстояния.
~1/p),
энергия и импульс передаются на меньшие
расстояния.
Вакуумные явления
Все явления переноса тесно связаны со
столкновениями между молекулами. Представляет интерес изучение
свойств газа в условиях, когда между молекулами нет столкновений.
Т.к. длина свободного пробега  обратно пропорциональна давлению, то при
уменьшении давления длина свободного пробега становится
сопоставимой с характерными размерами сосуда
L
обратно пропорциональна давлению, то при
уменьшении давления длина свободного пробега становится
сопоставимой с характерными размерами сосуда
L
|
|
|
(10) |
Такое состояние называется вакуумом. Понятие
вакуума является понятием относительным: чем меньше размеры сосуда,
тем при больших давлениях создаётся вакуум. Начиная с некоторого
давления (например, при давлении порядка
10-6 мм.
рт. ст.  достигает нескольких десятков метров),
длина свободного пробега становится больше размеров сосуда и
молекулы будут преимущественно сталкиваться со стенками сосуда, а
не с другими молекулами. Это приводит к существенному изменению
физического механизма всех явлений переноса. В условиях вакуума
теряет смысл говорить о давлении одной части газа на другую, а это
значит, что трение перестаёт быть внутренним. Имеет смысл говорить
только о силе трения, испытываемого движущимся телом. Теряет также
смысл понятие теплопроводности, как процесса передачи энергии от
одного слоя газа другому, следует говорить о теплопередаче между
стенками сосуда. Эффективное значение средней длины свободного
пробега становится приблизительно равным L (
достигает нескольких десятков метров),
длина свободного пробега становится больше размеров сосуда и
молекулы будут преимущественно сталкиваться со стенками сосуда, а
не с другими молекулами. Это приводит к существенному изменению
физического механизма всех явлений переноса. В условиях вакуума
теряет смысл говорить о давлении одной части газа на другую, а это
значит, что трение перестаёт быть внутренним. Имеет смысл говорить
только о силе трения, испытываемого движущимся телом. Теряет также
смысл понятие теплопроводности, как процесса передачи энергии от
одного слоя газа другому, следует говорить о теплопередаче между
стенками сосуда. Эффективное значение средней длины свободного
пробега становится приблизительно равным L ( = Const = L). Т.е. величина
= Const = L). Т.е. величина
 больше не зависит от концентрации
молекул газа в сосуде . Коэффициенты æ и η в
этом случае оказываются пропорциональными плотности
ρ, а
следовательно, и давлению p,
т.е. æ, η~
больше не зависит от концентрации
молекул газа в сосуде . Коэффициенты æ и η в
этом случае оказываются пропорциональными плотности
ρ, а
следовательно, и давлению p,
т.е. æ, η~ p~ρ.
Схематически зависимость коэффициентов æ и η от
давления газа показана на рис.4.
p~ρ.
Схематически зависимость коэффициентов æ и η от
давления газа показана на рис.4.

рис.4.
Примеры задач.
В данной самостоятельной работе мы приводим некоторый теоретически материал относящийся к явлениям переноса, молекулярным потокам и динамическому равновесию, а также разбираем две задачи по данной теме.
Первая задача.
Кубический сосуд объёмом V = 1 л заполнен воздухом. Одна из стенок поддерживается при температуре T1, противоположная ей — при температуре T2, остальные стенки теплоизолированы. Найдите отношение средних частот соударений молекул со стенками и рассмотрите два случая: а) давление в сосуде равно атмосферному p0 = 1 атм; б) сосуд откачан до давления p = 10
Решение:
Будем считать, что температуры T1 и T2 не очень сильно отличаются от 273 К. Тогда в случае а) средняя длина свободного пробега молекул во много раз меньше размеров сосуда. Поэтому частота f ударов молекул о стенку пропорциональна концентрации n и скорости v движения молекул в тонком слое, прилегающем к рассматриваемой стенке:

Так как давление, оказываемое газом на стенки сосуда, должно быть
одинаковым, то n1T1 = n2T2, откуда

Для того, чтобы рассмотреть случай б), оценим среднюю длину свободного пробега молекул L при давлении p = 10-9 атм. Так как

где L0 = 10-5 см. Отсюда получаем L ˜ 104 см. Это намного больше, чем расстояние между стенками кубического сосуда объёмом 1 литр, которое равно 10 см. Поэтому количество молекул, ударяющихся при давлении p в каждую из стенок за некоторый промежуток времени, будет одним и тем же, и f1/f2 = 1.
Вторая задача.
После тёплых дней резко ударил мороз, и поверхность озера покрылась льдом. Через сутки после похолодания толщина льда составила d1=3см. Строителям требуется переправить груз на противоположный берег озера, но для безопасности требуется лёд толщиной не менее d2=10см. Через сколько дней после установления морозов можно осуществить перевозку груза, если погода не изменится, а меры по искусственному ускорению процесса наращивания льда не предпринимаются?
Решение:
Лёд на поверхности озера образуется из-за оттока тепла от воды через толщу льда. Процесс этот достаточно медленный, поэтому будем считать, что внутри льда в любой момент времени существует стационарное — линейное — распределение температуры по толщине. Кроме того, будем пренебрегать малым количеством тепла, выделяющимся за счёт постепенного охлаждения нарастающего слоя льда, по сравнению с теплотой кристаллизации воды. Пусть в некоторый момент времени t слой льда имеет толщину x. Тогда количество теплоты ΔQ, проходящее за малый промежуток времени Δt через ледяной цилиндр с площадью основания S, равно
 ,
,
где ΔT — постоянная разность температур между водой и воздухом, η — коэффициент пропорциональности, называемый коэффициентом теплопроводности. Эта теплота отнимается от небольшого слоя воды, непосредственно примыкающего ко льду и превращающегося при замерзании в слой льда толщиной Δx:
 ,
,
где p — плотность льда, λ — удельная теплота замерзания воды. Приравнивая записанные выражения, получим, что
 ,
,
откуда  ,
,
то есть толщина слоя льда увеличивается пропорционально корню квадратному из времени, прошедшего с момента, когда мороз «ударил».
Следовательно, если за время τ1=1сутки на озере нарос слой льда толщиной d1=3смd1=3см, то слой толщиной d2=10см нарастёт за время
 ..
..
Список используемой литературы:
-
Задачи Московских городских олимпиад по физике, 1986-2005- 623 с.
-
Исследование теплопроводностии диффузии газов, Учебно-методическое пособие. Саратов: Издательский центр «Рата», 2008. – 36 с.

шағым қалдыра аласыз


























