1-лекция
Оқиғалар алгебрасы
1. Бастапқы жалпы шарт, сынау, оқиға.
2. Оқиғаларды класстарға бөлу .
3. Оқиғалар арасындағы байланыстар .
1. Оқиғалар алгебрасы.
1. Бастапқы жалпы шарт, сынау, оқиға. Бұл ұғымдарды түсіндіруді мысалдармен көрсетейік.
1-мысал. Металл теңгені тегіс еденге тастайық, сонда мына төмендегі құбылыстарды байқаймыз. Теңгені лақтыру үшін өзімізді белгілі бір қалыпқа келтіреміз. Одан соң бас бармақпен теңгенің бір ұшын жоғары қарай түртіп жібереміз. Онда ол шыр көбелек , белгілі бір биіктікке дейін көтеріліп, төмен қарай құлдилап еденге түседіде, бір неше рет секіректеп , жалпағыныан не тиін жағы не герб жағы жоғары қарап жатады. Сайып келгенде , теңге жалпағынан жатуы үшін көптеген қимыл әрекеттер жасалады, солардың жиынын бастапқы жалпы шарт деп атаймыз. Оның тиын не герб жағының жоғары жатуы , яғни бастапқы жалпы шарттың орындалу нәтижесі – оқиға деп айтылады.
2-мысал. Біртекті материалдардан жасалған симмертиялы кубтың(ойын тасының) әрбір жағы 1 ден 6 ға дейін нөмірленген болады. Оны бір рет лақтырғанда , яғни бастапқы жалпы шарт орындалғанда алты жағының біреуі жоғары қарап түседі, мұнда қай жағы түсседе оқиға болады.
3-мысал. Өзіміз қарапайым көріп жүрген суды 100оС ге дейін қыздырсақ, ол буға айналады. Судың буға айналуы –оқиға, ал осы бу пайда болғанға дейінгі барлық әрекеттер жиыны бастапқы жалпы шарт болады.
Бұдан былай бастапқы жалпы шарт термині орнына сынау, тәжірибе, эксперимент терминдерін қолданамыз. Сонымен сынау нәтижесін оқиға деп атауға келісеміз. Әдетте оқиғаларды үлкен әріптер А,В,С,... арқылы белгілейміз. Мысал үшін теңгенің тиын жағының пайда болуы А оқиғасы болса, герб жағының пайда болуы В оқиғасымен белгіленеді және т.с.с.
2. Оқиғаларды кластарға бөлу.
Анықтама. Сынау жүргізілгенде А оқиғасы пайда болуыда , пайда болмауыда мүмкін болса , ондай оқиғаны кездейсоқ оқиға деп айтамыз. Мұндай оқиғаларға 1,2-мысал жатады, өйткені сынау нәтижесінде теңгенің немесе кубтың белгіленген жағынан пайда боларын күн ілгері айта алмайыз. Сынау нәтижесінде оқиға (А оқиғасы) сөзсіз пайда болатын болса, ондай оқиғаны ақиқат оқиға дейді. Сынау нәтижесінде оқиғаның (А оқиғасы) пайда болуы мүмкін болмаса, ондай оқиғаны мүмкін емес оқиға деп йтамыз
Ақиқат оқиғаны U әрпімен, мүмкін емес оқиғаны V әрпімен белгілеу қабылданылған. Мысалы, кобдишаға салынған ақ шарлардың біреуін алсақ, оның ақ болып шығуы ақиқат оқиға да, басқа түсте болуы мүмкін емес оқиға. Сынау жүргізгенде екі оқиғаның бірі пайда болып, екіншісі пайда болмайтын оқиғаларды үйлесімсіз оқиғалар деп айтылады. Мәселен 2-мысалдағы А1,А2 (бірінші және екінші нөмірлі жақтар) оқиғалары- үйлесімсіз оқиғалар. Бұл мысалдағы кез келген екі оқиға да үйлесімсіз. Кез келген екі оқиғасы үйлесімсіз болатын оқиғалар жиынын қос-қостан үйлесімсіз оқиғалар дейді.
Сынау жүргізілгенде оқиғаның біреуінің пайда болуы екіншісінің пайда болуын жоққа шығармайтындай екі оқиғаны үйлесімді оқиғалар деп атайды. Мысалы, кубтың жұп нөмірінің пайда болуы (А оқиғасы) мен үш санына еселік нөмір пайда болуы В оқиғасы үйлесімді. Өйткені кубтың 6-нөмірінің пайда болуын көрсететін А6 оқиғасы В оқиғасы пайда болғанда да, А оқиғасы пайда болғанда да пайда болуы мүмкін.
Сынау нәтижесінде мүмкін оқиғалардың әйтеуір біреуінің сөзсіз пайда болуы ақиқат болса, ондай оқиғаны жалғыз ғана мүмкіндікті оқиға дейді. Жалғыз ғана мүмкіндікті оқиғалар оқиғалардың толық тобын немесе оқиғалардың толық жүйесін (системасын) құрады деп айтуға келісеміз. Мысалы, сынау нәтижесінде кубтың алты жағының біреуі (А оқиғасы) пайда болуы сөзсіз, сондықтан А1, А2, А3, А4, А5, А6 оқиғалары жалғыз ғана мүмкіндікті оқиғалар және олар оқиғалардың толық тобын құрайды. Сонымен қатар бұлар қос-қостан үйлесімсіз оқиғалар.
3.Оқиғалар арасындағы қатынастар. Оқиғаларға қолданатын
амалдар
Осы уақытқа дейін оқиғалар арасындағы кейбір қатынастарғана айтылған еді. Ал ықтималдықтар теориясының алдына қойған негізгі мақсатының бірі жеке оқиғалар ықтималдығы бойынша күрделі оқиғалар ықтималдығын анықтау болып табылады.
Бұл мәселені айқындау қосу, көбейту және тағыда басқа түрлі амалдар орындауға негізделеді. Бұларды баяндаудан бұрын сол оқиғалар арасындағы негізгі қатынастарды келтіріп, амалдарды орындап және көрнектілігін графикалық түрде көрсетейік.
1. А және В оқиғаларының кем дегенде біреуінің пайда болуын осы оқиғалардың қосындысы деп атайды. Оны АUВ немесе А+В арқылы белгілейміз, мұнда U-біріктіру (қосу) таңбасы. Сонымен, оқиғалардың қосындысы деп не А оқиғасы, не В оқиғасы, не А және В екеуі де пайда болатын оқиғаны ұғамыз. Оқиғаны өзіне-өзін қосқанда сол оқиғаның өзі шығады, яғни АUА=A. Сондай-ақ АUV=A, AUU=U болатынын көру қиын емес.
Екі оқиғаның бірігуін (қосындысын) оқиғалардың қалаған санына кеңейтуге болады, яғни A1UA2U…UAnU… (A1+A2+…+An+…), немесе i=1U¥Ai деп жазамыз. Мұны сынау нәтижесінде A1, A2,…,An,… оқиғаларының кем дегенде біреуінің пайда болуы деп ұғамыз. Ал бұл оқиғалар оқиғалардың толық тобын құраса, онда олардың қосындысы ақиқат оқиға болады. Мысалы, оқушының жақсы оқуы А оқиғасы, ал спортшы болуы В оқиғасы болсын. Осы екі оқиғаның қосындысы C=A U B оқушы жақсы оқыса да (А оқиғасы), спортшы болса да (В оқиғасы) немесе ол әрі жақсы оқитын әрі спортшы болса да (А және В оқиғаларының екеуі де) орындалады.
А және В оқиғалары қосындысының геометриялық кескінін көрсету үшін кездейсоқ оқиғаны жазықтықтағы фигура ретінде қарастырған қолайлы. Квадрат ішіндегі радиусы кіші дөңгелектегі нүктелер жиыны В оқиғасының пайда болуын кескіндейді, радиуысы үлкен дөңгелектегі нүктелер жиыны А оқиғасының пайда болуын кескіндейді десек, онда АUВ оқиғалар бірігуі екі дөңгелек жасаған облыстағы нүктелер жиынын көрсетеді, мұндағы А және В оқиғаларының екеуіне де жататын нүктелер тек бір рет қана есепке алынады.
2. А және В оқиғаларының бірге
пайда болуын олардың көбейтіндісі деп атайды да АВ (яғни А*В)
немесе А![]() В арқылы белгілейді,
мұндағы
В арқылы белгілейді,
мұндағы ![]() -қылысу (көбейту) таңбасы.
А*В-ны А мен В-ның бірге пайда болуы деп ұғамыз. Оқиғаны өзіне-өзін
көбейтсе, сол оқиғаның өзі шығады, яғни А∩А=А. Сондай-ақ
A∩V=V, A∩
U
=A.
-қылысу (көбейту) таңбасы.
А*В-ны А мен В-ның бірге пайда болуы деп ұғамыз. Оқиғаны өзіне-өзін
көбейтсе, сол оқиғаның өзі шығады, яғни А∩А=А. Сондай-ақ
A∩V=V, A∩
U
=A.
Аталған екі оқиғаның қиылысуын
(көбейтіндісін) оқиғалардың кез келген санына кеңейтуге болады,
яғни А1![]() A2
A2![]() …
…![]() An
An![]() … немесе
i=1∩¥Аі
деп жазамыз. Мұны сынау
нәтижесінде осы А1,А2,...,Аn... оқиғаларының барлығының
пайда болуы деп ұғамыз.
… немесе
i=1∩¥Аі
деп жазамыз. Мұны сынау
нәтижесінде осы А1,А2,...,Аn... оқиғаларының барлығының
пайда болуы деп ұғамыз.
3.А оқиғасы орындалып, В оқиғасы орындалмайтын оқиғаны А мен В-ның айырымы деп айтады және оны А-В немесе А \ В ( \ азайту таңбасы арқылы) белгілейміз.
4.Cимметриялы айыру амалы. Симметриялы айыру амалы деп А және В оқиғалар бірігуінен сол оқиғалар қиылысуының айырымынан құралған элементтер жиынын айтамыз:
А Å В : = ( А U В) \ ( А ∩ В) = { х | (хÎ А & х Ï В) Ú (х Ï А & х Î В) }.
5. Екі үйлесімсіз А және Ā
( ØА немесе А емес) оқиғалары
оқиғалардың толық тобын құраса, оларды қарама-қарсы оқиғалар деп
айтамыз. Олардың қосындысы ақиқат оқиға, яғни А U Ā
= U, ал көбейтіндісі –мүмкін емес
оқиға А∩ Ā = V,
сондай-ақ Ū
=
V
,
 = U
болуын байқау қиын
емес.
= U
болуын байқау қиын
емес.
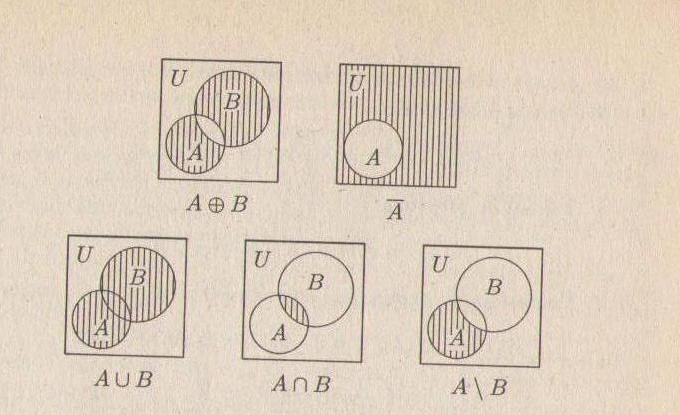
Жоғарыдағы сызбаларда А және В оқиғалардың қосындысы(бірігуі), көбейтіндісі(қиылысуы), айырымы, симметриялы айырымы және қарама-
қарсы оқиғалардың диаграммалары көрсетілген.
6. Сынау нәтижесінде пайда болған В оқиғасы екінші бір А оқиғасының да пайда болуын қамтамасыз етсе, онда В-ның пайда болуы А-ның пайда болуын ілестіреді деп айтады да мұны ВÌ А (жату, ену таңбасы) арқылы белгілейді.
Геометриялық талқылаудан төмендегідей тұжырымдар келіп шығады.
-
А Ì А болады,
-
А Ì В, В Ì С болса, онда А Ì С болады,
-
А Ì B болса, А U В = B және А ∩ В = А болады.
Буларға талдау жасауды оқырмандардың өздеріне тапсырамыз.
7.Сынау нәтижесінде пайда болған А оқиғасы В оқиғасыныңда пайда болуын қамтыса ( яғни А Ì В болса) және осы сынауда В оқиғасының пайда болуы А оқиғасының пайда болуын қамтыса (яғни В Ì А болса) , онда А және В оқиғаларды эквивалентті деп айтамызда оны А≡В ретінде белгілейміз. Өзара эквивалентті(тең) оқиғаларды бір-бірімен ауыстыруға болады. Сондықтан кез келген екі эквивалентті оқиғаны тепе-тең немесе тең оқиғалар депте айтамыз. Барлық ақиқат оқиғалар эквивалентті, сондаяқ барлық мүмкін емес оқиғаларда эквивалентті.
8.Қандай да оқиғаларға бірігу
( U ), қиылысу(∩) , ішінде жату(Ì ) және ішіне
алу(É) амалдарының қолданылуы дұрыс
болса, онда ол оқиғаларды сәйкес қарама-қарсы оқиғалармен ауыстырып
қолданғанда амалдар бір-бірімен ауысады, яғни U ∩ ға не ∩ U
ға, É
Ì
ға не
Ì
É
ға айналады. Сол себепті
төмендегі қасиеттер орын алады. Егер А
Ì
В болса,
онда  É
É
 ; егер
А É
В болса,
онда
; егер
А É
В болса,
онда  Ì
Ì
 ; егер
С = A∩B
болса,
онда
; егер
С = A∩B
болса,
онда  =
=  U
U
 ; егер
C=AU
B
болса,
онда
; егер
C=AU
B
болса,
онда  =
=  ∩
∩  болады.
болады.
9.Оқиғалар қосындысының анықтамасы бойынша АU В оқиғасы мен ВUА оқиғасы пара-пар, ал көбейтіндінің анықтамасы бойынша А∩ В мен В∩А пара пар оқиғалар. Бұл жайт оқиғалар саны екіден артық болсада орын алады. Сондықтан , оқиғалардың қосындысы мен көбейтіндісі үшін орын алмастыру заңы орындалады.
Сонымен оқиғалар арасындағы қатынастардан пайдаланып , төмендегідей қасиеттерді жазуымызға болады:
1) Идемпотенттік қасиеті. Элементтері бірдей oқиғалардың қосындысы немесе көбейтіндісі өзіне тең:
А È А =А, А Ç А = А;
2) Коммутативтілік(ауыстырымдылық) қасиеті. Қосу немесе көбейту амалдарын орындағанда оқиғалардың орны ауысқанымен нәтиже мәні өзгермейді :
А È В = В È А, А Ç В = В Ç А;
3) Ассоциативтілік(топталу) қасиеті. А,В,С оқиғалардың қосу немесе көбейту амалдарын біргелікте орындағанда жақшалардың орны ауысқанымен нәтиже мәні өзгермейді:
А È ( В È С) = ( А È В) È С,
А Ç ( ВÇ С) = ( А Ç В) ÇС;
4) Дистрибутивтік(терімділік) қасиеті:
АÈ (В Ç С) = (АÈ В) Ç (А È С)
А Ç (ВÈ С) = (А Ç В) È (А Ç С)
5) Жұтылу қасиеті:
(АÇ В) È А= А, (АÈ В) Ç А=А,
6) Мүмкін емес оқиға қасиеті:
АÈ V = А, А Ç V = V;
7) Ақиқат оқиға қасиеті:
А È U = U , А Ç U = А;
8) Екі рет терістік қасиеті:
 = А;
= А;
9) Де Морган заңдары:
 =
=  Ç
Ç
 ,
,  =
=  È
È
 ;
;
10) Толықтыру қасиеті:
А
È
 = U, А
Ç
= U, А
Ç
 = V
;
= V
;
11) Айырым үшін өрнек:
А \ В
= А
Ç

Жоғарыдағы келтірілген түрлендірулерді күрделі өрнектерді ықшамдау үшін пайдаланудың мәні зор-ақ.
Біздің мақсатымыз–тәжірибенің нәтижелерімен анықталатын құбылыс-тарды сипаттауға ыңғайлы математикалық модельді іздестіру. Бұл мәселе оқиғаны тек сынау нәтижесі деп қарастырумен шешілмейді. Сондықтан оны шешу үшін жиын мен оқиғаны ұштастырады, яғни тәжірибе нәтижелерінен құрылған әрбір жиынды оқиға ретінде қарастырады. Осылай қарастыру нәтижесінде ғана қойылған мақсат шешілетін болып отыр. Сондықтан, іздестіріліп отырған моделімізге жоғарыда келтірілген оқиғалар тобына , оларға қолданылатын бірігі, қиылысу, толықтыру және басқа амалдармен бұлардың қасиеттеріне(заңдарына) құрылған модельді алуға болатынын көреміз. Бұл моделді оқиғалар алгебрасы(өрісі) деп айтамыз.
Мысал-1. Кластан шақырылған кез келген
бір студенттің белгілі бір пәннен алған бағасы жақсы болуы А
оқиғасы, орташа болуы В оқиғасы, нашар болуы С оқиғасы болсын.
АUВ,  ,
,
 , АВ, А∩СU
В,
, АВ, А∩СU
В,  ,
,
 оқиғаларын сипаттап
беріңдер.
оқиғаларын сипаттап
беріңдер.
Шешуі. АU В оқиғасы А не В
оқиғаларының кемінде біреуінің пайда болатынын көрсетеді. Сондықтан
АU В оқиғасы деп студенттің жақсы немесе орташа оқитынын түсінеміз.
Ал,  оқиғасы АU В оқиғасына
қарама-қарсы оқиға, ол-студенттің нашар оқитынын көрсететін С
оқиғасы , яғни
оқиғасы АU В оқиғасына
қарама-қарсы оқиға, ол-студенттің нашар оқитынын көрсететін С
оқиғасы , яғни  = С. Осы
секілді
= С. Осы
секілді  = В болады. А∩В оқиғасы
- мүмкін емес оқиғас, себебі студенттің алған бағасы біруақытта
жақсыда, орташада болуы мүмкін емес. Сол секілді А∩С да мүмкін емес
оқиға. Ал, А∩СUВ =В болатынын байқау қиын емес. А оқиғасына қарама
–қарсы оқиға
= В болады. А∩В оқиғасы
- мүмкін емес оқиғас, себебі студенттің алған бағасы біруақытта
жақсыда, орташада болуы мүмкін емес. Сол секілді А∩С да мүмкін емес
оқиға. Ал, А∩СUВ =В болатынын байқау қиын емес. А оқиғасына қарама
–қарсы оқиға  студенттің орташа (В) не
нашар (С) оқуын сипаттайды, демек, А=ВU С. Ал
студенттің орташа (В) не
нашар (С) оқуын сипаттайды, демек, А=ВU С. Ал
 =
=  және
және  =А
болатынынан
=А
болатынынан  =А екендігі түсінікті.
Сол секілді
=А екендігі түсінікті.
Сол секілді  = В болатынын көрсету
қиын емес.
= В болатынын көрсету
қиын емес.
Мысал-2: Теңгені 1 рет тастағанда «герб» түсуі «сан» түсуіне мүмкіндік бермейді. Сондықтан «герб» түсті және «сан» түсті деген оқиғалар өзара үйлесімсіз.
Сынау жүргізгенде пайда болған оқиға ақиқат оқиға болса, онда ол жалғыз мүмкіндікті оқиға деп аталады.
Сынау нәтижесінде бірнеше оқиғалар пайда болуы мүмкін болса және олардың біреуінің пайда болу мүмкіндігі екіншісіне қарағанда артықшылығы болмаса мұндай оқиғалар тең мүмкіндікті оқиғалар деп аталады.
Мысал-3: Біртекті материалдардан жасалған симметриялы кубтың әрбір жағын 1-ден 6-ға дейінгі санлармен нөмірлейік. Оны бір рет лақтырғанда 6 жағының біреуі жоғары қарап түседі; қай жағы түссе де оқиға болады.
А1 – Бірінші нөмірлі жағы түсетін оқиға;
А2 – Екінші нөмірлі жағы түсетін оқиға;
А - жұп нөмірлі цифр жағы түсетін оқиға;
В - үш санына еселі цифр жағы түсетін оқиға;
U – 1 – 6 сандар түсетін оқиға;
V - бірінші және екінші нөмір қатар түсетін оқиға;
А1, А2 – үйлесімсіз оқиғалар;
А, В – үйлесімді оқиғалар ( Мысалы: 6 нөмірі түседі.);
 1
- бірінші нөмірі түспейтін
оқиға;
1
- бірінші нөмірі түспейтін
оқиға;
Ықтималдықтардың анықтамалары
1. Ықтималдықтардың классикалық анықтамасы .
2. Ықтималдықтардың геометриялық анықтамасы .
3. Статистикалық заңдылық және ықтималдықтың
жиіліктік анықтамасы.
-----------------------------------------------------------------------------
Ықтималдықтардың негізгі анықтамалары.
1. Ықтималдықтың классикалық анықтамасы
Ықтималдықтың классикалық анықтамасын алғаш рет берген Лаплас (1749-1827) еді. Ықтималдықтың бұл анықтамасы тең мүмкінліктің саны шекті элементар оқиғалар кеңістігінде қарастырылады және өте қарапайым.
«Тең мүмкіндік» немесе «тең
ықтималдық» ұғымдары алғашқы ұғымдарға жатады, олар формальды
анықтама беруді қажет етпейді. Жалпы сынау нәтижесінде бірнеше
элементар оқиғалар (нәтижелер, жағдайлар) пайда болуы мүмкін болса
және олардың біреуінің пайда болу мүмкіндігінің екіншісіне
қарағанда артықшылығы бар деп айта алмайтын болсақ, басқаша
айтқанда, сынау нәтижесінің симметриялы қасиеті болса, мұндай
элементар оқиғалар тең мүмкіндікті делінеді. Бұған 1-бөлімде
келтірілген 2-мысал айғақ. Өйткені кубтың әрбір жағының пайда болу
мүмкіндігі бірдей. Сондықтан бұлар тең мүмкіндікті (яғни тең
ықтималдықты) элементар оқиғалар болады.
е1,
е2,...,
еn
элементар оқиғалары тең
мүмкіндікті, қос-қостан үйлесімсіз және оқиғалардың толық тобын
(системасын) құраса, онда ол оқиғаларды сынаудың мүмкін (мүмкін
болатын) нәтижелерінің толық тобы немесе элементар оқиғалар
кеңістігі деп айтатынын көрдік, Сонда
{ }=
{e1,e2,…,en} кеңістігіндегі элементар
оқиғалардың жалпы санын n{
}=
{e1,e2,…,en} кеңістігіндегі элементар
оқиғалардың жалпы санын n{ } арқылы белгілесек,
әрбір элементар оқиғаның шығу мүмкіндігінің мөлшері, ықтималдығы, P
=
} арқылы белгілесек,
әрбір элементар оқиғаның шығу мүмкіндігінің мөлшері, ықтималдығы, P
= . Ал тең мүмкіндікті,
үйлесімсіз және оқиғалардың толық тобын құрайтын
e1,e2,…,en
элементар оқиғалардың біреуі
не бірнешеуі бір А оқиғасының пайда болуын тудыруы мүмкін, яғни
екінші сөзбен айтқанда, А оқиғасы тең мүмкіндікті бірнеше элементар
оқиғаларға бөлінеді және олардың кез келген біреуінің пайда
болуынан А оқиғасының пайда болуы шығатын болады. Мысалы, кубты бір
рет лақтырғанда оның кез келген тақ нөмірі
е1,е3,е5
пайда болуынан А оқиғасы пайда
болсын. Былайша айтқанда, А оқиғасы тақ нөмірлі
e1,e3,e5
үш оқиғаға бөлініп отыр. Бұл
тақ нөмірлі элементар оқиғаларды осы А оқиғасының пайда болуына
қолайлы оқиғалар дейміз. Бұлардың санын
m{
. Ал тең мүмкіндікті,
үйлесімсіз және оқиғалардың толық тобын құрайтын
e1,e2,…,en
элементар оқиғалардың біреуі
не бірнешеуі бір А оқиғасының пайда болуын тудыруы мүмкін, яғни
екінші сөзбен айтқанда, А оқиғасы тең мүмкіндікті бірнеше элементар
оқиғаларға бөлінеді және олардың кез келген біреуінің пайда
болуынан А оқиғасының пайда болуы шығатын болады. Мысалы, кубты бір
рет лақтырғанда оның кез келген тақ нөмірі
е1,е3,е5
пайда болуынан А оқиғасы пайда
болсын. Былайша айтқанда, А оқиғасы тақ нөмірлі
e1,e3,e5
үш оқиғаға бөлініп отыр. Бұл
тақ нөмірлі элементар оқиғаларды осы А оқиғасының пайда болуына
қолайлы оқиғалар дейміз. Бұлардың санын
m{ } арқылы белгілейміз
(m{
} арқылы белгілейміз
(m{ }=3).
}=3).
Анықтама. А оқиғасына қолайлы элементар
оқиғалар санының (m{ }) сынаудың тең
мүмкіндікті барлық элементар оқиғалары санына
(n{
}) сынаудың тең
мүмкіндікті барлық элементар оқиғалары санына
(n{ }) қатынасын А
оқиғасының ықтималдығы деп айтамыз және былай
жазамыз:
}) қатынасын А
оқиғасының ықтималдығы деп айтамыз және былай
жазамыз:
Р(А) =
 .
.
Бұдан былай
m=m{ },
n=n{
},
n=n{ } деп белгілеу
еңгіземіз, сонда
} деп белгілеу
еңгіземіз, сонда
Р(А) =
 .
.
Ықтималдықтың бұл анықтамасын классикалық анықтама немесе Лаплас моделі дейміз. Бұл айтылғандардан Лаплас моделі нәтижесі тең мүмкіндікті тәжірибелерді сипаттайды деп ұғамыз.
Енді Р(А) ықтималдығының қасиеттерін қарастырайық.
1о Р(А) ықтималдығы теріс емес функция, яғни Р(А) ³ 0.
2о
Р(А) ықтималдығы нормалданған
функция, яғни Р{ }=1.
}=1.
3о Қиылыспайтын (үйлесімсіз) А және В оқиғалары үшін Р(А+В) ықтималдығы аддитивті функция, яғни Р(А+В)=Р(А) +Р(В).
Бұл үшінші қасиетті ықтималдықтарды қосу теоремасы немесе ықтималдықтарды қосу заңы деп те атайды.
1-ші және 2-ші қасиеттер айқын көрініп тұр. Өйткені m ³ 0 және n > 0, m£n. Мұнан m>0 болса, Р(А) > 0, m=0 болса, Р(А)=Р(V)=0 (яғни мүмкін емес оқиға ықтималдығы). m=n болса, Р(А)=Р(U)=1 (яғни оқиқат оқиға ықтималдығы). Бұл екі қасиеттен 0 £ Р(А) £ 1 болатыны айқын көрініп тұр, яғни ықтималдық мәні 0 мен 1 арасындағы оң таңбалы сан екен.
Келтірілген қасиеттерден мүмкін емес (ақиқат) оқиға ықтималдығы нөлге (бірге) тең болуын көрдік. Бұл анықтама үшін осы сөйлемнің керісі де орын алады, яғни оқиға ықтималдығы нөлге (бірге) тең болса, ондай оқиғаның пайда болуы мүмкін емес (ақиқат). Ал ықтималдықтың басқа анықтамалары үшін бұл кері сөйлемнің орын алмауын байқаймыз (оны кейінгі бөлімдерде қарастырамыз). Ықтималдықтың классикалық анықтамасының бұл кемістігі сол бөлімде жетілтіріледі.
Ықтималдықтың классикалық анықтамасы өз уақытында ықтималдықтар теориясын құруға негіз болады. Біз мұны кездейсоқ оқиғалар заңдылығын математикалық абстракциялаудың алғашқы қарапайым сатысы – моделі дейміз. Ықтималдықтарды есептеу сынаудың жалпы саны мен оқиғаның пайда болуына қолайлы нәтижелер санын анықтауға тіреледі, бұл көп жағдайда үлкен қиындыққа ұшыратады. Оның үстіне, практикады кездесетін оқиғалар күрделі болып келеді де, олардың ықтималдығын табу үшін, ол оқиғаларды бірнеше қарапайым оқиғалардың қосындысы не көбейтіндісі түрінде жазып, солардың ықтималдықтары арқылы күрделі оқиға ықтималдығын анықтайды. Сондықтан да қарастырылып отырған оқиға ықтималдыңын екінші ықтималдық арқылы табудың маңызы өте-мөте зор. Ол үшін негізінен ықтималдықтарды қосу және көбейту теоремаларын пайдаланады.
Енді ықтималдықтың классикалық анықтамасын пайдалана отырып, оларды тікелей есептеуге бірнеше мысалдар келтірейік. Сонымен қатар тарихи мәні бар кейбір мысалдарды қарастырып, ықтималдықтар теориясының бірден қалыптаса қоймағанына көз жеткізейік.
Мысал-1. Жәшікте 10 шар бар. олардың 4-уі ақ 6-уы қызыл шар. Жәшіктегі шарларды араластырып жіберіп, қарамай тұрып, бір шарды алайық (сынау жүргізу). Алынған шар ақ шар болып шығуының (А оқиғасы) сандық мөлшерін (ықтималдығын) анықтау керек.
Шешуі. Әрбір шардың пайда болу
мүмкіндігі бірдей, яғни булар тең мүмкіндікті элементар оқиғалар.
Қалаған бір элементар оқиғаның шығу мүмкіндігінің сандық мөлшері
(ықтималдығы)  - ге тең:
n{
- ге тең:
n{ }=10. Барлық тең
мүмкіндікті 10 элементар оқиғалардың тек 4-уі ғана А оқиғасының
пайда болуына қолайлы элементар оқиғалар. Бұлардың санын (олар 4)
барлық элементар оқиғалар санына (олар 10) қатынасы
(
}=10. Барлық тең
мүмкіндікті 10 элементар оқиғалардың тек 4-уі ғана А оқиғасының
пайда болуына қолайлы элементар оқиғалар. Бұлардың санын (олар 4)
барлық элементар оқиғалар санына (олар 10) қатынасы
( ) осы оқиғаның пайда
болуының мүмкіндік дәрежесін көрсетеді. Мұны А оқиғасының пайда
болу ықтималдығы деп қабылдаймыз да Р(А) арқылы белгілейміз. Сонда
Р(А)=
) осы оқиғаның пайда
болуының мүмкіндік дәрежесін көрсетеді. Мұны А оқиғасының пайда
болу ықтималдығы деп қабылдаймыз да Р(А) арқылы белгілейміз. Сонда
Р(А)= .
.
Мысал-2. Ойын сүйегін лақтырғанда жұп сан шығуының ықтималдығы қандай?
Шешуі: Ойын сүйегі жалпы алты беттен, яғни 1 2 3 4 5 6 цифрларынан тұрады. Сонда n=6 және осы цифрлардағы жұп сандар саны үшеу, онда т=3. Сонымен ізделінді ықтималдық:
Р(А)=
Мысал-3. Жәшікте бірдей 20 шар бар. Оның 6-уы ақ шар, 4-уі көк шар, 10-ны қызыл шар. Жәшіктен кез келген бір шар алынады. Алынған шар: а)ақ шар (А оқиғасы); ә) қызыл шар (В оқиғасы); б) көк шар (С оқиғасы) болу ықтималдығын анықтау керек.
Шешуі: а) Шарлардың үлкендігі және салмағы бірдей болғандықтан, олардың шығу мүмкіндіктері де бірдей. Элементар оқиғалар саны n=20. А оқиғасына (ақ шардың шығуы) қолайлы элементар оқиғалар саны m=6. Демек,оның ықтималдығы
Р(А) =
 =
=  =0,3
=0,3
болады. Қалғандарын да осылай анықтау қиын емес, сонда: ә)0,5; б) 0,2.
Мысал-4. Теңге екі рет лақтырылды. Кем дегенде бір рет герб жағының шығу ықтималдығын анықтау керек.
Шешуі. Есептің дұрыс шешілуі (әсіресе, ықтималдыққа тиісті есептерді) есеп шартын талқылауға байланысты, бұл фактіні осы есептің шешуін талқылау арқылы көрсетейік.
Бірінші тәсіл (Даламбер талқылауы). Герб жағымен не бірінші, не екінші лақтырғанда түседі де тіпті түспейді. Сонымен, барлық элементар оқиғалар саны үшеу. Олардың ішінде А оқиғасының пайда болуына қолайлысы – екеу. Демек, іздеген ықтималдық Р(А)=2/3.
Екінші жолы: бірінші монетаны
бір рет лақтырғанда не герб жағынан, не тиын жағынан түсуі мүмкін.
Қай жағынан түссе де, бұл екінші рет лақтырғандағы монетаның герб
(Г) не тиын (Т) жағының түсуімен комбинациялынып келеді. Ақырында,
төмендегі тең мүмкіндікті тең 4 жағдай болады.
Олар  .
Мұнда Г-герб, Т-тиын. Есептің
шартына қолайлы элементар оқиғалар саны 3. Олай болса
ықтималдығы
.
Мұнда Г-герб, Т-тиын. Есептің
шартына қолайлы элементар оқиғалар саны 3. Олай болса
ықтималдығы
Р(А)
= =
0,75 не
75%.
=
0,75 не
75%.
Сонымен табылған екі ықтималдықтың қайсысы дұрыс. Соны анықтайық. Даламбердің қателігі мынада болған: ГТ және ТГ оқиғаларын бір оқиға деп алған. Шындығында бұлай болмайтыны екінші талқылаудан байқалады. Сонымен, екінші шешудің дұрыстығын байқаймыз.
Ықтималдықтарды есептеуде комбинаторика формуласын пайдаланудың қажеттігі туып отыр. Сондықтан комбинаторика ұғымын төменде келтіріп, оның формулаларын ықтималдықтарды есептеуге пайдалануды сол бөлімде толық қарастырамыз.
2. Ықтималдықтың геометриялық анықтамасы.
Алдындағы бөлімде қарастырылған тәжірибе нәтижелері шекті саналымды болып келді, практикада кездесетін есептердің басым көпшілігі бұл тәсілге келе бермейді. Себебі, тәжірибе нәтижелері саналымды шексіз, я саналымсыз жиын болуы мүмкін. Сондықтан ықтималдықтың классикалық анықтамасын сынау нәтижесінің саны шексіз тең мүмкіндікті тәжірибеге қолдануға болмайды. Осындай жағдайды сипаттауға ықтималдықтың геометриялық анықтамасы ыңғайлы. Оның үшін біз G жиында нүкте бірқалыпты деп ұйғарамыз, ал оның қандайда бір ішкі жиынын «g» ретінде белгілейміз (2-сызба).
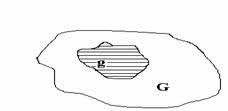
2-сызба
Ол уақытта G облысына лақтырылған нүктенің «g» облысына түсуін А оқиғасы деп белгілеп, оның ықтималдығына мынадай анықтама береміз.
Анықтама. G облысына кездейсоқ лақтырылған нүктенің оның g бөлігіне түсу ықтималдығы деп g өлшемінің G облыс өлшеміне қатынасына тең (ұзындық, аудан, көлем) болған шаманы айтамыз, яғни
Р(А) =
 .
.
Мұнда да ықтималдықтың классикалық анықтамасында көрсетілген үш қасиет орындалады:
1о . Р(g) ықтималдығы теріс емес функция, яғни Р(g) ³ 0.
2о
. Р(G) ықтималдығы нормалданған
функция, яғни Р( G)
=1.
G)
=1.
3о . Қиылыспайтын (үйлесімсіз) А және В оқиғалары үшін Р(А+В) ықтималдығы аддитивті функция, яғни Р(А+В)=Р(А) +Р(В).
Бұл соңғы қасиет үйлесімсіз оқиғалар саны шекті және саналымды шексіз болсада орын алады дейміз.
Геометриялық ықтималдықтар тәсілі биология, атомдық физика, астрономия және т.с.с. басқа салаларда да көптеген қолданыс тауып отыр. Айтып өтетін жайт-кез-келген құбылысты сипаттауға классикалықта, геометриялық тәсілді алуға болады. Бірақ геометриялық тәсілде алынған математикалық модель классикалық тәсілге қарағанда айқын емес. Бірақта бір реал құбылысты сипаттайтын әр түрлі модельге сәйкес түрлі ықтимал-дықтарды алуға болады.
Мысал-1. Қабырғалары а = 4 ке тең болған квадрат ішіне жанамалап шеңгбер сызылған(3- сызба). Квадрат ішіне кездейсоқ лақтырылған нүктенің шеңбер ішіне түсу(А оқиғасы) ықтималдығы неге тең ?
Шешуі: Жалпы квадрат ауданын G
десек, онда G= a2
= 16 болады. Ал, сызбадан
шеңбер радиусының R=2 ге тең екендігін оңай табамыз. Сонда шеңбер
ауданын g деп белгілесек, онда оның ауданы g =
pR2=
4p
болады. Анықтама бойынша
ізделінген ықтималдық Р(А) =  =
=
 .
.

![]()
![]()
![]()
д а=4
![]()
3-сызба
Егер мәселеде Ω элементар оқиғалар кеңістігі шексіз санамалы емес жиын болса, ал ωі элементар оқиғалар тең мүмкіндікті болса, онда бұл есепте ықтималдықтың геометриялық анықтамасын қолдануға болады деп есептейміз. Геометриялық тұрғыдан есеп шартын қарамастан нүктені белгілі бір G геометриялық облысқа лақтыру (кесінді, жазықтықтың немесе кеңістіктің бөлігі) шартына келтіру. Нүкте қарамастан лақтырылғандықтан, онда G облысының g кез келген щектеулі бөлігіне түсу мүмкіндіктері тең. Сондықтан нүктенің g (g Ì G) облысына түсу ықтималдығы g өлшеміне (ұзындық, аудан немесе көлем) пропорционал және g-ның пішіні мен орналасуына тәуелді емес.
Егер оқиғаны А нүктенің g (g Ì G) облысына түсуі десек. Онда бұл оқиғаның ықтималдығы осы нүкте пайда болатын g облыс өлшемінің барлық G өлшеміне қатынасына тең: Р(А)=Lg/LG немесе Р(А)=Sg/SG немесе Р(А)=Vg/VG , мұндағы L, S, V – сәйкес облыстың ұзындығы, ауданы немесе көлемі.
Мысал-2. – Радиусы R дөңгелек диск екі секторға бөлінген. Біреуінің доға ұзындығы R. Тез айналып жатқан дискіге оқ атылды. Оның доға ұзындығы R секторға түсу ықтималдығын табу қажет .
Шешуі.
A оқиғасы–доға
ұзындығы R секторға түсуі. P(A)=  .
.
S(сектор)=
 ·R·l формуласы бойынша S(сектор) =
·R·l формуласы бойынша S(сектор) =
 ·R·R = R2/2
,
·R·R = R2/2
,
S(дөңгелек) =
π·R2 .
Сондықтан
Р(А) =  = R2/(2πR2) =
= R2/(2πR2) =
 .
.
Мысал-3. Жауын тамшысы, ұзындығы 100 метр болатын түзу жүгіру жолына тамады. А оқиғасын «Тамшы старт сызығынан а метрден артық емес қашықтыққа тамады» деп анықтаймыз. А оқиғасының Р(А) ықтимал-дығы қандай? Мұнда жолдан тыс жерге таматын тамшылар қарастырыл-майды.
Шешуі. 50 метр жолға таматын
тамшылар 100 метр жолға таматын тамшылардан 2 есе аз екендігін
түсіну қиын емес. Сондықтан, мысалы, a=50 болса,
онда P(A)= =
=  . Егер a=25 болса, онда ұзындығы 25 метр
жол бөлігі бүкіл жолдан 4 есе қысқа, сол
себепті P(A)=
. Егер a=25 болса, онда ұзындығы 25 метр
жол бөлігі бүкіл жолдан 4 есе қысқа, сол
себепті P(A)= =
= . Жалпы алғанда ұзындығы а метр
жолға, а метр 100–ден неше есе
кіші болса, сонша есе аз тамшылар тамады.
Яғни P(A) =
. Жалпы алғанда ұзындығы а метр
жолға, а метр 100–ден неше есе
кіші болса, сонша есе аз тамшылар тамады.
Яғни P(A) =  .
.
Мысал-4. (Кездесу туралы мәселе).
Екі студент (А мен В) сағат 10 мен 11 аралығында кездесуге уәделескен. Қайсысы бұрын келсе, сонысы 20 минут күтеді, сол мезгілде екіншісі келмесе қайтып кетеді, яғни кездесу болмайды. Егер әрқайсысының сол уәделескен уақытта келуі бір-біріне тәуелсіз және кездесуі кездейсоқ болса, онда екі студенттің кездесу ықтималдығы неге тең ?
Шешуі. А ның уәделі жерге келу уақытын х, В-ның келуін у арқылы белгілейміз. Уақыт өлшемін минут деп қабылдасақ , онда тек | х –у | £ 20 мин. болғандағана кездеседі. Бұл жағдайда барлық нәтижелер жиыны мына теңсіздіктермен анықталады: 18(сағ)£ х £ 19(сағ) және 18(сағ) £ у £ 19(сағ).
Кездесуге қолайлы нәтижелер жиыны мына теңсіздікпен берілген:
| х –у | £ 20 немесе х -20 £ у £ х +20. Олар осы қолайлы нәтижелер сызылған жолақта орналасқан( 4 - сызба).

![]() у y=x+20
у y=x+20
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()

![]() y=x-20
y=x-20

![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 40
40
![]()
![]()
![]()
![]()
![]() g
g
![]()
![]()
![]() 20 G
20 G
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 20
40 60
20
40 60
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0
60 х
0
60 х
4-сызба
Бұл
сызбада Р(A1) +
P(A2) + …+
P(A ) + …=1. Ал, сол екі студент
уаделі жерде [0,t] аралығында
) + …=1. Ал, сол екі студент
уаделі жерде [0,t] аралығында  - уақытта кездесетін болса,
онда
- уақытта кездесетін болса,
онда
P(A) =
(t2-(t- )2)/t2
= 1-(1-
)2)/t2
= 1-(1-
 /t)2
/t)2
болады.
Дербес жағдайда t =
1,  = 1/3 болса, онда P(A) =
1-(2/3)2
=
5/9.
= 1/3 болса, онда P(A) =
1-(2/3)2
=
5/9.
3. Статистикалық заңдылық және ықтималдықтың жиіліктік анықтамасы
Ықтималдықтың классикалық анықтамасы сынау нәтижесі шектеулі сан рет және тең мүмкіндікті болатынына негізделеді. Сондықтан бұл анықтаманың қолданылу өрісі тар. Осы себепті ықтималдықтың жай есептерінен күрделі есептерін шешуге көшкенде, әсіресе, статистикалық құбылыстарды сипаттауға байланысты практикада қолданылатын мәселелерді шешкенде шамадан тыс көптеген қиыншылықтарды кездестіреміз. Өйткені, біріншіден, сынаудың мүмкін нәтижелері шектеулі шама болмауы мүмкін. Мысалы, қандай да бір тілдегі бір сөздің пайда болу ықтималдығын тапқанда, біз практика тұрғысынан шектеусіз жиынды кездестіреміз. Екіншіден, жүргізілген тәжірибе нәтижесін ылғи да тең ықтималды болады деу аса үлкен қиындық туғызады. Мысалы, ұл бала не қыз бала туу ықтималдығын анықтағанда симметрия және тең ықтималдыққа сүйеніп қорытынды жасауға болмайтынын биологиялық статистика дәлелдейді.
Құбылыстарды сипаттауға ықтималдықтың статистикалық анықтамасын қолданайық. Статистикалық анықтама тәжірибені сан рет қайталап, нәтижелердің тізбесін жасауға суйенеді. Тәжірибе көп жүргізілгенде оқиғаның бірнеше рет пайда болуы не пайда болмауы мүмкін. Оқиғаның пайда болу не пайда болмау санын бұдан былай жиілік немесе абсалюттік жиілік деп айтамыз. Ал жиіліктің барлық сынау санына қатынасын салыстырмалы жиілік деп айтуға келісеміз. Сонда сынаудың жалпы санын n десек және оқиғаның қайыра пайда болу санын (жиілігін) m дейміз. Сонда А оқиғасының салыстырмалы жиілігі мынадай есептелінеді:
f(А) =  . Жүргізілген сынау саны аз болса , жиілік тұрақты болмай
бір сынаудан екінші сынауға дейінгі өзгеріс артып отырады. Ал сынау
жеткілікті дәрежеде қайталанып отырса, онда А оқиғасының
салыстырмалы жиілігі тұрақтана түседі. Мұндай жағдайлар физика,
биология, экономика, техникалық бақылауларда және т.с.с. салаларда
көп байқалады. Мысал үшін метал теңгені бір рет тастағанда оның
герб жағымен түсу ықтималдығы ықтималдықтың классикалық анықтамасы
бойынша 0.5 екендігін білеміз. Бырақта бұл сынауды 2, 5, 10 және
оданда көп рет қайталасақ ықтималдық олар үшін барлық уақыт 0.5 ке
тең болмастығы айқын. Сондықтан жоғарыда айтылған жиілік заңдылығын
сынау өте көп жүргізілгенде анықтау үшін танымал математиктер
Бюффон және К.Пирсондардың метал теңгенің герб жағымен түсу
тәжірибесін жүргізген тәжірибе қорытындыларын кестеде(1-кесте)
келтіреміз:
. Жүргізілген сынау саны аз болса , жиілік тұрақты болмай
бір сынаудан екінші сынауға дейінгі өзгеріс артып отырады. Ал сынау
жеткілікті дәрежеде қайталанып отырса, онда А оқиғасының
салыстырмалы жиілігі тұрақтана түседі. Мұндай жағдайлар физика,
биология, экономика, техникалық бақылауларда және т.с.с. салаларда
көп байқалады. Мысал үшін метал теңгені бір рет тастағанда оның
герб жағымен түсу ықтималдығы ықтималдықтың классикалық анықтамасы
бойынша 0.5 екендігін білеміз. Бырақта бұл сынауды 2, 5, 10 және
оданда көп рет қайталасақ ықтималдық олар үшін барлық уақыт 0.5 ке
тең болмастығы айқын. Сондықтан жоғарыда айтылған жиілік заңдылығын
сынау өте көп жүргізілгенде анықтау үшін танымал математиктер
Бюффон және К.Пирсондардың метал теңгенің герб жағымен түсу
тәжірибесін жүргізген тәжірибе қорытындыларын кестеде(1-кесте)
келтіреміз:
1-кесте
|
Тәжірібе жүргізгендер |
Тәжірибе саны |
Герб жағымен түсу саны |
Салыстырмалы жиілігі |
|
Бюффон |
4040 |
2048 |
0.5080 |
|
Г.Пирсон |
12000 |
6019 |
0.5018 |
|
Г.Пирсон |
24000 |
12012 |
0.005 |
Мысал-1. 1935 жылы Швецияда туған ұл баланың статистикалық мәліметтері алынды (2-кесте). Мұнда ұл баланың туу жиілігі 0,518 санына жуық өзгеріп (тұрақсызданып) отырған. Осы сияқты бақылау 1871 жылдан 1900 жылға дейінгі аралықта жүргізілген. Бұл жылдары 2,5 миллионнан астам туған балалардың жынысын есепке алғанда, ұл бала тууының салыстырмалы жиілігі 0,514 болған.
|
Айы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-кесте
Бұл келтірілген мысалдардан сынау саны мейлінше көп болғанда салыс-тырмалы жиілік мәні тұрақтылық қалыпқа түсетінін байқаймыз. Біздің жоғарыдағы кестеміз бойынша салыстырмалы жиілік 0.5 ке жуықтайды. Сонымен, тәжірибелерде сынау саны мейлінше көп болса, салыстырмалы жиілік ƒ мәні тұрақтылық қалыпқа түсетінін байқаймыз. Екінші сөзбен айтқанда, кездейсоқ құбылыстарда қандай да объективті қасиеттер бар екендігі және оның тұрақтануға бейімділігі сезіледі.
Бұл қасиет сынау саны артқан сайын айқындала түседі, ал ол қасиет қандайда бір шамамен өлшенеді. Бұл шама бақылауға түскен құбылыстың объективті сандық сипаты болып табылады. Осы тұрақтыны(санды) А кездейсоқ оқиғаның ықтималдығы деп айтамыз. Ал оныда жоғарыдағыдай Р(А) арқылы белгілейміз. Осындай тәсілмен анықталған кездейсоқ оқиға ықтималдығын статистикалық ықтималдық деп айтамыз. Сонымен, ықтималдықтың статистикалық анықтамасын да Р(А) @ f(A) ретінде қабылдаймыз.
Ықтималдықтың жоғарыда келтірілген қасиеттері статистикалық тұрғыдан анықтағандада орындалады:
1°. Салыстырмалы жиілік m/n теріс таңбалы болуы мүмкін емес, себебі
m ³ 0, n ³ 0 демек Р(А) ³ 0.
2°. Ақиқат оқиға сынауда әрбір қайталауда пайда болады, сондықтан
m= n, демек Р(А) = 1.
3°. А және В оқиғалары үйлесімсіз болса, бұлардың қосындысының ықтималдығы олардың ықтималдықтарының қосындысына тең, яғни n –жалпы саны, m1 – А оқиғасының пайда болу жиілігі, m2- В оқиғасының пайда болу жиілігі болса, онда мынадай теңдік орындалады:
Р(А+В) = m1/n + m2/n = Р(А) + Р(В) .
Мысал-2. Сапасын тексеру үшін кездейсоқ алынған 100 детальдың 5-еуі жарамсыз болып шықты. Жарамсыз детель шығуының салыстырмалы жиілігін табыңдар.
Шешуі. Мұнда , тексеру(сынау) өткізілетін барлық детальдар саны
n = 100, ал жарамсыз детальдар саны m = 5, сондықтан салыстырмалы жиілік формуласын қолдансақ төмендегі оған сәйкес шаманы табамыз:
f (А) =
 =
=  = 0.05
.
= 0.05
.
Ал, бұл шаманы жоғарыда айтылған анықтама бойынша статистикалық ықтималдық деп айтамыз.
Енді статистикалық ықтималдықтарды өте маңызды сипаттайтын устазымыз Қ.Бектаев [ 1 ] қарастырған мысалды келтирейік.
Мысал-3. 10 жастағы 100 000 бала бақылауға алынып, олардың қаншасы 20 жасқа дейін, қаншасы 30 жасқа дейін т.т. қаншасы 100 жасқа дейін өмір сүргенін есептеп нәтижесін төмендегі кесте (3-кесте)түрінде келтірілген.
3-кесте
|
Адамның жасы |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
|
Өмір сүрген |
100000 |
96061 |
89685 |
82277 |
72785 |
58842 |
37977 |
13987 |
1273 |
Осы кестеде келтірілген мәліметтерді пайдаланып :
а) а ( а=20) жастағы адамның b( b=50, b=70, b=90 ) жасқа дейін өмір сүру ықтималдығын анықтау керек;
ә) a = 20 жастағы адамның b( b=30, b=50, b=70, b=90 ) жасқа жетпей дүние салу ықтималдығын анықтау керек;
б) куйеуі а( а=30 ) жаста , әйелі b( b=20) жаста . Екеуі бірге c( c=20, c=40,c=50) жыл өмір сүру ықтималдығын анықтау керек;
в) куйеуі а( а=23 ) , әйелі b( b=18) жаста, олар бірге c( c=45) жыл өмір сүру ықтималдығын анықтау керек;
г) куйеуі а( а=50 ) , әйелі b( b=45) жаста, ұлы c( c=25) жаста, үшеуінің бірге d( d=20,d=30,d=40) жыл өмір сүру ықтималдығын анықтау керек;
д) куйеуі а( а=40 ) , әйелі b( b=35) жаста, екеуі бірге c( c=70, c=80) жасқа дейін өмір сүре алмау ықтималдығын есептеу керек;
е) куйеуі а( а=40 ) жаста , әйелі b( b=30)жаста, c( c=30, c=40) жылдан соң кемінде біреуі өлмей қалу ықтималдығын анықтау керек.
Шешуі. Жақша ішіндегі мәліметтердің біреуі үшін ғана есепті шығарамыз, қалғандарын оқушыларға жүктейміз. Тексеру жеңіл болу үшін олардың жауабын келтіріп , тиісті талдауларды пайдаланамыз.
а) Кестеге қарағанда, адамның
жасы ұлғайған сайын олардың саны азайып барады, бұл заңды, әрі
түсінікті де. а
жастағы
адамның b
жасқа дейін өмір сүруін А
оқиғасы дейік, бұлардың саны m(b) болсын,
а
жастағы адамдар саны
n(a) дейік. Сонда А оқиғасының
ықтималдығы P(A) =  ,
,
ал, кесте бойынша a= 20 болғанда n(a) = 96061, b = 50 болғанда
m(b) =72795. Сонда Р(А)
=  =
0.758.
=
0.758.
Сонымен, 20 жастағы адамдардың орта есеппен 75.8 % -і 50 жасқа дейін, 39.5% - і 70 жасқа дейін, 1.3 %-і 90 жасқа дейін өмір сүреді екен. Егер b=a болғанда Р(А) =1 болатын еді, бұл факт адамның b жасқа дейін өмір сүреті-нінің ақиқаттығын көрсетеді.
ә) Белгілі бір жасқа дейін
өмір сүруді А оқиғасы десек, онда оның осы жасқа дейін өмір
сүрмеуі  оқиғасы
болады. а
= 20,
b
= 50 десек,
онда
оқиғасы
болады. а
= 20,
b
= 50 десек,
онда
Р( ) = 1 – P (A) =1
–
) = 1 – P (A) =1
–  =
=
 =
=  =
=
 =
02427.
=
02427.
Сонда 20 жастағы адамдардың орта есеппен 24.2 % - і 50 жасқа жетпей дүние салатынын байқаймыз. Ал, осы 20 жастағы адамдардың 30 жасқа жетпей 6.6 % -і, 70 жасқа жетпей 61.5 % - і дүние салатынын оп –оңай есептеуге болады.
б) Куйеуінің а жастан а + с жасқа дейін өмір сүруін А оқиғасы, ал әйелінің b жастан b + c жасқа дейін өмір сүруін В оқиғасы дейік. Сонда екеуінің бірге өмір сүруі күрделі оқиға АВ болады. Бұлар бір-біріне тәуелсіз оқиғалар, сондықтан :
Р(АВ) = P(A) P(B)
=  ·
·
 =
=  ·
·
 =
=
=
 ·
·  =
=

 =
0.695
.
=
0.695
.
Сонымен, екеуінің бірге өмір сүру ықтималдығы 0.695 ке тең, яғни осы көрсетілген жаста ерлі-зайыптылардың 69.5 % ті тағыда 20 жыл бірге өмір сүреді екен. Әрине, бұлардың жастары артқан сайын бірге өмір сүрушілер саны кеми түседі. Екеуі қосылғаннан бастап 40 жыл өмір сүру ықтималдығы 26 % , ал 50 жыл өмір сүру ықтималдығы 6.2 % болатынын анықтаңыздар.
в) Бұл мәселе де дәл б) пунктіндегі мәселе секілді шешіледі. Бірақ б) пункт-інде келтірілген жасқа сәйкес жиіліктер шамасы кестеде жоқ. Сондықтан интерполяциялау тәсілін қолданамыз. Оның үшін кестеде келтірілген он жыл ішіндегі әрбір жылдағы өлім санын бірдей деп аламыз. Сондықтан жұбайлардың бірге өмір сүру ықтималдығын анықтаудан бұрын n(20), n(18) , m(23+45)= m(68), m(18+45) = m(63) мәндері неге тең болатынын табамыз. n(23) жиілігі n(20) мен n(30) аралығында, демек мынау келіп шығады:
n(23) = n(20) –  · 3 = 96061 –
· 3 = 96061 –  · 3 = 96061 -
· 3 = 96061 -  · 3 =
· 3 =
96061 – 191278 @ 94148.
Қалғандары да осылай анықталады, сонда m(18) = 96848, m(68) = 42150, m(63) = 52582. Демек ,
Р(АВ)
=  ·
·  =
=  ·
·  = 072437.
= 072437.
г) Бұл жағдайда ұлының с жастан с+d жасқа дейін өмір сүруін С оқиғасы десек, онда мәселе А,В,С оқиғаларының бірге пайда болу ықтималдығын табуға келіп тіреледі. Демек,
Р(АВС) =
 ·
·  ·
·
 =
=  ·
·
 ·
·  =
07272.
=
07272.
Қалғандарын да осылай анықтасақ үшеуі бірге 30 жыл өмір сүру ықтималдығы 4.5 % -ке, ал бірге 40 жыл өмір сүру ықтималдығы 0.08 % - ке тең болады екен.
д) Куйеунің
өлуін  оқиғасы, әйелінің
өлуін
оқиғасы, әйелінің
өлуін  оқиғасы десек, онда
екеуінің бірге өмір сүрмеуі
оқиғасы десек, онда
екеуінің бірге өмір сүрмеуі  ·
· оқиғасы болады. Мұның
ықтималдығы мынаған тең:
оқиғасы болады. Мұның
ықтималдығы мынаған тең:
Р(
 ) =
P(
) =
P( ·P(
·P( ) = (1 – P(A))·(1-P(B))
=
) = (1 – P(A))·(1-P(B))
=  ·
·
 =
=
=
 ·
·  =
=
 ·
·  =
0.300.
=
0.300.
Ал, ерлі-зайыпты адамдар бірге 80 жасқа дейін өмір сүрмеу ықтималдығы 69.5 % болады екен.
е) Кемінде біреуінің өлмеуін А
оқиғасы дейік, онда оған қарама-қарсы оқиға
 екеуінің де өлуін
көрсетеді. Олай болса,
екеуінің де өлуін
көрсетеді. Олай болса,
Р( ) =
) =
 ·
·  =
=
 ·
·  =
=
=
 ·
·  =
0.185.
=
0.185.
Сонда ізделінген ықтималдық,
яғни 30 жылдан кейін кемінде біреуінің өмір сүру ықтималдығы Р(А) =
1- P(  ) = 1- 0.185 = 0.815.
Дәл осылай есептесек, 40 жылдан кейін кемінде біреуінің өмір сүру
ықтималдығы 48 % болатынын табу қиын
емес.
) = 1- 0.185 = 0.815.
Дәл осылай есептесек, 40 жылдан кейін кемінде біреуінің өмір сүру
ықтималдығы 48 % болатынын табу қиын
емес.
Мысал-4. Жоғарыдағы 3-кестені пайдаланып а(а =20, a=30, a=50, a=70, a=80) жастағы адамның ықтималды өмір сүруін анықтау керек. Ықтималды өмір сүру деп қазіргі жасынан бастап қайсі бір жасқа дейін өмір сүру ықтималдығы 0.5 ( бұл шама түрлі өлкелерде әр түрлі болуы мүмкін) болатын жасты түсінеміз.
Шешуі. Қайсібір жасқа дейін
өмір сүруін А оқиғасы дейік, онда сол жасқа дейін дүние
салуы  оқиғасы болады. Егер
Р(А) = 0.5 болса, онда
оқиғасы болады. Егер
Р(А) = 0.5 болса, онда
Р( ) = болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға болады.Мысалы, қаупсіздендіру
мекемелері де осыны негізге алады. Айталық, болжап отырған
жасымыз х
болсын .
Сонда
) = болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға болады.Мысалы, қаупсіздендіру
мекемелері де осыны негізге алады. Айталық, болжап отырған
жасымыз х
болсын .
Сонда
 = 0.5,
m(x)
=0.5·n(a
).
= 0.5,
m(x)
=0.5·n(a
).
Енді х- тің мәнін жоғарыдағы кестеден пайдаланып табамыз. а = 20 , m(x) = 0.5, n(20) = 48030,5 . Кестеде 48030,5 мәні жоқ, сондықтан сызықты интерполяциялауды орындаймыз. 48030,5 саны 58842 мен 37977 аралығында, демек, бұл санға сәйкес х жас 60 пен 70 аралығында болады. Дәлірек айтқанда,
х
= 60 +
 · 10 =
60+5,2 = 65,2
@
65,
· 10 =
60+5,2 = 65,2
@
65,
Осы тәсілді қолданып, жасы а = 306, а = 50, а = 70, а = 80 деп алып есептегенде, ықтималды өмір сүру жасының сәйкес 67, 77, 79, 86 сандарына тең болатынын табу қиын емес.
Мысал-5. Енді жоғарыдағы 3-кестені пайдаланып еліміздегі а =20 жастағы адамның ықтималды өмір сүруін анықтау қажет болсын. Интернет желісіндегі Қазақстан Республикасындағы адамдардың орташа өмір сүру ықтималдығы P(A) ≈ 0.72 ( бұл шама интернет желілерінде 72.05% ретінде көрсетілген ) екендігі көрсетілген.
Шешуі. Қайсібір
жасқа дейін өмір сүруін А оқиғасы дедік, онда сол жасқа дейін дүние
салуы  оқиғасы болады. Егер
Р(А) = 0.72 болса, онда
оқиғасы болады. Егер
Р(А) = 0.72 болса, онда
Р( ) = 0.28 болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға
болады.
) = 0.28 болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға
болады.
Айталық, болжап отырған жасымыз х болсын . Сонда
 =
P(
=
P( ) =
0.28,
m(x)
=0.28·n(a
).
) =
0.28,
m(x)
=0.28·n(a
).
Енді х- тің мәнін жоғарыдағы 3-кестеден пайдаланып табамыз. а = 20 , m(x) = 0,28 • n(20) = 0,28 • 96061 = 26897,08 . Кестеде 26897,08 мәні жоқ, сондықтан сызықты интерполяциялауды орындаймыз. 26897,08 саны 13989 мен 37977 аралығында, демек, бұл санға сәйкес х жас 70 пен 80 аралығында болады. Дәлірек айтқанда,
х = 70 +
 · 10 =
70+0,46•10 = 70+4,6
@
74,6.
· 10 =
70+0,46•10 = 70+4,6
@
74,6.
Жоғарыдағы 3-мысалда 10 жастағы 100 000 баланың 90 жасқа дейін өмір сүргені бақыланып, сол мәліметтер бойынша мәселелер құрастырылып шешілген. Алайда, бұл статистикалық мәліметтер қайжерде, кім жағынан 90 жыл жинақталғаны белгісіз. Сонда да ол мәліметтер шартты түрде жазылған деп есептейік. Тағыда ол мәліметтерде ерлер мен әйелдердің өмір суру ықтималдықтары барлық аралықтарда бірдей етіп алынған. Ал ол қазіргі заман ғылыми зерттеулеріне сәйкес келмейді. Сондықтан мәселеге анықтық еңгізу үшін төмендегідей мәліметтер гистограмма ретінде берілген және интернет желісінде көрсетілген Ұлттық экономикалық министрлігі статистика комитетінің деректерінен алынды(төмендегі гисторграмма).

|
Бұл гистограммада 100 жасқа дейін әр 5 жас арасындағы ерлер мен әйлдердің өмір сүру ықтималдықтары пайыз(%) ретіндегі қатынастары келтірілген. Көрініп тұрғандай белгілі жас аралықтарында ерлер мен әйелдердің өмір сүру ықтималдықтары әр түрлі екен. Мұнда бірінші бағана ерлердің , ал екінші бағана әйелдердің сол аралықтағы өмір сүру ықтималдықтарын білдіреді. Бұл гистограммаға сәйкес келетін мәліметтер 4-кестеде жазылған. 4-кесте |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Барлығы 18 157 336 |
Бұл деректер бойынша 2018 жыл басында Қазақстан Республикасындағы халық саны 18 миллионнан асқан, олардың 8 791297 і ер адамдар, 9366 039 і әйелдер , ал жалпы елімізде 18 157 336 адам өмір сүргені көрсетілген. Бұл мәліметтерден сол кезде елімізде әйелдердің ерлерге қарағанда 574 742 адамға көп болғаны көрініп тұр. Сол себептен Бектаев ағамыздың танымал мәселесіне қазіргі кездерде жиналған деректерді пайдаланып шешуді жөн көрдік.
Мысал-6. Туылғаннан бастап 100 жасқа дейін белгілі жас аралығындағы ерлер және әйелдердің саны, яғни 1-4 аралық жаста қаншасы, 5-9 жас аралығында қаншасы т.т. қаншасы 100 жасқа дейін өмір сүргендігі және олардың салыстырмалы түрдегі пайыздық көрсеткіші статистикалық мәліметтер ретінде анықталған(4-кесте).
Осы кестеде келтірілген мәліметтерді пайдаланып :
а) а ( а=20) жастағы адамның b( b=50, b=70, b=90 ) жасқа дейін өмір сүру ықтималдығын анықтау керек;
ә) a = 20 жастағы адамның b( b=30, b=50, b=70, b=90 ) жасқа жетпей дүние салу ықтималдығын анықтау керек;
б) куйеуі а( а=30 ) жаста , әйелі b( b=20) жаста . Екеуі бірге c( c=20, c=40,c=50) жыл өмір сүру ықтималдығын анықтау керек;
в) куйеуі а( а=23 ) , әйелі b( b=18) жаста, олар бірге c( c=45) жыл өмір сүру ықтималдығын анықтау керек;
г) куйеуі а( а=50 ) , әйелі b( b=45) жаста, ұлы c( c=25) жаста, үшеуінің бірге d( d=20,d=30,d=40) жыл өмір сүру ықтималдығын анықтау керек;
д) куйеуі а( а=40 ) , әйелі b( b=35) жаста, екеуі бірге c( c=70, c=80) жасқа дейін өмір сүре алмау ықтималдығын есептеу керек;
е) куйеуі а( а=40 ) жаста , әйелі b( b=30)жаста, c( c=30, c=40) жылдан соң кемінде біреуі өлмей қалу ықтималдығын анықтау керек.
Шешуі. Бұл мәселені шешу үшін 4-кестені 3-кесте ретінде ерлер және әйелдер үшін жеке-жеке құрастырамыз(5-кесте). Себебі ерлер мен әйелдердің өмір сүру ықтималдықтары әр түрлі.
5-кесте
|
Жас аралығы |
Ерлер саны |
Жалпы адамдар саны |
Жас аралығы |
Әйелдер саны |
|
жасы: 0 |
8 791 298 |
18 157 336 |
жасы: 0 |
9 366 038 |
|
жасы: 1-4 |
8 591 203 |
17 769 971 |
жасы: 1-4 |
9 178 768 |
|
жасы: 5-9 |
7 785 025 |
17 011 752 |
жасы: 5-9 |
8 420 549 |
|
жасы: 10-14 |
6 866 366 |
14 416 414 |
жасы: 10-14 |
7 550 048 |
|
жасы: 15-19 |
6 169 970 |
13 047 806 |
жасы: 15-19 |
6 884 838 |
|
жасы: 20-24 |
5 592 525 |
11 932 727 |
жасы: 20-24 |
6 340 202 |
|
жасы: 25-29 |
4 938 716 |
10 648 809 |
жасы: 25-29 |
5 710 093 |
|
жасы: 30-34 |
4 148 739 |
9 057 860 |
жасы: 30-34 |
4 909 121 |
|
жасы: 35-39 |
3 397 147 |
7 538 790 |
жасы: 35-39 |
4 141 643 |
|
жасы: 40-44 |
2 772 563 |
6 270 226 |
жасы: 40-44 |
3 497 663 |
|
жасы: 45-49 |
2 216 791 |
5 119 938 |
жасы: 45-49 |
2 903 147 |
|
жасы: 50-54 |
1 705 629 |
4 049 924 |
жасы: 50-54 |
2 344 295 |
|
жасы: 55-59 |
1 229 722 |
3 034 455 |
жасы: 55-59 |
1 804 733 |
|
жасы: 60-64 |
784 251 |
2 052 874 |
жасы: 60-64 |
1 268 623 |
|
жасы: 65-69 |
473 678 |
1 327 935 |
жасы: 65-69 |
854 257 |
|
жасы: 70-74 |
262 080 |
791 914 |
жасы: 70-74 |
529 834 |
|
жасы: 75-79 |
164 662 |
530 826 |
жасы: 75-79 |
366 164 |
|
жасы: 80-84 |
70 946 |
242 326 |
жасы: 80-84 |
171 380 |
|
жасы: 85-89 |
23 469 |
79 850 |
жасы: 85-89 |
63 165 |
|
жасы: 90-94 |
6 814 |
22 100 |
жасы: 90-94 |
16 956 |
|
жасы: 95-99 |
1670 |
3 806 |
жасы: 95-99 |
2 583 |
|
жасы: 100+ |
447 |
871 |
жасы: 100+ |
424 |
|
|
Жалпы саны 8 791 298 |
Жалпы саны 18 157 336 |
|
Жалпы саны 9 366 038 |
Ескерту: Мәселені
төмендегідей шешу үшін жоғарыдағы 3-мысалдың шешілу процесін толық
меңгерген болу қажет. Себебі 3-мысалдағы түсініктемелерді қайталап
жазып отырмаймыз. Сондада , кестеге қарағанда, адамның жасы
ұлғайған сайын олардың саны азайып баратындығын көреміз, бұл заңды,
әрі түсінікті де. а
жастағы
адамның b
жасқа дейін өмір сүруін А
оқиғасы дейік, бұлардың санын сәйкес ретінде ерлер үшін
mе(b), әйелдер үшін
mә
(b) болсын,
а
жастағы адамдар саны ерлер
үшін nе(a), әйелдер үшін
nә(a), ал аралықтағы адамдар санын
ерлер үшін nе(i-j), әйелдер үшін
nә(i-j) (мұнда,
i= ,
i=i+5, j=
,
i=i+5, j= ,
j=i+4, ) деп белгілейік( жалпы
адамдар саны үшінда осындай белгілеулар еңгізген
жөн).
,
j=i+4, ) деп белгілейік( жалпы
адамдар саны үшінда осындай белгілеулар еңгізген
жөн).
Жоғарыдағы мәселелерді шешу үшін төмендегідей өзгерістер еңгіземіз:
а) Бұл жерде
жастарын өзгеріссіз қалдырамыз және ерлер, не әйелдер
ескертілмегендіктен кестедегі жалпы адамдар санының өзгеріс
заңдылығын қолданамыз. Сонда А оқиғасының ықтималдығы P(A)
=  ал, кесте
бойынша a=
20 болғанда
nж(a) = 11 932
777, b
= 50
болғанда
ал, кесте
бойынша a=
20 болғанда
nж(a) = 11 932
777, b
= 50
болғанда
mж(b) =4 049 924. Сонда Р(А)
=  =
0,339.
=
0,339.
Сонымен, 20 жастағы адамдардың орта есеппен 33,9 % -і 50 жасқа дейін өмір сүреді екен. Бұл көпшілікке күман келтіру мүмкін, бырақта бұл 2018 жылғы статистикалық мәлімет бойынша есептелінді. Егер b=a болғанда Р(А) =1 болатын еді, бұл факт адамның b жасқа дейін өмір сүретінінің ақиқаттығын көрсетеді.
ә) (а) пункттегідей есептеу жүргіземіз.
б) Мұнда Р(А) ны есептеу үшін кестедегі 2-бағандағы(ерлер үшін) мәлімет-терді, ал Р(В) ны есептеу үшін кестедегі 5-бағандағы(әйелдер үшін) алынған мәліметтерден пайдаланамыз.
в) Бұл мәселе де дәл (б) пунктіндегі мәселе секілді шешіледі, бырақта (б) пунктінде келтірілген жасқа сәйкес жиіліктер шамасы кестеде жоқ. Сондықтан интерпалациялау әдісін қолданып 4-кестеде келтірілген сол аралықтағы адамдар(ерлер немесе әйелдер немесе жалпы) үшін 5 жыл ішіндегі әрбір жылдағы өлім санын бірдей деп аламыз және сол аралықтағы адамдар санын 5-ке бөліп біртіндеп қосу арқылы қажетті жасты табамыз. Дәл сұралған мәселе үшін толық тоқталайық. Сондықтан бізге қажетті болған ne(23), me(23+45) = me(68), nә(18), mә(18+45) = mә(63) мәндердің неге тең болатыны табайық.
ne(23) =
ne(20) -
 •4=
5 592 525 -
•4=
5 592 525 -  • 4 =
5 592 525-523047,2 =
5 069 477,8.
• 4 =
5 592 525-523047,2 =
5 069 477,8.
me(23+45) =
me(68)=
me(65)- •4
=
473 678-
•4
=
473 678-
 •4
=473 678-
169 278,4 =
304 399,6 .
•4
=473 678-
169 278,4 =
304 399,6 .
nә(18) =
nә(15)
- •4 = 6 884 838
-
•4 = 6 884 838
-  •4 = 6 884 838
– 435708,8 =
6 449 129,2.
•4 = 6 884 838
– 435708,8 =
6 449 129,2.
mә(18+45) =
mә(63)=
mә(60)
- •4
= 1 268
683-
•4
= 1 268
683-  •4
=
1 268 683 –
331 492,8 =
937 190,2.
•4
=
1 268 683 –
331 492,8 =
937 190,2.
Демек,
Р(А•В) =  •
•
 =
=  ·
·  = 0,06 •
0,145 =
0,0087.
= 0,06 •
0,145 =
0,0087.
г) Бұл жағдайда ұлының өмір сүруін С оқиғасы деп ерлерге жазылған мәліметтерден есептеп Р(А•В•С) ықтималдықты есептейміз.
д) Мұндада куйеуі және әйелі үшін жеке есептеліп 3-мысалдағыдай табылады.
е) (д) пункттегідей есептелінеді.
Жоғарыдағы ә), б), г), д) және е) пункттегі мәселелерді 3-мысалдағы тәсілдер көмегімен 4 және 5-кестелерді пайдаланып шешуді оқушылардың өзіне қалдырамыз.
3-лекция
Комбинаторикалық элементтер.
1. Комбинаторикалық элементтер ұғымы.
2. Құрылымдар санын есептеу формулалары.
3. Орналастыру заңдылықтары.
4. Комбинаторикада орын алмастыру қағидалары.
5. Теру және оның қасиеттері.
________________________________________________________________
Комбинаторикалық элементтер.
1. Комбинаторлы конфигурация негіздері
1) Комбинаторика – математика тарауларының бірі. Мұнда элементтер жиынының әртүрлі комбинациялары қарастырылып, олардың сандары есептелінеді.
Комбинаториканың негізгі мәселелері болып кезектегілерді айырып алуға болады: есептелу, санақтау, классификациялау және оптимизациялау. Егер кейбір қасиеттер немесе қасиеттер жиынтығына ие болған элементтер санын анықтау талап етілсе, онда бұл мәселе есептелу. Ал, егер бұл жерде элементтер тізімін көрсету қажет болса, онда ол санақтау болады. Егер есептелу өте үлкен сандарға алып келетін болса, онда ол сәйкес ретінде есептелудің орнына қандайда бір қатынастар көмегімен текқана кластарға бөлінеді. Оны біз классификациялау деп айтамыз. Кейбір мәселелердегі шешімдер жиынтығына функциялардың шамаларын енгізу мүмкін. Бұл функцияларда оптимизациялау мәселелері, яғни белгілі бір обьекттер жиынында функцияның экстремумын табу, болмаса экстремал мәндерге жете алатын кейбір немесе барлық нысандарды көрсету қарастырылады.
2) Комбинаторикалық құрылым деп қатар арнайы қасиеттерді қанағаттандыратын элементтердің шекті жиынтықтарының жайғасуын түсінеміз. Негізгі комбинаторикалық құрылымдарға теру, орналастыру және орын алмастырулар кіреді. Басқа көптеген құрылымдар осыларға алып келуі мүмкін.
Х=(х1,х2,….хn) жиын элементтерінен құралған (хі1,хі2,….хік), (k£n), элементтер жиналымы (набор) элементтердің k көлемдегі таңдамасы немесе (n,k)-таңдама деп айтылады. Элементтер құрамымен айырықшалыққа ие болған таңдамалар барлық уақыт әртүрлі болады. Егер таңдамада элементтер реті алдын – ала берілген болса, онда оны реттелген деп айтамыз. Екі реттелген таңдама элементтерінің келу ретімен ғана айырықшалыққа ие болса да әр түрлі деп есептеледі. Егер таңдамада элементтер реті белгісіз болса, онда оны реттелмеген таңдама деп айтамыз. Элементтері қайталануы мүмкін болған реттелген (n,k)-таңдама (n,k)-қайталамалы орналастыру немесе n элементтен әрқайсысы k- дан жасалған қайталамалы орналастыру деп айтамыз. Егер (n,k) – таңдаманың элементтері жұбымен әр түрлі болса, онда ол (n,k) – қайталамасыз орналастыру немесе n элементтен әрқайсысы k- дан жасалған қайталамасыз орналастыру деп айтылады. Қайталамасыз (n,n) – орналастыру n –элементтен n – нен алынған орын алмастырулар немесе n элементті орын алмастыру деп айтамыз.
Реттелген (n,k) –таңдамада n элементтен әрқайсысы к – дан алынған орналастыруларды бір – бірінен айырықшалығы не элементтерінде, не элементерінің орналасу ретінде болатын комбинациялар ретінде де қарастыру мүмкін. Оны біз теру деп айтамыз. Мұнда қайталанбайтын (n,k) – теру n – элементті жиынның k-элементті ішкі жиындары екендігіне мән беру қажет. Егер элементтер (n,k) –таңдамада қайталанбайтын болса, онда k £ n теңсіздік орындалады. Ал, қайталамалы таңдамалар үшін k>n шарт болуы мүмкін.
3) Комбинаторикада екі негізгі қағиданы көрсету мүмкін: қосу қағидасы және көбейту қағидасы.
Айталық , Х шекті жиын n элементтен құралған болсын. Онда Х тен алынған бір нысанды n тәсілмен таңдау мүмкін және ол ïХï=n ретінде жазылады. Егер Х және Ү – қиылыспайтын жиындар және ïХï=n,ïҮï=m болса ,онда ïХÈҮï=m+n болады. Бұл қасиетті бұданда көп жиындар үшін де қолдану мүмкін.
Айталық íХý - өздерінің жұбымен қиылыспайтын жүйе болсын:
Хі Ç Хj = Æ, і ¹j. Онда
êі=1È n Xі½= і=1 å nôХіô (1)
болады. Бұл қағиданы қосылу немесе альтернатив қағида деп айтылады.
Егер хÎ Х нысан n тәсілмен таңдалған және әрбір осындай тәсілден соң
уÎ Ү нысан m тәсілмен алынған болса, онда реттелген (х,у) жұптық таңдауы m ×n тәсілмен орындалуы мүмкін. Бұл көбейту қағидасы болады. Онда ол тағыда көп санды жиындарға қолдануға мүмкіндік береді. íХіý, і=1,2,….k, мұнда ôХіô=mі, жиынды жүйе үшін k санды (х1,х2,….хк), хі Î Хі, нысандардың реттелген тізбекті таңдамасы m1 × m2 ×…×mk тәсілмен орындалуы мүмкін.
Мысал. Қазақстандағы кез келген автомобил нөмірі АСССААА қалыптағы тізбектен тұрады, мұнда А латын алфавитіндегі әріптер, ал С кез келген ондық сан. Сонда мүмкін болған әр түрлі нөмірлер саны 35×10×10×10×35×35×35=1 500 625 000 болады.
Ал, қиылысатын жиындар үшін біраз
күрделі қатынастар орындалады. Бұл жерде кемінде біреуіне тиісті
болатын, яғни олардың бірігуіне тиісті Х,Ү жиындар үшін элементтер
саны 
ôХÈҮô=ôХô+ôҮô-ôХ ÇҮô (2)
формула арқылы табылатындығын көру қиын емес.
Ал үш Х,Ү,Z жиындар үшін,олардың бірігуіндегі элементтер саны
ôХÈҮÈ Zô=ôXô+ôYô+ôZô-ôXÇYô-ôXÇYô-ôXÇYô+ôXÇYÇ Zô (3)
тең болады. Бұл жерде (2) және (3)
қатынастарға басқашада сипат беру мүмкін. Егер, Х,Y,Z, жиындарды U
жалпылама жиынның ішкі жиыны ретінде қарастырсақ,
онда  =ôUô-ôX È Yô екендігі, ал одан
=ôUô-ôX È Yô екендігі, ал одан
 =ôUô-
(ôХô+ôҮô)+ôХ ÇҮô (4)
=ôUô-
(ôХô+ôҮô)+ôХ ÇҮô (4)
келіп шығады. Сол секілді:
 =ôUô-ôХô+ôҮô+ôZô)+(ôX ÇYô+ôX Ç Zô+ôYÇ Zô ) -
=ôUô-ôХô+ôҮô+ôZô)+(ôX ÇYô+ôX Ç Zô+ôYÇ Zô ) -
-ôX Ç Y Ç Zô (5)
теңдік орынды болады. Бұл жердегі (4) және (5) тендіктер енгізу және шығару қағидаларының дербес жағдайы болып есептелінеді.
Айталық, Р (1), Р (2),...., Р(n) болған n қасиет және Р(і), Р(j) қасиеттерге ие болған N элементті жиынның Ni элементті саны, жалпы айтқанда (Рі1), (Рі2),...,(Ріs) қасиеттерге ие болған Nі1і2…іs-элементтер саны қарастырылып жатқан болсын. Онда, осы қасиеттердің бірде-біреуінеде ие болмаған N(0)- дің элементтер саны таңбалары ауысып келетін төмендегідей алгебралық қосындымен анықталады:
N (0) =N - іå Nі + і<jåNij - …+ (-1)s× i1<i2<…<iså N i1i2…is + (-1)n ×N12….n . (6)
2. Комбинаторикалық құрылымдар санын есептеу
формулалары.
Орын алмастыруларды есептеу
Анықтама. Алмастырулар деп, бір-бірінен айырмашылығы oрналасу ретінде ғана болатын элементтер комбинацияларын айтады.
Сонымен, n элементтен n! алмастыру жасауға болады, оны Рn арқылы белгілейді: Рn = n! = 1. 2 . 3 . . . n.
a және b-екі элементтен, олардың ретін өзгертіп, екі алмастыру алуға болады: ab, ba. Үш (a, b, с ) элементтен 6 алмастыру алынады: abс, baс, bсa, aсb, сab, сba. Алмастырулар заңдылыққа бағынады: екі элементтен екі алмастыру, немесе 2! алмастыру алуға болады, 3 элементтен үшеуден 6 алмастыру, немесе – 3! алуға болады. Онда 4 элементтен төртеуден 4! =24 алмастыру алуға болады т.с.с.
Енді n элементтен келіп шығатын барлық орын алмастырулар тізбегінен кейбір алгоритмдерін қарастырайық.
а) Лексикографикалық немесе алфавиттік. Мұнда, тізбектелу индуктив түрде анықталады , яғни әр бір орын алмастыруға бірінші элемент көрсетілген, одан соң келетін барлық тізбектегілер:
1, ( алфавитті ретпен í2,….,ný тен алынған барлық орын алмастырулар );
2, (алфавитті ретпен í1,3,….,n ý тен алынған барлық орын алмастырулар);
3, (алфавитті ретпен í1,2,4,..….,n ý тен алынған барлық орын алмастырулар);
……………...............
k , (алфавитті ретпен í1,2,…..,k – 1 ,k + 1,….., n ý тен алынған барлық орын алмастырулар);
……………..............
n , (алфавитті ретпен í1,2,…..,n – 1 ý тен алынған барлық орын алмастырулар).
Мысал. n ═ 3 үшін
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
б) Бұл жерде орын алмастырулардың құрылымы сондай кезектесумен жайғасады, яғни екіншісінен бастап әр бір элемент алдынғысынан орындары дәл екі элементке ауысатындай айрықшалықта болады(осындай жағдай және осындай ауыстыру транспозиция деп айтылады). Мұндай орын алмастырулар тізбегі өте тиімді болуы мүмкін, егер қандайда бір мәселені (мысалы, комбинаторикалық) шешуде әр бір орын алмастырумен кейбір есептеулер байланысты және алдынғы орын алмастырулар үшін алынған дербес нәтижелерді қолдану мүмкіншілігі бар болса немесе егер тізбектегі орын алмастырулар бір-бірінен өте аз айрықшалықта болса.
Қазіргі кезеңде әр түрлі қатынастарда өте қолайлы, әсіресе бағдарламалау теориясы үшін тиімді болған осындай кезектесудің түрлі құрылу алгоритмдері бар.
в) Алдыңғы пункттің дербес жағдайы ретінде екі көршілес орын алмас-тырулар арасындағы айрықшалық жәнеде кіші болған кезектесуді қарастыру мүмкін. Олар екі көршілес элементтердің транспозициясы-мен айрықшаланады. Мұндай алгоритмнің мазмұны-индуктивті құрылым.
Айталық осыған дейін осы қасиетке ие болған 1,2,…..,(n – 1) элементтер кезектесуі құрылған болсын . Онда талап этілген 1,2,…..,n элементтердің орын алмастыру тізбектерін n ді мүмкін болған барлық тәсілдермен (олардың саны дәл n ) 1,2,…,(n-1) элементтердің әр бір орын алмастыруларының түрлі орындарына n -ді біртіндеп алға және артқа жылжыта отырып (n – 1)! рет) қою арқылы аламыз.
Төменде n ═ 2,3,4 үшін толық, ал n ═ 5 болғанда кезектесудің басы үшін осы алгоритм кесте ретінде бейнеленген. Бұл жерде (n) элемент қою әріппен жазылған, ал әр бір бағанның оң жағында 1, 2 ,…, ( n - 1 ) элементтердің транспозициясы көрсетілген:
n ═ 2 n ═ 3 n ═ 4 n ═ 5
------------------------------------------------------------------------------------------------------------
1 2 1 2 3 1 2 3 4 1 2 3 4 5
2 1 1 3 2 1 2 4 3 1 2 3 5 4
3 1 2 12 1 4 2 3 1 2 5 3 4
3 2 1 21 4 1 2 3 23 1 5 2 3 4
2 3 1 4 1 3 2 32 5 1 2 3 4 34
2 1 3 1 4 3 2 5 1 2 4 3 43
1 3 4 2 1 5 2 4 3
1 3 2 4 13 1 2 5 4 3
3 1 2 4 31 1 2 4 5 3
3 1 4 2 1 2 4 3 5 24
3 4 1 2 1 4 2 3 5 42
4 3 1 2 12 1 4 2 5 3
4 3 2 1 21 1 4 5 2 3
3 4 2 1 1 5 4 2 3
3 2 4 1 5 1 4 2 3 14
3 2 1 4 32 5 4 1 2 3
2 3 1 4 23 4 5 1 2 3
2 3 4 1 4 1 5 2 3
2 4 3 1 4 1 2 5 3
4 2 3 1 31 4 1 2 3 5 23
4 2 1 3 13 4 1 3 2 5 32
2 4 1 3 4 1 3 5 2
2 1 4 3 4 1 5 3 2
2 1 3 4 4 5 1 3 2
5 4 1 3 2 41
5 1 4 3 2 14
1 5 4 3 2
……………
Орналастыруларды есептеу.
Анықтама. Бір-бірінен айырмашылығы орналасу ретінде немесе құрамында болатын n элементтің m - нен жасалған комбинацияларын орналастырулар деп атайды.
Мысал үшін 4- элементтен әрбіреуінде 2- элемент болатын комбинациялар құрып, оның санын есептеу керек болсын. Сонда а, b, с, d элементтерінен екі – екіден комбинация құру төмендегідей болады.
Олар: аb, bс, bd, ас, аd, сd, bа, са, dа, сb, db, dс.
Қайталамасыз ( n,k) – орналастырулар саны Аkn көбейту қағидалары көмегімен анықталуы мүмкін. Бірінші k элементті орналастыру n тәсілмен таңдалады, ал екіншісі ( n – 1) тәсілмен, себебі бірінші алынған элемент қайталанбауы қажет. Сол секілді үшінші элементке (n-2) тәсіл ( егер к > 2 болса) қалады және т.с. жалғасады. Бұл жерде k элемент, яғни Аkn = n × ( n-1)× …..×(n –k+1) элемент, атап айтқанда n нен бастап біреуден кеміп баратын k көбейтінді тандалуы мүмкін. Басқаша айтқанда, n! =1×2× ….×n белгілеуді қолдансақ оны төмендегідей қолайлы жазуға болады:
Аkn = 
Мысал-1. А37 = 7! /4! = 7×6×5=210;
А47 =7! /3!=7×6×5×4=840;
А57 =7!/ 2!=7×6×5×4×3=2520.
Егер k=1 болса, онда А1n=n!/(n-1)! = n ; егер k= n-1 болса, онда Аn-1n =n!/1!=n!; егер k= n болса, онда Аnn=n!/0! = n! болатындығын көру қиын емес. Математикада формуланың бірмәнділігі және қолайлық үшін 0!=1 деп қабылданғандығын ескертеміз. Бұл жерде Аn-1n және Аnn сандарының тең екендігі айқын, себебі, егер n элементтен ( n-1) элемент тандалған болса, онда қалған жалғыз элементте сондай тәсілмен тандалған болады. Ал, ол
Аn-1n санын Аnn санымен салыстырғанда өзгертпейді. Сондықтан, n орын алмастыру Рn = n! болады.
Ал, қайталамалы (n,k)- орналастырулар n элементті алфавиттің k ұзындықтағы сөз тізбегі болады. Осы жерде көбейту қағидасынан пайдалана отырып әр түрлі қайталамалы (n,k) орналастырулар Аkn = nk болатындығын көру қиын емес. Шындығындада, реттелген тізбектегі n мүшенің әр біреуі бір-бірінен байланыссыз, саны k ға тең бола тұра, n тәсілмен тандалуы мүмкін.
Мысалдар. 1) { 0,1} алфавитіндегі k ұзындықтағы сөздер саны 2k ға тең, сол секілді k- элементті жиынның барлық ішкі жиындарыда сол санға тең, себебі жиын өзінің характеристикалық функциясымен бірмәнді беріледі. k-мәнді екілік сандардың мөлшері 2k-1 ге тең, себебі бұл жерде санның бірінші сатысы 1 ге тең болуы қажет.
2) k- мәнді ондық сандар ( яғни, дәл k сатыға ие болған) мөлшері 9×10k-1 ге тең, бұл жерде оларды біз {0,1,2, …..9} алфавитіндегі сөз ретінде қарастырдық, сонымен тағыда бұл сандардағы бірінші саты барлық уақыт 0 ден айрықша болуын ескертеміз.
Теру элементтерін есептеу.
Анықтама. Бір-бірінен айырмашылығы құрамында ең болмағанда бір элементі өзгеше болатын элементтер комбинацияларын n элементтен m – нен жасалған теру деп атайды.
Қайталамасыз ( n,k) теру санын Сkn немесе ( nk) арқылы белгілейміз және оларды биномиал коэффиценттер деп айтамыз. Себебі, олар х+у екімүшенің n- дәрежелі Ньютон биномы формуласындағы коэффициенттерге сәйкес келеді:
(х + у)n = k=0ån Ckn × xn-k × уk . (7)
Шындығындада,
хn-k ·
уk мүшенің алдындағы коэффициент n дана бір түрлі
(х+у) ×(х+у)×…..×(х+у) көбейтінділерінен k рет тандалған тәсілдер
санына тең. Ал, ол х және у тер көбейтіндісінің дәл
хn-k ·
уk реттік көбейтіндісінен тандалған. Қайталамасыз
(n, k) - теруді есептеу үшін қайталамасыз барлық (n,k)-
орналастырулар жиынын бір түрлі элементтер құрамына ие болатын
қатынастарға байланысты эквивалент кластарға бөліп қарастыру өте
қолайлы. Бұл жерде құрылымы бойынша айрықша болған элементтер әр
түрлі кластарда жатады. Әр бір класта бірдей k дана түрлі элементі
болған реттелген құрылымға ие болады, яғни олар k орын алмастыруды
сипаттайды және әр бір класта олардың саны k! ға тең болады. Осы
жерден қайталамасыз (n,k)- терулердің
Сkn саны Аkn/
k! ға тең, яғни Сkn
=  . (8)
. (8)
Бұл жерде k ның дерлік үлкен болмаған мәндерінде Сkn үшін соңғы өрнекті қолданған қолайлы, себебі өрнектің алымындада, бөліміндеде k данағана көбейтінді бар, яғни алымында n-нен бастап кеміп баратын натурал сандар қатары, ал бөлімінде 1 ден бастап өсү бойынша k ға дейінгі натурал сандар қатарының бөлігінен құралған. Дербес ретінде барлық уақыт С0n =1, C1n= n, C2n= n×(n-1)/2 болатындығын көру қиын емес. Тағыда, осы жерде егер k>n болса, онда Сkn=0 деп қабылдаймыз.
Мысал үшін 4 элементтен 2-ден жасалған теру саны
 ға тең,
яғни аb, ас, аd, bс, bd,
сd .
ға тең,
яғни аb, ас, аd, bс, bd,
сd .
Мысал-2: С38
=
 =
=  =
=
 =
56;
=
56;
С410
=  =
=
 =
=  =
210.
=
210.
Осы жерде биномиал коэфифенттердің кейбір қасиеттерін қарастырамыз:
1) Сkn = Cn-kn .
Бұл теңдік (8) формуладан келіп шығады, яғни n элементтен алынған k элементті тандама оған қосымша ретінде n элементтен алынған (n-k) элементті таңдамаға бірмәнді сәйкес келеді. Осы жерден және алдынғы теңдіктерден төмендегі қатынастар келіп шығады: Сnn =C0n=1,Cn-1n=C1n=n.
Мысал-3. С26
=
 =
15, С46
=
=
15, С46
=
 =
=  =
15.
=
15.
2) k=0ån Ckn = 2n.
Бұл теңдік (7) формуладағы х және у айнымалылар орнына 1 мәңді қою арқылы оңай табылады.
Мысалдар. 1+5+10+10+5+1=32 =25 ; 1+6+15+20+15+6+1=64=26.
-
k=0ån(-1)k ×Ckn= 0.
Бұл теңдіктіда (7) формулада х =1, у= -1 ауыстырулар арқылы оңай табу мүмкін.
Мысал. n=6 болғанда 1-6+15-20+15-6+1=0.
-
k=0 ån Ckn ×k = n×2n-1 .
Бұл теңдіктің ақиқаттығына сену үшін n элементті íа1,а2,….,аný әр бір теру үшін осы (k элементтен алынған) теру элементтеріне сәйкес келетін аі1,аі2,….,аік белгілер жеке бөліктерге жазып алынған деп есептейік. Мұнда 2- қасиет бойынша барлық бөліктер 2n ге тең. Онда барлық бөліктердегі белгілер қосындысының санын екі түрлі есептеу мүмкін:
а) Дәл k белгіні қамтитын Сkn белгілердің қосынды саны k × Сkn болады. Ал, қарастырылып жатқан теңдіктің сол жағында k=0,1,….,n үшін барлық бөліктердегі белгілердің жалпы саны алынады.
б) Егер барлық бөліктерден жазылған кейбір аі белгіні өшірсек , онда ол жерде қалған (n-1) элементті мүмкін болған барлық терулер қалады. Олардың саны 2n-1. Демек аі белгі дәл 2n -1 бөліктерде жазылған екен. Ал, осы жерден теңдіктің оң жақ бөлігіндегі жалпы белгілер саны n × 2n-1 болатындығын көреміз.
Мысал-4. n =5 болғанда : 0× 1+1×5+2×10+3×10+4×5+5×1=80=5×24.
Ал, n=6 болғанда: 0×1+1×6+2×15+3×20+4×15+5×6+6×1=192=6×25 болады.
5) Сkn= Ck-1n-1+Ckn-1 .
Бұл теңдік мынадай тұжырым арқылы келіп шығады. n элементті жиыннан кез келген бір х элементті белгілеп аламыз. Бұл жерде k элементті жиындардың барлық жиынтығын осы х элемент жату немесе жатпаулығына қарай екі қиылыспайтын кластарға бөлінеді. Бірінші класта Сk-1n-1 ішкі жиын, олар х ті және қалған (n-1) элементтің ішінен (k -1) элементті өз ішіне алады. Екінші класта Сkn-1 элемент болатындығы айқын.
Бұл теңдіктер Паскаль ұшбурышы деп аталатын (5- сызба) сұлбамен тығыз байланысты.
Егер осы ұшбурыштың жолдарын ретімен 0,1,2,… деп нөмірлесек , онда і-жол С0і ,С1і ,…..Сіі сандарына сәйкес келеді. 5-қасиет бойынша 1 санына тең болған шеткі диоганалдан басқа әрбір санды алдыңғы қатардағы үстінде жайғасқан екі санның қосындысы ретінде алу мүмкін. Бұл Паскаль ұшбурышын құру және сонымен бірге биномиал коэффициенттерді табудың өте қарапайым тәсілін береді. Мұнда, n-қатар (х+у)n биномының коэффициенттеріне сәйкес келеді.
Ескерту. Бұл жерде (5) қасиет реккуренттік қатынас мысалы ретінде сипатталады, яғни Сkn шама екі n және k аргументтердің функциясы ретінде қарастырылып, ол осы функция айнымалыларының басқа мәндері арқылы өрнектеледі.
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
6 1 6 15 20 15 6 1
7 1 7 21 35 35 21 7 1
8 1 8 28 56 70 56 28 8 1
9 1 9 36 84 126 126 84 36 9 1
10 1 10 45 120 210 252 210 120 45 11 1
…………………………………………………………….
5 – сызба
-
Сkm+n = s=0åk Csm Ck-sn ( Коши теңдігі).
Бұл теңдікті дәлелдеу үшін мынадай интерпретацияны қарастыру қолайлы.
Айталық , m ерлер және n әйелдерден құралған топтан k адамнан тұратын өкілдер таңдалатын болсын. Оны Сkm+n тәсілмен жасауға болады. Біздің (m+n) элементті жиынның барлық k элементті ішкі жиындарын өкілдердегі ерлер саны бойынша классификациялау мүмкін. s ерлерден тұратын k элементті өкілдерді алдын s ер кісілерді таңдау арқылы Сms тәсілмен , ал одан соң (k-s) әйел кісілерді Ck-sn тәсілмен алу мүмкін. Көбейту қағидасы бойынша k элементті өкілдер саны Сsm×Ck-sn , ал қосу қағидасы бойынша k элементті өкілдер саны теңдіктің оң бөлігі секілді осындай санға тең.
Мысал-5.
С410= С47+3 = С07× С43+ С17 × С33 +С27 ×С23+С37×С13 +С47 ×С03=
[ С43 = 0 екендігін есепке алсақ] = 7×1+21×3+35×3+35×1 = 210.
Қайталамалы (n,k) терудің Сkn санын алу үшін осындай әр бір теруге (яғни, n элементті жиыннан алынған реттелмеген k таңдау) екі мәнді í0,1ý алфавитінде мынадай тізбек сәйкес қоямыз . Бастапқыда, k таңдамаға енетін және әр бір аі элемент n жиынның і элементтер санына тең болған n натурал сандардың íаіý тізбегін құрастырамыз. Мұнда, кейбір аі элементтер 0 ге тең болуыда мүмкін. Ал, осы тізбектің n компоненттер қосындысы k ға тең.
Енді әр бір аі санды (нөлдермен бөле отырып) аі та бірлермен ауыстырып нөл және бірлерден тұратын тізбек құрастырамыз:
11…101…10…0
0…
ÈÈÈÈ ÈÈÈ ÇÇÇ
а1 а2 аі =0
Егер, кейбір элементтерде аі = 0 болса, онда сәйкес нөлдер арасында мүлдем бір саны болмайды. Басқаша айтқанда, (n-1) нөлдерден құралған тізбек n орынды анықтайды( сол жағынан барлық тізбектен бастап, ал оң жағынан әр бір нөлден бастап). і-ші орынға аі та бір қоямыз( мұнда, кейбір аі элемент 0 ге тең болуыда мүмкін).
Мысал-6. (1,1,3,4,4,4,4) ретіндегі (4,7) теруге (2,0,1,4) тізбек, тағыда өз кезегінде 1100101111 тізбек сәйкес келеді, ал (1,2,2,2,3,3,3) ретіндегі (4,7) теруге бастап (1,3,3,0) тізбек, сосын 1011101110 тізбек сәйкес келеді. Нәтижеде, (n-1) нөлдер және k бірлерден құралған жиналым, яғни (n-k+1) ұзындықтағы вектор келіп шығады. Керісінше, әр бір осындай векторға (n,k) теру сәйкес келеді, бұл жерде бірлер қатар келетін топтар аі санды анықтайды, ал олардың қосындысы k ға тең. Сондықтан
Ĉkn= Сkn+k-1=C n-1n+k-1 (9)
болады.
Осы (9) теңдікті басқаша жолменде алуға болады.
Айталық, (С1,С2,…,Сk)-қайталамалы (n,k) теру болсын, мұнда С1 £ С2 £. …£ Сk. Оған d1=c1+0,d2=c2+1,d3=c3+2,…,dk=ck+k-1 болған (d1,d2,….,dk) таңдаманы сәйкес қоямыз. Бұл жерде барлық di сандар әр түрлі , сондықтан (d1,d2,….,dk) таңдаманы қайталамасыз (n+k-1,k) теру секілді қарастыру мүмкін. Керісінше, әр бір қайталамасыз (n+k-1,k) теруге қайталамалы болуы мүмкін болған (n,k) теру сәйкес келеді. Осы жерден (9) теңдік келіп шығады.
Мысал-7. . Ĉ43=С46=С26=6×5/2=15.
4- кестеде 3
элементтен 4 еуден алынған барлық қайталамалы (3,4) теру өздеріне
сәйкес тізбектермен және оларға сәйкес қайталамасыз (6,4) теру
келтірілген. 

4-кесте
______________________________________________
1,1,1,1 4,0,0 111100 1 2 3 4
1,1,1,2 3,1,1 111010 1 2 3 5
1,1,1,3 3,0,1 111001 1 2 3 6
1,1,2,2 2,2,0 110110 1 2 4 5
1,1,2,3 2,1,1 110101 1 2 4 6
1,1,3,3 2,0,2 110011 1 2 5 6
1,2,2,2 1,3,0 101110 1 3 4 5
1,2,2,3 1,2,1 101101 1 3 4 6
1,2,3,3 1,1,2 101011 1 3 5 6
1,3,3,3 1,0,3 100111 1 4 5 6
2,2,2,2 0,4,0 011110 2 3 4 5
2,2,2,3 0,3,1 011101 2 3 4 6
2,2,3,3 0,2,2 011011 2 3 5 6
2,3,3,3 0,1,3 010111 2 4 5 6
3,3,3,3 0,0,4 001111 3 4 5 6
4. Бұл жерде n элементтен құралған а1 а2 …аn қайталамалы және қосымша шартты, яғни олардың әр бірінде бірінші типтегі b1 элементті, екінші типтегі b2 элементті, жалпы айтқанда і-типтегі (і ═ 1,2,…,r) bі элементті барлық мүмкін орналастыруларды қарастырамыз. Мұнда, b1+b2 + …br ═ n теңдік орындалатындығы айқын. Енді і-ші типтегі bі элементтерді барлығы әр түрлі болғанша бір бірінен айрықша болған bi1,…,bir элементтермен ауыстырамыз, яғни n орналастыру аламыз. Әр бір осындай жайғастыру b1! b2!…br! орналастыруды береді. Сондықтан, барлық қайталамалы орналастырулар саны төмендегі өрнек арқылы табылады:
 ,
мұнда,
b1+b2+….+br═
n.
,
мұнда,
b1+b2+….+br═
n.
Бұл сан полиномдық коэффициент деп айтылады, себебі ол (х1+х2+….+хr)n полиномды айнымалылар дәрежесі бойынша жіктеудегі х1b1x2b2….xrbr көбейтінді алдындағы коэффициентке тең. r ═2 болғанда биномиалдық коэффициенттер дербес жағдайда бейнеленеді.
5. Бір еңгізу және шығару ұстанымын қолдануға мысал ретінде «Тәртіпсіздік тұралы» мәселені» қарастырамыз: кез келген і ═ 1,2,…..,n үшін аі ≠ і болатын 1,2,….,n сандардың а1,а2,…,аn орын алмастырулар саны қанша?
Осы санды Dn арқылы белгілеп (6) формуладан пайдаланамыз. Бұл жерде N элементті n! дана а1,а2,…,аn орын алмастырулар, ал Р(і) қасиет аі = і (і ═ 1,2,…..,n) теңдікпен өрнектелетіндігін білдіреді.
Онда Nі1і2….іr ═ ( n – r)! өз орнында белгілі r символдар қалдырылған орын алмастырулар саны болады.
Ал, SNі1і2…іr өрнекте 1,2,…,n сандардан і1,і2,….,іr таңдау тәсілдерінің саны бойынша алынған Сrn қосындылар бар. Осы жерде (6) теңдікті қолдана отырып төмендегіні табамыз :
N (0) ═ n! – n .( n – 1)! + С2n .( n – 2)! - ….+ (-1)r . Сrn . ( n – r)! +….+(-1)n . 1 ═ n! – n . (n-1)! + n . (( n -1)/2) . (n-2)! - ….+(-1)r . (n . (n -1)...( n –r + 1)/r!) . (n –r)!+….+ (-1)n ═ n! . ( 1 -1 + 1/2 ! – 1/3! + …+ ( -1 )r r ! + …+ ( - 1)n / n! ).
Бұл жерде жақшаға алынған
1-1+ 1/2 ! -1/3 ! +….+ ( - 1)r / r ! + ….+ ( - 1)n / n!
қосынды е-1 сан үшін шексіз қатардың дербес қосындысы. Сондықтан Dn ге тең болған N ( 0 ) өрнек n ! / e ге жуық болған бутін сан, яғни
Dn/ n ! » e -1 . (10)
(10)- формуланың өте қарапайым сипаттамасы мынадай. Егер әр түрлі мекенжай үшін n хат кездейсоқ ретінде мекенжайлары жазылған n конвертке салып қойылған болса, онда n мекенжайдағы бірде бір адам 1/е » 0.368 санға жұық ықтималдықпен өздеріне арналған хатты алалмайды. Бұл теория қарама-қайшылықты көрінуі мүмкін, бірақта 10 немесе 10000 хаттар үшінда бұл ықтималдық шамамен бірдей.
6. Комбинаториканың классикалық мәселелерінен біреуі - берілген шектеулердің орындалуы арқылы кейбір нысандар жиынын қаншада бір «қораптарға» жайғастырудың тәсілдер санын анықтау болып табылады.
Егер екі Х және Y жиындар берілген болса, бұл жерде çХ÷ ═ n, çYç ═ m, онда Х ті нысандар, Y ті қораптар деп есептесек кез келген f : Х Þ Y функция сондай бір орналастыруды береді, яғни ол хі нысанды уі қорапқа жайғастырудай f (хі) ═ уі теңдікті бейнелейді.
Тағыда басқаша интерпретация-бояқтау . Айталық Y түстер жиыны және f (х) х нысанның түсі болсын. Онда, бұл мәселені кейбір шектеулерге сақтана отырып бояулар санын анықтауға алып келу мүмкін. Мұнда, жалпылама қағиданы сақтай отырып барлық уақыт Х ═ í1,2,….,ný , ал Y ═ í1,2,….,mý деп есептеуге келісеміз. Егер орналастыруға еш қандай шектеулер қойылмайтын болса , онда барлық
f : Х Þ Y функциялар саны mn ге тең, яғни әншейін қайталамалы (m,n) орналастыру болады.
Егер, әр бір қорап біреуден артық болмаған нысандарға ие болса, онда біз m ³ n болған қайталамасыз (m,n) орналастыруға ие боламыз. Олардың саны дәл Аnm ге тең, яғни реттелген m қораптардан n данасын таңдаймыз және оларға бір данадан саламыз. Егерде n>m болсашы, онда ондай орналастыру мүмкін еместігін көреміз. Осы жерде Дирихле ұстанымы деп аталатын немесе қораптар ұстанымы қағидасы, яғни егер m қорапта (m+1) немесе оданда көп тастар бар болса , онда кемінде бір қорапта біреуден артық тас болу ұстанымы өз күшіне енеді.
Егер біз n нысанды m қораптар бойынша әр бір қорап қатаң реттелген тізбек құрастыратындай (оларға жайғастырылған нысандардың әншейін реттелмеген жиыны емес) етіп жайғастырсақ , онда мұндай жайғастыруды n нысанды m қораптар бойынша реттелген орналастыру деп айтамыз. Олардың санын [ m] [n] арқылы белгілейміз және n ═ 0 үшін [ m] [0] ═ 1 деп қабылдасақ , жалпы жағдайда төмендегі формулаға ие боламыз:
[ m] [n] ═ m . ( m + 1) × ….× (m +n -1) ═ Аnm+n -1.
Дәлелдеу. Бұл жерде жаңа нысандарды біртіндеп қоса отырып реттелген орналастырулар құрамыз. Бірінші нысанды әзірше бос болған кез келген қорапқа жайғастырып m тәсілмен орналастыру мүмкін. Екіншіні (m+1) тәсілмен, яғни қалған (m-1) бос қораптардың біреуіне немесе бірінші нысан жайғасқан қораптың алдыңғы немесе кейінгі қорабына. Жалпы жағдайда , егер қорапта s нысан бар болса, онда кезектегі нысанды осы қорапқа (s+1) тәсілмен жайғастыру мүмкін. Сондықтан, егер k-қорапта і-нысанды орналастырудан алдын rk ( k ═ 1,2, ….,m; k═1Sm rk ═ і – 1) нысан бар болған болса, онда оны барлығы болып
( r1 + 1) + ….+ ( rm + 1 ) ═ ( rm + 1 ) ═ ( r 1 + ….+ rm ) + m ═ ( і – 1 ) + m
тәсілмен орналастыру мүмкін. Сонымен бірге дәлелдеудің индуктивті тәсілі төменде көрсетілген.
6-сызбада екі а және b элементтің үш қорапқа [ 3 ] [ 2] ═ 3 × 4 ═ 12 реттелген орналастыру тәсілі көрсетілген.
-
-
a
b
a
b
b
a
b
a
a,b
b,a
a
b
b
a
a,b
b,a
a,b
b,a
-
6-сызба
Енді жоғарыдағы анықтамалардан пайдаланып негізгі комбинаторикалық элементтердің қысқаша жазылу формулаларын келтіреміз.
Алмастырулар. Қайталанбайтын комбинация үшін алмастырулар саны
Рn = n! ,
қайталамалы комбинация үшін
 n(k1,k2,…,kn) =
n(k1,k2,…,kn) =
 ,
(k1!
+k2!+...+kn! =
n)
,
(k1!
+k2!+...+kn! =
n)
формуласымен табылады.
Орналастырулар. Қайталанбайтын комбинация үшін
орналастырулар саны
 , ал қайталамалы
комбинация үшін
, ал қайталамалы
комбинация үшін
 mn
=
nm
mn
=
nm
формуласымен табылады.
Терулер. Қайталанбайтын комбинация үшін терулер саны
 ,
,
ал қайталамалы коминация үшін
 mn= Сkn+k-1=C
n-1n+k-1 =
mn= Сkn+k-1=C
n-1n+k-1 =

формуласымен табылады.
Мысал-8. Спортлото ( 36-дан 5) ойынына қатысушы бір билет сатып алған. Оны толтыру жағдайлары нешеу және ұту ықтималдығы қандай?
Шешуі. Бір билет толтыру үшін ойын ережесі бойынша 1-ден 36-ға дейінгі натурал санның бесеуін сызу керек. Сызу тәртібі әртүрлі, оның саны

Сонымен, ұтысқа қатынасатын тең мүмкіндікті жағдайлар саны n = 376992. Бір билет иесінің ұту ықтималдығы

Мысал -9: Цехта 6 ер адам, 4 әйел адам жұмыс істейді. Табельдегі нөмірлері бойынша 7 адам таңдап алынды. Таңдап алынған адамдардың ішінде 3 әйел бар болуының ықтималдығын табу керек.
Шешуі: Табелбдегі нөмірлері бойынша барлығы 10 адамнан 7 адам таңдап алудың жалпы саны 10 элементтен 7 элемент бойынша алынған терулер саны сияқты есептелінеді, яғни:

Ал, 3 әйелді
табельдік нөмірлері бойынша 4 әйелдің ішінен таңдап алудың
саны  формула
бойынша:
формула
бойынша:

Сондай-ақ 6 ер
адамнан 4 ер адам таңдаудың саны: 
Енді, көбейту
ережесін пайдалансақ, таңдап алынған 7 адамның ішінде 3 әйел, 4 ер
адам болу мүмкіндіктерінің жалпы саны
 тең. Сонымен анықталғалы
отырған ықтималдық:
тең. Сонымен анықталғалы
отырған ықтималдық:  .
.
Мысал-10. Лотереяда 10 билет бар. Оның ішінде 3 билет ұтысты. Кездейсоқ таңдап алынған 5 билеттің ішінде 2 билеттің ұтысты болып шығуының ықтималдығы қандай?
Шешуі. n
=  =
= =
=
 = 4∙7∙9.
= 4∙7∙9.
3 билеттен 2 ұтыс билетін таңдау жолының санын анықтаймыз:
 =
=  =
=
 = 3.
= 3.
7 билеттен 3 ұтыссыз билетті таңдау жолының санын анықтаймыз:
 =
=  =
= =
=
 = 5∙7 =
35.
= 5∙7 =
35.
Сынақтың қолайлы
жағдайының санын көбейту әдісі бойынша табамыз:
m  ∙
∙ = 3∙5∙7. А оқиғасының
ықтималдығын анықтаймыз:
= 3∙5∙7. А оқиғасының
ықтималдығын анықтаймыз:
P (A)
=  =
=
Мысал-11. Бірдей карточкаларға жазылған А, А, А, Б, Р, С, Т әріптерінен: а) 7 әріптен алғанда неше алмастырулар шығады? ә) «АТБАСАР» сөзінің шығу ықтималдығын анықтау керек.
Шешуі. а) Іріктемегенде әріптер әр түрлі болса, «жеті» әріппен жазылатын сөздер саны 7! болар еді. Ал биздің мысалымызда үш әріп бірдей. Сондықтан 7 әріпті әр түрлі сөздер (оның басым көпшілігі мағынасыз тіркестер) саны 7!- дан кемид. Өйткені «А» әріптері өз ара орындарын ауыстырғанда жаңа сөз шықпайды. Сондықтан есепті шешу үшін алдымен бірдей сөз құрайтын алмастырулар санын анықтап аламыз. «А» әрпінің өз ара орын ауыстырулар саны3!. Бұл әр типтегі сөздердің қайталану саны болмақ.
Бұл жағдайда 7 әріпті сөздердің бір типі «АТБАСАР» деген сөзбен көрсетейік. Түсіну оңай болу үшін алдымен әріптерді 1-ден 7-ге дейінгі цифрлармен нөмірлейік. Осы сөз құралатын алмастырулардың түрлері төменде цифрлармен келтірілді:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Содан жеті әріптен тұратын әр түрлі
«сөздер»  =
=  =
4*5*6*7 =840
=
4*5*6*7 =840
Тәсілмен шығады екен. Ал, оның ықтималдығын классикалық анықтама бойынша оңай табамыз. n=840, m=1, сондықтан Р(А) = 1/840.
Мысал
-12. Теңдіктегі
 -нің мәнін
табыңыз:
-нің мәнін
табыңыз:  =
=
 .
.
Шешуі: Теру формуласы бойынша мынадай теңдікті жазамыз:
 =
=
 Þ
Þ
 =
=  Þ
(n-6)(n-5) =
30 Þ
Þ
(n-6)(n-5) =
30 Þ
n2 – 9n + 20 = 30 Þ n2 – 9n - 10 = 0 Þ ( n= 10, n=-1 ), комбинаторика заңдарында n текқана натурал сан болғандықтан n=-1 санды шешім деп қабылдай алмаймыз. Сондықтан n= 10 теңдіктің шешімі болады.
4-лекция
Ықтималдықтар алгебрасы
-
Ықтималдықтарды қосу заңдылықтары.
-
Шартты ықтималдық.
3. Ықтималдықтарды көбейту заңдылықтары..
________________________________________________________________
-
Ықтималдықтардың қосу заңдылықтары.
Ықтималдықтарды есептеу сынаудың жалпы саны мен оқиғаның пайда болуына қолайлы нәтижелер санын анықтауға келіп тіреледі. Бұларды тікелей есептеу көп жағдайда үлкен қиындыққа ұшыратады. Сондықтан да камбинаторика формулаларын пайдалануға мәжбүр болдық. Оның үстіне, практикада кездесетін оқиғалар күрделі болып келеді де, олардың ықтималдылығын табу үшін, ол оқиғаларды бірнеше қарапайым оқиғалардың қосындысы не көбейтіндісі түрінде жазып, солардың ықтималдығын анықтайды. Сондықтан да қарастырып отырған оқиға ықтималдығын екінші ықтималдылық арқылы табудың маңызы өте-мөте зор. Ол үшін негізінен ықтималдылықтарды қосу және көбейту теоремаларын пайдаланады. Енді алдымен қосу теоремасын, одан шығатын бірнеше салдарды қарастырайық.
Екі А және В оқиғаларының қосындысы деп С = А+В оқиғасына айтылады, бұл С – оқиғасы А – оқиғаның пайда болуынан, В – оқиғасының пайда болуынан, немесе А оқиғасының және В оқиғасының біруақытта пайда болуынан құралады.
Мысал-1: Екі атқыш нысанаға бір-бір реттен оқ атады, А – оқиғасы бірінші атқыштың нысанаға дәл тигізуі, В – оқиғасы екінші атқыштың нысанаға дәл тигізуі. С=А+В – оқиғасы бірінші атқыштың нысанаға дәл тигізуі немесе екінші атқыштың нысанаға дәл тигізуі немесе бірінші және екінші атқыштың да нысанаға дәл тигізуі.
Бірнеше оқиғалардың қосындысы деп, осы оқиғалардың кем дегенде біреуінің пайда болуынан тұратын оқиғаға айтылады. А+В+С оқиғасы: А,В,С не болмаса А және В, не болмаса А және С, яки В және С, яки А және В және С оқиғаларының кем дегенде біреуінің пайда болуынан тұратын оқиғаға айтылады.
А және В оқиғалары үйлесімсіз болып және олардың ықтималдықтары мәлім болса, онда А оқиғасының немесе В оқиғасының ықтималдығы қосу теоремасымен анықталады.
Теорема. Үйлесімсіз А және В оқиғалар қосындысының ықтималдығы олардың ықтымалдықтарының қосындысына тең
P(А+В) = P(А) + P (В) (1)
Дәлелдеуі.
n – тең мүмкіндікті үйлесімсіз оқиғалар саны болсын.
m1 – А оқиғасы үшін қолайлы оқиғалар саны
m2 – В оқиғасына қолайлы оқиғалар саны
Демек, 
 ,
,

Теорема. Егер А1, А2, ... , Аn үйлесімсіз оқиғалар болса, онда бұлардың қосындысының ықтималдығы әрқайсысының ықтималдықтарының қосындысына тең болады.
P(А1+А2 + ... + Аn) = P(А1) + P(А2) + ... + P (Аn) (2)
Салдар-1.
Қарама-қарсы А және  оқиғалары ықтималдықтарының
қосындысы 1-ге тең, яғни
оқиғалары ықтималдықтарының
қосындысы 1-ге тең, яғни
P(А) +
P( ) =
1
) =
1
Дәлелдеуі. А мен
 қосындысы ақиқат оқиға
болғандықтан P (
қосындысы ақиқат оқиға
болғандықтан P ( +А) = 1, үйлесімсіз
болғандықтан
+А) = 1, үйлесімсіз
болғандықтан
P
(А+ ) = P (А) +
P(
) = P (А) +
P( ) =
1
) =
1
Сондықтан p = P (А),
q = P ( ) деп белгілеп p + q =
1
) деп белгілеп p + q =
1
Салдар-2. Егер А1, А2, ..., Аn оқиғалары үйлесімсіз болса және оқиғалардың толық тобын құраса, онда
P(А1) + P(А2) + ... + P (Аn) = 1 болады.
Дәлелдеуі. Ұйғарым бойынша не А1, не А2,… , не Аn пайда болуы ақиқат, олай болса, бұлардың қосындысының ықтималдығы 1-ге тең, яғни
P(А1) + P(А2) + ... + P (Аn) = P(А1+А2 + ...+ Аn) = 1 (3)
Мысал-2: Ұн қоймасы ұннан жасалған
тағамдарды А, В, С қалаларының ұн зауыттарынан қабылдайды. Қойманың
ұнды А қаласынан қабылдауы P(А) = 0,6-ға тең, В қаласынан қабылдауы
ықтималдығы  =0,3-ке тең, ұнның С-қаласынан
қабылдау ықтималдығы P (С) –
табылсын.
=0,3-ке тең, ұнның С-қаласынан
қабылдау ықтималдығы P (С) –
табылсын.
Шешуі. Ұннан жасалған тағамдарды А, В және С қалаларынан қабылдау оқиғасы оқиғаның толық тобын құрайды. (3) формула бойынша 0,6+0,3+p(С) = 1 болады. Бұл жерде P(С) = 1 – 0,9 = 0,1.
Теорема. Екі оқиғаның кемінде біреуінің пайда болу ықтималдығы олардың ықтималдықтарының қосындысы мен оқиғалардың бірге пайда болу ықтималдығының айырмасына тең болады.
P(А+В) = P (А) + P (В) –P(А.В)
Дәлелдеуі. Егер А және В үйлесімді оқиғалар болса , онда А+В=А+(В-АВ) және В = А.*В+(В-А.*В) теңдіктерінің оң жағындағы қосылғыштар үйлесімсіз оқиғалар болады.
P(А+В) = P (А) + P (В-А.В)
P(В)=P(А
.В)+P(В-А.В)
 P(А+В)=P(А)+P(В)-P(А.В)
P(А+В)=P(А)+P(В)-P(А.В)
Мысал-3. Жәшікте бірдей 20 шар бар. Оның 7-уі қызыл түсті, 8-і көк түсті, 5-уі ақ түсті. Жәшіктен қалаған бір шар алынады. Оның түсті ( не қызыл түсті, не көк түсті) шар болу ықтималдылығын анықтау керек.
Шешуі. Тең мүмкіндікті, үйлесімсіз оқиғалардың толық тобын құрайтын жағдайлар саны n =20. Қызыл түсті шар шығуын В оқиғасы, түсті шар шығуын С оқиғасы десек, онда А үшін қолайлы жағдайлар m = 7, В үшін қолайлы жағдайлар m =8 болады. Сонда С оқиғасының болу ықтималдылығы р(С) = р(А+В)=p(A)+p(A)= не 75% болады.
Мысал-4. Лотерея ойынына 1000 билет қатысады.Бұлардың біреуі 200 сом ұтады, төртеуі 100 сомнан, жиырма бесі 20 сомнан және елуі 10 сомнан ұтады. Қалған билеттер ұтпайды. Алынған бір лотерея ұтысының 20 сомнан кем болмау ықтималдығын анықтау керек.
Шешуі. А - ұтыс 20
сомнан кем болмауын,  - ұтыс 200
сом,
- ұтыс 200
сом,  – ұтыс 100 сом,
ал
– ұтыс 100 сом,
ал  – ұтыс 20 сом болуды
көрсететін оқиғалар болсын. Сонда
– ұтыс 20 сом болуды
көрсететін оқиғалар болсын. Сонда 
 ,
,
 - қос-қостан
үйлесімсіз оқиғалар, өйткені лотереяға бір ғана ұтыс шығады. Олай
болса, А =
- қос-қостан
үйлесімсіз оқиғалар, өйткені лотереяға бір ғана ұтыс шығады. Олай
болса, А = 
 +
+  формула
бойынша
формула
бойынша
P (A)
= P
( + P
(
+ P
( + P
(
+ P
( =
=  +
+  +
+  = 0,
03.
= 0,
03.
Мысал-5. Жәшікте бірдей 50 деталь бар, оның 45-і жарамды, 5-і жарамсыз. Бақылаушы жәшіктен кез келген 10 детальді алып тексереді. Егер осы алынған таңдама ішінде жарамсыз деталь саны бірден артық болмаса, онда жәшіктегі қалған детальдарды тексерместен жарамды деп қабылдайды. Бұлайша қабылдау ықтималдығы неге тең?
Шешуі. Алынған 10
детальдың ішінде бірде-бір жарамсыз деталь болмауы А оқиғасы, тек
бір жарамсыз деталь болуы В оқиғасы болсын. А және В оқиғалары
үйлесімсіз. Олай болса, P (A+B) = P (A) + P (B) . 50 детальдан 10
детальдың  тәсілімен аламыз.А
оқиғасына қолайлы элементар оқиғалар саны
тәсілімен аламыз.А
оқиғасына қолайлы элементар оқиғалар саны
 өйткені алынған 10
детальдың ішінде бірде-бір жарамсыз деталь
жоқ:
өйткені алынған 10
детальдың ішінде бірде-бір жарамсыз деталь
жоқ:
P (A)
=  =
=
 =
=  =
= =
0,31.
=
0,31.
В оқиғасына қолайлы
элементар оқиғалар саны  =
=
 ∙
∙ өйткені алынған 10
детальдың біреуі жарамсызда қалған тоғызы жарамды. Жарамдысын
барлық жарамдылардан
өйткені алынған 10
детальдың біреуі жарамсызда қалған тоғызы жарамды. Жарамдысын
барлық жарамдылардан  тәсілмен алсақ,
жарамсыздардан
тәсілмен алсақ,
жарамсыздардан  аламыз. Оның әр бір
жарамсызы жарамды детальдармен комбинацияланып келеді,
яғни
аламыз. Оның әр бір
жарамсызы жарамды детальдармен комбинацияланып келеді,
яғни  болады.
болады.
Демек, P
(B)
= = 0,43.
= 0,43.
P (A+B)
=  +
+  = 0,31 + 0,43 =
0,74.
= 0,31 + 0,43 =
0,74.
-
Шартты ықтималдық.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болуы ықтималдығын өзгертпесе , онда оларды тәуелсіз оқиғалар деп атайды.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Анықтама. Егер екі оқиға тәуелсіз оқиғалар болса және бірінші оқиғаның пайда болуы ықтималдылығы екіншісіне байланысты болмаса мұндай оқиғалар ықтималдылығы шартсыз оқиғалар деп аталады.
Анықтама. Егер бір оқиғаның ықтималдылығын есептегенде комплексті шарттан басқа екінші оқиғаның пайда болуы, не пайда болмауы әсер етіп, оның ықтималдығын өзгертсе , мұндай ықтималдықты шартты ықтималдық деп атайды.
P (А/В) немесе PВ (А)
Мысал-1. Қобдишада 10 шар бар, оның төртеуі ақ, алтауы қызыл. Қобдишадан кез келген бір шарды алып, түсін белгілегеннен соң екіншісін алады. Бірінші алынған шар қызыл түсті болғанда екінші рет алынған шардың ақ түсті болу ықтималдығын анықтау керек.
Шешуі. Бұл мысалдың шешуі қобдишадан алынған бірінші шар түсі белгіленген соң екінші шарды алу алдында ол шар қайта қобдишаға салыну, әлде қайта салынбауына байланысты. Осы себеппен мысал екі тәсілмен шешіледі.
Бірінші
тәсіл. Қобдишадан бірінші рет
алынған шар түсі қызыл болуы В оқиғасы болсын,
онда  оқиғасы қобдишадан
алынған бірінші шар түсі қызыл емес, яғни ақ шар шығуы болады.
Екінші рет алынған шар түсі ақ шар болуы А оқиғасы болсын,
онда
оқиғасы қобдишадан
алынған бірінші шар түсі қызыл емес, яғни ақ шар шығуы болады.
Екінші рет алынған шар түсі ақ шар болуы А оқиғасы болсын,
онда  оқиғасы екінші ретте
қызыл шардың шығуы болады. Бірінші алынған шар түсі белгіленгеннен
кейін, ол шар қобдишаға қайта салынған себепті, шар екінші рет
алынғанда да қобдишадағы шарлар саны бастапқыдай болады.Сондықтан А
оқиғасының ықтималдығы оған дейін қобдишада қызыл шар шығуына
байланысты емес, өзгермейді және ол 0,4-ке тең. Бұдан В оқиғасының
пайда болуының А оқиғасының ықтималдығына әсері болмайтынын
байқаймыз. Демек, А және В оқиғалары бір-біріне тәуелсіз. Бұл жерде
А оқиғасының ықтималдығын есептегенде оның пайда болуына комплексті
шарттан өзге ешқандай шек қойылмайды. Егер екі оқиғаның біреуінің
пайда болуы екіншісінің пайда болу ықтималдығын өзгеретін болса,
ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Екінші
тәсіл. Тәжірибе шарты
1-мысалдағыдай, бірақ бірінші рет алынған шар қобдишаға қайта
салынбайды. Бұл жағдайда екінші ретте А оқиғасының пайда болу
ықтималдығы оның алдында қызыл шар (B), не ақ
шар
оқиғасы екінші ретте
қызыл шардың шығуы болады. Бірінші алынған шар түсі белгіленгеннен
кейін, ол шар қобдишаға қайта салынған себепті, шар екінші рет
алынғанда да қобдишадағы шарлар саны бастапқыдай болады.Сондықтан А
оқиғасының ықтималдығы оған дейін қобдишада қызыл шар шығуына
байланысты емес, өзгермейді және ол 0,4-ке тең. Бұдан В оқиғасының
пайда болуының А оқиғасының ықтималдығына әсері болмайтынын
байқаймыз. Демек, А және В оқиғалары бір-біріне тәуелсіз. Бұл жерде
А оқиғасының ықтималдығын есептегенде оның пайда болуына комплексті
шарттан өзге ешқандай шек қойылмайды. Егер екі оқиғаның біреуінің
пайда болуы екіншісінің пайда болу ықтималдығын өзгеретін болса,
ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Екінші
тәсіл. Тәжірибе шарты
1-мысалдағыдай, бірақ бірінші рет алынған шар қобдишаға қайта
салынбайды. Бұл жағдайда екінші ретте А оқиғасының пайда болу
ықтималдығы оның алдында қызыл шар (B), не ақ
шар  оқиғасы шығуына
байланысты. Егер бірінші сынауда қызыл шар шықса, онда екінші
сынауда ақ шар шығу ықтималдығы 4/9 болады. Егер бірінші
сынауда
оқиғасы шығуына
байланысты. Егер бірінші сынауда қызыл шар шықса, онда екінші
сынауда ақ шар шығу ықтималдығы 4/9 болады. Егер бірінші
сынауда  оқиғасы пайда болса (ақ
шар шықса), онда екінші ретте де ақ шар шығу (А оқиғасы)
ықтималдығы 3/9 = 1/3-ке тең. Осы сияқты, егербірінші сынауда қызыл
шар (
оқиғасы пайда болса (ақ
шар шықса), онда екінші ретте де ақ шар шығу (А оқиғасы)
ықтималдығы 3/9 = 1/3-ке тең. Осы сияқты, егербірінші сынауда қызыл
шар ( оқиғасы) не ақ шар
(
оқиғасы) не ақ шар
( оқиғасы) шықты десек,
онда екінші сынауда қызыл шар (
оқиғасы) шықты десек,
онда екінші сынауда қызыл шар ( оқиғасы) пайда болу
ықтималдығы сәйкес 5/9 және 2/3 сандарына
тең.
оқиғасы) пайда болу
ықтималдығы сәйкес 5/9 және 2/3 сандарына
тең.
Шартты
ықтималдық. 1-мысалда А оқиғасының
ықтималдығын есептегенде комплексті шарттан басқа В оқиғасының
пайда болу, не пайда болмауы әсер етіп, А оқиғасының ықтималдығын
өзгертіп отырады. Мұндай ықтималдыты шартты ықтималдық деп атайды.
Шартты ықтималдықты былай белгілейді: P (A/B)
немесе  (A). А және В
оқиғаларының тәуелсіздігін P (A/B)= P (A),
(A). А және В
оқиғаларының тәуелсіздігін P (A/B)= P (A),
 (A) = P (A)) түрінде
жазуға болады. 1- мысалдан
(A) = P (A)) түрінде
жазуға болады. 1- мысалдан
P (A) = P (A/B) =
0,4 , P (A) = P (A/ ) =
0,4
) =
0,4
Сондай-ақ
P
( ) = P
(
) = P
( /B)= 0,6 , P
(
/B)= 0,6 , P
( ) = P
(
) = P
( /
/
 ) = 0,6
.
) = 0,6
.
Егер А және В оқиғалары бір-біріне тәуелді болса, онда сол мысалдан
P (A) =
(A/B) , P
(A/B)=4/9
, P
(A/ ) =
1/3;
сондай-ақ
) =
1/3;
сондай-ақ
P
( /B) =5/9, P
(
/B) =5/9, P
( /B) =
2/3.
/B) =
2/3.
Шартты ықтималдықтың қасиеттері.
1. 0 ≤ P(А) ≤ 1
2. PВ(U) =1
3. PВ(V) = 0
4.Егер
А1 А2
болса,онда PВ
(А1)≤PВ(А2)
А2
болса,онда PВ
(А1)≤PВ(А2)
5.Егер А1=А2 болса, онда PВ (А1)=PВ(А2)
6.Егер А1...Аn үйлесімсіз және А=А1+...+Аn болса, онда
PВ (А)=PВ(А1)+...+ PВ(Аn)
70. А1...Аn – үйлесімсіз және олар оқиғалардың толық жүйеcін құраса, яғни
U =A1+…+ An , болса , онда PВ (U) = PВ (А1) + ...+ PВ (Аn) = 1
_ _
80.А және А – қарсы оқиғалар болса, онда Pв(А) =1-PВ(А).
-
Ықтималдықтардың көбейту теоремалары.
Теорема. Екі тәуелді оқиғаның көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығы мен сол оқиға пайда болғандaғы екінші оқиғаның шартты ықтималдығының көбейтіндісіне тең:
P(А * В) = P (А) * PА (В) = P(В) * PВ (А)
Дәлелдеуі.
n–тең мүмкіндікті үйлесімсіз және оқиғаның толық тобын құрайтын оқиғалар саны.
m- А- оқиғаға қолайлы ;
к – В –оқиғаға қолайлы;
r – А және В оқиғаға қолайлы.
P(А)=m/n; P(В)=k/n; P(А*В)=r/n; P(A.B)=r/n ;
PВ
(А) = r/k;бұл жерде r≤m, r≤k ;
r≤m, r≤k; PA(В) = r/m; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 P
(A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
.
P
(A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
.
Tеорема дәлелденді.
Мысал-2. Қобдишада 15 ұтысты, 10 ұтыссыз лотерея билеттері бар. Бір-бірлеп екі билет алынады (билет қаита салынбайды). Алынған екі билеттің де ұтатын билет болу ықтималдығын анықтау керек.
Шешуі: А- бірінші билеттің ұтуы.
В- екінші билетің ұтуы.
P(A)=15/25= 3/5; PA(B)=14/24=7/12;
Демек, P(A*B)=P(A)*PA(B)=3/5*7/12=0,35;
Теорема. А1,А2,…,Аn тәуелді оқиғалары көбейтіндісінің ықтималдығы мына формуламен өрнектеледі:
P(A1A2…An)=P(A1)* (A2)*
(A2)* (A3)
(A3)

 (An)
(An)
Дәлелдеуі. Мұны математикалық индукция әдісімен дәлелдейік.n=2 болғанда теорема дәлелденді, онда n=k мәнінде де бұл өрнек орын алады, яғни:
 болады.
Енді
болады.
Енді
n = k+1үшін теореманы дәлелдейік:
 деп алайық ,сонда
А =
В*Ак+1
болады.
деп алайық ,сонда
А =
В*Ак+1
болады.

Теорема. Екі тәуелсіз оқиғалар көбейтіндісінің ықтималдығы олардың шартсыз ықтималдықтарының көбейтіндісіне тең, яғни
P(A*В)=P(A)P(B) болады.
Дәлелдеуі. А және В оқиғалары тәуелсіз болғандықтан
P(A) = PВ(A) және P(B) = PA(B);P(A*В) = P(B)*PB(A) = P(B)*P(A)
Теорема. Егер А1, А2, ...,Аn оқиғалары жиынтығы бойынша тәуелсіз болса, онда олардың көбейтіндісінің ықтималдығы әрқайсысының ықтималдықтарының көбейтіндісіне тең, яғни:

Салдар. Егер А оқиғасы В-оқиғасына тәуелсіз болса, онда В оқиғасы А- оқиғасына да тәуелсіз болады.
Салдар. Егер А оқиғасы мен В-оқиғасы тәуелсіз болса, онда


 оқиғалары да
біріне-бірі тәуелсіз болады.
оқиғалары да
біріне-бірі тәуелсіз болады.
Мысал-3: Апатты хабарлау үшін бір-біріне тәуелсіз жұмыс істейтін екі сигналдаушы орнатылған. Апат кезінде сигналдаушының жұмыс істеу ықтималдығы бірінші сигналдаушы үшін
0,95 - ке,ал екіншісі үшін 0,9 – ға тең. Апат кезінде екі сигналдушының да жұмыс істеуінің ықтималдығын табу керек.
Шешуі.
А – оқиғасы бірінші сигналдаушы жұыс істейді.
В – оқиғасы екінші ситналдаушы жұыс істейді.
Бұл оқиғалардың сәйкес ықтималдықтары P(A) = 0,95 P(B) = 0,9 А оқиғасы мен В оқиғасы өзара тәуелсіз, сондықтан олардың бірге пайда болу ықтималдығы мынаған тең:
P (A*B) = P(A) *P (B) = 0,95* 0,9 = 0,855
Мысал-4. Үш оқушы біреуі монетті, екіншісі кубты лақтырды, ал үшіншісі колодадағы 36 картаның кез келген біреуін суырды. Осы жүргізген тәжірибелер нәтижесінде монеттің герб жағымен түсу (А оқиғасы), кубтың 4 ұпаймен түсу (В оқиғасы ), және суырған картаның тұз болып шығу (С оқиғасы ) ықтималдығын анықтау керек.
Шешуі. Өткен мысалдарды еске түсірсек,
р(А)=1/2, р(B)=1/6, р(C)=1/9.
Сонда іздеген ықтималдығымыз төмендегідей табылады:
Р(АВС)=p(A)*p(B)*p(C)=1/2*1/6*1/9=1/108=0,092.
5- сабақ
Шартты ықтималдық. Ықтималдықтардың көбейту теоремасы.
Толық ықтималдықтар формуласы. Байес формуласы.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болуы ықтималдығын өзгертпесе , онда оларды тәуелсіз оқиғалар деп атайды.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Анықтама. Егер екі оқиға тәуелсіз оқиғалар болса және бірінші оқиғаның пайда болуы ықтималдылығы екіншісіне байланысты болмаса мұндай оқиғалар ықтималдылығы шартсыз оқиғалар деп аталады.
Анықтама. Егер бір оқиғаның ықтималдылығын есептегенде комплексті шарттан басқа екінші оқиғаның пайда болуы, не пайда болмауы әсер етіп, оның ықтималдығын өзгертсе , мұндай ықтималдықты шартты ықтималдық деп атайды.
P (А/В) немесе PВ (А)
Мысалы. Жәшікте 10 шар бар, оның төртеуі ақ , алтауы қызыл. Жәшіктен кез-келген бір шарды алып, түсін анықтаған соң екіншісін алайық . Бірінші алынған шар қызыл болған жағдайда екінші алынған шардың ақ түсті болу ықтималдығы анықталсын.
Шешуі: бірінші тәсіл. ( алынған шар жәшікке қайта салынады.)
А -ақ шар алынады ( екінші ретте).
В - қызыл шар болуы оқиғасы .
Pв(А)=P(А) – тәуелсіз оқиғалар .


Екінші тәсіл. (Алынған шар жәшікке қайта салынбайды ).
 (А) =
(А) = 
 (А)
=
(А)
=
Шартты ықтималдықтың қасиеттері.
1. 0 ≤ P(А) ≤ 1
2. PВ(U) =1
3. PВ(V) = 0
4.Егер А1 А2
болса,онда PВ
(А1)≤PВ(А2)
А2
болса,онда PВ
(А1)≤PВ(А2)
5.Егер А1=А2 болса, онда PВ (А1)=PВ(А2)
6.Егер А1...Аn үйлесімсіз және А=А1+...+Аn болса, онда
PВ (А)=PВ(А1)+...+ PВ(Аn)
70. А1...Аn – үйлесімсіз және олар оқиғалардың толық жүйеcін құраса, яғни
U =A1+…+ An , болса , онда PВ (U) = PВ (А1) + ...+ PВ (Аn) = 1
_ _
80.А және А – қарсы оқиғалар болса, онда Pв(А) =1-PВ(А).
Теорема. Екі тәуелді оқиғаның көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығы мен сол оқиға пайда болғандaғы екінші оқиғаның шартты ықтималдығының көбейтіндісіне тең:
P(А * В) = P (А) * PА (В) = P(В) * PВ (А)
Дәлелдеуі.
n–тең мүмкіндікті үйлесімсіз және оқиғаның толық тобын құрайтын оқиғалар саны.
m- А- оқиғаға қолайлы ;
к – В –оқиғаға қолайлы;
r – А және В оқиғаға қолайлы.
P(А)=m/n; P(В)=k/n; P(А*В)=r/n; P(A.B)=r/n ;
PВ
(А) =
r/k;бұл жерде r≤m, r≤k ; r≤m, r≤k; PA(В) = r/m; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 P (A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
P (A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
теорема дәлелденді.
Мысал. Қобдишада 15 ұтысты, 10 ұтыссыз лотерея билеттері бар. Бір-бірлеп екі билет алынады (билет қаита салынбайды). Алынған екі билеттің де ұтатын билет болу ықтималдығын анықтау керек.
Шешуі: А- бірінші билеттің ұтуы.
В- екінші билетің ұтуы.
P(A)=15/25= 3/5; PA(B)=14/24=7/12;
Демек, P(A*B)=P(A)*PA(B)=3/5*7/12=0,35;
Теорема. А1,А2,…,Аn тәуелді оқиғалары көбейтіндісінің ықтималдығы мына формуламен өрнектеледі:
P(A1A2…An)=P(A1)* (A2)*
(A2)* (A3)
(A3)

 (An)
(An)
Дәлелдеуі. Мұны математикалық индукция әдісімен дәлелдейік.n=2 болғанда теорема дәлелденді, онда n=k мәнінде де бұл өрнек орын алады, яғни:
 болады. Енді
болады. Енді
n = k+1үшін теореманы дәлелдейік:
 деп алайық ,сонда А = В*Ак+1
болады.
деп алайық ,сонда А = В*Ак+1
болады.

Теорема. Екі тәуелсіз оқиғалар көбейтіндісінің ықтималдығы олардың шартсыз ықтималдықтарының көбейтіндісіне тең, яғни
P(A*В)=P(A)P(B) болады.
Дәлелдеуі. А және В оқиғалары тәуелсіз болғандықтан
P(A) = PВ(A) және P(B) = PA(B);P(A*В) = P(B)*PB(A) = P(B)*P(A)
Теорема. Егер А1, А2, ...,Аn оқиғалары жиынтығы бойынша тәуелсіз болса, онда олардың көбейтіндісінің ықтималдығы әрқайсысының ықтималдықтарының көбейтіндісіне тең, яғни:

Салдар. Егер А оқиғасы В-оқиғасына тәуелсіз болса, онда В оқиғасы А- оқиғасына да тәуелсіз болады.
Салдар. Егер А оқиғасы мен В-оқиғасы тәуелсіз болса, онда


 оқиғалары да біріне-бірі тәуелсіз
болады.
оқиғалары да біріне-бірі тәуелсіз
болады.
Мысал: Апатты хабарлау үшін бір-біріне тәуелсіз жұмыс істейтін екі сигналдаушы орнатылған. Апат кезінде сигналдаушының жұмыс істеу ықтималдығы бірінші сигналдаушы үшін
0,95 - ке,ал екіншісі үшін 0,9 – ға тең. Апат кезінде екі сигналдушының да жұмыс істеуінің ықтималдығын табу керек.
Шешуі.
А – оқиғасы бірінші сигналдаушы жұыс істейді.
В – оқиғасы екінші ситналдаушы жұыс істейді.
Бұл оқиғалардың сәйкес ықтималдықтары P(A) = 0,95 P(B) = 0,9 А оқиғасы мен В оқиғасы өзара тәуелсіз, сондықтан олардың бірге пайда болу ықтималдығы мынаған тең:
P (A*B) = P(A) *P (B) = 0,95* 0,9 = 0,855
Мысалды шешіңіз. Құрылыс отрядында 70% бірінші курс студенттері, ал 30% екінші курс студенттері. Бірінші курс студенттерінің ішінде 10%, ал екінші курс студенттерінің ішінде 5% қыздар бар. Барлық қыздар кезекпен асханада жұмыс істейді. Кез келген бір күнде тексергенде асханада бірінші курста оқитын қыз жұмыс істеп жатқандығының ықтималдығы қандай?
6- сабақ
Бернулли схемасы. Пуаcсон формуласы. Муавр-Лапластың локальдық теоремасы.
n санының үлкен мәндерінде тәжірибелердің қайталануында Бернулли формуласын пайдалану үлкен қиыншылықтар туғызады, себебі ол үлкен сандар үстінде амалдарды орындаумен байланысты.
Мысалы, Бернулли формуласында n = 50 m = 20; p = 0,1;
q = 0,9 болғанда Бернулли формуласы төмендегі көріністе болады:

Бұл жерде  ;
;  ;
; 



![]()
![]()
С![]() ол үшін ықтималдықты жеткілікті дәрежедегі дәлдікпен
анықтауға мүмкіндік беретін асимптотикалық формуладан пайдалану
қажеті болады.
ол үшін ықтималдықты жеткілікті дәрежедегі дәлдікпен
анықтауға мүмкіндік беретін асимптотикалық формуладан пайдалану
қажеті болады.
Бұндай дәрежедегі формуланы бірінші болып P = q
=  болғандағы Бернулли
схемасының дербес жағдайы үшін А.Муавр ойлап тапты. Сонан соң ол 0
және 1-ге тең болмаған Р жағдайы үшін ойлап тапқан П.С.Лапласпен
біріктірілді. Сондықтан бұл формула Муавр – Лаплас теоремасы деп
аталады.
болғандағы Бернулли
схемасының дербес жағдайы үшін А.Муавр ойлап тапты. Сонан соң ол 0
және 1-ге тең болмаған Р жағдайы үшін ойлап тапқан П.С.Лапласпен
біріктірілді. Сондықтан бұл формула Муавр – Лаплас теоремасы деп
аталады.
Теорема. Егер А оқиғасының әрбір
сынаудағы пайда болу ықтималдығы р- тұрақты болып, 0 мен 1 санына
тең болмаса (0 )және сынау саны
)және сынау саны  болса, онда оқиғаның дәл m – рет пайда болу
ықтималдығы
болса, онда оқиғаның дәл m – рет пайда болу
ықтималдығы  санының көбейтіндісі
санының көбейтіндісі  өрнегіне ұмтылады.
өрнегіне ұмтылады.
 мұндағы
мұндағы 
немесе

 функциясының мәндерінің,
функциясының мәндерінің,  үшін кітаптың соңында қосымшада №1 кестесі берілген,
ал
үшін кітаптың соңында қосымшада №1 кестесі берілген,
ал  болғанда да осы
кестеден пайдалануға болады, себебі
болғанда да осы
кестеден пайдалануға болады, себебі  функциясы жұп функция,
функциясы жұп функция, 
Дәлелдеуі. 

Енді 

Cтирлинг формуласынан пайдаланып Бернулли формуласын жазамыз.



![]()
![]()
![]()
![]()






Логарифм дейміз:

 ;
;
Логарифмдік функцияны дәрежелік қатарға жіктеу формуласын қолдаймыз.





 ;
;
потенцирлейміз:  ;
;
Сонымен  Теорема дәлелденді.
Теорема дәлелденді.
 тің қасиеттері.
тің қасиеттері.
10.
 жұп функция және оның графигі ОУ
осіне
симметриялы.
жұп функция және оның графигі ОУ
осіне
симметриялы.
20.
ОУ осімен у
=  графигі
графигі  нүктеде қиылысад
нүктеде қиылысад
30. ОХ
осімен
у қиылыспайды.
қиылыспайды.
Мысал. Нысанаға бір рет оқ атқанда оған тию ықтималдығы 0,8 – ге тең. Нысанаға 100 –рет оқ атылғанда оған 75 – рет тию ықтималдығы табылсын.
Шешуі. ![]()
Р = 0,8; n = 100; m = 75 екендігі берілген.
q = 1 – p = 1 – 0,8 = 0,2 екендігін табамыз.

х =-1,25 болғандағы  функциясының мәнін кітап соңындағы қосымшадағы №1 кестеден
іздейміз.
функциясының мәнін кітап соңындағы қосымшадағы №1 кестеден
іздейміз.
 ал
ал 
Олай болса, ізделінді ықтималдық

Жауабы: 
Егер  ал
ал  яғни
яғни  болса және m – нің мәні де жеткілікті түрде аз сан болса,
онда ізделінді ықтималдықты есептеуге Пуассонның жуықтап есептеу
формуласы қолданылады.
болса және m – нің мәні де жеткілікті түрде аз сан болса,
онда ізделінді ықтималдықты есептеуге Пуассонның жуықтап есептеу
формуласы қолданылады.
Мысал: Салыстырмалы жиіліктің ықтималдықтан (Р=3/8) ауытқуының абсолют шамасының 0,01-ден кем болмауының ықтималдығы 0,995-ке тең болуы үшін қанша тәуелсіз сынақтар жасау керек?
Шешуі: P=3/8; q=1-p=5/8;  0,01.
0,01.
Pn(k) .
.
Есептің шарты бойынша:  яғни 2Ф(0,01
яғни 2Ф(0,01 )=0,995.
)=0,995.
Сонда кестеден: 0,01 =2,8
=2,8




п=78400*0,234375
п=18375.
Тәуелсіз тәжірбиелердегі салыстырмалы жиіліктің тұрақты ықтималдықтан ауытқу ықтималдығы.
Мысал: А оқиғасының тәжірбиедегі пайда болған ықтималдығы 0,2-ге тең. Оқиғаның 400 тәжірбиеде 102 рет пайда болу ықтималдығын табу керек.
Шешуі: n=400, k=102, p=0,2; q=1-0,2=0,8.
Бұл есепті дәл шешуі Бернулли формуласымен табылады, бірақта бұл есепте сынақтар саны n=400 өте көп. Сондықтан Муавр-Лапластың локалдық формуласын пайдаланамыз. Ол үшін әуелі х-тің мәнін табамыз:
 Сонда
Сонда  Р400(102)
Р400(102)
7- сабақ
Кездейсоқ шамалар жайында жалпы түсінік. Дискретті кездейсоқ шамалар. Кездейсоқ шаманың ықтималдық тығыздығы. Кездейсоқ шамалардың тәуелсіздігі
Сынау нәтижесінде қандайда бір мүмкін мәнді қабылдайтын шаманы кездейсоқ шама деп атайды.
Егер кездейсоқ шамалардың қабылдаған мүмкін мәндерін жекелеп, айырып санауға келетін болса, мұндай шамаларды дискертті кездейсоқ шама деп атайды
Егер кездейсоқ шама белгілі аралықта біртұтас болса онда, яғни жекелеуге келмесе, онда оны үздіксіз кездейсоқ шама деп атайды.
Мысалы.
Ойын кубигін лақтырғанда ұпай санының пайда болуын көрейік, ұпай саны – кездейсоқ шама; 1,...,6 – мәндері.
Дискретті кездейсоқ шамалардың үлестіру заңдары.
Кездейсоқ шама мәндерімен оларға сәкес ықтималдықтарды байланыстыратын ереже дискретті шаманың үлестіру заңы деп аталады. Бұл заң таблица, график немесе формула түрінде өрнектеледі.
1. Дискретті кездейсоқ шамалардың кесте түрінде берілуі.
|
Х |
X1 |
X2 |
X3 |
… |
Xn |
|
P |
P1 |
P2 |
P3 |
… |
Pn |
Бұл жерде ықтималдықтар әр түрлі мәндерді қабылдайды.
р1+ р2 + ... + рn = 1
Mұндай кестені кезедейсоқ шаманың үлестірім кестесі
немесе үлестірім заңы деп атайды.
Мысал .
Алты бұйымнан тұратын партияның төртеуі жарамды. Қалай болса солай екі бұйым таңдап алынады. Таңдап алынған жарамды бұйымдар саны –Х–дискрет кездейсоқ шаманың үлестірім заңы құрылсын.
Шешуі. Х- кездейсоқ шама төмендегідей мүмкін болған мәндерді қабылдайды: x1= 0, x2= 1, x3=2. Оларға сәйкес ықтималдықтарды
 формуладан пайдаланып табамыз. (N –
партиядағы
формуладан пайдаланып табамыз. (N –
партиядағы
бұйымдар саны, n – партиядағы жарамды бұйымдар саны, m таңдап алынған бұйымдар саны, k – таңдап алынған бұйымдардың ішінде жарамдылар саны)



Ізделінді үлестірім заңын құрамыз:
|
X |
0 |
1 |
2 |
|
P |
|
|
|
Тексеру: 
Дискретті кездейсоқ шаманың график түрінде берілуі.
Дискретті кездейсоқ шаманың үлестіру заңын график түрінде бейнелеуге болады. Ол үшін жазықтықтағы тік бұрышты координаттар жүйесінде (хi; рi) нүктелерін белгілейді де, олардың ретіне қарай жалғастыратын кесінділер жүргізіледі. Шыққан фигураны үлестіру көпбұрышы деп атайды.
Мысал. Дискретті кездейсоқ шама Х мынадай үлестірім заңымен берілген:
|
Х |
2 |
4 |
5 |
6 |
|
Р |
0,3 |
0,1 |
0,2 |
0,4 |
Үлестіру көп бұрышын сызыңдар.
![]() P
P
0![]()
![]() .8
.8
0![]() .7
.7
0![]() .6
.6
0![]() .5
.5
0![]()
![]() .4
.4
0![]()
![]() .3
.3
0![]()
![]() .2
.2
0![]()
![]() .1
.1
![]()
![]()
![]()
![]()
![]() 0
0
![]() 0 x
0 x
-
4 5 6
Дискретті кездейсоқ шамалардың үлестірім заңдары
Х дискретті кездейсоқ шамасы ![]() мәндерін
мәндерін ![]() ықтималдықтарымен
қабылдасын
(
ықтималдықтарымен
қабылдасын
(![]() немесе
немесе ![]() ).
).
Х үлестірім заңы кестемен берілсін:
|
Х |
|
|
… |
|
… |
|
Р |
|
|
… |
|
… |
Бұл кесте үлестірім қатары деп
аталады. ![]() ,
, ![]() оқиғалары үйлесімсіз және толық топ
құрайды, яғни
оқиғалары үйлесімсіз және толық топ
құрайды, яғни ![]() .
.
Х үлестірім заңының графиктік түрде
берілуі: тік бұрышты координаталар жүйесінде абсцисса
осі бойына ![]() мәндері, ал ордината осіне – осы
мәндердің
мәндері, ал ордината осіне – осы
мәндердің ![]() ықтималдықтары салынады.
(
ықтималдықтары салынады.
(![]() ,
,![]() ) координаталы нүктелерді тізбектей кесінділермен
қосады. Пайда болған сынық сызықты үлестірімнің көпбұрышы деп
атайды.
) координаталы нүктелерді тізбектей кесінділермен
қосады. Пайда болған сынық сызықты үлестірімнің көпбұрышы деп
атайды.
Үлестірім заңының аналитикалық берілуі мүмкін мәндердің өз ықтималдықтарымен байланыстыратын формуланы айқындауды талап етеді. Бұндай формуланы кейбір кездейсоқ шамалар үшін ғана табуға болады.
Бернулли және Пуассон үлестірімдерін «Кездейсоқ шамалардың негізгі үлестірім заңдары» тақырыбында қарастырамыз.
8-сабақ
Кездейсоқ шамалардың үлестіру функциялары
Үзіліссіз кездейсоқ шамалар. Үлестірім функциясы
Үзіліссіз кездейсоқ шаманы үлестірім заңымен немесе үлестірім көпбұрышымен беруге болмайтындығы белгілі. Дискретті және үзіліссіз кездейсоқ шамалар үшін үлестірім заңын берудің универсал жолы бар.
Анықтама.
Х кездейсоқ шамасының үлестірім функциясы (немесе интегралдық функциясы, үлестірім заңы) деп әрбір х мәні үшін оқиғалар ықтималдығы X<x, яғни F(x)=P(X<x) (1) анықталатын F(x) функциясы айтылады.
![]() мәндерін қабылдайтын дискретті
Х кездейсоқ шамасы үшін (1) формула келесі түрде
жазылады
мәндерін қабылдайтын дискретті
Х кездейсоқ шамасы үшін (1) формула келесі түрде
жазылады ![]() ,
мұндағы
,
мұндағы ![]() қосындылау х-тен кіші
барлық
қосындылау х-тен кіші
барлық ![]() мәндеріне
салыстырмалылығын білдіреді. Сонымен, дискретті кездейсоқ шамасы
үшін бұл функция
үзілісті,
мәндеріне
салыстырмалылығын білдіреді. Сонымен, дискретті кездейсоқ шамасы
үшін бұл функция
үзілісті, ![]() - оның үзіліс нүктелері.
Үзіліссіз кездейсоқ шама
үшін F(x) үзіліссіз.
- оның үзіліс нүктелері.
Үзіліссіз кездейсоқ шама
үшін F(x) үзіліссіз.
F(x) қасиеттері
1) барлық х
үшін ![]() .
.
Бұл қасиет ықтималдық сияқты F(x) анықтамасынан шығады
2) F(x) кемімелі емес, яғни
егер ![]() ,
онда
,
онда ![]() .
.
Расында, ![]() болсын.
болсын. ![]() оқиғасын екі оқиғаның
қосындысы түрінде жазуға
болады:
оқиғасын екі оқиғаның
қосындысы түрінде жазуға
болады: ![]() . Бұл оқиғалар үйлесімсіз
болғандықтан, ықтималдықтарды қосу теоремасы
бойынша:
. Бұл оқиғалар үйлесімсіз
болғандықтан, ықтималдықтарды қосу теоремасы
бойынша: ![]() ,
бұдан
,
бұдан
![]()
![]() .
.
Кез келген ықтималдық теріс
емес болғандықтан, онда ![]() ,
яғни
,
яғни ![]() . Қасиет
дәлелденді.
. Қасиет
дәлелденді.
Салдар 1.
Кездейсоқ
шаманың ![]() аралығына түсу
ықтималдығы
аралығына түсу
ықтималдығы
![]() ,
,
бұл ![]() теңдігінен
шығады.
теңдігінен
шығады.
Салдар 2.
Кездейсоқ шама белгілі бір мәнді қабылдау
ықтималдығы нолге тең.
Егер ![]() формуласында
формуласында ![]() деп
алып,
деп
алып, ![]() кезде шекке көшсек,
онда
кезде шекке көшсек,
онда ![]() ,
, ![]() үзіліссіздіктерінен және
үзіліссіздіктерінен және
![]() .
.
Салдар 3.
![]() .
.
3)
Егер кездейсоқ шаманың мүмкін
мәндері ![]() интервалында жатса,
онда
интервалында жатса,
онда ![]() және
және ![]() ; үзіліссіз кездейсоқ шама үшін мүмкін
мәндері барлық сан осінде
жатса,
; үзіліссіз кездейсоқ шама үшін мүмкін
мәндері барлық сан осінде
жатса, ![]() және
және ![]() .
Аталып өткен қасиеттер үзіліссіз кездейсоқ шаманың графигін салуға
мүмкіндік береді:
.
Аталып өткен қасиеттер үзіліссіз кездейсоқ шаманың графигін салуға
мүмкіндік береді:
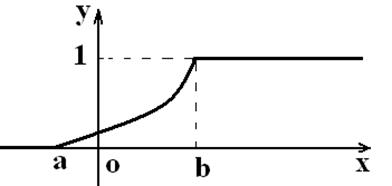
1 сурет
Айта кетелік, үзіліссіз кездейсоқ шаманы көбінесе үзіліссіз үлестірім функциясы бар шама ретінде анықталады.
Үлестірім тығыздығы
Үзіліссіз кездейсоқ шаманы үлестірім функциясынан басқа жолмен де беруге болады. Оның басты сипаттамасы – ықтималдықтардың үлестірім тығыздығы.
Анықтама.
Үзіліссіз кездейсоқ шаманың ықтималдықтарының
үлестірім тығыздығы (жәй үлестірім тығыздығы немесе
үлестірімнің дифференциалдық функциясы,
белгіленуі ![]() ) деп оның үлестірім функциясының туындысы
айтылады, яғни
) деп оның үлестірім функциясының туындысы
айтылады, яғни ![]() .
.
Үлестірім тығыздығының ықтималдық мағынасын анықтайық. Туындының анықтамасы бойынша
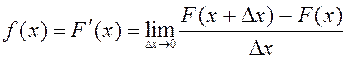 =
|
=
| ![]() қасиеті|
=
қасиеті|
= 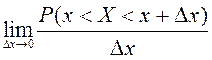 .
.
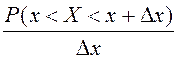 қатынасы
қатынасы ![]() интервалындағы орта ықтималдықты
білдіргендіктен,
интервалындағы орта ықтималдықты
білдіргендіктен, ![]() функциясы
функциясы ![]() нүктесіндегі және оның аймағындағы
ықтималдықты сипаттайды.
нүктесіндегі және оның аймағындағы
ықтималдықты сипаттайды.
Айта кетелік, үлестірімнің дифференциалдық функциясы, интегралдық функция сияқты үлестірім заңының бірі болады, бірақ интегралдық функция сияқты универсалды бола алмайды. Үлестірім тығыздығы тек үзіліссіз кездейсоқ шамалар үшін ғана анықталады.
f(x) қасиеттері
1. Х-тің ![]() интервалына түсу ықтималдығы келесі формула
бойынша анықталады:
интервалына түсу ықтималдығы келесі формула
бойынша анықталады:
 .
.
Расында, 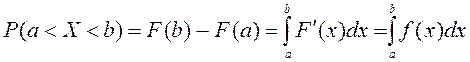 .
.
2. 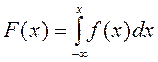 .
.
Расында,  .
.
3. ![]() үшін
үшін ![]() .
.
Расында, ![]() , бірақ
, бірақ ![]() кемімелі емес,
сондықтан
кемімелі емес,
сондықтан ![]() , олай болса
, олай болса ![]() .
.
4. 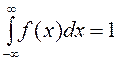 .
.
Бірінші
қасиетте ![]() деп есептейік,
онда
деп есептейік,
онда  , бірақ
, бірақ ![]() ақиқат оқиға,
сондықтан
ақиқат оқиға,
сондықтан ![]() . Яғни
. Яғни 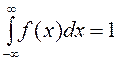 .
.
![]() үлестірім тығыздығының графигі
үлестірім қисығы деп аталады, келесі түрде
болады:
үлестірім тығыздығының графигі
үлестірім қисығы деп аталады, келесі түрде
болады:
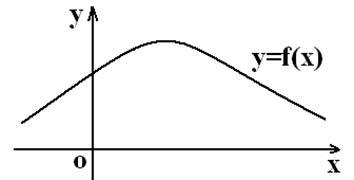
2 сурет
Егер анықталған интегралдың геометриялық
мағынасын еске түсірсек, яғни қисық сызықты трапецияның ауданы,
онда ![]() қасиеттерінің геометриялық интерпретациясын
аламыз.
қасиеттерінің геометриялық интерпретациясын
аламыз.
3
суретте жолақпен белгіленген облыстар сәйкес:
а) Х-тің ![]() интервалына түсу ықтималдығына тең;
б)
интервалына түсу ықтималдығына тең;
б) 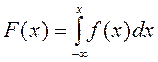 ; в)
; в) 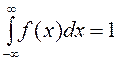 .
.
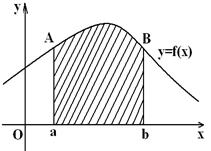
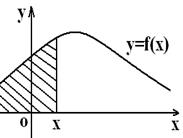
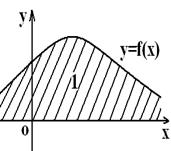
а) б) в)
3 сурет
Кездейсоқ шамалардың негізгі үлестірім заңдары
Дәріс мазмұны: биномдық үлестірім заңы, Пуассон, бірқалыпты, көрсеткіштік, қалыпты үлестірімдер.
Дәріс мақсаты: кездейсоқ шамалардың негізгі үлестірім заңдарымен таныстыру.
Биномдық үлестірім заңы
![]() – n тәуелсіз
сынақтарда А оқиғасының пайда болу
саны, р – әрбір
сынақта А оқиғасының пайда болу
ықтималдығы, q – пайда болмау ықтималдығы
болсын.
– n тәуелсіз
сынақтарда А оқиғасының пайда болу
саны, р – әрбір
сынақта А оқиғасының пайда болу
ықтималдығы, q – пайда болмау ықтималдығы
болсын. ![]() -тің мүмкін мәндері:
0,1,2,…, n. Бұл мүмкін мәндердің ықтималдықтары келесі
формуламен есептелінеді
-тің мүмкін мәндері:
0,1,2,…, n. Бұл мүмкін мәндердің ықтималдықтары келесі
формуламен есептелінеді ![]() =
=![]()
![]() ,
, ![]() (1).
(1).
Анықтама.
![]() дискретті кездейсоқ шамасының
үлестірімі үшін үлестірім заңы (1) формуласымен берілсе, онда ол
биномды үлестірім делінеді.
дискретті кездейсоқ шамасының
үлестірімі үшін үлестірім заңы (1) формуласымен берілсе, онда ол
биномды үлестірім делінеді.
Сонымен, бұл кездейсоқ шаманың үлестірім қатары:
|
Х |
0 |
1 |
2 |
… |
n |
|
Р(Х=k) |
|
|
|
… |
|
Үлестірім функциясы:
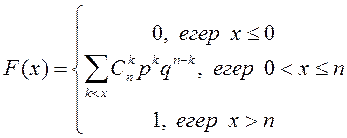 .
.
Сандық сипаттамаларды анықтау үшін дайын
формулаларды қолдануға болады, олар математикалық үміт пен
дисперсияның қасиеттерін анықтағанда
табылған. n тәуелсіз сынақта оқиғаның пайда болу
санының математикалық үміті мен
дисперсиясы: ![]() ,
, ![]() .
.
![]() интервалына түсу
ықтималдығы
интервалына түсу
ықтималдығы ![]() . формуласы бойынша
табылады.
. формуласы бойынша
табылады.
Бином заңы бойынша үлестірілген кездейсоқ шамаларды зерттеуді Mathcad жүйесінде арнайы енгізілген функциялар көмегімен жүргізуге болады ([7]).
Пуассон үлестірімі
Пуассон үлестірімі биномдық үлестірім
үшін шектік болып табылады, яғни сынақтар
саны n шексіз өседі, әрбір сынақта оқиғаның пайда
болу ықтималдығы р азаяды, бірақ ![]() көбейтіндісі тұрақты болып
қалады.
көбейтіндісі тұрақты болып
қалады.
Бұл жағдайда
оқиғаның k рет пайда болуы
(k=0,1,2,…,n,…) Пуассон формуласы бойынша
есептелінеді 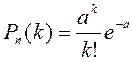 , ал үлестірім заңы осы формуламен берілетін
кездейсоқ шама Пуассон заңымен үлестірілген
делінеді.
, ал үлестірім заңы осы формуламен берілетін
кездейсоқ шама Пуассон заңымен үлестірілген
делінеді.
Бұл кездейсоқ шаманың үлестірім қатары:
|
Х |
0 |
1 |
2 |
… |
n |
… |
|
Р(Х=k) |
|
|
|
… |
|
… |
Сандық сипаттамаларын табамыз.
![]()
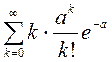 =
=![]()
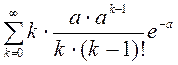 =
=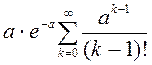 = =
= =![]() . Математикалық
үміті
. Математикалық
үміті ![]() . Дисперсиясы
. Дисперсиясы ![]() . Сонымен, Пуассон заңымен үлестірілген кездейсоқ
шамалар үшін математикалық үміт пен дисперсия өзара тең.
Пуассон заңының бұл қасиетін практикада зерттеліп отырған кездейсоқ
шамалар Пуассон заңымен үлестірілген гипотезасын тексеруде
қолданады. Пуассон заңы туралы жиі «сирек оқиғалар заңы» деп те
атайды. Пуассон заңымен үлестірілген кездейсоқ шамалар мысалы:
белгілі бір уақыт арасында катодтан ұшып шығатын электрондар
саны; t уақыт ішінде телефон станциясына келіп
түсетін қоңыраулар саны және
т.с.с.
. Сонымен, Пуассон заңымен үлестірілген кездейсоқ
шамалар үшін математикалық үміт пен дисперсия өзара тең.
Пуассон заңының бұл қасиетін практикада зерттеліп отырған кездейсоқ
шамалар Пуассон заңымен үлестірілген гипотезасын тексеруде
қолданады. Пуассон заңы туралы жиі «сирек оқиғалар заңы» деп те
атайды. Пуассон заңымен үлестірілген кездейсоқ шамалар мысалы:
белгілі бір уақыт арасында катодтан ұшып шығатын электрондар
саны; t уақыт ішінде телефон станциясына келіп
түсетін қоңыраулар саны және
т.с.с.
Бірқалыпты үлестірім
Мүмкін мәндері белгілі бір интервалда жататын және олардың барлығы бірдей мүмкіндікті болатын үзіліссіз кездейсоқ шамалар практикада кездеседі. Ондай шамалар бірқалыпты үлестірілген дейді.
Анықтама.
Егер [a,b]
кесіндісінде Х үзіліссіз кездейсоқ шамасының үлестірім
тығыздығы тұрақты, ал оның сыртында нолге тең
болса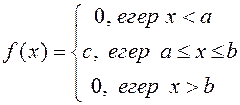 , онда үзіліссіз кездейсоқ шама бірқалыпты
үлестірілген деп аталады,
мұндағы с –
const.
, онда үзіліссіз кездейсоқ шама бірқалыпты
үлестірілген деп аталады,
мұндағы с –
const.
Сонымен, тығыздық графигі:
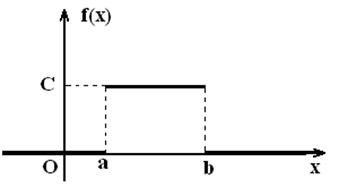
4 сурет
f(x) үлестірім тығыздығының қасиеттері
бойынша f(x) графигі
мен ОХ осімен шектелген фигураның ауданы 1-ге тең,
яғни ![]() немесе
немесе 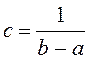 .
.
Олай болса, 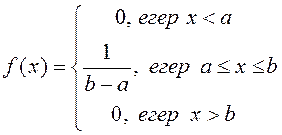 .
.
F(x) үлестірім функциясын табайық.
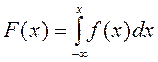 формуласы
бойынша
формуласы
бойынша ![]() болғанда
болғанда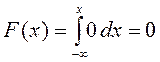 ;
;
егер ![]() , онда
, онда 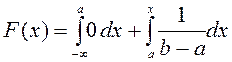 =
=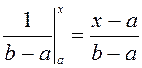 ;
;
егер ![]() , онда
, онда  .
.
Сонымен,
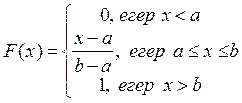 .
.
F(x) графигінің түрі:
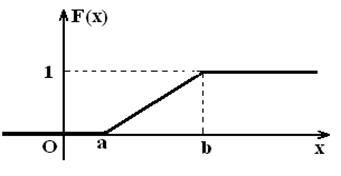
5 сурет
Бірқалыпты үлестірімнің сандық
сипаттамалары: математикалық
үміт 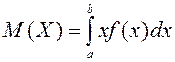 =
=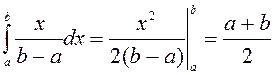 ; дисперсия
; дисперсия 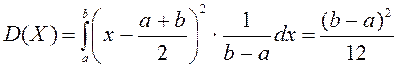 ; орта квадраттық
ауытқу
; орта квадраттық
ауытқу 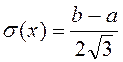 .
. ![]() интервалына түсу
ықтималдығы:
интервалына түсу
ықтималдығы:  =
=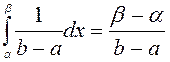 немесе
немесе ![]() . Бұл ықтималдық 6 суреттегі штрихталған
тіктөртбұрыштың ауданына тең
. Бұл ықтималдық 6 суреттегі штрихталған
тіктөртбұрыштың ауданына тең
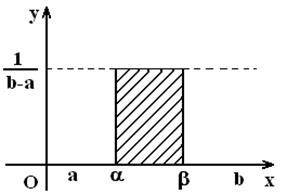
6 сурет
Көрсеткіштік үлестірім
Практикада ықтималдық теориясының қолданылуында, мысалы, сенімділік теориясында, жаппай қызмет ету теориясында және т.б. үлестірімнің көрсеткіштік немесе экспоненциалды заңы қолданылады.
Анықтама.
Егер үлестірім
тығыздығы 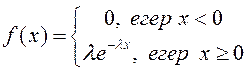 түрінде берілсе,
мұндағы
түрінде берілсе,
мұндағы ![]() >0 – үлестірім параметрі,
онда Х үзіліссіз кездейсоқ шамасы көрсеткіштік
заңмен үлестірілген
делінеді.
>0 – үлестірім параметрі,
онда Х үзіліссіз кездейсоқ шамасы көрсеткіштік
заңмен үлестірілген
делінеді.
Үлестірім функциясын
табайық 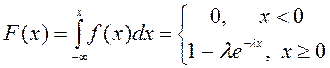 .
.
7 және 8 суреттерінде f(x), F(x) графиктері кескінделген
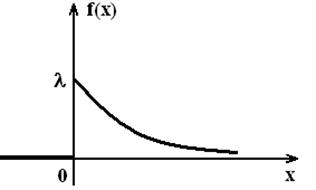
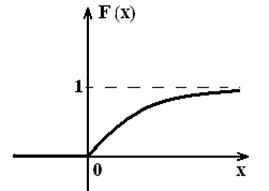
7 сурет 8 сурет
Көрсеткіштік үлестірімнің сандық сипаттамалары:
1)
математикалық үміт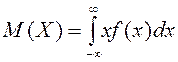 =
= 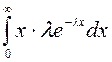 =
= ![]() =
=![]() ;
;
2)
дисперсия ![]() =
= 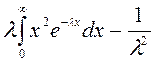 =
=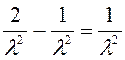 ;
;
3)
орта квадраттық ауытқуы 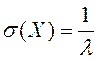 .
.
Сонымен, көрсеткіштік
үлестірімнің 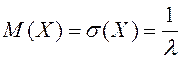 , бұл теңдікті практикада кездейсоқ шаманың
көрсеткіштік үлестірілген гипотезасын тексеруде
қолданады.
, бұл теңдікті практикада кездейсоқ шаманың
көрсеткіштік үлестірілген гипотезасын тексеруде
қолданады.
![]() интервалына түсу
ықтималдығы:
интервалына түсу
ықтималдығы:
![]() =
= ![]() .
.
Көрсеткіштік үлестірімнің сенімділік
теориясында қолданылуын қарастырайық. Кейбір қондырғыны, қарапайым
ба, күрделі ме, бұдан былай элемент деп атайтын боламыз.
Элемент ![]() моментінен бастап жұмысын бастасын,
ал
моментінен бастап жұмысын бастасын,
ал ![]() уақыттан соң жұмысын аяқтасын деп
ұйғарайық. Үзіліссіз кездейсоқ шаманы – элементтің мүлтіксіз
жұмыс істеу уақытын Т арқылы
белгілейік.
уақыттан соң жұмысын аяқтасын деп
ұйғарайық. Үзіліссіз кездейсоқ шаманы – элементтің мүлтіксіз
жұмыс істеу уақытын Т арқылы
белгілейік. ![]() үлестірім
функциясы
үлестірім
функциясы ![]() уақыт ішіндегі істен шығу ықтималдығын
анықтайды. Олай болса, сол уақыттағы мүлтіксіз жұмыс істеу
ықтималдығы (яғни
уақыт ішіндегі істен шығу ықтималдығын
анықтайды. Олай болса, сол уақыттағы мүлтіксіз жұмыс істеу
ықтималдығы (яғни ![]() қарама-қарсы оқиғаның
ықтималдығы):
қарама-қарсы оқиғаның
ықтималдығы):
![]()
![]() .
.
функциясын сенімділік функциясы деп атайды,
ол ![]() уақыт ішіндегі мүлтіксіз жұмыс істеу
ықтималдығын анықтайды. Т жиі көрсеткіштік
заңмен
уақыт ішіндегі мүлтіксіз жұмыс істеу
ықтималдығын анықтайды. Т жиі көрсеткіштік
заңмен
үлестірілген,
сонда ![]() , ал
, ал ![]() =
=![]() . Бұл
жағдайда
. Бұл
жағдайда ![]() сенімділіктің көрсеткіштік заңы деп
атайды, ал
сенімділіктің көрсеткіштік заңы деп
атайды, ал ![]() істен шығудың интенсивтілігін
анықтайды.
істен шығудың интенсивтілігін
анықтайды.
Қалыпты үлестірім
Үлестірімнің қалыпты заңы– ықтималдық теориясында маңызды заң. Мысалы қалыпты заңмен үлестірілген кездейсоқ шамалар: өлшеу және бақылаудың кездейсоқ қателері; оқ атқанда мәреден кездейсоқ жаңылуы кездейсоқ ауытқулары және т.б. Басқа заңдардан қалыпты заңның негізгі ерекшелігі – ол қандай да бір шарттарда басқа үлестірім заңдары ұмтылатын шектік заң болып табылады.
Анықтама.
 тығыздығымен сипатталатын кездейсоқ шаманың
ықтималдығының үлестірім заңы қалыпты заң деп
аталады.
тығыздығымен сипатталатын кездейсоқ шаманың
ықтималдығының үлестірім заңы қалыпты заң деп
аталады.
Сонымен, қалыпты үлестірім екі
параметрмен ![]() және
және ![]() анықталады. Осы параметрлердің ықтималдық
мағынасын ашайық.
анықталады. Осы параметрлердің ықтималдық
мағынасын ашайық.![]() болатындығын
көрсетейік:
болатындығын
көрсетейік:
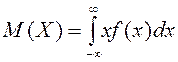 =
= =
= =…=
=…=![]() .
.
Толығырақ мәліметті [1], 145 беттен қараңыз. Сол
сияқты, ![]() :
:
![]()
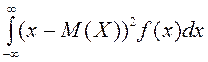 =
= =
= =
=
=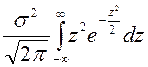 =
=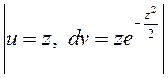 =…=
=…=![]() .
.
Бұдан орта квадраттық
ауытқу ![]() . Егер
. Егер ![]() =0 және
=0 және ![]() =1, онда қалыпты үлестірім нормаланған деп
аталады.
=1, онда қалыпты үлестірім нормаланған деп
аталады.
Ықтималдықтың қалыпты үлестірімінің
тығыздығының графигі қалыпты қисық немесе Гаусс қисығы деп
аталады.  функциясын математикалық талдау әдістерімен
зерттеп, оның графигін
саламыз:
функциясын математикалық талдау әдістерімен
зерттеп, оның графигін
саламыз:
а) анықталу
облысы ![]() ;
;
б) график ОХ осінен жоғары орналасқан,
себебі ![]() үшін
үшін ![]() ;
;
в) ![]() , яғни ОХ – көлденең
асимптота;
, яғни ОХ – көлденең
асимптота;
г) 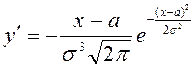 ,
, ![]()
![]()
![]() - кризистік
нүкте;
- кризистік
нүкте; ![]() егер
егер ![]() және
және ![]() егер
егер ![]() , онда
, онда ![]() ,
, 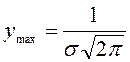 ;
;
д) екінші туынды арқылы иілу нүктесін
табамыз  және
және 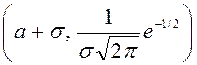 . Сонымен, Гаусс
қисығы:
. Сонымен, Гаусс
қисығы:
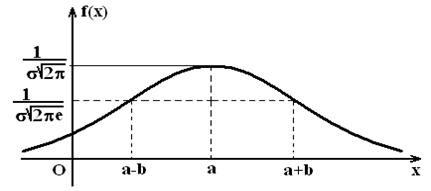
9 сурет
![]() және
және ![]() параметрлерінің өзгерісінің қалыпты
қисықтарға келтіретін әсері:
параметрлерінің өзгерісінің қалыпты
қисықтарға келтіретін әсері:
а)
бір ![]() болғанда
болғанда ![]() шамасының өзгеруі қалыпты қисықтың формасын
өзгертпейді, тек ОХ осі
бойында
шамасының өзгеруі қалыпты қисықтың формасын
өзгертпейді, тек ОХ осі
бойында ![]() болса
солға,
болса
солға, ![]() болса оңға
жылжиды;
болса оңға
жылжиды;
б) 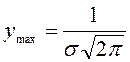 болғандықтан,
болғандықтан, ![]() өскен сайын максималды ордината кемиді және
керісінше; үлестірім қисығымен шектелген аудан әрқашан бірге тең
болғандықтан,
өскен сайын максималды ордината кемиді және
керісінше; үлестірім қисығымен шектелген аудан әрқашан бірге тең
болғандықтан, ![]() өзгергенде тек қисықтың формасы ғана
өзгереді:
өзгергенде тек қисықтың формасы ғана
өзгереді: ![]() өскен сайын ол жатық болады
және ОХ осі бойымен
созылады.
өскен сайын ол жатық болады
және ОХ осі бойымен
созылады.
Қалыпты үлестірілген кездейсоқ шаманың
берілген интервалға түсу ықтималдығын
табамыз ![]() :
:
 =
= 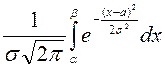 =
= =
=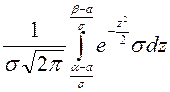 =
=
=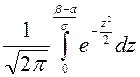 –
– 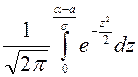 =
= = =
= =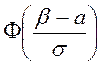 –
– 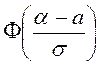 .
.
Лаплас функциясының мәндерін арнайы кестеден немесе Mathcad жүйесінде алынады. Бұл функцияның қасиеттері:
1) ![]() кез келген х үшін
анықталған;
кез келген х үшін
анықталған;
2) ![]() ;
; 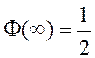 ;
;
3) ![]() , тақ
функция;
, тақ
функция;
4) ![]()
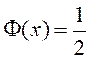 .
.
Сонымен, Лаплас функциясының графигі:
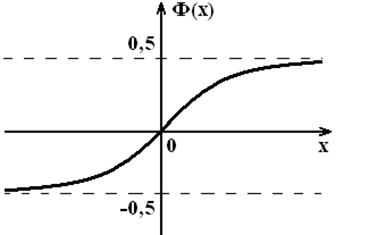
10 сурет
Лаплас функциясы арқылы қалыпты үлестірілген кездейсоқ шаманың F(x) үлестірім функциясы анықталады:
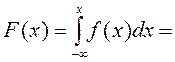
 =
=![]()
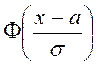 -
-![]() = =
= =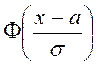 +
+ ![]() = =
= =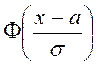 + 0,5.
+ 0,5.
Практикада ![]() қалыпты үлестірілген кездейсоқ
шаманың а – математикалық үміттен ауытқуының абсолют
шамасы бойынша
қалыпты үлестірілген кездейсоқ
шаманың а – математикалық үміттен ауытқуының абсолют
шамасы бойынша ![]() санынан кіші болу ықтималдығын,
яғни
санынан кіші болу ықтималдығын,
яғни ![]() басқаша айтқанда, бұл кездейсоқ шаманың
сейілу центрі
басқаша айтқанда, бұл кездейсоқ шаманың
сейілу центрі ![]() -ға салыстырмалы симметриялы интервалына түсу
ықтималдығын
-ға салыстырмалы симметриялы интервалына түсу
ықтималдығын ![]() есептеуге тура
келеді.
есептеуге тура
келеді.
Расында, ![]() болғандықтан,
болғандықтан,
![]() =
= ![]()
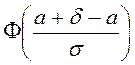 -
- 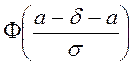 =
= .
.
Сонымен, ![]() аз болған сайын (яғни сейілу), соғырлым
қалыпты үлестірілген кездейсоқ
шаманың
аз болған сайын (яғни сейілу), соғырлым
қалыпты үлестірілген кездейсоқ
шаманың ![]() интервалына түсу ықтималдығы
үлкен.
интервалына түсу ықтималдығы
үлкен. ![]() -тің барлық мәндері енетіндей
центрі а нүктесінде болатын қандай интервал алуға
болатынын анықтайық.
-тің барлық мәндері енетіндей
центрі а нүктесінде болатын қандай интервал алуға
болатынын анықтайық. ![]() мәндерінің кестесін
қолданамыз:
мәндерінің кестесін
қолданамыз:
![]() =
=![]() =0,6826;
=0,6826;
![]() =
=![]() =0,9594;
=0,9594;
![]() =
=![]() =0,9973;
=0,9973; ![]() =
=![]() =0,999936.
=0,999936.
Сонымен, қалыпты үлестірілген кездейсоқ
шаманың барлық дерлік (~ 99,7%)
мәндері ![]() интервалына түседі. Бұл тұжырым «үш
сигма ережесі» деп аталады.
интервалына түседі. Бұл тұжырым «үш
сигма ережесі» деп аталады.
Мысал: Х кездейсоқ шаманың
үлестіру тығыздығы берілген. 
F(x) үлестіру формуласын табыңдар.
Шешуі: F(x) Осыдан х<0 болғанда f(x)=0 болатынын пайдалансақ,
F(x)
Осыдан х<0 болғанда f(x)=0 болатынын пайдалансақ,
F(x) . Енді
0<x<
. Енді
0<x< болғанда f(x)=sinx. Сондықтан: F(x)
болғанда f(x)=sinx. Сондықтан: F(x)

 .
.
Ақырында x> болғанда f(x)=0. Осыдан
болғанда f(x)=0. Осыдан
F(x)


 (-cosx
(-cosx )=-cos
)=-cos +cos0=1. Сонымен:
+cos0=1. Сонымен:

9- сабақ
Математикалық күтім және оның қасиеттері. Дисперсия және оның қасиеттері. Чебышев теңсіздігі
Үлестіру заңы кездейсоқ шаманы сипаттайтынын көрдік. Көптеген практикалық мәселелерді шешкенде кездейсоқ шаманың үлестіру заңын іздемей – ақ (оны анықтау кейде қиынға түседі), сол үлестірудің кейбір сандық синаттарымен қанағаттануға болады.
Анықтама. Дискретті кездейсоқ
шама Х – тің математикалық күтімі
деп оның барлық мүмкін
мәндерін сәкес ықтималдықтарына көбейтілген қосындысын айтамыз,
яғни 
Егер  қатар жинақсыз болса, онда математикалық күтім болмайды,
яғни
қатар жинақсыз болса, онда математикалық күтім болмайды,
яғни


Мысал. Бернулли схемасы бойынша үлестірілген кездейсоқ шаманың математикалық күтімін анықтау керек.




Математикалық күтімнің қасиеттері.
10. М(С) = С, С – тұрақты сан. Тұрақты санның математикалық күтімі сол тұрақты санға тең;
20. М(СХ) = С·М(Х) – тұрақтыны математикалық күтім таңбасының алдына шығаруға болады;
30. М(Х ± У) = М(Х)±М(У) – екі кездейсоқ шама қосындысының математикалық күтімі олардың математикалық күтімдерінің қосындысына тең.
40. М(Х·У) = М(Х)·М(У) – екі кездейсоқ шама көбейтіндісінің математикалық күтімі олардың математикалық күтімдерінің көбейтіндісіне тең.
Мысал.
|
Х |
0,21 |
0,54 |
0,61 |
|
Р |
0,1 |
0,5 |
0,4 |
Шешуі.
 §Дисперсия
§Дисперсия
Анықтама. Кездейсоқ шама мен оның математикалық күтімі айырымының квадратының математикалық күтімін дисперсия деп атайды.

 орташа квадраттық ауытқу.
орташа квадраттық ауытқу.
Мысалы. Пуассон заңы бойынша үлестірілген кездейсоқ шаманың дисперсиясын анықтау керек
 ;
; 



Дисперсияның қасиеттері .
10. Д(с) = 0 Тұрақтының дисперсиясы 0 – ге тең.
20. Д(сх) =
 (х) Тұрақтыны дисперсия таңбасының сыртына квадраттап
шығаруға болады.
(х) Тұрақтыны дисперсия таңбасының сыртына квадраттап
шығаруға болады.
30. Д(х ± у) = Д(х) ± Д(у)
40. Д(х · у) = Д(х) · Д(у) + [М(х)]2·Д(у) + [М(у)]2·Д(х)
Мысал . Үлестіру заңы бойынша берілген Х – дискертті кездейсоқ шаманың дисперсиясы және орташа квадраттық ауытқуы табылсын.
|
Х |
131 |
140 |
160 |
180 |
|
Р |
0,05 |
0,10 |
0,25 |
0,60 |
Шешуі. Д(х) = М(х)2 - [М(х)]2 формуласынан пайдаланамыз: Х – тің математикалық күтімін табамыз.
М(х) = 131·0,05 +140·0,1+ 160·0,25 + 180·0,60 = 6,55 + 14 + 40 +108 = =168,55
Х2 – тың үлестіру заңын жазамыз:
|
Х2 |
17161 |
19600 |
25600 |
32400 |
|
Р |
0,05 |
0,10 |
0,25 |
0,60 |
Х2 – тың математикалық күтімін табамыз:
М(х2) = 17161·0,05 +19600·0,10 + 25600·0,25 + 32400·0,60 = 858,05+1960 + 6400 +19440 = 28658,05
Ізделінді дисперсияны табамыз:
![]()
 28658,05-(168,55)2
= 28658,05 –
28409,1025 = 248,9475
28658,05-(168,55)2
= 28658,05 –
28409,1025 = 248,9475
Орташа квадраттық ауытқуды табамыз: σ(х) = √ 248.9475 ≈ 15.778 .
Үлкен заңдар заңы.
Мысал: Белгілі бір прибор тәуелсіз жұмыс істейтін 10 элементтен тұрады. Т уақыт ішінде әр элементтің жұмыс істемей қалған элементтердің орташа санының Ф (математикалық үміті) айырмасының абсолют шамасының:
1) екіден кем болуының;
2) екіден кем болмауының ықтималдықтарын бағалаңыз.
Шешуі: Есептің шарты бойынша: n=10, p=0,5, q=0,5
Сондықтан: М(х)=10*0,5=5, Д(х)=5*0,5=2,5
-
Р(
 <2)
<2)
-
Р(

 2)
2)
Сонымен:
Р( <2)
<2) , Р(
, Р(
 2)
2) .
.
10- сабақ
Үлкен сандар заңы. Орталық шектік теоремалар
Егер кездейсоқ шама х теріс таңбалы мәндерді қабылдамаса және оның математикалық күтімі шекті болса, онда бұл кездейсоқ шаманың қалаған оң таңбалы сан А-дан кем болмау ықтималдығы әрдайым математикалық күтімнің А-санына қатынасынан үлкен болмайды, яғни

Чебышев теңсіздігі.
Кездейсоқ шама Х өзінің математикалық күтімі М(х)-тен
ауытқуының абсолют шамасы  -нан кем болмау ықтималдығы дисперсия
D(х)-тің
-нан кем болмау ықтималдығы дисперсия
D(х)-тің  -ның квадратына қатынасынан үлкен болмайды,
яғни
-ның квадратына қатынасынан үлкен болмайды,
яғни


Чебышев теоремасы.
Егерде  тізбегі тәуелсіз кездейсоқ шамалар болса, олардың
дисперсиялары бар болып бір тұрақты С санымен шектелген, яғни
Д(х1)
тізбегі тәуелсіз кездейсоқ шамалар болса, олардың
дисперсиялары бар болып бір тұрақты С санымен шектелген, яғни
Д(х1) С, ... ,
Д(х
С, ... ,
Д(х )
) болса, онда кездейсоқ
шамалардың арифметикалық орташасының олардың математикалық
күтімдерінің арифметикалық орташасынан ауытқуының абсалютті шамасы,
қандай да бір оң таңбалы аз тұрақты сан
болса, онда кездейсоқ
шамалардың арифметикалық орташасының олардың математикалық
күтімдерінің арифметикалық орташасынан ауытқуының абсалютті шамасы,
қандай да бір оң таңбалы аз тұрақты сан  -нан үлкен болмауын, n мейлінше үлкен
болғанда
-нан үлкен болмауын, n мейлінше үлкен
болғанда 
бірге жуық ықтималдықпен мақұлдаймыз, яғни

Дәлелдеуі. Чебышев теңсіздігін пайдаланамыз.
х~ арифметикалық орташа.
арифметикалық орташа.
 ~
~ математикалық күтім
орташасы.
математикалық күтім
орташасы.


 болғандықтан
болғандықтан  өйткені
өйткені



 өйткені
өйткені 
Теорема дәлелденді.
Сонымен қатар  өрнегі де орынды.
өрнегі де орынды.
 жуық теңсіздік жеткілікті үлкен n-нің
барлық
жуық теңсіздік жеткілікті үлкен n-нің
барлық
мәнінде  дәлдікпен орындалады.
дәлдікпен орындалады.
Сенімділік ықтималдық Р және n, арасындағы тәуелділік
арасындағы тәуелділік  десек, онда формуламен
өрнектеледі.
десек, онда формуламен
өрнектеледі.
Мысал. Сенімділік 0,95,
дәлдігі 0,01-ге дейін болса, с =1 десек, онда
 теңсіздігі орындалуы үшін қосылғыш кездейсоқ шамалар саны
неге тең болатынын анықтау керек.
теңсіздігі орындалуы үшін қосылғыш кездейсоқ шамалар саны
неге тең болатынын анықтау керек.
Шешуі.



Бернулли теоремасы.
Егер әрбір тәуелсіз сынауда А оқиғасының пайда болу
ықтималдығы тұрақты  -ға тең болса, онда сынау саны n мейлінше үлкен
болғанда
-ға тең болса, онда сынау саны n мейлінше үлкен
болғанда  оқиғасының салыстырмалы жиілігі
оқиғасының салыстырмалы жиілігі  ықтималдық р-дан қандай да бір оң таңбалы аз
сан
ықтималдық р-дан қандай да бір оң таңбалы аз
сан  -нан үлкен болмауын
бірге жуық ықтималдықпен мақұлдаймыз,
яғни
-нан үлкен болмауын
бірге жуық ықтималдықпен мақұлдаймыз,
яғни

Дәлелдеуі. Салыстырмалы
жиілік  ді, математикалық күтімі р-ға, дисперсиясы
ді, математикалық күтімі р-ға, дисперсиясы
 ге тең кездейсоқ шаманы
қарастырамыз.
ге тең кездейсоқ шаманы
қарастырамыз.
Чебышев теңсіздігіне қойсақ  шығады.
шығады.  Теорема дәлелденді.
Теорема дәлелденді.
Сонымен n өскен сайын  р-ға 1-ге жуық ықтималдықпен
жуықтайды.
р-ға 1-ге жуық ықтималдықпен
жуықтайды.
Пуассон теоремасы.
Егер А оқиғасының ықтималдығы әрбір тәуелсіз сынауда
өзгеріп отырса, онда n- мейлінше үлкен  болғанда А оқиғасы пайда болуының салыстырмалы жиілігі
ықтималдықтардың
болғанда А оқиғасы пайда болуының салыстырмалы жиілігі
ықтималдықтардың
арифметикалық ортасы  мәнінен өте аз (
мәнінен өте аз ( )
айырмада болуын бірге жуық ықтималдықпен мақұлдаймыз,
яғни
)
айырмада болуын бірге жуық ықтималдықпен мақұлдаймыз,
яғни 
Дәлелдеуі.
 шамалардың әрқайсысы тек (1 не 0) мәніне
сәйкес
шамалардың әрқайсысы тек (1 не 0) мәніне
сәйкес  не
не

ықтималдықпен қабылдайтын кездейсоқ шамалар болсын. Мұнда кездейсоқ шамалар саны сынау санына тең.
 болады. Чебычев
теоремасынан
болады. Чебычев
теоремасынан


Теорема дәлелденді.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Ықтималдылық
Ықтималдылық
1-лекция
Оқиғалар алгебрасы
1. Бастапқы жалпы шарт, сынау, оқиға.
2. Оқиғаларды класстарға бөлу .
3. Оқиғалар арасындағы байланыстар .
1. Оқиғалар алгебрасы.
1. Бастапқы жалпы шарт, сынау, оқиға. Бұл ұғымдарды түсіндіруді мысалдармен көрсетейік.
1-мысал. Металл теңгені тегіс еденге тастайық, сонда мына төмендегі құбылыстарды байқаймыз. Теңгені лақтыру үшін өзімізді белгілі бір қалыпқа келтіреміз. Одан соң бас бармақпен теңгенің бір ұшын жоғары қарай түртіп жібереміз. Онда ол шыр көбелек , белгілі бір биіктікке дейін көтеріліп, төмен қарай құлдилап еденге түседіде, бір неше рет секіректеп , жалпағыныан не тиін жағы не герб жағы жоғары қарап жатады. Сайып келгенде , теңге жалпағынан жатуы үшін көптеген қимыл әрекеттер жасалады, солардың жиынын бастапқы жалпы шарт деп атаймыз. Оның тиын не герб жағының жоғары жатуы , яғни бастапқы жалпы шарттың орындалу нәтижесі – оқиға деп айтылады.
2-мысал. Біртекті материалдардан жасалған симмертиялы кубтың(ойын тасының) әрбір жағы 1 ден 6 ға дейін нөмірленген болады. Оны бір рет лақтырғанда , яғни бастапқы жалпы шарт орындалғанда алты жағының біреуі жоғары қарап түседі, мұнда қай жағы түсседе оқиға болады.
3-мысал. Өзіміз қарапайым көріп жүрген суды 100оС ге дейін қыздырсақ, ол буға айналады. Судың буға айналуы –оқиға, ал осы бу пайда болғанға дейінгі барлық әрекеттер жиыны бастапқы жалпы шарт болады.
Бұдан былай бастапқы жалпы шарт термині орнына сынау, тәжірибе, эксперимент терминдерін қолданамыз. Сонымен сынау нәтижесін оқиға деп атауға келісеміз. Әдетте оқиғаларды үлкен әріптер А,В,С,... арқылы белгілейміз. Мысал үшін теңгенің тиын жағының пайда болуы А оқиғасы болса, герб жағының пайда болуы В оқиғасымен белгіленеді және т.с.с.
2. Оқиғаларды кластарға бөлу.
Анықтама. Сынау жүргізілгенде А оқиғасы пайда болуыда , пайда болмауыда мүмкін болса , ондай оқиғаны кездейсоқ оқиға деп айтамыз. Мұндай оқиғаларға 1,2-мысал жатады, өйткені сынау нәтижесінде теңгенің немесе кубтың белгіленген жағынан пайда боларын күн ілгері айта алмайыз. Сынау нәтижесінде оқиға (А оқиғасы) сөзсіз пайда болатын болса, ондай оқиғаны ақиқат оқиға дейді. Сынау нәтижесінде оқиғаның (А оқиғасы) пайда болуы мүмкін болмаса, ондай оқиғаны мүмкін емес оқиға деп йтамыз
Ақиқат оқиғаны U әрпімен, мүмкін емес оқиғаны V әрпімен белгілеу қабылданылған. Мысалы, кобдишаға салынған ақ шарлардың біреуін алсақ, оның ақ болып шығуы ақиқат оқиға да, басқа түсте болуы мүмкін емес оқиға. Сынау жүргізгенде екі оқиғаның бірі пайда болып, екіншісі пайда болмайтын оқиғаларды үйлесімсіз оқиғалар деп айтылады. Мәселен 2-мысалдағы А1,А2 (бірінші және екінші нөмірлі жақтар) оқиғалары- үйлесімсіз оқиғалар. Бұл мысалдағы кез келген екі оқиға да үйлесімсіз. Кез келген екі оқиғасы үйлесімсіз болатын оқиғалар жиынын қос-қостан үйлесімсіз оқиғалар дейді.
Сынау жүргізілгенде оқиғаның біреуінің пайда болуы екіншісінің пайда болуын жоққа шығармайтындай екі оқиғаны үйлесімді оқиғалар деп атайды. Мысалы, кубтың жұп нөмірінің пайда болуы (А оқиғасы) мен үш санына еселік нөмір пайда болуы В оқиғасы үйлесімді. Өйткені кубтың 6-нөмірінің пайда болуын көрсететін А6 оқиғасы В оқиғасы пайда болғанда да, А оқиғасы пайда болғанда да пайда болуы мүмкін.
Сынау нәтижесінде мүмкін оқиғалардың әйтеуір біреуінің сөзсіз пайда болуы ақиқат болса, ондай оқиғаны жалғыз ғана мүмкіндікті оқиға дейді. Жалғыз ғана мүмкіндікті оқиғалар оқиғалардың толық тобын немесе оқиғалардың толық жүйесін (системасын) құрады деп айтуға келісеміз. Мысалы, сынау нәтижесінде кубтың алты жағының біреуі (А оқиғасы) пайда болуы сөзсіз, сондықтан А1, А2, А3, А4, А5, А6 оқиғалары жалғыз ғана мүмкіндікті оқиғалар және олар оқиғалардың толық тобын құрайды. Сонымен қатар бұлар қос-қостан үйлесімсіз оқиғалар.
3.Оқиғалар арасындағы қатынастар. Оқиғаларға қолданатын
амалдар
Осы уақытқа дейін оқиғалар арасындағы кейбір қатынастарғана айтылған еді. Ал ықтималдықтар теориясының алдына қойған негізгі мақсатының бірі жеке оқиғалар ықтималдығы бойынша күрделі оқиғалар ықтималдығын анықтау болып табылады.
Бұл мәселені айқындау қосу, көбейту және тағыда басқа түрлі амалдар орындауға негізделеді. Бұларды баяндаудан бұрын сол оқиғалар арасындағы негізгі қатынастарды келтіріп, амалдарды орындап және көрнектілігін графикалық түрде көрсетейік.
1. А және В оқиғаларының кем дегенде біреуінің пайда болуын осы оқиғалардың қосындысы деп атайды. Оны АUВ немесе А+В арқылы белгілейміз, мұнда U-біріктіру (қосу) таңбасы. Сонымен, оқиғалардың қосындысы деп не А оқиғасы, не В оқиғасы, не А және В екеуі де пайда болатын оқиғаны ұғамыз. Оқиғаны өзіне-өзін қосқанда сол оқиғаның өзі шығады, яғни АUА=A. Сондай-ақ АUV=A, AUU=U болатынын көру қиын емес.
Екі оқиғаның бірігуін (қосындысын) оқиғалардың қалаған санына кеңейтуге болады, яғни A1UA2U…UAnU… (A1+A2+…+An+…), немесе i=1U¥Ai деп жазамыз. Мұны сынау нәтижесінде A1, A2,…,An,… оқиғаларының кем дегенде біреуінің пайда болуы деп ұғамыз. Ал бұл оқиғалар оқиғалардың толық тобын құраса, онда олардың қосындысы ақиқат оқиға болады. Мысалы, оқушының жақсы оқуы А оқиғасы, ал спортшы болуы В оқиғасы болсын. Осы екі оқиғаның қосындысы C=A U B оқушы жақсы оқыса да (А оқиғасы), спортшы болса да (В оқиғасы) немесе ол әрі жақсы оқитын әрі спортшы болса да (А және В оқиғаларының екеуі де) орындалады.
А және В оқиғалары қосындысының геометриялық кескінін көрсету үшін кездейсоқ оқиғаны жазықтықтағы фигура ретінде қарастырған қолайлы. Квадрат ішіндегі радиусы кіші дөңгелектегі нүктелер жиыны В оқиғасының пайда болуын кескіндейді, радиуысы үлкен дөңгелектегі нүктелер жиыны А оқиғасының пайда болуын кескіндейді десек, онда АUВ оқиғалар бірігуі екі дөңгелек жасаған облыстағы нүктелер жиынын көрсетеді, мұндағы А және В оқиғаларының екеуіне де жататын нүктелер тек бір рет қана есепке алынады.
2. А және В оқиғаларының бірге
пайда болуын олардың көбейтіндісі деп атайды да АВ (яғни А*В)
немесе А![]() В арқылы белгілейді,
мұндағы
В арқылы белгілейді,
мұндағы ![]() -қылысу (көбейту) таңбасы.
А*В-ны А мен В-ның бірге пайда болуы деп ұғамыз. Оқиғаны өзіне-өзін
көбейтсе, сол оқиғаның өзі шығады, яғни А∩А=А. Сондай-ақ
A∩V=V, A∩
U
=A.
-қылысу (көбейту) таңбасы.
А*В-ны А мен В-ның бірге пайда болуы деп ұғамыз. Оқиғаны өзіне-өзін
көбейтсе, сол оқиғаның өзі шығады, яғни А∩А=А. Сондай-ақ
A∩V=V, A∩
U
=A.
Аталған екі оқиғаның қиылысуын
(көбейтіндісін) оқиғалардың кез келген санына кеңейтуге болады,
яғни А1![]() A2
A2![]() …
…![]() An
An![]() … немесе
i=1∩¥Аі
деп жазамыз. Мұны сынау
нәтижесінде осы А1,А2,...,Аn... оқиғаларының барлығының
пайда болуы деп ұғамыз.
… немесе
i=1∩¥Аі
деп жазамыз. Мұны сынау
нәтижесінде осы А1,А2,...,Аn... оқиғаларының барлығының
пайда болуы деп ұғамыз.
3.А оқиғасы орындалып, В оқиғасы орындалмайтын оқиғаны А мен В-ның айырымы деп айтады және оны А-В немесе А \ В ( \ азайту таңбасы арқылы) белгілейміз.
4.Cимметриялы айыру амалы. Симметриялы айыру амалы деп А және В оқиғалар бірігуінен сол оқиғалар қиылысуының айырымынан құралған элементтер жиынын айтамыз:
А Å В : = ( А U В) \ ( А ∩ В) = { х | (хÎ А & х Ï В) Ú (х Ï А & х Î В) }.
5. Екі үйлесімсіз А және Ā
( ØА немесе А емес) оқиғалары
оқиғалардың толық тобын құраса, оларды қарама-қарсы оқиғалар деп
айтамыз. Олардың қосындысы ақиқат оқиға, яғни А U Ā
= U, ал көбейтіндісі –мүмкін емес
оқиға А∩ Ā = V,
сондай-ақ Ū
=
V
,
 = U
болуын байқау қиын
емес.
= U
болуын байқау қиын
емес.

Жоғарыдағы сызбаларда А және В оқиғалардың қосындысы(бірігуі), көбейтіндісі(қиылысуы), айырымы, симметриялы айырымы және қарама-
қарсы оқиғалардың диаграммалары көрсетілген.
6. Сынау нәтижесінде пайда болған В оқиғасы екінші бір А оқиғасының да пайда болуын қамтамасыз етсе, онда В-ның пайда болуы А-ның пайда болуын ілестіреді деп айтады да мұны ВÌ А (жату, ену таңбасы) арқылы белгілейді.
Геометриялық талқылаудан төмендегідей тұжырымдар келіп шығады.
-
А Ì А болады,
-
А Ì В, В Ì С болса, онда А Ì С болады,
-
А Ì B болса, А U В = B және А ∩ В = А болады.
Буларға талдау жасауды оқырмандардың өздеріне тапсырамыз.
7.Сынау нәтижесінде пайда болған А оқиғасы В оқиғасыныңда пайда болуын қамтыса ( яғни А Ì В болса) және осы сынауда В оқиғасының пайда болуы А оқиғасының пайда болуын қамтыса (яғни В Ì А болса) , онда А және В оқиғаларды эквивалентті деп айтамызда оны А≡В ретінде белгілейміз. Өзара эквивалентті(тең) оқиғаларды бір-бірімен ауыстыруға болады. Сондықтан кез келген екі эквивалентті оқиғаны тепе-тең немесе тең оқиғалар депте айтамыз. Барлық ақиқат оқиғалар эквивалентті, сондаяқ барлық мүмкін емес оқиғаларда эквивалентті.
8.Қандай да оқиғаларға бірігу
( U ), қиылысу(∩) , ішінде жату(Ì ) және ішіне
алу(É) амалдарының қолданылуы дұрыс
болса, онда ол оқиғаларды сәйкес қарама-қарсы оқиғалармен ауыстырып
қолданғанда амалдар бір-бірімен ауысады, яғни U ∩ ға не ∩ U
ға, É
Ì
ға не
Ì
É
ға айналады. Сол себепті
төмендегі қасиеттер орын алады. Егер А
Ì
В болса,
онда  É
É
 ; егер
А É
В болса,
онда
; егер
А É
В болса,
онда  Ì
Ì
 ; егер
С = A∩B
болса,
онда
; егер
С = A∩B
болса,
онда  =
=  U
U
 ; егер
C=AU
B
болса,
онда
; егер
C=AU
B
болса,
онда  =
=  ∩
∩  болады.
болады.
9.Оқиғалар қосындысының анықтамасы бойынша АU В оқиғасы мен ВUА оқиғасы пара-пар, ал көбейтіндінің анықтамасы бойынша А∩ В мен В∩А пара пар оқиғалар. Бұл жайт оқиғалар саны екіден артық болсада орын алады. Сондықтан , оқиғалардың қосындысы мен көбейтіндісі үшін орын алмастыру заңы орындалады.
Сонымен оқиғалар арасындағы қатынастардан пайдаланып , төмендегідей қасиеттерді жазуымызға болады:
1) Идемпотенттік қасиеті. Элементтері бірдей oқиғалардың қосындысы немесе көбейтіндісі өзіне тең:
А È А =А, А Ç А = А;
2) Коммутативтілік(ауыстырымдылық) қасиеті. Қосу немесе көбейту амалдарын орындағанда оқиғалардың орны ауысқанымен нәтиже мәні өзгермейді :
А È В = В È А, А Ç В = В Ç А;
3) Ассоциативтілік(топталу) қасиеті. А,В,С оқиғалардың қосу немесе көбейту амалдарын біргелікте орындағанда жақшалардың орны ауысқанымен нәтиже мәні өзгермейді:
А È ( В È С) = ( А È В) È С,
А Ç ( ВÇ С) = ( А Ç В) ÇС;
4) Дистрибутивтік(терімділік) қасиеті:
АÈ (В Ç С) = (АÈ В) Ç (А È С)
А Ç (ВÈ С) = (А Ç В) È (А Ç С)
5) Жұтылу қасиеті:
(АÇ В) È А= А, (АÈ В) Ç А=А,
6) Мүмкін емес оқиға қасиеті:
АÈ V = А, А Ç V = V;
7) Ақиқат оқиға қасиеті:
А È U = U , А Ç U = А;
8) Екі рет терістік қасиеті:
 = А;
= А;
9) Де Морган заңдары:
 =
=  Ç
Ç
 ,
,  =
=  È
È
 ;
;
10) Толықтыру қасиеті:
А
È
 = U, А
Ç
= U, А
Ç
 = V
;
= V
;
11) Айырым үшін өрнек:
А \ В
= А
Ç

Жоғарыдағы келтірілген түрлендірулерді күрделі өрнектерді ықшамдау үшін пайдаланудың мәні зор-ақ.
Біздің мақсатымыз–тәжірибенің нәтижелерімен анықталатын құбылыс-тарды сипаттауға ыңғайлы математикалық модельді іздестіру. Бұл мәселе оқиғаны тек сынау нәтижесі деп қарастырумен шешілмейді. Сондықтан оны шешу үшін жиын мен оқиғаны ұштастырады, яғни тәжірибе нәтижелерінен құрылған әрбір жиынды оқиға ретінде қарастырады. Осылай қарастыру нәтижесінде ғана қойылған мақсат шешілетін болып отыр. Сондықтан, іздестіріліп отырған моделімізге жоғарыда келтірілген оқиғалар тобына , оларға қолданылатын бірігі, қиылысу, толықтыру және басқа амалдармен бұлардың қасиеттеріне(заңдарына) құрылған модельді алуға болатынын көреміз. Бұл моделді оқиғалар алгебрасы(өрісі) деп айтамыз.
Мысал-1. Кластан шақырылған кез келген
бір студенттің белгілі бір пәннен алған бағасы жақсы болуы А
оқиғасы, орташа болуы В оқиғасы, нашар болуы С оқиғасы болсын.
АUВ,  ,
,
 , АВ, А∩СU
В,
, АВ, А∩СU
В,  ,
,
 оқиғаларын сипаттап
беріңдер.
оқиғаларын сипаттап
беріңдер.
Шешуі. АU В оқиғасы А не В
оқиғаларының кемінде біреуінің пайда болатынын көрсетеді. Сондықтан
АU В оқиғасы деп студенттің жақсы немесе орташа оқитынын түсінеміз.
Ал,  оқиғасы АU В оқиғасына
қарама-қарсы оқиға, ол-студенттің нашар оқитынын көрсететін С
оқиғасы , яғни
оқиғасы АU В оқиғасына
қарама-қарсы оқиға, ол-студенттің нашар оқитынын көрсететін С
оқиғасы , яғни  = С. Осы
секілді
= С. Осы
секілді  = В болады. А∩В оқиғасы
- мүмкін емес оқиғас, себебі студенттің алған бағасы біруақытта
жақсыда, орташада болуы мүмкін емес. Сол секілді А∩С да мүмкін емес
оқиға. Ал, А∩СUВ =В болатынын байқау қиын емес. А оқиғасына қарама
–қарсы оқиға
= В болады. А∩В оқиғасы
- мүмкін емес оқиғас, себебі студенттің алған бағасы біруақытта
жақсыда, орташада болуы мүмкін емес. Сол секілді А∩С да мүмкін емес
оқиға. Ал, А∩СUВ =В болатынын байқау қиын емес. А оқиғасына қарама
–қарсы оқиға  студенттің орташа (В) не
нашар (С) оқуын сипаттайды, демек, А=ВU С. Ал
студенттің орташа (В) не
нашар (С) оқуын сипаттайды, демек, А=ВU С. Ал
 =
=  және
және  =А
болатынынан
=А
болатынынан  =А екендігі түсінікті.
Сол секілді
=А екендігі түсінікті.
Сол секілді  = В болатынын көрсету
қиын емес.
= В болатынын көрсету
қиын емес.
Мысал-2: Теңгені 1 рет тастағанда «герб» түсуі «сан» түсуіне мүмкіндік бермейді. Сондықтан «герб» түсті және «сан» түсті деген оқиғалар өзара үйлесімсіз.
Сынау жүргізгенде пайда болған оқиға ақиқат оқиға болса, онда ол жалғыз мүмкіндікті оқиға деп аталады.
Сынау нәтижесінде бірнеше оқиғалар пайда болуы мүмкін болса және олардың біреуінің пайда болу мүмкіндігі екіншісіне қарағанда артықшылығы болмаса мұндай оқиғалар тең мүмкіндікті оқиғалар деп аталады.
Мысал-3: Біртекті материалдардан жасалған симметриялы кубтың әрбір жағын 1-ден 6-ға дейінгі санлармен нөмірлейік. Оны бір рет лақтырғанда 6 жағының біреуі жоғары қарап түседі; қай жағы түссе де оқиға болады.
А1 – Бірінші нөмірлі жағы түсетін оқиға;
А2 – Екінші нөмірлі жағы түсетін оқиға;
А - жұп нөмірлі цифр жағы түсетін оқиға;
В - үш санына еселі цифр жағы түсетін оқиға;
U – 1 – 6 сандар түсетін оқиға;
V - бірінші және екінші нөмір қатар түсетін оқиға;
А1, А2 – үйлесімсіз оқиғалар;
А, В – үйлесімді оқиғалар ( Мысалы: 6 нөмірі түседі.);
 1
- бірінші нөмірі түспейтін
оқиға;
1
- бірінші нөмірі түспейтін
оқиға;
Ықтималдықтардың анықтамалары
1. Ықтималдықтардың классикалық анықтамасы .
2. Ықтималдықтардың геометриялық анықтамасы .
3. Статистикалық заңдылық және ықтималдықтың
жиіліктік анықтамасы.
-----------------------------------------------------------------------------
Ықтималдықтардың негізгі анықтамалары.
1. Ықтималдықтың классикалық анықтамасы
Ықтималдықтың классикалық анықтамасын алғаш рет берген Лаплас (1749-1827) еді. Ықтималдықтың бұл анықтамасы тең мүмкінліктің саны шекті элементар оқиғалар кеңістігінде қарастырылады және өте қарапайым.
«Тең мүмкіндік» немесе «тең
ықтималдық» ұғымдары алғашқы ұғымдарға жатады, олар формальды
анықтама беруді қажет етпейді. Жалпы сынау нәтижесінде бірнеше
элементар оқиғалар (нәтижелер, жағдайлар) пайда болуы мүмкін болса
және олардың біреуінің пайда болу мүмкіндігінің екіншісіне
қарағанда артықшылығы бар деп айта алмайтын болсақ, басқаша
айтқанда, сынау нәтижесінің симметриялы қасиеті болса, мұндай
элементар оқиғалар тең мүмкіндікті делінеді. Бұған 1-бөлімде
келтірілген 2-мысал айғақ. Өйткені кубтың әрбір жағының пайда болу
мүмкіндігі бірдей. Сондықтан бұлар тең мүмкіндікті (яғни тең
ықтималдықты) элементар оқиғалар болады.
е1,
е2,...,
еn
элементар оқиғалары тең
мүмкіндікті, қос-қостан үйлесімсіз және оқиғалардың толық тобын
(системасын) құраса, онда ол оқиғаларды сынаудың мүмкін (мүмкін
болатын) нәтижелерінің толық тобы немесе элементар оқиғалар
кеңістігі деп айтатынын көрдік, Сонда
{ }=
{e1,e2,…,en} кеңістігіндегі элементар
оқиғалардың жалпы санын n{
}=
{e1,e2,…,en} кеңістігіндегі элементар
оқиғалардың жалпы санын n{ } арқылы белгілесек,
әрбір элементар оқиғаның шығу мүмкіндігінің мөлшері, ықтималдығы, P
=
} арқылы белгілесек,
әрбір элементар оқиғаның шығу мүмкіндігінің мөлшері, ықтималдығы, P
= . Ал тең мүмкіндікті,
үйлесімсіз және оқиғалардың толық тобын құрайтын
e1,e2,…,en
элементар оқиғалардың біреуі
не бірнешеуі бір А оқиғасының пайда болуын тудыруы мүмкін, яғни
екінші сөзбен айтқанда, А оқиғасы тең мүмкіндікті бірнеше элементар
оқиғаларға бөлінеді және олардың кез келген біреуінің пайда
болуынан А оқиғасының пайда болуы шығатын болады. Мысалы, кубты бір
рет лақтырғанда оның кез келген тақ нөмірі
е1,е3,е5
пайда болуынан А оқиғасы пайда
болсын. Былайша айтқанда, А оқиғасы тақ нөмірлі
e1,e3,e5
үш оқиғаға бөлініп отыр. Бұл
тақ нөмірлі элементар оқиғаларды осы А оқиғасының пайда болуына
қолайлы оқиғалар дейміз. Бұлардың санын
m{
. Ал тең мүмкіндікті,
үйлесімсіз және оқиғалардың толық тобын құрайтын
e1,e2,…,en
элементар оқиғалардың біреуі
не бірнешеуі бір А оқиғасының пайда болуын тудыруы мүмкін, яғни
екінші сөзбен айтқанда, А оқиғасы тең мүмкіндікті бірнеше элементар
оқиғаларға бөлінеді және олардың кез келген біреуінің пайда
болуынан А оқиғасының пайда болуы шығатын болады. Мысалы, кубты бір
рет лақтырғанда оның кез келген тақ нөмірі
е1,е3,е5
пайда болуынан А оқиғасы пайда
болсын. Былайша айтқанда, А оқиғасы тақ нөмірлі
e1,e3,e5
үш оқиғаға бөлініп отыр. Бұл
тақ нөмірлі элементар оқиғаларды осы А оқиғасының пайда болуына
қолайлы оқиғалар дейміз. Бұлардың санын
m{ } арқылы белгілейміз
(m{
} арқылы белгілейміз
(m{ }=3).
}=3).
Анықтама. А оқиғасына қолайлы элементар
оқиғалар санының (m{ }) сынаудың тең
мүмкіндікті барлық элементар оқиғалары санына
(n{
}) сынаудың тең
мүмкіндікті барлық элементар оқиғалары санына
(n{ }) қатынасын А
оқиғасының ықтималдығы деп айтамыз және былай
жазамыз:
}) қатынасын А
оқиғасының ықтималдығы деп айтамыз және былай
жазамыз:
Р(А) =
 .
.
Бұдан былай
m=m{ },
n=n{
},
n=n{ } деп белгілеу
еңгіземіз, сонда
} деп белгілеу
еңгіземіз, сонда
Р(А) =
 .
.
Ықтималдықтың бұл анықтамасын классикалық анықтама немесе Лаплас моделі дейміз. Бұл айтылғандардан Лаплас моделі нәтижесі тең мүмкіндікті тәжірибелерді сипаттайды деп ұғамыз.
Енді Р(А) ықтималдығының қасиеттерін қарастырайық.
1о Р(А) ықтималдығы теріс емес функция, яғни Р(А) ³ 0.
2о
Р(А) ықтималдығы нормалданған
функция, яғни Р{ }=1.
}=1.
3о Қиылыспайтын (үйлесімсіз) А және В оқиғалары үшін Р(А+В) ықтималдығы аддитивті функция, яғни Р(А+В)=Р(А) +Р(В).
Бұл үшінші қасиетті ықтималдықтарды қосу теоремасы немесе ықтималдықтарды қосу заңы деп те атайды.
1-ші және 2-ші қасиеттер айқын көрініп тұр. Өйткені m ³ 0 және n > 0, m£n. Мұнан m>0 болса, Р(А) > 0, m=0 болса, Р(А)=Р(V)=0 (яғни мүмкін емес оқиға ықтималдығы). m=n болса, Р(А)=Р(U)=1 (яғни оқиқат оқиға ықтималдығы). Бұл екі қасиеттен 0 £ Р(А) £ 1 болатыны айқын көрініп тұр, яғни ықтималдық мәні 0 мен 1 арасындағы оң таңбалы сан екен.
Келтірілген қасиеттерден мүмкін емес (ақиқат) оқиға ықтималдығы нөлге (бірге) тең болуын көрдік. Бұл анықтама үшін осы сөйлемнің керісі де орын алады, яғни оқиға ықтималдығы нөлге (бірге) тең болса, ондай оқиғаның пайда болуы мүмкін емес (ақиқат). Ал ықтималдықтың басқа анықтамалары үшін бұл кері сөйлемнің орын алмауын байқаймыз (оны кейінгі бөлімдерде қарастырамыз). Ықтималдықтың классикалық анықтамасының бұл кемістігі сол бөлімде жетілтіріледі.
Ықтималдықтың классикалық анықтамасы өз уақытында ықтималдықтар теориясын құруға негіз болады. Біз мұны кездейсоқ оқиғалар заңдылығын математикалық абстракциялаудың алғашқы қарапайым сатысы – моделі дейміз. Ықтималдықтарды есептеу сынаудың жалпы саны мен оқиғаның пайда болуына қолайлы нәтижелер санын анықтауға тіреледі, бұл көп жағдайда үлкен қиындыққа ұшыратады. Оның үстіне, практикады кездесетін оқиғалар күрделі болып келеді де, олардың ықтималдығын табу үшін, ол оқиғаларды бірнеше қарапайым оқиғалардың қосындысы не көбейтіндісі түрінде жазып, солардың ықтималдықтары арқылы күрделі оқиға ықтималдығын анықтайды. Сондықтан да қарастырылып отырған оқиға ықтималдыңын екінші ықтималдық арқылы табудың маңызы өте-мөте зор. Ол үшін негізінен ықтималдықтарды қосу және көбейту теоремаларын пайдаланады.
Енді ықтималдықтың классикалық анықтамасын пайдалана отырып, оларды тікелей есептеуге бірнеше мысалдар келтірейік. Сонымен қатар тарихи мәні бар кейбір мысалдарды қарастырып, ықтималдықтар теориясының бірден қалыптаса қоймағанына көз жеткізейік.
Мысал-1. Жәшікте 10 шар бар. олардың 4-уі ақ 6-уы қызыл шар. Жәшіктегі шарларды араластырып жіберіп, қарамай тұрып, бір шарды алайық (сынау жүргізу). Алынған шар ақ шар болып шығуының (А оқиғасы) сандық мөлшерін (ықтималдығын) анықтау керек.
Шешуі. Әрбір шардың пайда болу
мүмкіндігі бірдей, яғни булар тең мүмкіндікті элементар оқиғалар.
Қалаған бір элементар оқиғаның шығу мүмкіндігінің сандық мөлшері
(ықтималдығы)  - ге тең:
n{
- ге тең:
n{ }=10. Барлық тең
мүмкіндікті 10 элементар оқиғалардың тек 4-уі ғана А оқиғасының
пайда болуына қолайлы элементар оқиғалар. Бұлардың санын (олар 4)
барлық элементар оқиғалар санына (олар 10) қатынасы
(
}=10. Барлық тең
мүмкіндікті 10 элементар оқиғалардың тек 4-уі ғана А оқиғасының
пайда болуына қолайлы элементар оқиғалар. Бұлардың санын (олар 4)
барлық элементар оқиғалар санына (олар 10) қатынасы
( ) осы оқиғаның пайда
болуының мүмкіндік дәрежесін көрсетеді. Мұны А оқиғасының пайда
болу ықтималдығы деп қабылдаймыз да Р(А) арқылы белгілейміз. Сонда
Р(А)=
) осы оқиғаның пайда
болуының мүмкіндік дәрежесін көрсетеді. Мұны А оқиғасының пайда
болу ықтималдығы деп қабылдаймыз да Р(А) арқылы белгілейміз. Сонда
Р(А)= .
.
Мысал-2. Ойын сүйегін лақтырғанда жұп сан шығуының ықтималдығы қандай?
Шешуі: Ойын сүйегі жалпы алты беттен, яғни 1 2 3 4 5 6 цифрларынан тұрады. Сонда n=6 және осы цифрлардағы жұп сандар саны үшеу, онда т=3. Сонымен ізделінді ықтималдық:
Р(А)=
Мысал-3. Жәшікте бірдей 20 шар бар. Оның 6-уы ақ шар, 4-уі көк шар, 10-ны қызыл шар. Жәшіктен кез келген бір шар алынады. Алынған шар: а)ақ шар (А оқиғасы); ә) қызыл шар (В оқиғасы); б) көк шар (С оқиғасы) болу ықтималдығын анықтау керек.
Шешуі: а) Шарлардың үлкендігі және салмағы бірдей болғандықтан, олардың шығу мүмкіндіктері де бірдей. Элементар оқиғалар саны n=20. А оқиғасына (ақ шардың шығуы) қолайлы элементар оқиғалар саны m=6. Демек,оның ықтималдығы
Р(А) =
 =
=  =0,3
=0,3
болады. Қалғандарын да осылай анықтау қиын емес, сонда: ә)0,5; б) 0,2.
Мысал-4. Теңге екі рет лақтырылды. Кем дегенде бір рет герб жағының шығу ықтималдығын анықтау керек.
Шешуі. Есептің дұрыс шешілуі (әсіресе, ықтималдыққа тиісті есептерді) есеп шартын талқылауға байланысты, бұл фактіні осы есептің шешуін талқылау арқылы көрсетейік.
Бірінші тәсіл (Даламбер талқылауы). Герб жағымен не бірінші, не екінші лақтырғанда түседі де тіпті түспейді. Сонымен, барлық элементар оқиғалар саны үшеу. Олардың ішінде А оқиғасының пайда болуына қолайлысы – екеу. Демек, іздеген ықтималдық Р(А)=2/3.
Екінші жолы: бірінші монетаны
бір рет лақтырғанда не герб жағынан, не тиын жағынан түсуі мүмкін.
Қай жағынан түссе де, бұл екінші рет лақтырғандағы монетаның герб
(Г) не тиын (Т) жағының түсуімен комбинациялынып келеді. Ақырында,
төмендегі тең мүмкіндікті тең 4 жағдай болады.
Олар  .
Мұнда Г-герб, Т-тиын. Есептің
шартына қолайлы элементар оқиғалар саны 3. Олай болса
ықтималдығы
.
Мұнда Г-герб, Т-тиын. Есептің
шартына қолайлы элементар оқиғалар саны 3. Олай болса
ықтималдығы
Р(А)
= =
0,75 не
75%.
=
0,75 не
75%.
Сонымен табылған екі ықтималдықтың қайсысы дұрыс. Соны анықтайық. Даламбердің қателігі мынада болған: ГТ және ТГ оқиғаларын бір оқиға деп алған. Шындығында бұлай болмайтыны екінші талқылаудан байқалады. Сонымен, екінші шешудің дұрыстығын байқаймыз.
Ықтималдықтарды есептеуде комбинаторика формуласын пайдаланудың қажеттігі туып отыр. Сондықтан комбинаторика ұғымын төменде келтіріп, оның формулаларын ықтималдықтарды есептеуге пайдалануды сол бөлімде толық қарастырамыз.
2. Ықтималдықтың геометриялық анықтамасы.
Алдындағы бөлімде қарастырылған тәжірибе нәтижелері шекті саналымды болып келді, практикада кездесетін есептердің басым көпшілігі бұл тәсілге келе бермейді. Себебі, тәжірибе нәтижелері саналымды шексіз, я саналымсыз жиын болуы мүмкін. Сондықтан ықтималдықтың классикалық анықтамасын сынау нәтижесінің саны шексіз тең мүмкіндікті тәжірибеге қолдануға болмайды. Осындай жағдайды сипаттауға ықтималдықтың геометриялық анықтамасы ыңғайлы. Оның үшін біз G жиында нүкте бірқалыпты деп ұйғарамыз, ал оның қандайда бір ішкі жиынын «g» ретінде белгілейміз (2-сызба).

2-сызба
Ол уақытта G облысына лақтырылған нүктенің «g» облысына түсуін А оқиғасы деп белгілеп, оның ықтималдығына мынадай анықтама береміз.
Анықтама. G облысына кездейсоқ лақтырылған нүктенің оның g бөлігіне түсу ықтималдығы деп g өлшемінің G облыс өлшеміне қатынасына тең (ұзындық, аудан, көлем) болған шаманы айтамыз, яғни
Р(А) =
 .
.
Мұнда да ықтималдықтың классикалық анықтамасында көрсетілген үш қасиет орындалады:
1о . Р(g) ықтималдығы теріс емес функция, яғни Р(g) ³ 0.
2о
. Р(G) ықтималдығы нормалданған
функция, яғни Р( G)
=1.
G)
=1.
3о . Қиылыспайтын (үйлесімсіз) А және В оқиғалары үшін Р(А+В) ықтималдығы аддитивті функция, яғни Р(А+В)=Р(А) +Р(В).
Бұл соңғы қасиет үйлесімсіз оқиғалар саны шекті және саналымды шексіз болсада орын алады дейміз.
Геометриялық ықтималдықтар тәсілі биология, атомдық физика, астрономия және т.с.с. басқа салаларда да көптеген қолданыс тауып отыр. Айтып өтетін жайт-кез-келген құбылысты сипаттауға классикалықта, геометриялық тәсілді алуға болады. Бірақ геометриялық тәсілде алынған математикалық модель классикалық тәсілге қарағанда айқын емес. Бірақта бір реал құбылысты сипаттайтын әр түрлі модельге сәйкес түрлі ықтимал-дықтарды алуға болады.
Мысал-1. Қабырғалары а = 4 ке тең болған квадрат ішіне жанамалап шеңгбер сызылған(3- сызба). Квадрат ішіне кездейсоқ лақтырылған нүктенің шеңбер ішіне түсу(А оқиғасы) ықтималдығы неге тең ?
Шешуі: Жалпы квадрат ауданын G
десек, онда G= a2
= 16 болады. Ал, сызбадан
шеңбер радиусының R=2 ге тең екендігін оңай табамыз. Сонда шеңбер
ауданын g деп белгілесек, онда оның ауданы g =
pR2=
4p
болады. Анықтама бойынша
ізделінген ықтималдық Р(А) =  =
=
 .
.

![]()
![]()
![]()
д а=4
![]()
3-сызба
Егер мәселеде Ω элементар оқиғалар кеңістігі шексіз санамалы емес жиын болса, ал ωі элементар оқиғалар тең мүмкіндікті болса, онда бұл есепте ықтималдықтың геометриялық анықтамасын қолдануға болады деп есептейміз. Геометриялық тұрғыдан есеп шартын қарамастан нүктені белгілі бір G геометриялық облысқа лақтыру (кесінді, жазықтықтың немесе кеңістіктің бөлігі) шартына келтіру. Нүкте қарамастан лақтырылғандықтан, онда G облысының g кез келген щектеулі бөлігіне түсу мүмкіндіктері тең. Сондықтан нүктенің g (g Ì G) облысына түсу ықтималдығы g өлшеміне (ұзындық, аудан немесе көлем) пропорционал және g-ның пішіні мен орналасуына тәуелді емес.
Егер оқиғаны А нүктенің g (g Ì G) облысына түсуі десек. Онда бұл оқиғаның ықтималдығы осы нүкте пайда болатын g облыс өлшемінің барлық G өлшеміне қатынасына тең: Р(А)=Lg/LG немесе Р(А)=Sg/SG немесе Р(А)=Vg/VG , мұндағы L, S, V – сәйкес облыстың ұзындығы, ауданы немесе көлемі.
Мысал-2. – Радиусы R дөңгелек диск екі секторға бөлінген. Біреуінің доға ұзындығы R. Тез айналып жатқан дискіге оқ атылды. Оның доға ұзындығы R секторға түсу ықтималдығын табу қажет .
Шешуі.
A оқиғасы–доға
ұзындығы R секторға түсуі. P(A)=  .
.
S(сектор)=
 ·R·l формуласы бойынша S(сектор) =
·R·l формуласы бойынша S(сектор) =
 ·R·R = R2/2
,
·R·R = R2/2
,
S(дөңгелек) =
π·R2 .
Сондықтан
Р(А) =  = R2/(2πR2) =
= R2/(2πR2) =
 .
.
Мысал-3. Жауын тамшысы, ұзындығы 100 метр болатын түзу жүгіру жолына тамады. А оқиғасын «Тамшы старт сызығынан а метрден артық емес қашықтыққа тамады» деп анықтаймыз. А оқиғасының Р(А) ықтимал-дығы қандай? Мұнда жолдан тыс жерге таматын тамшылар қарастырыл-майды.
Шешуі. 50 метр жолға таматын
тамшылар 100 метр жолға таматын тамшылардан 2 есе аз екендігін
түсіну қиын емес. Сондықтан, мысалы, a=50 болса,
онда P(A)= =
=  . Егер a=25 болса, онда ұзындығы 25 метр
жол бөлігі бүкіл жолдан 4 есе қысқа, сол
себепті P(A)=
. Егер a=25 болса, онда ұзындығы 25 метр
жол бөлігі бүкіл жолдан 4 есе қысқа, сол
себепті P(A)= =
= . Жалпы алғанда ұзындығы а метр
жолға, а метр 100–ден неше есе
кіші болса, сонша есе аз тамшылар тамады.
Яғни P(A) =
. Жалпы алғанда ұзындығы а метр
жолға, а метр 100–ден неше есе
кіші болса, сонша есе аз тамшылар тамады.
Яғни P(A) =  .
.
Мысал-4. (Кездесу туралы мәселе).
Екі студент (А мен В) сағат 10 мен 11 аралығында кездесуге уәделескен. Қайсысы бұрын келсе, сонысы 20 минут күтеді, сол мезгілде екіншісі келмесе қайтып кетеді, яғни кездесу болмайды. Егер әрқайсысының сол уәделескен уақытта келуі бір-біріне тәуелсіз және кездесуі кездейсоқ болса, онда екі студенттің кездесу ықтималдығы неге тең ?
Шешуі. А ның уәделі жерге келу уақытын х, В-ның келуін у арқылы белгілейміз. Уақыт өлшемін минут деп қабылдасақ , онда тек | х –у | £ 20 мин. болғандағана кездеседі. Бұл жағдайда барлық нәтижелер жиыны мына теңсіздіктермен анықталады: 18(сағ)£ х £ 19(сағ) және 18(сағ) £ у £ 19(сағ).
Кездесуге қолайлы нәтижелер жиыны мына теңсіздікпен берілген:
| х –у | £ 20 немесе х -20 £ у £ х +20. Олар осы қолайлы нәтижелер сызылған жолақта орналасқан( 4 - сызба).

![]() у y=x+20
у y=x+20
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()

![]() y=x-20
y=x-20

![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 40
40
![]()
![]()
![]()
![]()
![]() g
g
![]()
![]()
![]() 20 G
20 G
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 20
40 60
20
40 60
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0
60 х
0
60 х
4-сызба
Бұл
сызбада Р(A1) +
P(A2) + …+
P(A ) + …=1. Ал, сол екі студент
уаделі жерде [0,t] аралығында
) + …=1. Ал, сол екі студент
уаделі жерде [0,t] аралығында  - уақытта кездесетін болса,
онда
- уақытта кездесетін болса,
онда
P(A) =
(t2-(t- )2)/t2
= 1-(1-
)2)/t2
= 1-(1-
 /t)2
/t)2
болады.
Дербес жағдайда t =
1,  = 1/3 болса, онда P(A) =
1-(2/3)2
=
5/9.
= 1/3 болса, онда P(A) =
1-(2/3)2
=
5/9.
3. Статистикалық заңдылық және ықтималдықтың жиіліктік анықтамасы
Ықтималдықтың классикалық анықтамасы сынау нәтижесі шектеулі сан рет және тең мүмкіндікті болатынына негізделеді. Сондықтан бұл анықтаманың қолданылу өрісі тар. Осы себепті ықтималдықтың жай есептерінен күрделі есептерін шешуге көшкенде, әсіресе, статистикалық құбылыстарды сипаттауға байланысты практикада қолданылатын мәселелерді шешкенде шамадан тыс көптеген қиыншылықтарды кездестіреміз. Өйткені, біріншіден, сынаудың мүмкін нәтижелері шектеулі шама болмауы мүмкін. Мысалы, қандай да бір тілдегі бір сөздің пайда болу ықтималдығын тапқанда, біз практика тұрғысынан шектеусіз жиынды кездестіреміз. Екіншіден, жүргізілген тәжірибе нәтижесін ылғи да тең ықтималды болады деу аса үлкен қиындық туғызады. Мысалы, ұл бала не қыз бала туу ықтималдығын анықтағанда симметрия және тең ықтималдыққа сүйеніп қорытынды жасауға болмайтынын биологиялық статистика дәлелдейді.
Құбылыстарды сипаттауға ықтималдықтың статистикалық анықтамасын қолданайық. Статистикалық анықтама тәжірибені сан рет қайталап, нәтижелердің тізбесін жасауға суйенеді. Тәжірибе көп жүргізілгенде оқиғаның бірнеше рет пайда болуы не пайда болмауы мүмкін. Оқиғаның пайда болу не пайда болмау санын бұдан былай жиілік немесе абсалюттік жиілік деп айтамыз. Ал жиіліктің барлық сынау санына қатынасын салыстырмалы жиілік деп айтуға келісеміз. Сонда сынаудың жалпы санын n десек және оқиғаның қайыра пайда болу санын (жиілігін) m дейміз. Сонда А оқиғасының салыстырмалы жиілігі мынадай есептелінеді:
f(А) =  . Жүргізілген сынау саны аз болса , жиілік тұрақты болмай
бір сынаудан екінші сынауға дейінгі өзгеріс артып отырады. Ал сынау
жеткілікті дәрежеде қайталанып отырса, онда А оқиғасының
салыстырмалы жиілігі тұрақтана түседі. Мұндай жағдайлар физика,
биология, экономика, техникалық бақылауларда және т.с.с. салаларда
көп байқалады. Мысал үшін метал теңгені бір рет тастағанда оның
герб жағымен түсу ықтималдығы ықтималдықтың классикалық анықтамасы
бойынша 0.5 екендігін білеміз. Бырақта бұл сынауды 2, 5, 10 және
оданда көп рет қайталасақ ықтималдық олар үшін барлық уақыт 0.5 ке
тең болмастығы айқын. Сондықтан жоғарыда айтылған жиілік заңдылығын
сынау өте көп жүргізілгенде анықтау үшін танымал математиктер
Бюффон және К.Пирсондардың метал теңгенің герб жағымен түсу
тәжірибесін жүргізген тәжірибе қорытындыларын кестеде(1-кесте)
келтіреміз:
. Жүргізілген сынау саны аз болса , жиілік тұрақты болмай
бір сынаудан екінші сынауға дейінгі өзгеріс артып отырады. Ал сынау
жеткілікті дәрежеде қайталанып отырса, онда А оқиғасының
салыстырмалы жиілігі тұрақтана түседі. Мұндай жағдайлар физика,
биология, экономика, техникалық бақылауларда және т.с.с. салаларда
көп байқалады. Мысал үшін метал теңгені бір рет тастағанда оның
герб жағымен түсу ықтималдығы ықтималдықтың классикалық анықтамасы
бойынша 0.5 екендігін білеміз. Бырақта бұл сынауды 2, 5, 10 және
оданда көп рет қайталасақ ықтималдық олар үшін барлық уақыт 0.5 ке
тең болмастығы айқын. Сондықтан жоғарыда айтылған жиілік заңдылығын
сынау өте көп жүргізілгенде анықтау үшін танымал математиктер
Бюффон және К.Пирсондардың метал теңгенің герб жағымен түсу
тәжірибесін жүргізген тәжірибе қорытындыларын кестеде(1-кесте)
келтіреміз:
1-кесте
|
Тәжірібе жүргізгендер |
Тәжірибе саны |
Герб жағымен түсу саны |
Салыстырмалы жиілігі |
|
Бюффон |
4040 |
2048 |
0.5080 |
|
Г.Пирсон |
12000 |
6019 |
0.5018 |
|
Г.Пирсон |
24000 |
12012 |
0.005 |
Мысал-1. 1935 жылы Швецияда туған ұл баланың статистикалық мәліметтері алынды (2-кесте). Мұнда ұл баланың туу жиілігі 0,518 санына жуық өзгеріп (тұрақсызданып) отырған. Осы сияқты бақылау 1871 жылдан 1900 жылға дейінгі аралықта жүргізілген. Бұл жылдары 2,5 миллионнан астам туған балалардың жынысын есепке алғанда, ұл бала тууының салыстырмалы жиілігі 0,514 болған.
|
Айы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-кесте
Бұл келтірілген мысалдардан сынау саны мейлінше көп болғанда салыс-тырмалы жиілік мәні тұрақтылық қалыпқа түсетінін байқаймыз. Біздің жоғарыдағы кестеміз бойынша салыстырмалы жиілік 0.5 ке жуықтайды. Сонымен, тәжірибелерде сынау саны мейлінше көп болса, салыстырмалы жиілік ƒ мәні тұрақтылық қалыпқа түсетінін байқаймыз. Екінші сөзбен айтқанда, кездейсоқ құбылыстарда қандай да объективті қасиеттер бар екендігі және оның тұрақтануға бейімділігі сезіледі.
Бұл қасиет сынау саны артқан сайын айқындала түседі, ал ол қасиет қандайда бір шамамен өлшенеді. Бұл шама бақылауға түскен құбылыстың объективті сандық сипаты болып табылады. Осы тұрақтыны(санды) А кездейсоқ оқиғаның ықтималдығы деп айтамыз. Ал оныда жоғарыдағыдай Р(А) арқылы белгілейміз. Осындай тәсілмен анықталған кездейсоқ оқиға ықтималдығын статистикалық ықтималдық деп айтамыз. Сонымен, ықтималдықтың статистикалық анықтамасын да Р(А) @ f(A) ретінде қабылдаймыз.
Ықтималдықтың жоғарыда келтірілген қасиеттері статистикалық тұрғыдан анықтағандада орындалады:
1°. Салыстырмалы жиілік m/n теріс таңбалы болуы мүмкін емес, себебі
m ³ 0, n ³ 0 демек Р(А) ³ 0.
2°. Ақиқат оқиға сынауда әрбір қайталауда пайда болады, сондықтан
m= n, демек Р(А) = 1.
3°. А және В оқиғалары үйлесімсіз болса, бұлардың қосындысының ықтималдығы олардың ықтималдықтарының қосындысына тең, яғни n –жалпы саны, m1 – А оқиғасының пайда болу жиілігі, m2- В оқиғасының пайда болу жиілігі болса, онда мынадай теңдік орындалады:
Р(А+В) = m1/n + m2/n = Р(А) + Р(В) .
Мысал-2. Сапасын тексеру үшін кездейсоқ алынған 100 детальдың 5-еуі жарамсыз болып шықты. Жарамсыз детель шығуының салыстырмалы жиілігін табыңдар.
Шешуі. Мұнда , тексеру(сынау) өткізілетін барлық детальдар саны
n = 100, ал жарамсыз детальдар саны m = 5, сондықтан салыстырмалы жиілік формуласын қолдансақ төмендегі оған сәйкес шаманы табамыз:
f (А) =
 =
=  = 0.05
.
= 0.05
.
Ал, бұл шаманы жоғарыда айтылған анықтама бойынша статистикалық ықтималдық деп айтамыз.
Енді статистикалық ықтималдықтарды өте маңызды сипаттайтын устазымыз Қ.Бектаев [ 1 ] қарастырған мысалды келтирейік.
Мысал-3. 10 жастағы 100 000 бала бақылауға алынып, олардың қаншасы 20 жасқа дейін, қаншасы 30 жасқа дейін т.т. қаншасы 100 жасқа дейін өмір сүргенін есептеп нәтижесін төмендегі кесте (3-кесте)түрінде келтірілген.
3-кесте
|
Адамның жасы |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
|
Өмір сүрген |
100000 |
96061 |
89685 |
82277 |
72785 |
58842 |
37977 |
13987 |
1273 |
Осы кестеде келтірілген мәліметтерді пайдаланып :
а) а ( а=20) жастағы адамның b( b=50, b=70, b=90 ) жасқа дейін өмір сүру ықтималдығын анықтау керек;
ә) a = 20 жастағы адамның b( b=30, b=50, b=70, b=90 ) жасқа жетпей дүние салу ықтималдығын анықтау керек;
б) куйеуі а( а=30 ) жаста , әйелі b( b=20) жаста . Екеуі бірге c( c=20, c=40,c=50) жыл өмір сүру ықтималдығын анықтау керек;
в) куйеуі а( а=23 ) , әйелі b( b=18) жаста, олар бірге c( c=45) жыл өмір сүру ықтималдығын анықтау керек;
г) куйеуі а( а=50 ) , әйелі b( b=45) жаста, ұлы c( c=25) жаста, үшеуінің бірге d( d=20,d=30,d=40) жыл өмір сүру ықтималдығын анықтау керек;
д) куйеуі а( а=40 ) , әйелі b( b=35) жаста, екеуі бірге c( c=70, c=80) жасқа дейін өмір сүре алмау ықтималдығын есептеу керек;
е) куйеуі а( а=40 ) жаста , әйелі b( b=30)жаста, c( c=30, c=40) жылдан соң кемінде біреуі өлмей қалу ықтималдығын анықтау керек.
Шешуі. Жақша ішіндегі мәліметтердің біреуі үшін ғана есепті шығарамыз, қалғандарын оқушыларға жүктейміз. Тексеру жеңіл болу үшін олардың жауабын келтіріп , тиісті талдауларды пайдаланамыз.
а) Кестеге қарағанда, адамның
жасы ұлғайған сайын олардың саны азайып барады, бұл заңды, әрі
түсінікті де. а
жастағы
адамның b
жасқа дейін өмір сүруін А
оқиғасы дейік, бұлардың саны m(b) болсын,
а
жастағы адамдар саны
n(a) дейік. Сонда А оқиғасының
ықтималдығы P(A) =  ,
,
ал, кесте бойынша a= 20 болғанда n(a) = 96061, b = 50 болғанда
m(b) =72795. Сонда Р(А)
=  =
0.758.
=
0.758.
Сонымен, 20 жастағы адамдардың орта есеппен 75.8 % -і 50 жасқа дейін, 39.5% - і 70 жасқа дейін, 1.3 %-і 90 жасқа дейін өмір сүреді екен. Егер b=a болғанда Р(А) =1 болатын еді, бұл факт адамның b жасқа дейін өмір сүреті-нінің ақиқаттығын көрсетеді.
ә) Белгілі бір жасқа дейін
өмір сүруді А оқиғасы десек, онда оның осы жасқа дейін өмір
сүрмеуі  оқиғасы
болады. а
= 20,
b
= 50 десек,
онда
оқиғасы
болады. а
= 20,
b
= 50 десек,
онда
Р( ) = 1 – P (A) =1
–
) = 1 – P (A) =1
–  =
=
 =
=  =
=
 =
02427.
=
02427.
Сонда 20 жастағы адамдардың орта есеппен 24.2 % - і 50 жасқа жетпей дүние салатынын байқаймыз. Ал, осы 20 жастағы адамдардың 30 жасқа жетпей 6.6 % -і, 70 жасқа жетпей 61.5 % - і дүние салатынын оп –оңай есептеуге болады.
б) Куйеуінің а жастан а + с жасқа дейін өмір сүруін А оқиғасы, ал әйелінің b жастан b + c жасқа дейін өмір сүруін В оқиғасы дейік. Сонда екеуінің бірге өмір сүруі күрделі оқиға АВ болады. Бұлар бір-біріне тәуелсіз оқиғалар, сондықтан :
Р(АВ) = P(A) P(B)
=  ·
·
 =
=  ·
·
 =
=
=
 ·
·  =
=

 =
0.695
.
=
0.695
.
Сонымен, екеуінің бірге өмір сүру ықтималдығы 0.695 ке тең, яғни осы көрсетілген жаста ерлі-зайыптылардың 69.5 % ті тағыда 20 жыл бірге өмір сүреді екен. Әрине, бұлардың жастары артқан сайын бірге өмір сүрушілер саны кеми түседі. Екеуі қосылғаннан бастап 40 жыл өмір сүру ықтималдығы 26 % , ал 50 жыл өмір сүру ықтималдығы 6.2 % болатынын анықтаңыздар.
в) Бұл мәселе де дәл б) пунктіндегі мәселе секілді шешіледі. Бірақ б) пункт-інде келтірілген жасқа сәйкес жиіліктер шамасы кестеде жоқ. Сондықтан интерполяциялау тәсілін қолданамыз. Оның үшін кестеде келтірілген он жыл ішіндегі әрбір жылдағы өлім санын бірдей деп аламыз. Сондықтан жұбайлардың бірге өмір сүру ықтималдығын анықтаудан бұрын n(20), n(18) , m(23+45)= m(68), m(18+45) = m(63) мәндері неге тең болатынын табамыз. n(23) жиілігі n(20) мен n(30) аралығында, демек мынау келіп шығады:
n(23) = n(20) –  · 3 = 96061 –
· 3 = 96061 –  · 3 = 96061 -
· 3 = 96061 -  · 3 =
· 3 =
96061 – 191278 @ 94148.
Қалғандары да осылай анықталады, сонда m(18) = 96848, m(68) = 42150, m(63) = 52582. Демек ,
Р(АВ)
=  ·
·  =
=  ·
·  = 072437.
= 072437.
г) Бұл жағдайда ұлының с жастан с+d жасқа дейін өмір сүруін С оқиғасы десек, онда мәселе А,В,С оқиғаларының бірге пайда болу ықтималдығын табуға келіп тіреледі. Демек,
Р(АВС) =
 ·
·  ·
·
 =
=  ·
·
 ·
·  =
07272.
=
07272.
Қалғандарын да осылай анықтасақ үшеуі бірге 30 жыл өмір сүру ықтималдығы 4.5 % -ке, ал бірге 40 жыл өмір сүру ықтималдығы 0.08 % - ке тең болады екен.
д) Куйеунің
өлуін  оқиғасы, әйелінің
өлуін
оқиғасы, әйелінің
өлуін  оқиғасы десек, онда
екеуінің бірге өмір сүрмеуі
оқиғасы десек, онда
екеуінің бірге өмір сүрмеуі  ·
· оқиғасы болады. Мұның
ықтималдығы мынаған тең:
оқиғасы болады. Мұның
ықтималдығы мынаған тең:
Р(
 ) =
P(
) =
P( ·P(
·P( ) = (1 – P(A))·(1-P(B))
=
) = (1 – P(A))·(1-P(B))
=  ·
·
 =
=
=
 ·
·  =
=
 ·
·  =
0.300.
=
0.300.
Ал, ерлі-зайыпты адамдар бірге 80 жасқа дейін өмір сүрмеу ықтималдығы 69.5 % болады екен.
е) Кемінде біреуінің өлмеуін А
оқиғасы дейік, онда оған қарама-қарсы оқиға
 екеуінің де өлуін
көрсетеді. Олай болса,
екеуінің де өлуін
көрсетеді. Олай болса,
Р( ) =
) =
 ·
·  =
=
 ·
·  =
=
=
 ·
·  =
0.185.
=
0.185.
Сонда ізделінген ықтималдық,
яғни 30 жылдан кейін кемінде біреуінің өмір сүру ықтималдығы Р(А) =
1- P(  ) = 1- 0.185 = 0.815.
Дәл осылай есептесек, 40 жылдан кейін кемінде біреуінің өмір сүру
ықтималдығы 48 % болатынын табу қиын
емес.
) = 1- 0.185 = 0.815.
Дәл осылай есептесек, 40 жылдан кейін кемінде біреуінің өмір сүру
ықтималдығы 48 % болатынын табу қиын
емес.
Мысал-4. Жоғарыдағы 3-кестені пайдаланып а(а =20, a=30, a=50, a=70, a=80) жастағы адамның ықтималды өмір сүруін анықтау керек. Ықтималды өмір сүру деп қазіргі жасынан бастап қайсі бір жасқа дейін өмір сүру ықтималдығы 0.5 ( бұл шама түрлі өлкелерде әр түрлі болуы мүмкін) болатын жасты түсінеміз.
Шешуі. Қайсібір жасқа дейін
өмір сүруін А оқиғасы дейік, онда сол жасқа дейін дүние
салуы  оқиғасы болады. Егер
Р(А) = 0.5 болса, онда
оқиғасы болады. Егер
Р(А) = 0.5 болса, онда
Р( ) = болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға болады.Мысалы, қаупсіздендіру
мекемелері де осыны негізге алады. Айталық, болжап отырған
жасымыз х
болсын .
Сонда
) = болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға болады.Мысалы, қаупсіздендіру
мекемелері де осыны негізге алады. Айталық, болжап отырған
жасымыз х
болсын .
Сонда
 = 0.5,
m(x)
=0.5·n(a
).
= 0.5,
m(x)
=0.5·n(a
).
Енді х- тің мәнін жоғарыдағы кестеден пайдаланып табамыз. а = 20 , m(x) = 0.5, n(20) = 48030,5 . Кестеде 48030,5 мәні жоқ, сондықтан сызықты интерполяциялауды орындаймыз. 48030,5 саны 58842 мен 37977 аралығында, демек, бұл санға сәйкес х жас 60 пен 70 аралығында болады. Дәлірек айтқанда,
х
= 60 +
 · 10 =
60+5,2 = 65,2
@
65,
· 10 =
60+5,2 = 65,2
@
65,
Осы тәсілді қолданып, жасы а = 306, а = 50, а = 70, а = 80 деп алып есептегенде, ықтималды өмір сүру жасының сәйкес 67, 77, 79, 86 сандарына тең болатынын табу қиын емес.
Мысал-5. Енді жоғарыдағы 3-кестені пайдаланып еліміздегі а =20 жастағы адамның ықтималды өмір сүруін анықтау қажет болсын. Интернет желісіндегі Қазақстан Республикасындағы адамдардың орташа өмір сүру ықтималдығы P(A) ≈ 0.72 ( бұл шама интернет желілерінде 72.05% ретінде көрсетілген ) екендігі көрсетілген.
Шешуі. Қайсібір
жасқа дейін өмір сүруін А оқиғасы дедік, онда сол жасқа дейін дүние
салуы  оқиғасы болады. Егер
Р(А) = 0.72 болса, онда
оқиғасы болады. Егер
Р(А) = 0.72 болса, онда
Р( ) = 0.28 болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға
болады.
) = 0.28 болады. Қорытып
айтқанда, ықтималды өмір сүру деп қайсібір жасқа дейін өмір сүру
ықтималдығы сол жасқа дейін дүние салу ықтимал-дығына тең
болатын(болжанатын) жасты атауымызға
болады.
Айталық, болжап отырған жасымыз х болсын . Сонда
 =
P(
=
P( ) =
0.28,
m(x)
=0.28·n(a
).
) =
0.28,
m(x)
=0.28·n(a
).
Енді х- тің мәнін жоғарыдағы 3-кестеден пайдаланып табамыз. а = 20 , m(x) = 0,28 • n(20) = 0,28 • 96061 = 26897,08 . Кестеде 26897,08 мәні жоқ, сондықтан сызықты интерполяциялауды орындаймыз. 26897,08 саны 13989 мен 37977 аралығында, демек, бұл санға сәйкес х жас 70 пен 80 аралығында болады. Дәлірек айтқанда,
х = 70 +
 · 10 =
70+0,46•10 = 70+4,6
@
74,6.
· 10 =
70+0,46•10 = 70+4,6
@
74,6.
Жоғарыдағы 3-мысалда 10 жастағы 100 000 баланың 90 жасқа дейін өмір сүргені бақыланып, сол мәліметтер бойынша мәселелер құрастырылып шешілген. Алайда, бұл статистикалық мәліметтер қайжерде, кім жағынан 90 жыл жинақталғаны белгісіз. Сонда да ол мәліметтер шартты түрде жазылған деп есептейік. Тағыда ол мәліметтерде ерлер мен әйелдердің өмір суру ықтималдықтары барлық аралықтарда бірдей етіп алынған. Ал ол қазіргі заман ғылыми зерттеулеріне сәйкес келмейді. Сондықтан мәселеге анықтық еңгізу үшін төмендегідей мәліметтер гистограмма ретінде берілген және интернет желісінде көрсетілген Ұлттық экономикалық министрлігі статистика комитетінің деректерінен алынды(төмендегі гисторграмма).

|
Бұл гистограммада 100 жасқа дейін әр 5 жас арасындағы ерлер мен әйлдердің өмір сүру ықтималдықтары пайыз(%) ретіндегі қатынастары келтірілген. Көрініп тұрғандай белгілі жас аралықтарында ерлер мен әйелдердің өмір сүру ықтималдықтары әр түрлі екен. Мұнда бірінші бағана ерлердің , ал екінші бағана әйелдердің сол аралықтағы өмір сүру ықтималдықтарын білдіреді. Бұл гистограммаға сәйкес келетін мәліметтер 4-кестеде жазылған. 4-кесте |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Барлығы 18 157 336 |
Бұл деректер бойынша 2018 жыл басында Қазақстан Республикасындағы халық саны 18 миллионнан асқан, олардың 8 791297 і ер адамдар, 9366 039 і әйелдер , ал жалпы елімізде 18 157 336 адам өмір сүргені көрсетілген. Бұл мәліметтерден сол кезде елімізде әйелдердің ерлерге қарағанда 574 742 адамға көп болғаны көрініп тұр. Сол себептен Бектаев ағамыздың танымал мәселесіне қазіргі кездерде жиналған деректерді пайдаланып шешуді жөн көрдік.
Мысал-6. Туылғаннан бастап 100 жасқа дейін белгілі жас аралығындағы ерлер және әйелдердің саны, яғни 1-4 аралық жаста қаншасы, 5-9 жас аралығында қаншасы т.т. қаншасы 100 жасқа дейін өмір сүргендігі және олардың салыстырмалы түрдегі пайыздық көрсеткіші статистикалық мәліметтер ретінде анықталған(4-кесте).
Осы кестеде келтірілген мәліметтерді пайдаланып :
а) а ( а=20) жастағы адамның b( b=50, b=70, b=90 ) жасқа дейін өмір сүру ықтималдығын анықтау керек;
ә) a = 20 жастағы адамның b( b=30, b=50, b=70, b=90 ) жасқа жетпей дүние салу ықтималдығын анықтау керек;
б) куйеуі а( а=30 ) жаста , әйелі b( b=20) жаста . Екеуі бірге c( c=20, c=40,c=50) жыл өмір сүру ықтималдығын анықтау керек;
в) куйеуі а( а=23 ) , әйелі b( b=18) жаста, олар бірге c( c=45) жыл өмір сүру ықтималдығын анықтау керек;
г) куйеуі а( а=50 ) , әйелі b( b=45) жаста, ұлы c( c=25) жаста, үшеуінің бірге d( d=20,d=30,d=40) жыл өмір сүру ықтималдығын анықтау керек;
д) куйеуі а( а=40 ) , әйелі b( b=35) жаста, екеуі бірге c( c=70, c=80) жасқа дейін өмір сүре алмау ықтималдығын есептеу керек;
е) куйеуі а( а=40 ) жаста , әйелі b( b=30)жаста, c( c=30, c=40) жылдан соң кемінде біреуі өлмей қалу ықтималдығын анықтау керек.
Шешуі. Бұл мәселені шешу үшін 4-кестені 3-кесте ретінде ерлер және әйелдер үшін жеке-жеке құрастырамыз(5-кесте). Себебі ерлер мен әйелдердің өмір сүру ықтималдықтары әр түрлі.
5-кесте
|
Жас аралығы |
Ерлер саны |
Жалпы адамдар саны |
Жас аралығы |
Әйелдер саны |
|
жасы: 0 |
8 791 298 |
18 157 336 |
жасы: 0 |
9 366 038 |
|
жасы: 1-4 |
8 591 203 |
17 769 971 |
жасы: 1-4 |
9 178 768 |
|
жасы: 5-9 |
7 785 025 |
17 011 752 |
жасы: 5-9 |
8 420 549 |
|
жасы: 10-14 |
6 866 366 |
14 416 414 |
жасы: 10-14 |
7 550 048 |
|
жасы: 15-19 |
6 169 970 |
13 047 806 |
жасы: 15-19 |
6 884 838 |
|
жасы: 20-24 |
5 592 525 |
11 932 727 |
жасы: 20-24 |
6 340 202 |
|
жасы: 25-29 |
4 938 716 |
10 648 809 |
жасы: 25-29 |
5 710 093 |
|
жасы: 30-34 |
4 148 739 |
9 057 860 |
жасы: 30-34 |
4 909 121 |
|
жасы: 35-39 |
3 397 147 |
7 538 790 |
жасы: 35-39 |
4 141 643 |
|
жасы: 40-44 |
2 772 563 |
6 270 226 |
жасы: 40-44 |
3 497 663 |
|
жасы: 45-49 |
2 216 791 |
5 119 938 |
жасы: 45-49 |
2 903 147 |
|
жасы: 50-54 |
1 705 629 |
4 049 924 |
жасы: 50-54 |
2 344 295 |
|
жасы: 55-59 |
1 229 722 |
3 034 455 |
жасы: 55-59 |
1 804 733 |
|
жасы: 60-64 |
784 251 |
2 052 874 |
жасы: 60-64 |
1 268 623 |
|
жасы: 65-69 |
473 678 |
1 327 935 |
жасы: 65-69 |
854 257 |
|
жасы: 70-74 |
262 080 |
791 914 |
жасы: 70-74 |
529 834 |
|
жасы: 75-79 |
164 662 |
530 826 |
жасы: 75-79 |
366 164 |
|
жасы: 80-84 |
70 946 |
242 326 |
жасы: 80-84 |
171 380 |
|
жасы: 85-89 |
23 469 |
79 850 |
жасы: 85-89 |
63 165 |
|
жасы: 90-94 |
6 814 |
22 100 |
жасы: 90-94 |
16 956 |
|
жасы: 95-99 |
1670 |
3 806 |
жасы: 95-99 |
2 583 |
|
жасы: 100+ |
447 |
871 |
жасы: 100+ |
424 |
|
|
Жалпы саны 8 791 298 |
Жалпы саны 18 157 336 |
|
Жалпы саны 9 366 038 |
Ескерту: Мәселені
төмендегідей шешу үшін жоғарыдағы 3-мысалдың шешілу процесін толық
меңгерген болу қажет. Себебі 3-мысалдағы түсініктемелерді қайталап
жазып отырмаймыз. Сондада , кестеге қарағанда, адамның жасы
ұлғайған сайын олардың саны азайып баратындығын көреміз, бұл заңды,
әрі түсінікті де. а
жастағы
адамның b
жасқа дейін өмір сүруін А
оқиғасы дейік, бұлардың санын сәйкес ретінде ерлер үшін
mе(b), әйелдер үшін
mә
(b) болсын,
а
жастағы адамдар саны ерлер
үшін nе(a), әйелдер үшін
nә(a), ал аралықтағы адамдар санын
ерлер үшін nе(i-j), әйелдер үшін
nә(i-j) (мұнда,
i= ,
i=i+5, j=
,
i=i+5, j= ,
j=i+4, ) деп белгілейік( жалпы
адамдар саны үшінда осындай белгілеулар еңгізген
жөн).
,
j=i+4, ) деп белгілейік( жалпы
адамдар саны үшінда осындай белгілеулар еңгізген
жөн).
Жоғарыдағы мәселелерді шешу үшін төмендегідей өзгерістер еңгіземіз:
а) Бұл жерде
жастарын өзгеріссіз қалдырамыз және ерлер, не әйелдер
ескертілмегендіктен кестедегі жалпы адамдар санының өзгеріс
заңдылығын қолданамыз. Сонда А оқиғасының ықтималдығы P(A)
=  ал, кесте
бойынша a=
20 болғанда
nж(a) = 11 932
777, b
= 50
болғанда
ал, кесте
бойынша a=
20 болғанда
nж(a) = 11 932
777, b
= 50
болғанда
mж(b) =4 049 924. Сонда Р(А)
=  =
0,339.
=
0,339.
Сонымен, 20 жастағы адамдардың орта есеппен 33,9 % -і 50 жасқа дейін өмір сүреді екен. Бұл көпшілікке күман келтіру мүмкін, бырақта бұл 2018 жылғы статистикалық мәлімет бойынша есептелінді. Егер b=a болғанда Р(А) =1 болатын еді, бұл факт адамның b жасқа дейін өмір сүретінінің ақиқаттығын көрсетеді.
ә) (а) пункттегідей есептеу жүргіземіз.
б) Мұнда Р(А) ны есептеу үшін кестедегі 2-бағандағы(ерлер үшін) мәлімет-терді, ал Р(В) ны есептеу үшін кестедегі 5-бағандағы(әйелдер үшін) алынған мәліметтерден пайдаланамыз.
в) Бұл мәселе де дәл (б) пунктіндегі мәселе секілді шешіледі, бырақта (б) пунктінде келтірілген жасқа сәйкес жиіліктер шамасы кестеде жоқ. Сондықтан интерпалациялау әдісін қолданып 4-кестеде келтірілген сол аралықтағы адамдар(ерлер немесе әйелдер немесе жалпы) үшін 5 жыл ішіндегі әрбір жылдағы өлім санын бірдей деп аламыз және сол аралықтағы адамдар санын 5-ке бөліп біртіндеп қосу арқылы қажетті жасты табамыз. Дәл сұралған мәселе үшін толық тоқталайық. Сондықтан бізге қажетті болған ne(23), me(23+45) = me(68), nә(18), mә(18+45) = mә(63) мәндердің неге тең болатыны табайық.
ne(23) =
ne(20) -
 •4=
5 592 525 -
•4=
5 592 525 -  • 4 =
5 592 525-523047,2 =
5 069 477,8.
• 4 =
5 592 525-523047,2 =
5 069 477,8.
me(23+45) =
me(68)=
me(65)- •4
=
473 678-
•4
=
473 678-
 •4
=473 678-
169 278,4 =
304 399,6 .
•4
=473 678-
169 278,4 =
304 399,6 .
nә(18) =
nә(15)
- •4 = 6 884 838
-
•4 = 6 884 838
-  •4 = 6 884 838
– 435708,8 =
6 449 129,2.
•4 = 6 884 838
– 435708,8 =
6 449 129,2.
mә(18+45) =
mә(63)=
mә(60)
- •4
= 1 268
683-
•4
= 1 268
683-  •4
=
1 268 683 –
331 492,8 =
937 190,2.
•4
=
1 268 683 –
331 492,8 =
937 190,2.
Демек,
Р(А•В) =  •
•
 =
=  ·
·  = 0,06 •
0,145 =
0,0087.
= 0,06 •
0,145 =
0,0087.
г) Бұл жағдайда ұлының өмір сүруін С оқиғасы деп ерлерге жазылған мәліметтерден есептеп Р(А•В•С) ықтималдықты есептейміз.
д) Мұндада куйеуі және әйелі үшін жеке есептеліп 3-мысалдағыдай табылады.
е) (д) пункттегідей есептелінеді.
Жоғарыдағы ә), б), г), д) және е) пункттегі мәселелерді 3-мысалдағы тәсілдер көмегімен 4 және 5-кестелерді пайдаланып шешуді оқушылардың өзіне қалдырамыз.
3-лекция
Комбинаторикалық элементтер.
1. Комбинаторикалық элементтер ұғымы.
2. Құрылымдар санын есептеу формулалары.
3. Орналастыру заңдылықтары.
4. Комбинаторикада орын алмастыру қағидалары.
5. Теру және оның қасиеттері.
________________________________________________________________
Комбинаторикалық элементтер.
1. Комбинаторлы конфигурация негіздері
1) Комбинаторика – математика тарауларының бірі. Мұнда элементтер жиынының әртүрлі комбинациялары қарастырылып, олардың сандары есептелінеді.
Комбинаториканың негізгі мәселелері болып кезектегілерді айырып алуға болады: есептелу, санақтау, классификациялау және оптимизациялау. Егер кейбір қасиеттер немесе қасиеттер жиынтығына ие болған элементтер санын анықтау талап етілсе, онда бұл мәселе есептелу. Ал, егер бұл жерде элементтер тізімін көрсету қажет болса, онда ол санақтау болады. Егер есептелу өте үлкен сандарға алып келетін болса, онда ол сәйкес ретінде есептелудің орнына қандайда бір қатынастар көмегімен текқана кластарға бөлінеді. Оны біз классификациялау деп айтамыз. Кейбір мәселелердегі шешімдер жиынтығына функциялардың шамаларын енгізу мүмкін. Бұл функцияларда оптимизациялау мәселелері, яғни белгілі бір обьекттер жиынында функцияның экстремумын табу, болмаса экстремал мәндерге жете алатын кейбір немесе барлық нысандарды көрсету қарастырылады.
2) Комбинаторикалық құрылым деп қатар арнайы қасиеттерді қанағаттандыратын элементтердің шекті жиынтықтарының жайғасуын түсінеміз. Негізгі комбинаторикалық құрылымдарға теру, орналастыру және орын алмастырулар кіреді. Басқа көптеген құрылымдар осыларға алып келуі мүмкін.
Х=(х1,х2,….хn) жиын элементтерінен құралған (хі1,хі2,….хік), (k£n), элементтер жиналымы (набор) элементтердің k көлемдегі таңдамасы немесе (n,k)-таңдама деп айтылады. Элементтер құрамымен айырықшалыққа ие болған таңдамалар барлық уақыт әртүрлі болады. Егер таңдамада элементтер реті алдын – ала берілген болса, онда оны реттелген деп айтамыз. Екі реттелген таңдама элементтерінің келу ретімен ғана айырықшалыққа ие болса да әр түрлі деп есептеледі. Егер таңдамада элементтер реті белгісіз болса, онда оны реттелмеген таңдама деп айтамыз. Элементтері қайталануы мүмкін болған реттелген (n,k)-таңдама (n,k)-қайталамалы орналастыру немесе n элементтен әрқайсысы k- дан жасалған қайталамалы орналастыру деп айтамыз. Егер (n,k) – таңдаманың элементтері жұбымен әр түрлі болса, онда ол (n,k) – қайталамасыз орналастыру немесе n элементтен әрқайсысы k- дан жасалған қайталамасыз орналастыру деп айтылады. Қайталамасыз (n,n) – орналастыру n –элементтен n – нен алынған орын алмастырулар немесе n элементті орын алмастыру деп айтамыз.
Реттелген (n,k) –таңдамада n элементтен әрқайсысы к – дан алынған орналастыруларды бір – бірінен айырықшалығы не элементтерінде, не элементерінің орналасу ретінде болатын комбинациялар ретінде де қарастыру мүмкін. Оны біз теру деп айтамыз. Мұнда қайталанбайтын (n,k) – теру n – элементті жиынның k-элементті ішкі жиындары екендігіне мән беру қажет. Егер элементтер (n,k) –таңдамада қайталанбайтын болса, онда k £ n теңсіздік орындалады. Ал, қайталамалы таңдамалар үшін k>n шарт болуы мүмкін.
3) Комбинаторикада екі негізгі қағиданы көрсету мүмкін: қосу қағидасы және көбейту қағидасы.
Айталық , Х шекті жиын n элементтен құралған болсын. Онда Х тен алынған бір нысанды n тәсілмен таңдау мүмкін және ол ïХï=n ретінде жазылады. Егер Х және Ү – қиылыспайтын жиындар және ïХï=n,ïҮï=m болса ,онда ïХÈҮï=m+n болады. Бұл қасиетті бұданда көп жиындар үшін де қолдану мүмкін.
Айталық íХý - өздерінің жұбымен қиылыспайтын жүйе болсын:
Хі Ç Хj = Æ, і ¹j. Онда
êі=1È n Xі½= і=1 å nôХіô (1)
болады. Бұл қағиданы қосылу немесе альтернатив қағида деп айтылады.
Егер хÎ Х нысан n тәсілмен таңдалған және әрбір осындай тәсілден соң
уÎ Ү нысан m тәсілмен алынған болса, онда реттелген (х,у) жұптық таңдауы m ×n тәсілмен орындалуы мүмкін. Бұл көбейту қағидасы болады. Онда ол тағыда көп санды жиындарға қолдануға мүмкіндік береді. íХіý, і=1,2,….k, мұнда ôХіô=mі, жиынды жүйе үшін k санды (х1,х2,….хк), хі Î Хі, нысандардың реттелген тізбекті таңдамасы m1 × m2 ×…×mk тәсілмен орындалуы мүмкін.
Мысал. Қазақстандағы кез келген автомобил нөмірі АСССААА қалыптағы тізбектен тұрады, мұнда А латын алфавитіндегі әріптер, ал С кез келген ондық сан. Сонда мүмкін болған әр түрлі нөмірлер саны 35×10×10×10×35×35×35=1 500 625 000 болады.
Ал, қиылысатын жиындар үшін біраз
күрделі қатынастар орындалады. Бұл жерде кемінде біреуіне тиісті
болатын, яғни олардың бірігуіне тиісті Х,Ү жиындар үшін элементтер
саны 
ôХÈҮô=ôХô+ôҮô-ôХ ÇҮô (2)
формула арқылы табылатындығын көру қиын емес.
Ал үш Х,Ү,Z жиындар үшін,олардың бірігуіндегі элементтер саны
ôХÈҮÈ Zô=ôXô+ôYô+ôZô-ôXÇYô-ôXÇYô-ôXÇYô+ôXÇYÇ Zô (3)
тең болады. Бұл жерде (2) және (3)
қатынастарға басқашада сипат беру мүмкін. Егер, Х,Y,Z, жиындарды U
жалпылама жиынның ішкі жиыны ретінде қарастырсақ,
онда  =ôUô-ôX È Yô екендігі, ал одан
=ôUô-ôX È Yô екендігі, ал одан
 =ôUô-
(ôХô+ôҮô)+ôХ ÇҮô (4)
=ôUô-
(ôХô+ôҮô)+ôХ ÇҮô (4)
келіп шығады. Сол секілді:
 =ôUô-ôХô+ôҮô+ôZô)+(ôX ÇYô+ôX Ç Zô+ôYÇ Zô ) -
=ôUô-ôХô+ôҮô+ôZô)+(ôX ÇYô+ôX Ç Zô+ôYÇ Zô ) -
-ôX Ç Y Ç Zô (5)
теңдік орынды болады. Бұл жердегі (4) және (5) тендіктер енгізу және шығару қағидаларының дербес жағдайы болып есептелінеді.
Айталық, Р (1), Р (2),...., Р(n) болған n қасиет және Р(і), Р(j) қасиеттерге ие болған N элементті жиынның Ni элементті саны, жалпы айтқанда (Рі1), (Рі2),...,(Ріs) қасиеттерге ие болған Nі1і2…іs-элементтер саны қарастырылып жатқан болсын. Онда, осы қасиеттердің бірде-біреуінеде ие болмаған N(0)- дің элементтер саны таңбалары ауысып келетін төмендегідей алгебралық қосындымен анықталады:
N (0) =N - іå Nі + і<jåNij - …+ (-1)s× i1<i2<…<iså N i1i2…is + (-1)n ×N12….n . (6)
2. Комбинаторикалық құрылымдар санын есептеу
формулалары.
Орын алмастыруларды есептеу
Анықтама. Алмастырулар деп, бір-бірінен айырмашылығы oрналасу ретінде ғана болатын элементтер комбинацияларын айтады.
Сонымен, n элементтен n! алмастыру жасауға болады, оны Рn арқылы белгілейді: Рn = n! = 1. 2 . 3 . . . n.
a және b-екі элементтен, олардың ретін өзгертіп, екі алмастыру алуға болады: ab, ba. Үш (a, b, с ) элементтен 6 алмастыру алынады: abс, baс, bсa, aсb, сab, сba. Алмастырулар заңдылыққа бағынады: екі элементтен екі алмастыру, немесе 2! алмастыру алуға болады, 3 элементтен үшеуден 6 алмастыру, немесе – 3! алуға болады. Онда 4 элементтен төртеуден 4! =24 алмастыру алуға болады т.с.с.
Енді n элементтен келіп шығатын барлық орын алмастырулар тізбегінен кейбір алгоритмдерін қарастырайық.
а) Лексикографикалық немесе алфавиттік. Мұнда, тізбектелу индуктив түрде анықталады , яғни әр бір орын алмастыруға бірінші элемент көрсетілген, одан соң келетін барлық тізбектегілер:
1, ( алфавитті ретпен í2,….,ný тен алынған барлық орын алмастырулар );
2, (алфавитті ретпен í1,3,….,n ý тен алынған барлық орын алмастырулар);
3, (алфавитті ретпен í1,2,4,..….,n ý тен алынған барлық орын алмастырулар);
……………...............
k , (алфавитті ретпен í1,2,…..,k – 1 ,k + 1,….., n ý тен алынған барлық орын алмастырулар);
……………..............
n , (алфавитті ретпен í1,2,…..,n – 1 ý тен алынған барлық орын алмастырулар).
Мысал. n ═ 3 үшін
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
б) Бұл жерде орын алмастырулардың құрылымы сондай кезектесумен жайғасады, яғни екіншісінен бастап әр бір элемент алдынғысынан орындары дәл екі элементке ауысатындай айрықшалықта болады(осындай жағдай және осындай ауыстыру транспозиция деп айтылады). Мұндай орын алмастырулар тізбегі өте тиімді болуы мүмкін, егер қандайда бір мәселені (мысалы, комбинаторикалық) шешуде әр бір орын алмастырумен кейбір есептеулер байланысты және алдынғы орын алмастырулар үшін алынған дербес нәтижелерді қолдану мүмкіншілігі бар болса немесе егер тізбектегі орын алмастырулар бір-бірінен өте аз айрықшалықта болса.
Қазіргі кезеңде әр түрлі қатынастарда өте қолайлы, әсіресе бағдарламалау теориясы үшін тиімді болған осындай кезектесудің түрлі құрылу алгоритмдері бар.
в) Алдыңғы пункттің дербес жағдайы ретінде екі көршілес орын алмас-тырулар арасындағы айрықшалық жәнеде кіші болған кезектесуді қарастыру мүмкін. Олар екі көршілес элементтердің транспозициясы-мен айрықшаланады. Мұндай алгоритмнің мазмұны-индуктивті құрылым.
Айталық осыған дейін осы қасиетке ие болған 1,2,…..,(n – 1) элементтер кезектесуі құрылған болсын . Онда талап этілген 1,2,…..,n элементтердің орын алмастыру тізбектерін n ді мүмкін болған барлық тәсілдермен (олардың саны дәл n ) 1,2,…,(n-1) элементтердің әр бір орын алмастыруларының түрлі орындарына n -ді біртіндеп алға және артқа жылжыта отырып (n – 1)! рет) қою арқылы аламыз.
Төменде n ═ 2,3,4 үшін толық, ал n ═ 5 болғанда кезектесудің басы үшін осы алгоритм кесте ретінде бейнеленген. Бұл жерде (n) элемент қою әріппен жазылған, ал әр бір бағанның оң жағында 1, 2 ,…, ( n - 1 ) элементтердің транспозициясы көрсетілген:
n ═ 2 n ═ 3 n ═ 4 n ═ 5
------------------------------------------------------------------------------------------------------------
1 2 1 2 3 1 2 3 4 1 2 3 4 5
2 1 1 3 2 1 2 4 3 1 2 3 5 4
3 1 2 12 1 4 2 3 1 2 5 3 4
3 2 1 21 4 1 2 3 23 1 5 2 3 4
2 3 1 4 1 3 2 32 5 1 2 3 4 34
2 1 3 1 4 3 2 5 1 2 4 3 43
1 3 4 2 1 5 2 4 3
1 3 2 4 13 1 2 5 4 3
3 1 2 4 31 1 2 4 5 3
3 1 4 2 1 2 4 3 5 24
3 4 1 2 1 4 2 3 5 42
4 3 1 2 12 1 4 2 5 3
4 3 2 1 21 1 4 5 2 3
3 4 2 1 1 5 4 2 3
3 2 4 1 5 1 4 2 3 14
3 2 1 4 32 5 4 1 2 3
2 3 1 4 23 4 5 1 2 3
2 3 4 1 4 1 5 2 3
2 4 3 1 4 1 2 5 3
4 2 3 1 31 4 1 2 3 5 23
4 2 1 3 13 4 1 3 2 5 32
2 4 1 3 4 1 3 5 2
2 1 4 3 4 1 5 3 2
2 1 3 4 4 5 1 3 2
5 4 1 3 2 41
5 1 4 3 2 14
1 5 4 3 2
……………
Орналастыруларды есептеу.
Анықтама. Бір-бірінен айырмашылығы орналасу ретінде немесе құрамында болатын n элементтің m - нен жасалған комбинацияларын орналастырулар деп атайды.
Мысал үшін 4- элементтен әрбіреуінде 2- элемент болатын комбинациялар құрып, оның санын есептеу керек болсын. Сонда а, b, с, d элементтерінен екі – екіден комбинация құру төмендегідей болады.
Олар: аb, bс, bd, ас, аd, сd, bа, са, dа, сb, db, dс.
Қайталамасыз ( n,k) – орналастырулар саны Аkn көбейту қағидалары көмегімен анықталуы мүмкін. Бірінші k элементті орналастыру n тәсілмен таңдалады, ал екіншісі ( n – 1) тәсілмен, себебі бірінші алынған элемент қайталанбауы қажет. Сол секілді үшінші элементке (n-2) тәсіл ( егер к > 2 болса) қалады және т.с. жалғасады. Бұл жерде k элемент, яғни Аkn = n × ( n-1)× …..×(n –k+1) элемент, атап айтқанда n нен бастап біреуден кеміп баратын k көбейтінді тандалуы мүмкін. Басқаша айтқанда, n! =1×2× ….×n белгілеуді қолдансақ оны төмендегідей қолайлы жазуға болады:
Аkn = 
Мысал-1. А37 = 7! /4! = 7×6×5=210;
А47 =7! /3!=7×6×5×4=840;
А57 =7!/ 2!=7×6×5×4×3=2520.
Егер k=1 болса, онда А1n=n!/(n-1)! = n ; егер k= n-1 болса, онда Аn-1n =n!/1!=n!; егер k= n болса, онда Аnn=n!/0! = n! болатындығын көру қиын емес. Математикада формуланың бірмәнділігі және қолайлық үшін 0!=1 деп қабылданғандығын ескертеміз. Бұл жерде Аn-1n және Аnn сандарының тең екендігі айқын, себебі, егер n элементтен ( n-1) элемент тандалған болса, онда қалған жалғыз элементте сондай тәсілмен тандалған болады. Ал, ол
Аn-1n санын Аnn санымен салыстырғанда өзгертпейді. Сондықтан, n орын алмастыру Рn = n! болады.
Ал, қайталамалы (n,k)- орналастырулар n элементті алфавиттің k ұзындықтағы сөз тізбегі болады. Осы жерде көбейту қағидасынан пайдалана отырып әр түрлі қайталамалы (n,k) орналастырулар Аkn = nk болатындығын көру қиын емес. Шындығындада, реттелген тізбектегі n мүшенің әр біреуі бір-бірінен байланыссыз, саны k ға тең бола тұра, n тәсілмен тандалуы мүмкін.
Мысалдар. 1) { 0,1} алфавитіндегі k ұзындықтағы сөздер саны 2k ға тең, сол секілді k- элементті жиынның барлық ішкі жиындарыда сол санға тең, себебі жиын өзінің характеристикалық функциясымен бірмәнді беріледі. k-мәнді екілік сандардың мөлшері 2k-1 ге тең, себебі бұл жерде санның бірінші сатысы 1 ге тең болуы қажет.
2) k- мәнді ондық сандар ( яғни, дәл k сатыға ие болған) мөлшері 9×10k-1 ге тең, бұл жерде оларды біз {0,1,2, …..9} алфавитіндегі сөз ретінде қарастырдық, сонымен тағыда бұл сандардағы бірінші саты барлық уақыт 0 ден айрықша болуын ескертеміз.
Теру элементтерін есептеу.
Анықтама. Бір-бірінен айырмашылығы құрамында ең болмағанда бір элементі өзгеше болатын элементтер комбинацияларын n элементтен m – нен жасалған теру деп атайды.
Қайталамасыз ( n,k) теру санын Сkn немесе ( nk) арқылы белгілейміз және оларды биномиал коэффиценттер деп айтамыз. Себебі, олар х+у екімүшенің n- дәрежелі Ньютон биномы формуласындағы коэффициенттерге сәйкес келеді:
(х + у)n = k=0ån Ckn × xn-k × уk . (7)
Шындығындада,
хn-k ·
уk мүшенің алдындағы коэффициент n дана бір түрлі
(х+у) ×(х+у)×…..×(х+у) көбейтінділерінен k рет тандалған тәсілдер
санына тең. Ал, ол х және у тер көбейтіндісінің дәл
хn-k ·
уk реттік көбейтіндісінен тандалған. Қайталамасыз
(n, k) - теруді есептеу үшін қайталамасыз барлық (n,k)-
орналастырулар жиынын бір түрлі элементтер құрамына ие болатын
қатынастарға байланысты эквивалент кластарға бөліп қарастыру өте
қолайлы. Бұл жерде құрылымы бойынша айрықша болған элементтер әр
түрлі кластарда жатады. Әр бір класта бірдей k дана түрлі элементі
болған реттелген құрылымға ие болады, яғни олар k орын алмастыруды
сипаттайды және әр бір класта олардың саны k! ға тең болады. Осы
жерден қайталамасыз (n,k)- терулердің
Сkn саны Аkn/
k! ға тең, яғни Сkn
=  . (8)
. (8)
Бұл жерде k ның дерлік үлкен болмаған мәндерінде Сkn үшін соңғы өрнекті қолданған қолайлы, себебі өрнектің алымындада, бөліміндеде k данағана көбейтінді бар, яғни алымында n-нен бастап кеміп баратын натурал сандар қатары, ал бөлімінде 1 ден бастап өсү бойынша k ға дейінгі натурал сандар қатарының бөлігінен құралған. Дербес ретінде барлық уақыт С0n =1, C1n= n, C2n= n×(n-1)/2 болатындығын көру қиын емес. Тағыда, осы жерде егер k>n болса, онда Сkn=0 деп қабылдаймыз.
Мысал үшін 4 элементтен 2-ден жасалған теру саны
 ға тең,
яғни аb, ас, аd, bс, bd,
сd .
ға тең,
яғни аb, ас, аd, bс, bd,
сd .
Мысал-2: С38
=
 =
=  =
=
 =
56;
=
56;
С410
=  =
=
 =
=  =
210.
=
210.
Осы жерде биномиал коэфифенттердің кейбір қасиеттерін қарастырамыз:
1) Сkn = Cn-kn .
Бұл теңдік (8) формуладан келіп шығады, яғни n элементтен алынған k элементті тандама оған қосымша ретінде n элементтен алынған (n-k) элементті таңдамаға бірмәнді сәйкес келеді. Осы жерден және алдынғы теңдіктерден төмендегі қатынастар келіп шығады: Сnn =C0n=1,Cn-1n=C1n=n.
Мысал-3. С26
=
 =
15, С46
=
=
15, С46
=
 =
=  =
15.
=
15.
2) k=0ån Ckn = 2n.
Бұл теңдік (7) формуладағы х және у айнымалылар орнына 1 мәңді қою арқылы оңай табылады.
Мысалдар. 1+5+10+10+5+1=32 =25 ; 1+6+15+20+15+6+1=64=26.
-
k=0ån(-1)k ×Ckn= 0.
Бұл теңдіктіда (7) формулада х =1, у= -1 ауыстырулар арқылы оңай табу мүмкін.
Мысал. n=6 болғанда 1-6+15-20+15-6+1=0.
-
k=0 ån Ckn ×k = n×2n-1 .
Бұл теңдіктің ақиқаттығына сену үшін n элементті íа1,а2,….,аný әр бір теру үшін осы (k элементтен алынған) теру элементтеріне сәйкес келетін аі1,аі2,….,аік белгілер жеке бөліктерге жазып алынған деп есептейік. Мұнда 2- қасиет бойынша барлық бөліктер 2n ге тең. Онда барлық бөліктердегі белгілер қосындысының санын екі түрлі есептеу мүмкін:
а) Дәл k белгіні қамтитын Сkn белгілердің қосынды саны k × Сkn болады. Ал, қарастырылып жатқан теңдіктің сол жағында k=0,1,….,n үшін барлық бөліктердегі белгілердің жалпы саны алынады.
б) Егер барлық бөліктерден жазылған кейбір аі белгіні өшірсек , онда ол жерде қалған (n-1) элементті мүмкін болған барлық терулер қалады. Олардың саны 2n-1. Демек аі белгі дәл 2n -1 бөліктерде жазылған екен. Ал, осы жерден теңдіктің оң жақ бөлігіндегі жалпы белгілер саны n × 2n-1 болатындығын көреміз.
Мысал-4. n =5 болғанда : 0× 1+1×5+2×10+3×10+4×5+5×1=80=5×24.
Ал, n=6 болғанда: 0×1+1×6+2×15+3×20+4×15+5×6+6×1=192=6×25 болады.
5) Сkn= Ck-1n-1+Ckn-1 .
Бұл теңдік мынадай тұжырым арқылы келіп шығады. n элементті жиыннан кез келген бір х элементті белгілеп аламыз. Бұл жерде k элементті жиындардың барлық жиынтығын осы х элемент жату немесе жатпаулығына қарай екі қиылыспайтын кластарға бөлінеді. Бірінші класта Сk-1n-1 ішкі жиын, олар х ті және қалған (n-1) элементтің ішінен (k -1) элементті өз ішіне алады. Екінші класта Сkn-1 элемент болатындығы айқын.
Бұл теңдіктер Паскаль ұшбурышы деп аталатын (5- сызба) сұлбамен тығыз байланысты.
Егер осы ұшбурыштың жолдарын ретімен 0,1,2,… деп нөмірлесек , онда і-жол С0і ,С1і ,…..Сіі сандарына сәйкес келеді. 5-қасиет бойынша 1 санына тең болған шеткі диоганалдан басқа әрбір санды алдыңғы қатардағы үстінде жайғасқан екі санның қосындысы ретінде алу мүмкін. Бұл Паскаль ұшбурышын құру және сонымен бірге биномиал коэффициенттерді табудың өте қарапайым тәсілін береді. Мұнда, n-қатар (х+у)n биномының коэффициенттеріне сәйкес келеді.
Ескерту. Бұл жерде (5) қасиет реккуренттік қатынас мысалы ретінде сипатталады, яғни Сkn шама екі n және k аргументтердің функциясы ретінде қарастырылып, ол осы функция айнымалыларының басқа мәндері арқылы өрнектеледі.
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
6 1 6 15 20 15 6 1
7 1 7 21 35 35 21 7 1
8 1 8 28 56 70 56 28 8 1
9 1 9 36 84 126 126 84 36 9 1
10 1 10 45 120 210 252 210 120 45 11 1
…………………………………………………………….
5 – сызба
-
Сkm+n = s=0åk Csm Ck-sn ( Коши теңдігі).
Бұл теңдікті дәлелдеу үшін мынадай интерпретацияны қарастыру қолайлы.
Айталық , m ерлер және n әйелдерден құралған топтан k адамнан тұратын өкілдер таңдалатын болсын. Оны Сkm+n тәсілмен жасауға болады. Біздің (m+n) элементті жиынның барлық k элементті ішкі жиындарын өкілдердегі ерлер саны бойынша классификациялау мүмкін. s ерлерден тұратын k элементті өкілдерді алдын s ер кісілерді таңдау арқылы Сms тәсілмен , ал одан соң (k-s) әйел кісілерді Ck-sn тәсілмен алу мүмкін. Көбейту қағидасы бойынша k элементті өкілдер саны Сsm×Ck-sn , ал қосу қағидасы бойынша k элементті өкілдер саны теңдіктің оң бөлігі секілді осындай санға тең.
Мысал-5.
С410= С47+3 = С07× С43+ С17 × С33 +С27 ×С23+С37×С13 +С47 ×С03=
[ С43 = 0 екендігін есепке алсақ] = 7×1+21×3+35×3+35×1 = 210.
Қайталамалы (n,k) терудің Сkn санын алу үшін осындай әр бір теруге (яғни, n элементті жиыннан алынған реттелмеген k таңдау) екі мәнді í0,1ý алфавитінде мынадай тізбек сәйкес қоямыз . Бастапқыда, k таңдамаға енетін және әр бір аі элемент n жиынның і элементтер санына тең болған n натурал сандардың íаіý тізбегін құрастырамыз. Мұнда, кейбір аі элементтер 0 ге тең болуыда мүмкін. Ал, осы тізбектің n компоненттер қосындысы k ға тең.
Енді әр бір аі санды (нөлдермен бөле отырып) аі та бірлермен ауыстырып нөл және бірлерден тұратын тізбек құрастырамыз:
11…101…10…0
0…
ÈÈÈÈ ÈÈÈ ÇÇÇ
а1 а2 аі =0
Егер, кейбір элементтерде аі = 0 болса, онда сәйкес нөлдер арасында мүлдем бір саны болмайды. Басқаша айтқанда, (n-1) нөлдерден құралған тізбек n орынды анықтайды( сол жағынан барлық тізбектен бастап, ал оң жағынан әр бір нөлден бастап). і-ші орынға аі та бір қоямыз( мұнда, кейбір аі элемент 0 ге тең болуыда мүмкін).
Мысал-6. (1,1,3,4,4,4,4) ретіндегі (4,7) теруге (2,0,1,4) тізбек, тағыда өз кезегінде 1100101111 тізбек сәйкес келеді, ал (1,2,2,2,3,3,3) ретіндегі (4,7) теруге бастап (1,3,3,0) тізбек, сосын 1011101110 тізбек сәйкес келеді. Нәтижеде, (n-1) нөлдер және k бірлерден құралған жиналым, яғни (n-k+1) ұзындықтағы вектор келіп шығады. Керісінше, әр бір осындай векторға (n,k) теру сәйкес келеді, бұл жерде бірлер қатар келетін топтар аі санды анықтайды, ал олардың қосындысы k ға тең. Сондықтан
Ĉkn= Сkn+k-1=C n-1n+k-1 (9)
болады.
Осы (9) теңдікті басқаша жолменде алуға болады.
Айталық, (С1,С2,…,Сk)-қайталамалы (n,k) теру болсын, мұнда С1 £ С2 £. …£ Сk. Оған d1=c1+0,d2=c2+1,d3=c3+2,…,dk=ck+k-1 болған (d1,d2,….,dk) таңдаманы сәйкес қоямыз. Бұл жерде барлық di сандар әр түрлі , сондықтан (d1,d2,….,dk) таңдаманы қайталамасыз (n+k-1,k) теру секілді қарастыру мүмкін. Керісінше, әр бір қайталамасыз (n+k-1,k) теруге қайталамалы болуы мүмкін болған (n,k) теру сәйкес келеді. Осы жерден (9) теңдік келіп шығады.
Мысал-7. . Ĉ43=С46=С26=6×5/2=15.
4- кестеде 3
элементтен 4 еуден алынған барлық қайталамалы (3,4) теру өздеріне
сәйкес тізбектермен және оларға сәйкес қайталамасыз (6,4) теру
келтірілген. 

4-кесте
______________________________________________
1,1,1,1 4,0,0 111100 1 2 3 4
1,1,1,2 3,1,1 111010 1 2 3 5
1,1,1,3 3,0,1 111001 1 2 3 6
1,1,2,2 2,2,0 110110 1 2 4 5
1,1,2,3 2,1,1 110101 1 2 4 6
1,1,3,3 2,0,2 110011 1 2 5 6
1,2,2,2 1,3,0 101110 1 3 4 5
1,2,2,3 1,2,1 101101 1 3 4 6
1,2,3,3 1,1,2 101011 1 3 5 6
1,3,3,3 1,0,3 100111 1 4 5 6
2,2,2,2 0,4,0 011110 2 3 4 5
2,2,2,3 0,3,1 011101 2 3 4 6
2,2,3,3 0,2,2 011011 2 3 5 6
2,3,3,3 0,1,3 010111 2 4 5 6
3,3,3,3 0,0,4 001111 3 4 5 6
4. Бұл жерде n элементтен құралған а1 а2 …аn қайталамалы және қосымша шартты, яғни олардың әр бірінде бірінші типтегі b1 элементті, екінші типтегі b2 элементті, жалпы айтқанда і-типтегі (і ═ 1,2,…,r) bі элементті барлық мүмкін орналастыруларды қарастырамыз. Мұнда, b1+b2 + …br ═ n теңдік орындалатындығы айқын. Енді і-ші типтегі bі элементтерді барлығы әр түрлі болғанша бір бірінен айрықша болған bi1,…,bir элементтермен ауыстырамыз, яғни n орналастыру аламыз. Әр бір осындай жайғастыру b1! b2!…br! орналастыруды береді. Сондықтан, барлық қайталамалы орналастырулар саны төмендегі өрнек арқылы табылады:
 ,
мұнда,
b1+b2+….+br═
n.
,
мұнда,
b1+b2+….+br═
n.
Бұл сан полиномдық коэффициент деп айтылады, себебі ол (х1+х2+….+хr)n полиномды айнымалылар дәрежесі бойынша жіктеудегі х1b1x2b2….xrbr көбейтінді алдындағы коэффициентке тең. r ═2 болғанда биномиалдық коэффициенттер дербес жағдайда бейнеленеді.
5. Бір еңгізу және шығару ұстанымын қолдануға мысал ретінде «Тәртіпсіздік тұралы» мәселені» қарастырамыз: кез келген і ═ 1,2,…..,n үшін аі ≠ і болатын 1,2,….,n сандардың а1,а2,…,аn орын алмастырулар саны қанша?
Осы санды Dn арқылы белгілеп (6) формуладан пайдаланамыз. Бұл жерде N элементті n! дана а1,а2,…,аn орын алмастырулар, ал Р(і) қасиет аі = і (і ═ 1,2,…..,n) теңдікпен өрнектелетіндігін білдіреді.
Онда Nі1і2….іr ═ ( n – r)! өз орнында белгілі r символдар қалдырылған орын алмастырулар саны болады.
Ал, SNі1і2…іr өрнекте 1,2,…,n сандардан і1,і2,….,іr таңдау тәсілдерінің саны бойынша алынған Сrn қосындылар бар. Осы жерде (6) теңдікті қолдана отырып төмендегіні табамыз :
N (0) ═ n! – n .( n – 1)! + С2n .( n – 2)! - ….+ (-1)r . Сrn . ( n – r)! +….+(-1)n . 1 ═ n! – n . (n-1)! + n . (( n -1)/2) . (n-2)! - ….+(-1)r . (n . (n -1)...( n –r + 1)/r!) . (n –r)!+….+ (-1)n ═ n! . ( 1 -1 + 1/2 ! – 1/3! + …+ ( -1 )r r ! + …+ ( - 1)n / n! ).
Бұл жерде жақшаға алынған
1-1+ 1/2 ! -1/3 ! +….+ ( - 1)r / r ! + ….+ ( - 1)n / n!
қосынды е-1 сан үшін шексіз қатардың дербес қосындысы. Сондықтан Dn ге тең болған N ( 0 ) өрнек n ! / e ге жуық болған бутін сан, яғни
Dn/ n ! » e -1 . (10)
(10)- формуланың өте қарапайым сипаттамасы мынадай. Егер әр түрлі мекенжай үшін n хат кездейсоқ ретінде мекенжайлары жазылған n конвертке салып қойылған болса, онда n мекенжайдағы бірде бір адам 1/е » 0.368 санға жұық ықтималдықпен өздеріне арналған хатты алалмайды. Бұл теория қарама-қайшылықты көрінуі мүмкін, бірақта 10 немесе 10000 хаттар үшінда бұл ықтималдық шамамен бірдей.
6. Комбинаториканың классикалық мәселелерінен біреуі - берілген шектеулердің орындалуы арқылы кейбір нысандар жиынын қаншада бір «қораптарға» жайғастырудың тәсілдер санын анықтау болып табылады.
Егер екі Х және Y жиындар берілген болса, бұл жерде çХ÷ ═ n, çYç ═ m, онда Х ті нысандар, Y ті қораптар деп есептесек кез келген f : Х Þ Y функция сондай бір орналастыруды береді, яғни ол хі нысанды уі қорапқа жайғастырудай f (хі) ═ уі теңдікті бейнелейді.
Тағыда басқаша интерпретация-бояқтау . Айталық Y түстер жиыны және f (х) х нысанның түсі болсын. Онда, бұл мәселені кейбір шектеулерге сақтана отырып бояулар санын анықтауға алып келу мүмкін. Мұнда, жалпылама қағиданы сақтай отырып барлық уақыт Х ═ í1,2,….,ný , ал Y ═ í1,2,….,mý деп есептеуге келісеміз. Егер орналастыруға еш қандай шектеулер қойылмайтын болса , онда барлық
f : Х Þ Y функциялар саны mn ге тең, яғни әншейін қайталамалы (m,n) орналастыру болады.
Егер, әр бір қорап біреуден артық болмаған нысандарға ие болса, онда біз m ³ n болған қайталамасыз (m,n) орналастыруға ие боламыз. Олардың саны дәл Аnm ге тең, яғни реттелген m қораптардан n данасын таңдаймыз және оларға бір данадан саламыз. Егерде n>m болсашы, онда ондай орналастыру мүмкін еместігін көреміз. Осы жерде Дирихле ұстанымы деп аталатын немесе қораптар ұстанымы қағидасы, яғни егер m қорапта (m+1) немесе оданда көп тастар бар болса , онда кемінде бір қорапта біреуден артық тас болу ұстанымы өз күшіне енеді.
Егер біз n нысанды m қораптар бойынша әр бір қорап қатаң реттелген тізбек құрастыратындай (оларға жайғастырылған нысандардың әншейін реттелмеген жиыны емес) етіп жайғастырсақ , онда мұндай жайғастыруды n нысанды m қораптар бойынша реттелген орналастыру деп айтамыз. Олардың санын [ m] [n] арқылы белгілейміз және n ═ 0 үшін [ m] [0] ═ 1 деп қабылдасақ , жалпы жағдайда төмендегі формулаға ие боламыз:
[ m] [n] ═ m . ( m + 1) × ….× (m +n -1) ═ Аnm+n -1.
Дәлелдеу. Бұл жерде жаңа нысандарды біртіндеп қоса отырып реттелген орналастырулар құрамыз. Бірінші нысанды әзірше бос болған кез келген қорапқа жайғастырып m тәсілмен орналастыру мүмкін. Екіншіні (m+1) тәсілмен, яғни қалған (m-1) бос қораптардың біреуіне немесе бірінші нысан жайғасқан қораптың алдыңғы немесе кейінгі қорабына. Жалпы жағдайда , егер қорапта s нысан бар болса, онда кезектегі нысанды осы қорапқа (s+1) тәсілмен жайғастыру мүмкін. Сондықтан, егер k-қорапта і-нысанды орналастырудан алдын rk ( k ═ 1,2, ….,m; k═1Sm rk ═ і – 1) нысан бар болған болса, онда оны барлығы болып
( r1 + 1) + ….+ ( rm + 1 ) ═ ( rm + 1 ) ═ ( r 1 + ….+ rm ) + m ═ ( і – 1 ) + m
тәсілмен орналастыру мүмкін. Сонымен бірге дәлелдеудің индуктивті тәсілі төменде көрсетілген.
6-сызбада екі а және b элементтің үш қорапқа [ 3 ] [ 2] ═ 3 × 4 ═ 12 реттелген орналастыру тәсілі көрсетілген.
-
-
a
b
a
b
b
a
b
a
a,b
b,a
a
b
b
a
a,b
b,a
a,b
b,a
-
6-сызба
Енді жоғарыдағы анықтамалардан пайдаланып негізгі комбинаторикалық элементтердің қысқаша жазылу формулаларын келтіреміз.
Алмастырулар. Қайталанбайтын комбинация үшін алмастырулар саны
Рn = n! ,
қайталамалы комбинация үшін
 n(k1,k2,…,kn) =
n(k1,k2,…,kn) =
 ,
(k1!
+k2!+...+kn! =
n)
,
(k1!
+k2!+...+kn! =
n)
формуласымен табылады.
Орналастырулар. Қайталанбайтын комбинация үшін
орналастырулар саны
 , ал қайталамалы
комбинация үшін
, ал қайталамалы
комбинация үшін
 mn
=
nm
mn
=
nm
формуласымен табылады.
Терулер. Қайталанбайтын комбинация үшін терулер саны
 ,
,
ал қайталамалы коминация үшін
 mn= Сkn+k-1=C
n-1n+k-1 =
mn= Сkn+k-1=C
n-1n+k-1 =

формуласымен табылады.
Мысал-8. Спортлото ( 36-дан 5) ойынына қатысушы бір билет сатып алған. Оны толтыру жағдайлары нешеу және ұту ықтималдығы қандай?
Шешуі. Бір билет толтыру үшін ойын ережесі бойынша 1-ден 36-ға дейінгі натурал санның бесеуін сызу керек. Сызу тәртібі әртүрлі, оның саны

Сонымен, ұтысқа қатынасатын тең мүмкіндікті жағдайлар саны n = 376992. Бір билет иесінің ұту ықтималдығы

Мысал -9: Цехта 6 ер адам, 4 әйел адам жұмыс істейді. Табельдегі нөмірлері бойынша 7 адам таңдап алынды. Таңдап алынған адамдардың ішінде 3 әйел бар болуының ықтималдығын табу керек.
Шешуі: Табелбдегі нөмірлері бойынша барлығы 10 адамнан 7 адам таңдап алудың жалпы саны 10 элементтен 7 элемент бойынша алынған терулер саны сияқты есептелінеді, яғни:

Ал, 3 әйелді
табельдік нөмірлері бойынша 4 әйелдің ішінен таңдап алудың
саны  формула
бойынша:
формула
бойынша:

Сондай-ақ 6 ер
адамнан 4 ер адам таңдаудың саны: 
Енді, көбейту
ережесін пайдалансақ, таңдап алынған 7 адамның ішінде 3 әйел, 4 ер
адам болу мүмкіндіктерінің жалпы саны
 тең. Сонымен анықталғалы
отырған ықтималдық:
тең. Сонымен анықталғалы
отырған ықтималдық:  .
.
Мысал-10. Лотереяда 10 билет бар. Оның ішінде 3 билет ұтысты. Кездейсоқ таңдап алынған 5 билеттің ішінде 2 билеттің ұтысты болып шығуының ықтималдығы қандай?
Шешуі. n
=  =
= =
=
 = 4∙7∙9.
= 4∙7∙9.
3 билеттен 2 ұтыс билетін таңдау жолының санын анықтаймыз:
 =
=  =
=
 = 3.
= 3.
7 билеттен 3 ұтыссыз билетті таңдау жолының санын анықтаймыз:
 =
=  =
= =
=
 = 5∙7 =
35.
= 5∙7 =
35.
Сынақтың қолайлы
жағдайының санын көбейту әдісі бойынша табамыз:
m  ∙
∙ = 3∙5∙7. А оқиғасының
ықтималдығын анықтаймыз:
= 3∙5∙7. А оқиғасының
ықтималдығын анықтаймыз:
P (A)
=  =
=
Мысал-11. Бірдей карточкаларға жазылған А, А, А, Б, Р, С, Т әріптерінен: а) 7 әріптен алғанда неше алмастырулар шығады? ә) «АТБАСАР» сөзінің шығу ықтималдығын анықтау керек.
Шешуі. а) Іріктемегенде әріптер әр түрлі болса, «жеті» әріппен жазылатын сөздер саны 7! болар еді. Ал биздің мысалымызда үш әріп бірдей. Сондықтан 7 әріпті әр түрлі сөздер (оның басым көпшілігі мағынасыз тіркестер) саны 7!- дан кемид. Өйткені «А» әріптері өз ара орындарын ауыстырғанда жаңа сөз шықпайды. Сондықтан есепті шешу үшін алдымен бірдей сөз құрайтын алмастырулар санын анықтап аламыз. «А» әрпінің өз ара орын ауыстырулар саны3!. Бұл әр типтегі сөздердің қайталану саны болмақ.
Бұл жағдайда 7 әріпті сөздердің бір типі «АТБАСАР» деген сөзбен көрсетейік. Түсіну оңай болу үшін алдымен әріптерді 1-ден 7-ге дейінгі цифрлармен нөмірлейік. Осы сөз құралатын алмастырулардың түрлері төменде цифрлармен келтірілді:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Содан жеті әріптен тұратын әр түрлі
«сөздер»  =
=  =
4*5*6*7 =840
=
4*5*6*7 =840
Тәсілмен шығады екен. Ал, оның ықтималдығын классикалық анықтама бойынша оңай табамыз. n=840, m=1, сондықтан Р(А) = 1/840.
Мысал
-12. Теңдіктегі
 -нің мәнін
табыңыз:
-нің мәнін
табыңыз:  =
=
 .
.
Шешуі: Теру формуласы бойынша мынадай теңдікті жазамыз:
 =
=
 Þ
Þ
 =
=  Þ
(n-6)(n-5) =
30 Þ
Þ
(n-6)(n-5) =
30 Þ
n2 – 9n + 20 = 30 Þ n2 – 9n - 10 = 0 Þ ( n= 10, n=-1 ), комбинаторика заңдарында n текқана натурал сан болғандықтан n=-1 санды шешім деп қабылдай алмаймыз. Сондықтан n= 10 теңдіктің шешімі болады.
4-лекция
Ықтималдықтар алгебрасы
-
Ықтималдықтарды қосу заңдылықтары.
-
Шартты ықтималдық.
3. Ықтималдықтарды көбейту заңдылықтары..
________________________________________________________________
-
Ықтималдықтардың қосу заңдылықтары.
Ықтималдықтарды есептеу сынаудың жалпы саны мен оқиғаның пайда болуына қолайлы нәтижелер санын анықтауға келіп тіреледі. Бұларды тікелей есептеу көп жағдайда үлкен қиындыққа ұшыратады. Сондықтан да камбинаторика формулаларын пайдалануға мәжбүр болдық. Оның үстіне, практикада кездесетін оқиғалар күрделі болып келеді де, олардың ықтималдылығын табу үшін, ол оқиғаларды бірнеше қарапайым оқиғалардың қосындысы не көбейтіндісі түрінде жазып, солардың ықтималдығын анықтайды. Сондықтан да қарастырып отырған оқиға ықтималдығын екінші ықтималдылық арқылы табудың маңызы өте-мөте зор. Ол үшін негізінен ықтималдылықтарды қосу және көбейту теоремаларын пайдаланады. Енді алдымен қосу теоремасын, одан шығатын бірнеше салдарды қарастырайық.
Екі А және В оқиғаларының қосындысы деп С = А+В оқиғасына айтылады, бұл С – оқиғасы А – оқиғаның пайда болуынан, В – оқиғасының пайда болуынан, немесе А оқиғасының және В оқиғасының біруақытта пайда болуынан құралады.
Мысал-1: Екі атқыш нысанаға бір-бір реттен оқ атады, А – оқиғасы бірінші атқыштың нысанаға дәл тигізуі, В – оқиғасы екінші атқыштың нысанаға дәл тигізуі. С=А+В – оқиғасы бірінші атқыштың нысанаға дәл тигізуі немесе екінші атқыштың нысанаға дәл тигізуі немесе бірінші және екінші атқыштың да нысанаға дәл тигізуі.
Бірнеше оқиғалардың қосындысы деп, осы оқиғалардың кем дегенде біреуінің пайда болуынан тұратын оқиғаға айтылады. А+В+С оқиғасы: А,В,С не болмаса А және В, не болмаса А және С, яки В және С, яки А және В және С оқиғаларының кем дегенде біреуінің пайда болуынан тұратын оқиғаға айтылады.
А және В оқиғалары үйлесімсіз болып және олардың ықтималдықтары мәлім болса, онда А оқиғасының немесе В оқиғасының ықтималдығы қосу теоремасымен анықталады.
Теорема. Үйлесімсіз А және В оқиғалар қосындысының ықтималдығы олардың ықтымалдықтарының қосындысына тең
P(А+В) = P(А) + P (В) (1)
Дәлелдеуі.
n – тең мүмкіндікті үйлесімсіз оқиғалар саны болсын.
m1 – А оқиғасы үшін қолайлы оқиғалар саны
m2 – В оқиғасына қолайлы оқиғалар саны
Демек, 
 ,
,

Теорема. Егер А1, А2, ... , Аn үйлесімсіз оқиғалар болса, онда бұлардың қосындысының ықтималдығы әрқайсысының ықтималдықтарының қосындысына тең болады.
P(А1+А2 + ... + Аn) = P(А1) + P(А2) + ... + P (Аn) (2)
Салдар-1.
Қарама-қарсы А және  оқиғалары ықтималдықтарының
қосындысы 1-ге тең, яғни
оқиғалары ықтималдықтарының
қосындысы 1-ге тең, яғни
P(А) +
P( ) =
1
) =
1
Дәлелдеуі. А мен
 қосындысы ақиқат оқиға
болғандықтан P (
қосындысы ақиқат оқиға
болғандықтан P ( +А) = 1, үйлесімсіз
болғандықтан
+А) = 1, үйлесімсіз
болғандықтан
P
(А+ ) = P (А) +
P(
) = P (А) +
P( ) =
1
) =
1
Сондықтан p = P (А),
q = P ( ) деп белгілеп p + q =
1
) деп белгілеп p + q =
1
Салдар-2. Егер А1, А2, ..., Аn оқиғалары үйлесімсіз болса және оқиғалардың толық тобын құраса, онда
P(А1) + P(А2) + ... + P (Аn) = 1 болады.
Дәлелдеуі. Ұйғарым бойынша не А1, не А2,… , не Аn пайда болуы ақиқат, олай болса, бұлардың қосындысының ықтималдығы 1-ге тең, яғни
P(А1) + P(А2) + ... + P (Аn) = P(А1+А2 + ...+ Аn) = 1 (3)
Мысал-2: Ұн қоймасы ұннан жасалған
тағамдарды А, В, С қалаларының ұн зауыттарынан қабылдайды. Қойманың
ұнды А қаласынан қабылдауы P(А) = 0,6-ға тең, В қаласынан қабылдауы
ықтималдығы  =0,3-ке тең, ұнның С-қаласынан
қабылдау ықтималдығы P (С) –
табылсын.
=0,3-ке тең, ұнның С-қаласынан
қабылдау ықтималдығы P (С) –
табылсын.
Шешуі. Ұннан жасалған тағамдарды А, В және С қалаларынан қабылдау оқиғасы оқиғаның толық тобын құрайды. (3) формула бойынша 0,6+0,3+p(С) = 1 болады. Бұл жерде P(С) = 1 – 0,9 = 0,1.
Теорема. Екі оқиғаның кемінде біреуінің пайда болу ықтималдығы олардың ықтималдықтарының қосындысы мен оқиғалардың бірге пайда болу ықтималдығының айырмасына тең болады.
P(А+В) = P (А) + P (В) –P(А.В)
Дәлелдеуі. Егер А және В үйлесімді оқиғалар болса , онда А+В=А+(В-АВ) және В = А.*В+(В-А.*В) теңдіктерінің оң жағындағы қосылғыштар үйлесімсіз оқиғалар болады.
P(А+В) = P (А) + P (В-А.В)
P(В)=P(А
.В)+P(В-А.В)
 P(А+В)=P(А)+P(В)-P(А.В)
P(А+В)=P(А)+P(В)-P(А.В)
Мысал-3. Жәшікте бірдей 20 шар бар. Оның 7-уі қызыл түсті, 8-і көк түсті, 5-уі ақ түсті. Жәшіктен қалаған бір шар алынады. Оның түсті ( не қызыл түсті, не көк түсті) шар болу ықтималдылығын анықтау керек.
Шешуі. Тең мүмкіндікті, үйлесімсіз оқиғалардың толық тобын құрайтын жағдайлар саны n =20. Қызыл түсті шар шығуын В оқиғасы, түсті шар шығуын С оқиғасы десек, онда А үшін қолайлы жағдайлар m = 7, В үшін қолайлы жағдайлар m =8 болады. Сонда С оқиғасының болу ықтималдылығы р(С) = р(А+В)=p(A)+p(A)= не 75% болады.
Мысал-4. Лотерея ойынына 1000 билет қатысады.Бұлардың біреуі 200 сом ұтады, төртеуі 100 сомнан, жиырма бесі 20 сомнан және елуі 10 сомнан ұтады. Қалған билеттер ұтпайды. Алынған бір лотерея ұтысының 20 сомнан кем болмау ықтималдығын анықтау керек.
Шешуі. А - ұтыс 20
сомнан кем болмауын,  - ұтыс 200
сом,
- ұтыс 200
сом,  – ұтыс 100 сом,
ал
– ұтыс 100 сом,
ал  – ұтыс 20 сом болуды
көрсететін оқиғалар болсын. Сонда
– ұтыс 20 сом болуды
көрсететін оқиғалар болсын. Сонда 
 ,
,
 - қос-қостан
үйлесімсіз оқиғалар, өйткені лотереяға бір ғана ұтыс шығады. Олай
болса, А =
- қос-қостан
үйлесімсіз оқиғалар, өйткені лотереяға бір ғана ұтыс шығады. Олай
болса, А = 
 +
+  формула
бойынша
формула
бойынша
P (A)
= P
( + P
(
+ P
( + P
(
+ P
( =
=  +
+  +
+  = 0,
03.
= 0,
03.
Мысал-5. Жәшікте бірдей 50 деталь бар, оның 45-і жарамды, 5-і жарамсыз. Бақылаушы жәшіктен кез келген 10 детальді алып тексереді. Егер осы алынған таңдама ішінде жарамсыз деталь саны бірден артық болмаса, онда жәшіктегі қалған детальдарды тексерместен жарамды деп қабылдайды. Бұлайша қабылдау ықтималдығы неге тең?
Шешуі. Алынған 10
детальдың ішінде бірде-бір жарамсыз деталь болмауы А оқиғасы, тек
бір жарамсыз деталь болуы В оқиғасы болсын. А және В оқиғалары
үйлесімсіз. Олай болса, P (A+B) = P (A) + P (B) . 50 детальдан 10
детальдың  тәсілімен аламыз.А
оқиғасына қолайлы элементар оқиғалар саны
тәсілімен аламыз.А
оқиғасына қолайлы элементар оқиғалар саны
 өйткені алынған 10
детальдың ішінде бірде-бір жарамсыз деталь
жоқ:
өйткені алынған 10
детальдың ішінде бірде-бір жарамсыз деталь
жоқ:
P (A)
=  =
=
 =
=  =
= =
0,31.
=
0,31.
В оқиғасына қолайлы
элементар оқиғалар саны  =
=
 ∙
∙ өйткені алынған 10
детальдың біреуі жарамсызда қалған тоғызы жарамды. Жарамдысын
барлық жарамдылардан
өйткені алынған 10
детальдың біреуі жарамсызда қалған тоғызы жарамды. Жарамдысын
барлық жарамдылардан  тәсілмен алсақ,
жарамсыздардан
тәсілмен алсақ,
жарамсыздардан  аламыз. Оның әр бір
жарамсызы жарамды детальдармен комбинацияланып келеді,
яғни
аламыз. Оның әр бір
жарамсызы жарамды детальдармен комбинацияланып келеді,
яғни  болады.
болады.
Демек, P
(B)
= = 0,43.
= 0,43.
P (A+B)
=  +
+  = 0,31 + 0,43 =
0,74.
= 0,31 + 0,43 =
0,74.
-
Шартты ықтималдық.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болуы ықтималдығын өзгертпесе , онда оларды тәуелсіз оқиғалар деп атайды.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Анықтама. Егер екі оқиға тәуелсіз оқиғалар болса және бірінші оқиғаның пайда болуы ықтималдылығы екіншісіне байланысты болмаса мұндай оқиғалар ықтималдылығы шартсыз оқиғалар деп аталады.
Анықтама. Егер бір оқиғаның ықтималдылығын есептегенде комплексті шарттан басқа екінші оқиғаның пайда болуы, не пайда болмауы әсер етіп, оның ықтималдығын өзгертсе , мұндай ықтималдықты шартты ықтималдық деп атайды.
P (А/В) немесе PВ (А)
Мысал-1. Қобдишада 10 шар бар, оның төртеуі ақ, алтауы қызыл. Қобдишадан кез келген бір шарды алып, түсін белгілегеннен соң екіншісін алады. Бірінші алынған шар қызыл түсті болғанда екінші рет алынған шардың ақ түсті болу ықтималдығын анықтау керек.
Шешуі. Бұл мысалдың шешуі қобдишадан алынған бірінші шар түсі белгіленген соң екінші шарды алу алдында ол шар қайта қобдишаға салыну, әлде қайта салынбауына байланысты. Осы себеппен мысал екі тәсілмен шешіледі.
Бірінші
тәсіл. Қобдишадан бірінші рет
алынған шар түсі қызыл болуы В оқиғасы болсын,
онда  оқиғасы қобдишадан
алынған бірінші шар түсі қызыл емес, яғни ақ шар шығуы болады.
Екінші рет алынған шар түсі ақ шар болуы А оқиғасы болсын,
онда
оқиғасы қобдишадан
алынған бірінші шар түсі қызыл емес, яғни ақ шар шығуы болады.
Екінші рет алынған шар түсі ақ шар болуы А оқиғасы болсын,
онда  оқиғасы екінші ретте
қызыл шардың шығуы болады. Бірінші алынған шар түсі белгіленгеннен
кейін, ол шар қобдишаға қайта салынған себепті, шар екінші рет
алынғанда да қобдишадағы шарлар саны бастапқыдай болады.Сондықтан А
оқиғасының ықтималдығы оған дейін қобдишада қызыл шар шығуына
байланысты емес, өзгермейді және ол 0,4-ке тең. Бұдан В оқиғасының
пайда болуының А оқиғасының ықтималдығына әсері болмайтынын
байқаймыз. Демек, А және В оқиғалары бір-біріне тәуелсіз. Бұл жерде
А оқиғасының ықтималдығын есептегенде оның пайда болуына комплексті
шарттан өзге ешқандай шек қойылмайды. Егер екі оқиғаның біреуінің
пайда болуы екіншісінің пайда болу ықтималдығын өзгеретін болса,
ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Екінші
тәсіл. Тәжірибе шарты
1-мысалдағыдай, бірақ бірінші рет алынған шар қобдишаға қайта
салынбайды. Бұл жағдайда екінші ретте А оқиғасының пайда болу
ықтималдығы оның алдында қызыл шар (B), не ақ
шар
оқиғасы екінші ретте
қызыл шардың шығуы болады. Бірінші алынған шар түсі белгіленгеннен
кейін, ол шар қобдишаға қайта салынған себепті, шар екінші рет
алынғанда да қобдишадағы шарлар саны бастапқыдай болады.Сондықтан А
оқиғасының ықтималдығы оған дейін қобдишада қызыл шар шығуына
байланысты емес, өзгермейді және ол 0,4-ке тең. Бұдан В оқиғасының
пайда болуының А оқиғасының ықтималдығына әсері болмайтынын
байқаймыз. Демек, А және В оқиғалары бір-біріне тәуелсіз. Бұл жерде
А оқиғасының ықтималдығын есептегенде оның пайда болуына комплексті
шарттан өзге ешқандай шек қойылмайды. Егер екі оқиғаның біреуінің
пайда болуы екіншісінің пайда болу ықтималдығын өзгеретін болса,
ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Екінші
тәсіл. Тәжірибе шарты
1-мысалдағыдай, бірақ бірінші рет алынған шар қобдишаға қайта
салынбайды. Бұл жағдайда екінші ретте А оқиғасының пайда болу
ықтималдығы оның алдында қызыл шар (B), не ақ
шар  оқиғасы шығуына
байланысты. Егер бірінші сынауда қызыл шар шықса, онда екінші
сынауда ақ шар шығу ықтималдығы 4/9 болады. Егер бірінші
сынауда
оқиғасы шығуына
байланысты. Егер бірінші сынауда қызыл шар шықса, онда екінші
сынауда ақ шар шығу ықтималдығы 4/9 болады. Егер бірінші
сынауда  оқиғасы пайда болса (ақ
шар шықса), онда екінші ретте де ақ шар шығу (А оқиғасы)
ықтималдығы 3/9 = 1/3-ке тең. Осы сияқты, егербірінші сынауда қызыл
шар (
оқиғасы пайда болса (ақ
шар шықса), онда екінші ретте де ақ шар шығу (А оқиғасы)
ықтималдығы 3/9 = 1/3-ке тең. Осы сияқты, егербірінші сынауда қызыл
шар ( оқиғасы) не ақ шар
(
оқиғасы) не ақ шар
( оқиғасы) шықты десек,
онда екінші сынауда қызыл шар (
оқиғасы) шықты десек,
онда екінші сынауда қызыл шар ( оқиғасы) пайда болу
ықтималдығы сәйкес 5/9 және 2/3 сандарына
тең.
оқиғасы) пайда болу
ықтималдығы сәйкес 5/9 және 2/3 сандарына
тең.
Шартты
ықтималдық. 1-мысалда А оқиғасының
ықтималдығын есептегенде комплексті шарттан басқа В оқиғасының
пайда болу, не пайда болмауы әсер етіп, А оқиғасының ықтималдығын
өзгертіп отырады. Мұндай ықтималдыты шартты ықтималдық деп атайды.
Шартты ықтималдықты былай белгілейді: P (A/B)
немесе  (A). А және В
оқиғаларының тәуелсіздігін P (A/B)= P (A),
(A). А және В
оқиғаларының тәуелсіздігін P (A/B)= P (A),
 (A) = P (A)) түрінде
жазуға болады. 1- мысалдан
(A) = P (A)) түрінде
жазуға болады. 1- мысалдан
P (A) = P (A/B) =
0,4 , P (A) = P (A/ ) =
0,4
) =
0,4
Сондай-ақ
P
( ) = P
(
) = P
( /B)= 0,6 , P
(
/B)= 0,6 , P
( ) = P
(
) = P
( /
/
 ) = 0,6
.
) = 0,6
.
Егер А және В оқиғалары бір-біріне тәуелді болса, онда сол мысалдан
P (A) =
(A/B) , P
(A/B)=4/9
, P
(A/ ) =
1/3;
сондай-ақ
) =
1/3;
сондай-ақ
P
( /B) =5/9, P
(
/B) =5/9, P
( /B) =
2/3.
/B) =
2/3.
Шартты ықтималдықтың қасиеттері.
1. 0 ≤ P(А) ≤ 1
2. PВ(U) =1
3. PВ(V) = 0
4.Егер
А1 А2
болса,онда PВ
(А1)≤PВ(А2)
А2
болса,онда PВ
(А1)≤PВ(А2)
5.Егер А1=А2 болса, онда PВ (А1)=PВ(А2)
6.Егер А1...Аn үйлесімсіз және А=А1+...+Аn болса, онда
PВ (А)=PВ(А1)+...+ PВ(Аn)
70. А1...Аn – үйлесімсіз және олар оқиғалардың толық жүйеcін құраса, яғни
U =A1+…+ An , болса , онда PВ (U) = PВ (А1) + ...+ PВ (Аn) = 1
_ _
80.А және А – қарсы оқиғалар болса, онда Pв(А) =1-PВ(А).
-
Ықтималдықтардың көбейту теоремалары.
Теорема. Екі тәуелді оқиғаның көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығы мен сол оқиға пайда болғандaғы екінші оқиғаның шартты ықтималдығының көбейтіндісіне тең:
P(А * В) = P (А) * PА (В) = P(В) * PВ (А)
Дәлелдеуі.
n–тең мүмкіндікті үйлесімсіз және оқиғаның толық тобын құрайтын оқиғалар саны.
m- А- оқиғаға қолайлы ;
к – В –оқиғаға қолайлы;
r – А және В оқиғаға қолайлы.
P(А)=m/n; P(В)=k/n; P(А*В)=r/n; P(A.B)=r/n ;
PВ
(А) = r/k;бұл жерде r≤m, r≤k ;
r≤m, r≤k; PA(В) = r/m; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 P
(A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
.
P
(A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
.
Tеорема дәлелденді.
Мысал-2. Қобдишада 15 ұтысты, 10 ұтыссыз лотерея билеттері бар. Бір-бірлеп екі билет алынады (билет қаита салынбайды). Алынған екі билеттің де ұтатын билет болу ықтималдығын анықтау керек.
Шешуі: А- бірінші билеттің ұтуы.
В- екінші билетің ұтуы.
P(A)=15/25= 3/5; PA(B)=14/24=7/12;
Демек, P(A*B)=P(A)*PA(B)=3/5*7/12=0,35;
Теорема. А1,А2,…,Аn тәуелді оқиғалары көбейтіндісінің ықтималдығы мына формуламен өрнектеледі:
P(A1A2…An)=P(A1)* (A2)*
(A2)* (A3)
(A3)

 (An)
(An)
Дәлелдеуі. Мұны математикалық индукция әдісімен дәлелдейік.n=2 болғанда теорема дәлелденді, онда n=k мәнінде де бұл өрнек орын алады, яғни:
 болады.
Енді
болады.
Енді
n = k+1үшін теореманы дәлелдейік:
 деп алайық ,сонда
А =
В*Ак+1
болады.
деп алайық ,сонда
А =
В*Ак+1
болады.

Теорема. Екі тәуелсіз оқиғалар көбейтіндісінің ықтималдығы олардың шартсыз ықтималдықтарының көбейтіндісіне тең, яғни
P(A*В)=P(A)P(B) болады.
Дәлелдеуі. А және В оқиғалары тәуелсіз болғандықтан
P(A) = PВ(A) және P(B) = PA(B);P(A*В) = P(B)*PB(A) = P(B)*P(A)
Теорема. Егер А1, А2, ...,Аn оқиғалары жиынтығы бойынша тәуелсіз болса, онда олардың көбейтіндісінің ықтималдығы әрқайсысының ықтималдықтарының көбейтіндісіне тең, яғни:

Салдар. Егер А оқиғасы В-оқиғасына тәуелсіз болса, онда В оқиғасы А- оқиғасына да тәуелсіз болады.
Салдар. Егер А оқиғасы мен В-оқиғасы тәуелсіз болса, онда


 оқиғалары да
біріне-бірі тәуелсіз болады.
оқиғалары да
біріне-бірі тәуелсіз болады.
Мысал-3: Апатты хабарлау үшін бір-біріне тәуелсіз жұмыс істейтін екі сигналдаушы орнатылған. Апат кезінде сигналдаушының жұмыс істеу ықтималдығы бірінші сигналдаушы үшін
0,95 - ке,ал екіншісі үшін 0,9 – ға тең. Апат кезінде екі сигналдушының да жұмыс істеуінің ықтималдығын табу керек.
Шешуі.
А – оқиғасы бірінші сигналдаушы жұыс істейді.
В – оқиғасы екінші ситналдаушы жұыс істейді.
Бұл оқиғалардың сәйкес ықтималдықтары P(A) = 0,95 P(B) = 0,9 А оқиғасы мен В оқиғасы өзара тәуелсіз, сондықтан олардың бірге пайда болу ықтималдығы мынаған тең:
P (A*B) = P(A) *P (B) = 0,95* 0,9 = 0,855
Мысал-4. Үш оқушы біреуі монетті, екіншісі кубты лақтырды, ал үшіншісі колодадағы 36 картаның кез келген біреуін суырды. Осы жүргізген тәжірибелер нәтижесінде монеттің герб жағымен түсу (А оқиғасы), кубтың 4 ұпаймен түсу (В оқиғасы ), және суырған картаның тұз болып шығу (С оқиғасы ) ықтималдығын анықтау керек.
Шешуі. Өткен мысалдарды еске түсірсек,
р(А)=1/2, р(B)=1/6, р(C)=1/9.
Сонда іздеген ықтималдығымыз төмендегідей табылады:
Р(АВС)=p(A)*p(B)*p(C)=1/2*1/6*1/9=1/108=0,092.
5- сабақ
Шартты ықтималдық. Ықтималдықтардың көбейту теоремасы.
Толық ықтималдықтар формуласы. Байес формуласы.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болуы ықтималдығын өзгертпесе , онда оларды тәуелсіз оқиғалар деп атайды.
Анықтама. Егер екі оқиғаның бірінің пайда болуы екіншісінің пайда болу ықтималдығын өзгертетін болса, ондай екі оқиғаны тәуелді оқиғалар деп атайды.
Анықтама. Егер екі оқиға тәуелсіз оқиғалар болса және бірінші оқиғаның пайда болуы ықтималдылығы екіншісіне байланысты болмаса мұндай оқиғалар ықтималдылығы шартсыз оқиғалар деп аталады.
Анықтама. Егер бір оқиғаның ықтималдылығын есептегенде комплексті шарттан басқа екінші оқиғаның пайда болуы, не пайда болмауы әсер етіп, оның ықтималдығын өзгертсе , мұндай ықтималдықты шартты ықтималдық деп атайды.
P (А/В) немесе PВ (А)
Мысалы. Жәшікте 10 шар бар, оның төртеуі ақ , алтауы қызыл. Жәшіктен кез-келген бір шарды алып, түсін анықтаған соң екіншісін алайық . Бірінші алынған шар қызыл болған жағдайда екінші алынған шардың ақ түсті болу ықтималдығы анықталсын.
Шешуі: бірінші тәсіл. ( алынған шар жәшікке қайта салынады.)
А -ақ шар алынады ( екінші ретте).
В - қызыл шар болуы оқиғасы .
Pв(А)=P(А) – тәуелсіз оқиғалар .


Екінші тәсіл. (Алынған шар жәшікке қайта салынбайды ).
 (А) =
(А) = 
 (А)
=
(А)
=
Шартты ықтималдықтың қасиеттері.
1. 0 ≤ P(А) ≤ 1
2. PВ(U) =1
3. PВ(V) = 0
4.Егер А1 А2
болса,онда PВ
(А1)≤PВ(А2)
А2
болса,онда PВ
(А1)≤PВ(А2)
5.Егер А1=А2 болса, онда PВ (А1)=PВ(А2)
6.Егер А1...Аn үйлесімсіз және А=А1+...+Аn болса, онда
PВ (А)=PВ(А1)+...+ PВ(Аn)
70. А1...Аn – үйлесімсіз және олар оқиғалардың толық жүйеcін құраса, яғни
U =A1+…+ An , болса , онда PВ (U) = PВ (А1) + ...+ PВ (Аn) = 1
_ _
80.А және А – қарсы оқиғалар болса, онда Pв(А) =1-PВ(А).
Теорема. Екі тәуелді оқиғаның көбейтіндісінің ықтималдығы біреуінің шартсыз ықтималдығы мен сол оқиға пайда болғандaғы екінші оқиғаның шартты ықтималдығының көбейтіндісіне тең:
P(А * В) = P (А) * PА (В) = P(В) * PВ (А)
Дәлелдеуі.
n–тең мүмкіндікті үйлесімсіз және оқиғаның толық тобын құрайтын оқиғалар саны.
m- А- оқиғаға қолайлы ;
к – В –оқиғаға қолайлы;
r – А және В оқиғаға қолайлы.
P(А)=m/n; P(В)=k/n; P(А*В)=r/n; P(A.B)=r/n ;
PВ
(А) =
r/k;бұл жерде r≤m, r≤k ; r≤m, r≤k; PA(В) = r/m; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 P (A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
P (A*B) = P(A)
*PA
(B) =
P(B) *
PB
(A)
теорема дәлелденді.
Мысал. Қобдишада 15 ұтысты, 10 ұтыссыз лотерея билеттері бар. Бір-бірлеп екі билет алынады (билет қаита салынбайды). Алынған екі билеттің де ұтатын билет болу ықтималдығын анықтау керек.
Шешуі: А- бірінші билеттің ұтуы.
В- екінші билетің ұтуы.
P(A)=15/25= 3/5; PA(B)=14/24=7/12;
Демек, P(A*B)=P(A)*PA(B)=3/5*7/12=0,35;
Теорема. А1,А2,…,Аn тәуелді оқиғалары көбейтіндісінің ықтималдығы мына формуламен өрнектеледі:
P(A1A2…An)=P(A1)* (A2)*
(A2)* (A3)
(A3)

 (An)
(An)
Дәлелдеуі. Мұны математикалық индукция әдісімен дәлелдейік.n=2 болғанда теорема дәлелденді, онда n=k мәнінде де бұл өрнек орын алады, яғни:
 болады. Енді
болады. Енді
n = k+1үшін теореманы дәлелдейік:
 деп алайық ,сонда А = В*Ак+1
болады.
деп алайық ,сонда А = В*Ак+1
болады.

Теорема. Екі тәуелсіз оқиғалар көбейтіндісінің ықтималдығы олардың шартсыз ықтималдықтарының көбейтіндісіне тең, яғни
P(A*В)=P(A)P(B) болады.
Дәлелдеуі. А және В оқиғалары тәуелсіз болғандықтан
P(A) = PВ(A) және P(B) = PA(B);P(A*В) = P(B)*PB(A) = P(B)*P(A)
Теорема. Егер А1, А2, ...,Аn оқиғалары жиынтығы бойынша тәуелсіз болса, онда олардың көбейтіндісінің ықтималдығы әрқайсысының ықтималдықтарының көбейтіндісіне тең, яғни:

Салдар. Егер А оқиғасы В-оқиғасына тәуелсіз болса, онда В оқиғасы А- оқиғасына да тәуелсіз болады.
Салдар. Егер А оқиғасы мен В-оқиғасы тәуелсіз болса, онда


 оқиғалары да біріне-бірі тәуелсіз
болады.
оқиғалары да біріне-бірі тәуелсіз
болады.
Мысал: Апатты хабарлау үшін бір-біріне тәуелсіз жұмыс істейтін екі сигналдаушы орнатылған. Апат кезінде сигналдаушының жұмыс істеу ықтималдығы бірінші сигналдаушы үшін
0,95 - ке,ал екіншісі үшін 0,9 – ға тең. Апат кезінде екі сигналдушының да жұмыс істеуінің ықтималдығын табу керек.
Шешуі.
А – оқиғасы бірінші сигналдаушы жұыс істейді.
В – оқиғасы екінші ситналдаушы жұыс істейді.
Бұл оқиғалардың сәйкес ықтималдықтары P(A) = 0,95 P(B) = 0,9 А оқиғасы мен В оқиғасы өзара тәуелсіз, сондықтан олардың бірге пайда болу ықтималдығы мынаған тең:
P (A*B) = P(A) *P (B) = 0,95* 0,9 = 0,855
Мысалды шешіңіз. Құрылыс отрядында 70% бірінші курс студенттері, ал 30% екінші курс студенттері. Бірінші курс студенттерінің ішінде 10%, ал екінші курс студенттерінің ішінде 5% қыздар бар. Барлық қыздар кезекпен асханада жұмыс істейді. Кез келген бір күнде тексергенде асханада бірінші курста оқитын қыз жұмыс істеп жатқандығының ықтималдығы қандай?
6- сабақ
Бернулли схемасы. Пуаcсон формуласы. Муавр-Лапластың локальдық теоремасы.
n санының үлкен мәндерінде тәжірибелердің қайталануында Бернулли формуласын пайдалану үлкен қиыншылықтар туғызады, себебі ол үлкен сандар үстінде амалдарды орындаумен байланысты.
Мысалы, Бернулли формуласында n = 50 m = 20; p = 0,1;
q = 0,9 болғанда Бернулли формуласы төмендегі көріністе болады:

Бұл жерде  ;
;  ;
; 



![]()
![]()
С![]() ол үшін ықтималдықты жеткілікті дәрежедегі дәлдікпен
анықтауға мүмкіндік беретін асимптотикалық формуладан пайдалану
қажеті болады.
ол үшін ықтималдықты жеткілікті дәрежедегі дәлдікпен
анықтауға мүмкіндік беретін асимптотикалық формуладан пайдалану
қажеті болады.
Бұндай дәрежедегі формуланы бірінші болып P = q
=  болғандағы Бернулли
схемасының дербес жағдайы үшін А.Муавр ойлап тапты. Сонан соң ол 0
және 1-ге тең болмаған Р жағдайы үшін ойлап тапқан П.С.Лапласпен
біріктірілді. Сондықтан бұл формула Муавр – Лаплас теоремасы деп
аталады.
болғандағы Бернулли
схемасының дербес жағдайы үшін А.Муавр ойлап тапты. Сонан соң ол 0
және 1-ге тең болмаған Р жағдайы үшін ойлап тапқан П.С.Лапласпен
біріктірілді. Сондықтан бұл формула Муавр – Лаплас теоремасы деп
аталады.
Теорема. Егер А оқиғасының әрбір
сынаудағы пайда болу ықтималдығы р- тұрақты болып, 0 мен 1 санына
тең болмаса (0 )және сынау саны
)және сынау саны  болса, онда оқиғаның дәл m – рет пайда болу
ықтималдығы
болса, онда оқиғаның дәл m – рет пайда болу
ықтималдығы  санының көбейтіндісі
санының көбейтіндісі  өрнегіне ұмтылады.
өрнегіне ұмтылады.
 мұндағы
мұндағы 
немесе

 функциясының мәндерінің,
функциясының мәндерінің,  үшін кітаптың соңында қосымшада №1 кестесі берілген,
ал
үшін кітаптың соңында қосымшада №1 кестесі берілген,
ал  болғанда да осы
кестеден пайдалануға болады, себебі
болғанда да осы
кестеден пайдалануға болады, себебі  функциясы жұп функция,
функциясы жұп функция, 
Дәлелдеуі. 

Енді 

Cтирлинг формуласынан пайдаланып Бернулли формуласын жазамыз.



![]()
![]()
![]()
![]()






Логарифм дейміз:

 ;
;
Логарифмдік функцияны дәрежелік қатарға жіктеу формуласын қолдаймыз.





 ;
;
потенцирлейміз:  ;
;
Сонымен  Теорема дәлелденді.
Теорема дәлелденді.
 тің қасиеттері.
тің қасиеттері.
10.
 жұп функция және оның графигі ОУ
осіне
симметриялы.
жұп функция және оның графигі ОУ
осіне
симметриялы.
20.
ОУ осімен у
=  графигі
графигі  нүктеде қиылысад
нүктеде қиылысад
30. ОХ
осімен
у қиылыспайды.
қиылыспайды.
Мысал. Нысанаға бір рет оқ атқанда оған тию ықтималдығы 0,8 – ге тең. Нысанаға 100 –рет оқ атылғанда оған 75 – рет тию ықтималдығы табылсын.
Шешуі. ![]()
Р = 0,8; n = 100; m = 75 екендігі берілген.
q = 1 – p = 1 – 0,8 = 0,2 екендігін табамыз.

х =-1,25 болғандағы  функциясының мәнін кітап соңындағы қосымшадағы №1 кестеден
іздейміз.
функциясының мәнін кітап соңындағы қосымшадағы №1 кестеден
іздейміз.
 ал
ал 
Олай болса, ізделінді ықтималдық

Жауабы: 
Егер  ал
ал  яғни
яғни  болса және m – нің мәні де жеткілікті түрде аз сан болса,
онда ізделінді ықтималдықты есептеуге Пуассонның жуықтап есептеу
формуласы қолданылады.
болса және m – нің мәні де жеткілікті түрде аз сан болса,
онда ізделінді ықтималдықты есептеуге Пуассонның жуықтап есептеу
формуласы қолданылады.
Мысал: Салыстырмалы жиіліктің ықтималдықтан (Р=3/8) ауытқуының абсолют шамасының 0,01-ден кем болмауының ықтималдығы 0,995-ке тең болуы үшін қанша тәуелсіз сынақтар жасау керек?
Шешуі: P=3/8; q=1-p=5/8;  0,01.
0,01.
Pn(k) .
.
Есептің шарты бойынша:  яғни 2Ф(0,01
яғни 2Ф(0,01 )=0,995.
)=0,995.
Сонда кестеден: 0,01 =2,8
=2,8




п=78400*0,234375
п=18375.
Тәуелсіз тәжірбиелердегі салыстырмалы жиіліктің тұрақты ықтималдықтан ауытқу ықтималдығы.
Мысал: А оқиғасының тәжірбиедегі пайда болған ықтималдығы 0,2-ге тең. Оқиғаның 400 тәжірбиеде 102 рет пайда болу ықтималдығын табу керек.
Шешуі: n=400, k=102, p=0,2; q=1-0,2=0,8.
Бұл есепті дәл шешуі Бернулли формуласымен табылады, бірақта бұл есепте сынақтар саны n=400 өте көп. Сондықтан Муавр-Лапластың локалдық формуласын пайдаланамыз. Ол үшін әуелі х-тің мәнін табамыз:
 Сонда
Сонда  Р400(102)
Р400(102)
7- сабақ
Кездейсоқ шамалар жайында жалпы түсінік. Дискретті кездейсоқ шамалар. Кездейсоқ шаманың ықтималдық тығыздығы. Кездейсоқ шамалардың тәуелсіздігі
Сынау нәтижесінде қандайда бір мүмкін мәнді қабылдайтын шаманы кездейсоқ шама деп атайды.
Егер кездейсоқ шамалардың қабылдаған мүмкін мәндерін жекелеп, айырып санауға келетін болса, мұндай шамаларды дискертті кездейсоқ шама деп атайды
Егер кездейсоқ шама белгілі аралықта біртұтас болса онда, яғни жекелеуге келмесе, онда оны үздіксіз кездейсоқ шама деп атайды.
Мысалы.
Ойын кубигін лақтырғанда ұпай санының пайда болуын көрейік, ұпай саны – кездейсоқ шама; 1,...,6 – мәндері.
Дискретті кездейсоқ шамалардың үлестіру заңдары.
Кездейсоқ шама мәндерімен оларға сәкес ықтималдықтарды байланыстыратын ереже дискретті шаманың үлестіру заңы деп аталады. Бұл заң таблица, график немесе формула түрінде өрнектеледі.
1. Дискретті кездейсоқ шамалардың кесте түрінде берілуі.
|
Х |
X1 |
X2 |
X3 |
… |
Xn |
|
P |
P1 |
P2 |
P3 |
… |
Pn |
Бұл жерде ықтималдықтар әр түрлі мәндерді қабылдайды.
р1+ р2 + ... + рn = 1
Mұндай кестені кезедейсоқ шаманың үлестірім кестесі
немесе үлестірім заңы деп атайды.
Мысал .
Алты бұйымнан тұратын партияның төртеуі жарамды. Қалай болса солай екі бұйым таңдап алынады. Таңдап алынған жарамды бұйымдар саны –Х–дискрет кездейсоқ шаманың үлестірім заңы құрылсын.
Шешуі. Х- кездейсоқ шама төмендегідей мүмкін болған мәндерді қабылдайды: x1= 0, x2= 1, x3=2. Оларға сәйкес ықтималдықтарды
 формуладан пайдаланып табамыз. (N –
партиядағы
формуладан пайдаланып табамыз. (N –
партиядағы
бұйымдар саны, n – партиядағы жарамды бұйымдар саны, m таңдап алынған бұйымдар саны, k – таңдап алынған бұйымдардың ішінде жарамдылар саны)



Ізделінді үлестірім заңын құрамыз:
|
X |
0 |
1 |
2 |
|
P |
|
|
|
Тексеру: 
Дискретті кездейсоқ шаманың график түрінде берілуі.
Дискретті кездейсоқ шаманың үлестіру заңын график түрінде бейнелеуге болады. Ол үшін жазықтықтағы тік бұрышты координаттар жүйесінде (хi; рi) нүктелерін белгілейді де, олардың ретіне қарай жалғастыратын кесінділер жүргізіледі. Шыққан фигураны үлестіру көпбұрышы деп атайды.
Мысал. Дискретті кездейсоқ шама Х мынадай үлестірім заңымен берілген:
|
Х |
2 |
4 |
5 |
6 |
|
Р |
0,3 |
0,1 |
0,2 |
0,4 |
Үлестіру көп бұрышын сызыңдар.
![]() P
P
0![]()
![]() .8
.8
0![]() .7
.7
0![]() .6
.6
0![]() .5
.5
0![]()
![]() .4
.4
0![]()
![]() .3
.3
0![]()
![]() .2
.2
0![]()
![]() .1
.1
![]()
![]()
![]()
![]()
![]() 0
0
![]() 0 x
0 x
-
4 5 6
Дискретті кездейсоқ шамалардың үлестірім заңдары
Х дискретті кездейсоқ шамасы ![]() мәндерін
мәндерін ![]() ықтималдықтарымен
қабылдасын
(
ықтималдықтарымен
қабылдасын
(![]() немесе
немесе ![]() ).
).
Х үлестірім заңы кестемен берілсін:
|
Х |
|
|
… |
|
… |
|
Р |
|
|
… |
|
… |
Бұл кесте үлестірім қатары деп
аталады. ![]() ,
, ![]() оқиғалары үйлесімсіз және толық топ
құрайды, яғни
оқиғалары үйлесімсіз және толық топ
құрайды, яғни ![]() .
.
Х үлестірім заңының графиктік түрде
берілуі: тік бұрышты координаталар жүйесінде абсцисса
осі бойына ![]() мәндері, ал ордината осіне – осы
мәндердің
мәндері, ал ордината осіне – осы
мәндердің ![]() ықтималдықтары салынады.
(
ықтималдықтары салынады.
(![]() ,
,![]() ) координаталы нүктелерді тізбектей кесінділермен
қосады. Пайда болған сынық сызықты үлестірімнің көпбұрышы деп
атайды.
) координаталы нүктелерді тізбектей кесінділермен
қосады. Пайда болған сынық сызықты үлестірімнің көпбұрышы деп
атайды.
Үлестірім заңының аналитикалық берілуі мүмкін мәндердің өз ықтималдықтарымен байланыстыратын формуланы айқындауды талап етеді. Бұндай формуланы кейбір кездейсоқ шамалар үшін ғана табуға болады.
Бернулли және Пуассон үлестірімдерін «Кездейсоқ шамалардың негізгі үлестірім заңдары» тақырыбында қарастырамыз.
8-сабақ
Кездейсоқ шамалардың үлестіру функциялары
Үзіліссіз кездейсоқ шамалар. Үлестірім функциясы
Үзіліссіз кездейсоқ шаманы үлестірім заңымен немесе үлестірім көпбұрышымен беруге болмайтындығы белгілі. Дискретті және үзіліссіз кездейсоқ шамалар үшін үлестірім заңын берудің универсал жолы бар.
Анықтама.
Х кездейсоқ шамасының үлестірім функциясы (немесе интегралдық функциясы, үлестірім заңы) деп әрбір х мәні үшін оқиғалар ықтималдығы X<x, яғни F(x)=P(X<x) (1) анықталатын F(x) функциясы айтылады.
![]() мәндерін қабылдайтын дискретті
Х кездейсоқ шамасы үшін (1) формула келесі түрде
жазылады
мәндерін қабылдайтын дискретті
Х кездейсоқ шамасы үшін (1) формула келесі түрде
жазылады ![]() ,
мұндағы
,
мұндағы ![]() қосындылау х-тен кіші
барлық
қосындылау х-тен кіші
барлық ![]() мәндеріне
салыстырмалылығын білдіреді. Сонымен, дискретті кездейсоқ шамасы
үшін бұл функция
үзілісті,
мәндеріне
салыстырмалылығын білдіреді. Сонымен, дискретті кездейсоқ шамасы
үшін бұл функция
үзілісті, ![]() - оның үзіліс нүктелері.
Үзіліссіз кездейсоқ шама
үшін F(x) үзіліссіз.
- оның үзіліс нүктелері.
Үзіліссіз кездейсоқ шама
үшін F(x) үзіліссіз.
F(x) қасиеттері
1) барлық х
үшін ![]() .
.
Бұл қасиет ықтималдық сияқты F(x) анықтамасынан шығады
2) F(x) кемімелі емес, яғни
егер ![]() ,
онда
,
онда ![]() .
.
Расында, ![]() болсын.
болсын. ![]() оқиғасын екі оқиғаның
қосындысы түрінде жазуға
болады:
оқиғасын екі оқиғаның
қосындысы түрінде жазуға
болады: ![]() . Бұл оқиғалар үйлесімсіз
болғандықтан, ықтималдықтарды қосу теоремасы
бойынша:
. Бұл оқиғалар үйлесімсіз
болғандықтан, ықтималдықтарды қосу теоремасы
бойынша: ![]() ,
бұдан
,
бұдан
![]()
![]() .
.
Кез келген ықтималдық теріс
емес болғандықтан, онда ![]() ,
яғни
,
яғни ![]() . Қасиет
дәлелденді.
. Қасиет
дәлелденді.
Салдар 1.
Кездейсоқ
шаманың ![]() аралығына түсу
ықтималдығы
аралығына түсу
ықтималдығы
![]() ,
,
бұл ![]() теңдігінен
шығады.
теңдігінен
шығады.
Салдар 2.
Кездейсоқ шама белгілі бір мәнді қабылдау
ықтималдығы нолге тең.
Егер ![]() формуласында
формуласында ![]() деп
алып,
деп
алып, ![]() кезде шекке көшсек,
онда
кезде шекке көшсек,
онда ![]() ,
, ![]() үзіліссіздіктерінен және
үзіліссіздіктерінен және
![]() .
.
Салдар 3.
![]() .
.
3)
Егер кездейсоқ шаманың мүмкін
мәндері ![]() интервалында жатса,
онда
интервалында жатса,
онда ![]() және
және ![]() ; үзіліссіз кездейсоқ шама үшін мүмкін
мәндері барлық сан осінде
жатса,
; үзіліссіз кездейсоқ шама үшін мүмкін
мәндері барлық сан осінде
жатса, ![]() және
және ![]() .
Аталып өткен қасиеттер үзіліссіз кездейсоқ шаманың графигін салуға
мүмкіндік береді:
.
Аталып өткен қасиеттер үзіліссіз кездейсоқ шаманың графигін салуға
мүмкіндік береді:

1 сурет
Айта кетелік, үзіліссіз кездейсоқ шаманы көбінесе үзіліссіз үлестірім функциясы бар шама ретінде анықталады.
Үлестірім тығыздығы
Үзіліссіз кездейсоқ шаманы үлестірім функциясынан басқа жолмен де беруге болады. Оның басты сипаттамасы – ықтималдықтардың үлестірім тығыздығы.
Анықтама.
Үзіліссіз кездейсоқ шаманың ықтималдықтарының
үлестірім тығыздығы (жәй үлестірім тығыздығы немесе
үлестірімнің дифференциалдық функциясы,
белгіленуі ![]() ) деп оның үлестірім функциясының туындысы
айтылады, яғни
) деп оның үлестірім функциясының туындысы
айтылады, яғни ![]() .
.
Үлестірім тығыздығының ықтималдық мағынасын анықтайық. Туындының анықтамасы бойынша
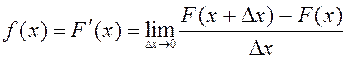 =
|
=
| ![]() қасиеті|
=
қасиеті|
= 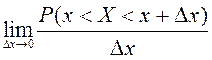 .
.
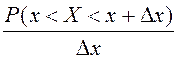 қатынасы
қатынасы ![]() интервалындағы орта ықтималдықты
білдіргендіктен,
интервалындағы орта ықтималдықты
білдіргендіктен, ![]() функциясы
функциясы ![]() нүктесіндегі және оның аймағындағы
ықтималдықты сипаттайды.
нүктесіндегі және оның аймағындағы
ықтималдықты сипаттайды.
Айта кетелік, үлестірімнің дифференциалдық функциясы, интегралдық функция сияқты үлестірім заңының бірі болады, бірақ интегралдық функция сияқты универсалды бола алмайды. Үлестірім тығыздығы тек үзіліссіз кездейсоқ шамалар үшін ғана анықталады.
f(x) қасиеттері
1. Х-тің ![]() интервалына түсу ықтималдығы келесі формула
бойынша анықталады:
интервалына түсу ықтималдығы келесі формула
бойынша анықталады:
 .
.
Расында, 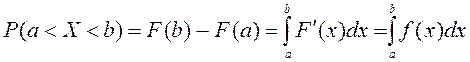 .
.
2. 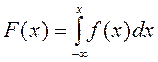 .
.
Расында,  .
.
3. ![]() үшін
үшін ![]() .
.
Расында, ![]() , бірақ
, бірақ ![]() кемімелі емес,
сондықтан
кемімелі емес,
сондықтан ![]() , олай болса
, олай болса ![]() .
.
4. 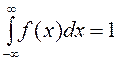 .
.
Бірінші
қасиетте ![]() деп есептейік,
онда
деп есептейік,
онда  , бірақ
, бірақ ![]() ақиқат оқиға,
сондықтан
ақиқат оқиға,
сондықтан ![]() . Яғни
. Яғни 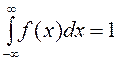 .
.
![]() үлестірім тығыздығының графигі
үлестірім қисығы деп аталады, келесі түрде
болады:
үлестірім тығыздығының графигі
үлестірім қисығы деп аталады, келесі түрде
болады:

2 сурет
Егер анықталған интегралдың геометриялық
мағынасын еске түсірсек, яғни қисық сызықты трапецияның ауданы,
онда ![]() қасиеттерінің геометриялық интерпретациясын
аламыз.
қасиеттерінің геометриялық интерпретациясын
аламыз.
3
суретте жолақпен белгіленген облыстар сәйкес:
а) Х-тің ![]() интервалына түсу ықтималдығына тең;
б)
интервалына түсу ықтималдығына тең;
б) 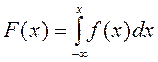 ; в)
; в) 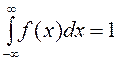 .
.



а) б) в)
3 сурет
Кездейсоқ шамалардың негізгі үлестірім заңдары
Дәріс мазмұны: биномдық үлестірім заңы, Пуассон, бірқалыпты, көрсеткіштік, қалыпты үлестірімдер.
Дәріс мақсаты: кездейсоқ шамалардың негізгі үлестірім заңдарымен таныстыру.
Биномдық үлестірім заңы
![]() – n тәуелсіз
сынақтарда А оқиғасының пайда болу
саны, р – әрбір
сынақта А оқиғасының пайда болу
ықтималдығы, q – пайда болмау ықтималдығы
болсын.
– n тәуелсіз
сынақтарда А оқиғасының пайда болу
саны, р – әрбір
сынақта А оқиғасының пайда болу
ықтималдығы, q – пайда болмау ықтималдығы
болсын. ![]() -тің мүмкін мәндері:
0,1,2,…, n. Бұл мүмкін мәндердің ықтималдықтары келесі
формуламен есептелінеді
-тің мүмкін мәндері:
0,1,2,…, n. Бұл мүмкін мәндердің ықтималдықтары келесі
формуламен есептелінеді ![]() =
=![]()
![]() ,
, ![]() (1).
(1).
Анықтама.
![]() дискретті кездейсоқ шамасының
үлестірімі үшін үлестірім заңы (1) формуласымен берілсе, онда ол
биномды үлестірім делінеді.
дискретті кездейсоқ шамасының
үлестірімі үшін үлестірім заңы (1) формуласымен берілсе, онда ол
биномды үлестірім делінеді.
Сонымен, бұл кездейсоқ шаманың үлестірім қатары:
|
Х |
0 |
1 |
2 |
… |
n |
|
Р(Х=k) |
|
|
|
… |
|
Үлестірім функциясы:
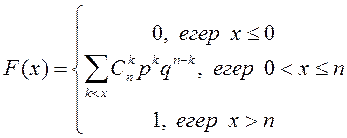 .
.
Сандық сипаттамаларды анықтау үшін дайын
формулаларды қолдануға болады, олар математикалық үміт пен
дисперсияның қасиеттерін анықтағанда
табылған. n тәуелсіз сынақта оқиғаның пайда болу
санының математикалық үміті мен
дисперсиясы: ![]() ,
, ![]() .
.
![]() интервалына түсу
ықтималдығы
интервалына түсу
ықтималдығы ![]() . формуласы бойынша
табылады.
. формуласы бойынша
табылады.
Бином заңы бойынша үлестірілген кездейсоқ шамаларды зерттеуді Mathcad жүйесінде арнайы енгізілген функциялар көмегімен жүргізуге болады ([7]).
Пуассон үлестірімі
Пуассон үлестірімі биномдық үлестірім
үшін шектік болып табылады, яғни сынақтар
саны n шексіз өседі, әрбір сынақта оқиғаның пайда
болу ықтималдығы р азаяды, бірақ ![]() көбейтіндісі тұрақты болып
қалады.
көбейтіндісі тұрақты болып
қалады.
Бұл жағдайда
оқиғаның k рет пайда болуы
(k=0,1,2,…,n,…) Пуассон формуласы бойынша
есептелінеді 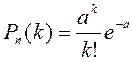 , ал үлестірім заңы осы формуламен берілетін
кездейсоқ шама Пуассон заңымен үлестірілген
делінеді.
, ал үлестірім заңы осы формуламен берілетін
кездейсоқ шама Пуассон заңымен үлестірілген
делінеді.
Бұл кездейсоқ шаманың үлестірім қатары:
|
Х |
0 |
1 |
2 |
… |
n |
… |
|
Р(Х=k) |
|
|
|
… |
|
… |
Сандық сипаттамаларын табамыз.
![]()
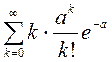 =
=![]()
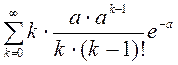 =
=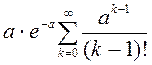 = =
= =![]() . Математикалық
үміті
. Математикалық
үміті ![]() . Дисперсиясы
. Дисперсиясы ![]() . Сонымен, Пуассон заңымен үлестірілген кездейсоқ
шамалар үшін математикалық үміт пен дисперсия өзара тең.
Пуассон заңының бұл қасиетін практикада зерттеліп отырған кездейсоқ
шамалар Пуассон заңымен үлестірілген гипотезасын тексеруде
қолданады. Пуассон заңы туралы жиі «сирек оқиғалар заңы» деп те
атайды. Пуассон заңымен үлестірілген кездейсоқ шамалар мысалы:
белгілі бір уақыт арасында катодтан ұшып шығатын электрондар
саны; t уақыт ішінде телефон станциясына келіп
түсетін қоңыраулар саны және
т.с.с.
. Сонымен, Пуассон заңымен үлестірілген кездейсоқ
шамалар үшін математикалық үміт пен дисперсия өзара тең.
Пуассон заңының бұл қасиетін практикада зерттеліп отырған кездейсоқ
шамалар Пуассон заңымен үлестірілген гипотезасын тексеруде
қолданады. Пуассон заңы туралы жиі «сирек оқиғалар заңы» деп те
атайды. Пуассон заңымен үлестірілген кездейсоқ шамалар мысалы:
белгілі бір уақыт арасында катодтан ұшып шығатын электрондар
саны; t уақыт ішінде телефон станциясына келіп
түсетін қоңыраулар саны және
т.с.с.
Бірқалыпты үлестірім
Мүмкін мәндері белгілі бір интервалда жататын және олардың барлығы бірдей мүмкіндікті болатын үзіліссіз кездейсоқ шамалар практикада кездеседі. Ондай шамалар бірқалыпты үлестірілген дейді.
Анықтама.
Егер [a,b]
кесіндісінде Х үзіліссіз кездейсоқ шамасының үлестірім
тығыздығы тұрақты, ал оның сыртында нолге тең
болса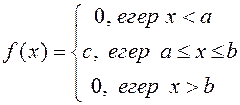 , онда үзіліссіз кездейсоқ шама бірқалыпты
үлестірілген деп аталады,
мұндағы с –
const.
, онда үзіліссіз кездейсоқ шама бірқалыпты
үлестірілген деп аталады,
мұндағы с –
const.
Сонымен, тығыздық графигі:

4 сурет
f(x) үлестірім тығыздығының қасиеттері
бойынша f(x) графигі
мен ОХ осімен шектелген фигураның ауданы 1-ге тең,
яғни ![]() немесе
немесе 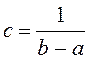 .
.
Олай болса, 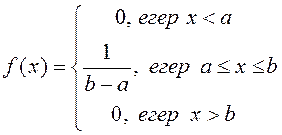 .
.
F(x) үлестірім функциясын табайық.
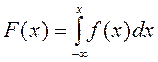 формуласы
бойынша
формуласы
бойынша ![]() болғанда
болғанда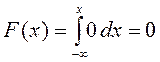 ;
;
егер ![]() , онда
, онда 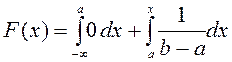 =
=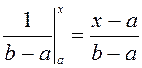 ;
;
егер ![]() , онда
, онда  .
.
Сонымен,
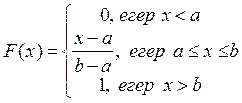 .
.
F(x) графигінің түрі:

5 сурет
Бірқалыпты үлестірімнің сандық
сипаттамалары: математикалық
үміт 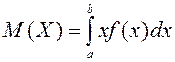 =
=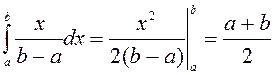 ; дисперсия
; дисперсия 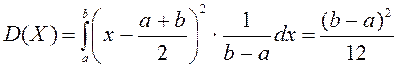 ; орта квадраттық
ауытқу
; орта квадраттық
ауытқу 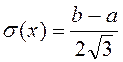 .
. ![]() интервалына түсу
ықтималдығы:
интервалына түсу
ықтималдығы:  =
=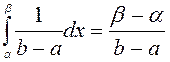 немесе
немесе ![]() . Бұл ықтималдық 6 суреттегі штрихталған
тіктөртбұрыштың ауданына тең
. Бұл ықтималдық 6 суреттегі штрихталған
тіктөртбұрыштың ауданына тең

6 сурет
Көрсеткіштік үлестірім
Практикада ықтималдық теориясының қолданылуында, мысалы, сенімділік теориясында, жаппай қызмет ету теориясында және т.б. үлестірімнің көрсеткіштік немесе экспоненциалды заңы қолданылады.
Анықтама.
Егер үлестірім
тығыздығы 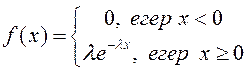 түрінде берілсе,
мұндағы
түрінде берілсе,
мұндағы ![]() >0 – үлестірім параметрі,
онда Х үзіліссіз кездейсоқ шамасы көрсеткіштік
заңмен үлестірілген
делінеді.
>0 – үлестірім параметрі,
онда Х үзіліссіз кездейсоқ шамасы көрсеткіштік
заңмен үлестірілген
делінеді.
Үлестірім функциясын
табайық 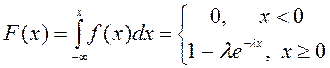 .
.
7 және 8 суреттерінде f(x), F(x) графиктері кескінделген


7 сурет 8 сурет
Көрсеткіштік үлестірімнің сандық сипаттамалары:
1)
математикалық үміт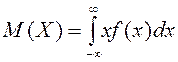 =
= 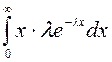 =
= ![]() =
=![]() ;
;
2)
дисперсия ![]() =
= 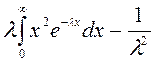 =
=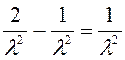 ;
;
3)
орта квадраттық ауытқуы 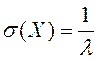 .
.
Сонымен, көрсеткіштік
үлестірімнің 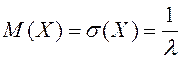 , бұл теңдікті практикада кездейсоқ шаманың
көрсеткіштік үлестірілген гипотезасын тексеруде
қолданады.
, бұл теңдікті практикада кездейсоқ шаманың
көрсеткіштік үлестірілген гипотезасын тексеруде
қолданады.
![]() интервалына түсу
ықтималдығы:
интервалына түсу
ықтималдығы:
![]() =
= ![]() .
.
Көрсеткіштік үлестірімнің сенімділік
теориясында қолданылуын қарастырайық. Кейбір қондырғыны, қарапайым
ба, күрделі ме, бұдан былай элемент деп атайтын боламыз.
Элемент ![]() моментінен бастап жұмысын бастасын,
ал
моментінен бастап жұмысын бастасын,
ал ![]() уақыттан соң жұмысын аяқтасын деп
ұйғарайық. Үзіліссіз кездейсоқ шаманы – элементтің мүлтіксіз
жұмыс істеу уақытын Т арқылы
белгілейік.
уақыттан соң жұмысын аяқтасын деп
ұйғарайық. Үзіліссіз кездейсоқ шаманы – элементтің мүлтіксіз
жұмыс істеу уақытын Т арқылы
белгілейік. ![]() үлестірім
функциясы
үлестірім
функциясы ![]() уақыт ішіндегі істен шығу ықтималдығын
анықтайды. Олай болса, сол уақыттағы мүлтіксіз жұмыс істеу
ықтималдығы (яғни
уақыт ішіндегі істен шығу ықтималдығын
анықтайды. Олай болса, сол уақыттағы мүлтіксіз жұмыс істеу
ықтималдығы (яғни ![]() қарама-қарсы оқиғаның
ықтималдығы):
қарама-қарсы оқиғаның
ықтималдығы):
![]()
![]() .
.
функциясын сенімділік функциясы деп атайды,
ол ![]() уақыт ішіндегі мүлтіксіз жұмыс істеу
ықтималдығын анықтайды. Т жиі көрсеткіштік
заңмен
уақыт ішіндегі мүлтіксіз жұмыс істеу
ықтималдығын анықтайды. Т жиі көрсеткіштік
заңмен
үлестірілген,
сонда ![]() , ал
, ал ![]() =
=![]() . Бұл
жағдайда
. Бұл
жағдайда ![]() сенімділіктің көрсеткіштік заңы деп
атайды, ал
сенімділіктің көрсеткіштік заңы деп
атайды, ал ![]() істен шығудың интенсивтілігін
анықтайды.
істен шығудың интенсивтілігін
анықтайды.
Қалыпты үлестірім
Үлестірімнің қалыпты заңы– ықтималдық теориясында маңызды заң. Мысалы қалыпты заңмен үлестірілген кездейсоқ шамалар: өлшеу және бақылаудың кездейсоқ қателері; оқ атқанда мәреден кездейсоқ жаңылуы кездейсоқ ауытқулары және т.б. Басқа заңдардан қалыпты заңның негізгі ерекшелігі – ол қандай да бір шарттарда басқа үлестірім заңдары ұмтылатын шектік заң болып табылады.
Анықтама.
 тығыздығымен сипатталатын кездейсоқ шаманың
ықтималдығының үлестірім заңы қалыпты заң деп
аталады.
тығыздығымен сипатталатын кездейсоқ шаманың
ықтималдығының үлестірім заңы қалыпты заң деп
аталады.
Сонымен, қалыпты үлестірім екі
параметрмен ![]() және
және ![]() анықталады. Осы параметрлердің ықтималдық
мағынасын ашайық.
анықталады. Осы параметрлердің ықтималдық
мағынасын ашайық.![]() болатындығын
көрсетейік:
болатындығын
көрсетейік:
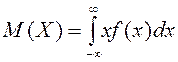 =
= =
= =…=
=…=![]() .
.
Толығырақ мәліметті [1], 145 беттен қараңыз. Сол
сияқты, ![]() :
:
![]()
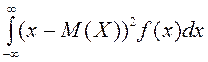 =
= =
= =
=
=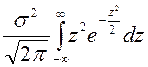 =
=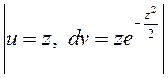 =…=
=…=![]() .
.
Бұдан орта квадраттық
ауытқу ![]() . Егер
. Егер ![]() =0 және
=0 және ![]() =1, онда қалыпты үлестірім нормаланған деп
аталады.
=1, онда қалыпты үлестірім нормаланған деп
аталады.
Ықтималдықтың қалыпты үлестірімінің
тығыздығының графигі қалыпты қисық немесе Гаусс қисығы деп
аталады.  функциясын математикалық талдау әдістерімен
зерттеп, оның графигін
саламыз:
функциясын математикалық талдау әдістерімен
зерттеп, оның графигін
саламыз:
а) анықталу
облысы ![]() ;
;
б) график ОХ осінен жоғары орналасқан,
себебі ![]() үшін
үшін ![]() ;
;
в) ![]() , яғни ОХ – көлденең
асимптота;
, яғни ОХ – көлденең
асимптота;
г) 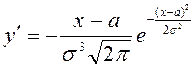 ,
, ![]()
![]()
![]() - кризистік
нүкте;
- кризистік
нүкте; ![]() егер
егер ![]() және
және ![]() егер
егер ![]() , онда
, онда ![]() ,
, 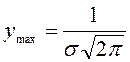 ;
;
д) екінші туынды арқылы иілу нүктесін
табамыз  және
және 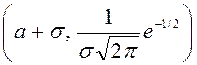 . Сонымен, Гаусс
қисығы:
. Сонымен, Гаусс
қисығы:

9 сурет
![]() және
және ![]() параметрлерінің өзгерісінің қалыпты
қисықтарға келтіретін әсері:
параметрлерінің өзгерісінің қалыпты
қисықтарға келтіретін әсері:
а)
бір ![]() болғанда
болғанда ![]() шамасының өзгеруі қалыпты қисықтың формасын
өзгертпейді, тек ОХ осі
бойында
шамасының өзгеруі қалыпты қисықтың формасын
өзгертпейді, тек ОХ осі
бойында ![]() болса
солға,
болса
солға, ![]() болса оңға
жылжиды;
болса оңға
жылжиды;
б) 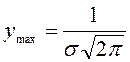 болғандықтан,
болғандықтан, ![]() өскен сайын максималды ордината кемиді және
керісінше; үлестірім қисығымен шектелген аудан әрқашан бірге тең
болғандықтан,
өскен сайын максималды ордината кемиді және
керісінше; үлестірім қисығымен шектелген аудан әрқашан бірге тең
болғандықтан, ![]() өзгергенде тек қисықтың формасы ғана
өзгереді:
өзгергенде тек қисықтың формасы ғана
өзгереді: ![]() өскен сайын ол жатық болады
және ОХ осі бойымен
созылады.
өскен сайын ол жатық болады
және ОХ осі бойымен
созылады.
Қалыпты үлестірілген кездейсоқ шаманың
берілген интервалға түсу ықтималдығын
табамыз ![]() :
:
 =
= 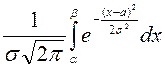 =
= =
=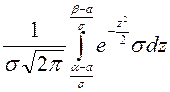 =
=
=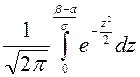 –
– 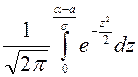 =
= = =
= =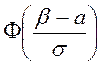 –
– 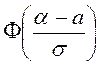 .
.
Лаплас функциясының мәндерін арнайы кестеден немесе Mathcad жүйесінде алынады. Бұл функцияның қасиеттері:
1) ![]() кез келген х үшін
анықталған;
кез келген х үшін
анықталған;
2) ![]() ;
; 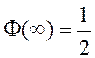 ;
;
3) ![]() , тақ
функция;
, тақ
функция;
4) ![]()
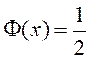 .
.
Сонымен, Лаплас функциясының графигі:

10 сурет
Лаплас функциясы арқылы қалыпты үлестірілген кездейсоқ шаманың F(x) үлестірім функциясы анықталады:
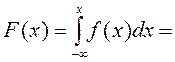
 =
=![]()
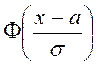 -
-![]() = =
= =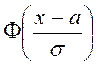 +
+ ![]() = =
= =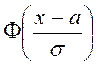 + 0,5.
+ 0,5.
Практикада ![]() қалыпты үлестірілген кездейсоқ
шаманың а – математикалық үміттен ауытқуының абсолют
шамасы бойынша
қалыпты үлестірілген кездейсоқ
шаманың а – математикалық үміттен ауытқуының абсолют
шамасы бойынша ![]() санынан кіші болу ықтималдығын,
яғни
санынан кіші болу ықтималдығын,
яғни ![]() басқаша айтқанда, бұл кездейсоқ шаманың
сейілу центрі
басқаша айтқанда, бұл кездейсоқ шаманың
сейілу центрі ![]() -ға салыстырмалы симметриялы интервалына түсу
ықтималдығын
-ға салыстырмалы симметриялы интервалына түсу
ықтималдығын ![]() есептеуге тура
келеді.
есептеуге тура
келеді.
Расында, ![]() болғандықтан,
болғандықтан,
![]() =
= ![]()
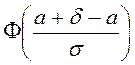 -
- 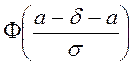 =
= .
.
Сонымен, ![]() аз болған сайын (яғни сейілу), соғырлым
қалыпты үлестірілген кездейсоқ
шаманың
аз болған сайын (яғни сейілу), соғырлым
қалыпты үлестірілген кездейсоқ
шаманың ![]() интервалына түсу ықтималдығы
үлкен.
интервалына түсу ықтималдығы
үлкен. ![]() -тің барлық мәндері енетіндей
центрі а нүктесінде болатын қандай интервал алуға
болатынын анықтайық.
-тің барлық мәндері енетіндей
центрі а нүктесінде болатын қандай интервал алуға
болатынын анықтайық. ![]() мәндерінің кестесін
қолданамыз:
мәндерінің кестесін
қолданамыз:
![]() =
=![]() =0,6826;
=0,6826;
![]() =
=![]() =0,9594;
=0,9594;
![]() =
=![]() =0,9973;
=0,9973; ![]() =
=![]() =0,999936.
=0,999936.
Сонымен, қалыпты үлестірілген кездейсоқ
шаманың барлық дерлік (~ 99,7%)
мәндері ![]() интервалына түседі. Бұл тұжырым «үш
сигма ережесі» деп аталады.
интервалына түседі. Бұл тұжырым «үш
сигма ережесі» деп аталады.
Мысал: Х кездейсоқ шаманың
үлестіру тығыздығы берілген. 
F(x) үлестіру формуласын табыңдар.
Шешуі: F(x) Осыдан х<0 болғанда f(x)=0 болатынын пайдалансақ,
F(x)
Осыдан х<0 болғанда f(x)=0 болатынын пайдалансақ,
F(x) . Енді
0<x<
. Енді
0<x< болғанда f(x)=sinx. Сондықтан: F(x)
болғанда f(x)=sinx. Сондықтан: F(x)

 .
.
Ақырында x> болғанда f(x)=0. Осыдан
болғанда f(x)=0. Осыдан
F(x)


 (-cosx
(-cosx )=-cos
)=-cos +cos0=1. Сонымен:
+cos0=1. Сонымен:

9- сабақ
Математикалық күтім және оның қасиеттері. Дисперсия және оның қасиеттері. Чебышев теңсіздігі
Үлестіру заңы кездейсоқ шаманы сипаттайтынын көрдік. Көптеген практикалық мәселелерді шешкенде кездейсоқ шаманың үлестіру заңын іздемей – ақ (оны анықтау кейде қиынға түседі), сол үлестірудің кейбір сандық синаттарымен қанағаттануға болады.
Анықтама. Дискретті кездейсоқ
шама Х – тің математикалық күтімі
деп оның барлық мүмкін
мәндерін сәкес ықтималдықтарына көбейтілген қосындысын айтамыз,
яғни 
Егер  қатар жинақсыз болса, онда математикалық күтім болмайды,
яғни
қатар жинақсыз болса, онда математикалық күтім болмайды,
яғни


Мысал. Бернулли схемасы бойынша үлестірілген кездейсоқ шаманың математикалық күтімін анықтау керек.




Математикалық күтімнің қасиеттері.
10. М(С) = С, С – тұрақты сан. Тұрақты санның математикалық күтімі сол тұрақты санға тең;
20. М(СХ) = С·М(Х) – тұрақтыны математикалық күтім таңбасының алдына шығаруға болады;
30. М(Х ± У) = М(Х)±М(У) – екі кездейсоқ шама қосындысының математикалық күтімі олардың математикалық күтімдерінің қосындысына тең.
40. М(Х·У) = М(Х)·М(У) – екі кездейсоқ шама көбейтіндісінің математикалық күтімі олардың математикалық күтімдерінің көбейтіндісіне тең.
Мысал.
|
Х |
0,21 |
0,54 |
0,61 |
|
Р |
0,1 |
0,5 |
0,4 |
Шешуі.
 §Дисперсия
§Дисперсия
Анықтама. Кездейсоқ шама мен оның математикалық күтімі айырымының квадратының математикалық күтімін дисперсия деп атайды.

 орташа квадраттық ауытқу.
орташа квадраттық ауытқу.
Мысалы. Пуассон заңы бойынша үлестірілген кездейсоқ шаманың дисперсиясын анықтау керек
 ;
; 



Дисперсияның қасиеттері .
10. Д(с) = 0 Тұрақтының дисперсиясы 0 – ге тең.
20. Д(сх) =
 (х) Тұрақтыны дисперсия таңбасының сыртына квадраттап
шығаруға болады.
(х) Тұрақтыны дисперсия таңбасының сыртына квадраттап
шығаруға болады.
30. Д(х ± у) = Д(х) ± Д(у)
40. Д(х · у) = Д(х) · Д(у) + [М(х)]2·Д(у) + [М(у)]2·Д(х)
Мысал . Үлестіру заңы бойынша берілген Х – дискертті кездейсоқ шаманың дисперсиясы және орташа квадраттық ауытқуы табылсын.
|
Х |
131 |
140 |
160 |
180 |
|
Р |
0,05 |
0,10 |
0,25 |
0,60 |
Шешуі. Д(х) = М(х)2 - [М(х)]2 формуласынан пайдаланамыз: Х – тің математикалық күтімін табамыз.
М(х) = 131·0,05 +140·0,1+ 160·0,25 + 180·0,60 = 6,55 + 14 + 40 +108 = =168,55
Х2 – тың үлестіру заңын жазамыз:
|
Х2 |
17161 |
19600 |
25600 |
32400 |
|
Р |
0,05 |
0,10 |
0,25 |
0,60 |
Х2 – тың математикалық күтімін табамыз:
М(х2) = 17161·0,05 +19600·0,10 + 25600·0,25 + 32400·0,60 = 858,05+1960 + 6400 +19440 = 28658,05
Ізделінді дисперсияны табамыз:
![]()
 28658,05-(168,55)2
= 28658,05 –
28409,1025 = 248,9475
28658,05-(168,55)2
= 28658,05 –
28409,1025 = 248,9475
Орташа квадраттық ауытқуды табамыз: σ(х) = √ 248.9475 ≈ 15.778 .
Үлкен заңдар заңы.
Мысал: Белгілі бір прибор тәуелсіз жұмыс істейтін 10 элементтен тұрады. Т уақыт ішінде әр элементтің жұмыс істемей қалған элементтердің орташа санының Ф (математикалық үміті) айырмасының абсолют шамасының:
1) екіден кем болуының;
2) екіден кем болмауының ықтималдықтарын бағалаңыз.
Шешуі: Есептің шарты бойынша: n=10, p=0,5, q=0,5
Сондықтан: М(х)=10*0,5=5, Д(х)=5*0,5=2,5
-
Р(
 <2)
<2)
-
Р(

 2)
2)
Сонымен:
Р( <2)
<2) , Р(
, Р(
 2)
2) .
.
10- сабақ
Үлкен сандар заңы. Орталық шектік теоремалар
Егер кездейсоқ шама х теріс таңбалы мәндерді қабылдамаса және оның математикалық күтімі шекті болса, онда бұл кездейсоқ шаманың қалаған оң таңбалы сан А-дан кем болмау ықтималдығы әрдайым математикалық күтімнің А-санына қатынасынан үлкен болмайды, яғни

Чебышев теңсіздігі.
Кездейсоқ шама Х өзінің математикалық күтімі М(х)-тен
ауытқуының абсолют шамасы  -нан кем болмау ықтималдығы дисперсия
D(х)-тің
-нан кем болмау ықтималдығы дисперсия
D(х)-тің  -ның квадратына қатынасынан үлкен болмайды,
яғни
-ның квадратына қатынасынан үлкен болмайды,
яғни


Чебышев теоремасы.
Егерде  тізбегі тәуелсіз кездейсоқ шамалар болса, олардың
дисперсиялары бар болып бір тұрақты С санымен шектелген, яғни
Д(х1)
тізбегі тәуелсіз кездейсоқ шамалар болса, олардың
дисперсиялары бар болып бір тұрақты С санымен шектелген, яғни
Д(х1) С, ... ,
Д(х
С, ... ,
Д(х )
) болса, онда кездейсоқ
шамалардың арифметикалық орташасының олардың математикалық
күтімдерінің арифметикалық орташасынан ауытқуының абсалютті шамасы,
қандай да бір оң таңбалы аз тұрақты сан
болса, онда кездейсоқ
шамалардың арифметикалық орташасының олардың математикалық
күтімдерінің арифметикалық орташасынан ауытқуының абсалютті шамасы,
қандай да бір оң таңбалы аз тұрақты сан  -нан үлкен болмауын, n мейлінше үлкен
болғанда
-нан үлкен болмауын, n мейлінше үлкен
болғанда 
бірге жуық ықтималдықпен мақұлдаймыз, яғни

Дәлелдеуі. Чебышев теңсіздігін пайдаланамыз.
х~ арифметикалық орташа.
арифметикалық орташа.
 ~
~ математикалық күтім
орташасы.
математикалық күтім
орташасы.


 болғандықтан
болғандықтан  өйткені
өйткені



 өйткені
өйткені 
Теорема дәлелденді.
Сонымен қатар  өрнегі де орынды.
өрнегі де орынды.
 жуық теңсіздік жеткілікті үлкен n-нің
барлық
жуық теңсіздік жеткілікті үлкен n-нің
барлық
мәнінде  дәлдікпен орындалады.
дәлдікпен орындалады.
Сенімділік ықтималдық Р және n, арасындағы тәуелділік
арасындағы тәуелділік  десек, онда формуламен
өрнектеледі.
десек, онда формуламен
өрнектеледі.
Мысал. Сенімділік 0,95,
дәлдігі 0,01-ге дейін болса, с =1 десек, онда
 теңсіздігі орындалуы үшін қосылғыш кездейсоқ шамалар саны
неге тең болатынын анықтау керек.
теңсіздігі орындалуы үшін қосылғыш кездейсоқ шамалар саны
неге тең болатынын анықтау керек.
Шешуі.



Бернулли теоремасы.
Егер әрбір тәуелсіз сынауда А оқиғасының пайда болу
ықтималдығы тұрақты  -ға тең болса, онда сынау саны n мейлінше үлкен
болғанда
-ға тең болса, онда сынау саны n мейлінше үлкен
болғанда  оқиғасының салыстырмалы жиілігі
оқиғасының салыстырмалы жиілігі  ықтималдық р-дан қандай да бір оң таңбалы аз
сан
ықтималдық р-дан қандай да бір оң таңбалы аз
сан  -нан үлкен болмауын
бірге жуық ықтималдықпен мақұлдаймыз,
яғни
-нан үлкен болмауын
бірге жуық ықтималдықпен мақұлдаймыз,
яғни

Дәлелдеуі. Салыстырмалы
жиілік  ді, математикалық күтімі р-ға, дисперсиясы
ді, математикалық күтімі р-ға, дисперсиясы
 ге тең кездейсоқ шаманы
қарастырамыз.
ге тең кездейсоқ шаманы
қарастырамыз.
Чебышев теңсіздігіне қойсақ  шығады.
шығады.  Теорема дәлелденді.
Теорема дәлелденді.
Сонымен n өскен сайын  р-ға 1-ге жуық ықтималдықпен
жуықтайды.
р-ға 1-ге жуық ықтималдықпен
жуықтайды.
Пуассон теоремасы.
Егер А оқиғасының ықтималдығы әрбір тәуелсіз сынауда
өзгеріп отырса, онда n- мейлінше үлкен  болғанда А оқиғасы пайда болуының салыстырмалы жиілігі
ықтималдықтардың
болғанда А оқиғасы пайда болуының салыстырмалы жиілігі
ықтималдықтардың
арифметикалық ортасы  мәнінен өте аз (
мәнінен өте аз ( )
айырмада болуын бірге жуық ықтималдықпен мақұлдаймыз,
яғни
)
айырмада болуын бірге жуық ықтималдықпен мақұлдаймыз,
яғни 
Дәлелдеуі.
 шамалардың әрқайсысы тек (1 не 0) мәніне
сәйкес
шамалардың әрқайсысы тек (1 не 0) мәніне
сәйкес  не
не

ықтималдықпен қабылдайтын кездейсоқ шамалар болсын. Мұнда кездейсоқ шамалар саны сынау санына тең.
 болады. Чебычев
теоремасынан
болады. Чебычев
теоремасынан


Теорема дәлелденді.

шағым қалдыра аласыз