
Урок геометрии в 8 классе
Тема: «Высота, биссектриса и медиана треугольника»
Учитель: Мейманова А.А.
Урок геометрии в 8 классе
Мейманова Айнагуль Амангельдовна - учитель математики и физики, дефектолог, КГУ Специальная (коррекционная) школа – интернат №1с ограниченными возможностями в развитии
г. Петропавловск
Тема: Медиана, биссектриса и высота треугольника.
Цель: ввести понятия высоты, медианы и биссектрисы треугольника, уметь их различать и строить.
Задачи:
-
Ввести новые понятия высоты, медианы и биссектрисы треугольника.
-
Способствовать формированию устойчивого познавательного интереса к изучению геометрии.
-
Развивать логическое мышление учащихся.
Тип урока: урок закрепления
Формы организации учебной деятельности: коллективная, индивидуальная
Оборудование и наглядность урока: модели треугольников , изготовленные из плотного цветного картона; презентация к уроку «Медиана, биссектриса и высота треугольника»; тесты
Ход урока
-
Организационный момент.
-
Сообщение темы урока .
Математику не зря называют царицей наук, ей больше, чем какой-либо другой науке свойственны красота, изящность и точность. Постараемся это доказать при построении медианы, биссектрисы и высоты. Знания не просто надо иметь, но и нужно уметь их показывать, что вы и сделаете на сегодняшнем уроке, а я в этом вам помогу.
Безусловно, центровой фигурой является треугольник. Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о геометрии треугольника как о самостоятельном разделе геометрии.
( слайд с показом предметов принимающих форму треугольника)
-
Итак, глядя на рисунок, какая геометрическая фигура изображена ? (Треугольник).
А что называется треугольником? (Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).
-
Сколько у него элементов? (6)
-
Назовите элементы треугольника. (Три стороны и три угла).
-
Как найти периметр треугольника?( величины всех сторон сложить)
-
Какие виды треугольника вы знаете? (прямоугольный, равнобедренный, равносторонний, остроугольный, тупоугольный) на доске выбрать под каким номером изображен тот или иной вид треугольника
-
Кто из вас слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? {Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто – Рико и полуостровом Флорида}.
-
А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.
III. Объяснение нового материала.
1. Медиана.
-
Начертите треугольник АВС и найдите середину стороны ВС – точку К.
-
Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).
-
Соедините точку К с вершиной А. Отрезок АК называется медианой треугольника.
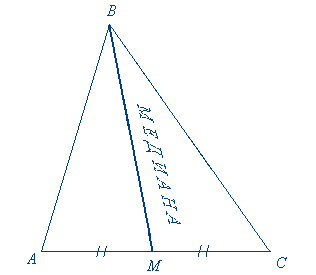
Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника
-
Сколько медиан можно провести в треугольнике?(3).
-
“Проведите” три медианы в треугольнике.
-
Какое свойство медиан вы заметили? (В любом треугольнике все медианы пересекаются в одной точке).
-
Эта точка называется центром тяжести треугольника. Запишите в тетрадях:
АК – медиана, ВК = КС
ВТ– медиана, АТ = ТС
СР– медиана, АР = РВ
О – точка пересечения медиан
2. Высота.
-
Начертите треугольник АВС
-
С помощью чертёжного угольника из вершины В проведём перпендикуляр ВН к прямой АС. Он называется высотой треугольника.
Запись на доске: ВН АС, Н АС.
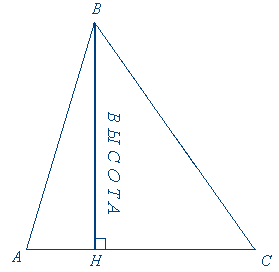
Определение. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
-
Сколько высот имеет треугольник? (3).
-
“Постройте” все три высоты в треугольнике.
-
Обладают ли высоты аналогичным свойством, что и медианы? (Да).
-
А если треугольник тупоугольный, то как построить высоты? (Провести дополнительные полупрямые)
-
Как вы думаете, что является высотой в прямоугольном треугольнике? (катеты)
Физминутка
Поднимает руки класс-это раз
Повернулась голова-это два
Руки вниз, вперед смотри - это три
Руки в стороны пошире развернули на четыре
С силой их к плечам прижать - это пять
Всем ребятам тихо сесть - это шесть.
3. Биссектриса.
-
Вспомните определение биссектрисы угла.
Определение. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
-
Постройте еще один треугольник АВС
-
Теперь постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС.
Запись на доске:
AF- биссектриса, ‹ CАF = ‹ FАB
BK - биссектриса, ‹ CBK = ‹ АBK
CS - биссектриса, ‹ АCS = ‹ BCS
О - точка пересечения биссектрис.
Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.
Постройте все три биссектрисы в вашем треугольнике.
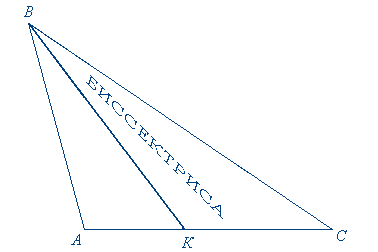
Сформулируйте свойство биссектрис треугольника. (В любом треугольнике биссектрисы пересекаются в одной точке).
Конечно, геометрия – наука серьёзная, и изучатьть её надо серьёзно и вдумчиво. Но и забавные стихи и весёлые “геометрические” зверята помогают учению.
В ысота похожа на кота,
ысота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.
(Стихи иллюстрируются весёлым рисунком).
Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас.
Биссектриса – это
крыса,
Которая бегает по углам
И делит угол пополам.
IV. Контроль усвоения учащимися нового материала.
-
Выполним тестовые задания ( показ слайдов)
1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.
а) Отрезок, соединяющий вершину треугольника с серединой ______________, называется ___________ треугольника.
(Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника).
б) Из точки, не лежащей на
прямой, можно провести перпендикуляр к этой прямой, и притом
_____________.
(Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом единственный).
2. Верны ли следующие утверждения?
а) В любом треугольнике
можно провести три медианы. (Да).
б) Точка пересечения высот любого треугольника
лежит внутри треугольника. (Не всегда).
в) Все биссектрисы треугольника пересекаются в одной точке.
(Да).
-
Работа в парах. На каждой парте лежат три треугольника, разносторонние, разных цветов. На одном из них изображены три медианы, на другом – высоты, на третьем – биссектрисы.
-
Покажите треугольник с изображением высот. ( красные).
-
Поднимите треугольник, на котором изображены медианы. ( жёлтые и оранжевые).
-
Покажите треугольник с изображением биссектрис. (Зелёные).
(Учащиеся поднимают треугольники).
-
С какими новыми геометрическими понятиями вы сегодня познакомились? (Медиана, биссектриса, высота).
-
Оказывается, не так и дружны между собой эти геометрические понятия. Послушаем их спор ( говорят дети)
|
Три девицы, три сестрицы |
Если циркулем владеешь,
В спор вмешался
треугольник: |
V. Подведение итога урока.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Урок геометрии в 7 классе на тему: Медиана, биссектриса и высота треугольника
Урок геометрии в 7 классе на тему: Медиана, биссектриса и высота треугольника
Урок геометрии в 8 классе
Тема: «Высота, биссектриса и медиана треугольника»
Учитель: Мейманова А.А.
Урок геометрии в 8 классе
Мейманова Айнагуль Амангельдовна - учитель математики и физики, дефектолог, КГУ Специальная (коррекционная) школа – интернат №1с ограниченными возможностями в развитии
г. Петропавловск
Тема: Медиана, биссектриса и высота треугольника.
Цель: ввести понятия высоты, медианы и биссектрисы треугольника, уметь их различать и строить.
Задачи:
-
Ввести новые понятия высоты, медианы и биссектрисы треугольника.
-
Способствовать формированию устойчивого познавательного интереса к изучению геометрии.
-
Развивать логическое мышление учащихся.
Тип урока: урок закрепления
Формы организации учебной деятельности: коллективная, индивидуальная
Оборудование и наглядность урока: модели треугольников , изготовленные из плотного цветного картона; презентация к уроку «Медиана, биссектриса и высота треугольника»; тесты
Ход урока
-
Организационный момент.
-
Сообщение темы урока .
Математику не зря называют царицей наук, ей больше, чем какой-либо другой науке свойственны красота, изящность и точность. Постараемся это доказать при построении медианы, биссектрисы и высоты. Знания не просто надо иметь, но и нужно уметь их показывать, что вы и сделаете на сегодняшнем уроке, а я в этом вам помогу.
Безусловно, центровой фигурой является треугольник. Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о геометрии треугольника как о самостоятельном разделе геометрии.
( слайд с показом предметов принимающих форму треугольника)
-
Итак, глядя на рисунок, какая геометрическая фигура изображена ? (Треугольник).
А что называется треугольником? (Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).
-
Сколько у него элементов? (6)
-
Назовите элементы треугольника. (Три стороны и три угла).
-
Как найти периметр треугольника?( величины всех сторон сложить)
-
Какие виды треугольника вы знаете? (прямоугольный, равнобедренный, равносторонний, остроугольный, тупоугольный) на доске выбрать под каким номером изображен тот или иной вид треугольника
-
Кто из вас слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? {Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто – Рико и полуостровом Флорида}.
-
А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.
III. Объяснение нового материала.
1. Медиана.
-
Начертите треугольник АВС и найдите середину стороны ВС – точку К.
-
Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).
-
Соедините точку К с вершиной А. Отрезок АК называется медианой треугольника.

Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника
-
Сколько медиан можно провести в треугольнике?(3).
-
“Проведите” три медианы в треугольнике.
-
Какое свойство медиан вы заметили? (В любом треугольнике все медианы пересекаются в одной точке).
-
Эта точка называется центром тяжести треугольника. Запишите в тетрадях:
АК – медиана, ВК = КС
ВТ– медиана, АТ = ТС
СР– медиана, АР = РВ
О – точка пересечения медиан
2. Высота.
-
Начертите треугольник АВС
-
С помощью чертёжного угольника из вершины В проведём перпендикуляр ВН к прямой АС. Он называется высотой треугольника.
Запись на доске: ВН АС, Н АС.

Определение. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.
-
Сколько высот имеет треугольник? (3).
-
“Постройте” все три высоты в треугольнике.
-
Обладают ли высоты аналогичным свойством, что и медианы? (Да).
-
А если треугольник тупоугольный, то как построить высоты? (Провести дополнительные полупрямые)
-
Как вы думаете, что является высотой в прямоугольном треугольнике? (катеты)
Физминутка
Поднимает руки класс-это раз
Повернулась голова-это два
Руки вниз, вперед смотри - это три
Руки в стороны пошире развернули на четыре
С силой их к плечам прижать - это пять
Всем ребятам тихо сесть - это шесть.
3. Биссектриса.
-
Вспомните определение биссектрисы угла.
Определение. Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
-
Постройте еще один треугольник АВС
-
Теперь постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС.
Запись на доске:
AF- биссектриса, ‹ CАF = ‹ FАB
BK - биссектриса, ‹ CBK = ‹ АBK
CS - биссектриса, ‹ АCS = ‹ BCS
О - точка пересечения биссектрис.
Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.
Постройте все три биссектрисы в вашем треугольнике.

Сформулируйте свойство биссектрис треугольника. (В любом треугольнике биссектрисы пересекаются в одной точке).
Конечно, геометрия – наука серьёзная, и изучатьть её надо серьёзно и вдумчиво. Но и забавные стихи и весёлые “геометрические” зверята помогают учению.
В ысота похожа на кота,
ысота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.
(Стихи иллюстрируются весёлым рисунком).
Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас.


Биссектриса – это
крыса,
Которая бегает по углам
И делит угол пополам.
IV. Контроль усвоения учащимися нового материала.
-
Выполним тестовые задания ( показ слайдов)
1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.
а) Отрезок, соединяющий вершину треугольника с серединой ______________, называется ___________ треугольника.
(Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника).
б) Из точки, не лежащей на
прямой, можно провести перпендикуляр к этой прямой, и притом
_____________.
(Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом единственный).
2. Верны ли следующие утверждения?
а) В любом треугольнике
можно провести три медианы. (Да).
б) Точка пересечения высот любого треугольника
лежит внутри треугольника. (Не всегда).
в) Все биссектрисы треугольника пересекаются в одной точке.
(Да).
-
Работа в парах. На каждой парте лежат три треугольника, разносторонние, разных цветов. На одном из них изображены три медианы, на другом – высоты, на третьем – биссектрисы.
-
Покажите треугольник с изображением высот. ( красные).
-
Поднимите треугольник, на котором изображены медианы. ( жёлтые и оранжевые).
-
Покажите треугольник с изображением биссектрис. (Зелёные).
(Учащиеся поднимают треугольники).
-
С какими новыми геометрическими понятиями вы сегодня познакомились? (Медиана, биссектриса, высота).
-
Оказывается, не так и дружны между собой эти геометрические понятия. Послушаем их спор ( говорят дети)
|
Три девицы, три сестрицы |
Если циркулем владеешь,
В спор вмешался
треугольник: |
V. Подведение итога урока.

шағым қалдыра аласыз
















