
Значение математики в медицине
Жексенова Назира Кенжебаевна
Преподаватель математики, Высший медицинский колледж “Даналық” им. З.Г.Мурзагуловой,
г.Астана
Аннотация
В данной работе рассматривается роль и значение математических методов в современной медицине. Исследование направлено на анализ того, каким образом математические модели способствуют повышению точности диагностики, эффективности лечения и качеству медицинских исследований. В теоретической части приведён обзор основных направлений применения математики в медицине, включая математическое моделирование биологических процессов и использование вычислительных методов.
Практическая часть включает два примера. Первый — анализ однокамерной фармакокинетической модели амоксициллина, в рамках которого рассчитаны основные параметры (период полувыведения, клиренс и т.д.) и продемонстрирована возможность предсказания поведения препарата в организме. Второй пример — применение модели SIR для анализа распространения инфекционных заболеваний, что позволяет прогнозировать динамику эпидемии, определять меры по её сдерживанию и планировать вакцинацию. Работа подчёркивает практическую значимость математического подхода в клинической практике и здравоохранении в целом.
Полученные результаты подтверждают гипотезу о высокой эффективности использования математических методов в медицине и подчёркивают необходимость дальнейшего развития междисциплинарных исследований на стыке математики и медицинских наук.
Ключевые слова
Математическое моделирование, фармакокинетика, SIR-модель, медицина, диагностика, эпидемия, клиренс.
Введение
Актуальность темы
Современная медицина стремительно развивается благодаря внедрению инновационных технологий и научных подходов, среди которых особое место занимает математика. Математические методы позволяют глубже понять сложные физиологические процессы, строить прогнозы распространения заболеваний, оптимизировать схемы лечения и разрабатывать персонализированные подходы к терапии. В эпоху цифровизации здравоохранения, появления биоинформатики, больших данных и машинного обучения, значимость точных расчетов и математического моделирования становится как никогда важной. Особенно актуальной данная тема стала в условиях глобальных вызовов, таких как пандемии, при которых математические модели служат основой для принятия решений на государственном уровне. Эти обстоятельства обуславливают возрастающий интерес исследователей к роли математики в медицине, что отражается в многочисленных научных работах. В мировой научной литературе накоплен обширный материал, посвящённый применению математики в медицине. Так, Х. Хеткот и его коллеги разработали математические модели эпидемий, включая классическую модель SIR. Многочисленные исследования в области фармакокинетики опираются на дифференциальные уравнения для описания динамики лекарственных веществ в организме. Кроме того, активно развиваются математические подходы к анализу изображений, моделированию биологических тканей, прогнозированию исходов лечения и оценке рисков. Однако интеграция математических методов в повседневную клиническую практику нередко осуществляется фрагментарно, что требует разработки единой междисциплинарной стратегии внедрения.
Цель исследования
Целью данной работы является определение роли и значения математических методов в медицинских исследованиях и практике, а также изучение того, каким образом математические инструменты способствуют развитию здравоохранения.
Гипотеза
Предполагается, что использование математических методов в медицине существенно повышает точность диагностики, эффективность лечения и качество медицинских исследований.
Задачи исследования
-
Изучить основные области применения математики в медицине;
-
Рассмотреть конкретные примеры математического моделирования в диагностике и терапии;
-
Оценить влияние математических методов на качество медицинской помощи.
Объект и предмет исследования
Объект исследования — математические методы и модели, применяемые в различных областях медицины. Предмет исследования — особенности использования математических инструментов для диагностики, лечения и анализа медицинских процессов.
Методы исследования
В ходе работы использовались аналитический обзор научной литературы, сравнительный анализ математических моделей, а также компьютерные программы для имитационного моделирования процессов, происходящих в организме человека или в системе здравоохранения.
Практическая значимость
Результаты данного исследования могут быть полезны врачам, медицинским исследователям, преподавателям и студентам, стремящимся применять математические методы в клинической практике и научной работе. Эффективное использование математического аппарата способствует не только повышению качества диагностики и лечения, но и развитию профилактических стратегий, улучшению управления ресурсами здравоохранения и ускорению научного прогресса.
1 Глава. Теоретическая часть
1.1 История развития применения математики в медицине
Математика является неотъемлемой частью медицины, обеспечивая необходимую точность и основу для практических вычислений в работе каждого врача. Врач должен владеть базовыми математическими навыками, такими как работа с процентами, анализ статистических данных, чтение и построение графиков, использование пропорций, умение обращаться с различными единицами измерения, а также умение выполнять точные расчеты по формулам. Именно благодаря математике медицина приобретает необходимую точность, без которой невозможен успешный лечебный процесс.
Исторически взаимосвязь математики и медицины насчитывает несколько тысяч лет. В Древнем Египте применялись точные дозировки лекарственных средств, разработанные для различных заболеваний. Врач из Индии Сушрута первым заметил связь между распространением малярии и комарами, а также между чумой и грызунами, что можно рассматривать как ранние проявления статистического и логического анализа.
В средневековье арабский ученый Аль-Кинди в своём труде «De Gradibus» внедрил измерительные методы в медицину, что способствовало развитию более точного подхода к лечению. В XI веке Ибн аль-Хайсам завершил работу над книгой по оптике, которая стала важным вкладом в офтальмологию и хирургическую практику, опираясь на точные математические расчеты и формулы.
В эпоху Возрождения, в XV веке, появились первые очки с вогнутыми линзами для коррекции близорукости, что тоже основывалось на точных вычислениях оптических параметров. Леонардо да Винчи создал знаменитый рисунок «Витрувианский человек», отражающий идеальные пропорции человеческого тела, а в начале XIX века Филипп Боццини изобрёл первый эндоскоп, использующий принципы симметрии и точности.
В середине XIX века (1842 год) Кроуфорд Лонг провёл первую операцию под анестезией эфиром, что требовало правильных пропорций и расчетов дозы. В 1895 году Вильгельм Рентген открыл рентгеновское излучение и его использование для медицинской диагностики, что стало возможным благодаря применению математической системы координат. В XX веке Ганс Бергер разработал метод электроэнцефалографии, основывающийся на анализе графиков биоэлектрической активности мозга.
Дальнейшее развитие медицинской техники сопровождалось созданием портативных дефибрилляторов (Фрэнк Пантридж, 1965 год), магнитно-резонансных томографов (Реймонд Дамадьян, 1980 год), а также имплантацией автономных искусственных сердец (2001 год), где точные математические расчеты и системы координат играют ключевую роль.
В биологических науках математические методы долгое время использовались ограниченно, поскольку биологические объекты и процессы характеризуются высокой сложностью и вариабельностью. Тем не менее, начиная с конца XIX века, ученые, такие как Фрэнсис Гальтон и Карл Пирсон, заложили основы математической статистики, которая стала незаменимым инструментом для анализа биомедицинских данных.
С 1940-х годов математика активно интегрируется в биомедицину через развитие кибернетики и информатики. Сегодня математические методы широко применяются в биофизике, биохимии, генетике, физиологии, а также в разработке медицинских приборов и биотехнических систем, что свидетельствует о постоянном расширении роли математики в медицине.
1.2 Роль математики в современной медицине
Математика занимает ключевое место в современной медицине, обеспечивая точность расчетов, достоверность диагностических данных и объективность в принятии клинических решений. Медицинская практика невозможна без базовых и прикладных математических знаний, которые охватывают работу с пропорциями, анализом статистических данных, измерениями, графическим представлением информации и расчетами по формулам. Каждому врачу, вне зависимости от его специализации, необходимо уверенно владеть математическим аппаратом, так как даже простая ошибка в расчётах может повлиять на здоровье пациента.
Связь математики и медицины существует на протяжении тысячелетий. Уже в Древнем Египте целители использовали определенные дозировки лекарств, подбирая их с учётом массы тела и тяжести заболевания. В средние века арабские и индийские учёные начали применять логические и количественные методы для диагностики и лечения. Например, индийский врач Сушрута установил связь между насекомыми и распространением заболеваний, что по сути стало прообразом эпидемиологического моделирования.
С течением времени медицинская наука всё больше полагалась на математический аппарат. Появление оптических приборов, анатомических измерений, эндоскопов, рентгеновского излучения, ультразвуковой и томографической диагностики стало возможным благодаря развитию геометрии, алгебры, математической физики и систем координат. Симметрия, пропорции, точные расчёты – всё это сделало возможным создание точных медицинских инструментов и технологий.
Сестринское дело также требует математической грамотности. Медицинским сёстрам необходимо уметь рассчитывать дозировки лекарств, знать правила перевода единиц измерения, находить цену деления шкалы шприца, точно соблюдать пропорции при приготовлении растворов и анальгетиков. Ошибка в пропорции может привести к неправильной дозе, что особенно критично при работе с детьми и пожилыми пациентами.
Фармакология полностью опирается на точные математические вычисления. Расчёт дозировки активного вещества, подбор пропорций химических компонентов и прогнозирование воздействия препарата на организм невозможны без формул, уравнений и моделей. Особенно важна математика при разработке новых лекарственных средств и клинических испытаниях, где применяются методы биостатистики и вероятностного анализа.
Педиатрия активно использует математическую статистику, поскольку новорождённые и маленькие дети не могут описать своё самочувствие. Диагностические данные интерпретируются через усреднённые значения, такие как среднее арифметическое, мода и медиана, позволяя врачам выявить отклонения от нормы и начать лечение.
Ортопедия использует геометрию и симметрию тела для выявления нарушений осанки и заболеваний опорно-двигательного аппарата. Диагностика сколиоза, плоскостопия или разницы в длине конечностей невозможна без измерений и расчётов.
Кардиология активно использует математические методы при расшифровке электрокардиограмм (ЭКГ), где сигнал сердца отображается в виде графиков, основанных на функциях типа y=sinx и y=cosx. Электроды фиксируют биоэлектрическую активность сердца, преобразуя её в графическую форму, анализ которой требует знания амплитуд, частот и интервалов – базовых математических понятий.
Вирусология и эпидемиология полагаются на математические модели распространения инфекций, включая геометрические прогрессии, статистические расчеты, теорию вероятностей. Знание скорости размножения вируса и коэффициента заражения позволяет прогнозировать эпидемии и разрабатывать стратегии сдерживания.
Гастроэнтерология использует современные методы диагностики – эндоскопию, томографию, ультразвук – для визуализации органов пищеварительной системы. Эти методы основаны на принципах проецирования и координатной системы (оси X, Y, Z), что позволяет точно определить размеры и структуру внутренних органов.
Даже общий анализ крови невозможен без применения математики: доли лейкоцитов, гемоглобина, эритроцитов выражаются в процентах, а сами анализаторы используют алгоритмы для обработки биохимических параметров. Таким образом, математика в медицине не ограничивается только вычислениями. Она пронизывает все этапы – от диагностики до лечения, от разработки лекарств до хирургии. Современная медицина невозможна без количественных методов, а математическая подготовка становится неотъемлемой частью профессиональной компетенции медицинского работника.
2 Глава. Практическая часть
2.1. Анализ фармакокинетической модели препарата
В рамках практической части исследования был проведён анализ фармакокинетической модели препарата амоксициллин, который широко используется в медицинской терапии. Как отмечают Gabrielsson и Weiner [1] , такая модель особенно полезна для описания препаратов с быстрым распределением в организме, к которым относится амоксициллин. Целью анализа было определить, как математические модели позволяют предсказать поведение лекарственного средства в организме пациента, включая его всасывание, распределение, метаболизм и выведение (ADME). Амоксициллин – это широко применяемый β-лактамный антибиотик, назначаемый при различных бактериальных инфекциях. Для оптимизации его дозирования особенно важно учитывать фармакокинетические характеристики, которые могут быть точно описаны с помощью математических моделей.
В данном анализе используется классическая однокамерная модель с внутривенным болюсным введением, при которой препарат мгновенно поступает в центральный компартмент (кровоток). Концентрация препарата в крови при этом описывается экспоненциальным уравнением, что соответствует модели первого порядка выведения, часто применяемой для простых случаев, когда препарат быстро распределяется по организму, а его выведение можно аппроксимировать экспоненциальным убыванием.
Модель описывается следующим дифференциальным уравнением:

-
 – концентрация в крови в момент
времениt,
– концентрация в крови в момент
времениt, -
 – начальная концентрация,
– начальная концентрация, -
 – константа скорости
выведения.
– константа скорости
выведения.
Этот подход, подробно рассмотренный в работе Gibaldi и Perrier [2], позволяет прогнозировать концентрацию лекарственного вещества в плазме крови после однократного введения. Для анализа были использованы следующие реальные параметры, характерные для амоксициллина у взрослых:
|
Параметр |
Значение |
|
Доза препарата |
1000 мг |
|
Объем распределения |
18 л |
|
Константа выведения |
0.3466 |
|
Начальная концентрация |
55.56 мг/л (1000 мг / 18 л) |
Расчёт основных фармакокинетических показателей
-
Период полувыведения

-
Клиренс

Примерные значения концентрации в первые часы после введения:
|
Время (ч) |
Концентрация мг/л |
|
0.00 |
55.56 |
|
0.12 |
53.27 |
|
0.24 |
51.08 |
|
0.36 |
48.98 |
|
0.48 |
46.96 |
|
0.61 |
45.03 |
|
0.73 |
43.18 |
|
0.85 |
41.40 |
|
0.97 |
39.70 |
|
1.09 |
38.06 |
На графике ниже показана динамика снижения концентрации амоксициллина в крови:
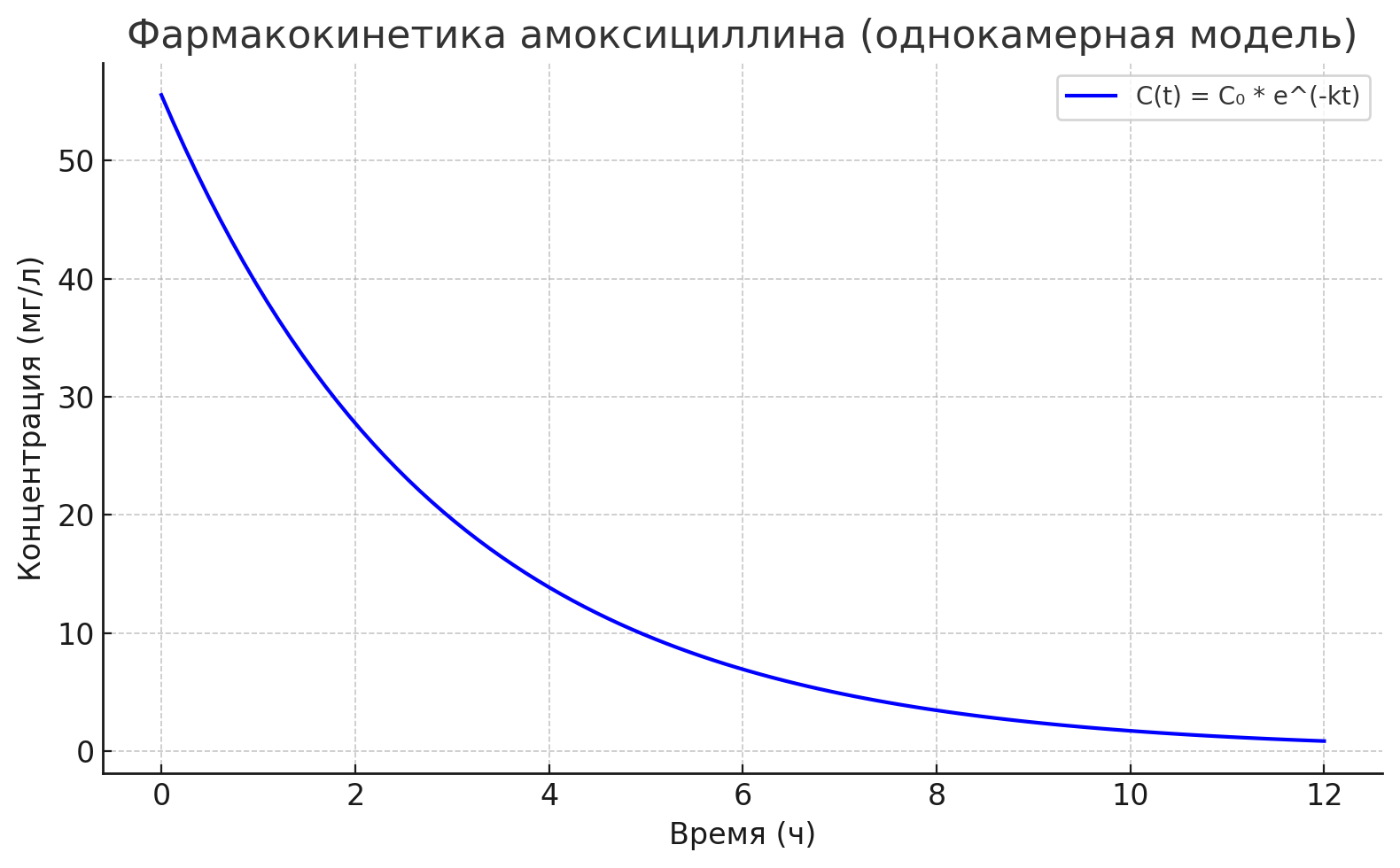
Рис.1 Динамика снижения концентрации амоксициллина в крови
Полученные данные позволяют прогнозировать эффективность и безопасность терапии. Период полувыведения амоксициллина составляет 2 часа, что, согласно исследованиям Craig [3], требует введения препарата каждые 6-8 часов для поддержания терапевтической концентрации (5-25 мг/л). Особое значение имеет расчет клиренса (6.24 л/ч), который, как отмечает Wagner [4], соответствует показателям пациентов с нормальной функцией почек. При почечной недостаточности данный параметр требует коррекции дозировки, поскольку, как демонстрируют Andes и соавт. [5], выведение амоксициллина происходит преимущественно почками. Эти выводы подтверждаются результатами наших расчетов (рис. 1).
2.2. Математические модели распространения инфекционных заболеваний: значение для диагностики, прогноза и здравоохранения
Инфекционные заболевания остаются одной из главных угроз общественному здоровью, особенно в условиях глобализации, урбанизации и изменяющегося климата. Прогнозирование и управление эпидемиями требуют точных и обоснованных решений, что делает математическое моделирование незаменимым инструментом современной эпидемиологии. Одним из наиболее известных подходов является модель SIR, которая позволяет описывать динамику инфекционного процесса и оценивать влияние различных интервенций, включая вакцинацию, карантинные меры и ограничение контактов [6].
Теоретическая основа: модель SIR
Модель SIR (susceptible-infected-recovered) делит популяцию на три группы:
-
S(t) — восприимчивые к заболеванию;
-
I(t) — инфицированные;
-
R(t) — выздоровевшие или погибшие.
Система дифференциальных уравнений имеет следующий вид:
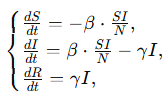
где,
-
 – коэффициент заражения (передачи
инфекции),
– коэффициент заражения (передачи
инфекции), -
 – коэффициент выздоровления (обратная величина
средней продолжительности болезни),
– коэффициент выздоровления (обратная величина
средней продолжительности болезни), -
N=S+I+R – общее население.
Ключевым параметром является базовое репродуктивное число:
 , которое отражает среднее число лиц, которых
заражает один инфицированный в полностью восприимчивой популяции.
Если
, которое отражает среднее число лиц, которых
заражает один инфицированный в полностью восприимчивой популяции.
Если  , эпидемия распространяется,
если
, эпидемия распространяется,
если  – затухает [7].
– затухает [7].
Для наглядной демонстрации важности математического подхода рассмотрим гипотетическую популяцию численностью 1 миллион человек. Пусть:
-
Начальное число инфицированных:I(0)=1,
-
β=0.3
 =0.1 (соответствует средней
продолжительности болезни 10 дней).
=0.1 (соответствует средней
продолжительности болезни 10 дней).
Рассчитаем:

Это означает, что каждый заражённый человек в среднем инфицирует трёх других, что потенциально приводит к экспоненциальному росту числа случаев заболевания.
Результаты численного моделирования с помощью метода Эйлера представлены на графике:
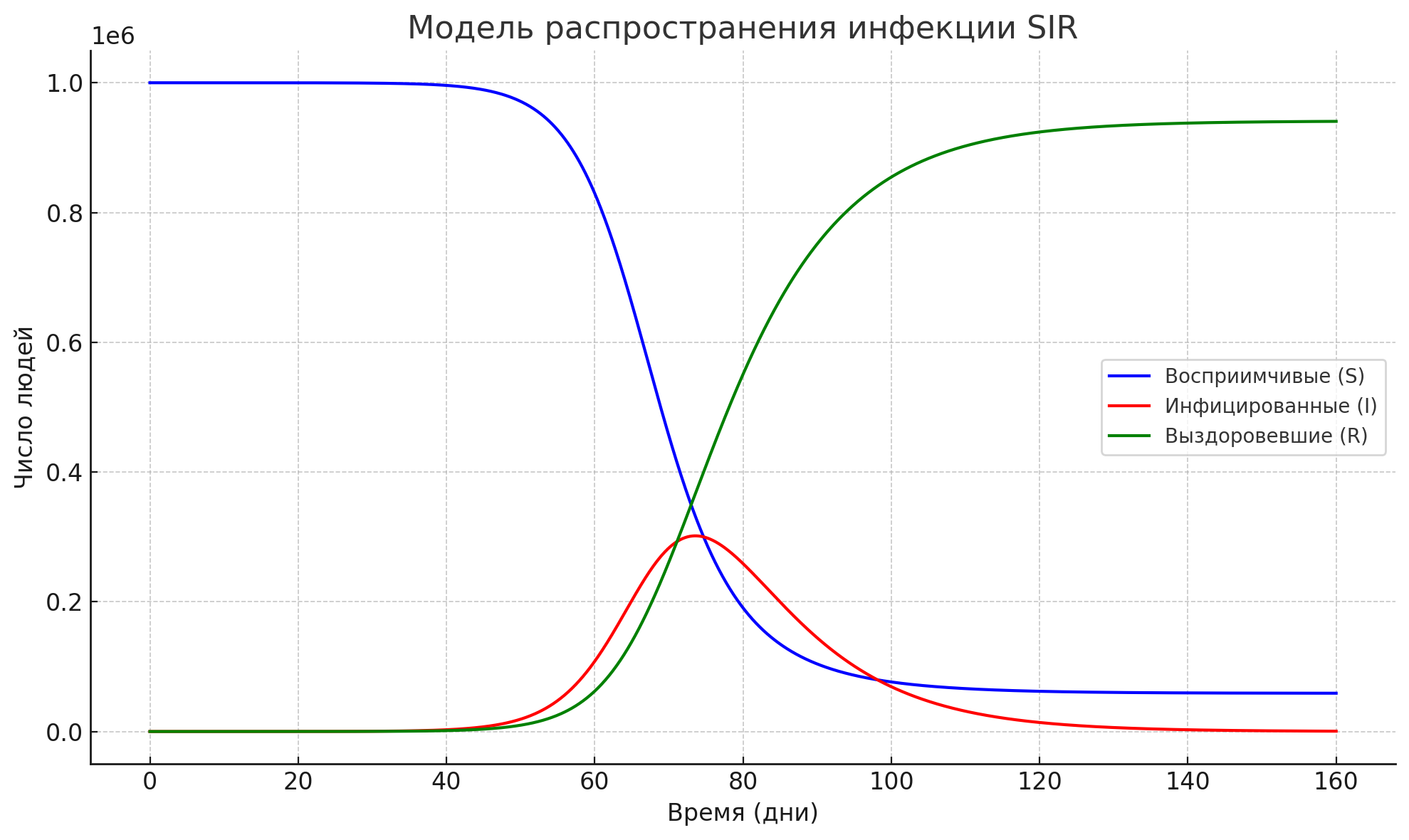
График демонстрирует типичную форму эпидемической кривой: быстрое увеличение числа инфицированных, последующий пик и спад с одновременным ростом количества выздоровевших.
Практическое значение модели
Модель SIR и её расширения (SEIR, SIRD, модели с вакцинацией) используются в реальных сценариях здравоохранения:
-
Прогнозирование эпидемий.
В период пандемии COVID-19 модели позволяли оценить сроки достижения пика заболеваемости и потребность в госпитальных койках [6]. -
Оценка коллективного иммунитета.
Для прекращения эпидемии необходимо вакцинировать:
 населения,
населения,
что
является ключевым критерием при планировании вакцинационных
кампаний [7].
Использование моделей позволяет спрогнозировать пиковую нагрузку на
систему здравоохранения (ИВЛ, койки, персонал) [8]. Применение
математических моделей, таких как SIR, представляет собой яркий
пример интеграции математики в медицину. Эти модели не только
позволяют глубже понять поведение инфекционных заболеваний, но и
служат основой для принятия критически важных решений в
здравоохранении. Современная медицина немыслима без математического
анализа, особенно в условиях глобальных эпидемических
угроз.
Заключение
В ходе проведенного исследования была подтверждена высокая значимость математических методов в современной медицине. Анализ научной литературы и практических примеров показал, что применение математического моделирования, статистических анализов и вычислительных алгоритмов позволяет врачам и исследователям глубже понимать физиологические процессы, прогнозировать развитие заболеваний и разрабатывать более эффективные методы диагностики и лечения.
Была доказана справедливость выдвинутой гипотезы: интеграция математических инструментов в медицинскую практику действительно способствует повышению точности диагностики, оптимизации лечебных процедур и улучшению результатов медицинских исследований. Особенно актуально использование таких методов в области эпидемиологии, фармакологии, биомеханики и медицинской визуализации.
Поставленные задачи были выполнены: изучены основные области применения математики в медицине, рассмотрены конкретные примеры моделей и алгоритмов, оценено их влияние на качество и эффективность медицинской помощи.
Таким образом, можно сделать вывод, что дальнейшее развитие междисциплинарных исследований на стыке математики и медицины является важным шагом на пути к созданию интеллектуальных систем здравоохранения, персонализированного лечения и научно обоснованного управления медицинскими ресурсами.
Практическая значимость работы заключается в том, что полученные результаты могут быть использованы в образовательной и научной деятельности, а также служить основой для разработки новых подходов в медицинской практике, где математические методы будут играть ключевую роль.
Литература
[1]. Габриэльссон Я., Вайнер Д. Анализ фармакокинетических и фармакодинамических данных: концепции и приложения. 5-е изд. Швеция: Swedish Pharmaceutical Press; 2016. 1168 с. (In English)
[2]. Гибалди М., Перье Д. Фармакокинетика. 2-е изд. Нью-Йорк: Marcel Dekker; 1982. 494 с. (In English)
[3]. Крейг У.А. Фармакокинетические/фармакодинамические параметры: обоснование дозирования антибактериальных препаратов у животных и людей // Clinical Infectious Diseases. 1998. Т. 26, № 1. С. 1-12. (In English)
[4]. Вагнер Дж.Г. Основы клинической фармакокинетики. Гамильтон: Drug Intelligence Publications; 1993. 331 с. (In English)
[5]. Андес Д., Крейг У.А. Фармакокинетика и фармакодинамика антибиотиков у животных и людей // Clinical Microbiology and Infection. 2002. Т. 8, № 2. С. 79-86. (In English)
[6]. Хеткоут Х.У. Математика инфекционных заболеваний // SIAM Review. 2000. Т. 42, № 4. С. 599-653. (In English)
[7]. Андерсон Р.М., Мэй Р.М. Инфекционные болезни человека: динамика и контроль. Оксфорд: Oxford University Press; 1992. 757 с.
[8]. Фергюсон Н.М. [и др.] Влияние нефармацевтических вмешательств (NPI) на снижение смертности от COVID-19 и нагрузку на систему здравоохранения: Отчет группы реагирования Имперского колледжа. 2020. 20 с.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
Значение математики в медицине
Значение математики в медицине
Значение математики в медицине
Жексенова Назира Кенжебаевна
Преподаватель математики, Высший медицинский колледж “Даналық” им. З.Г.Мурзагуловой,
г.Астана
Аннотация
В данной работе рассматривается роль и значение математических методов в современной медицине. Исследование направлено на анализ того, каким образом математические модели способствуют повышению точности диагностики, эффективности лечения и качеству медицинских исследований. В теоретической части приведён обзор основных направлений применения математики в медицине, включая математическое моделирование биологических процессов и использование вычислительных методов.
Практическая часть включает два примера. Первый — анализ однокамерной фармакокинетической модели амоксициллина, в рамках которого рассчитаны основные параметры (период полувыведения, клиренс и т.д.) и продемонстрирована возможность предсказания поведения препарата в организме. Второй пример — применение модели SIR для анализа распространения инфекционных заболеваний, что позволяет прогнозировать динамику эпидемии, определять меры по её сдерживанию и планировать вакцинацию. Работа подчёркивает практическую значимость математического подхода в клинической практике и здравоохранении в целом.
Полученные результаты подтверждают гипотезу о высокой эффективности использования математических методов в медицине и подчёркивают необходимость дальнейшего развития междисциплинарных исследований на стыке математики и медицинских наук.
Ключевые слова
Математическое моделирование, фармакокинетика, SIR-модель, медицина, диагностика, эпидемия, клиренс.
Введение
Актуальность темы
Современная медицина стремительно развивается благодаря внедрению инновационных технологий и научных подходов, среди которых особое место занимает математика. Математические методы позволяют глубже понять сложные физиологические процессы, строить прогнозы распространения заболеваний, оптимизировать схемы лечения и разрабатывать персонализированные подходы к терапии. В эпоху цифровизации здравоохранения, появления биоинформатики, больших данных и машинного обучения, значимость точных расчетов и математического моделирования становится как никогда важной. Особенно актуальной данная тема стала в условиях глобальных вызовов, таких как пандемии, при которых математические модели служат основой для принятия решений на государственном уровне. Эти обстоятельства обуславливают возрастающий интерес исследователей к роли математики в медицине, что отражается в многочисленных научных работах. В мировой научной литературе накоплен обширный материал, посвящённый применению математики в медицине. Так, Х. Хеткот и его коллеги разработали математические модели эпидемий, включая классическую модель SIR. Многочисленные исследования в области фармакокинетики опираются на дифференциальные уравнения для описания динамики лекарственных веществ в организме. Кроме того, активно развиваются математические подходы к анализу изображений, моделированию биологических тканей, прогнозированию исходов лечения и оценке рисков. Однако интеграция математических методов в повседневную клиническую практику нередко осуществляется фрагментарно, что требует разработки единой междисциплинарной стратегии внедрения.
Цель исследования
Целью данной работы является определение роли и значения математических методов в медицинских исследованиях и практике, а также изучение того, каким образом математические инструменты способствуют развитию здравоохранения.
Гипотеза
Предполагается, что использование математических методов в медицине существенно повышает точность диагностики, эффективность лечения и качество медицинских исследований.
Задачи исследования
-
Изучить основные области применения математики в медицине;
-
Рассмотреть конкретные примеры математического моделирования в диагностике и терапии;
-
Оценить влияние математических методов на качество медицинской помощи.
Объект и предмет исследования
Объект исследования — математические методы и модели, применяемые в различных областях медицины. Предмет исследования — особенности использования математических инструментов для диагностики, лечения и анализа медицинских процессов.
Методы исследования
В ходе работы использовались аналитический обзор научной литературы, сравнительный анализ математических моделей, а также компьютерные программы для имитационного моделирования процессов, происходящих в организме человека или в системе здравоохранения.
Практическая значимость
Результаты данного исследования могут быть полезны врачам, медицинским исследователям, преподавателям и студентам, стремящимся применять математические методы в клинической практике и научной работе. Эффективное использование математического аппарата способствует не только повышению качества диагностики и лечения, но и развитию профилактических стратегий, улучшению управления ресурсами здравоохранения и ускорению научного прогресса.
1 Глава. Теоретическая часть
1.1 История развития применения математики в медицине
Математика является неотъемлемой частью медицины, обеспечивая необходимую точность и основу для практических вычислений в работе каждого врача. Врач должен владеть базовыми математическими навыками, такими как работа с процентами, анализ статистических данных, чтение и построение графиков, использование пропорций, умение обращаться с различными единицами измерения, а также умение выполнять точные расчеты по формулам. Именно благодаря математике медицина приобретает необходимую точность, без которой невозможен успешный лечебный процесс.
Исторически взаимосвязь математики и медицины насчитывает несколько тысяч лет. В Древнем Египте применялись точные дозировки лекарственных средств, разработанные для различных заболеваний. Врач из Индии Сушрута первым заметил связь между распространением малярии и комарами, а также между чумой и грызунами, что можно рассматривать как ранние проявления статистического и логического анализа.
В средневековье арабский ученый Аль-Кинди в своём труде «De Gradibus» внедрил измерительные методы в медицину, что способствовало развитию более точного подхода к лечению. В XI веке Ибн аль-Хайсам завершил работу над книгой по оптике, которая стала важным вкладом в офтальмологию и хирургическую практику, опираясь на точные математические расчеты и формулы.
В эпоху Возрождения, в XV веке, появились первые очки с вогнутыми линзами для коррекции близорукости, что тоже основывалось на точных вычислениях оптических параметров. Леонардо да Винчи создал знаменитый рисунок «Витрувианский человек», отражающий идеальные пропорции человеческого тела, а в начале XIX века Филипп Боццини изобрёл первый эндоскоп, использующий принципы симметрии и точности.
В середине XIX века (1842 год) Кроуфорд Лонг провёл первую операцию под анестезией эфиром, что требовало правильных пропорций и расчетов дозы. В 1895 году Вильгельм Рентген открыл рентгеновское излучение и его использование для медицинской диагностики, что стало возможным благодаря применению математической системы координат. В XX веке Ганс Бергер разработал метод электроэнцефалографии, основывающийся на анализе графиков биоэлектрической активности мозга.
Дальнейшее развитие медицинской техники сопровождалось созданием портативных дефибрилляторов (Фрэнк Пантридж, 1965 год), магнитно-резонансных томографов (Реймонд Дамадьян, 1980 год), а также имплантацией автономных искусственных сердец (2001 год), где точные математические расчеты и системы координат играют ключевую роль.
В биологических науках математические методы долгое время использовались ограниченно, поскольку биологические объекты и процессы характеризуются высокой сложностью и вариабельностью. Тем не менее, начиная с конца XIX века, ученые, такие как Фрэнсис Гальтон и Карл Пирсон, заложили основы математической статистики, которая стала незаменимым инструментом для анализа биомедицинских данных.
С 1940-х годов математика активно интегрируется в биомедицину через развитие кибернетики и информатики. Сегодня математические методы широко применяются в биофизике, биохимии, генетике, физиологии, а также в разработке медицинских приборов и биотехнических систем, что свидетельствует о постоянном расширении роли математики в медицине.
1.2 Роль математики в современной медицине
Математика занимает ключевое место в современной медицине, обеспечивая точность расчетов, достоверность диагностических данных и объективность в принятии клинических решений. Медицинская практика невозможна без базовых и прикладных математических знаний, которые охватывают работу с пропорциями, анализом статистических данных, измерениями, графическим представлением информации и расчетами по формулам. Каждому врачу, вне зависимости от его специализации, необходимо уверенно владеть математическим аппаратом, так как даже простая ошибка в расчётах может повлиять на здоровье пациента.
Связь математики и медицины существует на протяжении тысячелетий. Уже в Древнем Египте целители использовали определенные дозировки лекарств, подбирая их с учётом массы тела и тяжести заболевания. В средние века арабские и индийские учёные начали применять логические и количественные методы для диагностики и лечения. Например, индийский врач Сушрута установил связь между насекомыми и распространением заболеваний, что по сути стало прообразом эпидемиологического моделирования.
С течением времени медицинская наука всё больше полагалась на математический аппарат. Появление оптических приборов, анатомических измерений, эндоскопов, рентгеновского излучения, ультразвуковой и томографической диагностики стало возможным благодаря развитию геометрии, алгебры, математической физики и систем координат. Симметрия, пропорции, точные расчёты – всё это сделало возможным создание точных медицинских инструментов и технологий.
Сестринское дело также требует математической грамотности. Медицинским сёстрам необходимо уметь рассчитывать дозировки лекарств, знать правила перевода единиц измерения, находить цену деления шкалы шприца, точно соблюдать пропорции при приготовлении растворов и анальгетиков. Ошибка в пропорции может привести к неправильной дозе, что особенно критично при работе с детьми и пожилыми пациентами.
Фармакология полностью опирается на точные математические вычисления. Расчёт дозировки активного вещества, подбор пропорций химических компонентов и прогнозирование воздействия препарата на организм невозможны без формул, уравнений и моделей. Особенно важна математика при разработке новых лекарственных средств и клинических испытаниях, где применяются методы биостатистики и вероятностного анализа.
Педиатрия активно использует математическую статистику, поскольку новорождённые и маленькие дети не могут описать своё самочувствие. Диагностические данные интерпретируются через усреднённые значения, такие как среднее арифметическое, мода и медиана, позволяя врачам выявить отклонения от нормы и начать лечение.
Ортопедия использует геометрию и симметрию тела для выявления нарушений осанки и заболеваний опорно-двигательного аппарата. Диагностика сколиоза, плоскостопия или разницы в длине конечностей невозможна без измерений и расчётов.
Кардиология активно использует математические методы при расшифровке электрокардиограмм (ЭКГ), где сигнал сердца отображается в виде графиков, основанных на функциях типа y=sinx и y=cosx. Электроды фиксируют биоэлектрическую активность сердца, преобразуя её в графическую форму, анализ которой требует знания амплитуд, частот и интервалов – базовых математических понятий.
Вирусология и эпидемиология полагаются на математические модели распространения инфекций, включая геометрические прогрессии, статистические расчеты, теорию вероятностей. Знание скорости размножения вируса и коэффициента заражения позволяет прогнозировать эпидемии и разрабатывать стратегии сдерживания.
Гастроэнтерология использует современные методы диагностики – эндоскопию, томографию, ультразвук – для визуализации органов пищеварительной системы. Эти методы основаны на принципах проецирования и координатной системы (оси X, Y, Z), что позволяет точно определить размеры и структуру внутренних органов.
Даже общий анализ крови невозможен без применения математики: доли лейкоцитов, гемоглобина, эритроцитов выражаются в процентах, а сами анализаторы используют алгоритмы для обработки биохимических параметров. Таким образом, математика в медицине не ограничивается только вычислениями. Она пронизывает все этапы – от диагностики до лечения, от разработки лекарств до хирургии. Современная медицина невозможна без количественных методов, а математическая подготовка становится неотъемлемой частью профессиональной компетенции медицинского работника.
2 Глава. Практическая часть
2.1. Анализ фармакокинетической модели препарата
В рамках практической части исследования был проведён анализ фармакокинетической модели препарата амоксициллин, который широко используется в медицинской терапии. Как отмечают Gabrielsson и Weiner [1] , такая модель особенно полезна для описания препаратов с быстрым распределением в организме, к которым относится амоксициллин. Целью анализа было определить, как математические модели позволяют предсказать поведение лекарственного средства в организме пациента, включая его всасывание, распределение, метаболизм и выведение (ADME). Амоксициллин – это широко применяемый β-лактамный антибиотик, назначаемый при различных бактериальных инфекциях. Для оптимизации его дозирования особенно важно учитывать фармакокинетические характеристики, которые могут быть точно описаны с помощью математических моделей.
В данном анализе используется классическая однокамерная модель с внутривенным болюсным введением, при которой препарат мгновенно поступает в центральный компартмент (кровоток). Концентрация препарата в крови при этом описывается экспоненциальным уравнением, что соответствует модели первого порядка выведения, часто применяемой для простых случаев, когда препарат быстро распределяется по организму, а его выведение можно аппроксимировать экспоненциальным убыванием.
Модель описывается следующим дифференциальным уравнением:

-
 – концентрация в крови в момент
времениt,
– концентрация в крови в момент
времениt, -
 – начальная концентрация,
– начальная концентрация, -
 – константа скорости
выведения.
– константа скорости
выведения.
Этот подход, подробно рассмотренный в работе Gibaldi и Perrier [2], позволяет прогнозировать концентрацию лекарственного вещества в плазме крови после однократного введения. Для анализа были использованы следующие реальные параметры, характерные для амоксициллина у взрослых:
|
Параметр |
Значение |
|
Доза препарата |
1000 мг |
|
Объем распределения |
18 л |
|
Константа выведения |
0.3466 |
|
Начальная концентрация |
55.56 мг/л (1000 мг / 18 л) |
Расчёт основных фармакокинетических показателей
-
Период полувыведения

-
Клиренс

Примерные значения концентрации в первые часы после введения:
|
Время (ч) |
Концентрация мг/л |
|
0.00 |
55.56 |
|
0.12 |
53.27 |
|
0.24 |
51.08 |
|
0.36 |
48.98 |
|
0.48 |
46.96 |
|
0.61 |
45.03 |
|
0.73 |
43.18 |
|
0.85 |
41.40 |
|
0.97 |
39.70 |
|
1.09 |
38.06 |
На графике ниже показана динамика снижения концентрации амоксициллина в крови:

Рис.1 Динамика снижения концентрации амоксициллина в крови
Полученные данные позволяют прогнозировать эффективность и безопасность терапии. Период полувыведения амоксициллина составляет 2 часа, что, согласно исследованиям Craig [3], требует введения препарата каждые 6-8 часов для поддержания терапевтической концентрации (5-25 мг/л). Особое значение имеет расчет клиренса (6.24 л/ч), который, как отмечает Wagner [4], соответствует показателям пациентов с нормальной функцией почек. При почечной недостаточности данный параметр требует коррекции дозировки, поскольку, как демонстрируют Andes и соавт. [5], выведение амоксициллина происходит преимущественно почками. Эти выводы подтверждаются результатами наших расчетов (рис. 1).
2.2. Математические модели распространения инфекционных заболеваний: значение для диагностики, прогноза и здравоохранения
Инфекционные заболевания остаются одной из главных угроз общественному здоровью, особенно в условиях глобализации, урбанизации и изменяющегося климата. Прогнозирование и управление эпидемиями требуют точных и обоснованных решений, что делает математическое моделирование незаменимым инструментом современной эпидемиологии. Одним из наиболее известных подходов является модель SIR, которая позволяет описывать динамику инфекционного процесса и оценивать влияние различных интервенций, включая вакцинацию, карантинные меры и ограничение контактов [6].
Теоретическая основа: модель SIR
Модель SIR (susceptible-infected-recovered) делит популяцию на три группы:
-
S(t) — восприимчивые к заболеванию;
-
I(t) — инфицированные;
-
R(t) — выздоровевшие или погибшие.
Система дифференциальных уравнений имеет следующий вид:
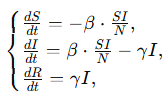
где,
-
 – коэффициент заражения (передачи
инфекции),
– коэффициент заражения (передачи
инфекции), -
 – коэффициент выздоровления (обратная величина
средней продолжительности болезни),
– коэффициент выздоровления (обратная величина
средней продолжительности болезни), -
N=S+I+R – общее население.
Ключевым параметром является базовое репродуктивное число:
 , которое отражает среднее число лиц, которых
заражает один инфицированный в полностью восприимчивой популяции.
Если
, которое отражает среднее число лиц, которых
заражает один инфицированный в полностью восприимчивой популяции.
Если  , эпидемия распространяется,
если
, эпидемия распространяется,
если  – затухает [7].
– затухает [7].
Для наглядной демонстрации важности математического подхода рассмотрим гипотетическую популяцию численностью 1 миллион человек. Пусть:
-
Начальное число инфицированных:I(0)=1,
-
β=0.3
 =0.1 (соответствует средней
продолжительности болезни 10 дней).
=0.1 (соответствует средней
продолжительности болезни 10 дней).
Рассчитаем:

Это означает, что каждый заражённый человек в среднем инфицирует трёх других, что потенциально приводит к экспоненциальному росту числа случаев заболевания.
Результаты численного моделирования с помощью метода Эйлера представлены на графике:

График демонстрирует типичную форму эпидемической кривой: быстрое увеличение числа инфицированных, последующий пик и спад с одновременным ростом количества выздоровевших.
Практическое значение модели
Модель SIR и её расширения (SEIR, SIRD, модели с вакцинацией) используются в реальных сценариях здравоохранения:
-
Прогнозирование эпидемий.
В период пандемии COVID-19 модели позволяли оценить сроки достижения пика заболеваемости и потребность в госпитальных койках [6]. -
Оценка коллективного иммунитета.
Для прекращения эпидемии необходимо вакцинировать:
 населения,
населения,
что
является ключевым критерием при планировании вакцинационных
кампаний [7].
Использование моделей позволяет спрогнозировать пиковую нагрузку на
систему здравоохранения (ИВЛ, койки, персонал) [8]. Применение
математических моделей, таких как SIR, представляет собой яркий
пример интеграции математики в медицину. Эти модели не только
позволяют глубже понять поведение инфекционных заболеваний, но и
служат основой для принятия критически важных решений в
здравоохранении. Современная медицина немыслима без математического
анализа, особенно в условиях глобальных эпидемических
угроз.
Заключение
В ходе проведенного исследования была подтверждена высокая значимость математических методов в современной медицине. Анализ научной литературы и практических примеров показал, что применение математического моделирования, статистических анализов и вычислительных алгоритмов позволяет врачам и исследователям глубже понимать физиологические процессы, прогнозировать развитие заболеваний и разрабатывать более эффективные методы диагностики и лечения.
Была доказана справедливость выдвинутой гипотезы: интеграция математических инструментов в медицинскую практику действительно способствует повышению точности диагностики, оптимизации лечебных процедур и улучшению результатов медицинских исследований. Особенно актуально использование таких методов в области эпидемиологии, фармакологии, биомеханики и медицинской визуализации.
Поставленные задачи были выполнены: изучены основные области применения математики в медицине, рассмотрены конкретные примеры моделей и алгоритмов, оценено их влияние на качество и эффективность медицинской помощи.
Таким образом, можно сделать вывод, что дальнейшее развитие междисциплинарных исследований на стыке математики и медицины является важным шагом на пути к созданию интеллектуальных систем здравоохранения, персонализированного лечения и научно обоснованного управления медицинскими ресурсами.
Практическая значимость работы заключается в том, что полученные результаты могут быть использованы в образовательной и научной деятельности, а также служить основой для разработки новых подходов в медицинской практике, где математические методы будут играть ключевую роль.
Литература
[1]. Габриэльссон Я., Вайнер Д. Анализ фармакокинетических и фармакодинамических данных: концепции и приложения. 5-е изд. Швеция: Swedish Pharmaceutical Press; 2016. 1168 с. (In English)
[2]. Гибалди М., Перье Д. Фармакокинетика. 2-е изд. Нью-Йорк: Marcel Dekker; 1982. 494 с. (In English)
[3]. Крейг У.А. Фармакокинетические/фармакодинамические параметры: обоснование дозирования антибактериальных препаратов у животных и людей // Clinical Infectious Diseases. 1998. Т. 26, № 1. С. 1-12. (In English)
[4]. Вагнер Дж.Г. Основы клинической фармакокинетики. Гамильтон: Drug Intelligence Publications; 1993. 331 с. (In English)
[5]. Андес Д., Крейг У.А. Фармакокинетика и фармакодинамика антибиотиков у животных и людей // Clinical Microbiology and Infection. 2002. Т. 8, № 2. С. 79-86. (In English)
[6]. Хеткоут Х.У. Математика инфекционных заболеваний // SIAM Review. 2000. Т. 42, № 4. С. 599-653. (In English)
[7]. Андерсон Р.М., Мэй Р.М. Инфекционные болезни человека: динамика и контроль. Оксфорд: Oxford University Press; 1992. 757 с.
[8]. Фергюсон Н.М. [и др.] Влияние нефармацевтических вмешательств (NPI) на снижение смертности от COVID-19 и нагрузку на систему здравоохранения: Отчет группы реагирования Имперского колледжа. 2020. 20 с.

шағым қалдыра аласыз


















