#1 слайд
АЙНАЛУ ДЕНЕЛЕРІ АЙНАЛУ ДЕНЕЛЕРІ

1 слайд

#2 слайд
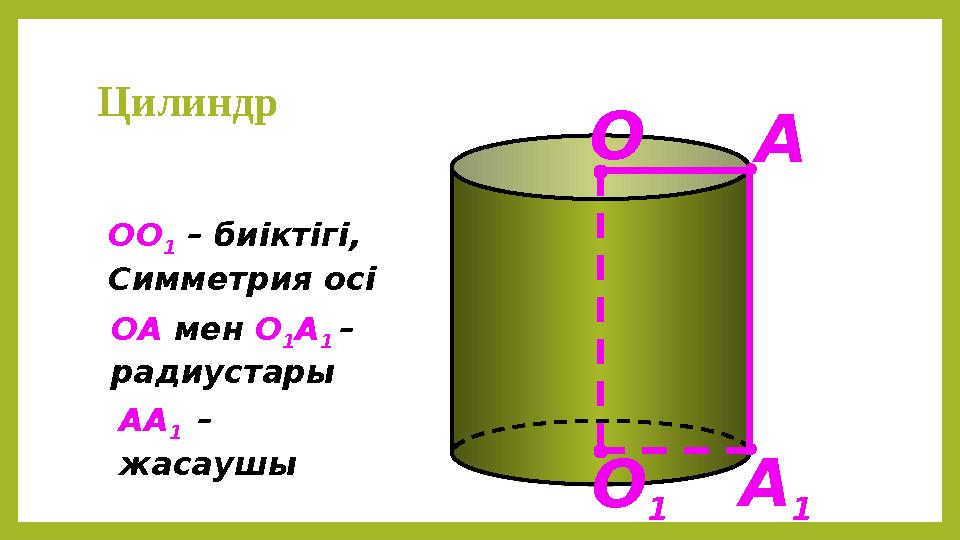
ОО 1 – биіктігі, Симметрия осі ОА мен О 1А 1 – радиустары АА 1 – жасаушы А А 1 О О 1 Цилиндр

2 слайд

#3 слайд
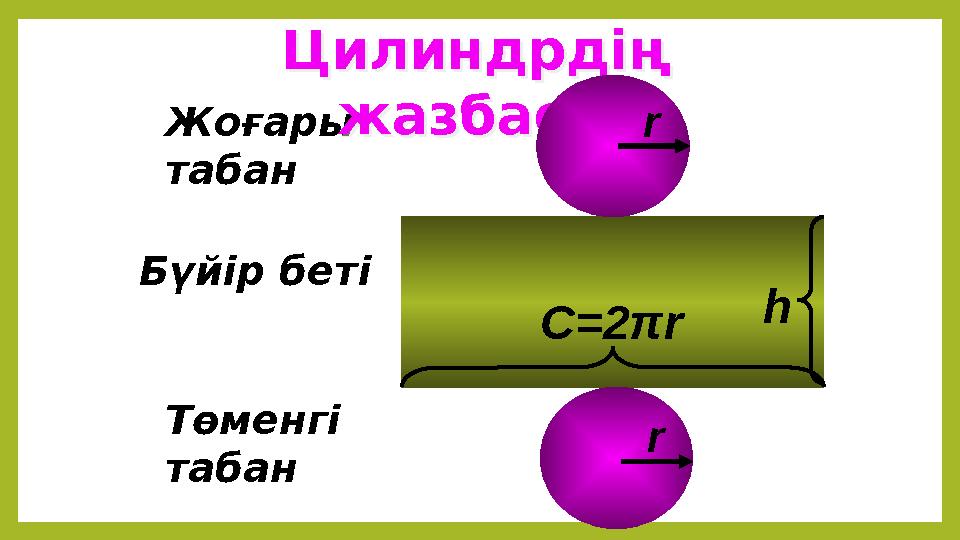
Жоғары табан Төменгі табан Бүйір бетіЦилиндрдің жазбасы Цилиндрдің жазбасы C=2πr r h r

3 слайд

#4 слайд
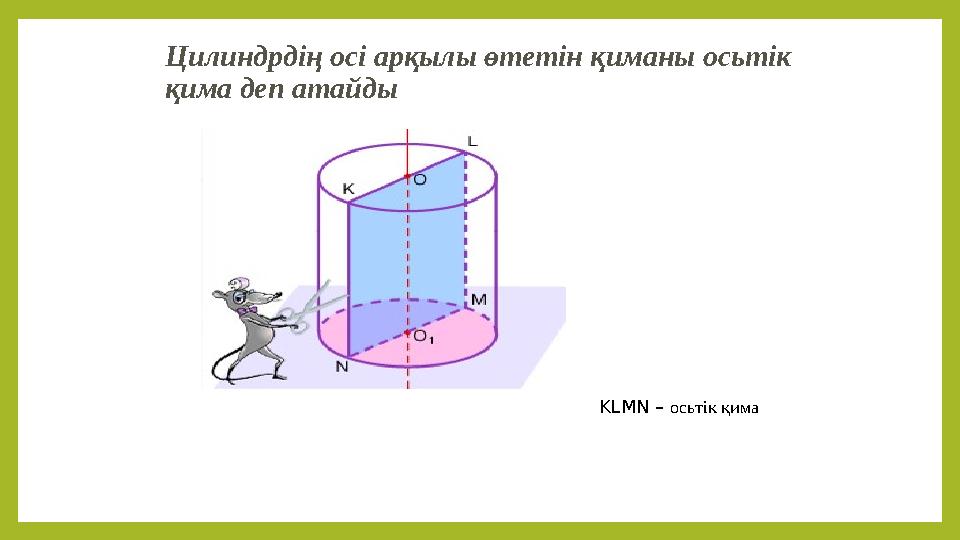
Цилиндрдің осі арқылы өтетін қиманы осьтік қима деп атайды KLMN – осьтік қима

4 слайд

#5 слайд
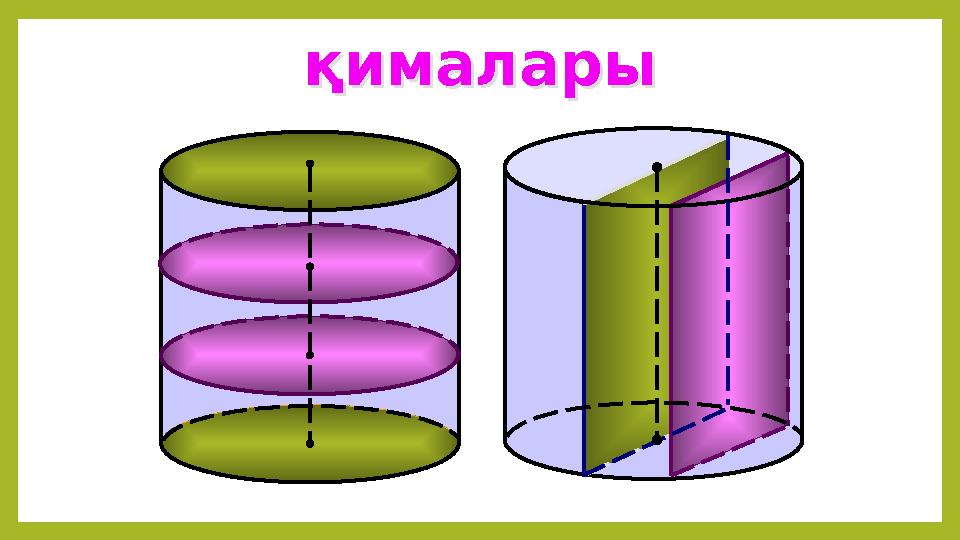
қималарықималары

5 слайд

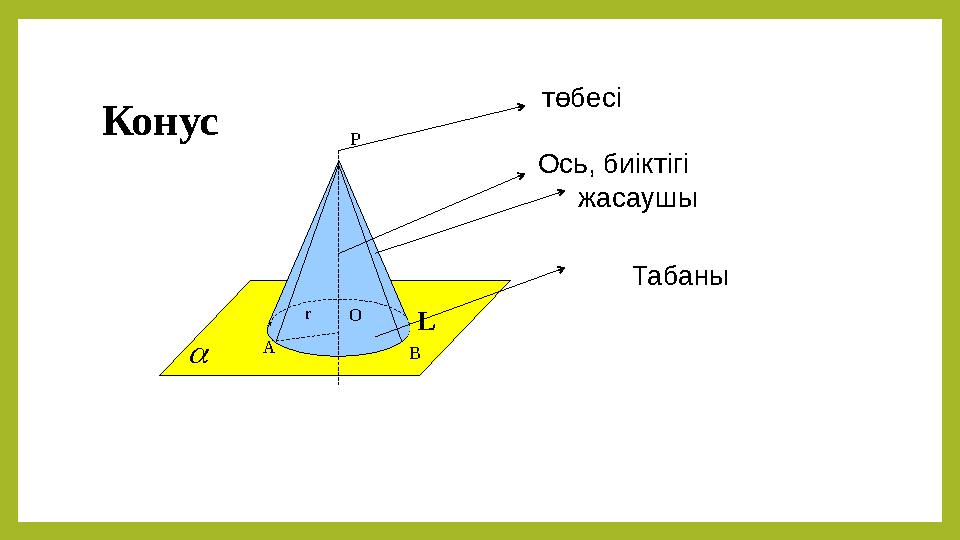
#6 слайд
 Р Оr А В L төбесі Ось, биіктігі жасаушы Табаны Конус

6 слайд

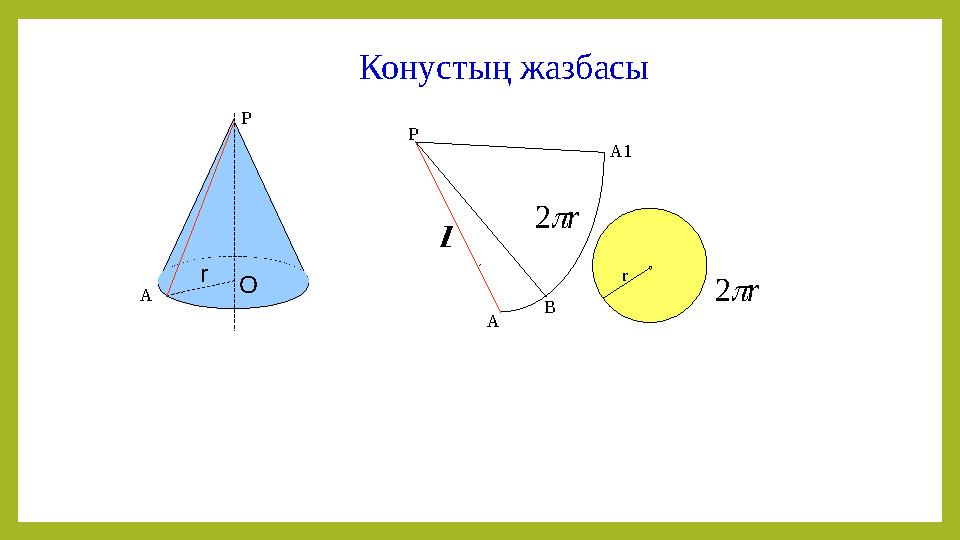
#7 слайд
Конустың жазбасы Р А В А1 r Р А О r l l r2 r2

7 слайд

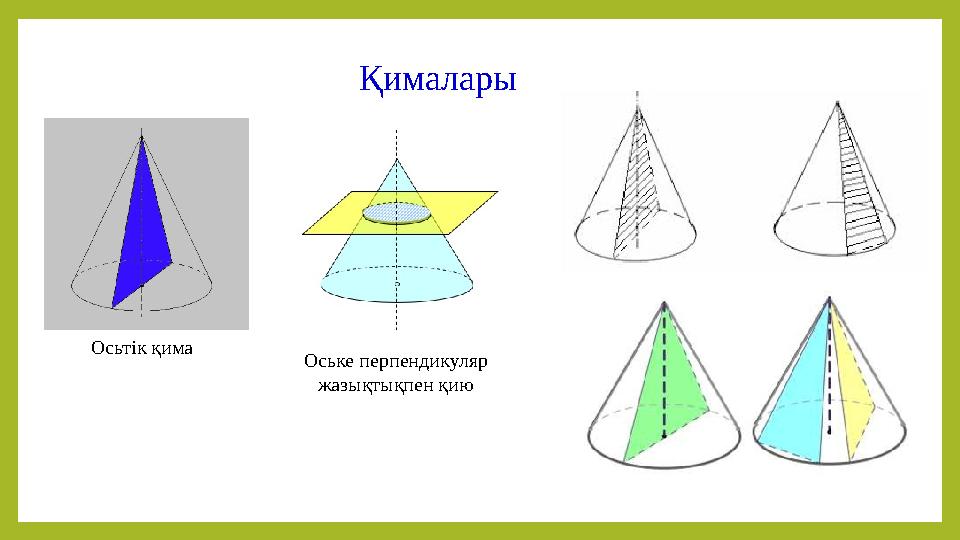
#8 слайд
Қималары Осьтік қима Оське перпендикуляр жазықтықпен қию

8 слайд

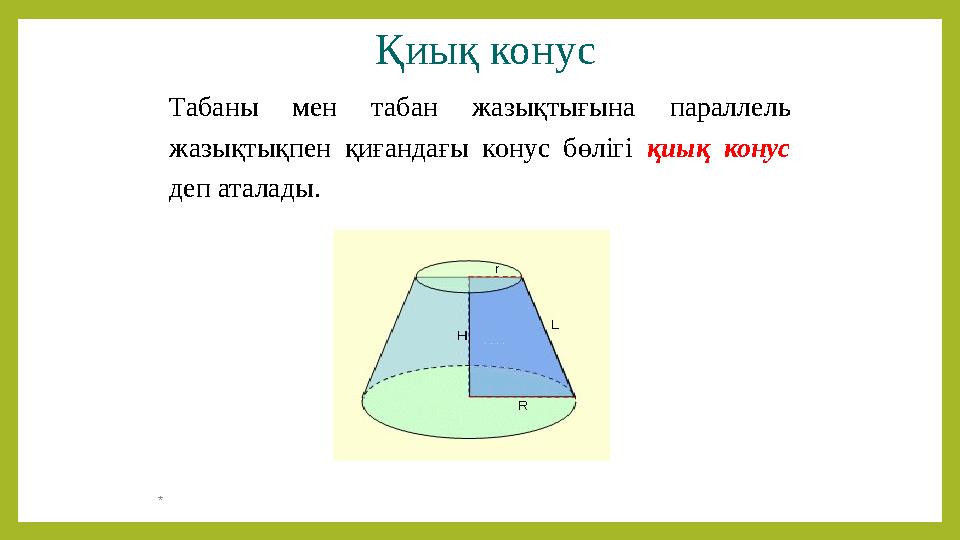
#9 слайд
Қиық конус Табаны мен табан жазықтығына параллель жазықтықпен қиғандағы конус бөлігі қиық конус деп аталады. *

9 слайд

#10 слайд
Негізгі анықтамалар •Қиық конус табандары деп берілген конус табаны мен жазықтықпен қиғандағы дөңгелекті атайды. •Қиық конустың табандарының центрлерін қосатын кесіндіні қиық конустың биіктігі деп аталады. •Қиық конусты шектейтін конустық беттің бөлігі оның бүйір беті деп, ал конустық бетті жасайтын кесінділер жасаушылары деп аталады. •Қиық конустың радиустары деп табандарының радиустарын атайды. Н L R r *

10 слайд

#11 слайд
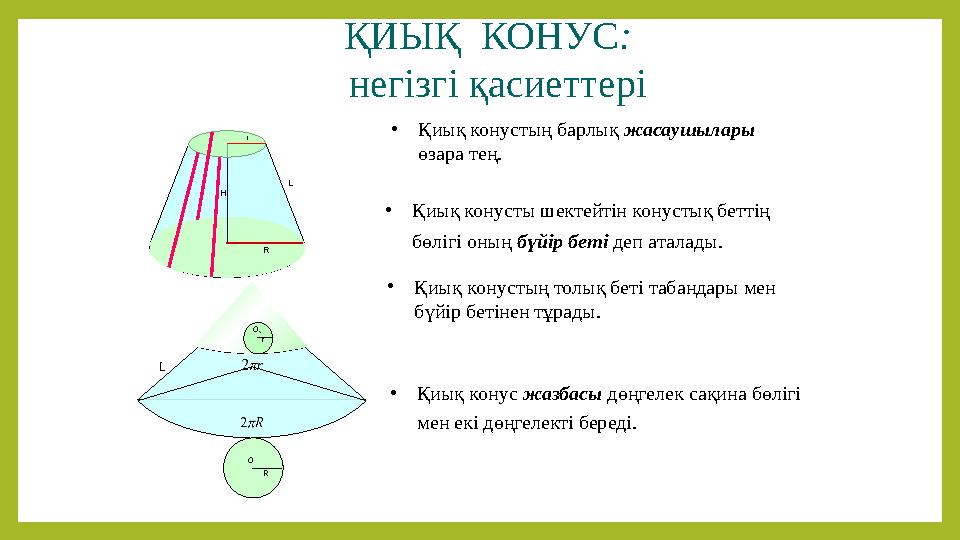
ҚИЫҚ КОНУС: негізгі қасиеттері •Қиық конустың барлық жасаушылары өзара тең. •Қиық конусты шектейтін конустық беттің бөлігі оның бүйір беті деп аталады. Н L r R •Қиық конустың толық беті табандары мен бүйір бетінен тұрады. L R О О 1 r •Қиық конус жазбасы дөңгелек сақина бөлігі мен екі дөңгелекті береді.

11 слайд

#12 слайд

12 слайд

#13 слайд
Сфера архитектурада

13 слайд

#14 слайд
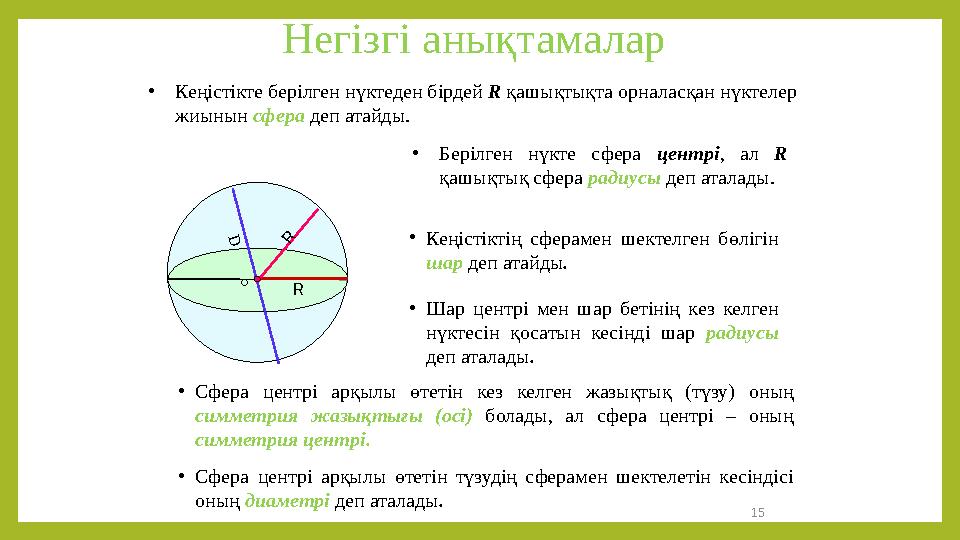
Сфера және шар Шар деп жарты дөңгелекті өз диаметрінен айналдырғанда шыққан денені (фигураны) айтады. Сфера деп жарты шеңберді өз диаметрінен айналдырғанда шыққан денені (фигураны) айтады.

14 слайд

#15 слайд
Негізгі анықтамалар •Кеңістікте берілген нүктеден бірдей R қашықтықта орналасқан нүктелер жиынын сфера деп атайды. •Берілген нүкте сфера центрі, ал R қашықтық cфера радиусы деп аталады. •Кеңістіктің сферамен шектелген бөлігін шар деп атайды. •Шар центрі мен шар бетінің кез келген нүктесін қосатын кесінді шар радиусы деп аталады. •Сфера центрі арқылы өтетін кез келген жазықтық (түзу) оның симметрия жазықтығы (осі) болады, ал сфера центрі – оның симметрия центрі. •Сфера центрі арқылы өтетін түзудің сферамен шектелетін кесіндісі оның диаметрі деп аталады. R R R D O R 15

15 слайд

#16 слайд

16 слайд

#17 слайд
АЙНАЛУ ДЕНЕЛЕРІНІҢ БЕТ АУДАНДАРЫ

17 слайд

#18 слайд
Цилиндрдің бүйір бетінің ауданы, цилиндрдің толық бетінің ауданы S т.б.  = 2S таб  + S б.б ; S т.б.  – цилиндрдің толық бетінің ауданы; S таб  – цилиндрдің табанының ауданы; S б.б.  – цилиндрдің бүйір бетінің ауданы; S т.б.  = 2 πR 2  + 2 πR h = 2 πR(R +h).

18 слайд

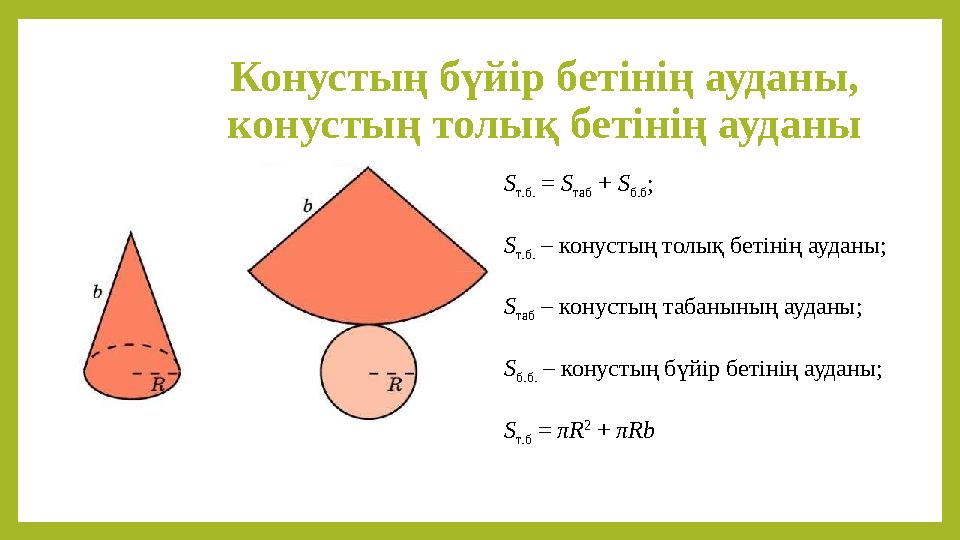
#19 слайд
Конустың бүйір бетінің ауданы, конустың толық бетінің ауданы S т.б.  = S таб  + S б.б ; S т.б.  – конустың толық бетінің ауданы; S таб  – конустың табанының ауданы; S б.б.  – конустың бүйір бетінің ауданы; S т.б  = πR 2  + πRb

19 слайд

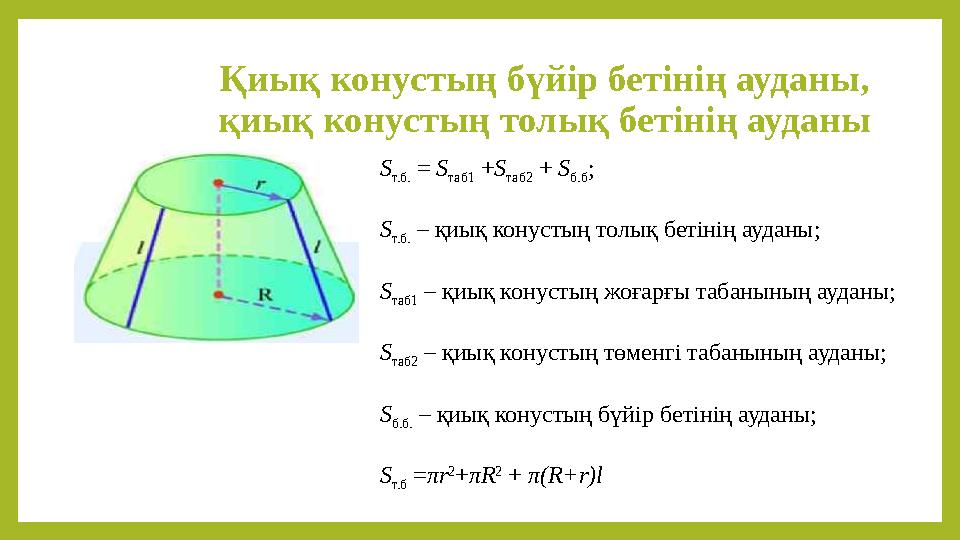
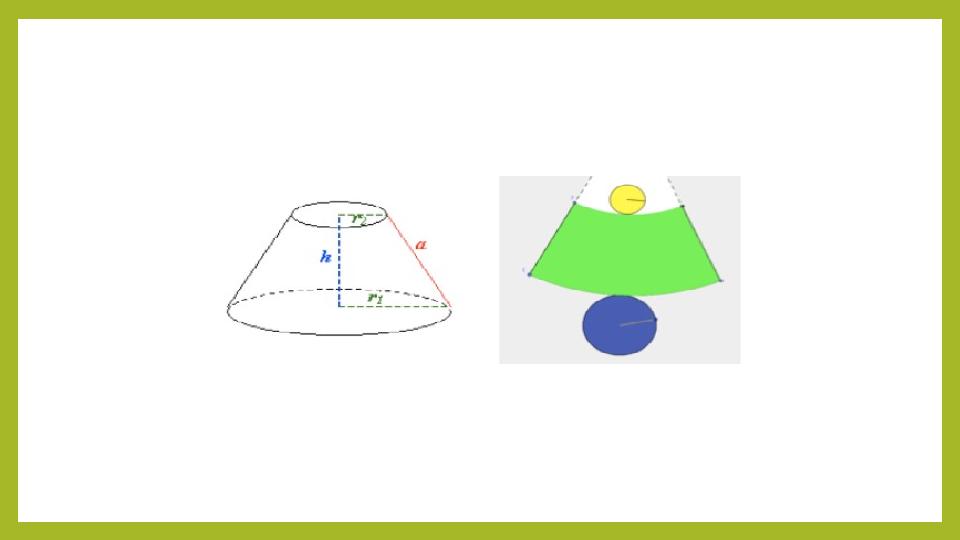
#20 слайд
Қиық конустың бүйір бетінің ауданы, қиық конустың толық бетінің ауданы S т.б.  = S таб1  +S таб2  + S б.б ; S т.б.  – қиық конустың толық бетінің ауданы; S таб1  – қиық конустың жоғарғы табанының ауданы; S таб2  – қиық конустың төменгі табанының ауданы; S б.б.  – қиық конустың бүйір бетінің ауданы; S т.б  =πr 2 +πR 2  + π(R+r)l

20 слайд

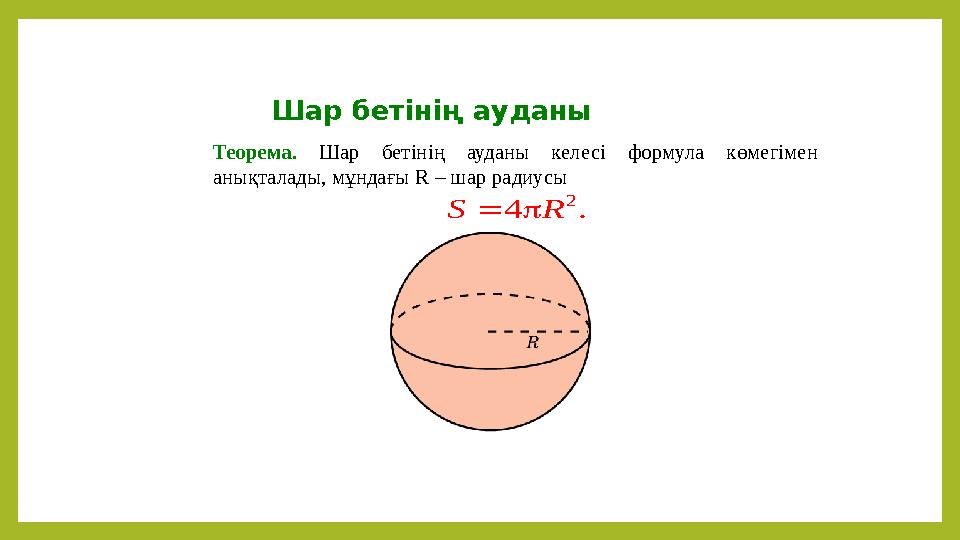
#21 слайд
Шар бетінің ауданы Теорема. Шар бетінің ауданы келесі формула көмегімен анықталады, мұндағы R – шар радиусы 2 4 .S R 

21 слайд

#22 слайд
АЙНАЛУ ДЕНЕЛЕРІНІҢ КӨЛЕМДЕРІ

22 слайд

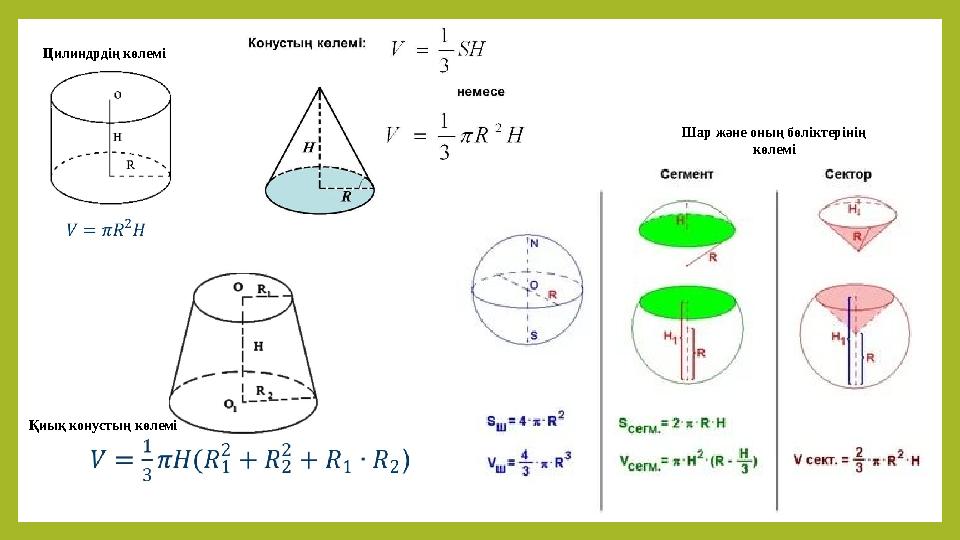
#23 слайд
Цилиндрдің көлемі Қиық конустың көлемі Шар және оның бөліктерінің көлемі

23 слайд

#24 слайд
№1 тапсырма. •Конус табанының радиусы 85 см, ал жасаушысы мен конус осі арасындағы 30 0 . Конус көлемін табыңыз. (сызбаны міндетті түрде GeoGebra –да салып көрсетіңіз)

24 слайд

#25 слайд
№2 тапсырма. Асфальт тегістейтін көліктің дөңгелегінің диаметрі – 120 см, ал ені – 2 м. Егер ол 30 рет айналым жасаса, қанша метр квадрат жол салуы мүмкін екенін табыңыз. Жауабын м 2 арқылы беріңіз.

25 слайд

#26 слайд
Осы тақырып бойынша өзіңіздің ерекше әдістемеңізбен немесе жаңалығыңызбен бөлісіңіз. •Түрлі графикалық редакторлардың мүмкіндіктері •Ерекше тапсырмалар •Кейбір тапсырмалардың шешу жолдары •Лайфхак •және тағы басқа бағытта тәжірибеңізбен бөлісуге болады

26 слайд