Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия


#1 слайд
Аксиомы стереометрии
и их следствия
1 слайд
Аксиомы стереометрии и их следствия

#2 слайд
Учебные цели:
•
10.3.1.1 знать и применять аксиомы стереометрии и
их следствия;
•
10.5.2.1 владеть техникой выполнения простейших
стереометрических чертежей.
2 слайд
Учебные цели: • 10.3.1.1 знать и применять аксиомы стереометрии и их следствия; • 10.5.2.1 владеть техникой выполнения простейших стереометрических чертежей.
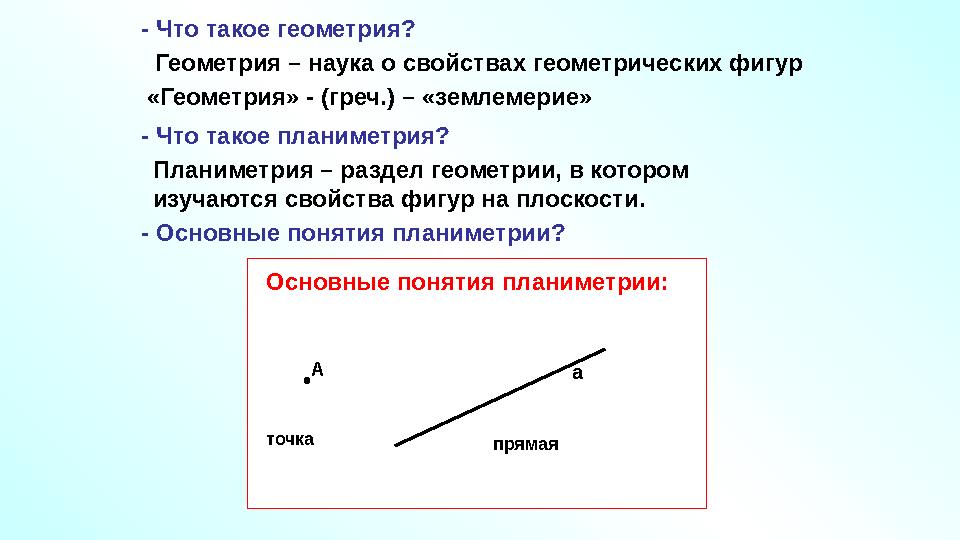
#3 слайд
- Что такое геометрия?
Геометрия – наука о свойствах геометрических фигур
«Геометрия» - (греч.) – «землемерие»
- Что такое планиметрия?
Планиметрия – раздел геометрии, в котором
изучаются свойства фигур на плоскости.
А
аОсновные понятия планиметрии:
точка
прямая- Основные понятия планиметрии?
3 слайд
- Что такое геометрия? Геометрия – наука о свойствах геометрических фигур «Геометрия» - (греч.) – «землемерие» - Что такое планиметрия? Планиметрия – раздел геометрии, в котором изучаются свойства фигур на плоскости. А аОсновные понятия планиметрии: точка прямая- Основные понятия планиметрии?
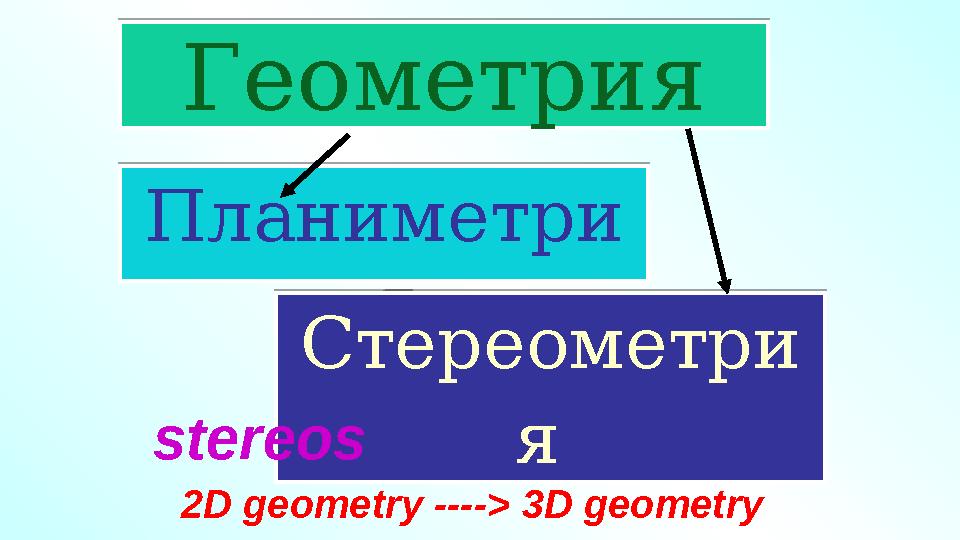
#4 слайд
Геометрия
Планиметри
я
Стереометри
я stereos
2D geometry ----> 3D geometryГеометрия Планиметри
я Стереометри
я
4 слайд
Геометрия Планиметри я Стереометри я stereos 2D geometry ----> 3D geometryГеометрия Планиметри я Стереометри я

#5 слайд
- раздел геометрии,
в котором
изучаются свойства
фигур в
пространстве
5 слайд
- раздел геометрии, в котором изучаются свойства фигур в пространстве
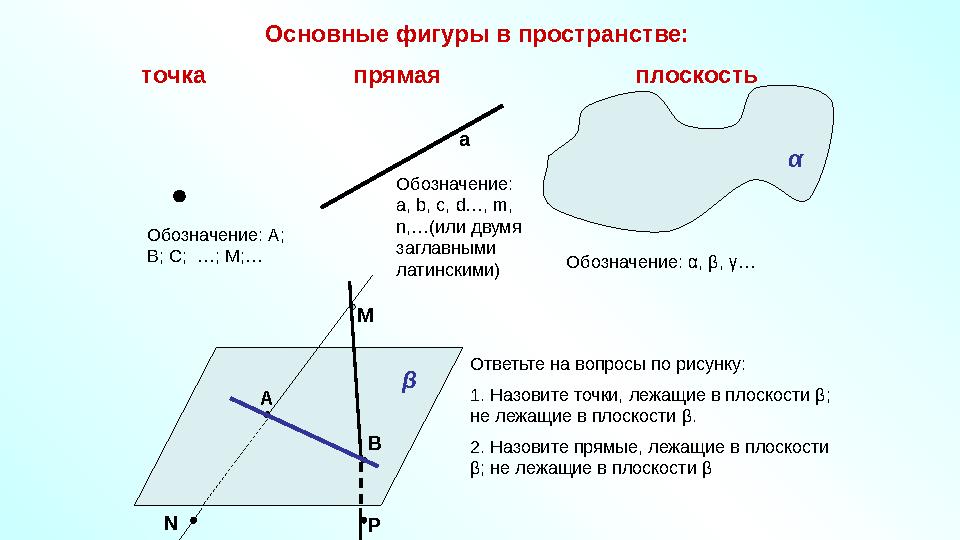
#6 слайд
Основные фигуры в пространстве:
точка прямая плоскость
α
βОбозначение: А;
В; С; …; М;… а
А
ВМ
N
Р Обозначение:
a, b, с, d…, m,
n,… (или двумя
заглавными
латинскими) Обозначение: α , β , γ …
Ответьте на вопросы по рисунку:
1. Назовите точки, лежащие в плоскости β ;
не лежащие в плоскости β .
2. Назовите прямые, лежащие в плоскости
β ; не лежащие в плоскости β
6 слайд
Основные фигуры в пространстве: точка прямая плоскость α βОбозначение: А; В; С; …; М;… а А ВМ N Р Обозначение: a, b, с, d…, m, n,… (или двумя заглавными латинскими) Обозначение: α , β , γ … Ответьте на вопросы по рисунку: 1. Назовите точки, лежащие в плоскости β ; не лежащие в плоскости β . 2. Назовите прямые, лежащие в плоскости β ; не лежащие в плоскости β
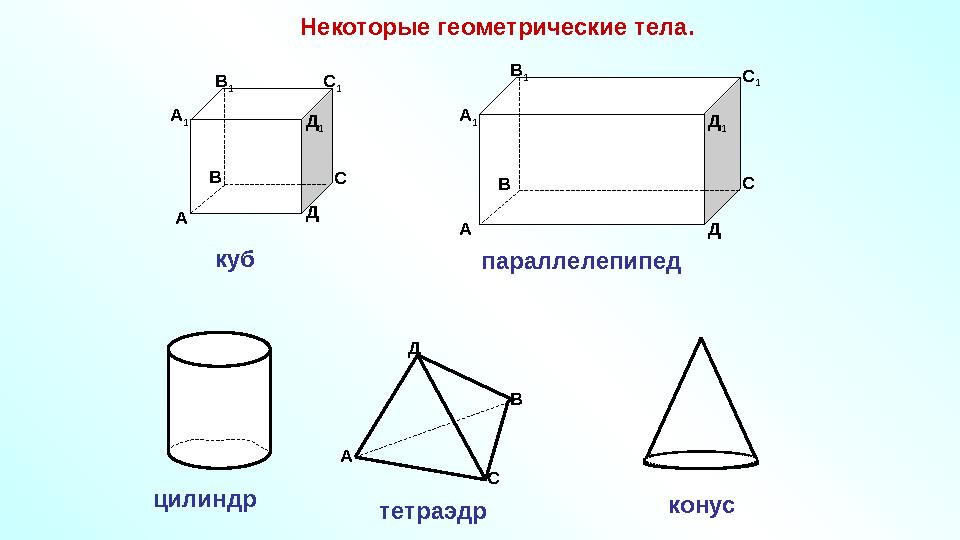
#7 слайд
Некоторые геометрические тела.
А В
С
ДД
1 С
1В
1
А
1
куб А В С
ДА
1 В
1
С
1
Д
1
параллелепипед
А В
СД
тетраэдрцилиндр
конус
7 слайд
Некоторые геометрические тела. А В С ДД 1 С 1В 1 А 1 куб А В С ДА 1 В 1 С 1 Д 1 параллелепипед А В СД тетраэдрцилиндр конус

#8 слайд
Назовите какие геометрические тела вам напоминают предметы,
изображенные на этих рисунках:
Назовите предметы из окружающей вас обстановки ( нашей классной
комнаты) напоминающие вам геометрические тела.
8 слайд
Назовите какие геометрические тела вам напоминают предметы, изображенные на этих рисунках: Назовите предметы из окружающей вас обстановки ( нашей классной комнаты) напоминающие вам геометрические тела.
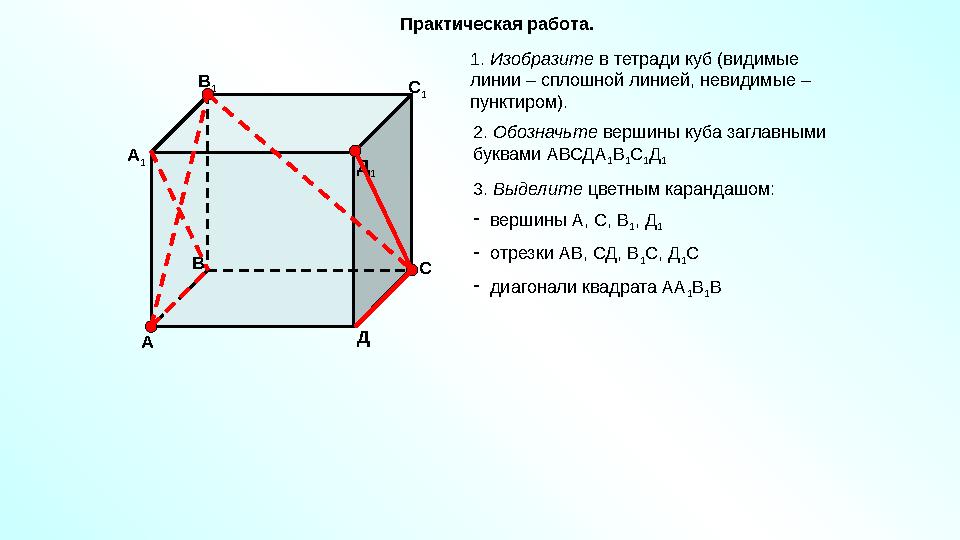
#9 слайд
Практическая работа.
1. Изобразите в тетради куб (видимые
линии – сплошной линией, невидимые –
пунктиром).
2. Обозначьте вершины куба заглавными
буквами АВСДА
1 В
1 С
1 Д
1
А В
С
ДД
1 С
1В
1
А
1
3. Выделите цветным карандашом:
-
вершины А, С, В
1 , Д
1
-
отрезки АВ, СД, В
1 С, Д
1 С
-
диагонали квадрата АА
1 В
1 В
9 слайд
Практическая работа. 1. Изобразите в тетради куб (видимые линии – сплошной линией, невидимые – пунктиром). 2. Обозначьте вершины куба заглавными буквами АВСДА 1 В 1 С 1 Д 1 А В С ДД 1 С 1В 1 А 1 3. Выделите цветным карандашом: - вершины А, С, В 1 , Д 1 - отрезки АВ, СД, В 1 С, Д 1 С - диагонали квадрата АА 1 В 1 В

#10 слайд
- Что такое аксиома?
Аксиома – это утверждение о свойствах
геометрических фигур, принимается в качестве
исходных положений, на основе которых доказываются
далее теоремы и вообще строится вся геометрия.
Аксиомы планиметрии:
- через любые две точки можно провести прямую и
притом только одну.
-
из трех точек прямой одна, и только одна, лежит
между двумя другими.
-
имеются по крайней мере три точки, не лежащие
на одной прямой…
10 слайд
- Что такое аксиома? Аксиома – это утверждение о свойствах геометрических фигур, принимается в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия. Аксиомы планиметрии: - через любые две точки можно провести прямую и притом только одну. - из трех точек прямой одна, и только одна, лежит между двумя другими. - имеются по крайней мере три точки, не лежащие на одной прямой…
#11 слайд
α А
11 слайд
α А
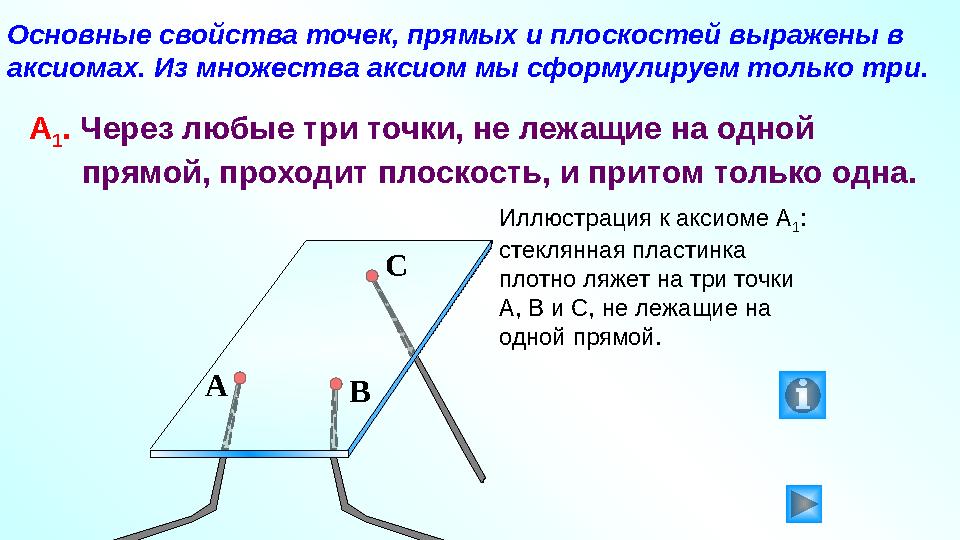
#12 слайд
Основные свойства точек, прямых и плоскостей выражены в
аксиомах. Из множества аксиом мы сформулируем только три.
А
1 . Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
Иллюстрация к аксиоме А
1 :
стеклянная пластинка
плотно ляжет на три точки
А, В и С, не лежащие на
одной прямой.
A
B C
12 слайд
Основные свойства точек, прямых и плоскостей выражены в аксиомах. Из множества аксиом мы сформулируем только три. А 1 . Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Иллюстрация к аксиоме А 1 : стеклянная пластинка плотно ляжет на три точки А, В и С, не лежащие на одной прямой. A B C
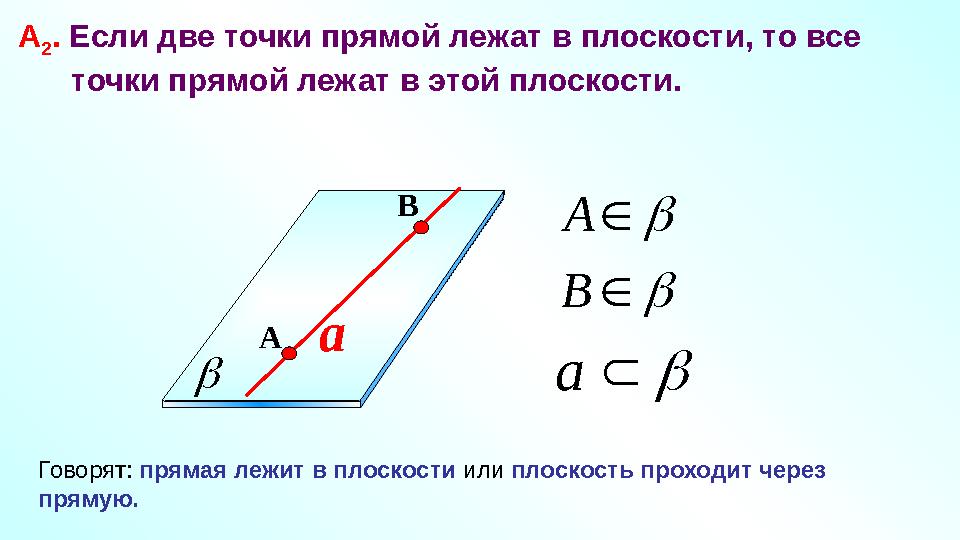
#13 слайд
a аА
2 . Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
A B
В
А
Говорят: прямая лежит в плоскости или плоскость проходит через
прямую.
13 слайд
a аА 2 . Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. A B В А Говорят: прямая лежит в плоскости или плоскость проходит через прямую.
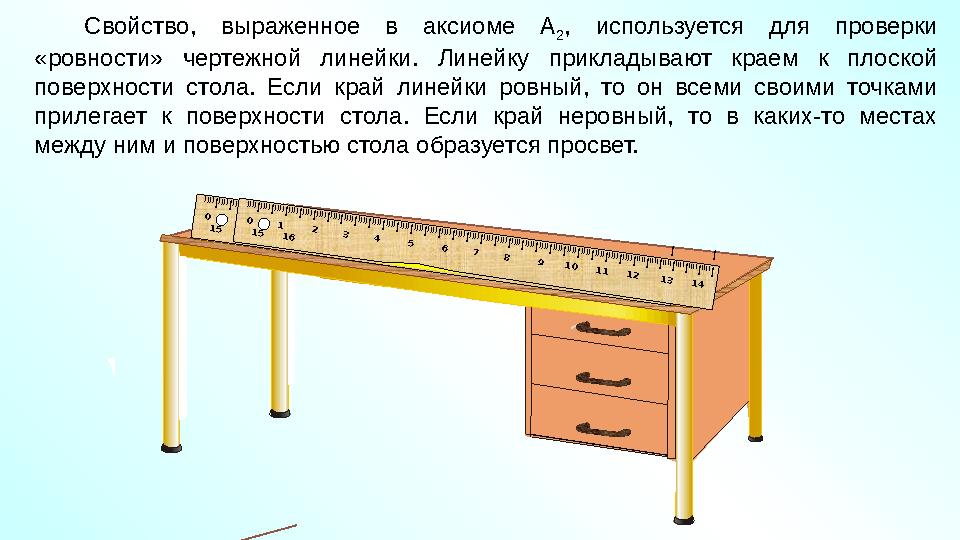
#14 слайд
Свойство, выраженное в аксиоме А
2 , используется для проверки
«ровности» чертежной линейки. Линейку прикладывают краем к плоской
поверхности стола. Если край линейки ровный, то он всеми своими точками
прилегает к поверхности стола. Если край неровный, то в каких-то местах
между ним и поверхностью стола образуется просвет.IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
I
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
15 16
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
I
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
15 16
14 слайд
Свойство, выраженное в аксиоме А 2 , используется для проверки «ровности» чертежной линейки. Линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный, то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII I 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII I 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
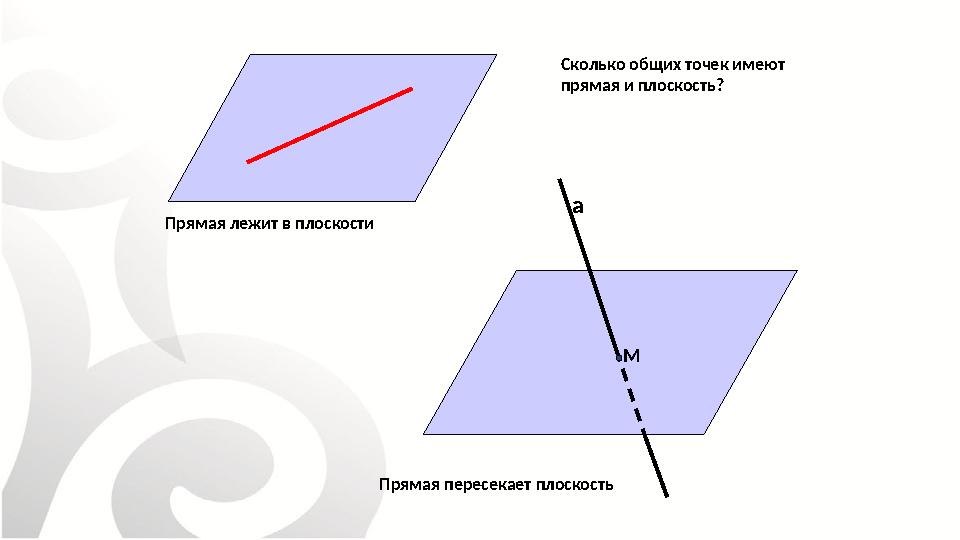
#15 слайд
а
МПрямая лежит в плоскости
Прямая пересекает плоскость Сколько общих точек имеют
прямая и плоскость?
15 слайд
а МПрямая лежит в плоскости Прямая пересекает плоскость Сколько общих точек имеют прямая и плоскость?
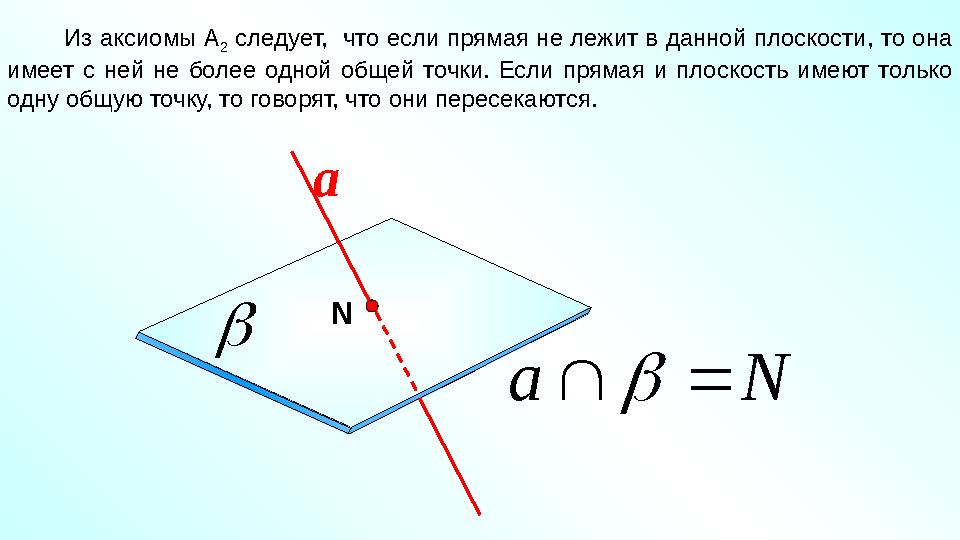
#16 слайд
N а Из аксиомы А
2 следует, что если прямая не лежит в данной плоскости, то она
имеет с ней не более одной общей точки. Если прямая и плоскость имеют только
одну общую точку, то говорят, что они пересекаются.
a
N
16 слайд
N а Из аксиомы А 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются. a N
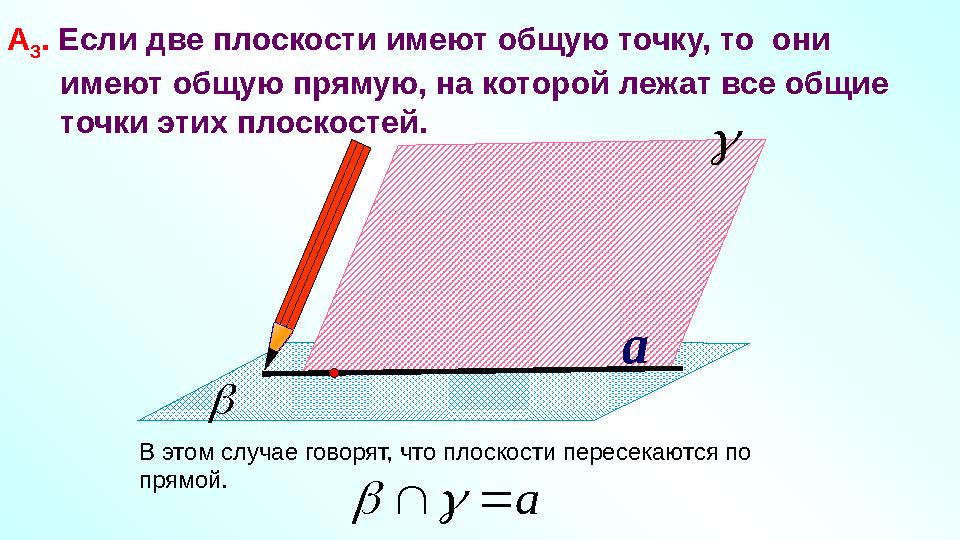
#17 слайд
aА
3 . Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
В этом случае говорят, что плоскости пересекаются по
прямой.
a
17 слайд
aА 3 . Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой. a
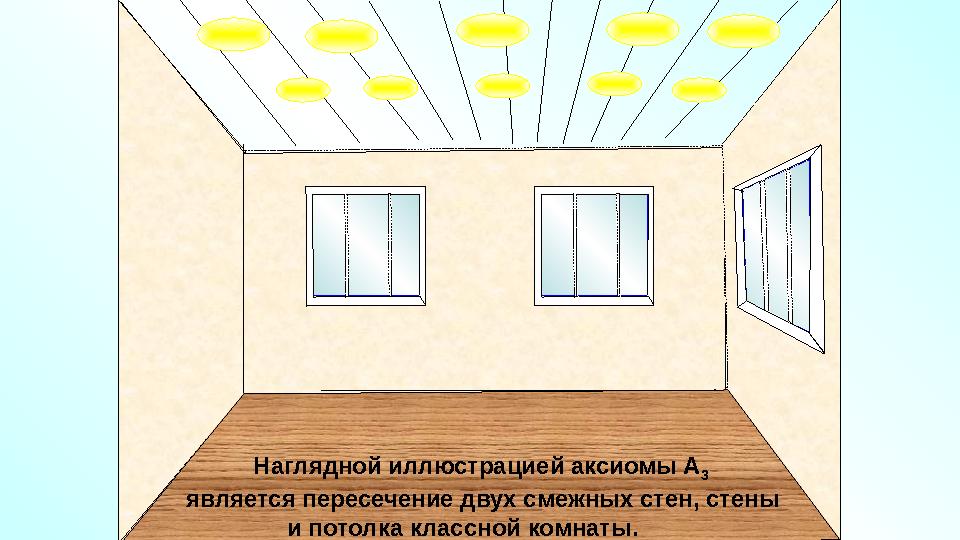
#18 слайд
Наглядной иллюстрацией аксиомы А
3
является пересечение двух смежных стен, стены
и потолка классной комнаты.
18 слайд
Наглядной иллюстрацией аксиомы А 3 является пересечение двух смежных стен, стены и потолка классной комнаты.
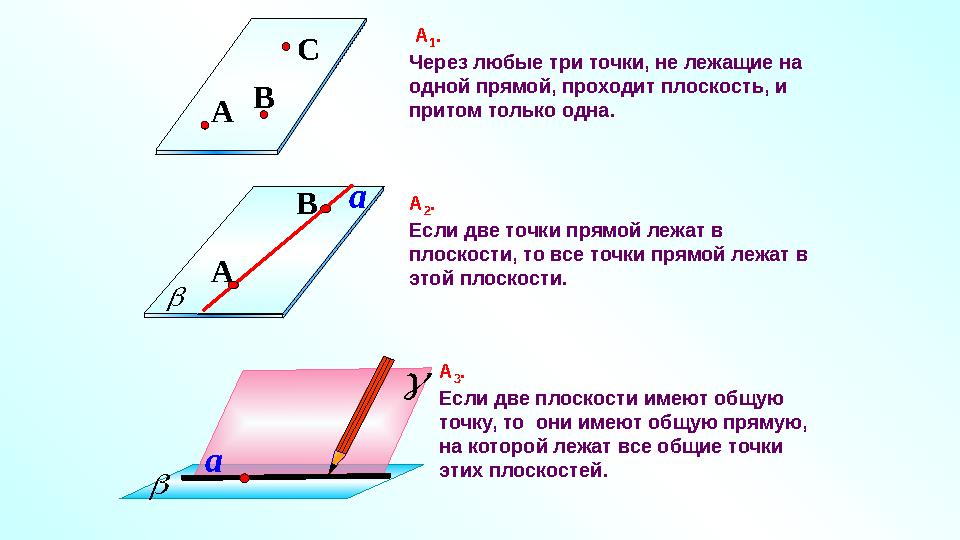
#19 слайд
А
1 .
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.C
A B
А
2 .
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости. a
A B
a А
3 .
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки
этих плоскостей.
19 слайд
А 1 . Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.C A B А 2 . Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. a A B a А 3 . Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
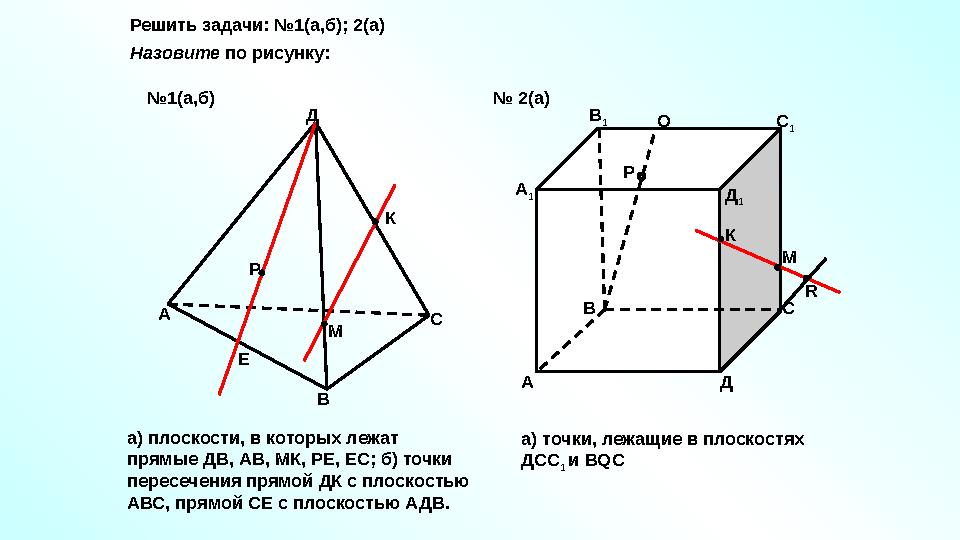
#20 слайд
Решить задачи: №1(а,б); 2(а)
А
В СД
Р
Е К
М
А В С
ДА
1 В
1
С
1
Д
1Q
P
RК
МНазовите по рисунку:
а) плоскости, в которых лежат
прямые ДВ, АВ, МК, РЕ, ЕС; б) точки
пересечения прямой ДК с плоскостью
АВС, прямой СЕ с плоскостью АДВ. а) точки, лежащие в плоскостях
ДСС
1 и В Q С№ 1(а,б) № 2(а)
20 слайд
Решить задачи: №1(а,б); 2(а) А В СД Р Е К М А В С ДА 1 В 1 С 1 Д 1Q P RК МНазовите по рисунку: а) плоскости, в которых лежат прямые ДВ, АВ, МК, РЕ, ЕС; б) точки пересечения прямой ДК с плоскостью АВС, прямой СЕ с плоскостью АДВ. а) точки, лежащие в плоскостях ДСС 1 и В Q С№ 1(а,б) № 2(а)
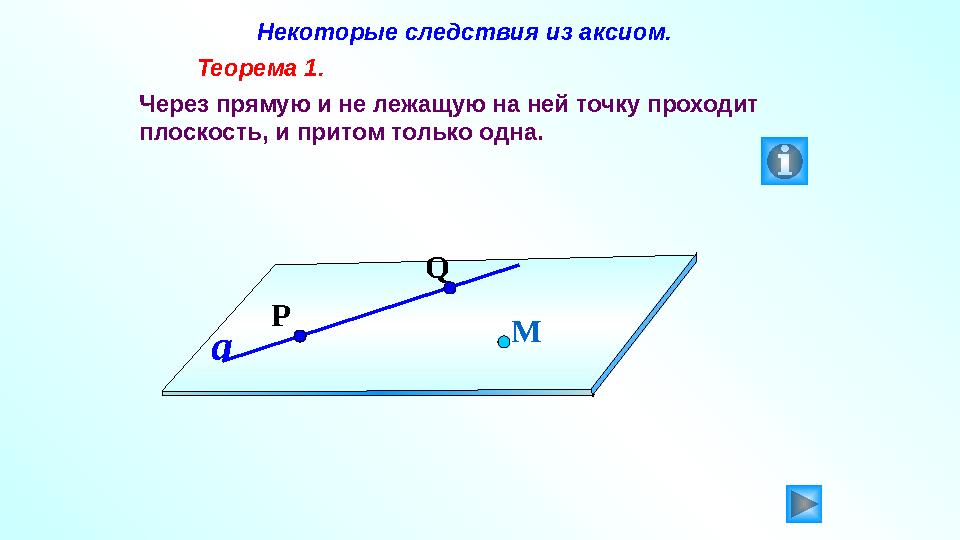
#21 слайд
Некоторые следствия из аксиом.
Теорема 1.
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
М
a Q
P
21 слайд
Некоторые следствия из аксиом. Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. М a Q P
#22 слайд
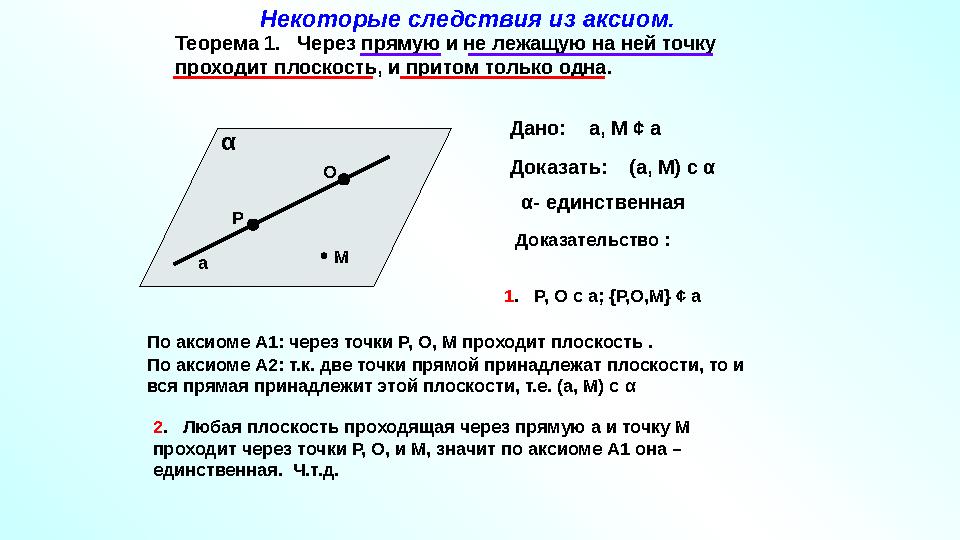
Теорема 1. Через прямую и не лежащую на ней точку
проходит плоскость, и притом только одна.
Дано: а, М ¢ а
Доказать: (а, М) с α
α - единственная
а Мα
Доказательство :
1 . Р, О с а; { Р,О,М } ¢ аР О
По аксиоме А1: через точки Р, О, М проходит плоскость .
По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и
вся прямая принадлежит этой плоскости, т.е. (а, М) с α
2 . Любая плоскость проходящая через прямую а и точку М
проходит через точки Р, О, и М, значит по аксиоме А1 она –
единственная. Ч.т.д. Некоторые следствия из аксиом.
22 слайд
Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Дано: а, М ¢ а Доказать: (а, М) с α α - единственная а Мα Доказательство : 1 . Р, О с а; { Р,О,М } ¢ аР О По аксиоме А1: через точки Р, О, М проходит плоскость . По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости, т.е. (а, М) с α 2 . Любая плоскость проходящая через прямую а и точку М проходит через точки Р, О, и М, значит по аксиоме А1 она – единственная. Ч.т.д. Некоторые следствия из аксиом.
#23 слайд
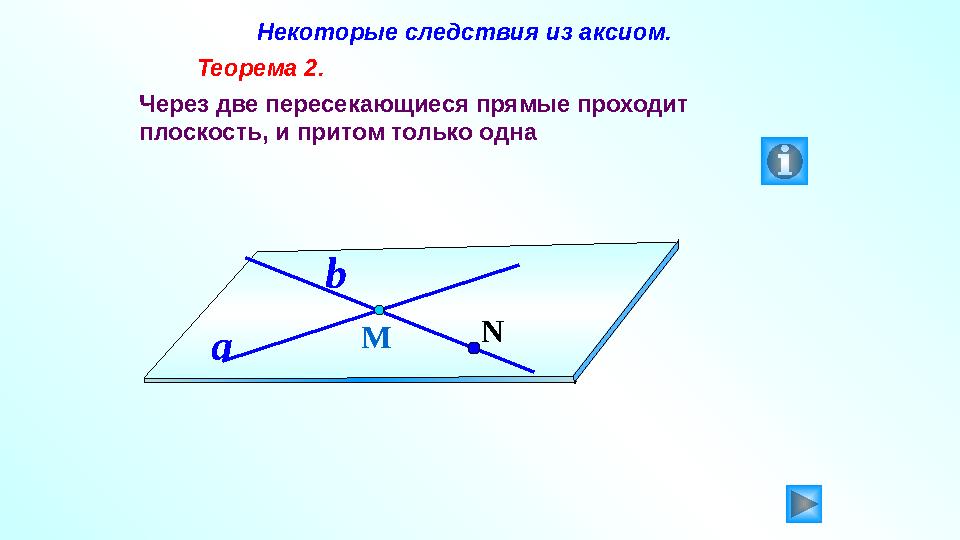
Некоторые следствия из аксиом.
Теорема 2.
Через две пересекающиеся прямые проходит
плоскость, и притом только одна
М
a b
N
23 слайд
Некоторые следствия из аксиом. Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна М a b N
#24 слайд
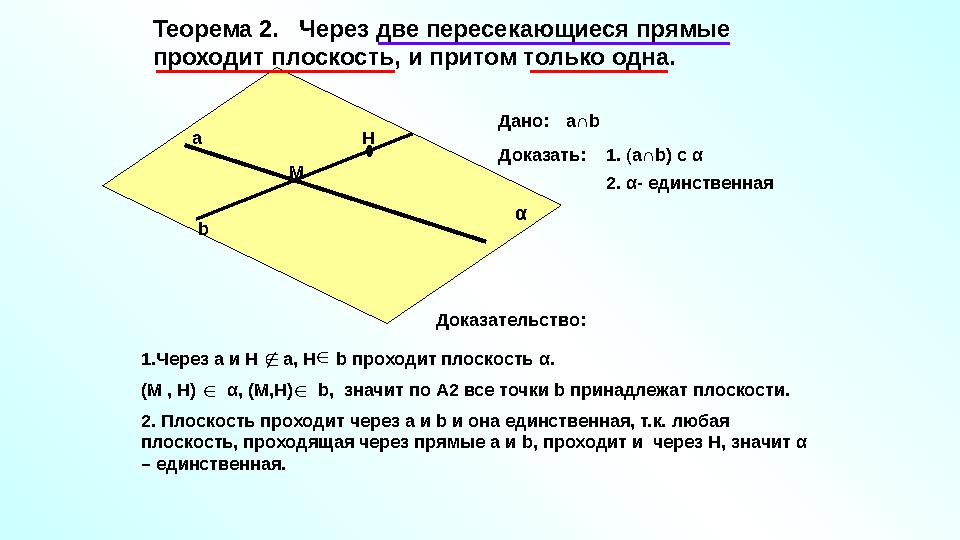
Теорема 2. Через две пересекающиеся прямые
проходит плоскость, и притом только одна.
Дано: а∩ b
Доказать: 1. ( а∩ b ) с α
2. α - единственнаяа
b М Н
α
Доказательство:
1.Через а и Н а, Н b проходит плоскость α .
(М , Н) α , (М,Н) b , значит по А2 все точки b принадлежат плоскости.
2. Плоскость проходит через а и b и она единственная, т.к. любая
плоскость, проходящая через прямые а и b , проходит и через Н, значит α
– единственная.
24 слайд
Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна. Дано: а∩ b Доказать: 1. ( а∩ b ) с α 2. α - единственнаяа b М Н α Доказательство: 1.Через а и Н а, Н b проходит плоскость α . (М , Н) α , (М,Н) b , значит по А2 все точки b принадлежат плоскости. 2. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b , проходит и через Н, значит α – единственная.
#25 слайд
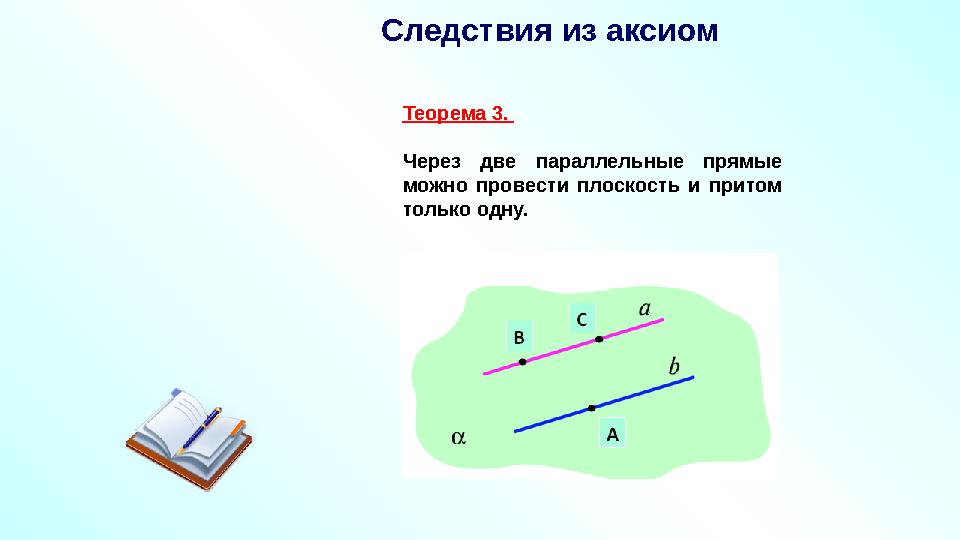
Теорема 3.
Через две параллельные прямые
можно провести плоскость и притом
только одну.
Следствия из аксиом
25 слайд
Теорема 3. Через две параллельные прямые можно провести плоскость и притом только одну. Следствия из аксиом
#26 слайд
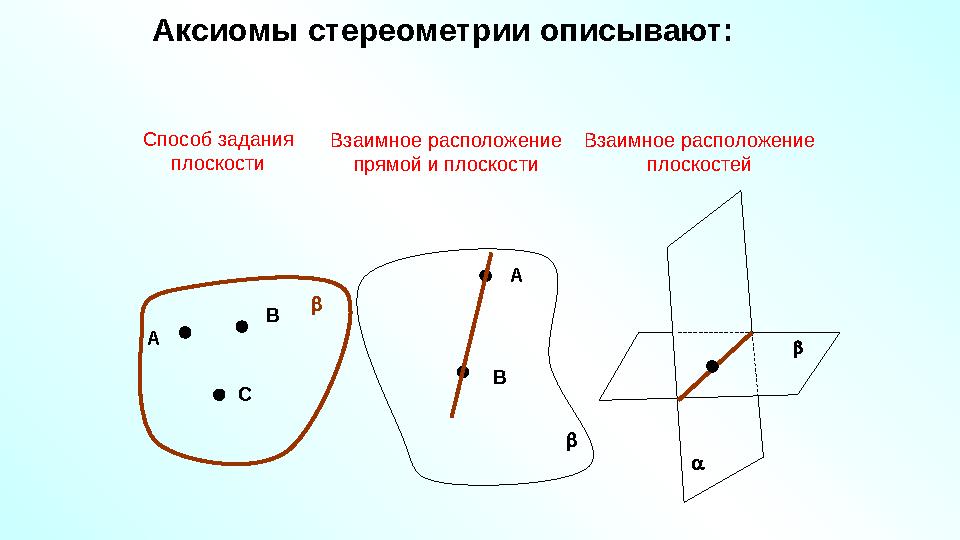
Аксиомы стереометрии описывают:
А В
С Способ задания
плоскости
А
ВВзаимное расположение
прямой и плоскости
a Взаимное расположение
плоскостей
26 слайд
Аксиомы стереометрии описывают: А В С Способ задания плоскости А ВВзаимное расположение прямой и плоскости a Взаимное расположение плоскостей
#27 слайд
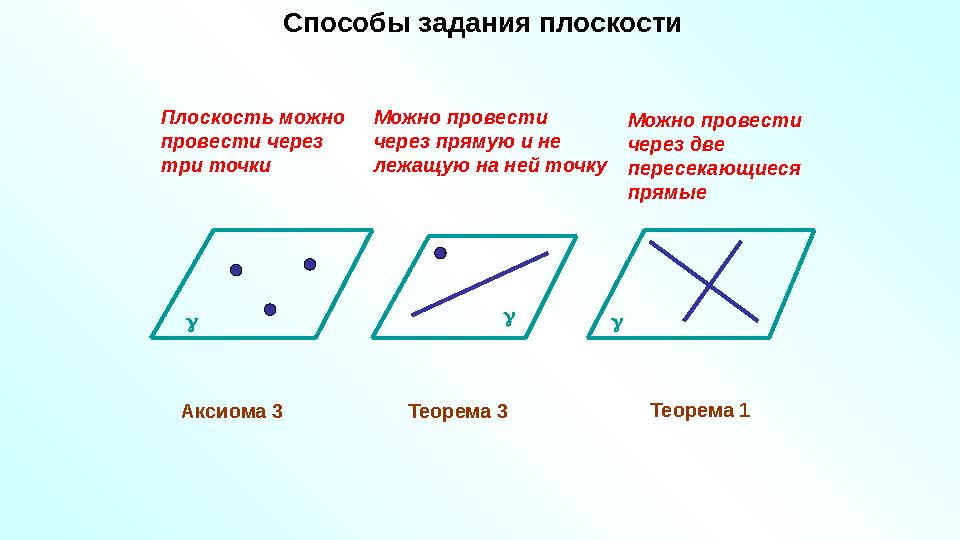
Способы задания плоскости
Плоскость можно
провести через
три точки
Можно провести
через прямую и не
лежащую на ней точку
Аксиома 3 Теорема 3
Теорема 1Можно провести
через две
пересекающиеся
прямые
27 слайд
Способы задания плоскости Плоскость можно провести через три точки Можно провести через прямую и не лежащую на ней точку Аксиома 3 Теорема 3 Теорема 1Можно провести через две пересекающиеся прямые
#28 слайд
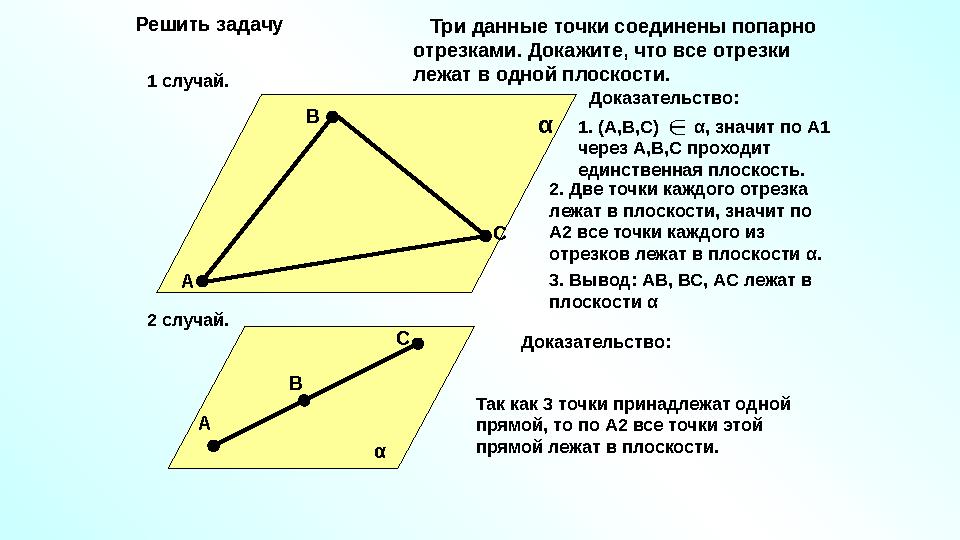
Решить задачу
А В
С α Три данные точки соединены попарно
отрезками. Докажите, что все отрезки
лежат в одной плоскости.
Доказательство:
1. (А,В,С) α , значит по А1
через А,В,С проходит
единственная плоскость.
2. Две точки каждого отрезка
лежат в плоскости, значит по
А2 все точки каждого из
отрезков лежат в плоскости α .
3. Вывод: АВ, ВС, АС лежат в
плоскости α1 случай.
А В С
α2 случай.
Доказательство:
Так как 3 точки принадлежат одной
прямой, то по А2 все точки этой
прямой лежат в плоскости.
28 слайд
Решить задачу А В С α Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости. Доказательство: 1. (А,В,С) α , значит по А1 через А,В,С проходит единственная плоскость. 2. Две точки каждого отрезка лежат в плоскости, значит по А2 все точки каждого из отрезков лежат в плоскости α . 3. Вывод: АВ, ВС, АС лежат в плоскости α1 случай. А В С α2 случай. Доказательство: Так как 3 точки принадлежат одной прямой, то по А2 все точки этой прямой лежат в плоскости.
#29 слайд
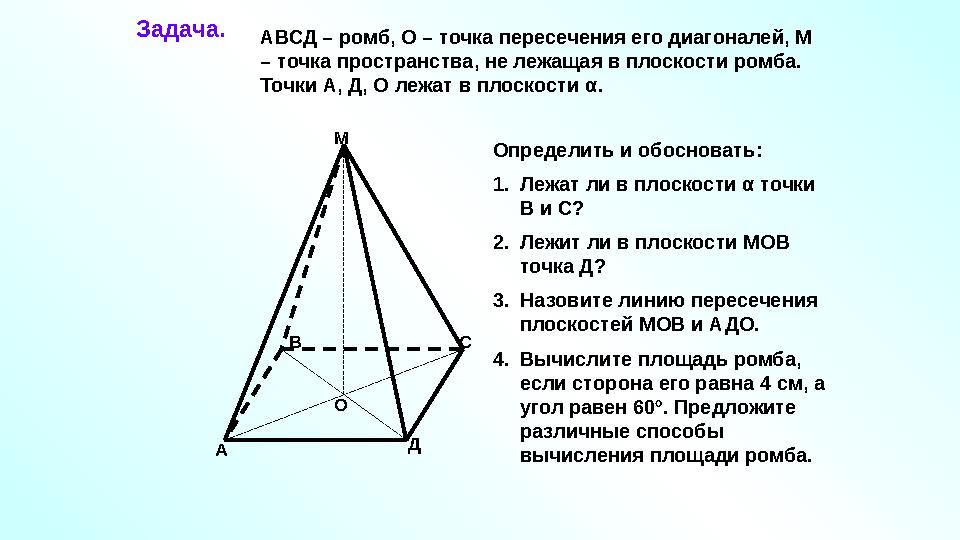
Задача.
А В
С
ДМ
ОАВСД – ромб, О – точка пересечения его диагоналей, М
– точка пространства, не лежащая в плоскости ромба.
Точки А, Д, О лежат в плоскости α .
Определить и обосновать:
1. Лежат ли в плоскости α точки
В и С?
2. Лежит ли в плоскости МОВ
точка Д?
3. Назовите линию пересечения
плоскостей МОВ и АДО.
4. Вычислите площадь ромба,
если сторона его равна 4 см, а
угол равен 60 º . Предложите
различные способы
вычисления площади ромба.
29 слайд
Задача. А В С ДМ ОАВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α . Определить и обосновать: 1. Лежат ли в плоскости α точки В и С? 2. Лежит ли в плоскости МОВ точка Д? 3. Назовите линию пересечения плоскостей МОВ и АДО. 4. Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60 º . Предложите различные способы вычисления площади ромба.
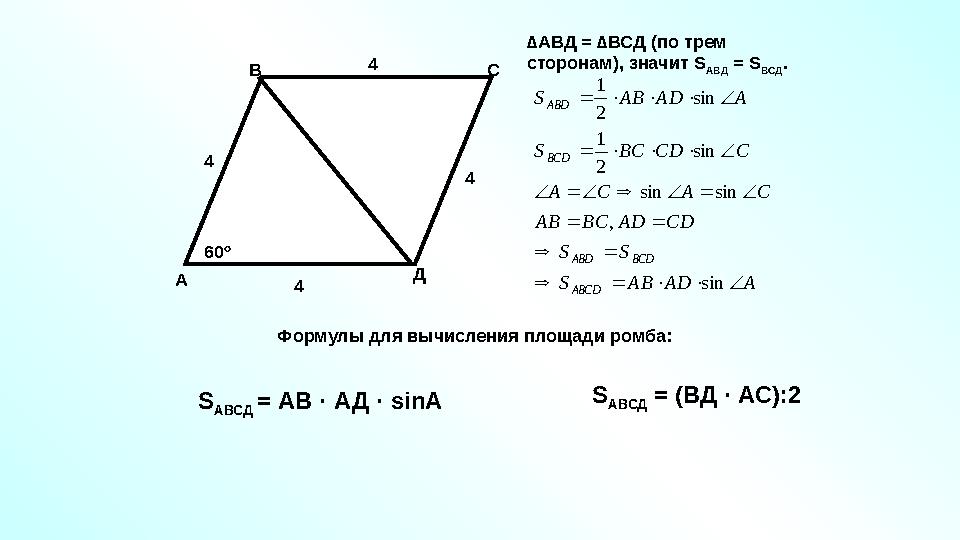
#30 слайд
А В
С
Д60 º4
44
4
S
АВСД = АВ · АД · sinA S
АВСД = (ВД · АС):2 Формулы для вычисления площади ромба: ∆ АВД = ∆ВСД (по трем
сторонам), значит S
АВД = S
ВСД .A AD AB S
S S
CD AD BC AB
C A C A
C CD BC S
A AD AB S
ABCD
BCD ABD
BCD
ABD
sin
,
sin sin
sin
2
1
sin
2
1
30 слайд
А В С Д60 º4 44 4 S АВСД = АВ · АД · sinA S АВСД = (ВД · АС):2 Формулы для вычисления площади ромба: ∆ АВД = ∆ВСД (по трем сторонам), значит S АВД = S ВСД .A AD AB S S S CD AD BC AB C A C A C CD BC S A AD AB S ABCD BCD ABD BCD ABD sin , sin sin sin 2 1 sin 2 1
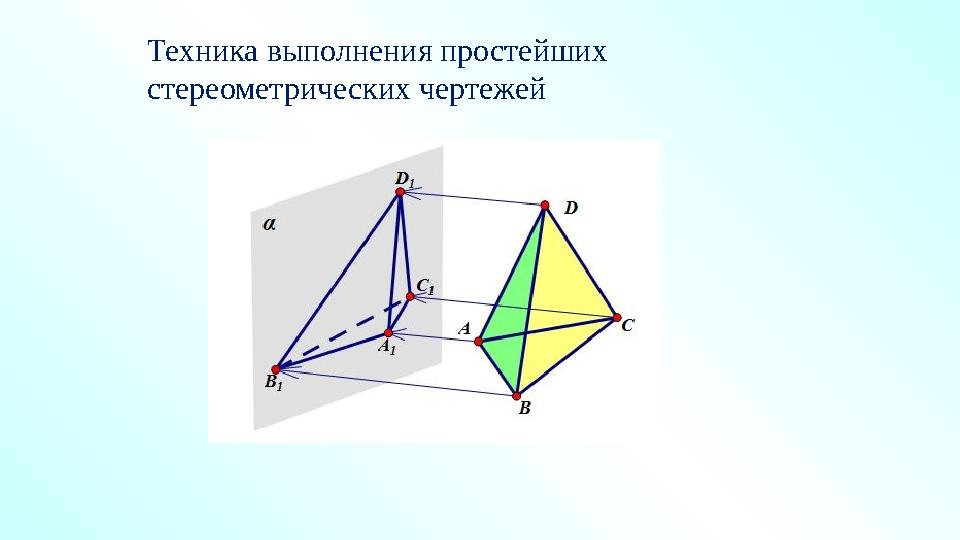
#31 слайд
Техника выполнения простейших
стереометрических чертежей
31 слайд
Техника выполнения простейших стереометрических чертежей
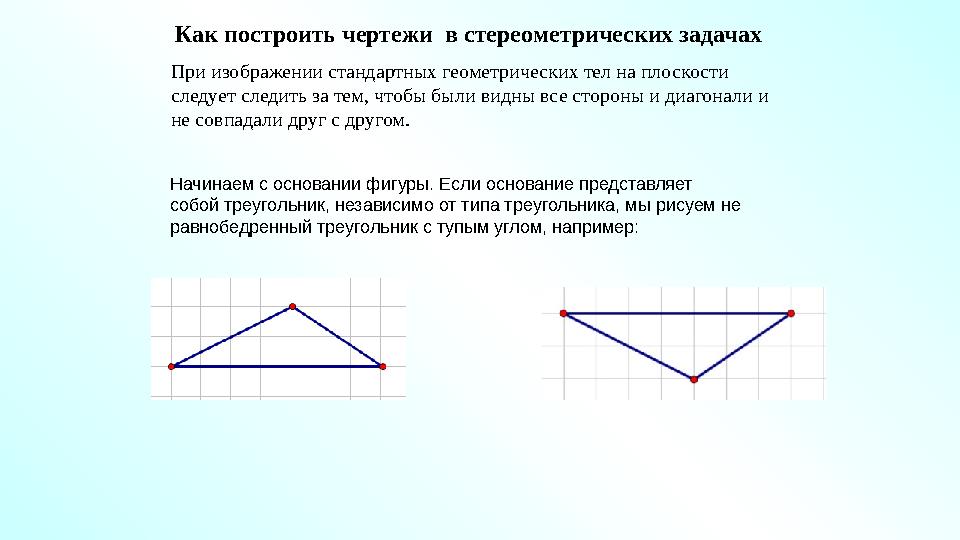
#32 слайд
Как построить чертежи в стереометрических задачах
При изображении стандартных геометрических тел на плоскости
следует следить за тем, чтобы были видны все стороны и диагонали и
не совпадали друг с другом.
Начинаем с основании фигуры. Если основание представляет
собой треугольник, независимо от типа треугольника, мы рисуем не
равнобедренный треугольник с тупым углом, например:
32 слайд
Как построить чертежи в стереометрических задачах При изображении стандартных геометрических тел на плоскости следует следить за тем, чтобы были видны все стороны и диагонали и не совпадали друг с другом. Начинаем с основании фигуры. Если основание представляет собой треугольник, независимо от типа треугольника, мы рисуем не равнобедренный треугольник с тупым углом, например:
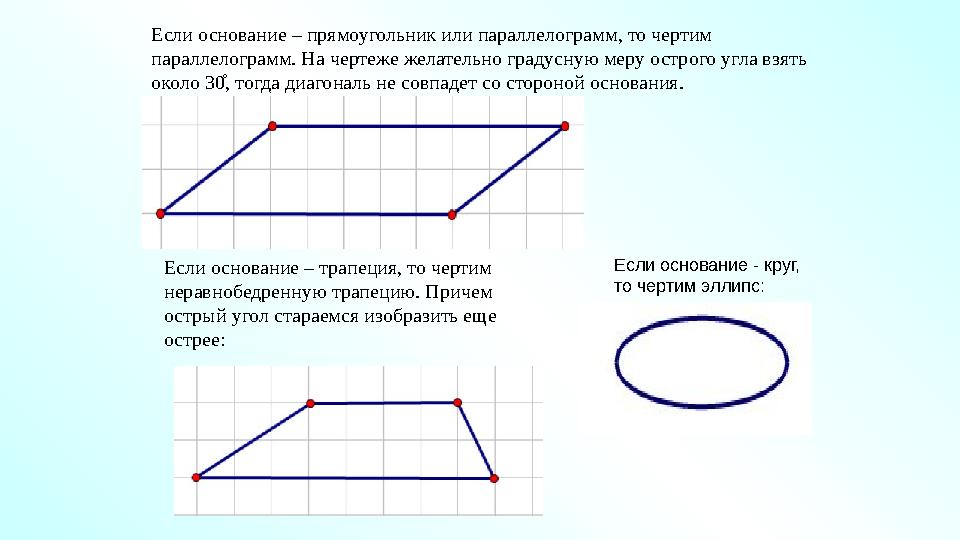
#33 слайд
Если основание – трапеция, то чертим
неравнобедренную трапецию. Причем
острый угол стараемся изобразить еще
острее: Если основание - круг,
то чертим эллипс:Если основание – прямоугольник или параллелограмм, то чертим
параллелограмм. На чертеже желательно градусную меру острого угла взять
около 301 , тогда диагональ не совпадет со стороной основания.
33 слайд
Если основание – трапеция, то чертим неравнобедренную трапецию. Причем острый угол стараемся изобразить еще острее: Если основание - круг, то чертим эллипс:Если основание – прямоугольник или параллелограмм, то чертим параллелограмм. На чертеже желательно градусную меру острого угла взять около 301 , тогда диагональ не совпадет со стороной основания.
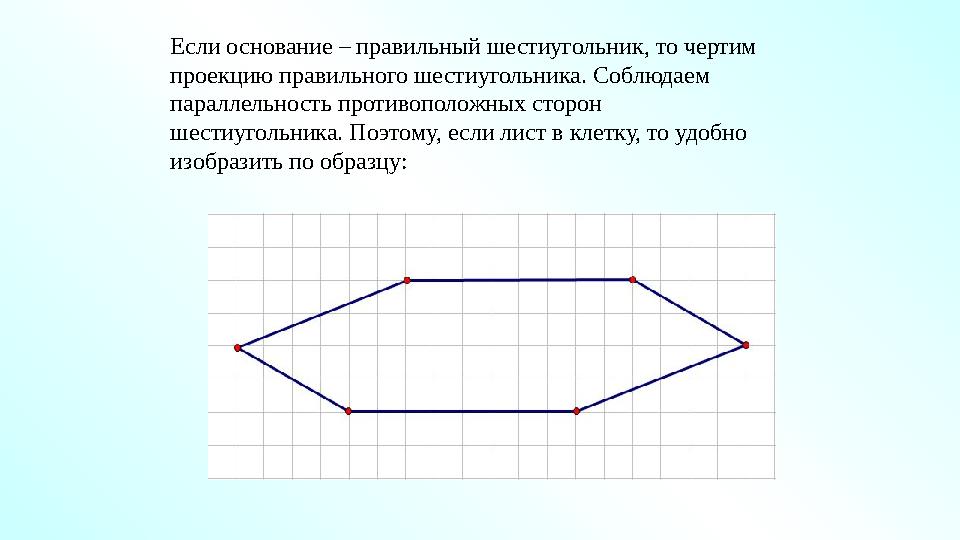
#34 слайд
Если основание – правильный шестиугольник, то чертим
проекцию правильного шестиугольника. Соблюдаем
параллельность противоположных сторон
шестиугольника. Поэтому, если лист в клетку, то удобно
изобразить по образцу:
34 слайд
Если основание – правильный шестиугольник, то чертим проекцию правильного шестиугольника. Соблюдаем параллельность противоположных сторон шестиугольника. Поэтому, если лист в клетку, то удобно изобразить по образцу:
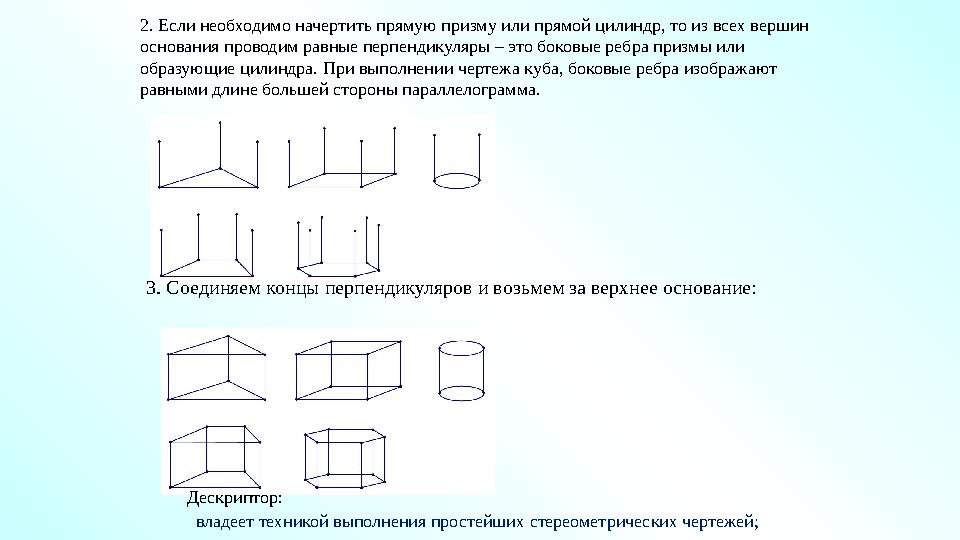
#35 слайд
3. Соединяем концы перпендикуляров и возьмем за верхнее основание:2. Если необходимо начертить прямую призму или прямой цилиндр, то из всех вершин
основания проводим равные перпендикуляры – это боковые ребра призмы или
образующие цилиндра. При выполнении чертежа куба, боковые ребра изображают
равными длине большей стороны параллелограмма.
Дескриптор:
владеет техникой выполнения простейших стереометрических чертежей;
35 слайд
3. Соединяем концы перпендикуляров и возьмем за верхнее основание:2. Если необходимо начертить прямую призму или прямой цилиндр, то из всех вершин основания проводим равные перпендикуляры – это боковые ребра призмы или образующие цилиндра. При выполнении чертежа куба, боковые ребра изображают равными длине большей стороны параллелограмма. Дескриптор: владеет техникой выполнения простейших стереометрических чертежей;
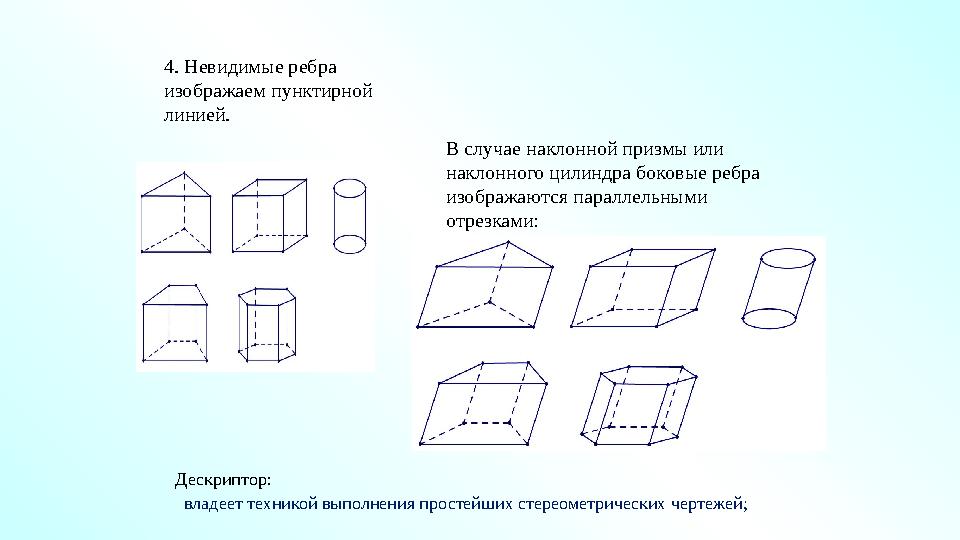
#36 слайд
4. Невидимые ребра
изображаем пунктирной
линией.
В случае наклонной призмы или
наклонного цилиндра боковые ребра
изображаются параллельными
отрезками:
Дескриптор:
владеет техникой выполнения простейших стереометрических чертежей;
36 слайд
4. Невидимые ребра изображаем пунктирной линией. В случае наклонной призмы или наклонного цилиндра боковые ребра изображаются параллельными отрезками: Дескриптор: владеет техникой выполнения простейших стереометрических чертежей;
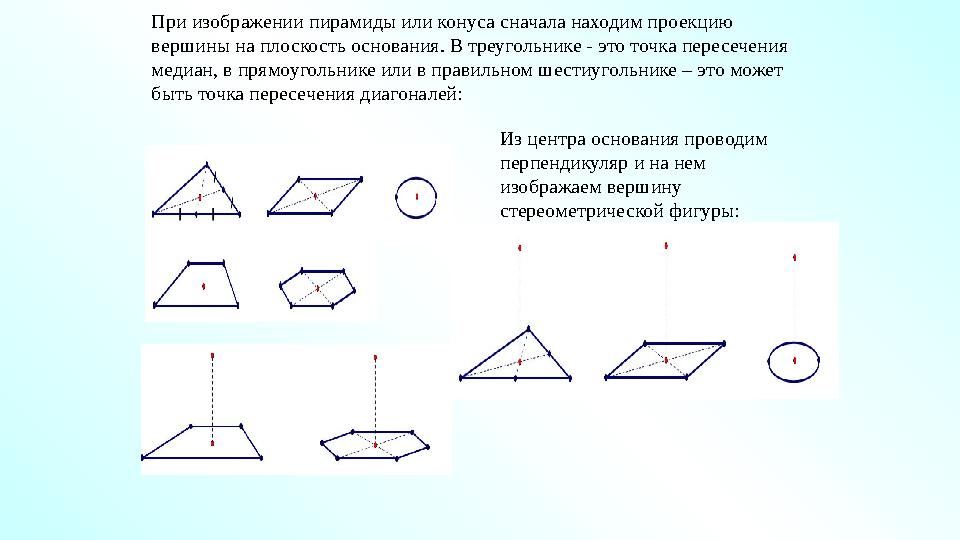
#37 слайд
Из центра основания проводим
перпендикуляр и на нем
изображаем вершину
стереометрической фигуры:При изображении пирамиды или конуса сначала находим проекцию
вершины на плоскость основания. В треугольнике - это точка пересечения
медиан, в прямоугольнике или в правильном шестиугольнике – это может
быть точка пересечения диагоналей:
37 слайд
Из центра основания проводим перпендикуляр и на нем изображаем вершину стереометрической фигуры:При изображении пирамиды или конуса сначала находим проекцию вершины на плоскость основания. В треугольнике - это точка пересечения медиан, в прямоугольнике или в правильном шестиугольнике – это может быть точка пересечения диагоналей:
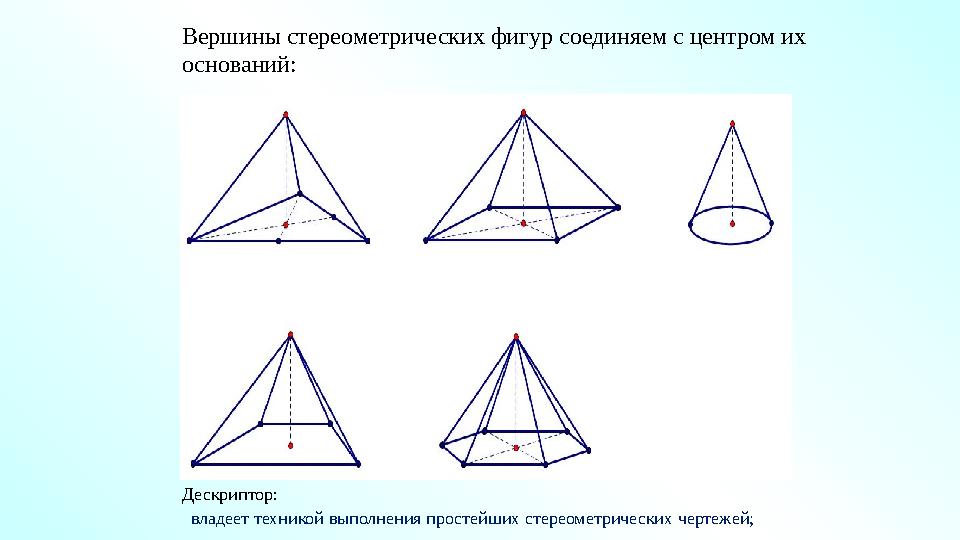
#38 слайд
Вершины стереометрических фигур соединяем с центром их
оснований:
Дескриптор:
владеет техникой выполнения простейших стереометрических чертежей;
38 слайд
Вершины стереометрических фигур соединяем с центром их оснований: Дескриптор: владеет техникой выполнения простейших стереометрических чертежей;
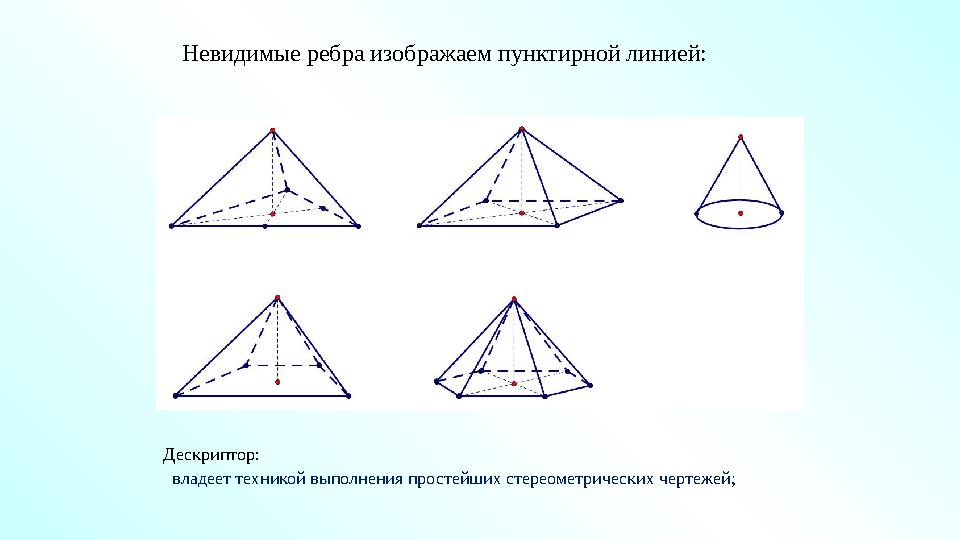
#39 слайд
Невидимые ребра изображаем пунктирной линией:
Дескриптор:
владеет техникой выполнения простейших стереометрических чертежей;
39 слайд
Невидимые ребра изображаем пунктирной линией: Дескриптор: владеет техникой выполнения простейших стереометрических чертежей;
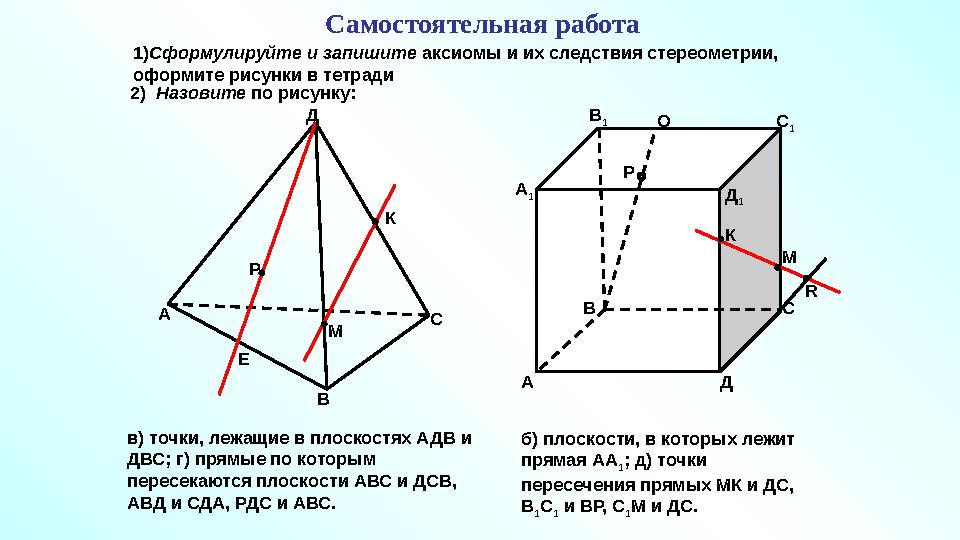
#40 слайд
А
В СД
Р
Е К
М
А В С
ДА
1 В
1
С
1
Д
1Q
P
RК
М2) Назовите по рисунку:
в) точки, лежащие в плоскостях АДВ и
ДВС; г) прямые по которым
пересекаются плоскости АВС и ДСВ,
АВД и СДА, РДС и АВС. б) плоскости, в которых лежит
прямая АА
1 ; д) точки
пересечения прямых МК и ДС,
В
1 С
1 и ВР, С
1 М и ДС.1) Сформулируйте и запишите аксиомы и их следствия стереометрии,
оформите рисунки в тетради Самостоятельная работа
40 слайд
А В СД Р Е К М А В С ДА 1 В 1 С 1 Д 1Q P RК М2) Назовите по рисунку: в) точки, лежащие в плоскостях АДВ и ДВС; г) прямые по которым пересекаются плоскости АВС и ДСВ, АВД и СДА, РДС и АВС. б) плоскости, в которых лежит прямая АА 1 ; д) точки пересечения прямых МК и ДС, В 1 С 1 и ВР, С 1 М и ДС.1) Сформулируйте и запишите аксиомы и их следствия стереометрии, оформите рисунки в тетради Самостоятельная работа
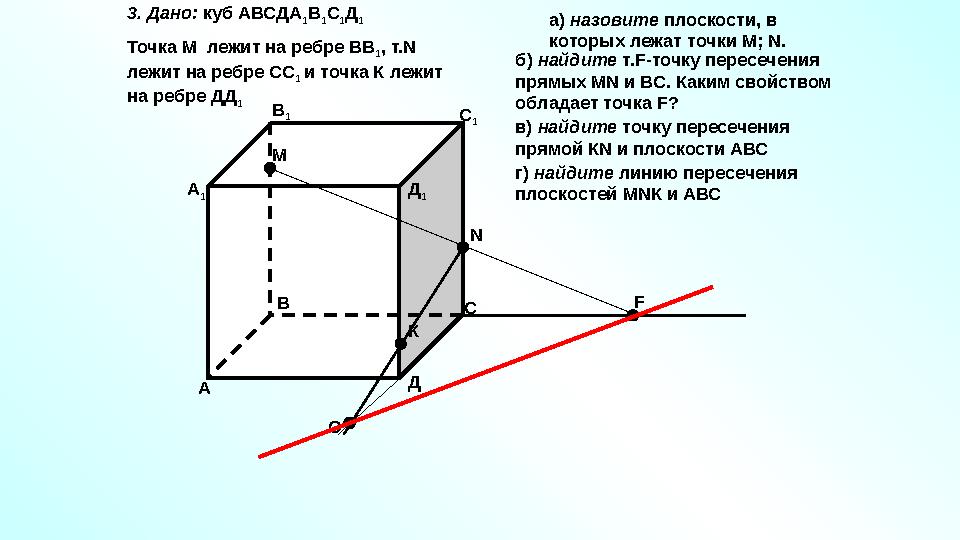
#41 слайд
А В
С
ДА
1 В
1
С
1
Д
1М
N
F
К3. Дано: куб АВСДА
1 В
1 С
1 Д
1
Точка М лежит на ребре ВВ
1 , т. N
лежит на ребре СС
1 и точка К лежит
на ребре ДД
1 а) назовите плоскости, в
которых лежат точки М; N .
б) найдите т. F- точку пересечения
прямых М N и ВС. Каким свойством
обладает точка F ?
в) найдите точку пересечения
прямой К N и плоскости АВС
О г) найдите линию пересечения
плоскостей М N К и АВС
41 слайд
А В С ДА 1 В 1 С 1 Д 1М N F К3. Дано: куб АВСДА 1 В 1 С 1 Д 1 Точка М лежит на ребре ВВ 1 , т. N лежит на ребре СС 1 и точка К лежит на ребре ДД 1 а) назовите плоскости, в которых лежат точки М; N . б) найдите т. F- точку пересечения прямых М N и ВС. Каким свойством обладает точка F ? в) найдите точку пересечения прямой К N и плоскости АВС О г) найдите линию пересечения плоскостей М N К и АВС
#42 слайд
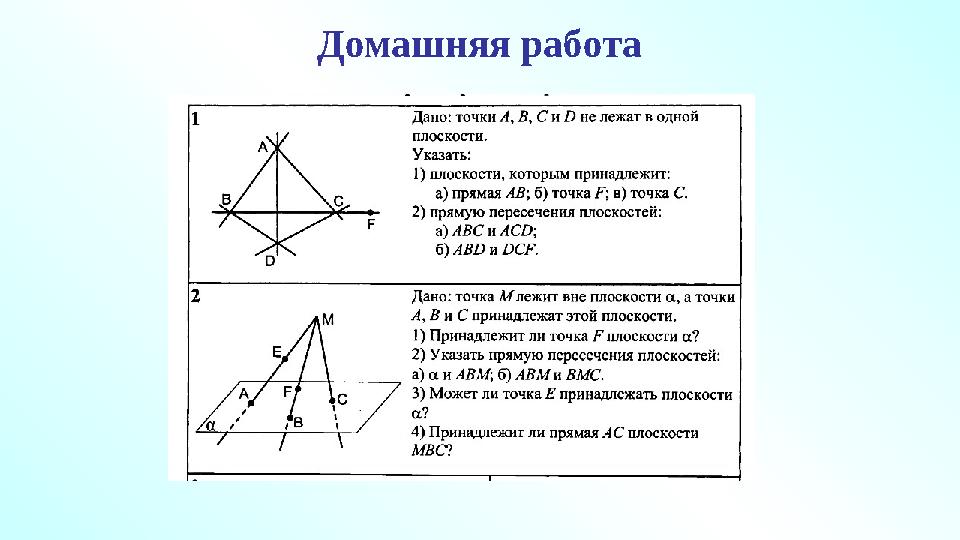
Домашняя работа
42 слайд
Домашняя работа
#43 слайд
43 слайд

#44 слайд
6. Точка С – общая точка плоскостей α и β. Прямая l проходит через точку С. Верно ли, что
плоскости α и β пересекаются по прямой l . Ответ обоснуйте.
7. Через прямую а и точку А можно провести две различные плоскости. Каково взаимное
расположение точки А и прямой а ? Ответ обоснуйте.
8. Прямые a , b и c имеют общую точку. Верно ли, что данные прямые лежат в одной
плоскости? Ответ обоснуйте.
9. Плоскости α и β пересекаются по прямой l . Прямая а лежит в плоскости α и пересекает
плоскость β. Каково взаимное расположение прямых а и l ? Ответ обоснуйте.
10. Четыре прямые попарно пересекаются. Верно ли, что если три из них лежат в одной
плоскости, то все четыре прямые лежат в одной плоскости? Ответ обоснуйте.
44 слайд
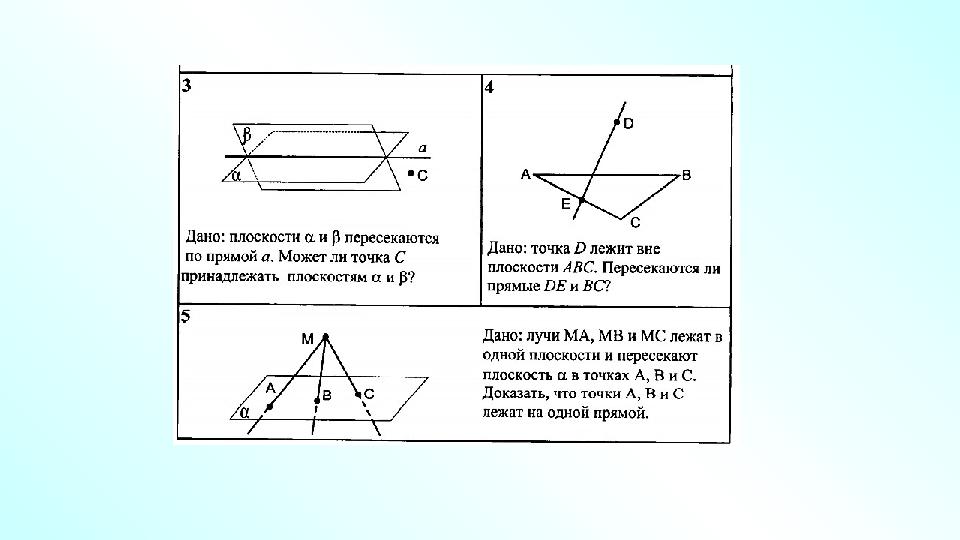
6. Точка С – общая точка плоскостей α и β. Прямая l проходит через точку С. Верно ли, что плоскости α и β пересекаются по прямой l . Ответ обоснуйте. 7. Через прямую а и точку А можно провести две различные плоскости. Каково взаимное расположение точки А и прямой а ? Ответ обоснуйте. 8. Прямые a , b и c имеют общую точку. Верно ли, что данные прямые лежат в одной плоскости? Ответ обоснуйте. 9. Плоскости α и β пересекаются по прямой l . Прямая а лежит в плоскости α и пересекает плоскость β. Каково взаимное расположение прямых а и l ? Ответ обоснуйте. 10. Четыре прямые попарно пересекаются. Верно ли, что если три из них лежат в одной плоскости, то все четыре прямые лежат в одной плоскости? Ответ обоснуйте.

шағым қалдыра аласыз
















