Аксиомы стереометрии. Взаимное расположение двух прямых в пространстве. Параллельность прямой и плоскости.

1 слайд
Аксиомы стереометрии Взаимное расположение двух прямых Преподаватель Айменова Сая Смагуловна Взаимное расположение прямой и плоскости

2 слайд
ГеометрияГеометрия ПланиметрияПланиметрия СтереометриСтереометри яя stereos - объемный, пространственный metreo - измеряюГеометрияГеометрия ПланиметрияПланиметрия СтереометриСтереометри яя

3 слайд
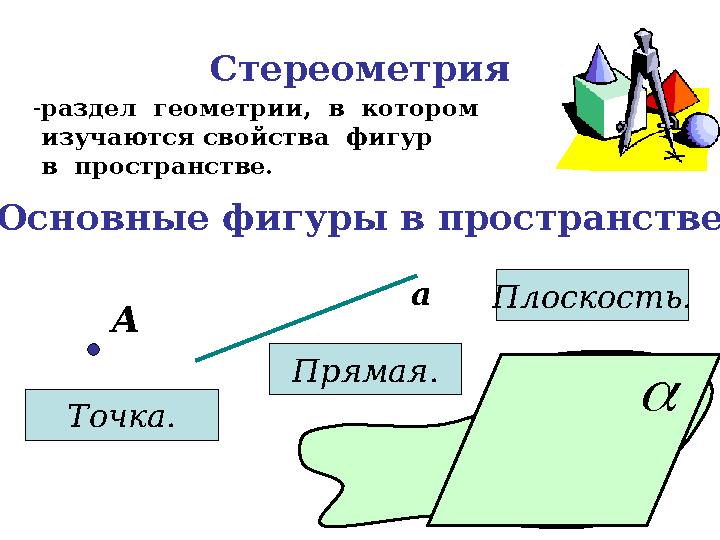
Стереометрия - раздел геометрии, в котором изучаются свойства фигур в пространстве. Основные фигуры в пространстве А Точка. а Прямая. Плоскость. 

4 слайд
A, B, C, … a, b, c, … или A В , B С , CD, …,  ,  , 

5 слайд
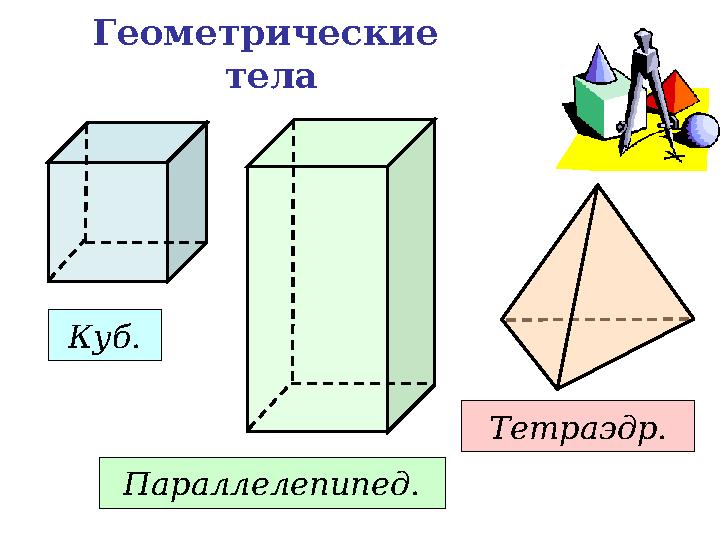
Геометрические тела Куб. Параллелепипед. Тетраэдр.

6 слайд
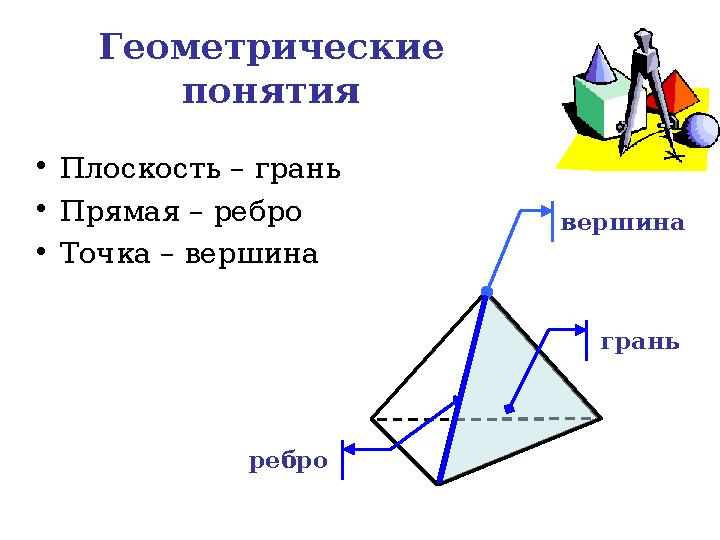
Геометрические понятия • Плоскость – грань • Прямая – ребро • Точка – вершина вершина грань ребро

7 слайд
Аксиома (от греч. ax íõ ma – принятие положения) исходное положение научной теории, принимаемое без доказательства

8 слайд
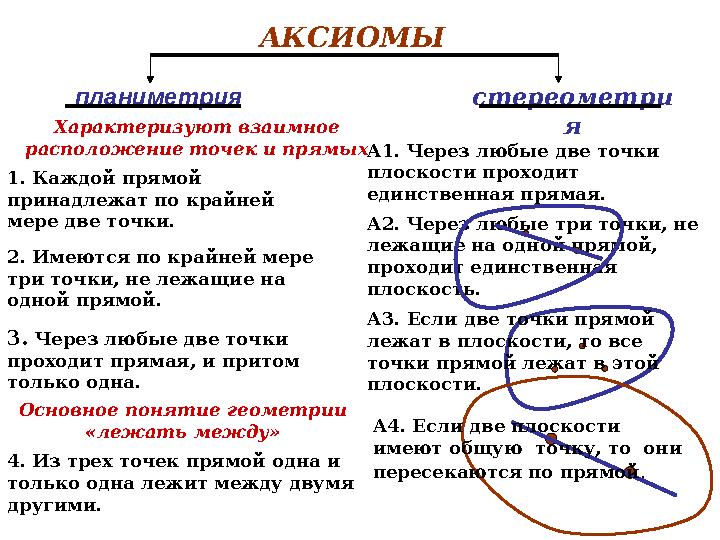
АКСИОМЫ планиметрия стереометри я 1. Каждой прямой принадлежат по крайней мере две точки. 2. Имеются по крайней мере три точки, не лежащие на одной прямой. 3. Через любые две точки проходит прямая, и притом только одна. Характеризуют взаимное расположение точек и прямых Основное понятие геометрии «лежать между» 4. Из трех точек прямой одна и только одна лежит между двумя другими. А2. Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость. А3. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. А4. Если две плоскости имеют общую точку, то они пересекаются по прямой .А1. Через любые две точки плоскости проходит единственная прямая.

9 слайд
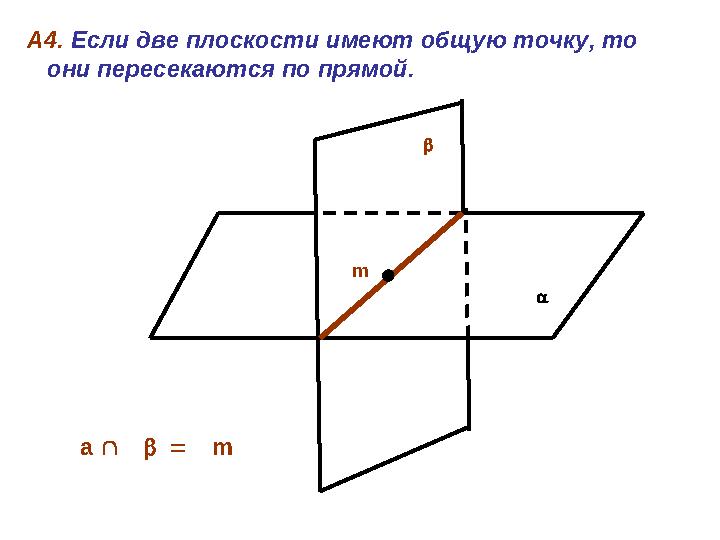
А4. Если две плоскости имеют общую точку, то они пересекаются по прямой.  а  m m

10 слайд
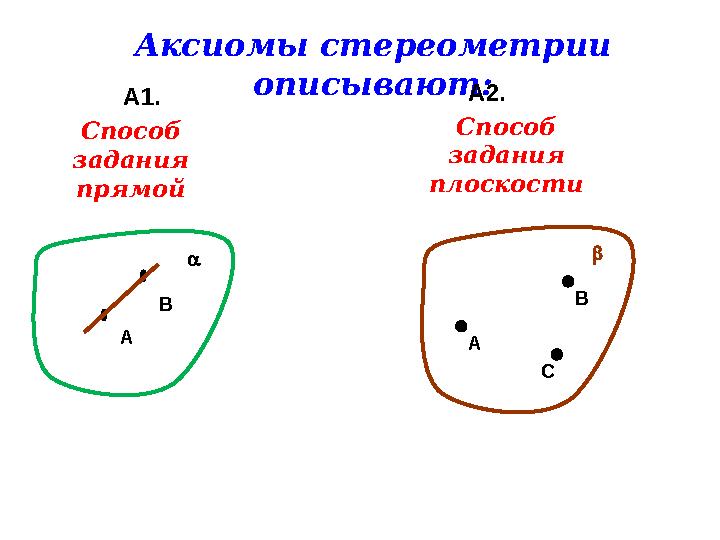
Аксиомы стереометрии описывают: А1. А2. А В С Способ задания прямой  Способ задания плоскости А В

11 слайд
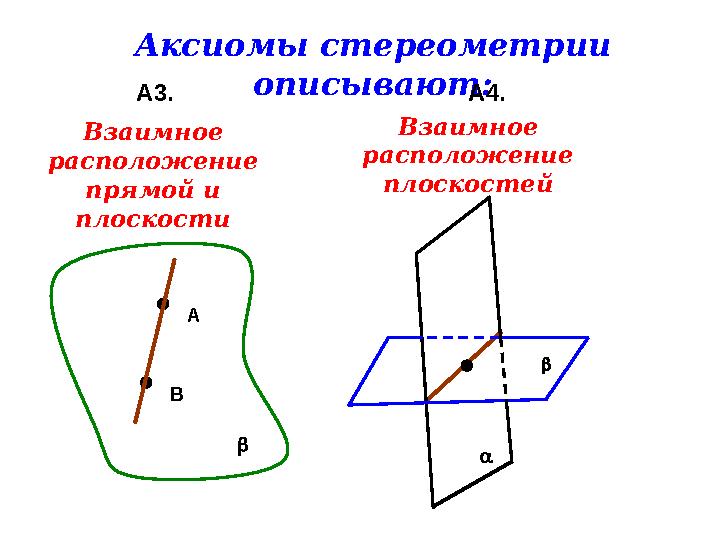
Аксиомы стереометрии описывают: А3. А4. А ВВзаимное расположение прямой и плоскости  Взаимное расположение плоскостей

12 слайд
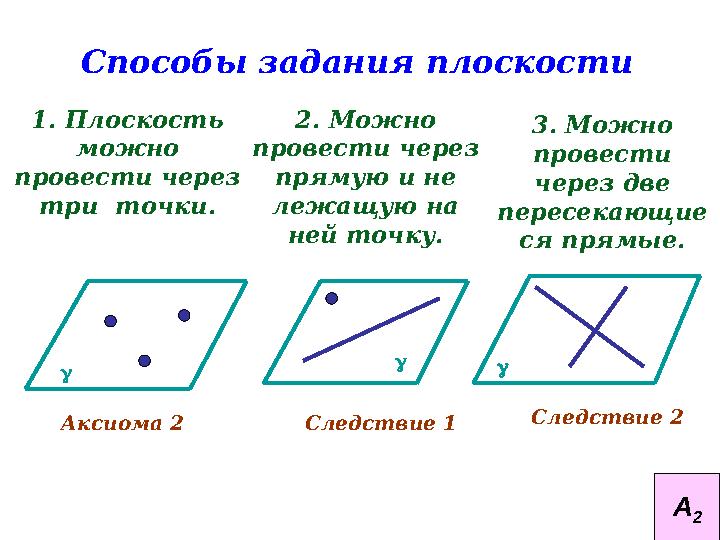
Способы задания плоскости 1. Плоскость можно провести через три точки. 2. Можно провести через прямую и не лежащую на ней точку. Аксиома 2 Следствие 1  Следствие 2 3. Можно провести через две пересекающие ся прямые. А 2

13 слайд
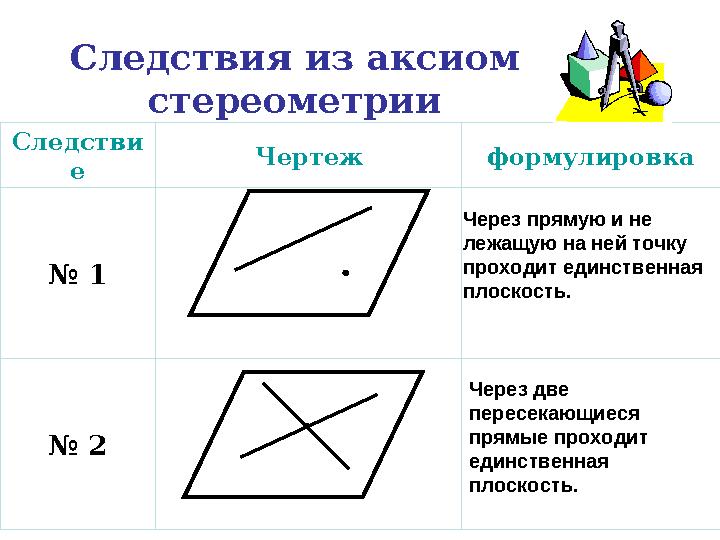
Следствия из аксиом стереометрии Следстви е Чертеж формулировка № 1 № 2 Через прямую и не лежащую на ней точку проходит единственная плоскость. Через две пересекающиеся прямые проходит единственная плоскость.

14 слайд
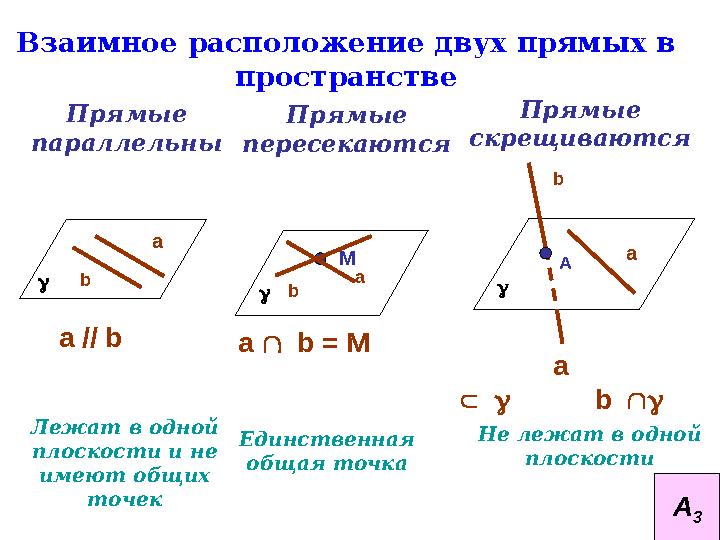
Взаимное расположение двух прямых в пространстве Прямые параллельны Прямые пересекаются Прямые скрещиваются Единственная общая точка Не лежат в одной плоскостиa // b а  b = M а   b  А 3 а b  М а b  аb A Лежат в одной плоскости и не имеют общих точек

15 слайд
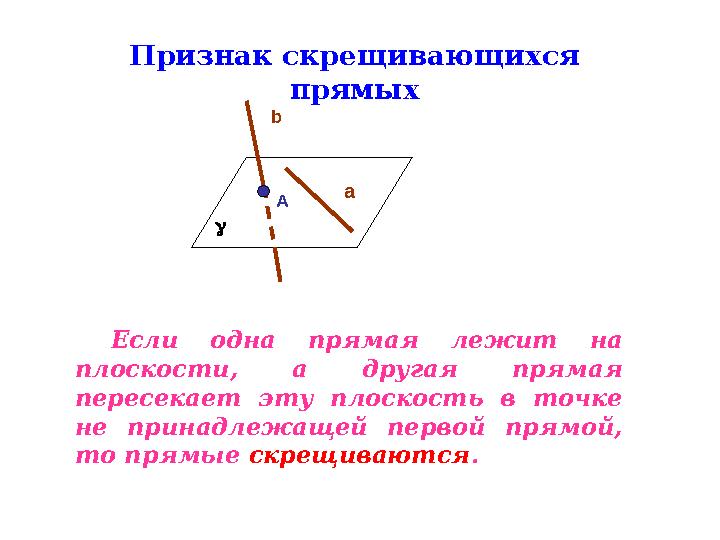
Признак скрещивающихся прямых  аb A Если одна прямая лежит на плоскости, а другая прямая пересекает эту плоскость в точке не принадлежащей первой прямой, то прямые скрещиваются .

16 слайд
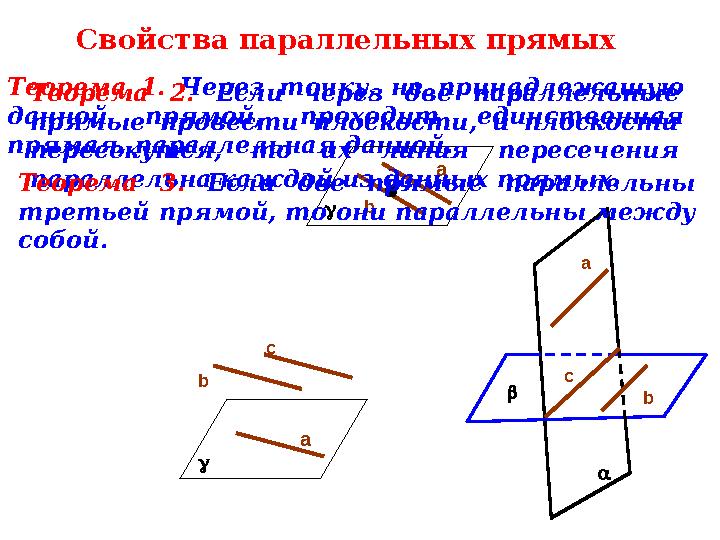
Свойства параллельных прямых bТеорема 1. Через точку, не принадлежащую данной прямой, проходит единственная прямая, параллельная данной.  а а bТеорема 2. Если через две параллельные прямые провести плоскости, и плоскости пересекутся, то их линия пересечения параллельна каждой из данных прямых. сТеорема 3. Если две прямые параллельны третьей прямой, то они параллельны между собой.  аb c

17 слайд
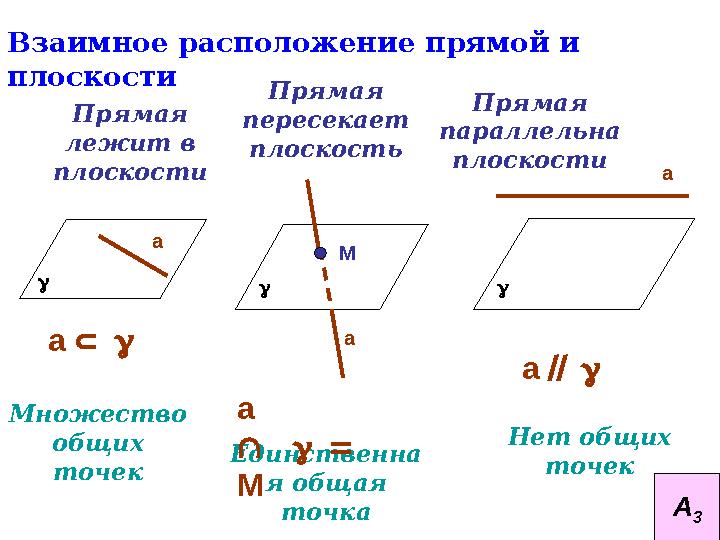
Взаимное расположение прямой и плоскости Прямая лежит в плоскости Прямая пересекает плоскость Прямая параллельна плоскости Множество общих точек Единственна я общая точка Нет общих точек а  аМ  а а  а  М а  А 3

18 слайд
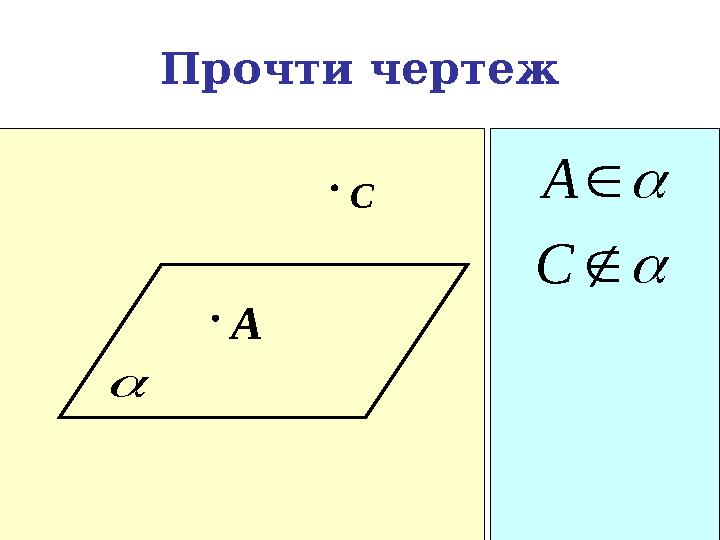
Прочти чертеж A С   A   C

19 слайд
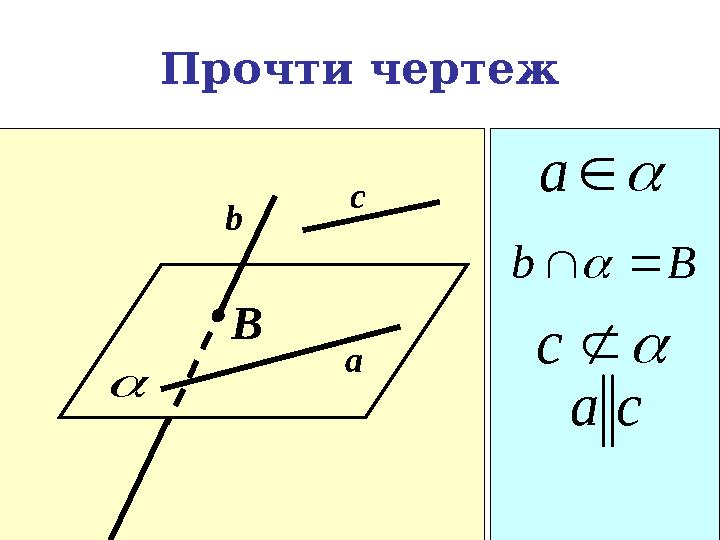
Прочти чертеж B c   a B b    b a   c c a

20 слайд
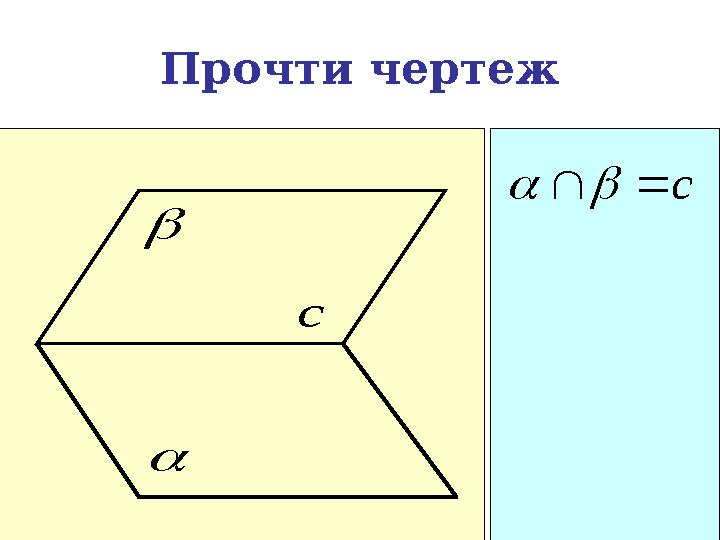
Прочти чертеж c      c

21 слайд
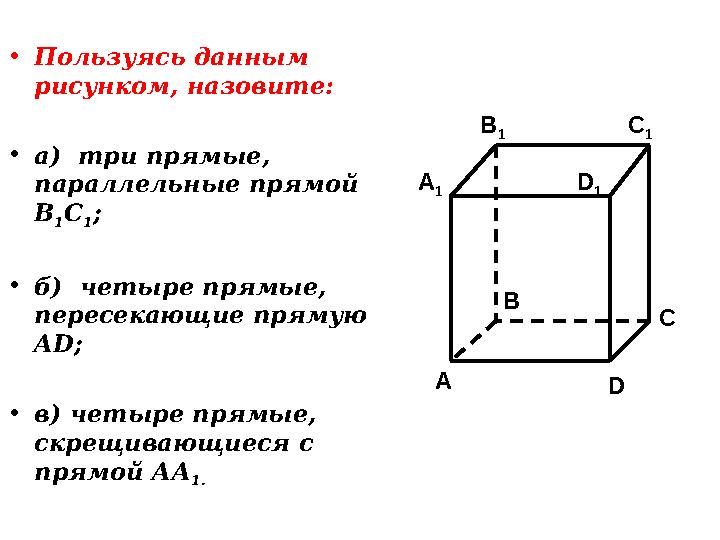
• Пользуясь данным рисунком, назовите: • а) три прямые, параллельные прямой В 1 С 1 ; • б) четыре прямые, пересекающие прямую AD ; • в) четыре прямые, скрещивающиеся с прямой АА 1. C 1 CA 1 B 1 D 1 A B D

22 слайд
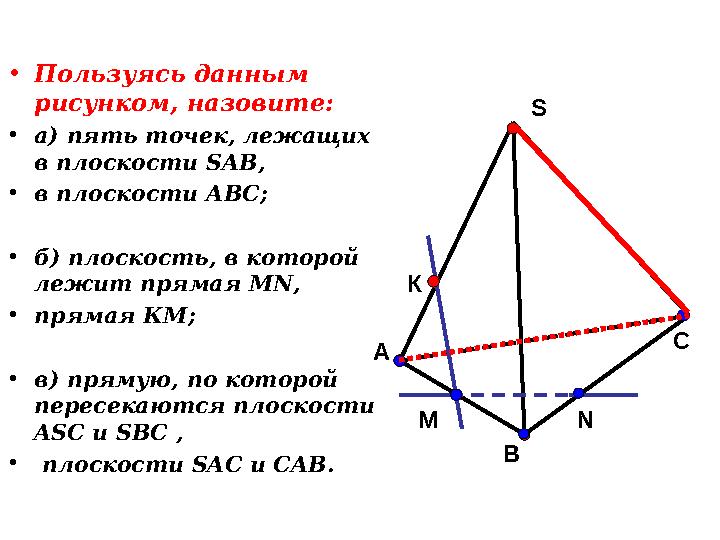
• Пользуясь данным рисунком, назовите: • а) пять точек, лежащих в плоскости SAB , • в плоскости АВС; • б) плоскость, в которой лежит прямая MN , • прямая КМ; • в) прямую, по которой пересекаются плоскости ASC и SBC , • плоскости SAC и CAB . К А ВМ S N C

23 слайд
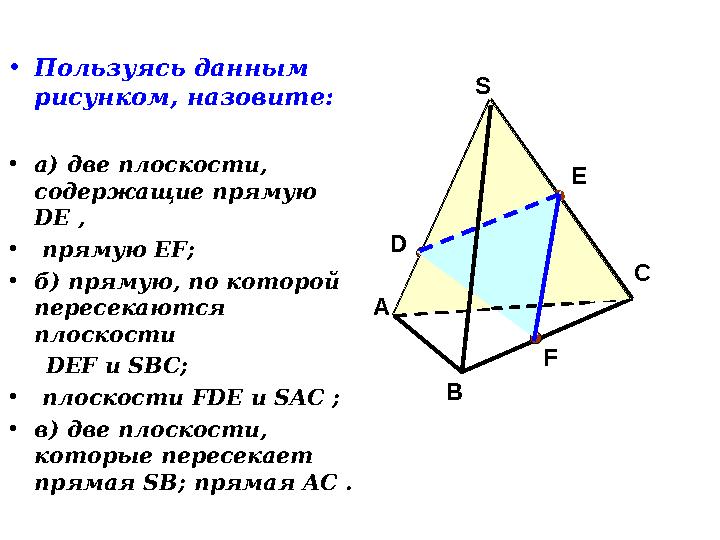
• Пользуясь данным рисунком, назовите: • а) две плоскости, содержащие прямую DE , • прямую EF ; • б) прямую, по которой пересекаются плоскости DEF и SBC ; • плоскости FDE и SAC ; • в) две плоскости, которые пересекает прямая SB ; прямая AC . А С В S D F E

24 слайд
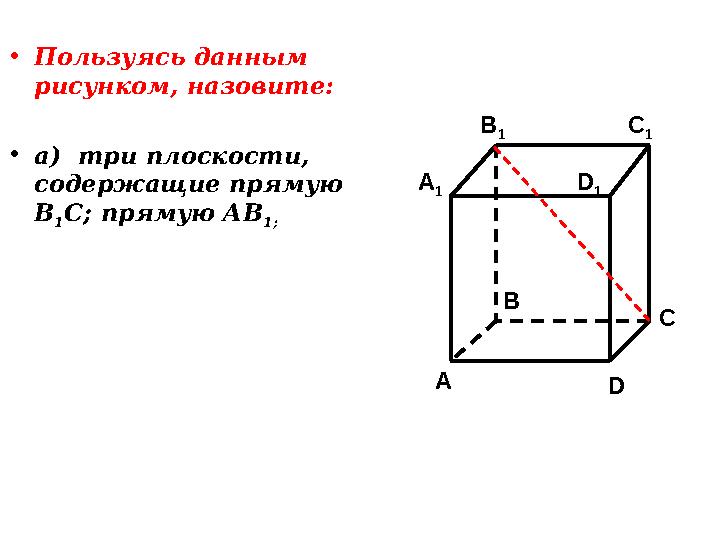
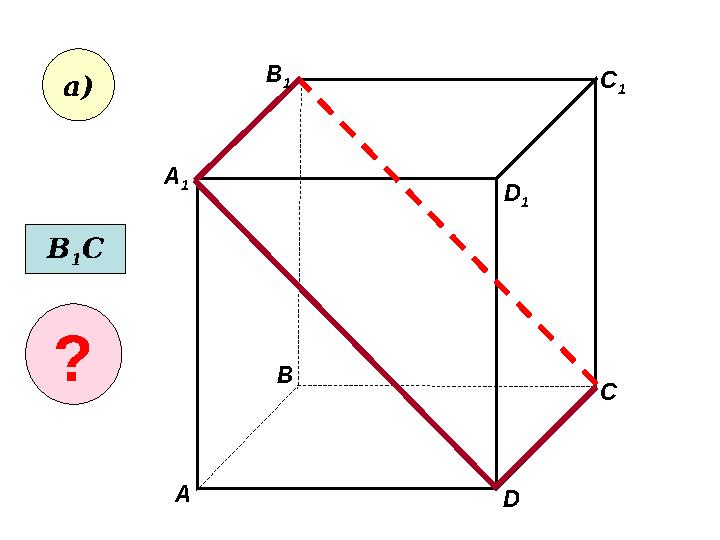
• Пользуясь данным рисунком, назовите: • а) три плоскости, содержащие прямую В 1 С; прямую АВ 1; C 1 CA 1 B 1 D 1 A B D

25 слайд
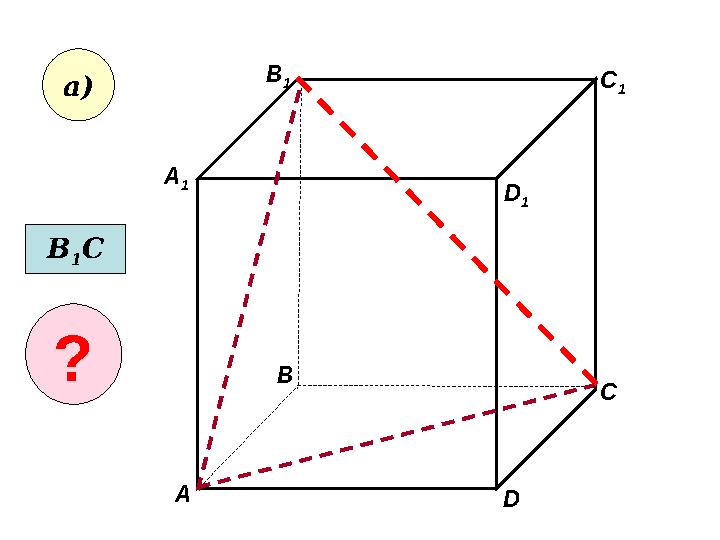
АА 1 ВВ 1 СD 1 D C 1 а) В 1 С ?

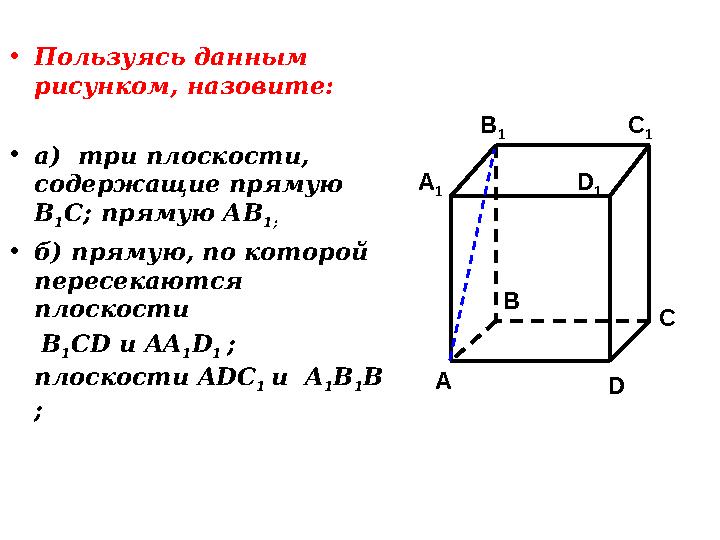
26 слайд
АА 1 ВВ 1 СD 1 D C 1 а) В 1 С ?

27 слайд
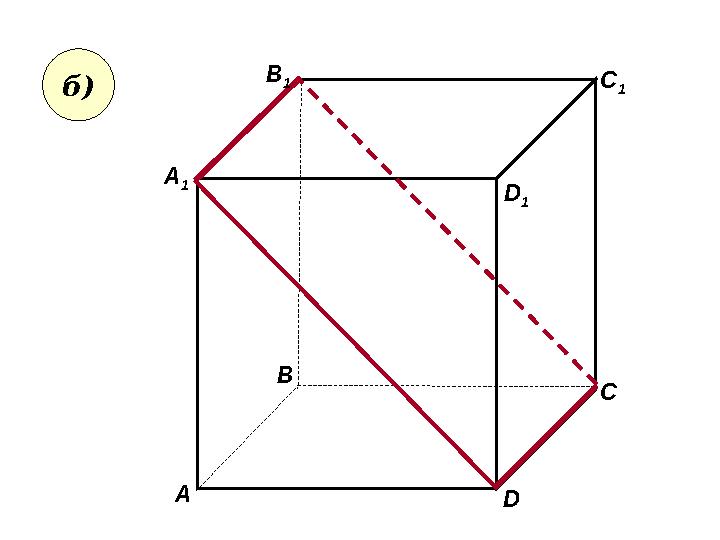
• Пользуясь данным рисунком, назовите: • а) три плоскости, содержащие прямую В 1 С; прямую АВ 1; • б) прямую, по которой пересекаются плоскости B 1 CD и AA 1 D 1 ; плоскости ADC 1 и A 1 B 1 B ; C 1 CA 1 B 1 D 1 A B D

28 слайд
АА 1 ВВ 1 СD 1 D C 1 б)

29 слайд
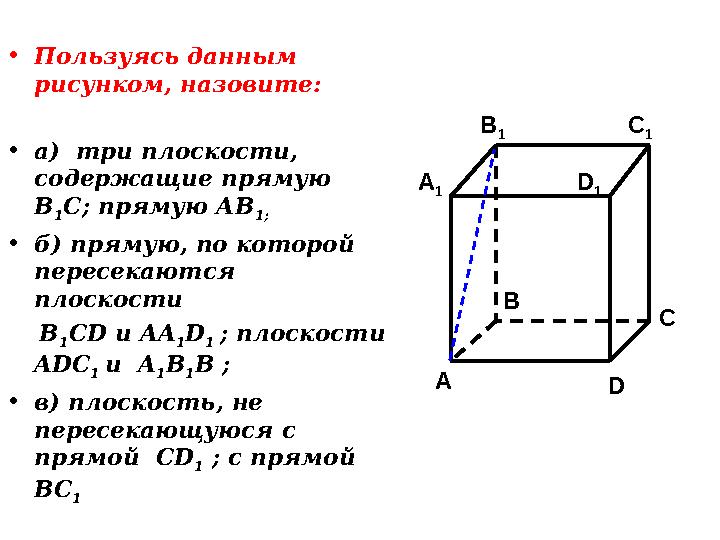
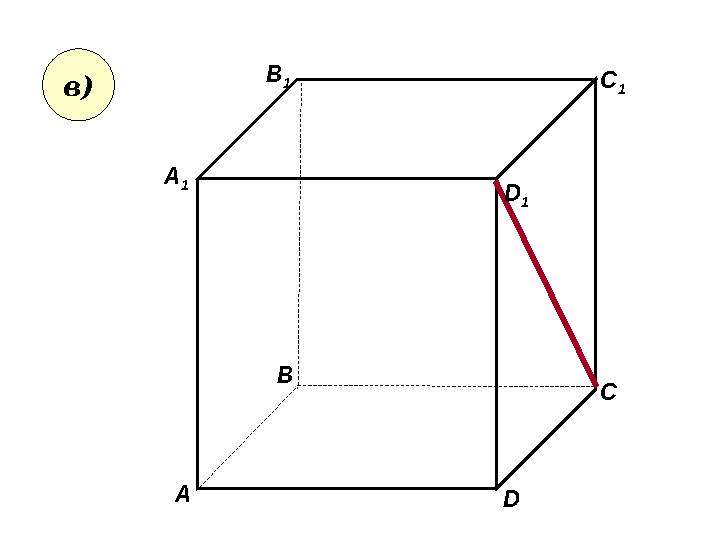
• Пользуясь данным рисунком, назовите: • а) три плоскости, содержащие прямую В 1 С; прямую АВ 1; • б) прямую, по которой пересекаются плоскости B 1 CD и AA 1 D 1 ; плоскости ADC 1 и A 1 B 1 B ; • в) плоскость, не пересекающуюся с прямой CD 1 ; с прямой BC 1 CC 1 A 1 B 1 D 1 A B D

30 слайд
АА 1 ВВ 1 СD 1 D C 1 в)

31 слайд
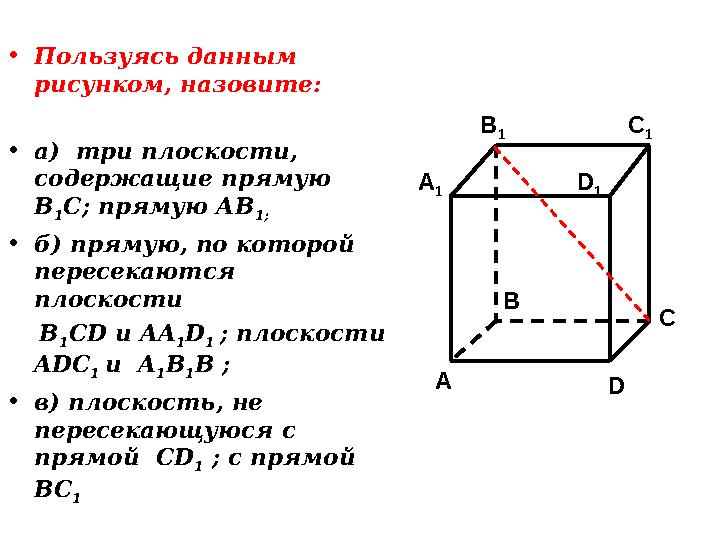
• Пользуясь данным рисунком, назовите: • а) три плоскости, содержащие прямую В 1 С; прямую АВ 1; • б) прямую, по которой пересекаются плоскости B 1 CD и AA 1 D 1 ; плоскости ADC 1 и A 1 B 1 B ; • в) плоскость, не пересекающуюся с прямой CD 1 ; с прямой BC 1 CC 1 A 1 B 1 D 1 A B D

32 слайд
Ответьте на вопросы: • Верно ли, что две прямые параллельны, если они не имеют общих точек? • Верно ли, что если две прямые не пересекаются, то они параллельны? • Верно ли, что через две точки можно провести множество плоскостей? • Верно ли, что если две прямые лежат в одной плоскости, то они параллельны? • Верно ли, что если две плоскости имеют общую точку, то они пересекаются по прямой? • Могут ли две пересекающиеся прямые не лежать в одной плоскости? Нет Нет Да Нет Да Да

33 слайд
Домашнее задание: 1) Выучить аксиомы и следствия из них. 2) Выучить определения и теоремы Успехов!