Ашық сабақ Көпбұрыш және оның түрлері 7 сынып

1 слайд
Дұрыс көпбұрыштар және олардың қасиеттері. Дұрыс көпбұрыштарды құру

2 слайд
Сабақтың мақсаты Барлық оқушылар:  көпбұрыш және оның түрлері н сипаттайды ; Оқушылардың басым бөлігі:  көпбұрыштың диагональдарын анықтай алады; Кейбір оқушылар:  дұрыс көпбұрыш сала алады.

3 слайд
Сыныпты топқа бөлу Үй тапсырмасын тексеру Дәптерлерін алмастырып, бірін-бірі бағалау

4 слайд
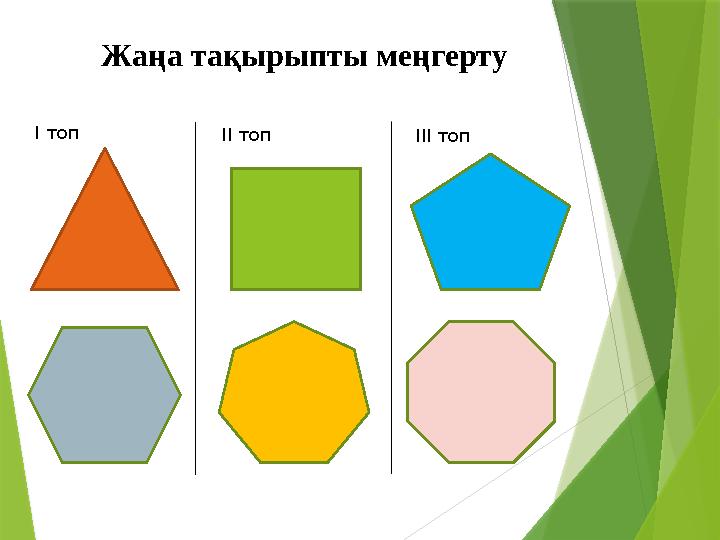
Жаңа тақырыпты меңгерту І топ ІІ топ ІІІ топ

5 слайд
Оқушылармен кері байланыс «Білемін» «Білдім» «Білгім келеді»

6 слайд
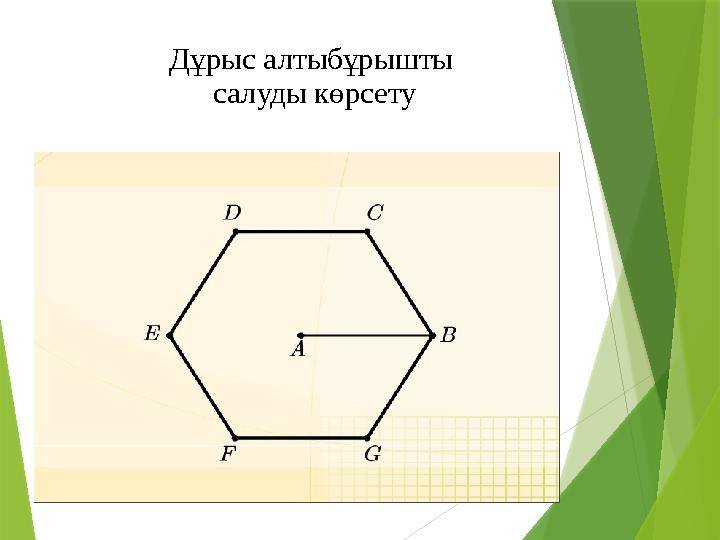
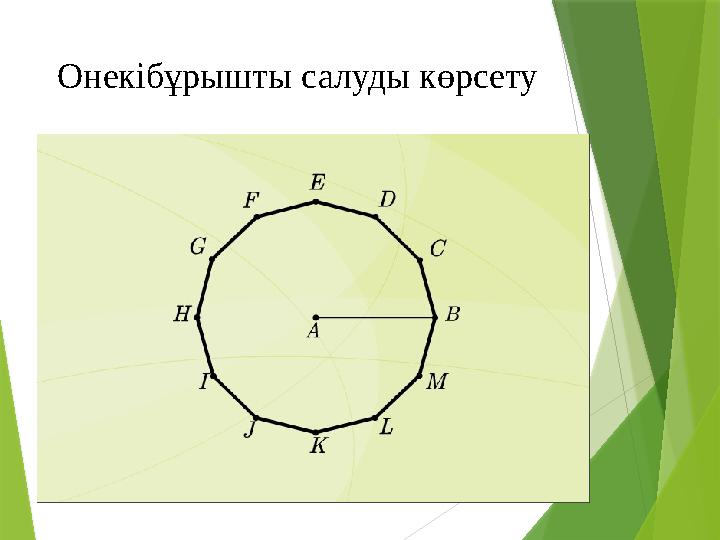
Дұрыс алтыбұрышты салуды көрсету

7 слайд
Онекібұрыш ты салуды көрсету

8 слайд
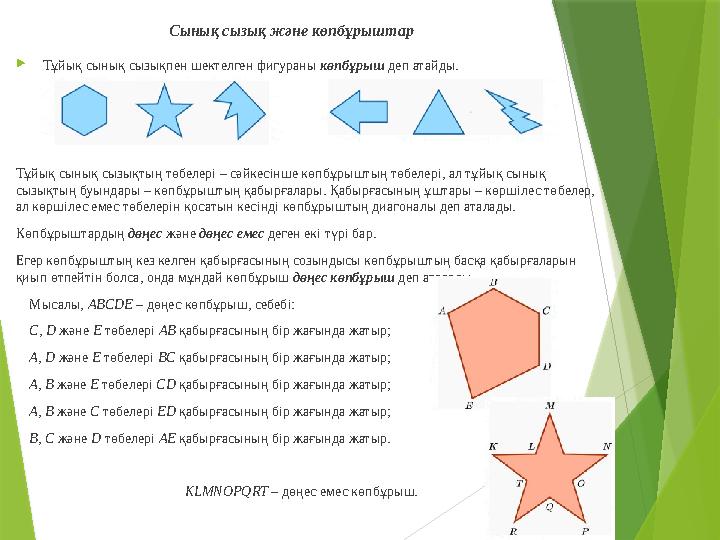
Сынық сызық және көпбұрыштар  Тұйық сынық сызықпен шектелген фигураны  көпбұрыш  деп атайды. Тұйық сынық сызықтың төбелері – сәйкесінше көпбұрыштың төбелері, ал тұйық сынық сызықтың буындары – көпбұрыштың қабырғалары. Қабырғасының ұштары – көршілес төбелер, ал көршілес емес төбелерін қосатын кесінді көпбұрыштың диагоналы деп аталады. Көпбұрыштардың  дөңес  және  дөңес емес  деген екі түрі бар. Егер көпбұрыштың кез келген қабырғасының созындысы көпбұрыштың басқа қабырғаларын қиып өтпейтін болса, онда мұндай көпбұрыш  дөңес көпбұрыш  деп аталады. Мысалы,  ABCDE  – дөңес көпбұрыш, себебі: C ,  D   және  E   төбелері  AB   қабырғасының бір жағында жатыр; A ,  D   және  E   төбелері  BC   қабырғасының бір жағында жатыр; A ,  B   және  E   төбелері  CD   қабырғасының бір жағында жатыр; A ,  B   және  C   төбелері  ED   қабырғасының бір жағында жатыр; B ,  C   және  D   төбелері  AE   қабырғасының бір жағында жатыр. KLMNOPQRT  – дөңес емес көпбұрыш.

9 слайд
Дөңес көпбұрыштың түрлері  Егер дөңес көпбұрыштың барлық қабырғалары мен барлық бұрыштары тең болса, онда оны  дұрыс көпбұрыш  деп атайды. Дұрыс көпбұрыштың негізгі қасиеттері 1-қасиет.  Дұрыс көпбұрыштарға сырттай және іштей сызылған шеңберлердің центрлері беттеседі. 2-қасиет.  Дұрыс  n - бұрыштың ішкі бұрыштарының қосындысы 180° · ( n  – 2)- ге тең. Дәлелдеуі.  Дұрыс  n - бұрыштың бір төбесінен жүргізілген барлық диагональдары оны үшбұрыштарға бөледі. Үшбұрыштың ішкі бұрыштарының қосындысы 180°-қа тең болғандықтан,  n - бұрыштың ішкі бұрыштарының қосындысы 180° · ( n  – 2)- ге тең. 2-қасиет дәлелденді. Мысалы, дөңес бесбұрышты  ABCDE   көпбұрышының ішкі бұрыштарының қосындысы 180° · (5 – 2) = 540°-қа тең 3-қасиет.  Кез келген дөңес көпбұрыштың әрбір төбесінен бір-бірден алынған сыртқы бұрыштарының қосындысы 360°-қа тең. Дәлелдеуі.  Көпбұрыштың бір төбесіндегі ішкі және сыртқы бұрышының қосындысы 180°-қа тең. Көпбұрыштың n төбесі болғандықтан, оның барлық ішкі және сыртқы бұрыштарының қосындысы 180° ·  n , ал ішкі бұрыштарының қосындысы  180° · ( n  – 2)- ге тең. Онда көпбұрыштың сыртқы бұрыштарының қосындысы  180° ·  n  – ( n  – 2) · 180° = 360°- қа тең.

10 слайд
3-қасиет дәлелденді. Дұрыс көпбұрышқа сырттай және іштей сызылған шеңберлерді салу негізінде келесідей дұрыс көпбұрышты салу алгортимін аламыз:  360º - ты  n - ге бөлу керек.  Белгілі центрі мен радиусы берілген шеңбер салу керек.  Центрінен өзара тең  n - бұрыш салу керек.  Шеңбермен қиылысқанға дейін сәулелер салу керек.  Қиылысу нүктелерін қосу керек. Дұрыс  n - бұрышты көпбұрыш алынады. n  > 4  болғанда, дұрыс  n - бұрышты көпбұрыш салу үшін көпбұрышқа сырттай сызылған шеңбер қолданылады.

11 слайд
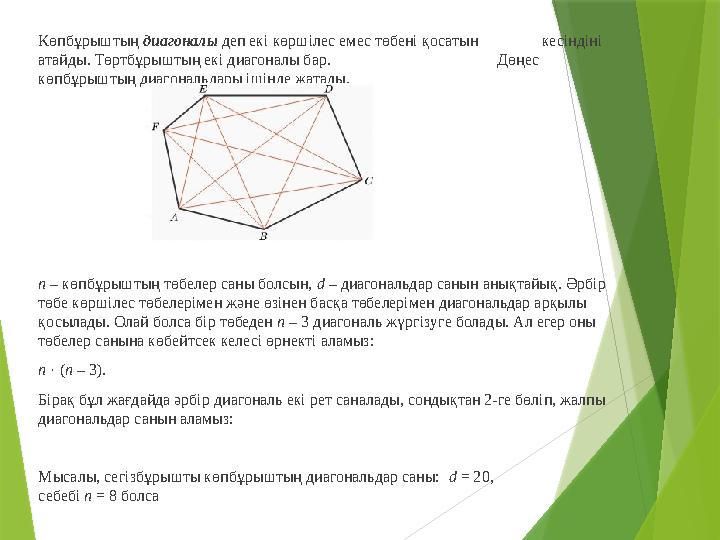
Көпбұрыштың  диагоналы  деп екі көршілес емес төбені қосатын кесіндіні атайды. Төртбұрыштың екі диагоналы бар. Дөңес көпбұрыштың диагональдары ішінде жатады. n  – көпбұрыштың төбелер саны болсын,  d  – диагональдар санын анықтайық. Әрбір төбе көршілес төбелерімен және өзінен басқа төбелерімен диагональдар арқылы қосылады. Олай болса бір төбеден  n  – 3  диагональ жүргізуге болады. Ал егер оны төбелер санына көбейтсек келесі өрнекті аламыз: n  · ( n  – 3). Бірақ бұл жағдайда әрбір диагональ екі рет саналады, сондықтан 2-ге бөліп, жалпы диагональдар санын аламыз: Мысалы, сегізбұрышты көпбұрыштың диагональдар саны:  d  = 20, себебі  n  = 8  болса  

12 слайд
Жаңа тақырыпқа байланысты есептер шешу 1 мысал. Периметрі 360 см болатын дұрыс 18-бұрышты көпбұрыштың қабырғасын тап. Жауабы: қабырғасы см-ге тең. 2 мысал. Көпбұрыштың төбесінен 18 диагональ өткізу мүмкін. Бұл қандай көпбұрыш? А) 16-бұрыш Ә) 18-бұрыш Б) 20-бұрыш В) 15-бұрыш Г) 21-бұрыш 3 мысал. Қабырғалары мен диагоналдарының саны бірдей көпбұрышты тап.

13 слайд
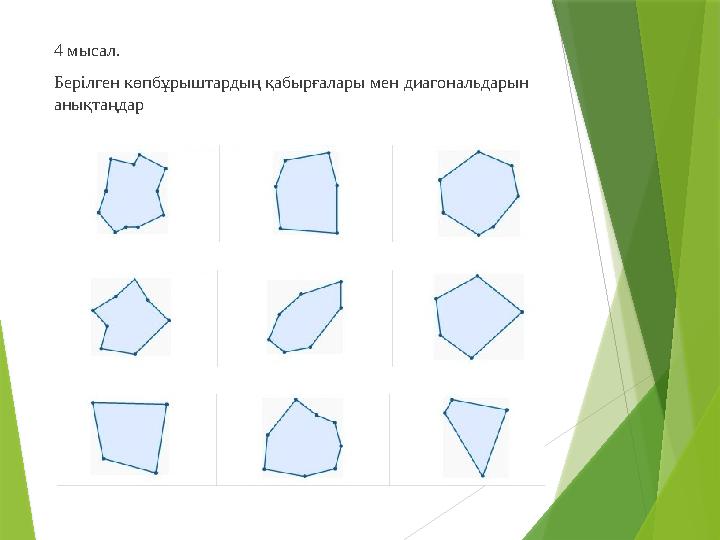
4 мысал. Берілген көпбұрыштардың қабырғалары мен диагональдарын анықтаңдар

14 слайд
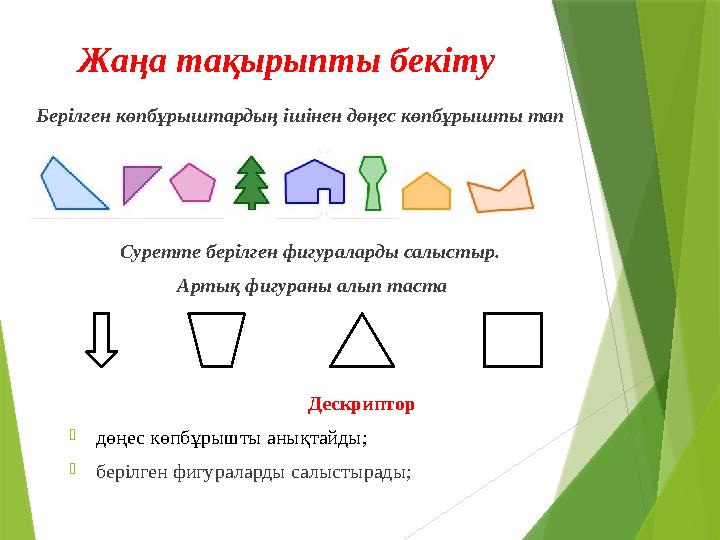
Жаңа тақырыпты бекіту Берілген көпбұрыштардың ішінен дөңес көпбұрышты тап Суретте берілген фигураларды салыстыр. Артық фигураны алып таста Дескриптор - дөңес көпбұрышты анықтайды; - берілген фигураларды салыстырады;

15 слайд
Бағалауы - орташа - жақсы - керемет

16 слайд
Жеке жұмыс «Тест»  № 1 сұрақ. Дөңес алтыбұрыштың қабырғасы 3 см-ге тең. Алтыбұрыштың периметрін тап. А) 16 см Б) 18 см В) 30 см Д) 10 см  № 2 сұрақ. Сегізбұрыштың бір қабырғасы – 5 см, ал қалған қабырғалары 2 см- ге тең. Сегізбұрыштың периметрін тап. А) 18 см Б) 21 см В) 25 см Д) 19 см  № 3 сұрақ. Дөңес төртбұрыштың неше диагоналы бар? А) 3 Б) 2 В) 1 Д) 4  № 4 сұрақ. Дөңес бесбұрыштың неше диагоналы бар екенін тап. А) 5 Б) 7 В) 4 Д) 3  № 5 сұрақ. Диагональдарының саны 35-ке тең дөңес көпбұрышты тап. А) онбұрыш Б) жетібұрыш В) тоғызбұрыш Д) он екі бұрыш № Дескриптор 1 Есептерді шешеді 2 Жауаптарын табады

17 слайд
Қорытындылау Рефлексия. Алма ағашы

18 слайд
Үйге тапсырма: Дұрыс көпбұрыштарды салу: 5; 6; 7; 8; 9; 10; 12 дұрыс көпбұрыштарын сыз

19 слайд
Назарларыңызға рахмет !!!