Материалдар / Бір айнымалысы бар теңдеулер және теңсіздіктер

Бір айнымалысы бар теңдеулер және теңсіздіктер

Материал туралы қысқаша түсінік

6 сынып, "Қызық екен" интеллектуалдық ойыны

Бекмахан Айбек Ғабиденұлы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

24 Қазан 2020

1814

0 рет жүктелген

Математика Барлық материалдар 6 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 39

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
1Бір айнымалысы бар сызықтық теңдеулер және теңсіздіктер.

1 слайд

1Бір айнымалысы бар сызықтық теңдеулер және теңсіздіктер.

2 слайд
2Сабақтың барысы: 1 . Ұ й ы м д а с т ы р у2 . Ж а ң а с а б а қ3 . ” Қ ы з ы қ е к е н ” т о к ш о у4 . Қ о р ы т ы н д ы л а у

2 слайд

2Сабақтың барысы: 1 . Ұ й ы м д а с т ы р у2 . Ж а ң а с а б а қ3 . ” Қ ы з ы қ е к е н ” т о к ш о у4 . Қ о р ы т ы н д ы л а у

3 слайд
Ұйымдастыру: а) Сәлемдесу ә) Оқушылар тізімін тексеру. Сабаққа деген назарын аударту

3 слайд

Ұйымдастыру: а) Сәлемдесу ә) Оқушылар тізімін тексеру. Сабаққа деген назарын аударту

4 слайд
Теңдеу. Теңдеудің түбірі.Теңдеудің түбірі - теңдеуді тура санды теңдікке айналдырады.х = 5 - 2Анықтама . ах= b түріндегі теңдеу (мұндағы х –айнымалы, а және b – қандай да бір сандар) бір айнымалысы бар сызықтық теңдеу деп аталады.

4 слайд

Теңдеу. Теңдеудің түбірі.Теңдеудің түбірі - теңдеуді тура санды теңдікке айналдырады.х = 5 - 2Анықтама . ах= b түріндегі теңдеу (мұндағы х –айнымалы, а және b – қандай да бір сандар) бір айнымалысы бар сызықтық теңдеу деп аталады.

5 слайд

6 слайд
• Түбірлері бірдей теңдеулер мәндес теңдеулер деп аталады • Теңдеуді шешу барысында теңдеу мәндес теңдеуге түрлендіріледі. • 4(х-3) =0 4x-12=0 • теңдеулері мәндес теңдеулер, себебі екі теңдеудің де түбірі 3-ке тең

6 слайд

• Түбірлері бірдей теңдеулер мәндес теңдеулер деп аталады • Теңдеуді шешу барысында теңдеу мәндес теңдеуге түрлендіріледі. • 4(х-3) =0 4x-12=0 • теңдеулері мәндес теңдеулер, себебі екі теңдеудің де түбірі 3-ке тең

7 слайд
Теңдеудің түбірін табайық: Біз теңдеуді шештік!Теңдеуді шешіп – теңдеуді тура теңдікке айналдыратын айнымалының мәнін таптық

7 слайд

Теңдеудің түбірін табайық: Біз теңдеуді шештік!Теңдеуді шешіп – теңдеуді тура теңдікке айналдыратын айнымалының мәнін таптық

8 слайд
Теңдеуді шешіңдер : 2(3х - 1) = 4(х + 3) Теңдеуді шешу үшін берілген теңдеуді мәндес теңдеуге түрлендіреміз. a х = b Түріне келтіреміз: 2(3х - 1) = 4(х + 3) 6х – 2 = 4х + 12 6х – 4х = 2 + 12 2х = 14 х = 14 : 2 х = 7 - теңдеудің бір түбірі бар

8 слайд

Теңдеуді шешіңдер : 2(3х - 1) = 4(х + 3) Теңдеуді шешу үшін берілген теңдеуді мәндес теңдеуге түрлендіреміз. a х = b Түріне келтіреміз: 2(3х - 1) = 4(х + 3) 6х – 2 = 4х + 12 6х – 4х = 2 + 12 2х = 14 х = 14 : 2 х = 7 - теңдеудің бір түбірі бар

9 слайд
19.04.2012 www.konspekturoka.ru 9Теңдеудің шексіз көп түбірі бар. Теңдеуді шешіңдер : 2(3х - 1) = 4(х + 3) – 14 + 2х Түріне келтіреміз a х = b 2(3х - 1) = 4(х + 3) – 14 + 2х 6х – 2 = 4х + 12 – 14 + 2х 6х – 4x - 2х = 2 + 12 – 14 0 · x = 0 Х-тің кез келген мәнінде теңдік тура болады: 0 = 0 x – кез келген сан (а = 0, b = 0)

9 слайд

19.04.2012 www.konspekturoka.ru 9Теңдеудің шексіз көп түбірі бар. Теңдеуді шешіңдер : 2(3х - 1) = 4(х + 3) – 14 + 2х Түріне келтіреміз a х = b 2(3х - 1) = 4(х + 3) – 14 + 2х 6х – 2 = 4х + 12 – 14 + 2х 6х – 4x - 2х = 2 + 12 – 14 0 · x = 0 Х-тің кез келген мәнінде теңдік тура болады: 0 = 0 x – кез келген сан (а = 0, b = 0)

10 слайд
Теңдеулерді шешуде қолданылатын теңдеудің қасиеттері: 1. Теңдеудегі қосылғыштың таңбасын қарама – қарсыға өзгертіп, оны теңдеудің бір жағынан екінші жағына көшіргенде теңдеу мәндес теңдеуге түрленеді . 2. Теңдеулің екі жағын да нөлден өзге бірдей санға көбейткенде немесе бөлгенде теңдеу мәндес теңдеуге түрленеді .

10 слайд

Теңдеулерді шешуде қолданылатын теңдеудің қасиеттері: 1. Теңдеудегі қосылғыштың таңбасын қарама – қарсыға өзгертіп, оны теңдеудің бір жағынан екінші жағына көшіргенде теңдеу мәндес теңдеуге түрленеді . 2. Теңдеулің екі жағын да нөлден өзге бірдей санға көбейткенде немесе бөлгенде теңдеу мәндес теңдеуге түрленеді .

11 слайд
11Теңдеуді шешейік: (35 + у) – 15 = 31 19.01.2016 35 + у = 31 + 15 35 + у = 46 y = 46 -35Теңдеуді шеш – бұл дегеніміз барлық түбірлерін табу немесе шешімі жоқ екендігін дәлелдеу

11 слайд

11Теңдеуді шешейік: (35 + у) – 15 = 31 19.01.2016 35 + у = 31 + 15 35 + у = 46 y = 46 -35Теңдеуді шеш – бұл дегеніміз барлық түбірлерін табу немесе шешімі жоқ екендігін дәлелдеу

12 слайд
www.konspekturoka.ru 12Теңдеуді шешпей қай жауап дұрыс болатынын айтып көр. 87 + (32 – х) = 105 19.01.2016

12 слайд

www.konspekturoka.ru 12Теңдеуді шешпей қай жауап дұрыс болатынын айтып көр. 87 + (32 – х) = 105 19.01.2016

13 слайд
www.konspekturoka.ru 1387 + (32 – 14) = 105 87 + (32 – 42) = 7787 + (32 – х) = 105 87 + (32 – 0) = 119 87 + (32 – 12) = 107 19.04.2012

13 слайд

www.konspekturoka.ru 1387 + (32 – 14) = 105 87 + (32 – 42) = 7787 + (32 – х) = 105 87 + (32 – 0) = 119 87 + (32 – 12) = 107 19.04.2012

14 слайд
14.Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеулерді шешуде: координаталық түзудегі А(а) және B(b) нүктелерінің арақашықтығы пайдаланылады: b a  • санның модулінің анықтамасының        , 0 , , 0 , болса егера а болса егера а а формуласы пайдаланылады. 0  а а а   b a ab   0 ,   b b a b a 2 2 a a  Есептеулерде модулдьдің негізгі қасиеттері де пайдаланылады :; ; ; ;

14 слайд

14.Айнымалысы модуль таңбасының ішінде берілген бір айнымалысы бар сызықтық теңдеулерді шешуде: координаталық түзудегі А(а) және B(b) нүктелерінің арақашықтығы пайдаланылады: b a  • санның модулінің анықтамасының        , 0 , , 0 , болса егера а болса егера а а формуласы пайдаланылады. 0  а а а   b a ab   0 ,   b b a b a 2 2 a a  Есептеулерде модулдьдің негізгі қасиеттері де пайдаланылады :; ; ; ;

15 слайд
15Екі санды өрнектің теңсіздік белгісімен ( «>» немесе «<» ) жазылуы санды теңсіздік деп аталады. Теңсіздік белгісінің сол жағындағы жазуды теңсіздіктің сол жақ бөлігі деп, ал оң жағындағы жазуды теңсіздіктің оң жақ бөлігі деп атайды. .   Егер теңсіздіктер < немесе > белгілерімен жазылса, қатаң теңсіздіктер деп аталады. Егер (артық немесе тең) және (кем немесе тең) белгілерімен жазылса, қатаң емес теңсіздіктер деп аталады.  

15 слайд

15Екі санды өрнектің теңсіздік белгісімен ( «>» немесе «<» ) жазылуы санды теңсіздік деп аталады. Теңсіздік белгісінің сол жағындағы жазуды теңсіздіктің сол жақ бөлігі деп, ал оң жағындағы жазуды теңсіздіктің оң жақ бөлігі деп атайды. .   Егер теңсіздіктер < немесе > белгілерімен жазылса, қатаң теңсіздіктер деп аталады. Егер (артық немесе тең) және (кем немесе тең) белгілерімен жазылса, қатаң емес теңсіздіктер деп аталады.  

16 слайд
16

16 слайд

17 слайд
17А және В сан аралықтарының кем дегенде біреуіне тиісті сандар жиынын А және В сан аралықтарының бірігуі деп атайды . Мысалы : аралығын А және В сан аралықтарының қиылысуы деп атайды. Мысалы : А сан аралығына да, В сан аралығына да тиісті сандардан ғана тұратын В А        14; 5 14; 2 9; 5            10; 1 15; 1 10; 3     

17 слайд

17А және В сан аралықтарының кем дегенде біреуіне тиісті сандар жиынын А және В сан аралықтарының бірігуі деп атайды . Мысалы : аралығын А және В сан аралықтарының қиылысуы деп атайды. Мысалы : А сан аралығына да, В сан аралығына да тиісті сандардан ғана тұратын В А        14; 5 14; 2 9; 5            10; 1 15; 1 10; 3     

18 слайд
18• Бір айнымалысы бар сызықтық теңсіздік .b ax  және түріндегі теңсіздіктер бір айнымалысы бар сызықтық теңсіздіктер деп аталады. Мұндағы а және b – қандай да бір сандар, х – айнымалы(белгісіз). Бір айнымалысы бар теңсіздіктің шешімі деп, айнымалының теңсіздікті тура санды теңсіздікке мәндерінің жиынын айтады. b ax  Теңсіздікті шешу дегеніміз – оның барлық шешімдер жиынын табу немесе шешімдерінің болмайтынын дәлелдеу. • Мәндес теңсіздіктер. Шешімдері бірдей теңсіздіктер мәндес теңсіздіктер деп аталады. Шешімдері болмайтын теңсіздіктер де мәндес теңсіздіктер болып есептеледі

18 слайд

18• Бір айнымалысы бар сызықтық теңсіздік .b ax  және түріндегі теңсіздіктер бір айнымалысы бар сызықтық теңсіздіктер деп аталады. Мұндағы а және b – қандай да бір сандар, х – айнымалы(белгісіз). Бір айнымалысы бар теңсіздіктің шешімі деп, айнымалының теңсіздікті тура санды теңсіздікке мәндерінің жиынын айтады. b ax  Теңсіздікті шешу дегеніміз – оның барлық шешімдер жиынын табу немесе шешімдерінің болмайтынын дәлелдеу. • Мәндес теңсіздіктер. Шешімдері бірдей теңсіздіктер мәндес теңсіздіктер деп аталады. Шешімдері болмайтын теңсіздіктер де мәндес теңсіздіктер болып есептеледі

19 слайд
191 • Егер теңсіздік құрамындағы қосылғыш теңсіздіктің бір жақ бөлігінен екінші жақ бөлігіне қарама-қарсы таңбамен көшірілсе, берілген теңсіздік мәндес теңсіздікке түрленеді. 2 • Егер теңсіздіктің екі жақ бөлігі де бірдей оң санға көбейтілсе немесе бөлінсе, берілген теңсіздік мәндес теңсіздікке түрленеді. 3 • Егер теңсіздіктің екі жақ бөлігі де бірдей теріс санға көбейтіліп немесе бөлініп, сонымен бірге теңсіздік белгісі қарама- қарсы теңсіздік белгісіне өзгертілсе, берілген теңсіздік мәндес теңсіздікке түрленеді.Теңсіздікті мәндес теңсіздікке түрлендіру ережесі.

19 слайд

191 • Егер теңсіздік құрамындағы қосылғыш теңсіздіктің бір жақ бөлігінен екінші жақ бөлігіне қарама-қарсы таңбамен көшірілсе, берілген теңсіздік мәндес теңсіздікке түрленеді. 2 • Егер теңсіздіктің екі жақ бөлігі де бірдей оң санға көбейтілсе немесе бөлінсе, берілген теңсіздік мәндес теңсіздікке түрленеді. 3 • Егер теңсіздіктің екі жақ бөлігі де бірдей теріс санға көбейтіліп немесе бөлініп, сонымен бірге теңсіздік белгісі қарама- қарсы теңсіздік белгісіне өзгертілсе, берілген теңсіздік мәндес теңсіздікке түрленеді.Теңсіздікті мәндес теңсіздікке түрлендіру ережесі.

20 слайд
20Теңсіздіктер жүйесін шешу дегеніміз – ондағы теңсіздіктердің әрқайсысын тура санды теңсіздікке айналдыратын айнымалының мәндерінің жиынын табу немесе шешімдерінің болмайтындығын дәлелдеу. Бір айнымалысы бар сызықтық теңсіздіктер жүйесінің шешімдерін табу үшін: • Жүйедегі теңсіздіктердің әрқайсысының шешімдерін табу керек; • Табылған шешімдерді бір координаталық түзуде кескіндеу керек; • Координаталық түзуден жүйедегі теңсіздіктердің ортақ шешімдерін табу керек немесе бірде-бір шешімі болмайтындығын дәлелдеу керек.

20 слайд

20Теңсіздіктер жүйесін шешу дегеніміз – ондағы теңсіздіктердің әрқайсысын тура санды теңсіздікке айналдыратын айнымалының мәндерінің жиынын табу немесе шешімдерінің болмайтындығын дәлелдеу. Бір айнымалысы бар сызықтық теңсіздіктер жүйесінің шешімдерін табу үшін: • Жүйедегі теңсіздіктердің әрқайсысының шешімдерін табу керек; • Табылған шешімдерді бір координаталық түзуде кескіндеу керек; • Координаталық түзуден жүйедегі теңсіздіктердің ортақ шешімдерін табу керек немесе бірде-бір шешімі болмайтындығын дәлелдеу керек.

21 слайд
21

21 слайд

22 слайд
22Бір айнымалысы бар сызықтық теңсіздіктер Теңдеу құруға берілген есептер Айнымалысы модуль таңбасының ішінде берілген теңсіздіктерСан аралықтары Теңсіздіктер жүйесін шешуТеңдеудің түбіріБір айнымалысы бар сызықтық теңдеулерСанды теңдік Мәндес теңдеуСанды теңсіздіктерАйнымалысы модуль таңбасының ішінде берілген теңдеулер???

22 слайд

22Бір айнымалысы бар сызықтық теңсіздіктер Теңдеу құруға берілген есептер Айнымалысы модуль таңбасының ішінде берілген теңсіздіктерСан аралықтары Теңсіздіктер жүйесін шешуТеңдеудің түбіріБір айнымалысы бар сызықтық теңдеулерСанды теңдік Мәндес теңдеуСанды теңсіздіктерАйнымалысы модуль таңбасының ішінде берілген теңдеулер???

23 слайд
23Координаталық түзуді пайдаланып, берілген сан аралықтарының бірігуін, қиылысуын жазыңыздар: 1) (- 8 ; 6] [-5 ; 8 ) 2)     4 ; 5 3 ;       [-5;6]   4 ;  

23 слайд

23Координаталық түзуді пайдаланып, берілген сан аралықтарының бірігуін, қиылысуын жазыңыздар: 1) (- 8 ; 6] [-5 ; 8 ) 2)     4 ; 5 3 ;       [-5;6]   4 ;  

24 слайд
24Теңсіздікті шешіңіз:х х х х 4 3 4 5 6 2 7        4 , 0 ;   1) 2) 11 3 2 7    х [2;4]

24 слайд

24Теңсіздікті шешіңіз:х х х х 4 3 4 5 6 2 7        4 , 0 ;   1) 2) 11 3 2 7    х [2;4]

25 слайд
25Ұзындығы 12 см тік төртбұрыш және қабырғасы осы тік төртбұрыштың енінен 1 см кем квадрат берілген. Квадраттың периметрі берілген тік төртбұрыштың периметрінен 10 см кем. Тік төртбұрыштың ені неше сантиметр? 9 см

25 слайд

25Ұзындығы 12 см тік төртбұрыш және қабырғасы осы тік төртбұрыштың енінен 1 см кем квадрат берілген. Квадраттың периметрі берілген тік төртбұрыштың периметрінен 10 см кем. Тік төртбұрыштың ені неше сантиметр? 9 см

26 слайд
261. Қос теңсіздікті шешіңдер және оның шешімдері болатын бүтін сандар жиынын жазыңдар:5 1 2    x {-5,-4,2,3} 2. Теңсіздікті шешіңдер: |2x+1|<3 (-2;1)

26 слайд

261. Қос теңсіздікті шешіңдер және оның шешімдері болатын бүтін сандар жиынын жазыңдар:5 1 2    x {-5,-4,2,3} 2. Теңсіздікті шешіңдер: |2x+1|<3 (-2;1)

27 слайд
27Тура санды теңдіктерді мүшелеп қосуды орындаңдар: 1)0,6-2 =-1.4 және 2+1,8 = 3,8: 2)1,7+6 = 7 . 7 және 0,5-1,7 = -1,2 2.4=2.4 6.5=6.5

27 слайд

27Тура санды теңдіктерді мүшелеп қосуды орындаңдар: 1)0,6-2 =-1.4 және 2+1,8 = 3,8: 2)1,7+6 = 7 . 7 және 0,5-1,7 = -1,2 2.4=2.4 6.5=6.5

28 слайд
285 1 2 4 3 1 15 7 4       x х х 2 3 5 4 5 3 8 9 5 x х x     x=-8 x=-3Те ңдеуді шешіңдер:

28 слайд

285 1 2 4 3 1 15 7 4       x х х 2 3 5 4 5 3 8 9 5 x х x     x=-8 x=-3Те ңдеуді шешіңдер:

29 слайд
29Теңдеуді шешіп, түбірін табыңдар:3 11 2 7 4 5     х x Х =13 8x-9=3x+8 X=3.4

29 слайд

29Теңдеуді шешіп, түбірін табыңдар:3 11 2 7 4 5     х x Х =13 8x-9=3x+8 X=3.4

30 слайд
30Теңсіздіктер жүйесінің шешімдерін табыңдар:       1 3 1 7 2 x x [-3;4)          3 2 ) 3 ( 5 3 ) 1 ( 3 x x x x (-4;0)

30 слайд

30Теңсіздіктер жүйесінің шешімдерін табыңдар:       1 3 1 7 2 x x [-3;4)          3 2 ) 3 ( 5 3 ) 1 ( 3 x x x x (-4;0)

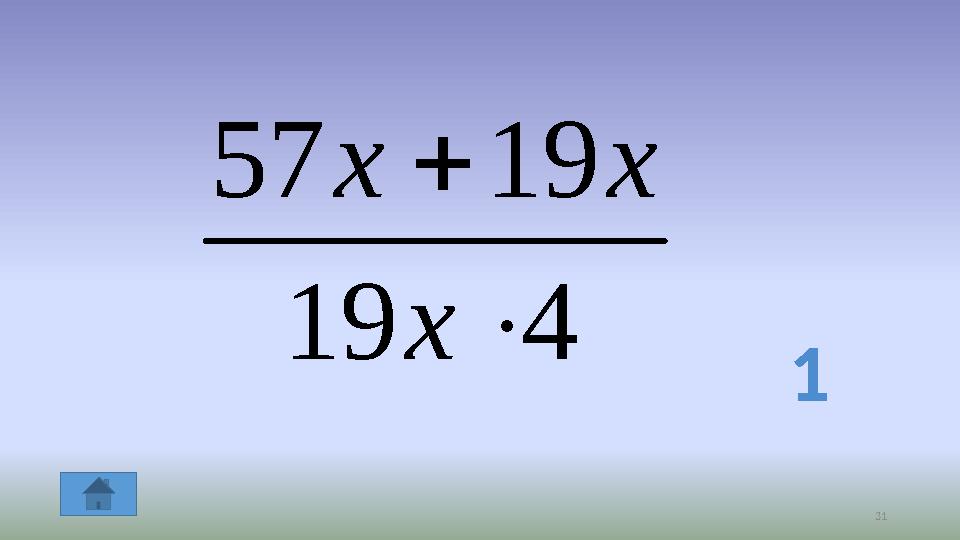
31 слайд
3114 19 19 57   x x x

31 слайд

3114 19 19 57   x x x

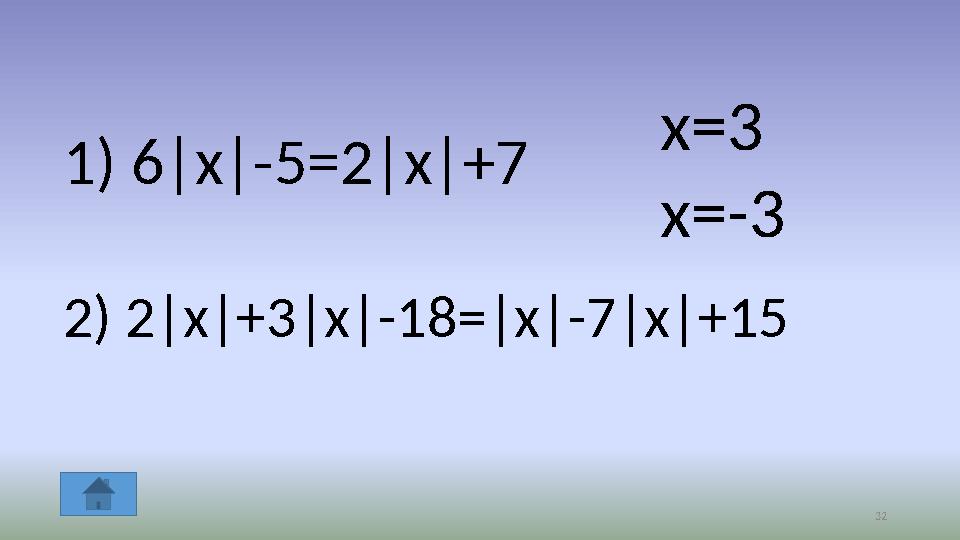
32 слайд
321) 6|x|-5=2|x|+7 x=3 x=-3 2) 2|x|+3|x|-18=|x|-7|x|+15

32 слайд

321) 6|x|-5=2|x|+7 x=3 x=-3 2) 2|x|+3|x|-18=|x|-7|x|+15

33 слайд
33Ұзындығы 7 см, ені 4см тіктөртбұрыштың ауданын қабырғасы 5 см квадраттың ауданымен салыстырыңдар. Салыстыру нәтижесін теңсіздік түрінде жазыңдар.2 5 4 7  

33 слайд

33Ұзындығы 7 см, ені 4см тіктөртбұрыштың ауданын қабырғасы 5 см квадраттың ауданымен салыстырыңдар. Салыстыру нәтижесін теңсіздік түрінде жазыңдар.2 5 4 7  