Дұрыс көпжақтар
Дұрыс көпжақтар


#1 слайд
Дұрыс көпжақтар
1 слайд
Дұрыс көпжақтар

#2 слайд
Оқу мақсаты
11.1.6-Дұрыс көпжақтың анықтамасын білу
Дұрыс көпжақтардың негізгі қасиеттерін және оларды
сипаттайтын критерийлерді түсіну.
Дұрыс көпжақтың түрлерін ажырата білу
Әрбір дұрыс көпжақтың бірегей ерекшеліктерін, олардың
атауларын және формаларын танып, айырмашылықтарын
анықтау.
2 слайд
Оқу мақсаты 11.1.6-Дұрыс көпжақтың анықтамасын білу Дұрыс көпжақтардың негізгі қасиеттерін және оларды сипаттайтын критерийлерді түсіну. Дұрыс көпжақтың түрлерін ажырата білу Әрбір дұрыс көпжақтың бірегей ерекшеліктерін, олардың атауларын және формаларын танып, айырмашылықтарын анықтау.

#3 слайд
Дұрыс көпжақ тар дегеніміз не?
Дұрыс көпжақ – бұл барлық жақтары бірдей дұрыс
көпбұрыштардан тұратын, барлық төбелерінде бірдей мөлшерде
жақтары түйісетін дөңес көпжақ.
Бұл анықтама геометриядағы ең симметриялы және әдемі пішіндерді
сипаттайды. Олар сондай-ақ "Платон денелері" деп те аталады,
себебі ежелгі грек философы Платон оларды табиғаттың бес
элементімен байланыстырған.
3 слайд
Дұрыс көпжақ тар дегеніміз не? Дұрыс көпжақ – бұл барлық жақтары бірдей дұрыс көпбұрыштардан тұратын, барлық төбелерінде бірдей мөлшерде жақтары түйісетін дөңес көпжақ. Бұл анықтама геометриядағы ең симметриялы және әдемі пішіндерді сипаттайды. Олар сондай-ақ "Платон денелері" деп те аталады, себебі ежелгі грек философы Платон оларды табиғаттың бес элементімен байланыстырған.

#4 слайд
Дұрыс көпжақтардың сипаттамалары
•Барлық жақтары дұрыс көпбұрыштар: Әрбір жақ бірдей
қабырғалы және бірдей бұрышты болады (мысалы, теңқабырғалы
үшбұрыш немесе квадрат).
•Барлық жақтары өзара тең: Көпжақтың барлық
жақтары бір-біріне тең өлшемде болады.
•Барлық төбелерінде бірдей жақтар түйіседі: Әр
төбеге бірдей сан жақтар жиналады.
•Дөңес пішін: Көпжақтың кез келген екі нүктесін қосатын
кесінді толығымен көпжақтың ішінде жатады.
Бұл қасиеттер дұрыс көпжақтарды ерекше етеді және олардың тек бес түрі ғана бар екенін көрсетеді.
4 слайд
Дұрыс көпжақтардың сипаттамалары •Барлық жақтары дұрыс көпбұрыштар: Әрбір жақ бірдей қабырғалы және бірдей бұрышты болады (мысалы, теңқабырғалы үшбұрыш немесе квадрат). •Барлық жақтары өзара тең: Көпжақтың барлық жақтары бір-біріне тең өлшемде болады. •Барлық төбелерінде бірдей жақтар түйіседі: Әр төбеге бірдей сан жақтар жиналады. •Дөңес пішін: Көпжақтың кез келген екі нүктесін қосатын кесінді толығымен көпжақтың ішінде жатады. Бұл қасиеттер дұрыс көпжақтарды ерекше етеді және олардың тек бес түрі ғана бар екенін көрсетеді.
#5 слайд
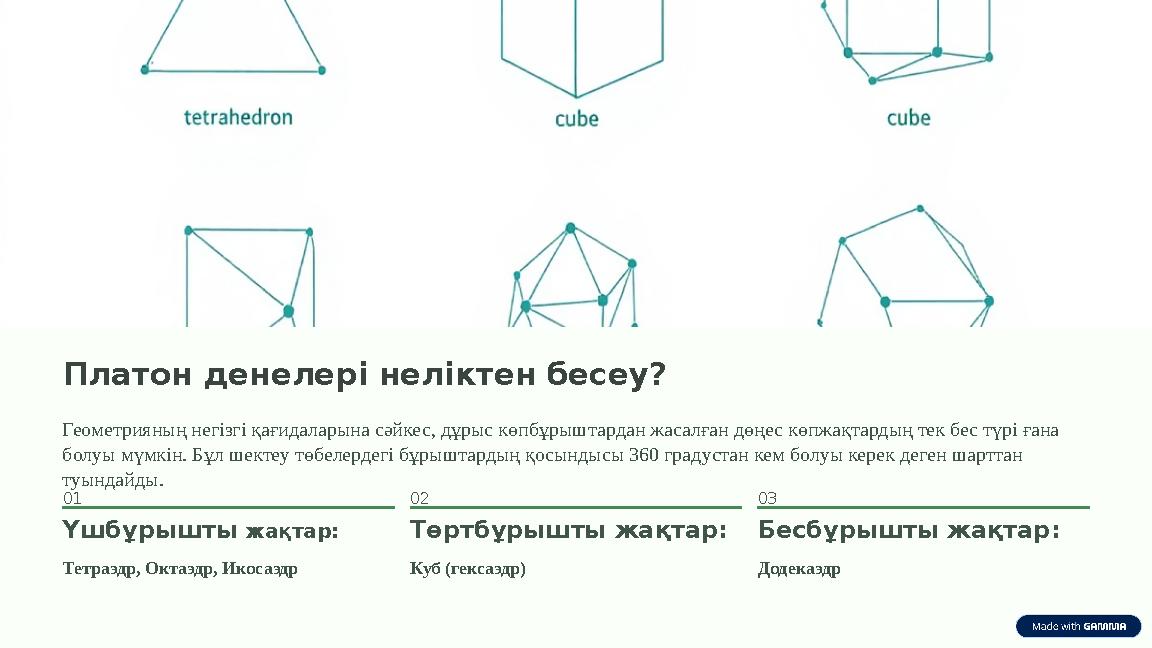
Платон денелері неліктен бесеу?
Геометрияның негізгі қағидаларына сәйкес, дұрыс көпбұрыштардан жасалған дөңес көпжақтардың тек бес түрі ғана
болуы мүмкін. Бұл шектеу төбелердегі бұрыштардың қосындысы 360 градустан кем болуы керек деген шарттан
туындайды.
01
Үшбұрышты жақтар:
Тетраэдр, Октаэдр, Икосаэдр
02
Төртбұрышты жақтар:
Куб (гексаэдр)
03
Бесбұрышты жақтар:
Додекаэдр
5 слайд
Платон денелері неліктен бесеу? Геометрияның негізгі қағидаларына сәйкес, дұрыс көпбұрыштардан жасалған дөңес көпжақтардың тек бес түрі ғана болуы мүмкін. Бұл шектеу төбелердегі бұрыштардың қосындысы 360 градустан кем болуы керек деген шарттан туындайды. 01 Үшбұрышты жақтар: Тетраэдр, Октаэдр, Икосаэдр 02 Төртбұрышты жақтар: Куб (гексаэдр) 03 Бесбұрышты жақтар: Додекаэдр
#6 слайд
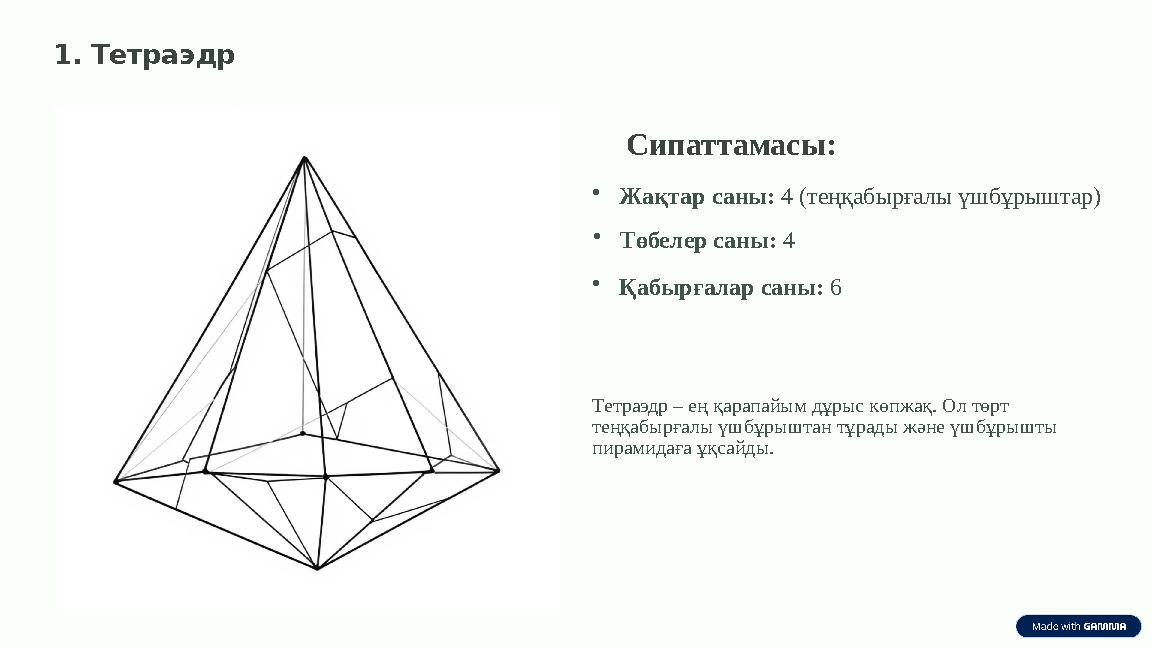
1. Тетраэдр
Сипаттамасы:
•Жақтар саны: 4 (теңқабырғалы үшбұрыштар)
•Төбелер саны: 4
•Қабырғалар саны: 6
Тетраэдр – ең қарапайым дұрыс көпжақ. Ол төрт
теңқабырғалы үшбұрыштан тұрады және үшбұрышты
пирамидаға ұқсайды.
Ежелгі Грецияда Платон тетраэдрді отпен байланыстырған, себебі оның ұштары өткір болып келеді.
6 слайд
1. Тетраэдр Сипаттамасы: •Жақтар саны: 4 (теңқабырғалы үшбұрыштар) •Төбелер саны: 4 •Қабырғалар саны: 6 Тетраэдр – ең қарапайым дұрыс көпжақ. Ол төрт теңқабырғалы үшбұрыштан тұрады және үшбұрышты пирамидаға ұқсайды. Ежелгі Грецияда Платон тетраэдрді отпен байланыстырған, себебі оның ұштары өткір болып келеді.

#7 слайд
2. Гексаэдр (Куб)
Сипаттамасы:
•Жақтар саны: 6 (квадраттар)
•Төбелер саны: 8
•Қабырғалар саны: 12
Куб – күнделікті өмірде жиі кездесетін дұрыс көпжақ.
Оның барлық жақтары квадрат пішіндес.
Платон кубты жермен байланыстырған, себебі ол тұрақты және берік пішінге ие.
7 слайд
2. Гексаэдр (Куб) Сипаттамасы: •Жақтар саны: 6 (квадраттар) •Төбелер саны: 8 •Қабырғалар саны: 12 Куб – күнделікті өмірде жиі кездесетін дұрыс көпжақ. Оның барлық жақтары квадрат пішіндес. Платон кубты жермен байланыстырған, себебі ол тұрақты және берік пішінге ие.
#8 слайд
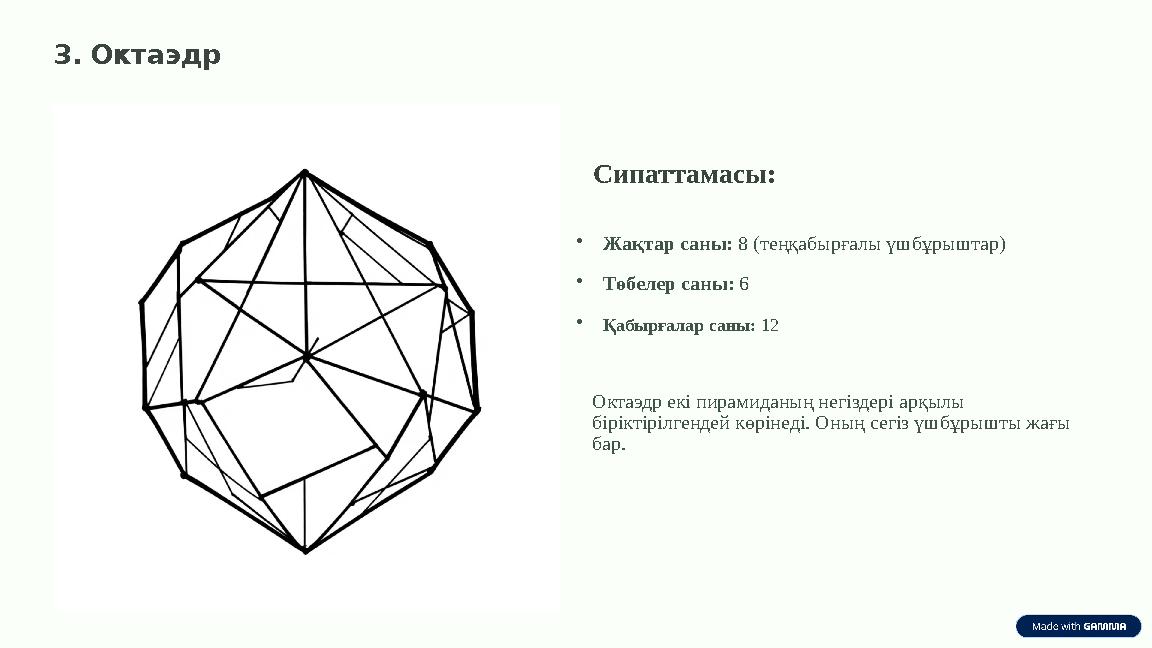
3. Октаэдр
Сипаттамасы:
•Жақтар саны: 8 (теңқабырғалы үшбұрыштар)
•Төбелер саны: 6
•Қабырғалар саны: 12
Октаэдр екі пирамиданың негіздері арқылы
біріктірілгендей көрінеді. Оның сегіз үшбұрышты жағы
бар.
Платон октаэдрді ауамен байланыстырды, себебі ол жеңіл және ұшатын пішінге ие.
8 слайд
3. Октаэдр Сипаттамасы: •Жақтар саны: 8 (теңқабырғалы үшбұрыштар) •Төбелер саны: 6 •Қабырғалар саны: 12 Октаэдр екі пирамиданың негіздері арқылы біріктірілгендей көрінеді. Оның сегіз үшбұрышты жағы бар. Платон октаэдрді ауамен байланыстырды, себебі ол жеңіл және ұшатын пішінге ие.

#9 слайд
4. Додекаэдр
Сипаттамасы:
•Жақтар саны: 12 (дұрыс бесбұрыштар)
•Төбелер саны: 20
•Қабырғалар саны: 30
Додекаэдр – 12 дұрыс бесбұрыштан тұратын күрделірек
пішін. Оның әр төбесінде үш бесбұрыш түйіседі.
Платон додекаэдрді Ғаламмен байланыстырған, себебі оның күрделілігі мен әртүрлілігі ғарыштың шексіздігін еске түсіреді.
9 слайд
4. Додекаэдр Сипаттамасы: •Жақтар саны: 12 (дұрыс бесбұрыштар) •Төбелер саны: 20 •Қабырғалар саны: 30 Додекаэдр – 12 дұрыс бесбұрыштан тұратын күрделірек пішін. Оның әр төбесінде үш бесбұрыш түйіседі. Платон додекаэдрді Ғаламмен байланыстырған, себебі оның күрделілігі мен әртүрлілігі ғарыштың шексіздігін еске түсіреді.
#10 слайд
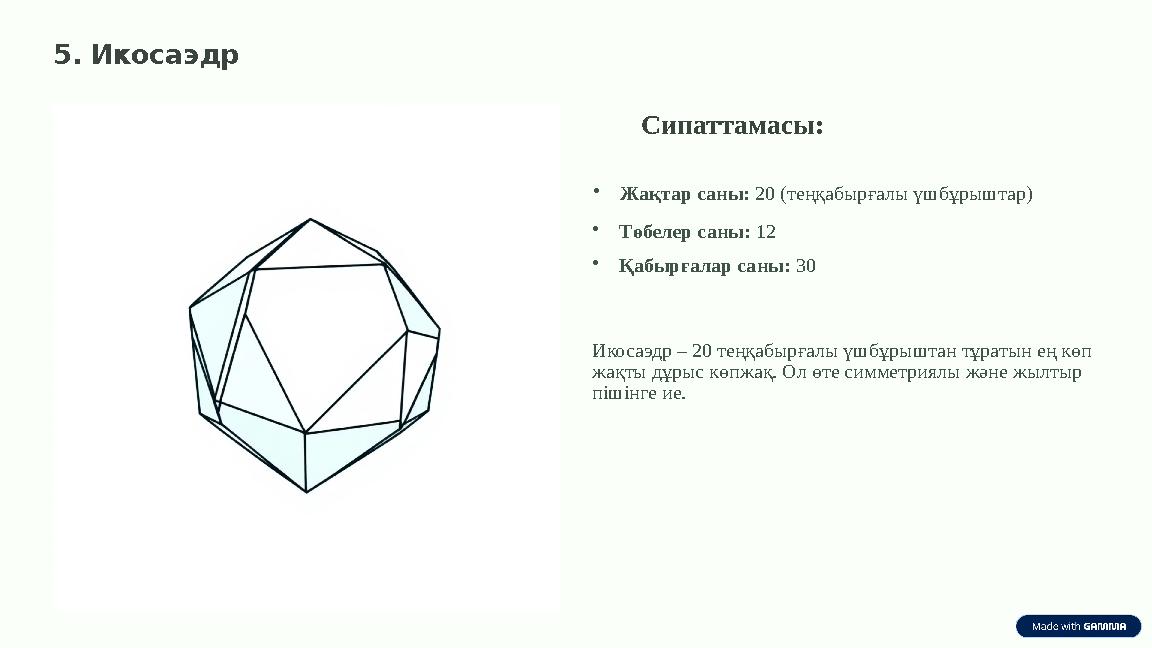
5. Икосаэдр
Сипаттамасы:
•Жақтар саны: 20 (теңқабырғалы үшбұрыштар)
•Төбелер саны: 12
•Қабырғалар саны: 30
Икосаэдр – 20 теңқабырғалы үшбұрыштан тұратын ең көп
жақты дұрыс көпжақ. Ол өте симметриялы және жылтыр
пішінге ие.
Платон икосаэдрді сумен байланыстырған, себебі оның көп жақтары су тамшысының домалақтығын еске түсіреді.
10 слайд
5. Икосаэдр Сипаттамасы: •Жақтар саны: 20 (теңқабырғалы үшбұрыштар) •Төбелер саны: 12 •Қабырғалар саны: 30 Икосаэдр – 20 теңқабырғалы үшбұрыштан тұратын ең көп жақты дұрыс көпжақ. Ол өте симметриялы және жылтыр пішінге ие. Платон икосаэдрді сумен байланыстырған, себебі оның көп жақтары су тамшысының домалақтығын еске түсіреді.

шағым қалдыра аласыз
















