Функцияның қасиеттерін талдау және графиктер
Функцияның қасиеттерін талдау және графиктер


#1 слайд
Сармсакова Нурасыл Батыргалиевна
1Функцияның қасиеттерін талдау және графиктер
1 слайд
Сармсакова Нурасыл Батыргалиевна 1Функцияның қасиеттерін талдау және графиктер

#2 слайд
Жұмыстың өзектілігі:
функциялардың схема түрінде немесе олардың
графиктерін дәл тұрғызу математиканың маңызды
есептерінің бірі. Графиктерді тұрғызу техникасын емін –
еркін меңгеру көптеген тапсырмаларды шешуге
көмектеседі және кей жағдайларда оларды шешудің
жалғыз жолы болып табылады. Сонымен қатар,
функциялардың графиктерін тұрғыза білу шеберлігі
үлкен тәуелсіз қызығушылық тудырады.
2
2 слайд
Жұмыстың өзектілігі: функциялардың схема түрінде немесе олардың графиктерін дәл тұрғызу математиканың маңызды есептерінің бірі. Графиктерді тұрғызу техникасын емін – еркін меңгеру көптеген тапсырмаларды шешуге көмектеседі және кей жағдайларда оларды шешудің жалғыз жолы болып табылады. Сонымен қатар, функциялардың графиктерін тұрғыза білу шеберлігі үлкен тәуелсіз қызығушылық тудырады. 2

#3 слайд
мақсаты:
міндеті:
функцияның негізгі қасиеттерін зерттеу және олардың
функцияның графигін салуға қажеттілігін нақтылау;
функциялардың графиктерін тұрғызудың математика
курсында кездесетін әдістерін жүйелеу, салыстыру;
математикада бұл тақырыптың маңызын және мектеп
математика курсында қажеттілігін көрсету.
тақырып бойынша теориялық материалдарды жүйелі
жинақтау;
теориялық материалда қолдану есептерінің шешу
әдістерін көрсету;
осы теориялық материалдарды практикада қолдана
білу дағдысын қалыптастыру .
3
3 слайд
мақсаты: міндеті: функцияның негізгі қасиеттерін зерттеу және олардың функцияның графигін салуға қажеттілігін нақтылау; функциялардың графиктерін тұрғызудың математика курсында кездесетін әдістерін жүйелеу, салыстыру; математикада бұл тақырыптың маңызын және мектеп математика курсында қажеттілігін көрсету. тақырып бойынша теориялық материалдарды жүйелі жинақтау; теориялық материалда қолдану есептерінің шешу әдістерін көрсету; осы теориялық материалдарды практикада қолдана білу дағдысын қалыптастыру . 3

#4 слайд
I. Функция туралы негізгі түсініктер
1.1.Функциялық тәуелділік және функцияның графигі .
1.2. Функцияның қасиеттері
1.3. Элементар функциялар
І тарауда функция туралы негізгі түсініктер,функциялық
тәуелділік және функцияның графигі, функцияның берілу
тәсілдері,функцияның анықталу және өзгеру аймағы, функцияның
қасиеттері, қарапайым элементар функциялар қарастырылды.
Әрбір тақырыпша мысалдар, дәлелдеулермен берілді.
4
4 слайд
I. Функция туралы негізгі түсініктер 1.1.Функциялық тәуелділік және функцияның графигі . 1.2. Функцияның қасиеттері 1.3. Элементар функциялар І тарауда функция туралы негізгі түсініктер,функциялық тәуелділік және функцияның графигі, функцияның берілу тәсілдері,функцияның анықталу және өзгеру аймағы, функцияның қасиеттері, қарапайым элементар функциялар қарастырылды. Әрбір тақырыпша мысалдар, дәлелдеулермен берілді. 4

#5 слайд
Функция (латынша –орындау, іске асыру) –математиканың
бір айнымалы шаманың өзге бір шамаға тәуелділігін
өрнектейтін негізгі ұғымдардың бірі. Функция
анықтамаларындағы «шама» деген сөз кең мағынада
ұғынылады: оның сан болуы да мүмкін, дерексіз сан
(нақты немесе комплекс), бірнеше сан (яғни кеңістіктің
нүктелері) және кез келген жиынның элементтері де
болуы мүмкін. Шама нақты сан болған жағдайда
«функция» ұғымы былайша анықталады: әрбір санына
берілген жиынындағы саны сәйкес қойылған. Функция
график түрінде де, кесте түрінде де беріледі.
«Функция» ғылыми атауы 1692 жылы неміс математигі Готфрид
Лейбництің (1646 -1716) еңбектерінде аталған. Бірақ оның мағынасы
қазіргі кездегіден басқаша болған. Функцияның қазіргі кездегі
біздердің түсінігімізге жақын келетін анықтамасын 1718 жылы
швейцар математигі Иоганн Бернулли (1667 – 1748) тұжырымдап:
«функция – айнымалылар мен тұрақтылардан құралған шама» деген.
5
5 слайд
Функция (латынша –орындау, іске асыру) –математиканың бір айнымалы шаманың өзге бір шамаға тәуелділігін өрнектейтін негізгі ұғымдардың бірі. Функция анықтамаларындағы «шама» деген сөз кең мағынада ұғынылады: оның сан болуы да мүмкін, дерексіз сан (нақты немесе комплекс), бірнеше сан (яғни кеңістіктің нүктелері) және кез келген жиынның элементтері де болуы мүмкін. Шама нақты сан болған жағдайда «функция» ұғымы былайша анықталады: әрбір санына берілген жиынындағы саны сәйкес қойылған. Функция график түрінде де, кесте түрінде де беріледі. «Функция» ғылыми атауы 1692 жылы неміс математигі Готфрид Лейбництің (1646 -1716) еңбектерінде аталған. Бірақ оның мағынасы қазіргі кездегіден басқаша болған. Функцияның қазіргі кездегі біздердің түсінігімізге жақын келетін анықтамасын 1718 жылы швейцар математигі Иоганн Бернулли (1667 – 1748) тұжырымдап: «функция – айнымалылар мен тұрақтылардан құралған шама» деген. 5

#6 слайд
Кестелік әдіс
Ауысша әдіс х аргументі және у функциясының мәндерінің
арасында пайда болатын функционалдық тәуелділік әртүрлі
әдістермен берілуі мүмкін.
6
Графикалық әдіс
Аналитикалық әдіс
6 слайд
Кестелік әдіс Ауысша әдіс х аргументі және у функциясының мәндерінің арасында пайда болатын функционалдық тәуелділік әртүрлі әдістермен берілуі мүмкін. 6 Графикалық әдіс Аналитикалық әдіс

#7 слайд
II. Графиктерді салу кезіндегі
функцияларды зерттеу әдістемесі
2.1. Сызықтық көбейткіштердің көбейтіндісі түрінде берілген
дәрежелі функциялар
2.2. Бөлшек – рациональды функциялар
ІІ тарау графиктерді салу кезіндегі функцияларды зерттеу
әдістемесі. Бұл тарауда сызықтық көбейткіштің көбейтіндісі
түрінде берілген дәрежелі функциялар, бөлшек –
рациональды функцияларды оқытудың әдістемесін
қарастырдым.
7
7 слайд
II. Графиктерді салу кезіндегі функцияларды зерттеу әдістемесі 2.1. Сызықтық көбейткіштердің көбейтіндісі түрінде берілген дәрежелі функциялар 2.2. Бөлшек – рациональды функциялар ІІ тарау графиктерді салу кезіндегі функцияларды зерттеу әдістемесі. Бұл тарауда сызықтық көбейткіштің көбейтіндісі түрінде берілген дәрежелі функциялар, бөлшек – рациональды функцияларды оқытудың әдістемесін қарастырдым. 7

#8 слайд
II. Графиктерді салу кезіндегі функцияларды
зерттеу әдістемесі
Функцияларды зерттеу төмендегідей ретпен жүргізіледі:
1.Функцияның анықталу обылысын немесе үзіліс нүктесін табу;
2.Функцияның жұп немесе тақтығын анықтау;
3.Функцияның периодтылығын анықтау;
4.Функцияның нөлдерін анықтау;
5.Функцияның тұрақты таңбалы интервалдарын және осы
интервалдардағы функциялардың таңбасын анықтау;
6. Функцияның бағытын зерттеу, горизонтальді асимптотаны
табу;
7.Вертикаль және көлбеу асимптоталарды табу;
8.Асимптота жақындағандағы бағытын зерттеу;
9.Функцияның ең үлкен және ең кіші мәндерін табу.
8
8 слайд
II. Графиктерді салу кезіндегі функцияларды зерттеу әдістемесі Функцияларды зерттеу төмендегідей ретпен жүргізіледі: 1.Функцияның анықталу обылысын немесе үзіліс нүктесін табу; 2.Функцияның жұп немесе тақтығын анықтау; 3.Функцияның периодтылығын анықтау; 4.Функцияның нөлдерін анықтау; 5.Функцияның тұрақты таңбалы интервалдарын және осы интервалдардағы функциялардың таңбасын анықтау; 6. Функцияның бағытын зерттеу, горизонтальді асимптотаны табу; 7.Вертикаль және көлбеу асимптоталарды табу; 8.Асимптота жақындағандағы бағытын зерттеу; 9.Функцияның ең үлкен және ең кіші мәндерін табу. 8

#9 слайд
Сызықтық көбейткіштің көбейтіндісі
түрінде берілген дәрежелі функциялар) )...( )( ( 2 1 n a x a x a x y
функция барлық сан осінде
анықталған;
периодты емес ;
асимптоталары жоқ;
x
| | y
9 болғанда функция
шексіз өседі немесе кемиді , яғни
функцияның үзіліссіздігі
салдарынан функцияның ең
үлкен және ең кіші мәндері
болады;
9 слайд
Сызықтық көбейткіштің көбейтіндісі түрінде берілген дәрежелі функциялар) )...( )( ( 2 1 n a x a x a x y функция барлық сан осінде анықталған; периодты емес ; асимптоталары жоқ; x | | y 9 болғанда функция шексіз өседі немесе кемиді , яғни функцияның үзіліссіздігі салдарынан функцияның ең үлкен және ең кіші мәндері болады;
#10 слайд
функциясының графигін салайық. )
2
)(
2
1
( ) 2 )(
2
3
2(
x x x x x y
Функцияның нөлдері:
2 ,
4
3
, 0,
2
1
,
2
x
y
x
2
2
1
0
4
3 2
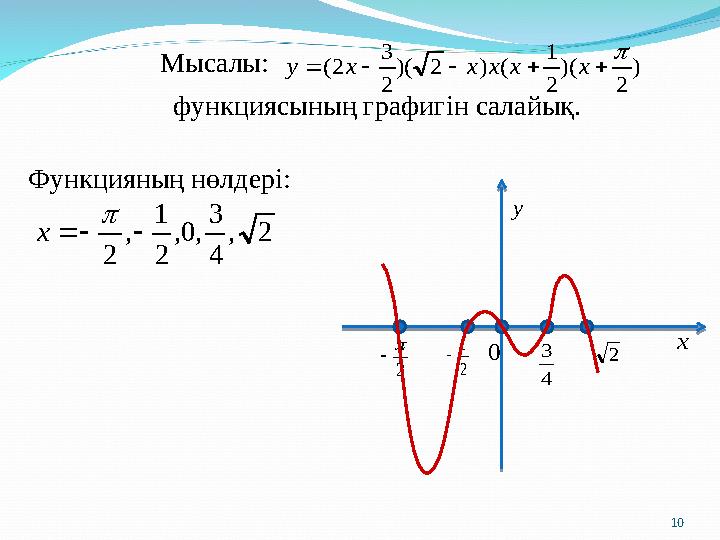
Мысалы:
10
10 слайд
функциясының графигін салайық. ) 2 )( 2 1 ( ) 2 )( 2 3 2( x x x x x y Функцияның нөлдері: 2 , 4 3 , 0, 2 1 , 2 x y x 2 2 1 0 4 3 2 Мысалы: 10
#11 слайд
n
n
x a x a a y ...
1 0
түріндегі екі
мүшенің көбейтіндісі
(мүмкін болса) түрінде
көрсету керек;
|a| кішірейткенде
нөлдер бір-біріне
жақындайды.
) ( a x
2 2
) )( ( a x a x a x y
x
y
0
2x y
2 2
a x y
a a
11
2 a
11 слайд
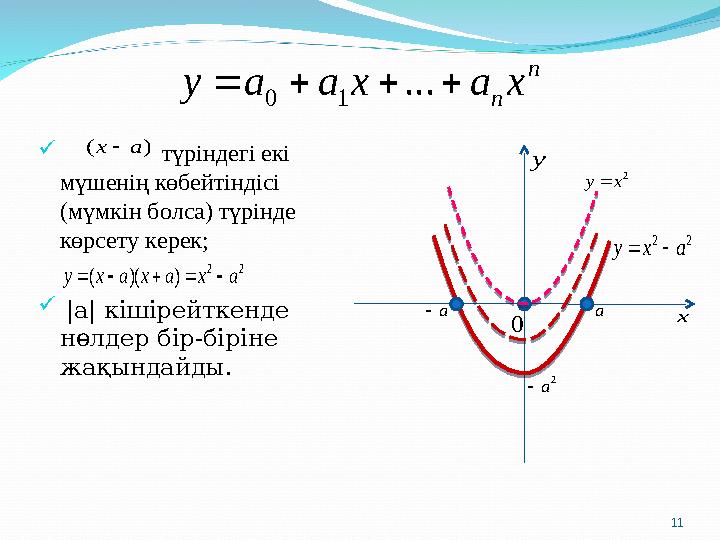
n n x a x a a y ... 1 0 түріндегі екі мүшенің көбейтіндісі (мүмкін болса) түрінде көрсету керек; |a| кішірейткенде нөлдер бір-біріне жақындайды. ) ( a x 2 2 ) )( ( a x a x a x y x y 0 2x y 2 2 a x y a a 11 2 a
#12 слайд
функцияның
нөлдері болып
табылады;
|a| кішірейткенде
нөлдер бір-біріне
жақындайды.x a x a x ) )( (
a x
x
y
0 a a
3
x y
x a x a x y ) )( (
12
12 слайд
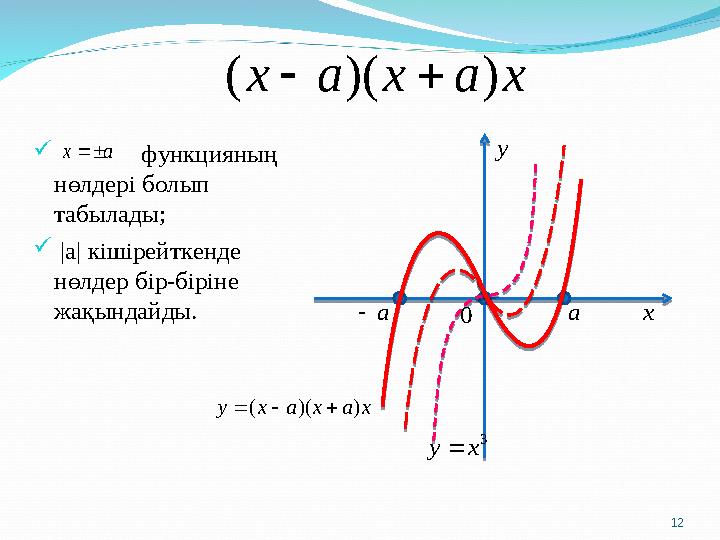
функцияның нөлдері болып табылады; |a| кішірейткенде нөлдер бір-біріне жақындайды.x a x a x ) )( ( a x x y 0 a a 3 x y x a x a x y ) )( ( 12

#13 слайд
натурал сандарnk
n
k k
a x a x a x y ) ...( ) ( ) ( 2 1
2 1
n k k k ,..., , 2 1
егер нөл жұп еселі болса, онда функцияның
графигі Ох осін қимайды (жанап өтеді), яғни
функция таңбасын өзгертпейді;
егер нөл тақ еселі (бір еселі болған жағдайы да )
болса, онда функцияның графигі Ох осін қияды.
13
13 слайд
натурал сандарnk n k k a x a x a x y ) ...( ) ( ) ( 2 1 2 1 n k k k ,..., , 2 1 егер нөл жұп еселі болса, онда функцияның графигі Ох осін қимайды (жанап өтеді), яғни функция таңбасын өзгертпейді; егер нөл тақ еселі (бір еселі болған жағдайы да ) болса, онда функцияның графигі Ох осін қияды. 13
#14 слайд
функциясының графигін салу керек.3 4 2
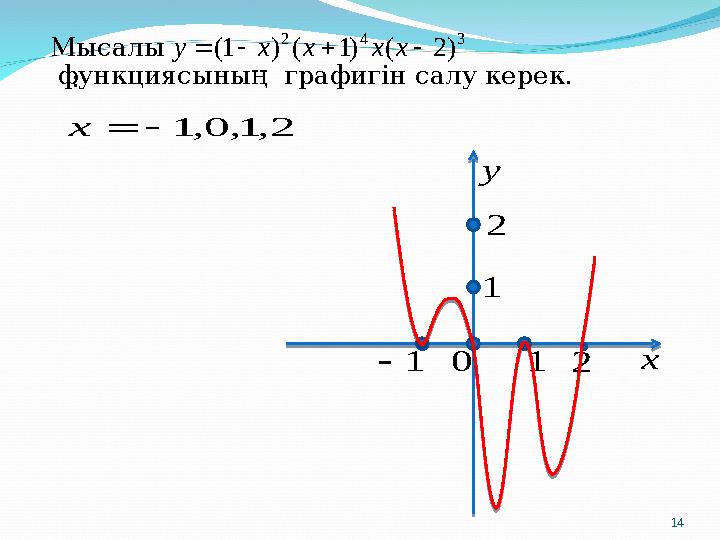
) 2 ( ) 1 ( ) 1( x x x x yМысалы
:
2 , 1, 0 , 1 x
x
y
0 1 1 2
1
2
14
14 слайд
функциясының графигін салу керек.3 4 2 ) 2 ( ) 1 ( ) 1( x x x x yМысалы : 2 , 1, 0 , 1 x x y 0 1 1 2 1 2 14

#15 слайд
ІІІ. Фукциялардың графиктерін салудың негізгі әдістері
3.1. Түрлендірулер әдісі
3.2. Күрделі түрлендірулер
3.3. Модуль белгісі бар функциялар. Функцияның графигіне
қолданылатын алгебралық амалдар
функциялардың графиктерін салудың негізгі әдістері
(параллель көшіру, шағылу (бейнелеу), деформация, модуль
белгісі бар функциялар, функциялардың графигіне
қолданылатын алгебралық амалдар). Функцияны зерттегенде
функцияның анықталу және өзгеру аймағын, оның кему
немесе өсу аймағын, асимптоталарын, таңба тұрақтылығын т.б
табуға мүмкіндік туындайды. Алайда көптеген функциялардың
графиктерін салған кезде функцияның аналитикалық өрнегін
жеңілдететін және графиктерді салуды оңайлататын әртүрлі
әдістерді қолдану арқылы мұндай зерттеулерді қысқартуға
болады. Осы тарау дәл осындай әдістерді көрсетуге арналған,
ол көптеген функциялардың графиктерін салу үшін
практикалық құрал ретінде қызмет ете алады.
15
15 слайд
ІІІ. Фукциялардың графиктерін салудың негізгі әдістері 3.1. Түрлендірулер әдісі 3.2. Күрделі түрлендірулер 3.3. Модуль белгісі бар функциялар. Функцияның графигіне қолданылатын алгебралық амалдар функциялардың графиктерін салудың негізгі әдістері (параллель көшіру, шағылу (бейнелеу), деформация, модуль белгісі бар функциялар, функциялардың графигіне қолданылатын алгебралық амалдар). Функцияны зерттегенде функцияның анықталу және өзгеру аймағын, оның кему немесе өсу аймағын, асимптоталарын, таңба тұрақтылығын т.б табуға мүмкіндік туындайды. Алайда көптеген функциялардың графиктерін салған кезде функцияның аналитикалық өрнегін жеңілдететін және графиктерді салуды оңайлататын әртүрлі әдістерді қолдану арқылы мұндай зерттеулерді қысқартуға болады. Осы тарау дәл осындай әдістерді көрсетуге арналған, ол көптеген функциялардың графиктерін салу үшін практикалық құрал ретінде қызмет ете алады. 15
![функцияның графигін салудың этаптық сұлбасы 16b a wx f A y ) (Функцияны )] ( [ w a x w f A в y түрінде жазай функцияның графигін салудың этаптық сұлбасы 16b a wx f A y ) (Функцияны )] ( [ w a x w f A в y түрінде жазай](https://api.ust.kz/storage/files/materials/ppt/image/2021/march/d17/1616010861-16.jpeg)
#16 слайд
функцияның графигін салудың
этаптық сұлбасы
16b a wx f A y ) (Функцияны
)] ( [
w
a
x w f A в y түрінде жазайық.
)] ( [
w
a x w f A в y
абсцисса осін
в бірлікке жылжыту
)] ( [ .1
w
a x w f A y
ордината осін
w
а бірлікке жылжыту
] [ .2 wx f A y
абсцисса осіне қатысты бейнелеу
) ( .3 wx f A y
ордината осі бойымен графикті сығу немесе созу
) ( .4 wx f y
ордината осіне қатысты бейнелеу
) ( .5 x w f y
абсцисса осі бойында графикті сығу немесе созу
) ( .6 x f y
16 слайд
функцияның графигін салудың этаптық сұлбасы 16b a wx f A y ) (Функцияны )] ( [ w a x w f A в y түрінде жазайық. )] ( [ w a x w f A в y абсцисса осін в бірлікке жылжыту )] ( [ .1 w a x w f A y ордината осін w а бірлікке жылжыту ] [ .2 wx f A y абсцисса осіне қатысты бейнелеу ) ( .3 wx f A y ордината осі бойымен графикті сығу немесе созу ) ( .4 wx f y ордината осіне қатысты бейнелеу ) ( .5 x w f y абсцисса осі бойында графикті сығу немесе созу ) ( .6 x f y

#17 слайд
IV. Теңдеу мен теңсіздіктердің графиктері
4.1. Нүктелердің геометриялық орны
4.2.Күрделі функциялардың графиктерін салу. Мысалдар
Нүктелердің геометриялық орны және күрделі
функциялардың графиктерін салу тұжырымдалды.
Практикада көбіне және екі айнымалылар
арасындағы бірмәнді емес тәуелділік жиі кездеседі,
яғни -тің бірмәніне -тің екі немесе одан да көп мәні
сәйкес келетін немесе осы айнымалылар арасындағы
тәуелділік теңсіздік арқылы берілетін жағдайлар. Осы
сияқты тәуелділіктер нүктенің геометриялық орны
түсінігімен тығыз байланысты.
17
17 слайд
IV. Теңдеу мен теңсіздіктердің графиктері 4.1. Нүктелердің геометриялық орны 4.2.Күрделі функциялардың графиктерін салу. Мысалдар Нүктелердің геометриялық орны және күрделі функциялардың графиктерін салу тұжырымдалды. Практикада көбіне және екі айнымалылар арасындағы бірмәнді емес тәуелділік жиі кездеседі, яғни -тің бірмәніне -тің екі немесе одан да көп мәні сәйкес келетін немесе осы айнымалылар арасындағы тәуелділік теңсіздік арқылы берілетін жағдайлар. Осы сияқты тәуелділіктер нүктенің геометриялық орны түсінігімен тығыз байланысты. 17

#18 слайд
V. Функцияның графиктерін қолдану есептері
Функцияның графиктерін әртүрлі тапсырмаларды шешу үшін
пайдалану. Функцияның графигін тұрғыза білу негізгі
мақсат емес. Көбіне графиктерді салу функцияның
қасиеттерін зерттеумен байланысты. Бірақта графиктерді
салу қажеттілігі мұнымен шектелмейді. Бірқатар
жағдайларда графиктер теңдеудің және теңсіздіктің
шешімін табуды жеңілдетеді .Графиктік әдіс қолданбалы
тапсырмаларды шешу кезінде де жиі қолданылады. Бұл
тарауда мен сұрақтар мен салуларда толық тоқталмай,
графиктерді қолдануды көрсететін бірнеше мысалдарды
қарастырдым.
18
18 слайд
V. Функцияның графиктерін қолдану есептері Функцияның графиктерін әртүрлі тапсырмаларды шешу үшін пайдалану. Функцияның графигін тұрғыза білу негізгі мақсат емес. Көбіне графиктерді салу функцияның қасиеттерін зерттеумен байланысты. Бірақта графиктерді салу қажеттілігі мұнымен шектелмейді. Бірқатар жағдайларда графиктер теңдеудің және теңсіздіктің шешімін табуды жеңілдетеді .Графиктік әдіс қолданбалы тапсырмаларды шешу кезінде де жиі қолданылады. Бұл тарауда мен сұрақтар мен салуларда толық тоқталмай, графиктерді қолдануды көрсететін бірнеше мысалдарды қарастырдым. 18

шағым қалдыра аласыз
















