ЖИ көмекші
Гомотетия: қасиеттері, түрлері және мысалдары
Тақырып бойынша 11 материал табылды
Гомотетия: қасиеттері, түрлері және мысалдары
Материал туралы қысқаша түсінік
Гомотетия - жазықтықтағы геометриялық өзгеріс, мұнда центр деп аталатын бекітілген нүктеден (O) қашықтықтар ортақ көбейткішке көбейтіледі. Осылайша әрбір Р нүктесі түрленудің басқа Р 'көбейтіндісіне сәйкес келеді және олар О нүктесімен тураланады.Сонымен, гомотетия дегеніміз екі геометриялық фигуралар арасындағы сәйкестік туралы, мұнда өзгертілген нүктелер гомотетикалық деп аталады және олар бекітілген нүктемен және бір-біріне параллель кесінділермен тураланған.
Материалдың қысқаша нұсқасы
1 / 20
Жүктеу
Бөлісу
ЖИ арқылы жасау
Слайдтың жеке беттері
#1 слайд
Преобразование подобия.
Гомотетия .
Цель урока: Рассмотреть одно из
важнейших преобразований подобия –
гомотетию.
1 слайд
Преобразование подобия. Гомотетия . Цель урока: Рассмотреть одно из важнейших преобразований подобия – гомотетию.
#2 слайд
2
а
2 слайд
2 а
#3 слайд
3А
3 слайд
3А
#4 слайд
4а
4 слайд
4а
#5 слайд
5А
5 слайд
5А
#6 слайд
6
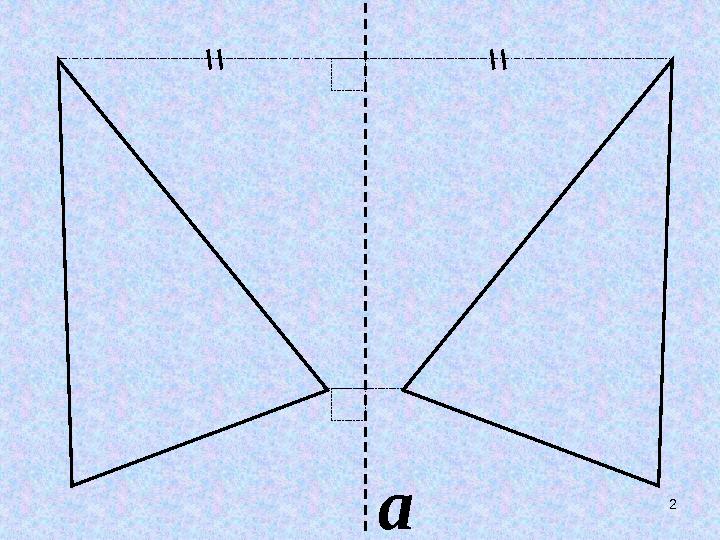
ОСЕВАЯ
СИММЕТРИЯ
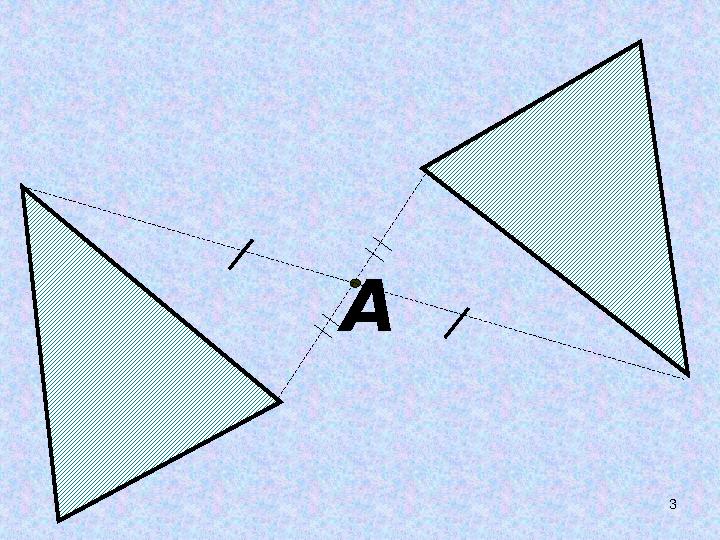
ЦЕНТРАЛЬНАЯ
СИММЕТРИЯ
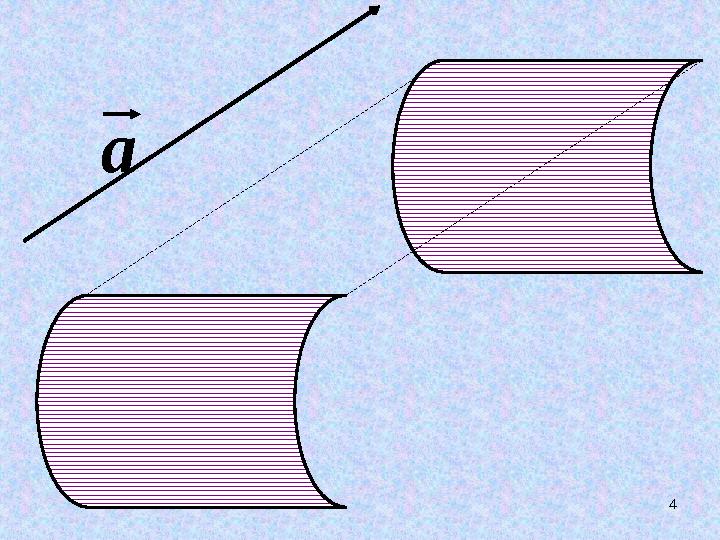
ПАРАЛЛЕЛЬНЫЙ
ПЕРЕНОС
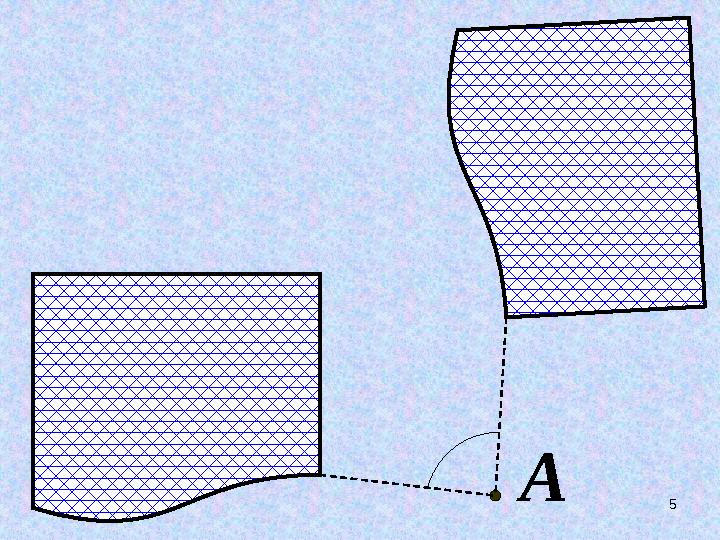
ПОВОРОТ Д
В
И
Ж
Е
Н
И
Е
6 слайд
6 ОСЕВАЯ СИММЕТРИЯ ЦЕНТРАЛЬНАЯ СИММЕТРИЯ ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ПОВОРОТ Д В И Ж Е Н И Е
#7 слайд
7Свойства движения:
При движении прямая переходит
в прямую, луч – в луч, отрезок – в
отрезок.
Сохраняются расстояния между
точками.
Сохраняются углы между
лучами.
7 слайд
7Свойства движения: При движении прямая переходит в прямую, луч – в луч, отрезок – в отрезок. Сохраняются расстояния между точками. Сохраняются углы между лучами.
#8 слайд
8Следствие
:
При движении фигура
переходит в равную ей
фигуру!!!
8 слайд
8Следствие : При движении фигура переходит в равную ей фигуру!!!
#9 слайд
9ГОМОТЕТИЯ.
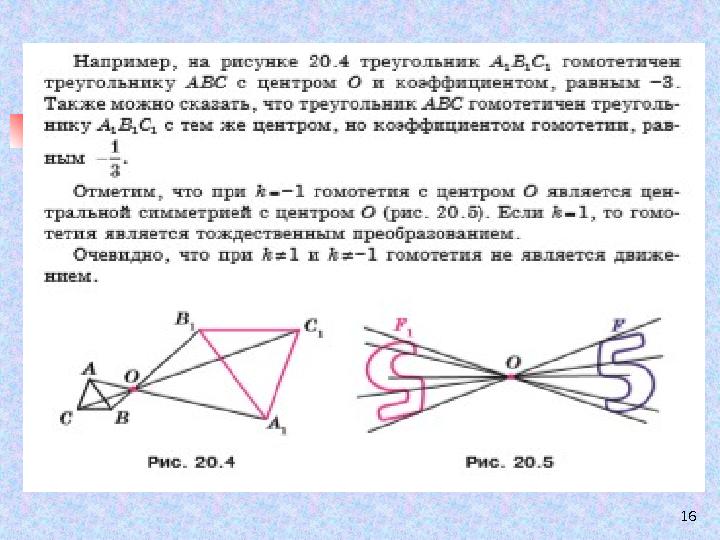
Гомотетия – одно из важнейших
преобразований подобия.
9 слайд
9ГОМОТЕТИЯ. Гомотетия – одно из важнейших преобразований подобия.
#10 слайд
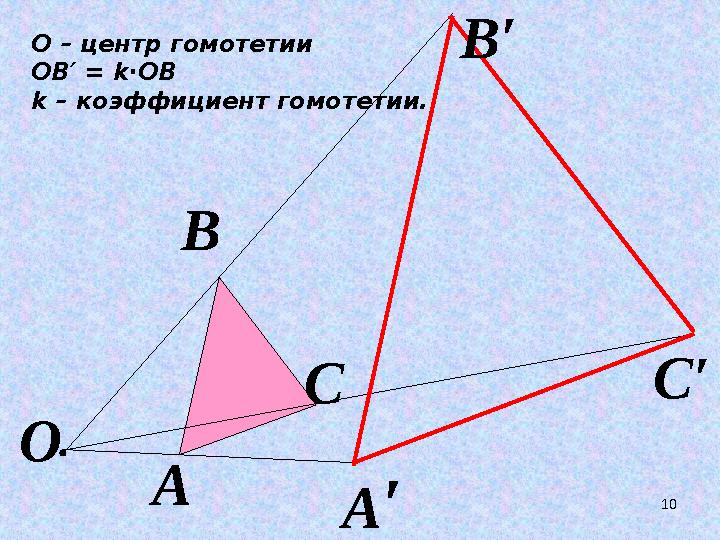
10О – центр гомотетии
ОВ′ = k ∙ОВ
k – коэффициент гомотетии.
О
А
А ′В В ′
С С ′
10 слайд
10О – центр гомотетии ОВ′ = k ∙ОВ k – коэффициент гомотетии. О А А ′В В ′ С С ′
#11 слайд
11При гомотетии
сохраняются только
углы!!!
11 слайд
11При гомотетии сохраняются только углы!!!
#12 слайд
12Рассмотрим случаи:
1 случай: k > 0
а) k > 1
б) k < 1
2 случай: k < 0
12 слайд
12Рассмотрим случаи: 1 случай: k > 0 а) k > 1 б) k < 1 2 случай: k < 0
#13 слайд
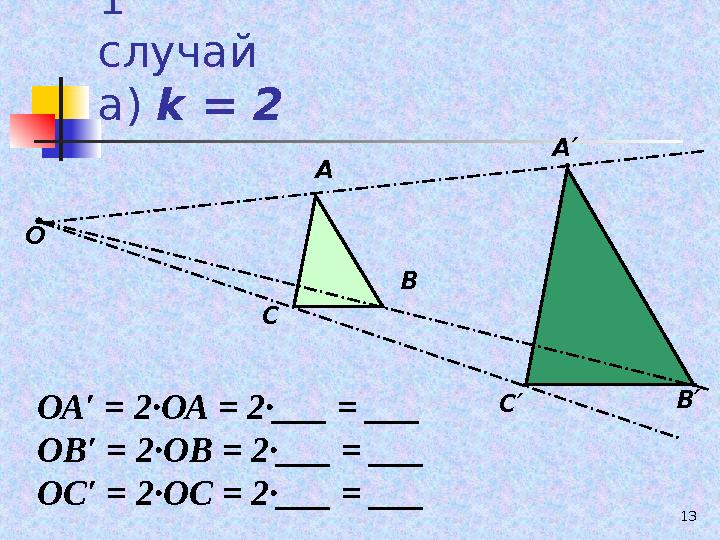
131
случай
а) k = 2
А
В
С А ′
В ′
С ′О
ОА′ = 2∙ОА = 2∙___ = ___
ОВ′ = 2∙ОВ = 2∙___ = ___
ОС′ = 2∙ОС = 2∙___ = ___
13 слайд
131 случай а) k = 2 А В С А ′ В ′ С ′О ОА′ = 2∙ОА = 2∙___ = ___ ОВ′ = 2∙ОВ = 2∙___ = ___ ОС′ = 2∙ОС = 2∙___ = ___
#14 слайд
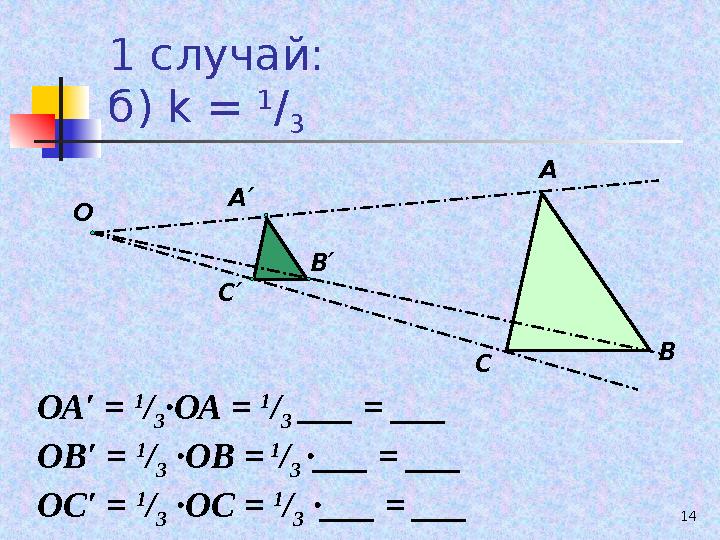
141 случай:
б) k = 1
/
3
А
В
СО А ′
В ′
С ′
ОА′ = 1
/
3 ∙ОА = 1
/
3 ___ = ___
ОВ′ = 1
/
3 ∙ОВ = 1
/
3 ∙___ = ___
ОС′ = 1
/
3 ∙ОС = 1
/
3 ∙___ = ___
14 слайд
141 случай: б) k = 1 / 3 А В СО А ′ В ′ С ′ ОА′ = 1 / 3 ∙ОА = 1 / 3 ___ = ___ ОВ′ = 1 / 3 ∙ОВ = 1 / 3 ∙___ = ___ ОС′ = 1 / 3 ∙ОС = 1 / 3 ∙___ = ___
#15 слайд
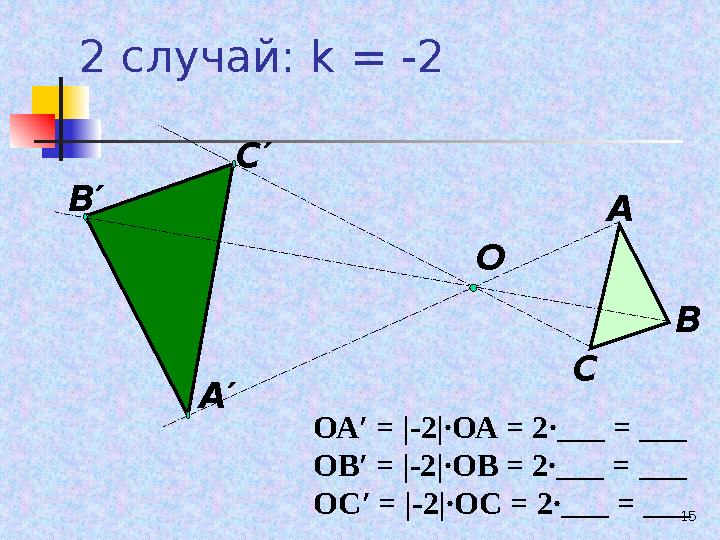
152 случай: k = -2
О А
В
С
А′В′ С′
ОА′ = |- 2 | ∙ОА = 2∙___ = ___
ОВ′ = |- 2 | ∙ОВ = 2∙___ = ___
ОС′ = |- 2 | ∙ОС = 2∙___ = ___
15 слайд
152 случай: k = -2 О А В С А′В′ С′ ОА′ = |- 2 | ∙ОА = 2∙___ = ___ ОВ′ = |- 2 | ∙ОВ = 2∙___ = ___ ОС′ = |- 2 | ∙ОС = 2∙___ = ___
#16 слайд
16
16 слайд
16
#17 слайд
17
17 слайд
17
#18 слайд
18
18 слайд
18
#19 слайд
19
19 слайд
19
Файл форматы:
pptx
07.06.2022
5330
Жүктеу
ЖИ арқылы жасау
Жариялаған:
Бұл материалды қолданушы жариялаған. Ustaz Tilegi ақпаратты жеткізуші ғана болып табылады. Жарияланған материалдың мазмұны мен авторлық құқық толықтай автордың жауапкершілігінде. Егер материал авторлық құқықты бұзады немесе сайттан алынуы тиіс деп есептесеңіз,
шағым қалдыра аласыз
шағым қалдыра аласыз
