Графтағы алгоритмдері. Дейкстра алгоритмі.
Графтағы алгоритмдері. Дейкстра алгоритмі.


#1 слайд
Графтағы
алгоритмдері.
Дейкстра алгоритмі.
1 слайд
Графтағы алгоритмдері. Дейкстра алгоритмі.

#2 слайд
Дейкстра
алгоритм і
деген не
және ол не
үшін
керек?
Ең қысқа жолды табудың мысалын
қарастырайық. Қалалық аймақтарды
байланыстыратын автомобиль
жолдарының желісі берілген. Кейбір
жолдар бір бағытта жүреді. Қала
орталығынан ауданның әр қаласына
ең қысқа жолдарды табыңыз.
Бұл мәселені шешу үшін Дайкстра
алгоритмін - 1959 жылы
голландиялық ғалым Э.Дейкстра
ойлап тапқан графиктер бойынша
алгоритмді қолдануға болады.
Графтың бір шыңынан басқаларына
дейін ең қысқа қашықтықты табады.
Теріс салмақ жиектері жоқ
графиктер үшін ғана жұмыс істейді.
2 слайд
Дейкстра алгоритм і деген не және ол не үшін керек? Ең қысқа жолды табудың мысалын қарастырайық. Қалалық аймақтарды байланыстыратын автомобиль жолдарының желісі берілген. Кейбір жолдар бір бағытта жүреді. Қала орталығынан ауданның әр қаласына ең қысқа жолдарды табыңыз. Бұл мәселені шешу үшін Дайкстра алгоритмін - 1959 жылы голландиялық ғалым Э.Дейкстра ойлап тапқан графиктер бойынша алгоритмді қолдануға болады. Графтың бір шыңынан басқаларына дейін ең қысқа қашықтықты табады. Теріс салмақ жиектері жоқ графиктер үшін ғана жұмыс істейді.
#3 слайд
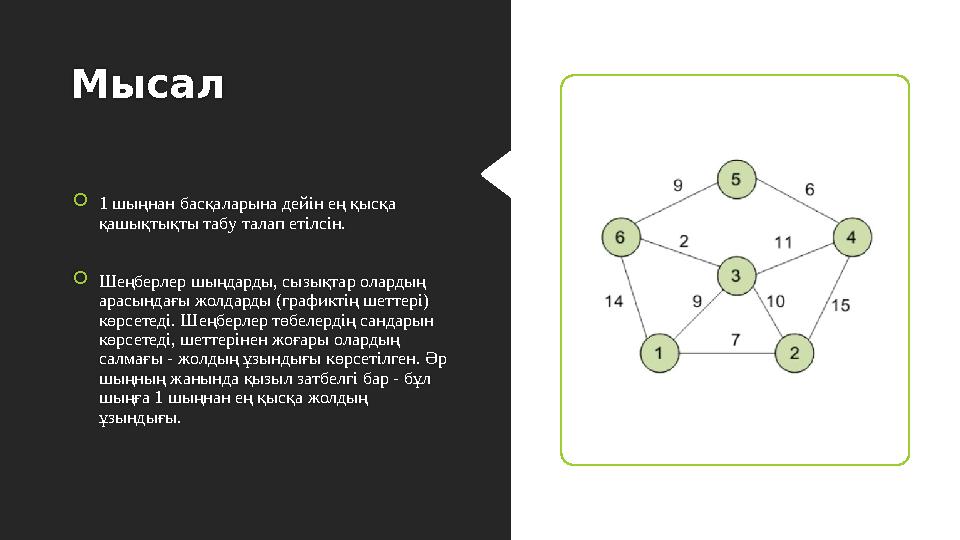
Мысал
1 шыңнан басқаларына дейін ең қысқа
қашықтықты табу талап етілсін.
Шеңберлер шыңдарды, сызықтар олардың
арасындағы жолдарды (графиктің шеттері)
көрсетеді. Шеңберлер төбелердің сандарын
көрсетеді, шеттерінен жоғары олардың
салмағы - жолдың ұзындығы көрсетілген. Әр
шыңның жанында қызыл затбелгі бар - бұл
шыңға 1 шыңнан ең қысқа жолдың
ұзындығы.
3 слайд
Мысал 1 шыңнан басқаларына дейін ең қысқа қашықтықты табу талап етілсін. Шеңберлер шыңдарды, сызықтар олардың арасындағы жолдарды (графиктің шеттері) көрсетеді. Шеңберлер төбелердің сандарын көрсетеді, шеттерінен жоғары олардың салмағы - жолдың ұзындығы көрсетілген. Әр шыңның жанында қызыл затбелгі бар - бұл шыңға 1 шыңнан ең қысқа жолдың ұзындығы.
#4 слайд
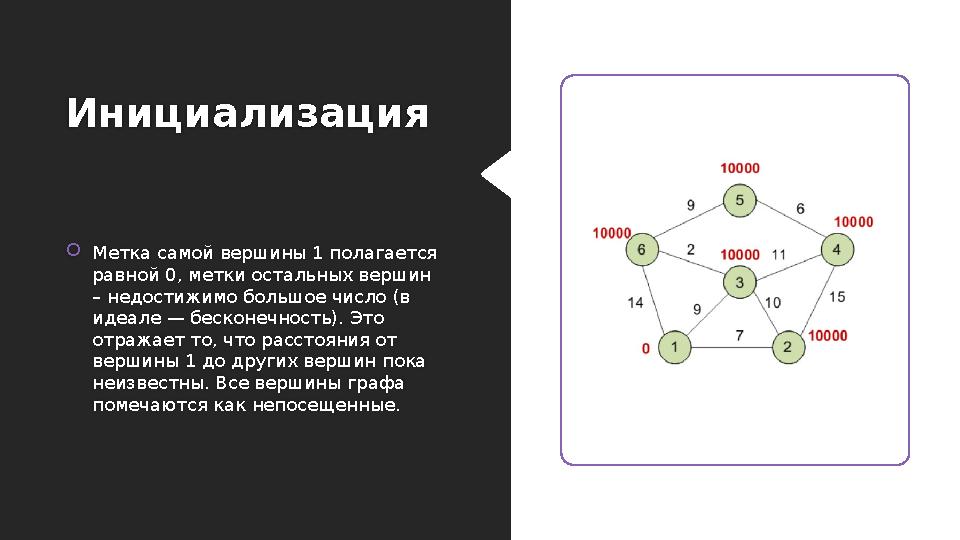
Инициализация
Метка самой вершины 1 полагается
равной 0, метки остальных вершин
– недостижимо большое число (в
идеале — бесконечность). Это
отражает то, что расстояния от
вершины 1 до других вершин пока
неизвестны. Все вершины графа
помечаются как непосещенные.
4 слайд
Инициализация Метка самой вершины 1 полагается равной 0, метки остальных вершин – недостижимо большое число (в идеале — бесконечность). Это отражает то, что расстояния от вершины 1 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.

#5 слайд
Бірінші қадам
1 шыңында минималды затбелгі бар, оның көршілері - 2, 3 және 6
шыңдары. Біз шыңның көршілерін кезекпен айналып өтеміз.
1 шыңының бірінші көршісі - 2 шыңы, өйткені оған жол ұзындығы
минималды. 1 шыңы арқылы өтетін жолдың ұзындығы 1 шыңына
дейінгі ең қысқа қашықтықтың қосындысына (оның белгісінің мәні)
және 1-ден 2-ге дейінгі жиектің ұзындығына тең, яғни 0 + 7 = 7. Бұл
2-шыңның қазіргі таңбасынан аз (10000), сондықтан 2-шыңның жаңа
белгісі 7-ге тең.
Сол сияқты барлық басқа көршілер үшін жол ұзындығын табамыз (3
және 6 шыңдары).
1 шыңының барлық көршілері тексеріледі. 1 шыңына дейінгі ең аз
қашықтық соңғы болып саналады және қайта қарауға жатпайды. 1
шыңы барған ретінде белгіленеді.
5 слайд
Бірінші қадам 1 шыңында минималды затбелгі бар, оның көршілері - 2, 3 және 6 шыңдары. Біз шыңның көршілерін кезекпен айналып өтеміз. 1 шыңының бірінші көршісі - 2 шыңы, өйткені оған жол ұзындығы минималды. 1 шыңы арқылы өтетін жолдың ұзындығы 1 шыңына дейінгі ең қысқа қашықтықтың қосындысына (оның белгісінің мәні) және 1-ден 2-ге дейінгі жиектің ұзындығына тең, яғни 0 + 7 = 7. Бұл 2-шыңның қазіргі таңбасынан аз (10000), сондықтан 2-шыңның жаңа белгісі 7-ге тең. Сол сияқты барлық басқа көршілер үшін жол ұзындығын табамыз (3 және 6 шыңдары). 1 шыңының барлық көршілері тексеріледі. 1 шыңына дейінгі ең аз қашықтық соңғы болып саналады және қайта қарауға жатпайды. 1 шыңы барған ретінде белгіленеді.
#6 слайд
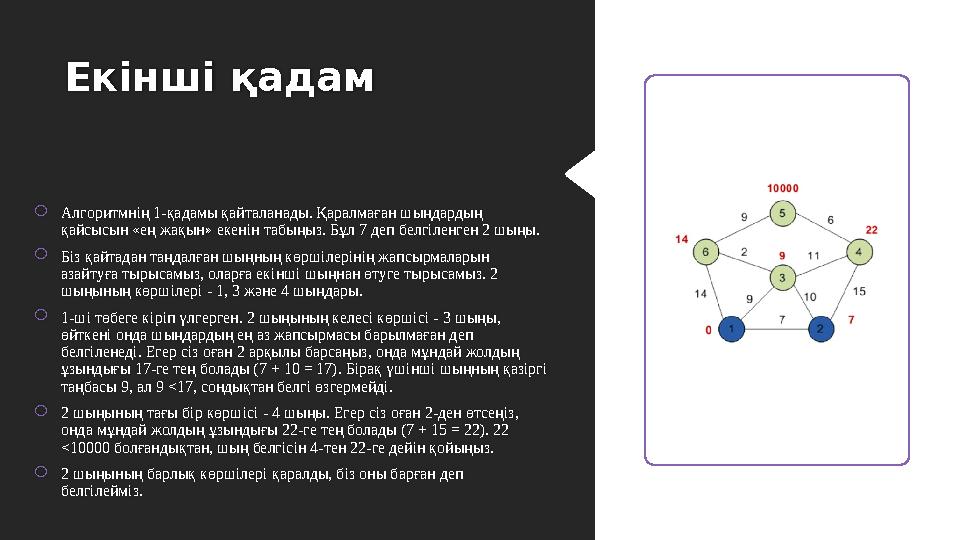
Екінші қадам
Алгоритмнің 1-қадамы қайталанады. Қаралмаған шыңдардың
қайсысын «ең жақын» екенін табыңыз. Бұл 7 деп белгіленген 2 шыңы.
Біз қайтадан таңдалған шыңның көршілерінің жапсырмаларын
азайтуға тырысамыз, оларға екінші шыңнан өтуге тырысамыз. 2
шыңының көршілері - 1, 3 және 4 шыңдары.
1-ші төбеге кіріп үлгерген. 2 шыңының келесі көршісі - 3 шыңы,
өйткені онда шыңдардың ең аз жапсырмасы барылмаған деп
белгіленеді. Егер сіз оған 2 арқылы барсаңыз, онда мұндай жолдың
ұзындығы 17-ге тең болады (7 + 10 = 17). Бірақ үшінші шыңның қазіргі
таңбасы 9, ал 9 <17, сондықтан белгі өзгермейді.
2 шыңының тағы бір көршісі - 4 шыңы. Егер сіз оған 2-ден өтсеңіз,
онда мұндай жолдың ұзындығы 22-ге тең болады (7 + 15 = 22). 22
<10000 болғандықтан, шың белгісін 4-тен 22-ге дейін қойыңыз.
2 шыңының барлық көршілері қаралды, біз оны барған деп
белгілейміз.
6 слайд
Екінші қадам Алгоритмнің 1-қадамы қайталанады. Қаралмаған шыңдардың қайсысын «ең жақын» екенін табыңыз. Бұл 7 деп белгіленген 2 шыңы. Біз қайтадан таңдалған шыңның көршілерінің жапсырмаларын азайтуға тырысамыз, оларға екінші шыңнан өтуге тырысамыз. 2 шыңының көршілері - 1, 3 және 4 шыңдары. 1-ші төбеге кіріп үлгерген. 2 шыңының келесі көршісі - 3 шыңы, өйткені онда шыңдардың ең аз жапсырмасы барылмаған деп белгіленеді. Егер сіз оған 2 арқылы барсаңыз, онда мұндай жолдың ұзындығы 17-ге тең болады (7 + 10 = 17). Бірақ үшінші шыңның қазіргі таңбасы 9, ал 9 <17, сондықтан белгі өзгермейді. 2 шыңының тағы бір көршісі - 4 шыңы. Егер сіз оған 2-ден өтсеңіз, онда мұндай жолдың ұзындығы 22-ге тең болады (7 + 15 = 22). 22 <10000 болғандықтан, шың белгісін 4-тен 22-ге дейін қойыңыз. 2 шыңының барлық көршілері қаралды, біз оны барған деп белгілейміз.
#7 слайд
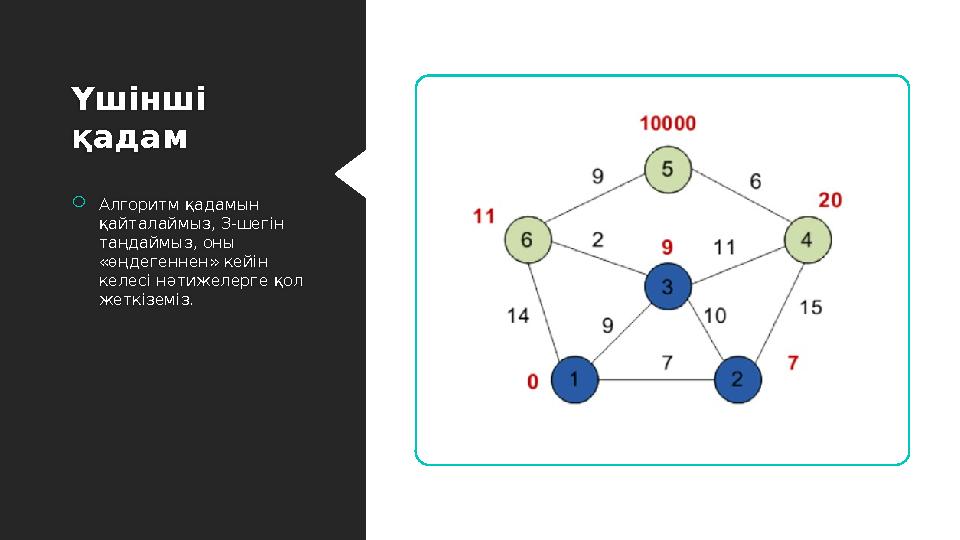
Үшінші
қадам
Алгоритм қадамын
қайталаймыз, 3-шегін
таңдаймыз, оны
«өңдегеннен» кейін
келесі нәтижелерге қол
жеткіземіз.
7 слайд
Үшінші қадам Алгоритм қадамын қайталаймыз, 3-шегін таңдаймыз, оны «өңдегеннен» кейін келесі нәтижелерге қол жеткіземіз.

#8 слайд
Т өртінші Қадам
8 слайд
Т өртінші Қадам
#9 слайд
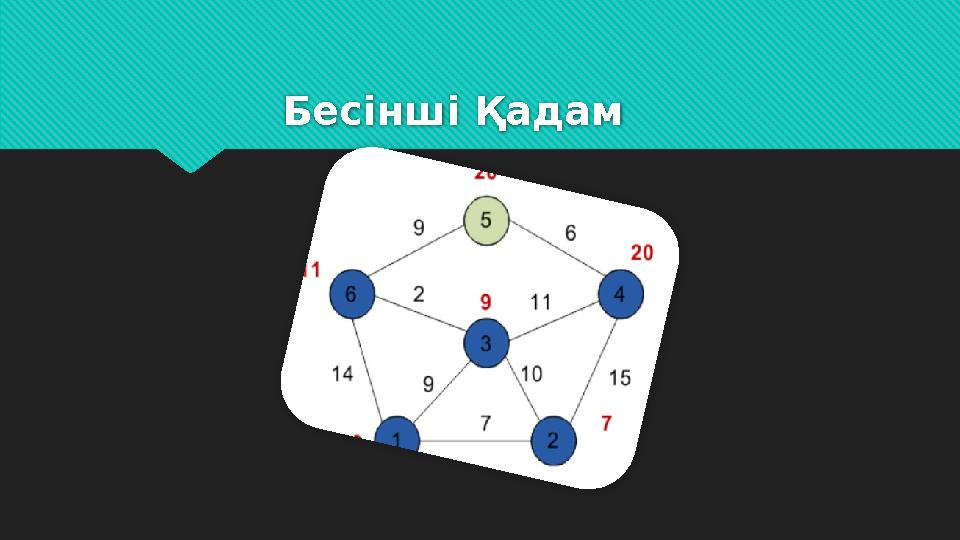
Бесінші Қадам
9 слайд
Бесінші Қадам
#10 слайд
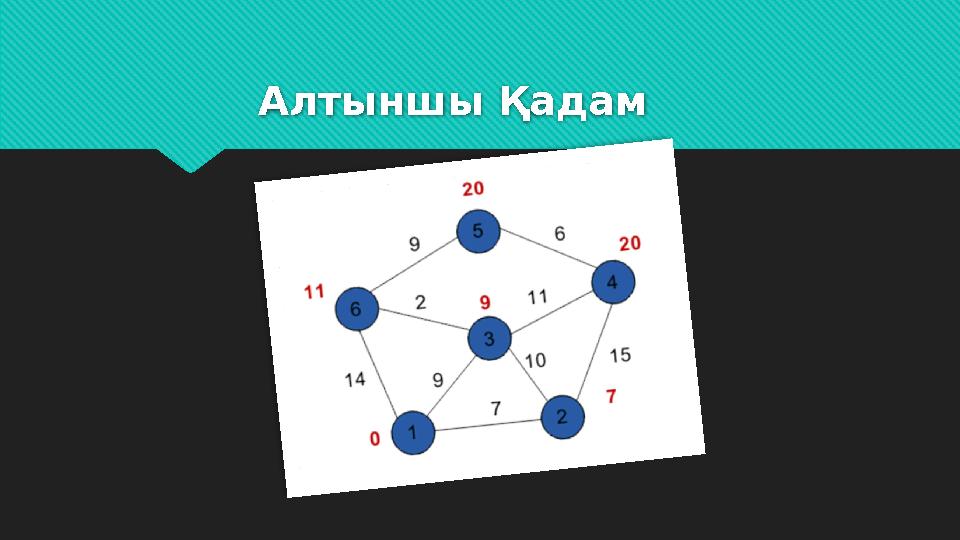
Алтыншы Қадам
10 слайд
Алтыншы Қадам

#11 слайд
Есеп немен
аякталды ?
Осылайша, 1 шыңнан 5 шыңға дейінгі ең қысқа жол 1
- 3 - 6 - 5 шыңдары арқылы өтетін жол болады,
өйткені осылайша біз 20-ға тең минималды салмақ
аламыз.
Ең қысқа жолдың шығуын қарастырайық. Біз әр
шыңның жол ұзындығын білеміз, енді шыңдарды
соңынан қарастырамыз. Соңғы шыңды қарастырайық
(бұл жағдайда 5 шың), және ол байланысқан барлық
шыңдар үшін сәйкес шеттің салмағын соңғы шыңның
жол ұзындығынан шығару арқылы жол ұзындығын
табамыз.
Сонымен, 5 шыңының ұзындығы 20-ға тең, ол 6 және
4 шыңдарымен байланысқан.
6 шыңы үшін біз салмақты 20 - 9 = 11 аламыз (сәйкес
келеді).
4 шыңы үшін біз 20 - 6 = 14 салмағын аламыз (сәйкес
келмеді).
Егер нәтижесінде біз қарастырылып отырған шыңның
жол ұзындығымен сәйкес келетін мән алсақ (бұл
жағдайда 6 шың), онда дәл осы жерден соңғы шыңға
көшу жүзеге асырылды. Бұл шыңды біз қалаған
жолмен белгілейміз.
Әрі қарай, біз 6-шыңға жеткен шекті анықтаймыз.
Сонымен, біз басымызға жеткенше.
Егер осындай траверстің нәтижесінде қандай да бір
қадамда бізде бірнеше шыңдар үшін бірдей мәндер
болса, онда олардың кез-келгенін алуға болады -
бірнеше жолдың ұзындығы бірдей болады.
11 слайд
Есеп немен аякталды ? Осылайша, 1 шыңнан 5 шыңға дейінгі ең қысқа жол 1 - 3 - 6 - 5 шыңдары арқылы өтетін жол болады, өйткені осылайша біз 20-ға тең минималды салмақ аламыз. Ең қысқа жолдың шығуын қарастырайық. Біз әр шыңның жол ұзындығын білеміз, енді шыңдарды соңынан қарастырамыз. Соңғы шыңды қарастырайық (бұл жағдайда 5 шың), және ол байланысқан барлық шыңдар үшін сәйкес шеттің салмағын соңғы шыңның жол ұзындығынан шығару арқылы жол ұзындығын табамыз. Сонымен, 5 шыңының ұзындығы 20-ға тең, ол 6 және 4 шыңдарымен байланысқан. 6 шыңы үшін біз салмақты 20 - 9 = 11 аламыз (сәйкес келеді). 4 шыңы үшін біз 20 - 6 = 14 салмағын аламыз (сәйкес келмеді). Егер нәтижесінде біз қарастырылып отырған шыңның жол ұзындығымен сәйкес келетін мән алсақ (бұл жағдайда 6 шың), онда дәл осы жерден соңғы шыңға көшу жүзеге асырылды. Бұл шыңды біз қалаған жолмен белгілейміз. Әрі қарай, біз 6-шыңға жеткен шекті анықтаймыз. Сонымен, біз басымызға жеткенше. Егер осындай траверстің нәтижесінде қандай да бір қадамда бізде бірнеше шыңдар үшін бірдей мәндер болса, онда олардың кез-келгенін алуға болады - бірнеше жолдың ұзындығы бірдей болады.

#12 слайд
Дейкстра
алгоритмінің іске
асуы
Квадрат матрица графиктің салмағын
сақтау үшін қолданылады. Жолдар мен
бағандардың тақырыптарында графиктің
шыңдары бар. Ал графикалық доғалардың
салмақтары кестенің ішкі ұяшықтарына
орналастырылған. Графикте циклдар жоқ,
сондықтан матрицаның негізгі
диагоналында нөлдік мәндер бар.
12 слайд
Дейкстра алгоритмінің іске асуы Квадрат матрица графиктің салмағын сақтау үшін қолданылады. Жолдар мен бағандардың тақырыптарында графиктің шыңдары бар. Ал графикалық доғалардың салмақтары кестенің ішкі ұяшықтарына орналастырылған. Графикте циклдар жоқ, сондықтан матрицаның негізгі диагоналында нөлдік мәндер бар.

шағым қалдыра аласыз
















