Материалдар / Көпжақтар. Призма

Көпжақтар. Призма

Материал туралы қысқаша түсінік

Ұстаздарға

Бахытова Рысжан Оралбайқызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

02 Маусым 2018

1477

2 рет жүктелген

Геометрия Презентация 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 10

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
КөпжақКөпжақ Жоспары:Жоспары: Бахытова Р.О

1 слайд

КөпжақКөпжақ Жоспары:Жоспары: Бахытова Р.О

2 слайд
Жоспары:Көпжақ КөпжақПризма ПризмаМысал Мысал

2 слайд

Жоспары:Көпжақ КөпжақПризма ПризмаМысал Мысал

3 слайд
Көпжақ дегеніміз беті саны шектеулі жазық көпбұрыштардан құралатын дене. Егер көпжақ өзінің бетін құрайтын әрбір жазық көпбұрыш жазықтығының бір жағына орналасқан болса, оны дөңес көпжақ деп атайды.Осындай жазықтық пен дөңес көпжақтың бетінің ортақ бөлігі жақ деп аталады.Дөңес көпжақтың жақтары дөңес көпбұрыштар болып келеді.Жақтардың қабырғаларын- көпжақтың қырлары деп,ал төбелерін көпжақтың төбелері деп атайды. Көпжақ

3 слайд

Көпжақ дегеніміз беті саны шектеулі жазық көпбұрыштардан құралатын дене. Егер көпжақ өзінің бетін құрайтын әрбір жазық көпбұрыш жазықтығының бір жағына орналасқан болса, оны дөңес көпжақ деп атайды.Осындай жазықтық пен дөңес көпжақтың бетінің ортақ бөлігі жақ деп аталады.Дөңес көпжақтың жақтары дөңес көпбұрыштар болып келеді.Жақтардың қабырғаларын- көпжақтың қырлары деп,ал төбелерін көпжақтың төбелері деп атайды. Көпжақ

4 слайд
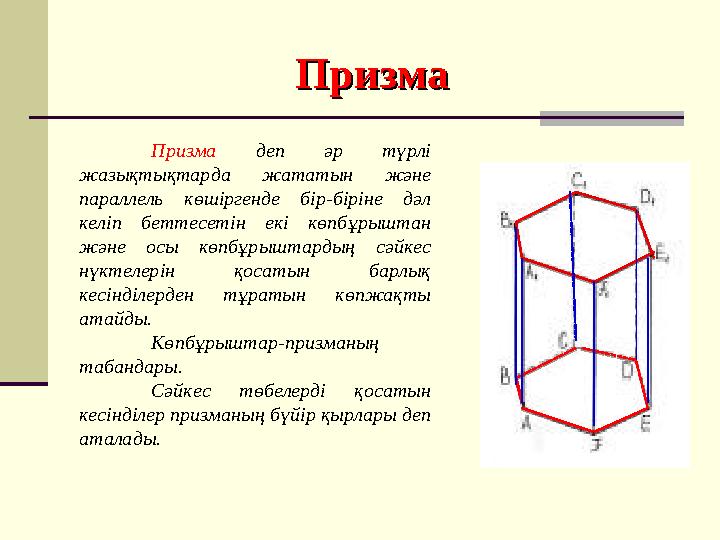
Призма деп әр түрлі жазықтықтарда жататын және параллель көшіргенде бір-біріне дәл келіп беттесетін екі көпбұрыштан және осы көпбұрыштардың сәйкес нүктелерін қосатын барлық кесінділерден тұратын көпжақты атайды. Көпбұрыштар-призманың табандары. Сәйкес төбелерді қосатын кесінділер призманың бүйір қырлары деп аталады. ПризмаПризма

4 слайд

Призма деп әр түрлі жазықтықтарда жататын және параллель көшіргенде бір-біріне дәл келіп беттесетін екі көпбұрыштан және осы көпбұрыштардың сәйкес нүктелерін қосатын барлық кесінділерден тұратын көпжақты атайды. Көпбұрыштар-призманың табандары. Сәйкес төбелерді қосатын кесінділер призманың бүйір қырлары деп аталады. ПризмаПризма

5 слайд
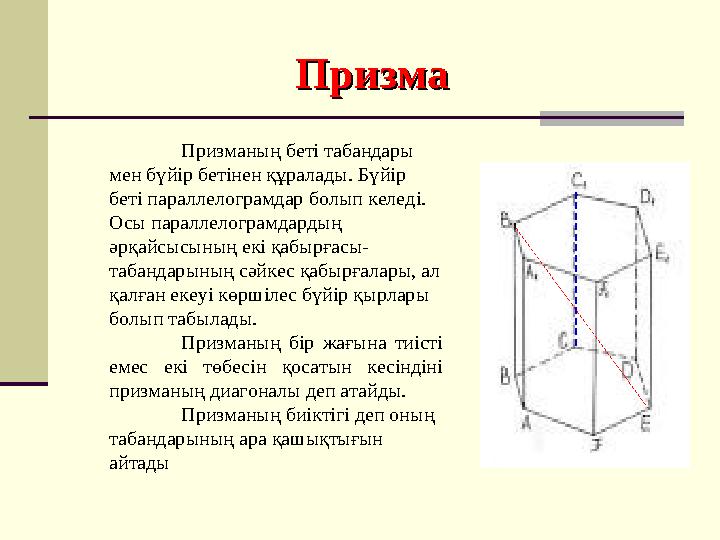
Призманың беті табандары мен бүйір бетінен құралады. Бүйір беті параллелограмдар болып келеді. Осы параллелограмдардың әрқайсысының екі қабырғасы- табандарының сәйкес қабырғалары, ал қалған екеуі көршілес бүйір қырлары болып табылады. Призманың бір жағына тиісті емес екі төбесін қосатын кесіндіні призманың диагоналы деп атайды. Призманың биіктігі деп оның табандарының ара қашықтығын айтады ПризмаПризма

5 слайд

Призманың беті табандары мен бүйір бетінен құралады. Бүйір беті параллелограмдар болып келеді. Осы параллелограмдардың әрқайсысының екі қабырғасы- табандарының сәйкес қабырғалары, ал қалған екеуі көршілес бүйір қырлары болып табылады. Призманың бір жағына тиісті емес екі төбесін қосатын кесіндіні призманың диагоналы деп атайды. Призманың биіктігі деп оның табандарының ара қашықтығын айтады ПризмаПризма

6 слайд
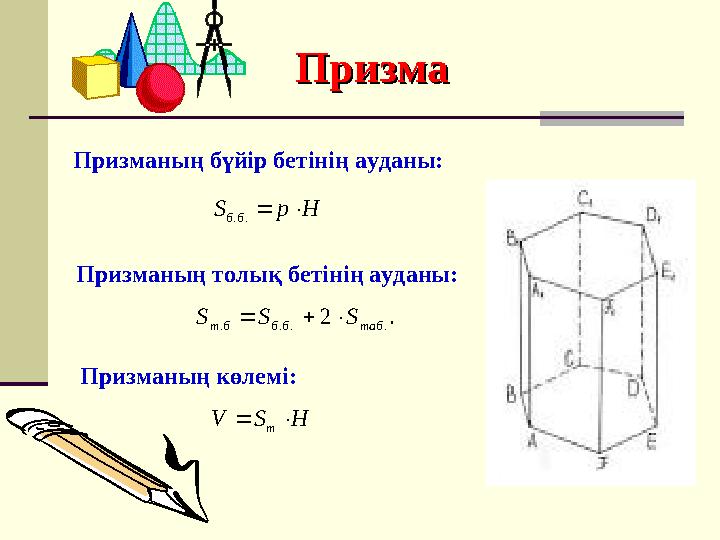
ПризмаПризма Призманың толық бетінің ауданы: .2 .... таббббт SSS  Призманың бүйір бетінің ауданы: HpS бб  .. Призманың көлемі: HSV т 

6 слайд

ПризмаПризма Призманың толық бетінің ауданы: .2 .... таббббт SSS  Призманың бүйір бетінің ауданы: HpS бб  .. Призманың көлемі: HSV т 

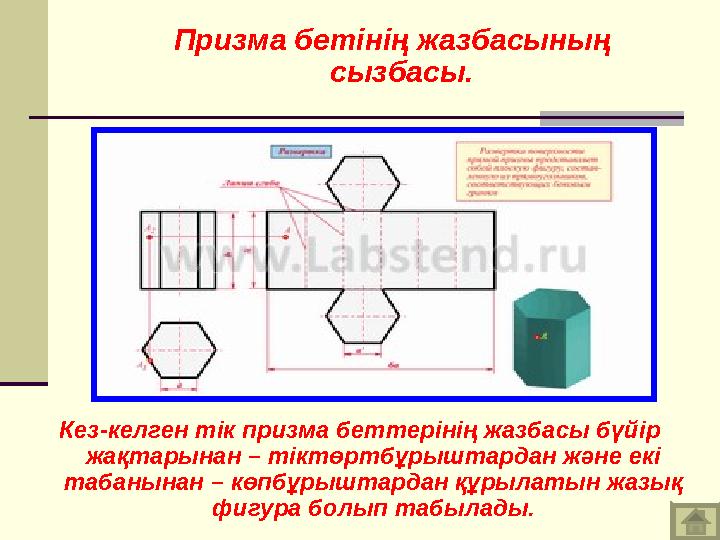
7 слайд
Кез-келген тік призма беттерінің жазбасы бүйір жақтарынан – тіктөртбұрыштардан және екі табанынан – көпбұрыштардан құрылатын жазық фигура болып табылады. Призма бетінің жазбасының сызбасы.

7 слайд

Кез-келген тік призма беттерінің жазбасы бүйір жақтарынан – тіктөртбұрыштардан және екі табанынан – көпбұрыштардан құрылатын жазық фигура болып табылады. Призма бетінің жазбасының сызбасы.

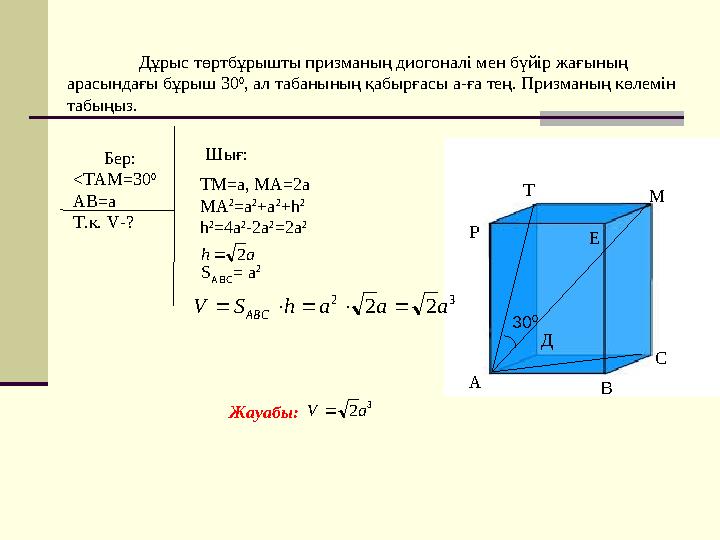
8 слайд
Дұрыс төртбұрышты призманың диогоналі мен бүйір жағының арасындағы бұрыш 30 0 , ал табанының қабырғасы а-ға тең. Призманың көлемін табыңыз. Бер: <TAM=30 0 AB=a Т.к. V-? Д А Р Т М Е С В Шығ: TM=a, MA=2a MA 2 =a 2 +a 2 +h 2 h 2 =4a 2 -2a 2 =2a 2 S ABC = a 2 32 22 aaahSV ABC  Жауабы: 3 2aV 30 0 ah2

8 слайд

Дұрыс төртбұрышты призманың диогоналі мен бүйір жағының арасындағы бұрыш 30 0 , ал табанының қабырғасы а-ға тең. Призманың көлемін табыңыз. Бер: <TAM=30 0 AB=a Т.к. V-? Д А Р Т М Е С В Шығ: TM=a, MA=2a MA 2 =a 2 +a 2 +h 2 h 2 =4a 2 -2a 2 =2a 2 S ABC = a 2 32 22 aaahSV ABC  Жауабы: 3 2aV 30 0 ah2

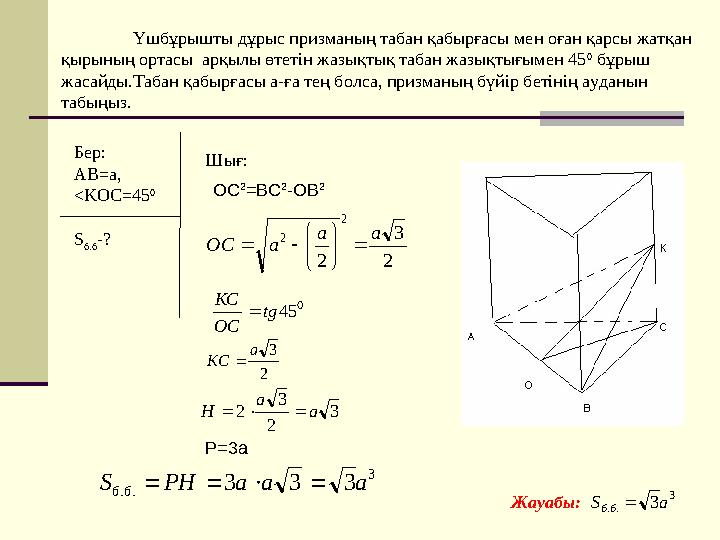
9 слайд
Үшбұрышты дұрыс призманың табан қабырғасы мен оған қарсы жатқан қырының ортасы арқылы өтетін жазықтық табан жазықтығымен 45 0 бұрыш жасайды.Табан қабырғасы а-ға тең болса, призманың бүйір бетінің ауданын табыңыз. Бер: AB=a, <KOC=45 0 S б.б -? Шығ: 2 3 2 2 2 аа аОС        OC 2 =BC 2 -OB 2 0 45tg ОС КС  2 3а KC 3 2 3 2 a a H  P=3a 3 .. 333 aaaPHS бб  3 .. 3aS бб Жауабы:

9 слайд

Үшбұрышты дұрыс призманың табан қабырғасы мен оған қарсы жатқан қырының ортасы арқылы өтетін жазықтық табан жазықтығымен 45 0 бұрыш жасайды.Табан қабырғасы а-ға тең болса, призманың бүйір бетінің ауданын табыңыз. Бер: AB=a, <KOC=45 0 S б.б -? Шығ: 2 3 2 2 2 аа аОС        OC 2 =BC 2 -OB 2 0 45tg ОС КС  2 3а KC 3 2 3 2 a a H  P=3a 3 .. 333 aaaPHS бб  3 .. 3aS бб Жауабы: