Материалдар / Көпжақтың қималары 11 сынып

Көпжақтың қималары 11 сынып

Материал туралы қысқаша түсінік

11 сынып геоеметрия есептерін шешуде және ҰБТ есептерін шешуде қолдану

Муратбекова Ильвира Абдразаковна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

03 Желтоқсан 2020

1872

3 рет жүктелген

Геометрия Презентация 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 31

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
КӨПЖАҚТАРДЫҢ КӨПЖАҚТАРДЫҢ ҚИМАЛАРЫҚИМАЛАРЫ

1 слайд

КӨПЖАҚТАРДЫҢ КӨПЖАҚТАРДЫҢ ҚИМАЛАРЫҚИМАЛАРЫ

2 слайд
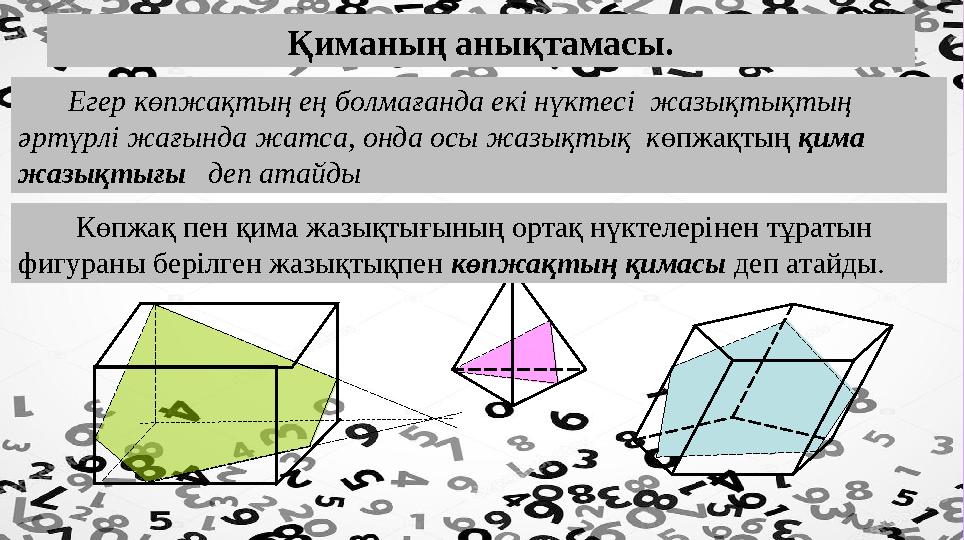
Қиманың анықтамасы. Егер көпжақтың ең болмағанда екі нүктесі жазықтықтың әртүрлі жағында жатса, онда осы жазықтық к өпжақтың қима жазықтығы деп атайды Көпжақ пен қима жазықтығының ортақ нүктелерінен тұратын фигураны берілген жазықтықпен көпжақтың қимасы деп атайды .

2 слайд

Қиманың анықтамасы. Егер көпжақтың ең болмағанда екі нүктесі жазықтықтың әртүрлі жағында жатса, онда осы жазықтық к өпжақтың қима жазықтығы деп атайды Көпжақ пен қима жазықтығының ортақ нүктелерінен тұратын фигураны берілген жазықтықпен көпжақтың қимасы деп атайды .

3 слайд
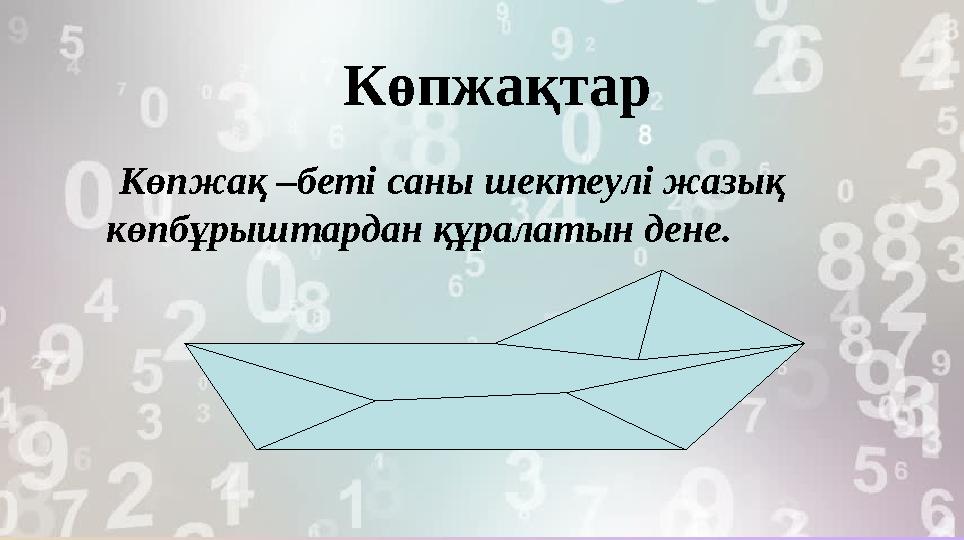
Көпжақтар Көпжақ –беті саны шектеулі жазық көпбұрыштардан құралатын дене.

3 слайд

Көпжақтар Көпжақ –беті саны шектеулі жазық көпбұрыштардан құралатын дене.

4 слайд
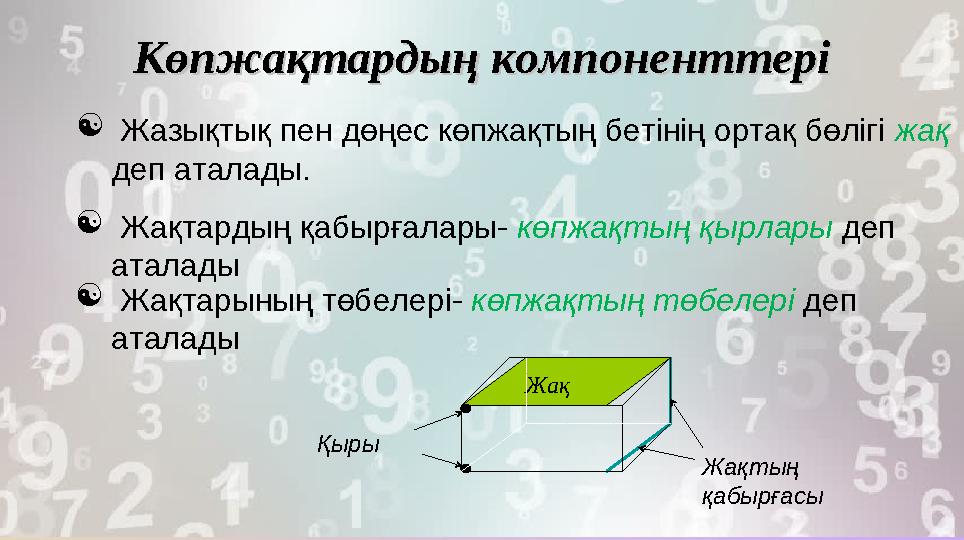
Көпжақтардың компоненттеріКөпжақтардың компоненттері  Жазықтық пен дөңес көпжақтың бетінің ортақ бөлігі жақ деп аталады. Жақтың қабырғасы Жақ Қыры Жақтардың қабырғалары- көпжақтың қырлары деп аталады  Жақтарының төбелері- көпжақтың төбелері деп аталады

4 слайд

Көпжақтардың компоненттеріКөпжақтардың компоненттері  Жазықтық пен дөңес көпжақтың бетінің ортақ бөлігі жақ деп аталады. Жақтың қабырғасы Жақ Қыры Жақтардың қабырғалары- көпжақтың қырлары деп аталады  Жақтарының төбелері- көпжақтың төбелері деп аталады

5 слайд
Көпжақ , үш өлшемді кеңістікте – бірнеше (шектеулі) жазық көпбұрыштан құрылған геометриялық бет. Көпжақ құрамындағы көпбұрыштың әрбір қабырғасы оған іргелес екінші көпбұрыштың да қабырғасы болып саналады. Ал әрбір көпбұрыштан іргелес көпбұрыштар арқылы кез келген көпбұрышқа өтуге болады. Жазық көпбұрыштарды көпжақтың жақтары деп, екі көпбұрыштың ортақ қабырғасын көпжақтың қырлары деп, ал көпбұрыштардың төбелерін көпжақтың төбелері деп атайды.

5 слайд

Көпжақ , үш өлшемді кеңістікте – бірнеше (шектеулі) жазық көпбұрыштан құрылған геометриялық бет. Көпжақ құрамындағы көпбұрыштың әрбір қабырғасы оған іргелес екінші көпбұрыштың да қабырғасы болып саналады. Ал әрбір көпбұрыштан іргелес көпбұрыштар арқылы кез келген көпбұрышқа өтуге болады. Жазық көпбұрыштарды көпжақтың жақтары деп, екі көпбұрыштың ортақ қабырғасын көпжақтың қырлары деп, ал көпбұрыштардың төбелерін көпжақтың төбелері деп атайды.

6 слайд
Дұрыс көпжақ Барлық жақтары тең және дұрыс, барлық төбелеріндегі көп жақты бұрыштары тең және дұрыс болатын көпжақ дұрыс көпжақ деп аталады. Бар болғаны 5 дұрыс көпжақ бар. Олар - куб, тетраэдр, октаэдр, икосаэдр, додекаэдр (бұлар Платон денелері деп аталады). Жақ Жақ , көп жақтың жағы - көпжақтың қырларымен шектелген беттерінің бөлігі болып табылатын жазық көпбұрыш.

6 слайд

Дұрыс көпжақ Барлық жақтары тең және дұрыс, барлық төбелеріндегі көп жақты бұрыштары тең және дұрыс болатын көпжақ дұрыс көпжақ деп аталады. Бар болғаны 5 дұрыс көпжақ бар. Олар - куб, тетраэдр, октаэдр, икосаэдр, додекаэдр (бұлар Платон денелері деп аталады). Жақ Жақ , көп жақтың жағы - көпжақтың қырларымен шектелген беттерінің бөлігі болып табылатын жазық көпбұрыш.

7 слайд
Дөңес көпжақ Егер көпбұрыштың барлық төбесі кез келген жағы арқылы жүргізілген жазықтықтың бір жағында орналасса, онда оны дөңес көпжақ деп атайды.

7 слайд

Дөңес көпжақ Егер көпбұрыштың барлық төбесі кез келген жағы арқылы жүргізілген жазықтықтың бір жағында орналасса, онда оны дөңес көпжақ деп атайды.

8 слайд
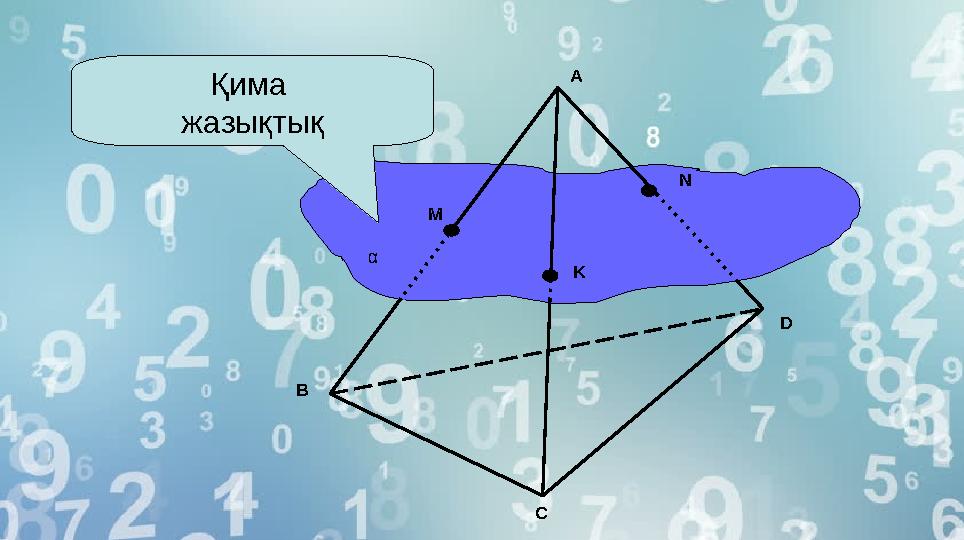
Қима жазықтық А В С DM N Kα

8 слайд

Қима жазықтық А В С DM N Kα

9 слайд
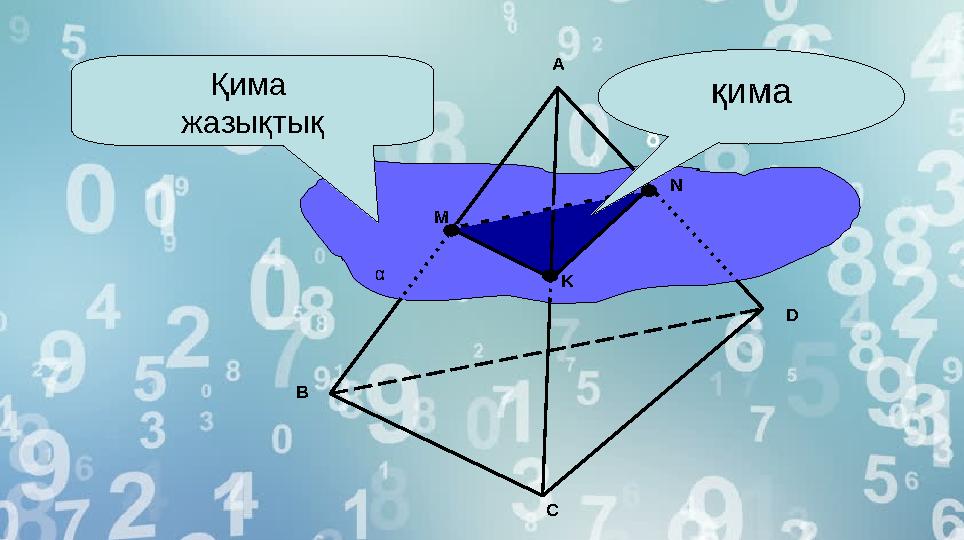
Қима жазықтық қимаA B C DM N Kα

9 слайд

Қима жазықтық қимаA B C DM N Kα

10 слайд

11 слайд

12 слайд
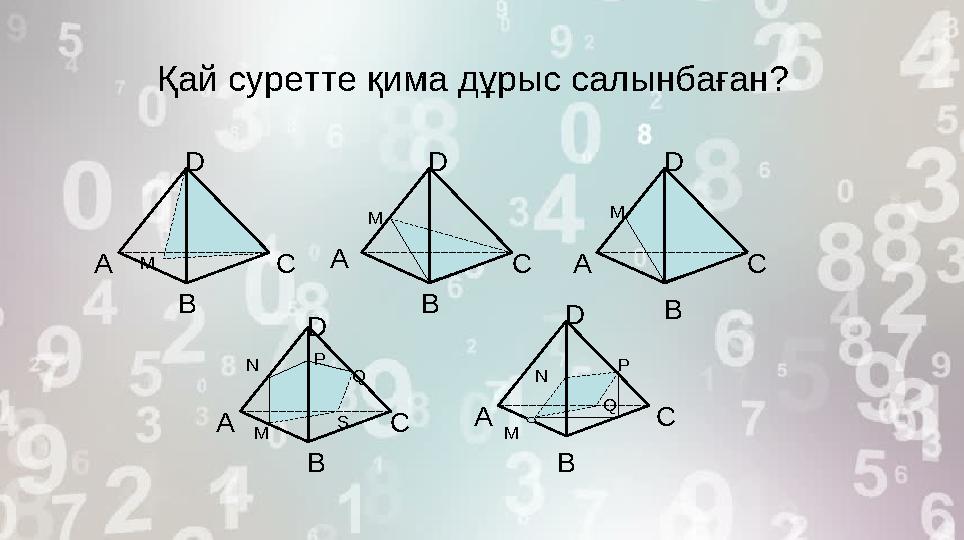
Қай суретте қима дұрыс салынбаған? BА А А А АD D D D D BB B B C CC C C N M M M M M NQP P Q S

12 слайд

Қай суретте қима дұрыс салынбаған? BА А А А АD D D D D BB B B C CC C C N M M M M M NQP P Q S

13 слайд
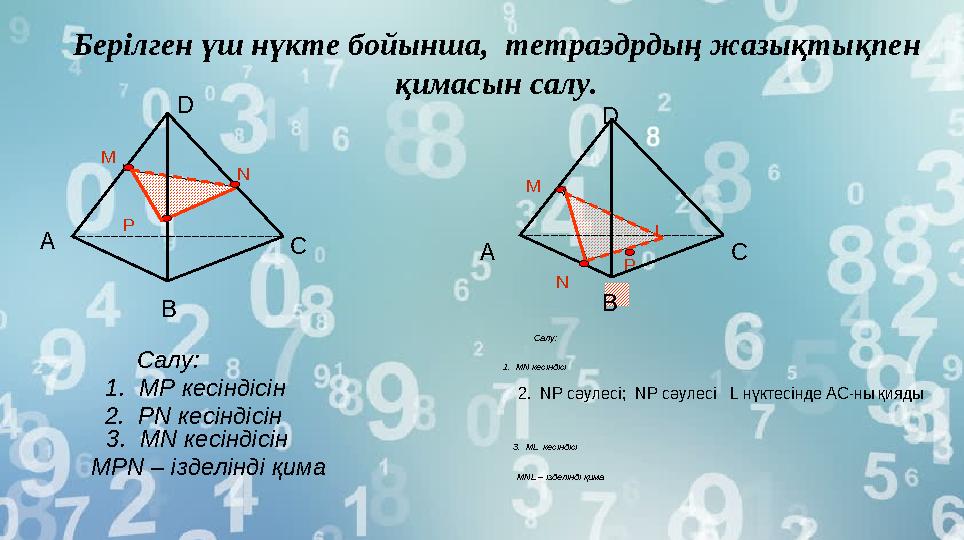
P NБерілген үш нүкте бойынша, тетраэдрдың жазықтықпен қимасын салу. Салу : А В СD PM N 2. PN кесіндісін А В СD M L 1. MP кесіндісін Салу: 3. MN кесіндісін MPN – ізделінді қима 1. MN кесіндісі 2. NP сәулесі ; NP сәулесі L нүктесінде АС-ны қияды 3. ML кесіндісі MNL – ізделінді қима

13 слайд

P NБерілген үш нүкте бойынша, тетраэдрдың жазықтықпен қимасын салу. Салу : А В СD PM N 2. PN кесіндісін А В СD M L 1. MP кесіндісін Салу: 3. MN кесіндісін MPN – ізделінді қима 1. MN кесіндісі 2. NP сәулесі ; NP сәулесі L нүктесінде АС-ны қияды 3. ML кесіндісі MNL – ізделінді қима

14 слайд
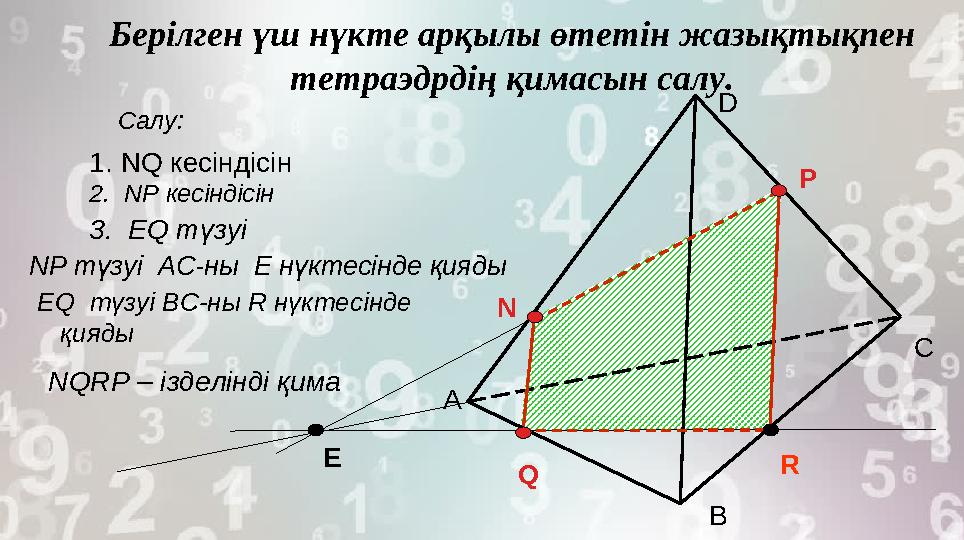
Берілген үш нүкте арқылы өтетін жазықтықпен тетраэдрдің қимасын салу. Салу: А С В D N P Q RE1. NQ кесіндісін 2. NP кесіндісін NP түзуі АС-ны Е нүктесінде қияды3. EQ түзуі EQ түзуі BC -ны R нүктесінде қияды NQRP – ізделінді қима

14 слайд

Берілген үш нүкте арқылы өтетін жазықтықпен тетраэдрдің қимасын салу. Салу: А С В D N P Q RE1. NQ кесіндісін 2. NP кесіндісін NP түзуі АС-ны Е нүктесінде қияды3. EQ түзуі EQ түзуі BC -ны R нүктесінде қияды NQRP – ізделінді қима

15 слайд
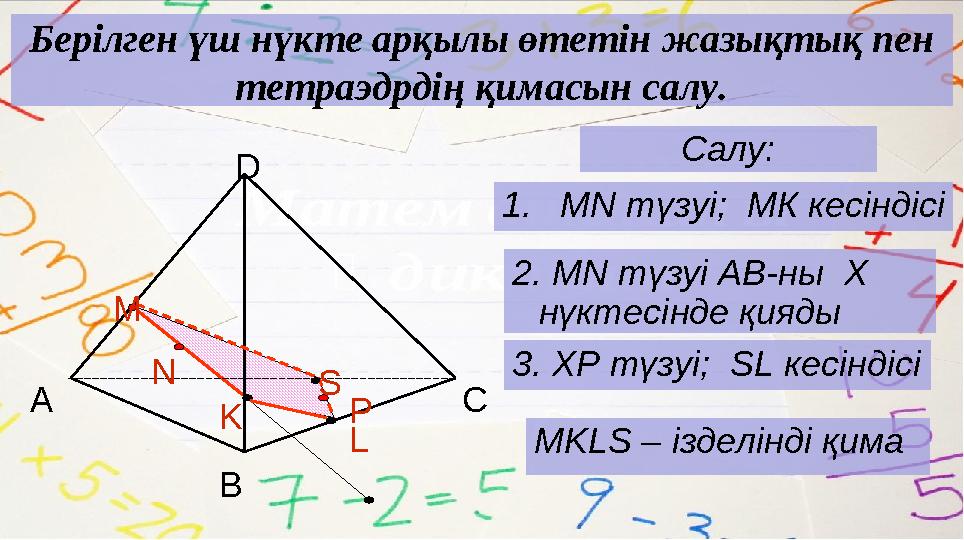
Берілген үш нүкте арқылы өтетін жазықтық пен тетраэдрдің қимасын салу. Салу: 1. MN түзуі ; МК кесіндісі 2. MN түзуі АВ-ны Х нүктесінде қияды 3. ХР түзуі; SL кесіндісі MKLS – ізделінді қимаА B CD M N P K S L

15 слайд

Берілген үш нүкте арқылы өтетін жазықтық пен тетраэдрдің қимасын салу. Салу: 1. MN түзуі ; МК кесіндісі 2. MN түзуі АВ-ны Х нүктесінде қияды 3. ХР түзуі; SL кесіндісі MKLS – ізделінді қимаА B CD M N P K S L

16 слайд
Аксиоматикалық тәсіл Із салу тәсілі Әдістің мәні фигураның кез-келген бетінің жазықтығымен кесу жазықтығының қиылысу сызығының кескіні болып табылатын көмекші түзу салу болып табылады. Кесу жазықтығының төменгі табан жазықтығымен қиылысу сызығының кескінін салу өте ыңғайлы. Бұл сызық кесілген жазықтық ізі деп аталады. Іздеуді пайдаланып, кескіннің бүйір жиектерінде немесе шеттерінде орналасқан кесілген жазықтық нүктелерінің кескіндерін салу оңай..

16 слайд

Аксиоматикалық тәсіл Із салу тәсілі Әдістің мәні фигураның кез-келген бетінің жазықтығымен кесу жазықтығының қиылысу сызығының кескіні болып табылатын көмекші түзу салу болып табылады. Кесу жазықтығының төменгі табан жазықтығымен қиылысу сызығының кескінін салу өте ыңғайлы. Бұл сызық кесілген жазықтық ізі деп аталады. Іздеуді пайдаланып, кескіннің бүйір жиектерінде немесе шеттерінде орналасқан кесілген жазықтық нүктелерінің кескіндерін салу оңай..

17 слайд
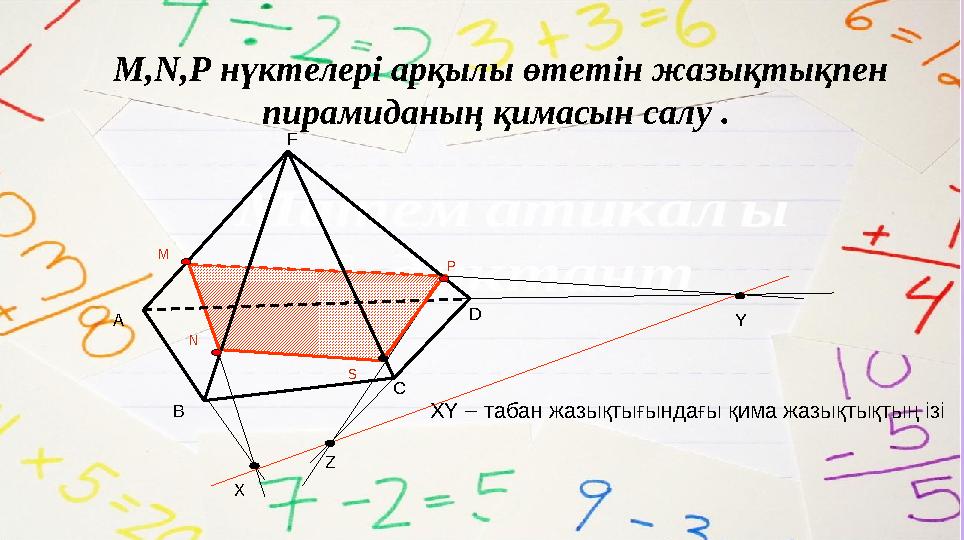
M,N,P нүктелері арқылы өтетін жазықтықпен пирамиданың қимасын салу . XY – табан жазықтығындағы қима жазықтықтың ізі D C BА Z Y XM N P SF

17 слайд

M,N,P нүктелері арқылы өтетін жазықтықпен пирамиданың қимасын салу . XY – табан жазықтығындағы қима жазықтықтың ізі D C BА Z Y XM N P SF

18 слайд
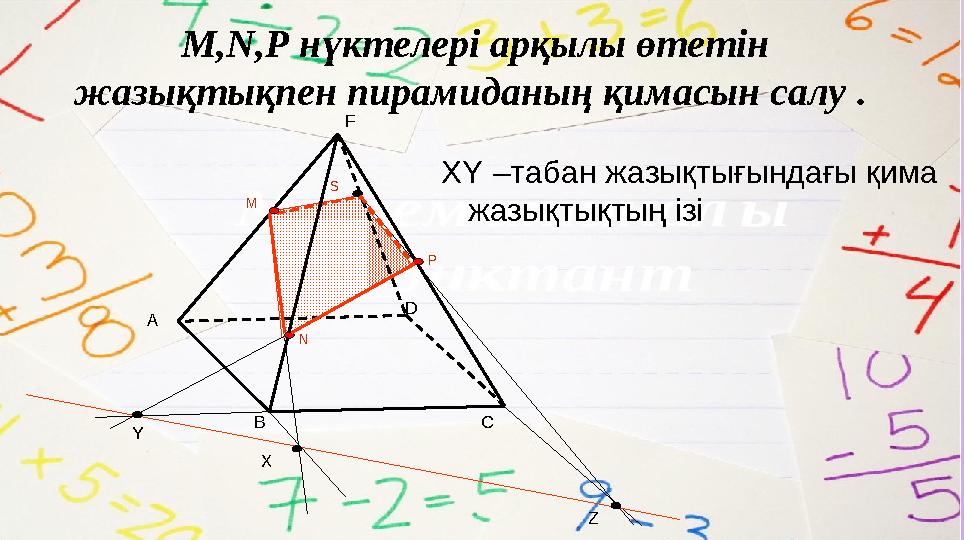
XY – табан жазықтығындағы қима жазықтықтың ізі D CB ZY XM N PSM,N,P нүктелері арқылы өтетін жазықтықпен пирамиданың қимасын салу . А F

18 слайд

XY – табан жазықтығындағы қима жазықтықтың ізі D CB ZY XM N PSM,N,P нүктелері арқылы өтетін жазықтықпен пирамиданың қимасын салу . А F

19 слайд
1 мысал Төрт бұрышты дұрыс пирамиданың табан қабырғасы а-ға тең және оның диагонал қимасы табанымен тең. Пирамиданың бүйір беті мен көлемін анықтаңыздар.

19 слайд

1 мысал Төрт бұрышты дұрыс пирамиданың табан қабырғасы а-ға тең және оның диагонал қимасы табанымен тең. Пирамиданың бүйір беті мен көлемін анықтаңыздар.

20 слайд
2 мысал Үш бұрышты дұрыс призманың бүйір қыры табан биіктігімен тең, ал осы бүйір қыр мен табан биіктігі арқылы жүргізілген қиманың ауданы Q-ге тең. Призма көлемін табыңыздар.

20 слайд

2 мысал Үш бұрышты дұрыс призманың бүйір қыры табан биіктігімен тең, ал осы бүйір қыр мен табан биіктігі арқылы жүргізілген қиманың ауданы Q-ге тең. Призма көлемін табыңыздар.

21 слайд
3 мысал

21 слайд

3 мысал

22 слайд
4 мысал Цилиндрдің жасаушысына перпендикуляр жүргізілген қиманың ауданы М-ге тең, ал осьтік қимасының ауданы N-ге тең. Сол цилиндрдің беті мен көлемін табыңыздар.

22 слайд

4 мысал Цилиндрдің жасаушысына перпендикуляр жүргізілген қиманың ауданы М-ге тең, ал осьтік қимасының ауданы N-ге тең. Сол цилиндрдің беті мен көлемін табыңыздар.

23 слайд
5 мысал Шар, осьтік қимасы квадрат болатын цилиндр және конус алынған. Цилиндр мен конустың табандары бірдей, ал олардың биіктіктері шардың диаметріне тең. Цилиндр, шар және конус көлемдерінің қатынасын табыңыздар.

23 слайд

5 мысал Шар, осьтік қимасы квадрат болатын цилиндр және конус алынған. Цилиндр мен конустың табандары бірдей, ал олардың биіктіктері шардың диаметріне тең. Цилиндр, шар және конус көлемдерінің қатынасын табыңыздар.

24 слайд
6 мысал кубында А, және . қабырғаларының ортасынан қима жүргізілген. Егер қ има ауданы болса, текше қырын табыңыз.1 1 1 1 D C B ABCDA 1 C D D 1 6 50 Шешуі: Біз қабырғаны белгілейміз : Сонда мұнда - осы тапсырмада ауданы қима проекциясының ауданы. Жауабы: 10. . 1 a С С  2 2 2 a CD AD AC    AC C 1    : 90 1    CA C . 3 2 1 2 1 a C C AC AC    3 2 3 2 cos 1 1     a a AC AC AC C , cos    кима пр S S пр S ABCD , 10 100 100 3 2 6 50 2        a а S пр . 10 1  CC Шешуі: Біз қабырғаны белгілейміз : Сонда мұнда - осы тапсырмада ауданы қима проекциясының ауданы. Жауабы: 10.

24 слайд

6 мысал кубында А, және . қабырғаларының ортасынан қима жүргізілген. Егер қ има ауданы болса, текше қырын табыңыз.1 1 1 1 D C B ABCDA 1 C D D 1 6 50 Шешуі: Біз қабырғаны белгілейміз : Сонда мұнда - осы тапсырмада ауданы қима проекциясының ауданы. Жауабы: 10. . 1 a С С  2 2 2 a CD AD AC    AC C 1    : 90 1    CA C . 3 2 1 2 1 a C C AC AC    3 2 3 2 cos 1 1     a a AC AC AC C , cos    кима пр S S пр S ABCD , 10 100 100 3 2 6 50 2        a а S пр . 10 1  CC Шешуі: Біз қабырғаны белгілейміз : Сонда мұнда - осы тапсырмада ауданы қима проекциясының ауданы. Жауабы: 10.

25 слайд
7 мысал Тура үшбұрышты призмада негіз жақтары 10,17 және 21-ге тең, ал призманың биіктігі - 18. Бүйір қырынан және түбінің кіші биіктігінен жүргізілген қима ауданын табыңыз. Шешуі: ( Герон формуласы ) Үшбұрышта ең кіші-үлкен жағына жүргізілген биіктік. Біздің жағдайда ең аз биіктігі BH болады. Жауабы: 144.    84 7 4 3 3 7 14 24             c p b p a p p S ABC 144 8 18 8 21 2 1 84 21 2 1 1 1 1              BH BB S BH BH BH S HH BB ABC Шешуі: ( Герон формуласы ) Үшбұрышта ең кіші-үлкен жағына жүргізілген биіктік. Біздің жағдайда ең аз биіктігі BH болады. Жауабы: 144.

25 слайд

7 мысал Тура үшбұрышты призмада негіз жақтары 10,17 және 21-ге тең, ал призманың биіктігі - 18. Бүйір қырынан және түбінің кіші биіктігінен жүргізілген қима ауданын табыңыз. Шешуі: ( Герон формуласы ) Үшбұрышта ең кіші-үлкен жағына жүргізілген биіктік. Біздің жағдайда ең аз биіктігі BH болады. Жауабы: 144.    84 7 4 3 3 7 14 24             c p b p a p p S ABC 144 8 18 8 21 2 1 84 21 2 1 1 1 1              BH BB S BH BH BH S HH BB ABC Шешуі: ( Герон формуласы ) Үшбұрышта ең кіші-үлкен жағына жүргізілген биіктік. Біздің жағдайда ең аз биіктігі BH болады. Жауабы: 144.

26 слайд
8 мысал Оң төртбұрышты пирамиданың биіктігі 80-ге тең, негізінің жағы -120. Пирамиданың бүйірлік қырының ортасынан өтетін қима ауданын есептеңіз. Шешуі: Қима - тең трапеция. 1 ) 2) 3) 4) Жауабы: 4500.KLMN 2 60 2 1 2 120 : 2 2        AC AO DC AD AC ACD 34 20 6400 7200 : 2 2       OE AO AE AEO 34 10 2 1   AE KL 34 10   KL MN 120   AB KN 60 2 1   CD LM 50 900 34 100 30 2 2 2          KH LK LH LM KH KH 4500 50 2 120 60 2        LH KN LM Sкима Шешуі: Қима - тең трапеция. 1 ) 2) 3) 4) Жауабы: 4500.

26 слайд

8 мысал Оң төртбұрышты пирамиданың биіктігі 80-ге тең, негізінің жағы -120. Пирамиданың бүйірлік қырының ортасынан өтетін қима ауданын есептеңіз. Шешуі: Қима - тең трапеция. 1 ) 2) 3) 4) Жауабы: 4500.KLMN 2 60 2 1 2 120 : 2 2        AC AO DC AD AC ACD 34 20 6400 7200 : 2 2       OE AO AE AEO 34 10 2 1   AE KL 34 10   KL MN 120   AB KN 60 2 1   CD LM 50 900 34 100 30 2 2 2          KH LK LH LM KH KH 4500 50 2 120 60 2        LH KN LM Sкима Шешуі: Қима - тең трапеция. 1 ) 2) 3) 4) Жауабы: 4500.

27 слайд
9 мысал Дұрыс төртбұрышты пирамиданың көлемін анықтаңыз, оның бүйір қабырғаларының бұрышын негізінің жазықтығымен және оның диагоналды қимасының ауданын біліңіз. Шешуі: 1) Яғни 2) Белгілейміз: 3) Жауабы:      tg S h ctg h h S AO EO S ctg h AC ctg h ctg EO AO AEO AEC                  . 2 ; :  tg S EO   x AD   2 2 2 2 2 2 4 2 ctg h AD DC AD AC        ctg S ctg tg S AD       2 2 2 2    ctg S S tg S ctg S EO AD EO S V 3 2 2 3 1 3 1 3 1 2           ctg S S 3 2 Шешуі: 1) Яғни 2) Белгілейміз: 3) Жауабы:

27 слайд

9 мысал Дұрыс төртбұрышты пирамиданың көлемін анықтаңыз, оның бүйір қабырғаларының бұрышын негізінің жазықтығымен және оның диагоналды қимасының ауданын біліңіз. Шешуі: 1) Яғни 2) Белгілейміз: 3) Жауабы:      tg S h ctg h h S AO EO S ctg h AC ctg h ctg EO AO AEO AEC                  . 2 ; :  tg S EO   x AD   2 2 2 2 2 2 4 2 ctg h AD DC AD AC        ctg S ctg tg S AD       2 2 2 2    ctg S S tg S ctg S EO AD EO S V 3 2 2 3 1 3 1 3 1 2           ctg S S 3 2 Шешуі: 1) Яғни 2) Белгілейміз: 3) Жауабы:

28 слайд
10 мысал Дұрыс үшбұрышты пирамиданың биіктігі 10-ға тең, негізі 10-ға тең. Негіздің бір жағынан жүргізілген қима ауданын қарға қарсы қырға перпендикуляр етіп анықтаңыз. Шешуі: 1 ) 2 ) 3) 4) Жауабы: 37,5.3 10 3 3 :      BC BO a R ABC 3 5 2 2    CE CB EB 3 20 3 100 100 : 2 2       OB DO DB DBO EBF DBO   ~ 2 15 20 3 3 50 3 5 3 20 10        EF EF EB DB EF DO 5. 37 2 15 10 2 1 2 1       EF AC S Дұрыс үшбұрышты пирамиданың биіктігі 10-ға тең, негізі 10-ға тең. Негіздің бір жағынан жүргізілген қима ауданын қарға қарсы қырға перпендикуляр етіп анықтаңыз. Шешуі: 1 ) 2 ) 3) 4) Жауабы: 37,5.

28 слайд

10 мысал Дұрыс үшбұрышты пирамиданың биіктігі 10-ға тең, негізі 10-ға тең. Негіздің бір жағынан жүргізілген қима ауданын қарға қарсы қырға перпендикуляр етіп анықтаңыз. Шешуі: 1 ) 2 ) 3) 4) Жауабы: 37,5.3 10 3 3 :      BC BO a R ABC 3 5 2 2    CE CB EB 3 20 3 100 100 : 2 2       OB DO DB DBO EBF DBO   ~ 2 15 20 3 3 50 3 5 3 20 10        EF EF EB DB EF DO 5. 37 2 15 10 2 1 2 1       EF AC S Дұрыс үшбұрышты пирамиданың биіктігі 10-ға тең, негізі 10-ға тең. Негіздің бір жағынан жүргізілген қима ауданын қарға қарсы қырға перпендикуляр етіп анықтаңыз. Шешуі: 1 ) 2 ) 3) 4) Жауабы: 37,5.

29 слайд
Пайданылған әдебиеттер: 1. Смирнова И.М., Смирнов В.А. УМК по геометрии. [Онлайн] 30 01 2012 ж. http://www.gcro.ru/mat-met-help/448-geom . 2. Сканави М.И. Математикадын конкурстық есептер жинағы 3. https://ppt-online.org/220570Пайданылған әдебиеттер: 1. Смирнова И.М., Смирнов В.А. УМК по геометрии. [Онлайн] 30 01 2012 ж. http://www.gcro.ru/mat-met-help/448-geom . 2. Сканави М.И. Математикадын конкурстық есептер жинағы 3. https://ppt-online.org/220570

29 слайд

Пайданылған әдебиеттер: 1. Смирнова И.М., Смирнов В.А. УМК по геометрии. [Онлайн] 30 01 2012 ж. http://www.gcro.ru/mat-met-help/448-geom . 2. Сканави М.И. Математикадын конкурстық есептер жинағы 3. https://ppt-online.org/220570Пайданылған әдебиеттер: 1. Смирнова И.М., Смирнов В.А. УМК по геометрии. [Онлайн] 30 01 2012 ж. http://www.gcro.ru/mat-met-help/448-geom . 2. Сканави М.И. Математикадын конкурстық есептер жинағы 3. https://ppt-online.org/220570

30 слайд