Көрсеткіштік теңдеулерді шешудің жалпы әдістері

1 слайд
№37 жалпы орта мектеп Тақырыбы: Көрсеткіштік теңдеулерді шешудің жалпы әдістері

1 слайд

2 слайд
Сабақтың мақсаты: Білімділік: Көрсеткіштік функцияның анықтамасын, қасиеттерін көрсеткіштік теңдеулерді шешуге дұрыс қолдана білуге үйрету. Дамытушылық: Оқушының көрсеткіштік теңдеулерді және жалпы теңдеулерді шеше алу,білім - білік дағдыларын дамыту; логикалық ойлауын, ауызша және жазбаша тіл байлығын дамыту. Тәрбиелік: Өзіндік ізденісін, шығармашылық қызмет тәжірибесін қалыптастыру, жақсы жолдастық қарым- қатынасқа тәрбиелеу.

2 слайд

3 слайд
Сабақтың барысы: 1.Ұйымдастыру кезеңі (оқушылармен амандасу, түгелдеу). 2. Өткенді қайталау. 3. Қайталау сұрақтары 4. Мысалдар келтіру. 5.Тест тапсырмасы (жинақтау) 6.Бекіту сұрақтары: 7.Бағалау. 8.Үйге тапсырма.

3 слайд

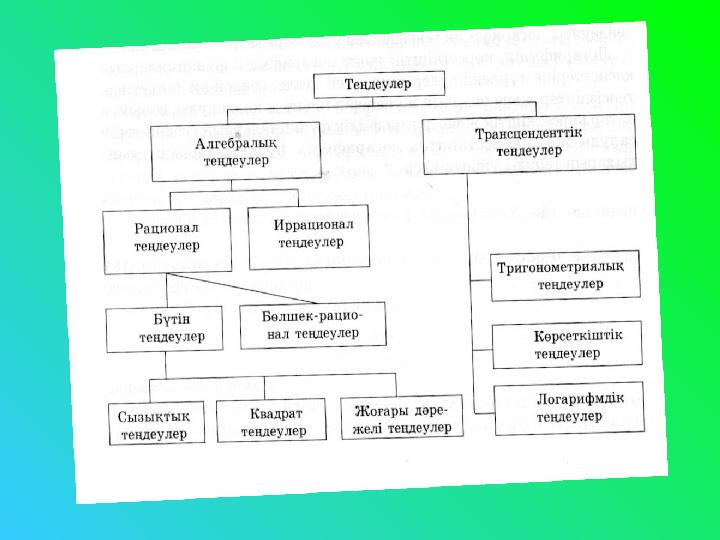
4 слайд

4 слайд

5 слайд
Қайталау сұрақтары: 1. Көрсеткіштік теңдеу дегеніміз не? 2. Көрсеткіштік функция қасиеттерін тұжырымдаңдар. 3. Қасиеттеріне байланысты ауызша есептер беріледі. 2 х+3   = 2 x 2 ∙ 3 3 2x-1 = 3 2x 3 ∙ -1 = 3 2x 1/3 ∙ (а/в) -n = (в/а) n ; a -n = 1/an т.с.с.

5 слайд

6 слайд
Көрсеткіштік теңдеулерді шешу тәсілдері: 1.Бірдей негізге келтіру А)Қарапайым көрсеткіштік теңдеу Б)Ортақ көбейткішті жақша сыртына шығару В)Көбейткіштерге жіктеу арқылы 2.Жаңа айнымалыны енгізу А)Квадрат теңдеуге келтіру Б)Біртекті теңдеу В)Жасанды тәсіл 3.Графиктік тәсіл 4.Теңдеудің екі жағында логарифмдеу

6 слайд

7 слайд
a>1a>1 0<a<10<a<1 Анықталу облысыАнықталу облысы D(y)=RD(y)=R D(y)=RD(y)=R Мәндерінің жиыныМәндерінің жиыныЕЕ(y)=(0;+∞)(y)=(0;+∞) ЕЕ(y)=(0;+∞)(y)=(0;+∞) Жұп, тақтығыЖұп, тақтығы Жұп та, тақ та емесЖұп та, тақ та емесЖұп та, тақ та емесЖұп та, тақ та емес Функция нольдеріФункция нольдері(0;1) OY (0;1) OY OX OX өсімен қиылысу өсімен қиылысу нүктесі жоқнүктесі жоқ (0;1) OY (0;1) OY OX OX өсімен қиылысу өсімен қиылысу нүктесі жоқнүктесі жоқ Таңба тұрақты Таңба тұрақты аралықтарыаралықтары Бүкіл сан өсінде оң Бүкіл сан өсінде оң мәндер қабылдайдымәндер қабылдайды Бүкіл сан өсінде оң мәндер Бүкіл сан өсінде оң мәндер қабылдайдықабылдайды Өсу, кему Өсу, кему аралықтарыаралықтары (-(-∞;+∞) өседі∞;+∞) өседі (-(-∞;+∞) кемиді∞;+∞) кемиді Экстремум Экстремум нүктелерінүктелері жоқжоқ жоқжоқ асимптотасыасимптотасы УУ=0=0 горизонталь горизонталь У=0 У=0 горизонтальгоризонталь 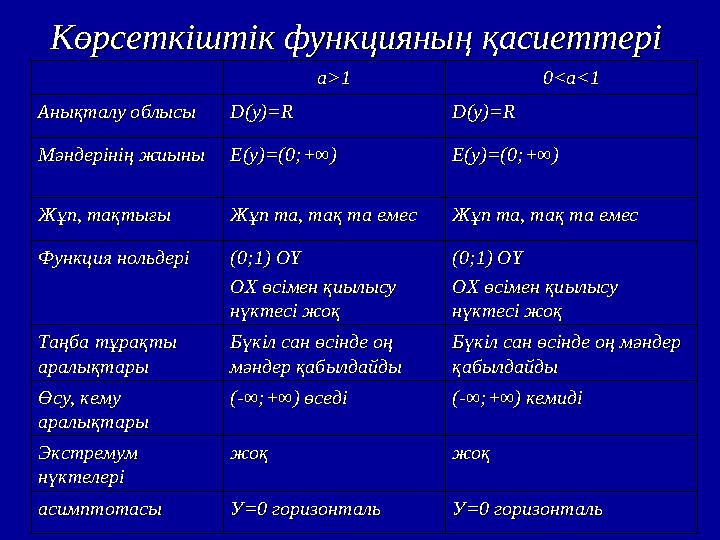Көрсеткіштік функцияның қасиеттеріКөрсеткіштік функцияның қасиеттері

7 слайд

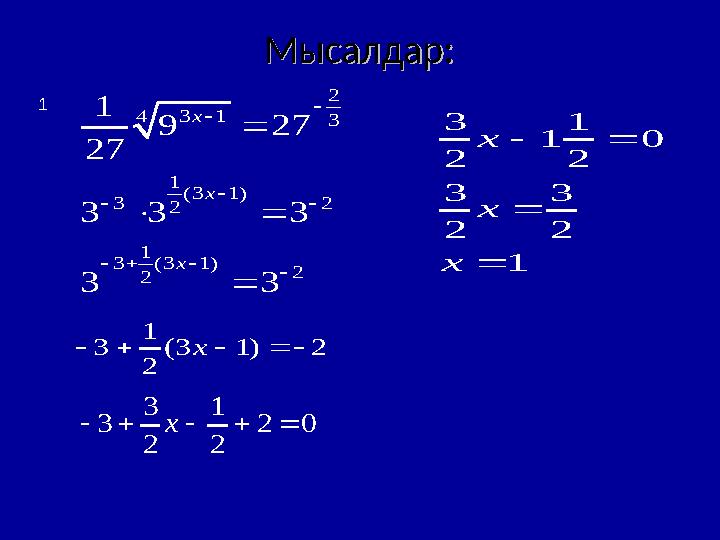
8 слайд
2 3 14 3 1 (3 1) 3 22 1 3 (3 1) 22 1 9 27 27 3 3 3 3 3 x x x              1 3 (3 1) 2 2 x    3 1 3 2 0 2 2 x     3 1 1 0 2 2 3 3 2 2 1 x x x     Мысалдар:Мысалдар: 1

8 слайд

9 слайд
Мысалдар:Мысалдар: 22. а). а) жауабыжауабы:: б)б) берілген теңдеуді логарифмдаймызберілген теңдеуді логарифмдаймыз:: жауабыжауабы:: 3 log 4 3 3 4 3 3 log 4 x x x    3 log 4x 2 1 3 3 5 x x   2 1 3 lg3 lg5 (2 1)lg3 (3 )lg5 2 lg3 lg3 3lg5 lg5 2 lg3 lg5 3lg5 lg3 (2lg3 lg5) 3lg5 lg3 3lg5 lg3 2lg3 lg5 x x x x x x x x x x                   3lg5 lg3 2lg3 lg5 x    3 log 4x

9 слайд

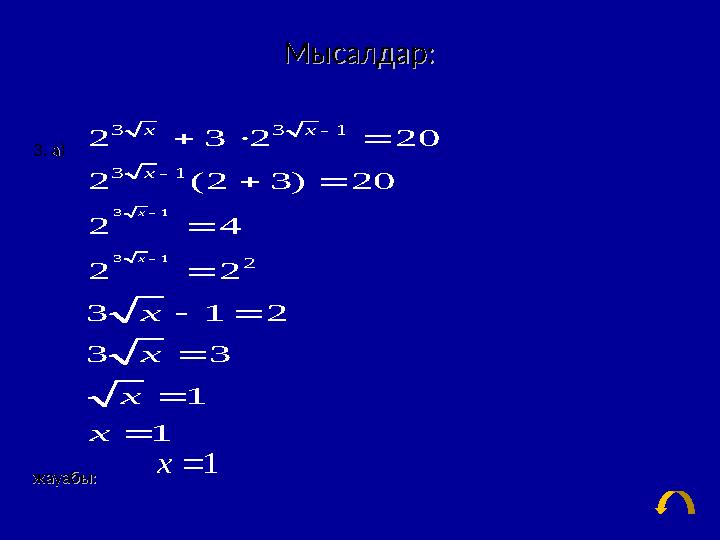
10 слайд
Мысалдар:Мысалдар: 33. а). а) жауабыжауабы:: 3 1 3 1 3 3 1 3 1 2 2 32 20 2 (2 3) 20 2 4 2 2 3 1 2 3 3 1 1 x x x x x x x x x                 1x

10 слайд

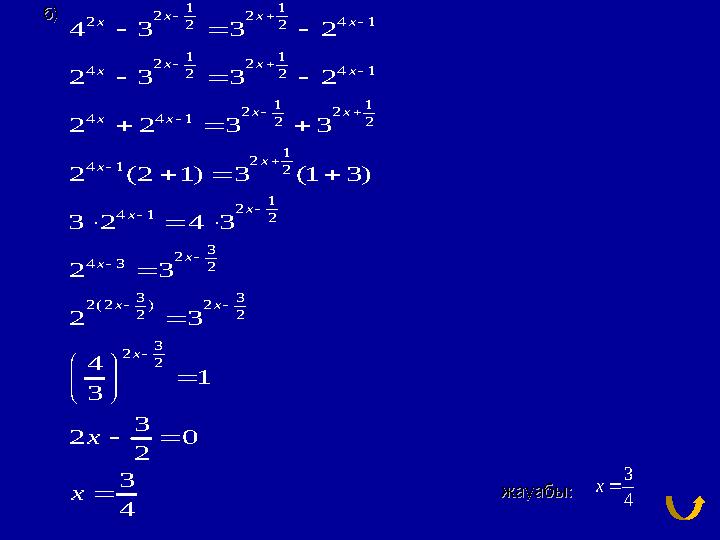
11 слайд
б)б) жауабы:жауабы: 1 1 2 2 2 4 1 2 2 1 1 2 2 4 4 1 2 2 1 1 2 2 4 4 1 2 2 1 2 4 1 2 1 2 4 1 2 3 2 4 3 2 3 3 2(2 ) 2 2 2 3 2 2 4 3 3 2 2 3 3 2 2 2 3 3 2 (2 1) 3 (1 3) 3 2 4 3 2 3 2 3 4 1 3 3 2 0 2 3 4 x x x x x x x x x x x x x x x x x x x x x x x                                              3 4 x

11 слайд

12 слайд
Мысалдар:Мысалдар: 44.. 2 2 4 5 x y   2 3 2 2 3 2 2 5 3 2 5 5 2 5 3 5 , x x x x x у             0y 2 3 2 4 2 2 5 5 5 5 5 2 3 0 x x y y y         5a 2b 3c 1 2 1 4 1 5 1 4 0,6 5 y y       

12 слайд

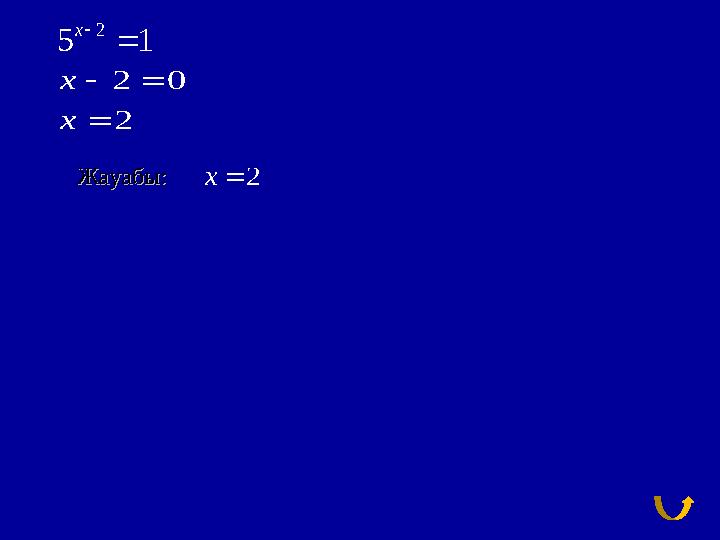
13 слайд
2 0 2 x x    : 2Ответ x 2 5 1 х  Жауабы:Жауабы:

13 слайд

14 слайд
Мысалдар:Мысалдар: 55.. 3 3 3 2 2 1 3 12 3 1 3 3 12 0 3 . .3 0 3 3 12 3 1 0 3 , 0 27 12 1 0 27 x x x x x x x x тк y y y y a                         12b 1c 1 2 1 3 1 9 y y        1 3 3 1 3 9 x x       

14 слайд

15 слайд
1 2 3 3 3 3 1 2 : 1; 2 x x x x Ответ           Жауабы: -1, -2Жауабы: -1, -2

15 слайд

16 слайд
Мысалдар:Мысалдар: 66.. . . Теңдеудің түбірі болмайды, сондықтан ос өрнеккке Теңдеудің түбірі болмайды, сондықтан ос өрнеккке бөліп жібереміз:бөліп жібереміз: жаңа айнымалы енгіземіз:жаңа айнымалы енгіземіз: , , 1 1 1 2 2 1 1 1 1 4 6 9 2 2 3 3 0 x x x x x x x                         2 1 3 0 x       2 1 1 2 2 1 0 3 3 x x                        1 2 3 x y         0y 2 1 0y y   1a 1b 1c

16 слайд

17 слайд
уу>0>0 шартына қайшы келеді шартына қайшы келеді = =>> 1 2 1 5 2 1 5 2 y y         1 2 1 5 3 2 x          1,5 1,5 1 1 5 log 2 1 1 5 log 2 x x       1,5 1 : 1 5 log 2 Ответ x                Жауабы:Жауабы:

17 слайд

18 слайд
Қарапайым көрсеткіштік теңдеулер А) 3 х =27 Ә) 5 x-2 =25 Б) (3/7) x =49/9 В) 2 x+8 =1/32 Г) 6 x-4 =-6 Ғ) 3 x+2 +3 x =90 Д) (2/3) x ∙(3/2) X =1 е) 4 x²+2х =1 Ж) 5 1-|x| =25

18 слайд

19 слайд
қорытындылау: 1. Көрсеткіштік теңдеулерді шешудің қандай әдістерін қарастырдық? 2. Көрсеткіштік теңдеулерді шығару қандай теңдеулерге алып келеді? 3. Тест есептерін шығарғанда қандай тәсілдерді қолданған тиімді?

19 слайд

20 слайд
Тест • Көрсеткіштік теңдеуді орнына қою арқылы тексеріп жауабын табу ұсынылады. • 1. Теңдеуді шешіңіз : 2 x + 2 x-3 =18 • А) х=-4 B) x=4 C) x= 0.4 D ) x= -0.4 E) x= 2 • 2. Теңдеуді шешіңіз : 0.8 2x-3 = 1 • А) х=1.5 B) x=-1.5 C) x= 0.15 D ) x= -0.15 E) x= 2/3 • 3. Теңдеуді шешіңіз : 7 2x = 4 • А) х=3log₇ 2 B) x=2log₇ 4 C) x = log₇ 2 D) x= 4 7 /2 E) x=4/7 • 4. Теңдеуді шешіңіз : 2 7-3x = (1/2) x-4 А) х=-4 B) x=4 C) x= 0.4 D ) x= -0.4 E) x= 2 5. Теңдеуді шешіңіз : 7 (x+1)(x+2) = 1 • А) -1;2 B) -1;3 C) -2;1 D ) -2;-1 E) -3;1 • 6. Теңдеуді шешіңіз: 7 cosx =1 • А) π/2 +2πn,п∈ Z B) πn, n∈Z C) πn/2, n ∈Z D) 2πn, n ∈Z E) π/2+πn, n ∈Z • 7. Теңдеуді шешіңіз: 4 x -10 2 x-1 -24 =0 • А) х=4 B) x=-4 C) x= 2 D ) x= 1 E) x= 3 • 8.Теңдеу түбірлерінің қосындысын табыңдар: 2 x²-3х =0,25 • А) 2 B) 6 C) 4 D ) 3 E) 5 • 9. Теңдеу түбірлерінің көбейтіндісін табыңдар: (2 x+4 ) x-3 =0,5 x ·4 x-4 • А) 4 B) -2 C) 0 D ) 2 E) -4 • 10. 4 √x -0.5 x-3 = 0 теңдеуінің түбірі x₀ болса, онда -x₀³ -3x₀² +2x₀-5 – тің мәні • А) -5 B) -7 C) -9 D ) -12 E) -11 • 1 3 log 4x 3 log 4x 3 log 4x

20 слайд

21 слайд
ҮЙГЕ ТАПСЫРМА С тобы №280-293беттегі көрсеткіштік теңдеулер

21 слайд

22 слайд
1.В 2.А 3.С 4.В 5.Д 6.Е 7.Е 8. Д 9.Е 10.В

22 слайд