2024-2025 оқу жылына арналған
қысқа мерзімді сабақ жоспарларын
Жүктеп алғыңыз келеді ме?
ҚР Білім және Ғылым министірлігінің стандартымен жасалған
Математика
Материал туралы қысқаша түсінік
Бұл материал математика пәніне арналған, қазақ мектептерінде сабақ беретін мұғалімдерге арналған. Орта мектепте қолдануға ұсынылған материалдар. Презентация арқылы оқушыларға сабақ түсіндіру оңайлана түседі. Жай бөлшектерді көбейту және бөлу.
Авторы:
27 Қаңтар 2018
377
1 рет жүктелген
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 10
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
1 слайд
2 слайд
Геометрияда «салу есептері» деп аталатын
ерекше есептер бар.Салу есептері сызба
құралдарының көмегімен орындалады.
Кейбір салу есептерін шешуде сызғыш пен
циркуль пайдаланылады.
Сызғышты пйдаланып:
-Берілген нүкте арқылы өтетінтүзулерді жүргізуге
болады.
-Берілген екі нүкте арқылы түзу жүргізуге
болады.3) кез келген түзуді жүргізуге болады.
Циркульды пайдаланып:
-Берілген нүктені центр етіп алып, радиусы
берілген кесіндіге тең шеңбер салуға болады.
-Берілген кесіндіге тең кесінді салуға болады.
Сызғыш пен циркульды бірге пайдаланғанда
мүмкіндік артады
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
I
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
15 16
2 слайд
Геометрияда «салу есептері» деп аталатын ерекше есептер бар.Салу есептері сызба құралдарының көмегімен орындалады. Кейбір салу есептерін шешуде сызғыш пен циркуль пайдаланылады. Сызғышты пйдаланып: -Берілген нүкте арқылы өтетінтүзулерді жүргізуге болады. -Берілген екі нүкте арқылы түзу жүргізуге болады.3) кез келген түзуді жүргізуге болады. Циркульды пайдаланып: -Берілген нүктені центр етіп алып, радиусы берілген кесіндіге тең шеңбер салуға болады. -Берілген кесіндіге тең кесінді салуға болады. Сызғыш пен циркульды бірге пайдаланғанда мүмкіндік артады IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII I 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
3 слайд
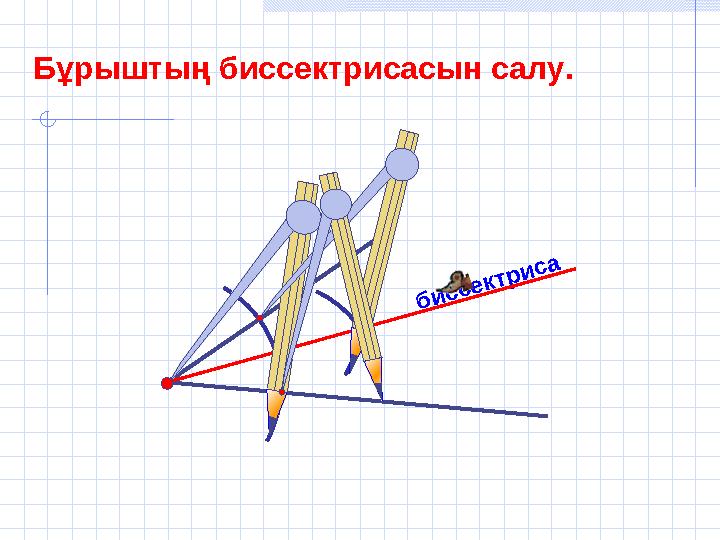
биссектриса
Бұрыштың биссектрисасын салу.
3 слайд
биссектриса Бұрыштың биссектрисасын салу.
4 слайд
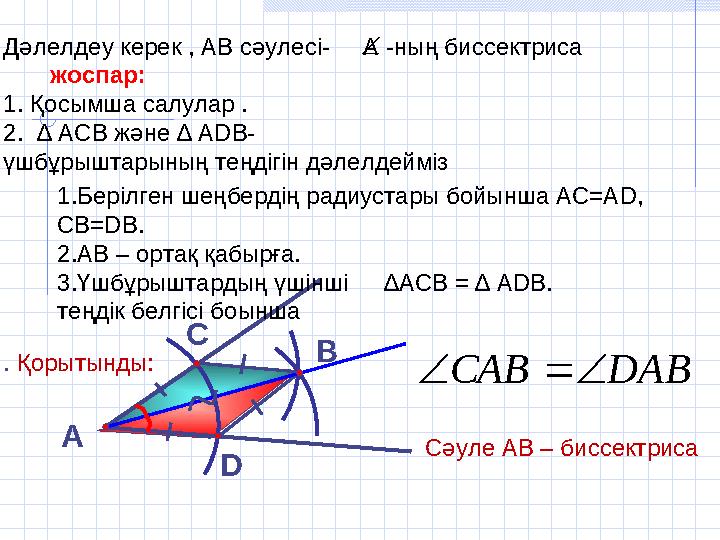
Дәлелдеу керек , АВ сәулесі- А -ның биссектриса
жоспар:
1.Қосымша салулар .
2. ∆ АСВ және ∆ АDB-
үшбұрыштарының теңдігін дәлелдейміз
. Қорытынды:
А
В
С
D
1.Берілген шеңбердің радиустары бойынша АС=АD,
СВ=DB.
2.АВ – ортақ қабырға.
3.Үшбұрыштардың үшінші
теңдік белгісі боынша
∆АСВ = ∆ АDВ.
DABСАВ
Сәуле АВ – биссектриса
4 слайд
Дәлелдеу керек , АВ сәулесі- А -ның биссектриса жоспар: 1.Қосымша салулар . 2. ∆ АСВ және ∆ АDB- үшбұрыштарының теңдігін дәлелдейміз . Қорытынды: А В С D 1.Берілген шеңбердің радиустары бойынша АС=АD, СВ=DB. 2.АВ – ортақ қабырға. 3.Үшбұрыштардың үшінші теңдік белгісі боынша ∆АСВ = ∆ АDВ. DABСАВ Сәуле АВ – биссектриса
5 слайд
Q
P
В
А
М
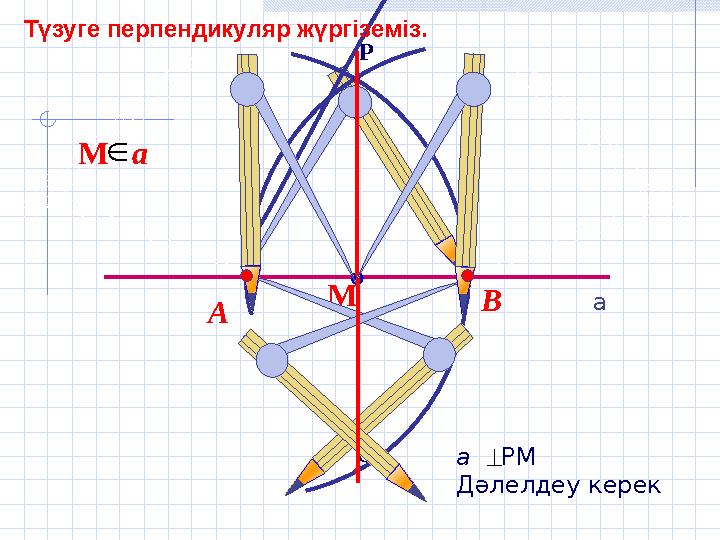
а РМ
Дәлелдеу керек
М a
Түзуге перпендикуляр жүргіземіз.
а
5 слайд
Q P В А М а РМ Дәлелдеу керек М a Түзуге перпендикуляр жүргіземіз. а
6 слайд
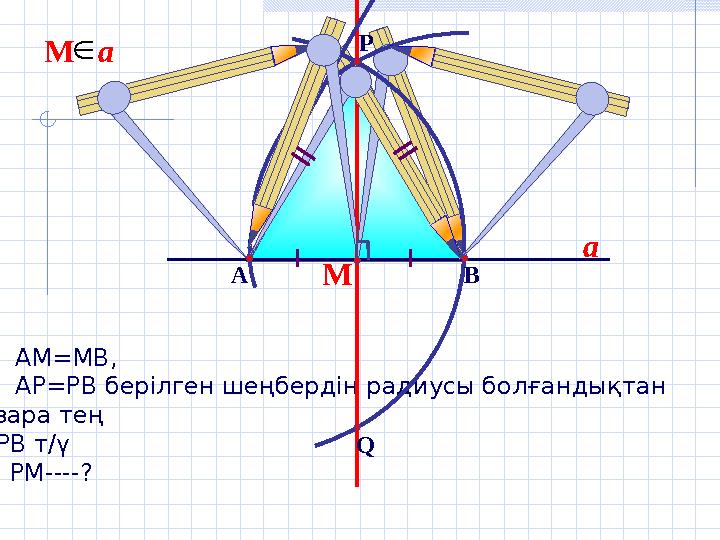
1.АМ=МВ,
2.АР=РВ берілген шеңбердің радиусы болғандықтан
өзара тең
АРВ т/ү
3. РМ----?
М
М a
a
ВА
Q
P
6 слайд
1.АМ=МВ, 2.АР=РВ берілген шеңбердің радиусы болғандықтан өзара тең АРВ т/ү 3. РМ----? М М a a ВА Q P
7 слайд
a
N
М
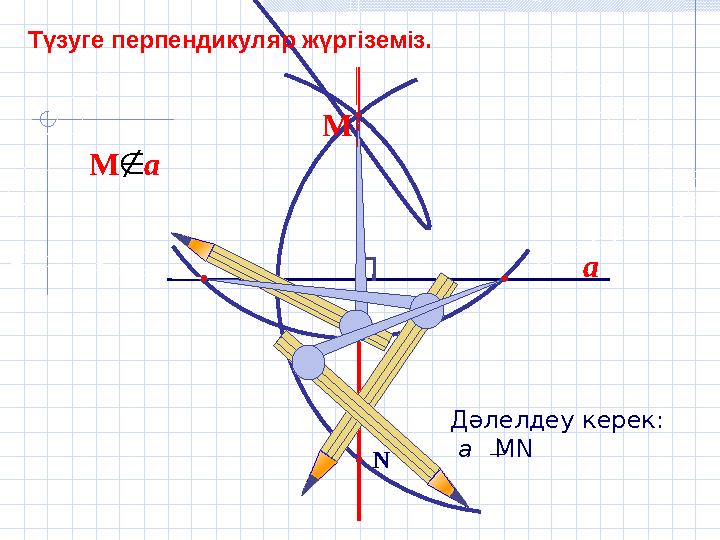
Түзуге перпендикуляр жүргіземіз.
Дәлелдеу керек:
а MN
М a
7 слайд
a N М Түзуге перпендикуляр жүргіземіз. Дәлелдеу керек: а MN М a
8 слайд
a
N
B
М a
AC
1 = 2
12
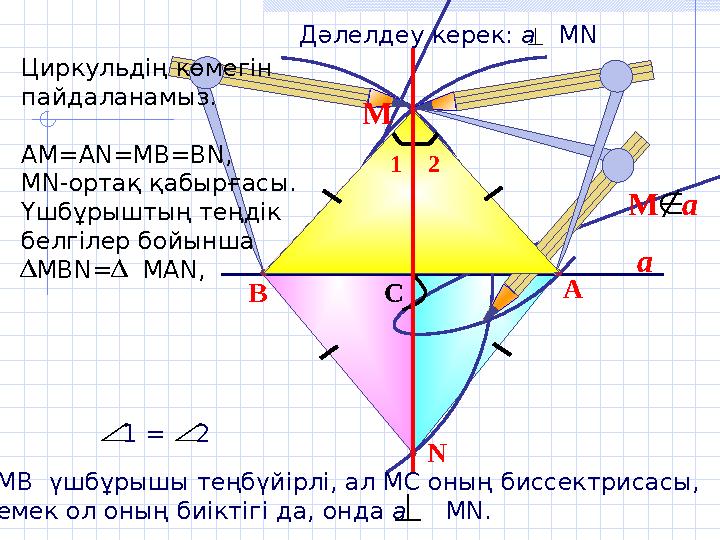
АМВ үшбұрышы теңбүйірлі, ал МС оның биссектрисасы,
демек ол оның биіктігі да, онда а МN.
М
Дәлелдеу керек: а MN
Циркульдің көмегін
пайдаланамыз.
АМ=АN=MB=BN,
МN-ортақ қабырғасы.
Үшбұрыштың теңдік
белгілер бойынша
MВN= MAN,
8 слайд
a N B М a AC 1 = 2 12 АМВ үшбұрышы теңбүйірлі, ал МС оның биссектрисасы, демек ол оның биіктігі да, онда а МN. М Дәлелдеу керек: а MN Циркульдің көмегін пайдаланамыз. АМ=АN=MB=BN, МN-ортақ қабырғасы. Үшбұрыштың теңдік белгілер бойынша MВN= MAN,
9 слайд
Пысықтау сүрақтары.
Салу есептерінің басқа есептерден
айырмашылығы қандай?
Үйге тапсырма. § 19. 4. 85 – бет
Бағалау
9 слайд
Пысықтау сүрақтары. Салу есептерінің басқа есептерден айырмашылығы қандай? Үйге тапсырма. § 19. 4. 85 – бет Бағалау
