Материалдар / Открытый урок "Щелочи и их свойства"

Открытый урок "Щелочи и их свойства"

Материал туралы қысқаша түсінік

Проблемно-поисковый подход удачно реализуется при проведении химического эксперимента. Одно дело просто провести химическую реакцию, совсем другое – провести химическое исследование. Много времени в учебных курсах отвожу на проведение практических и лабораторных работ, иногда сверхпрограммных. Убеждена, что только, дав возможность ученику попробовать себя в роли исследователя, экспериментатора, можно добиться усвоения учебного материала. Теория без практики ничто, поэтому групповой и индивидуальный исследовательский эксперимент - частый гость на моих уроках.

Абитов Жаслан Сакенович

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

18 Желтоқсан 2017

329

0 рет жүктелген

Химия Ашық сабақ 8 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 34

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Обобщающий урок Обобщающий урок по темепо теме Формулы Формулы сокращенсокращен ного ного умножениумножени яя

1 слайд

Обобщающий урок Обобщающий урок по темепо теме Формулы Формулы сокращенсокращен ного ного умножениумножени яя

2 слайд
Историческая Историческая страницастраница

2 слайд

Историческая Историческая страницастраница

3 слайд
ЧислоЧисло – арифмос (греч.) – арифмос (греч.) ГеометрияГеометрия – – гео – земля (греч.), метрео – гео – земля (греч.), метрео – меряю (греч.) меряю (греч.) Аль джебрАль джебр – – восстановление (арабск.)восстановление (арабск.)

3 слайд

ЧислоЧисло – арифмос (греч.) – арифмос (греч.) ГеометрияГеометрия – – гео – земля (греч.), метрео – гео – земля (греч.), метрео – меряю (греч.) меряю (греч.) Аль джебрАль джебр – – восстановление (арабск.)восстановление (арабск.)

4 слайд
Евклид. «Начала». Издание 1482 г.Евклид. «Начала». Издание 1482 г.

4 слайд

Евклид. «Начала». Издание 1482 г.Евклид. «Начала». Издание 1482 г.

5 слайд
Евклид. «Начала».Евклид. «Начала». «Если отрезок как-либо разбит на два «Если отрезок как-либо разбит на два отрезка, то площадь квадрата, отрезка, то площадь квадрата, построенного на всем отрезке, равна построенного на всем отрезке, равна сумме площадей квадратов, сумме площадей квадратов, построенных на каждом из двух построенных на каждом из двух отрезков, и удвоенный площади отрезков, и удвоенный площади прямоугольника, сторонами которого прямоугольника, сторонами которого служат эти два отрезка.»служат эти два отрезка.» Суть этой фразы в формулеСуть этой фразы в формуле (а + (а + b)b) 22 = a = a 22 + 2ab + b + 2ab + b 22

5 слайд

Евклид. «Начала».Евклид. «Начала». «Если отрезок как-либо разбит на два «Если отрезок как-либо разбит на два отрезка, то площадь квадрата, отрезка, то площадь квадрата, построенного на всем отрезке, равна построенного на всем отрезке, равна сумме площадей квадратов, сумме площадей квадратов, построенных на каждом из двух построенных на каждом из двух отрезков, и удвоенный площади отрезков, и удвоенный площади прямоугольника, сторонами которого прямоугольника, сторонами которого служат эти два отрезка.»служат эти два отрезка.» Суть этой фразы в формулеСуть этой фразы в формуле (а + (а + b)b) 22 = a = a 22 + 2ab + b + 2ab + b 22

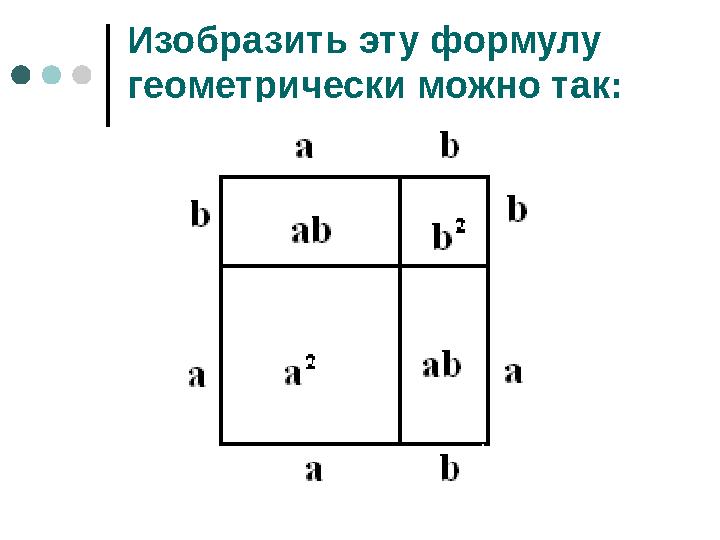
6 слайд
Изобразить эту формулу геометрически можно так:

6 слайд

Изобразить эту формулу геометрически можно так:

7 слайд
Три способа формулировки Три способа формулировки математических утверждений:математических утверждений: 1)1) СловесныйСловесный – понятный, но – понятный, но длинный, неудобный;длинный, неудобный; 2)2) ГеометрическийГеометрический – наглядный, – наглядный, но не всегда удобный для вычисления;но не всегда удобный для вычисления; 3)3) СимвольныйСимвольный – краткий, легко – краткий, легко запоминающийся.запоминающийся.

7 слайд

Три способа формулировки Три способа формулировки математических утверждений:математических утверждений: 1)1) СловесныйСловесный – понятный, но – понятный, но длинный, неудобный;длинный, неудобный; 2)2) ГеометрическийГеометрический – наглядный, – наглядный, но не всегда удобный для вычисления;но не всегда удобный для вычисления; 3)3) СимвольныйСимвольный – краткий, легко – краткий, легко запоминающийся.запоминающийся.

8 слайд
Аль джебрАль джебр – – восстановление (арабск.)восстановление (арабск.) algebralgebr

8 слайд

Аль джебрАль джебр – – восстановление (арабск.)восстановление (арабск.) algebralgebr

9 слайд
ТренировочТренировоч ные ные упражненияупражнения

9 слайд

ТренировочТренировоч ные ные упражненияупражнения

10 слайд
Составьте по описанию Составьте по описанию алгебраические выражения:алгебраические выражения: 1.1. Сумма квадратов чисел а и Сумма квадратов чисел а и bb .. 2.2. Разность между числом Разность между числом mm и и удвоенной суммой чисел а и удвоенной суммой чисел а и bb .. 3.3. Квадрат разности чисел Квадрат разности чисел bb и а. и а. 4.4. Разность квадратов чисел а и Разность квадратов чисел а и bb , , умноженная на сумму этих умноженная на сумму этих чисел.чисел.

10 слайд

Составьте по описанию Составьте по описанию алгебраические выражения:алгебраические выражения: 1.1. Сумма квадратов чисел а и Сумма квадратов чисел а и bb .. 2.2. Разность между числом Разность между числом mm и и удвоенной суммой чисел а и удвоенной суммой чисел а и bb .. 3.3. Квадрат разности чисел Квадрат разности чисел bb и а. и а. 4.4. Разность квадратов чисел а и Разность квадратов чисел а и bb , , умноженная на сумму этих умноженная на сумму этих чисел.чисел.

11 слайд
Запишите в виде степени Запишите в виде степени выражения:выражения:2 с 2 b 2 а ; 2 b 2 а 25 ; 3 у 3 х 125 1 ; 2 с 2 b 2 а .

11 слайд

Запишите в виде степени Запишите в виде степени выражения:выражения:2 с 2 b 2 а ; 2 b 2 а 25 ; 3 у 3 х 125 1 ; 2 с 2 b 2 а .

12 слайд
Найдите неизвестное х:Найдите неизвестное х: 1.1. (2(2 44 )) хх = 2 = 2 1212 ;; 2.2. 1010 хх = 10000; = 10000; 3.3. 55 33  5 5 44 = 5 = 5 2 + х2 + х ;; 4.4. 0,10,1 хх = 0,01. = 0,01.

12 слайд

Найдите неизвестное х:Найдите неизвестное х: 1.1. (2(2 44 )) хх = 2 = 2 1212 ;; 2.2. 1010 хх = 10000; = 10000; 3.3. 55 33  5 5 44 = 5 = 5 2 + х2 + х ;; 4.4. 0,10,1 хх = 0,01. = 0,01.

13 слайд
Заполните пропуски в Заполните пропуски в формулах:формулах: (а +…)(а +…) 22 = … + 2а = … + 2а bb + … ; + … ; (а … (а … bb )) …… = а = а 22 – 2а – 2а bb + … ; + … ; аа 33 - … = (а – - … = (а – bb )(… + а)(… + а bb + …); + …); аа 33 + + bb 3 3 = (… …)(а= (… …)(а 22 … + … + bb 22 );); аа 22 – – bb 22 = (… = (… bb )(а – …). )(а – …).

13 слайд

Заполните пропуски в Заполните пропуски в формулах:формулах: (а +…)(а +…) 22 = … + 2а = … + 2а bb + … ; + … ; (а … (а … bb )) …… = а = а 22 – 2а – 2а bb + … ; + … ; аа 33 - … = (а – - … = (а – bb )(… + а)(… + а bb + …); + …); аа 33 + + bb 3 3 = (… …)(а= (… …)(а 22 … + … + bb 22 );); аа 22 – – bb 22 = (… = (… bb )(а – …). )(а – …).

14 слайд
Расширение Расширение знаний по знаний по формулам формулам сокращенного сокращенного умноженияумножения

14 слайд

Расширение Расширение знаний по знаний по формулам формулам сокращенного сокращенного умноженияумножения

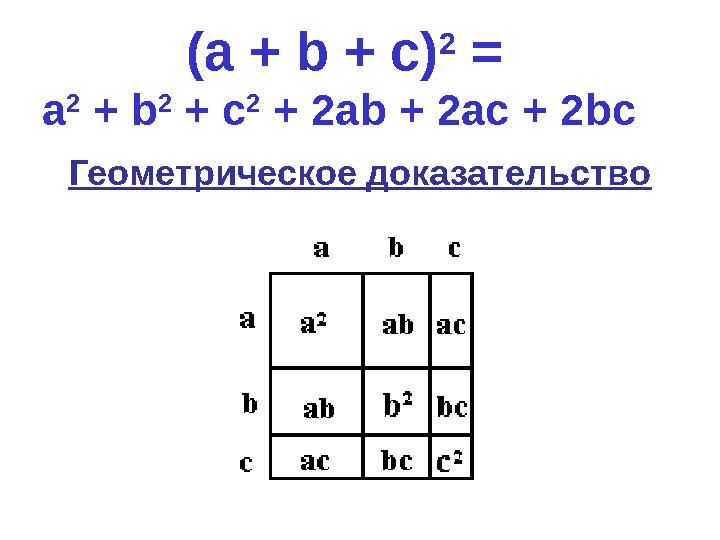
15 слайд
(а + b + с) 2 = а 2 + b 2 + с 2 + 2а b + 2ас + 2 b с Геометрическое доказательство

15 слайд

(а + b + с) 2 = а 2 + b 2 + с 2 + 2а b + 2ас + 2 b с Геометрическое доказательство

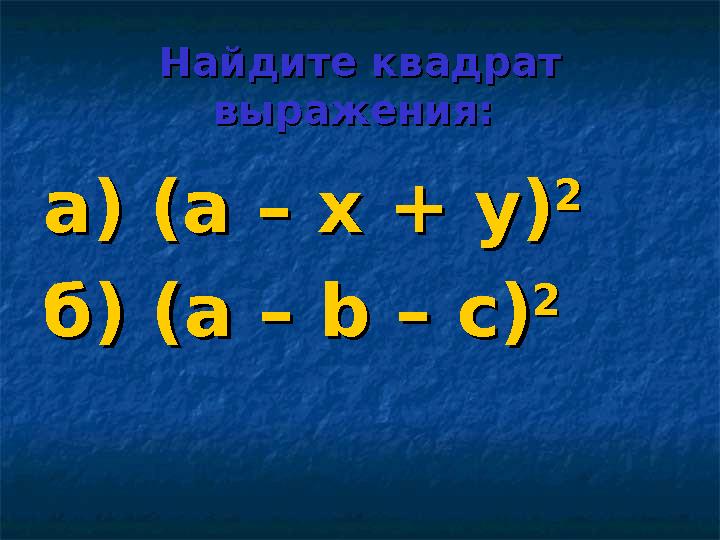
16 слайд
Найдите квадрат Найдите квадрат выражения:выражения: а) (а – х + у)а) (а – х + у) 22 б) (а – б) (а – bb – с) – с) 22

16 слайд

Найдите квадрат Найдите квадрат выражения:выражения: а) (а – х + у)а) (а – х + у) 22 б) (а – б) (а – bb – с) – с) 22

17 слайд
Треугольник Треугольник ПаскаляПаскаля

17 слайд

Треугольник Треугольник ПаскаляПаскаля

18 слайд
Блез Паскаль (1623 – 1662)

18 слайд

Блез Паскаль (1623 – 1662)

19 слайд
Рассмотрим двучлены: (а + b) 0 = 1 (a + b) 1 = a + b (a + b) 2 = a 2 + 2ab + b 2 (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

19 слайд

Рассмотрим двучлены: (а + b) 0 = 1 (a + b) 1 = a + b (a + b) 2 = a 2 + 2ab + b 2 (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

20 слайд
Составим таблицу из их коэффициентов: 1 1 1 1 2 1 1 3 3 1

20 слайд

Составим таблицу из их коэффициентов: 1 1 1 1 2 1 1 3 3 1

21 слайд
Закон образования Закон образования коэффициентовкоэффициентов 1 - 2 0 1 1 - 2 1 1 2 1 - 2 2 1 3 3 1 - 2 3

21 слайд

Закон образования Закон образования коэффициентовкоэффициентов 1 - 2 0 1 1 - 2 1 1 2 1 - 2 2 1 3 3 1 - 2 3

22 слайд
Вариации числа Вариации числа 100100

22 слайд

Вариации числа Вариации числа 100100

23 слайд
Рассмотрим комбинации Рассмотрим комбинации числа 100:числа 100:100 = 50 + 50; 100 = 38 + 62; 99 99 99 100   ; 101 101 101 100   ; 100 = (1 + 2 + 3 + 4) 2 ; 100 = 1 3 + 2 3 + 3 3 + 4 3 .

23 слайд

Рассмотрим комбинации Рассмотрим комбинации числа 100:числа 100:100 = 50 + 50; 100 = 38 + 62; 99 99 99 100   ; 101 101 101 100   ; 100 = (1 + 2 + 3 + 4) 2 ; 100 = 1 3 + 2 3 + 3 3 + 4 3 .

24 слайд
Изменив положение Изменив положение одной цифры, одной цифры, добейтесь, чтобы добейтесь, чтобы равенство 102 = равенство 102 = 100 было верным.100 было верным.

24 слайд

Изменив положение Изменив положение одной цифры, одной цифры, добейтесь, чтобы добейтесь, чтобы равенство 102 = равенство 102 = 100 было верным.100 было верным.

25 слайд
Примеры вариантов Примеры вариантов некоторых формул:некоторых формул: aa 22 + + bb 22 = (a + b) = (a + b) 22 – 2ab – 2ab aa 22 + b + b 22 = (a – b) = (a – b) 22 + 2ab + 2ab аа 22 = (a – b)(a + b) + b = (a – b)(a + b) + b 22

25 слайд

Примеры вариантов Примеры вариантов некоторых формул:некоторых формул: aa 22 + + bb 22 = (a + b) = (a + b) 22 – 2ab – 2ab aa 22 + b + b 22 = (a – b) = (a – b) 22 + 2ab + 2ab аа 22 = (a – b)(a + b) + b = (a – b)(a + b) + b 22

26 слайд
Вычисление Вычисление квадрата числаквадрата числа

26 слайд

Вычисление Вычисление квадрата числаквадрата числа

27 слайд
a 2 = а 2 – b 2 + b 2 = (a – b)(a + b) + b 2 , где b – дополнение числа а до круглого числа. Пример. Вычислите 986 2 1. Круглое число 1000. а = 986, b = 14, а + b = 1000, a – b = 972. 2. 986 2 = 972  1000 + 14 2 = 972000 + 196 = 972196.

27 слайд

a 2 = а 2 – b 2 + b 2 = (a – b)(a + b) + b 2 , где b – дополнение числа а до круглого числа. Пример. Вычислите 986 2 1. Круглое число 1000. а = 986, b = 14, а + b = 1000, a – b = 972. 2. 986 2 = 972  1000 + 14 2 = 972000 + 196 = 972196.

28 слайд
Вычислите:Вычислите: 1)1) 195 195 22 2)2) 488 488 22

28 слайд

Вычислите:Вычислите: 1)1) 195 195 22 2)2) 488 488 22

29 слайд
МатематическиМатематически й софизмй софизм

29 слайд

МатематическиМатематически й софизмй софизм

30 слайд
Докажем, что 4 = 5.1. Рассмотрим две разности: 16 – 36 и 25 – 45. 2. Добавим число 4 81 . Имеем: 4 81 45 25 4 81 36 16      . 3. Представим эти выражения так: 2 2 9 2 9 5 2 2 5 2 2 9 2 9 4 2 2 4                      . 4. Используем формулу: 2 2 9 5 2 2 9 4                . 5. Получаем: 2 9 5 2 9 4    , 4 = 5.

30 слайд

Докажем, что 4 = 5.1. Рассмотрим две разности: 16 – 36 и 25 – 45. 2. Добавим число 4 81 . Имеем: 4 81 45 25 4 81 36 16      . 3. Представим эти выражения так: 2 2 9 2 9 5 2 2 5 2 2 9 2 9 4 2 2 4                      . 4. Используем формулу: 2 2 9 5 2 2 9 4                . 5. Получаем: 2 9 5 2 9 4    , 4 = 5.

31 слайд
Домашнее задание 1. Обратите внимание на пирамиды чисел: а) 1  8 + 1 = 9, 12  8 + 2 = 98, 123  8 + 3 = 987. А как дальше? б) 1 2 = 1, 11 2 = 121, 111 2 = ? 2. Возведите в степень: а) (2а – b + c) 2 ; б) (а + b ) 4 . 3. Вычислите: а) 976 2 ; б) 295 2 .

31 слайд

Домашнее задание 1. Обратите внимание на пирамиды чисел: а) 1  8 + 1 = 9, 12  8 + 2 = 98, 123  8 + 3 = 987. А как дальше? б) 1 2 = 1, 11 2 = 121, 111 2 = ? 2. Возведите в степень: а) (2а – b + c) 2 ; б) (а + b ) 4 . 3. Вычислите: а) 976 2 ; б) 295 2 .

32 слайд
… Мне мудрость не чужда была земная, Разгадки тайн ища, не ведал сна я. За семьдесят перевалило мне, Что ж я узнал! - Что ничего не знаю. Омар Хайям

32 слайд

… Мне мудрость не чужда была земная, Разгадки тайн ища, не ведал сна я. За семьдесят перевалило мне, Что ж я узнал! - Что ничего не знаю. Омар Хайям

33 слайд
Обобщающий урок Обобщающий урок по темепо теме Формулы Формулы сокращенсокращен ного ного умноженумножен ияия

33 слайд

Обобщающий урок Обобщающий урок по темепо теме Формулы Формулы сокращенсокращен ного ного умноженумножен ияия